耦合传输线分析学习笔记(六)不对称耦合微带线Z参数矩阵推导与应用

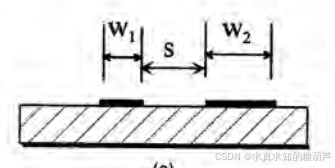
图1 不对称耦合微带线

这里讨论的是如图1剖面不对称，在图2中左右1和3端口、2和4端口满足对称条件

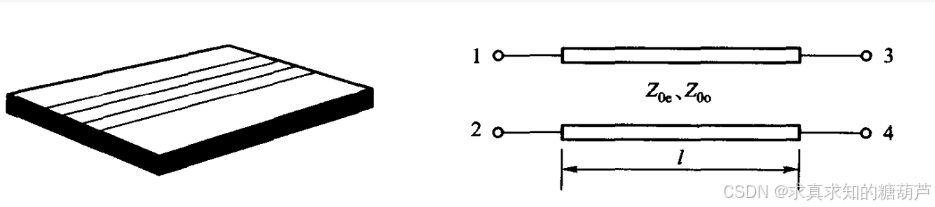
图2 端口顺序定义

参考前面的5篇文章中我们推出了如下公式

U1U2\]=\[11k−1k\]\[UeIUoI\](1) \\left\[\\begin{array}{l} U_{1} \\\\ U_{2} \\end{array}\\right\]=\\left\[\\begin{array}{cc} 1 \& 1 \\\\ k \& -\\frac{1}{k} \\end{array}\\right\]\\left\[\\begin{array}{l} U_{\\mathrm{e}}\^{I} \\\\ U_{\\mathrm{o}}\^{I} \\end{array}\\right\] \\quad(1) \[U1U2\]=\[1k1−k1\]\[UeIUoI\](1) \[U3U4\]=\[11k−1k\]\[UeIIUoII\](2) \\left\[\\begin{array}{l} U_{3} \\\\ U_{4} \\end{array}\\right\]=\\left\[\\begin{array}{cc} 1 \& 1 \\\\ k \& -\\frac{1}{k} \\end{array}\\right\]\\left\[\\begin{array}{l} U_{\\mathrm{e}}\^{II} \\\\ U_{\\mathrm{o}}\^{II} \\end{array}\\right\] \\quad(2) \[U3U4\]=\[1k1−k1\]\[UeIIUoII\](2) \[IeIIoI\]=kk2+1\[1k1k−1\]\[I1I2\](3) \\left\[\\begin{array}{l} I_{\\mathrm{e}}\^{I} \\\\ I_{\\mathrm{o}}\^{I} \\end{array}\\right\]=\\frac{k}{k\^{2}+1}\\left\[\\begin{array}{cc} \\frac{1}{k} \& 1 \\\\ k \& -1 \\end{array}\\right\]\\left\[\\begin{array}{l} I_{1} \\\\ I_{2} \\end{array}\\right\] \\quad(3) \[IeIIoI\]=k2+1k\[k1k1−1\]\[I1I2\](3) \[IeIIIoII\]=kk2+1\[1k1k−1\]\[I3I4\](4) \\left\[\\begin{array}{l} I_{\\mathrm{e}}\^{II} \\\\ I_{\\mathrm{o}}\^{II} \\end{array}\\right\]=\\frac{k}{k\^{2}+1}\\left\[\\begin{array}{cc} \\frac{1}{k} \& 1 \\\\ k \& -1 \\end{array}\\right\]\\left\[\\begin{array}{l} I_{3} \\\\ I_{4} \\end{array}\\right\] \\quad(4) \[IeIIIoII\]=k2+1k\[k1k1−1\]\[I3I4\](4) 传输线ABCD矩阵可以由如下二式表示 \[Ue1Ie1\]=\[cos⁡θejZ0esin⁡θejY0esin⁡θecos⁡θe\]\[UeIIIeII\](5) \\begin{bmatrix} U_e\^1 \\\\ I_e\^1 \\end{bmatrix} = \\begin{bmatrix} \\cos \\theta_e \& j Z_{0e} \\sin \\theta_e \\\\ j Y_{0e} \\sin \\theta_e \& \\cos \\theta_e \\end{bmatrix} \\begin{bmatrix} U_e\^{II} \\\\ I_e\^{II} \\end{bmatrix}\\qquad(5) \[Ue1Ie1\]=\[cosθejY0esinθejZ0esinθecosθe\]\[UeIIIeII\](5) \[Uo1Io1\]=\[cos⁡θojZ0osin⁡θojY0osin⁡θocos⁡θo\]\[UoIIIoII\](6) \\begin{bmatrix} U_o\^1 \\\\ I_o\^1 \\end{bmatrix} = \\begin{bmatrix} \\cos \\theta_o \& j Z_{0o} \\sin \\theta_o \\\\ j Y_{0o} \\sin \\theta_o \& \\cos \\theta_o \\end{bmatrix} \\begin{bmatrix} U_o\^{II} \\\\ I_o\^{II} \\end{bmatrix}\\qquad(6) \[Uo1Io1\]=\[cosθojY0osinθojZ0osinθocosθo\]\[UoIIIoII\](6) （这里 Y0e=1/Z0e,Y0o=1/Z0oY_{0e} = 1/Z_{0e}, Y_{0o} = 1/Z_{0o}Y0e=1/Z0e,Y0o=1/Z0o）  分析思路：下面我们需要将去耦后的传输线ABCD参数转换为二端口的Z参数矩阵。通过**奇偶模分解法，**将四端口网络分解为偶模和奇模两个独立的二端口网络，然后通过**前后两个变换矩阵**组合得到整体Z参数。  图3 变换矩阵Z参数求解思路 #### 1. 变量定义与变换关系 设四端口网络的端口电压和电流（定义所有电流流入网络为正）为： Vp=\[U1,U2,U3,U4\]T,Ip=\[I1,I2,I3,I4\]T. \\mathbf{V}_p = \[U_1, U_2, U_3, U_4\]\^T, \\quad \\mathbf{I}_p = \[I_1, I_2, I_3, I_4\]\^T. Vp=\[U1,U2,U3,U4\]T,Ip=\[I1,I2,I3,I4\]T. 奇偶模电压、电流定义为： Vm=\[UeI,UeII,UoI,UoII\]T,Im=\[IeI,IeII,IoI,IoII\]T. \\mathbf{V}_m = \[U_e\^I, U_e\^{II}, U_o\^I, U_o\^{II}\]\^T, \\quad \\mathbf{I}_m = \[I_e\^I, I_e\^{II}, I_o\^I, I_o\^{II}\]\^T. Vm=\[UeI,UeII,UoI,UoII\]T,Im=\[IeI,IeII,IoI,IoII\]T. 根据式(1)-(4)，变换关系为： \[U1U2\]=M\[UeIUoI\],\[U3U4\]=M\[UeIIUoII\],M=\[11k−1/k\]. \\begin{bmatrix} U_1 \\\\ U_2 \\end{bmatrix} = \\mathbf{M} \\begin{bmatrix} U_e\^I \\\\ U_o\^I \\end{bmatrix}, \\quad \\begin{bmatrix} U_3 \\\\ U_4 \\end{bmatrix} = \\mathbf{M} \\begin{bmatrix} U_e\^{II} \\\\ U_o\^{II} \\end{bmatrix}, \\quad \\mathbf{M} = \\begin{bmatrix} 1 \& 1 \\\\ k \& -1/k \\end{bmatrix}. \[U1U2\]=M\[UeIUoI\],\[U3U4\]=M\[UeIIUoII\],M=\[1k1−1/k\]. \[IeIIoI\]=N\[I1I2\],\[IeIIIoII\]=N\[I3I4\],N=kk2+1\[1/k1k−1\]=M−1. \\begin{bmatrix} I_e\^I \\\\ I_o\^I \\end{bmatrix} = \\mathbf{N} \\begin{bmatrix} I_1 \\\\ I_2 \\end{bmatrix}, \\quad \\begin{bmatrix} I_e\^{II} \\\\ I_o\^{II} \\end{bmatrix} = \\mathbf{N} \\begin{bmatrix} I_3 \\\\ I_4 \\end{bmatrix}, \\quad \\mathbf{N} = \\frac{k}{k\^2+1} \\begin{bmatrix} 1/k \& 1 \\\\ k \& -1 \\end{bmatrix} = \\mathbf{M}\^{-1}. \[IeIIoI\]=N\[I1I2\],\[IeIIIoII\]=N\[I3I4\],N=k2+1k\[1/kk1−1\]=M−1. 根据以上关系，整体**电压变换矩阵 TV\\mathbf{T}_VTV和电流变换矩阵 TI\\mathbf{T}_ITI**满足： Vp=TVVm,Im=TIIp. \\mathbf{V}_p = \\mathbf{T}_V \\mathbf{V}_m, \\quad \\mathbf{I}_m = \\mathbf{T}_I \\mathbf{I}_p. Vp=TVVm,Im=TIIp. 具体表达式如下： TV=\[1010k0−1/k001010k0−1/k\],TI=Tv−1=1k2+1\[1k00001kk2−k0000k2−k\] \\mathbf{T}_V = \\begin{bmatrix} 1 \& 0 \& 1 \& 0 \\\\ k \& 0 \& -1/k \& 0 \\\\ 0 \& 1 \& 0 \& 1 \\\\ 0 \& k \& 0 \& -1/k \\end{bmatrix}, \\quad \\mathbf{T}_I = \\mathbf{T}_v\^{-1} = \\frac{1}{k\^2+1} \\begin{bmatrix} 1 \& k \& 0 \& 0 \\\\ 0 \& 0 \& 1 \& k \\\\ k\^2 \& -k \& 0 \& 0 \\\\ 0 \& 0 \& k\^2 \& -k \\end{bmatrix} TV= 1k00001k1−1/k00001−1/k ,TI=Tv−1=k2+11 10k20k0−k0010k20k0−k #### 2. 模态阻抗矩阵 偶模和奇模二端口网络（均为传输线段）的ABCD参数如式(5)(6)所示。可以根据ABCD到Z参数二端口转换公式转换为Z参数（电流均定义为流入）得： 偶模二端口Z参数矩阵： Ze=\[Z11eZ12eZ21eZ22e\]=\[−jZ0ecot⁡θe−jZ0ecsc⁡θe−jZ0ecsc⁡θe−jZ0ecot⁡θe\]. \\mathbf{Z}_e = \\begin{bmatrix} Z_{11}\^e \& Z_{12}\^e \\\\ Z_{21}\^e \& Z_{22}\^e \\end{bmatrix} = \\begin{bmatrix} -jZ_{0e}\\cot\\theta_e \& -jZ_{0e}\\csc\\theta_e \\\\ -jZ_{0e}\\csc\\theta_e \& -jZ_{0e}\\cot\\theta_e \\end{bmatrix}. Ze=\[Z11eZ21eZ12eZ22e\]=\[−jZ0ecotθe−jZ0ecscθe−jZ0ecscθe−jZ0ecotθe\]. 奇模二端口Z参数矩阵： Zo=\[Z11oZ12oZ21oZ22o\]=\[−jZ0ocot⁡θo−jZ0ocsc⁡θo−jZ0ocsc⁡θo−jZ0ocot⁡θo\]. \\mathbf{Z}_o = \\begin{bmatrix} Z_{11}\^o \& Z_{12}\^o \\\\ Z_{21}\^o \& Z_{22}\^o \\end{bmatrix} = \\begin{bmatrix} -jZ_{0o}\\cot\\theta_o \& -jZ_{0o}\\csc\\theta_o \\\\ -jZ_{0o}\\csc\\theta_o \& -jZ_{0o}\\cot\\theta_o \\end{bmatrix}. Zo=\[Z11oZ21oZ12oZ22o\]=\[−jZ0ocotθo−jZ0ocscθo−jZ0ocscθo−jZ0ocotθo\]. 由于**两模态独立** ，整个模态域的4×4阻抗矩阵为分块对角阵： Zm=\[Ze00Zo\]. \\mathbf{Z}_m = \\begin{bmatrix} \\mathbf{Z}_e \& \\mathbf{0} \\\\ \\mathbf{0} \& \\mathbf{Z}_o \\end{bmatrix}. Zm=\[Ze00Zo\]. #### 3. 四端口Z参数矩阵 由 Vm=ZmIm\\mathbf{V}_m = \\mathbf{Z}_m \\mathbf{I}_mVm=ZmIm和上述变换，得： Vp=TVZmTIIp. \\mathbf{V}_p = \\mathbf{T}_V \\mathbf{Z}_m \\mathbf{T}_I \\mathbf{I}_p. Vp=TVZmTIIp. 故四端口Z参数矩阵为： Zp=TVZmTI. \\mathbf{Z}_p = \\mathbf{T}_V \\mathbf{Z}_m \\mathbf{T}_I. Zp=TVZmTI. 代入 TV\\mathbf{T}_VTV、Zm\\mathbf{Z}_mZm、TI\\mathbf{T}_ITI 并进行矩阵乘法，可得各Z参数表达式。 Z11=1k2+1\[Z11e+k2Z11o\]=−jk2+1(Z0ecot⁡θe+k2Z0ocot⁡θo),Z12=kk2+1\[Z11e−Z11o\]=−jkk2+1(Z0ecot⁡θe−Z0ocot⁡θo),Z13=1k2+1\[Z12e+k2Z12o\]=−jk2+1(Z0ecsc⁡θe+k2Z0ocsc⁡θo),Z14=kk2+1\[Z12e−Z12o\]=−jkk2+1(Z0ecsc⁡θe−Z0ocsc⁡θo),Z22=1k2+1\[k2Z11e+Z11o\]=−jk2+1(k2Z0ecot⁡θe+Z0ocot⁡θo),Z23=kk2+1\[Z12e−Z12o\]=Z14,Z24=1k2+1\[k2Z12e+Z12o\]=−jk2+1(k2Z0ecsc⁡θe+Z0ocsc⁡θo),Z33=Z11,Z34=Z12,Z44=Z22. \\begin{aligned} Z_{11} \&= \\frac{1}{k\^2+1}\\left\[ Z_{11}\^e + k\^2 Z_{11}\^o \\right\] = -\\frac{j}{k\^2+1}\\left( Z_{0e}\\cot\\theta_e + k\^2 Z_{0o}\\cot\\theta_o \\right), \\\\ Z_{12} \&= \\frac{k}{k\^2+1}\\left\[ Z_{11}\^e - Z_{11}\^o \\right\] = -\\frac{j k}{k\^2+1}\\left( Z_{0e}\\cot\\theta_e - Z_{0o}\\cot\\theta_o \\right), \\\\ Z_{13} \&= \\frac{1}{k\^2+1}\\left\[ Z_{12}\^e + k\^2 Z_{12}\^o \\right\] = -\\frac{j}{k\^2+1}\\left( Z_{0e}\\csc\\theta_e + k\^2 Z_{0o}\\csc\\theta_o \\right), \\\\ Z_{14} \&= \\frac{k}{k\^2+1}\\left\[ Z_{12}\^e - Z_{12}\^o \\right\] = -\\frac{j k}{k\^2+1}\\left( Z_{0e}\\csc\\theta_e - Z_{0o}\\csc\\theta_o \\right), \\\\ Z_{22} \&= \\frac{1}{k\^2+1}\\left\[ k\^2 Z_{11}\^e + Z_{11}\^o \\right\] = -\\frac{j}{k\^2+1}\\left( k\^2 Z_{0e}\\cot\\theta_e + Z_{0o}\\cot\\theta_o \\right), \\\\ Z_{23} \&= \\frac{k}{k\^2+1}\\left\[ Z_{12}\^e - Z_{12}\^o \\right\] = Z_{14}, \\\\ Z_{24} \&= \\frac{1}{k\^2+1}\\left\[ k\^2 Z_{12}\^e + Z_{12}\^o \\right\] = -\\frac{j}{k\^2+1}\\left( k\^2 Z_{0e}\\csc\\theta_e + Z_{0o}\\csc\\theta_o \\right), \\\\ Z_{33} \&= Z_{11}, \\quad Z_{34} = Z_{12}, \\quad Z_{44} = Z_{22}. \\end{aligned} Z11Z12Z13Z14Z22Z23Z24Z33=k2+11\[Z11e+k2Z11o\]=−k2+1j(Z0ecotθe+k2Z0ocotθo),=k2+1k\[Z11e−Z11o\]=−k2+1jk(Z0ecotθe−Z0ocotθo),=k2+11\[Z12e+k2Z12o\]=−k2+1j(Z0ecscθe+k2Z0ocscθo),=k2+1k\[Z12e−Z12o\]=−k2+1jk(Z0ecscθe−Z0ocscθo),=k2+11\[k2Z11e+Z11o\]=−k2+1j(k2Z0ecotθe+Z0ocotθo),=k2+1k\[Z12e−Z12o\]=Z14,=k2+11\[k2Z12e+Z12o\]=−k2+1j(k2Z0ecscθe+Z0ocscθo),=Z11,Z34=Z12,Z44=Z22. 其余元素由互易性和对称性确定：Zij=ZjiZ_{ij} = Z_{ji}Zij=Zji，且由于结构对称（端口1与3、2与4在几何上对称），有Z33=Z11Z_{33}=Z_{11}Z33=Z11、Z44=Z22Z_{44}=Z_{22}Z44=Z22、Z34=Z12Z_{34}=Z_{12}Z34=Z12、Z13=Z31Z_{13}=Z_{31}Z13=Z31 等。 Z=−jk2+1\[Z0ecot⁡θe+k2Z0ocot⁡θok(Z0ecot⁡θe−Z0ocot⁡θo)Z0esin⁡θe+k2Z0osin⁡θok(Z0esin⁡θe−Z0osin⁡θo)k(Z0ecot⁡θe−Z0ocot⁡θo)k2Z0ecot⁡θe+Z0ocot⁡θok(Z0esin⁡θe−Z0osin⁡θo)k2Z0esin⁡θe+Z0osin⁡θoZ0esin⁡θe+k2Z0osin⁡θok(Z0esin⁡θe−Z0osin⁡θo)Z0ecot⁡θe+k2Z0ocot⁡θok(Z0ecot⁡θe−Z0ocot⁡θo)k(Z0esin⁡θe−Z0osin⁡θo)k2Z0esin⁡θe+Z0osin⁡θok(Z0ecot⁡θe−Z0ocot⁡θo)k2Z0ecot⁡θe+Z0ocot⁡θo\] Z = \\frac{-j}{k\^2+1} \\begin{bmatrix} Z_{0e} \\cot\\theta_e + k\^2 Z_{0o} \\cot\\theta_o \& k (Z_{0e} \\cot\\theta_e - Z_{0o} \\cot\\theta_o) \& \\dfrac{Z_{0e}}{\\sin\\theta_e} + k\^2 \\dfrac{Z_{0o}}{\\sin\\theta_o} \& k \\left( \\dfrac{Z_{0e}}{\\sin\\theta_e} - \\dfrac{Z_{0o}}{\\sin\\theta_o} \\right) \\\\\[8pt\] k (Z_{0e} \\cot\\theta_e - Z_{0o} \\cot\\theta_o) \& k\^2 Z_{0e} \\cot\\theta_e + Z_{0o} \\cot\\theta_o \& k \\left( \\dfrac{Z_{0e}}{\\sin\\theta_e} - \\dfrac{Z_{0o}}{\\sin\\theta_o} \\right) \& k\^2 \\dfrac{Z_{0e}}{\\sin\\theta_e} + \\dfrac{Z_{0o}}{\\sin\\theta_o} \\\\\[8pt\] \\dfrac{Z_{0e}}{\\sin\\theta_e} + k\^2 \\dfrac{Z_{0o}}{\\sin\\theta_o} \& k \\left( \\dfrac{Z_{0e}}{\\sin\\theta_e} - \\dfrac{Z_{0o}}{\\sin\\theta_o} \\right) \& Z_{0e} \\cot\\theta_e + k\^2 Z_{0o} \\cot\\theta_o \& k (Z_{0e} \\cot\\theta_e - Z_{0o} \\cot\\theta_o) \\\\\[8pt\] k \\left( \\dfrac{Z_{0e}}{\\sin\\theta_e} - \\dfrac{Z_{0o}}{\\sin\\theta_o} \\right) \& k\^2 \\dfrac{Z_{0e}}{\\sin\\theta_e} + \\dfrac{Z_{0o}}{\\sin\\theta_o} \& k (Z_{0e} \\cot\\theta_e - Z_{0o} \\cot\\theta_o) \& k\^2 Z_{0e} \\cot\\theta_e + Z_{0o} \\cot\\theta_o \\end{bmatrix} Z=k2+1−j Z0ecotθe+k2Z0ocotθok(Z0ecotθe−Z0ocotθo)sinθeZ0e+k2sinθoZ0ok(sinθeZ0e−sinθoZ0o)k(Z0ecotθe−Z0ocotθo)k2Z0ecotθe+Z0ocotθok(sinθeZ0e−sinθoZ0o)k2sinθeZ0e+sinθoZ0osinθeZ0e+k2sinθoZ0ok(sinθeZ0e−sinθoZ0o)Z0ecotθe+k2Z0ocotθok(Z0ecotθe−Z0ocotθo)k(sinθeZ0e−sinθoZ0o)k2sinθeZ0e+sinθoZ0ok(Z0ecotθe−Z0ocotθo)k2Z0ecotθe+Z0ocotθo #### 小结一下  当k=1k=1k=1（对称耦合微带线）时，上述结果退化为经典对称耦合线Z参数： Z11=Z22=Z33=Z44=−j2(Z0ecot⁡θe+Z0ocot⁡θo),Z12=Z21=Z34=Z43=−j2(Z0ecot⁡θe−Z0ocot⁡θo),Z13=Z31=Z24=Z42=−j2(Z0ecsc⁡θe+Z0ocsc⁡θo),Z14=Z41=Z23=Z32=−j2(Z0ecsc⁡θe−Z0ocsc⁡θo). \\begin{aligned} Z_{11} \&= Z_{22} = Z_{33} = Z_{44} = -\\frac{j}{2}(Z_{0e}\\cot\\theta_e + Z_{0o}\\cot\\theta_o), \\\\ Z_{12} \&= Z_{21} = Z_{34} = Z_{43} = -\\frac{j}{2}(Z_{0e}\\cot\\theta_e - Z_{0o}\\cot\\theta_o), \\\\ Z_{13} \&= Z_{31} = Z_{24} = Z_{42} = -\\frac{j}{2}(Z_{0e}\\csc\\theta_e + Z_{0o}\\csc\\theta_o), \\\\ Z_{14} \&= Z_{41} = Z_{23} = Z_{32} = -\\frac{j}{2}(Z_{0e}\\csc\\theta_e - Z_{0o}\\csc\\theta_o). \\end{aligned} Z11Z12Z13Z14=Z22=Z33=Z44=−2j(Z0ecotθe+Z0ocotθo),=Z21=Z34=Z43=−2j(Z0ecotθe−Z0ocotθo),=Z31=Z24=Z42=−2j(Z0ecscθe+Z0ocscθo),=Z41=Z23=Z32=−2j(Z0ecscθe−Z0ocscθo).  参数模比系数（ke=k,ko=1/kk_e=k, k_o=1/kke=k,ko=1/k 1、2端口偶模电压比例系数） kkk 表征了不对称程度，k≠1k \\neq 1k=1 时，端口1与2、3与4的阻抗不再相同.  这种推导方法通过**模态分解与变换，将复杂的不对称耦合线四端口网络分析转化为两个独立传输线模型的组合，**是分析耦合线结构的有效手段，**相比四端口矩阵直接相互直接转换要简单很多** 。前面第(四)节中（参考梁老师简明微波书2-12节）我们用该方法推导出了**耦合微带线的A参数矩阵** ，同时在**RF and Microwave Coupled-Line Circuits** 书中第四章也用该方法推出了四端口耦合线的**S参数矩阵** 。  **当对称均匀时（k=1k=1k=1，θe=θo\\theta_e = \\theta_oθe=θo），矩阵将大幅简化**，可退化为上一节（五）中我们推出来的均匀对称耦合线节的Z参数形式。 Z=−j2sin⁡θ\[cos⁡θ(Z0e+Z0o)cos⁡θ(Z0e−Z0o)Z0e+Z0oZ0e−Z0ocos⁡θ(Z0e−Z0o)cos⁡θ(Z0e+Z0o)Z0e−Z0oZ0e+Z0o(Z0e+Z0o)(Z0e−Z0o)cos⁡θ(Z0e+Z0o)cos⁡θ(Z0e−Z0o)(Z0e−Z0o)(Z0e+Z0o)cos⁡θ(Z0e−Z0o)cos⁡θ(Z0e+Z0o)\] \\boxed{ Z = \\frac{-j}{2\\sin\\theta} \\begin{bmatrix} \\cos\\theta (Z_{0e}+Z_{0o}) \& \\cos\\theta (Z_{0e}-Z_{0o}) \& Z_{0e}+Z_{0o} \& Z_{0e}-Z_{0o} \\\\ \\cos\\theta (Z_{0e}-Z_{0o}) \& \\cos\\theta (Z_{0e}+Z_{0o}) \& Z_{0e}-Z_{0o} \& Z_{0e}+Z_{0o} \\\\ (Z_{0e}+Z_{0o}) \& (Z_{0e}-Z_{0o}) \& \\cos\\theta (Z_{0e}+Z_{0o}) \& \\cos\\theta (Z_{0e}-Z_{0o}) \\\\ (Z_{0e}-Z_{0o}) \& (Z_{0e}+Z_{0o}) \& \\cos\\theta (Z_{0e}-Z_{0o}) \& \\cos\\theta (Z_{0e}+Z_{0o}) \\end{bmatrix} } Z=2sinθ−j cosθ(Z0e+Z0o)cosθ(Z0e−Z0o)(Z0e+Z0o)(Z0e−Z0o)cosθ(Z0e−Z0o)cosθ(Z0e+Z0o)(Z0e−Z0o)(Z0e+Z0o)Z0e+Z0oZ0e−Z0ocosθ(Z0e+Z0o)cosθ(Z0e−Z0o)Z0e−Z0oZ0e+Z0ocosθ(Z0e−Z0o)cosθ(Z0e+Z0o) ### 应用：如何应用？类似第五节 从给定的四端口阻抗矩阵ZZZ反求五个参数（Z0eZ_{0e}Z0e、Z0oZ_{0o}Z0o、θe\\theta_eθe、θo\\theta_oθo、kkk）可以按如下方法： #### 提取矩阵独立元素 给定对称的 ZZZ 矩阵，我们取以下六个独立元素： Z11, Z12, Z13, Z14, Z22, Z24 Z_{11},\\ Z_{12},\\ Z_{13},\\ Z_{14},\\ Z_{22},\\ Z_{24} Z11, Z12, Z13, Z14, Z22, Z24 并验证对称性：Z21=Z12Z_{21}=Z_{12}Z21=Z12，Z23=Z14Z_{23}=Z_{14}Z23=Z14，Z33=Z11Z_{33}=Z_{11}Z33=Z11，Z34=Z12Z_{34}=Z_{12}Z34=Z12，Z44=Z22Z_{44}=Z_{22}Z44=Z22。**实际画的版图可能不那么理想。** #### 求解不对称系数 kkk 利用 Z11Z_{11}Z11、Z12Z_{12}Z12、Z22Z_{22}Z22 建立关于kkk 的方程： Z12k2+(Z11−Z22)k−Z12=0 Z_{12} k\^2 + (Z_{11} - Z_{22}) k - Z_{12} = 0 Z12k2+(Z11−Z22)k−Z12=0 解得： k=−(Z11−Z22)±(Z11−Z22)2+4Z1222Z12(7) k = \\frac{-(Z_{11}-Z_{22}) \\pm \\sqrt{(Z_{11}-Z_{22})\^2 + 4Z_{12}\^2}}{2Z_{12}}\\quad{(7)} k=2Z12−(Z11−Z22)±(Z11−Z22)2+4Z122 (7) 选取正实根（通常 k\>0k\>0k\>0），若两根均为正，需结合后续步骤选择合理的解。 #### 计算中间变量A,B,C,DA, B, C, DA,B,C,D 定义： α=1k2+1 \\alpha = \\frac{1}{k\^2+1} α=k2+11 计算： A=12\[(Z11+Z22)+k2+1kZ12\]B=12\[(Z11+Z22)−k2+1kZ12\]C=12\[(Z13+Z24)+k2+1kZ14\]D=12\[(Z13+Z24)−k2+1kZ14\](8) \\begin{aligned} A \&= \\frac{1}{2}\\left\[ (Z_{11}+Z_{22}) + \\frac{k\^2+1}{k} Z_{12} \\right\] \\\\ B \&= \\frac{1}{2}\\left\[ (Z_{11}+Z_{22}) - \\frac{k\^2+1}{k} Z_{12} \\right\] \\\\ C \&= \\frac{1}{2}\\left\[ (Z_{13}+Z_{24}) + \\frac{k\^2+1}{k} Z_{14} \\right\] \\\\ D \&= \\frac{1}{2}\\left\[ (Z_{13}+Z_{24}) - \\frac{k\^2+1}{k} Z_{14} \\right\] \\end{aligned}\\quad{(8)} ABCD=21\[(Z11+Z22)+kk2+1Z12\]=21\[(Z11+Z22)−kk2+1Z12\]=21\[(Z13+Z24)+kk2+1Z14\]=21\[(Z13+Z24)−kk2+1Z14\](8) 其中 A=Z0ecot⁡θeA = Z_{0e} \\cot\\theta_eA=Z0ecotθe，B=Z0ocot⁡θoB = Z_{0o} \\cot\\theta_oB=Z0ocotθo，C=Z0e/sin⁡θeC = Z_{0e}/\\sin\\theta_eC=Z0e/sinθe，D=Z0o/sin⁡θoD = Z_{0o}/\\sin\\theta_oD=Z0o/sinθo。 #### 求解偶模和奇模参数 * **偶模** ： Z0e=C2−A2(取正值) Z_{0e} = \\sqrt{C\^2 - A\^2} \\quad (\\text{取正值}) Z0e=C2−A2 (取正值) cos⁡θe=AC,θe=arccos⁡(AC)∈\[0,π\] \\cos\\theta_e = \\frac{A}{C}, \\quad \\theta_e = \\arccos\\left(\\frac{A}{C}\\right) \\in \[0, \\pi\] cosθe=CA,θe=arccos(CA)∈\[0,π

或联合 sin⁡θe=Z0e/C\sin\theta_e = Z_{0e}/Csinθe=Z0e/C确定象限。

• 奇模 ：
  Z0o=D2−B2(取正值) Z_{0o} = \sqrt{D^2 - B^2} \quad (\text{取正值}) Z0o=D2−B2 (取正值)
  cos⁡θo=BD,θo=arccos⁡(BD)∈[0,π] \cos\theta_o = \frac{B}{D}, \quad \theta_o = \arccos\left(\frac{B}{D}\right) \in [0, \pi] cosθo=DB,θo=arccos(DB)∈[0,π]

检查求得的Z0eZ_{0e}Z0e、Z0oZ_{0o}Z0o是否为正实数，θe\theta_eθe、θo\theta_oθo是否为实数。若kkk 有两个正根，需将两组解代入验证，选取使所有参数物理合理（如 Z0e,Z0o>0Z_{0e}, Z_{0o}>0Z0e,Z0o>0，0<θe,θo<π0<\theta_e,\theta_o<\pi0<θe,θo<π）的一组。若 Z12=0Z_{12}=0Z12=0 或Z11=Z22Z_{11}=Z_{22}Z11=Z22（可能退化为对称耦合线或解不唯一）。