前言
上一章我们讲解了PID控制器的使用,这一篇算是额外补充的,我们将用MATLAB代码和Simulink的基本模块(不使用PID control)来搭建一个PID控制器,一方面是希望能够加深大家对PID控制器的了解,一方面也是希望通过这个已知逻辑的底层实现,大家能够更熟练的使用MATLAB以及Simulink。
一、 核心原理
这边我们再复习一下上一章讲到的PID基本原理,方便后面的实现。
- PID 结构 :
- P(比例):反应当前的误差,消除误差最快。
- I(积分) :反应累积的误差,用于消除静差。
- D(微分) :反应误差的变化趋势,具有超前预判作用,能减少超调。
- PID 的表现形式 :
- 并联型(Parallel) :C(s)=Kp+Kis+KdsC(s) = K_p + \frac{K_i}{s} + K_d sC(s)=Kp+sKi+Kds(MATLAB 默认)。
- 标准型(Standard) :C(s)=Kp(1+1Tis+Tds)C(s) = K_p (1 + \frac{1}{T_i s} + T_d s)C(s)=Kp(1+Tis1+Tds)。
- 整定方法 :
- 传统法:齐格勒-尼科尔斯(Ziegler-Nichols)经验公式。
- 自动法:基于频率响应的自动整定技术(MATLAB 强项)。
- 最优法:利用 ITAE、ISE 等误差性能指标进行最优化搜索。
二、题目

三、 建模部分(Simulink)
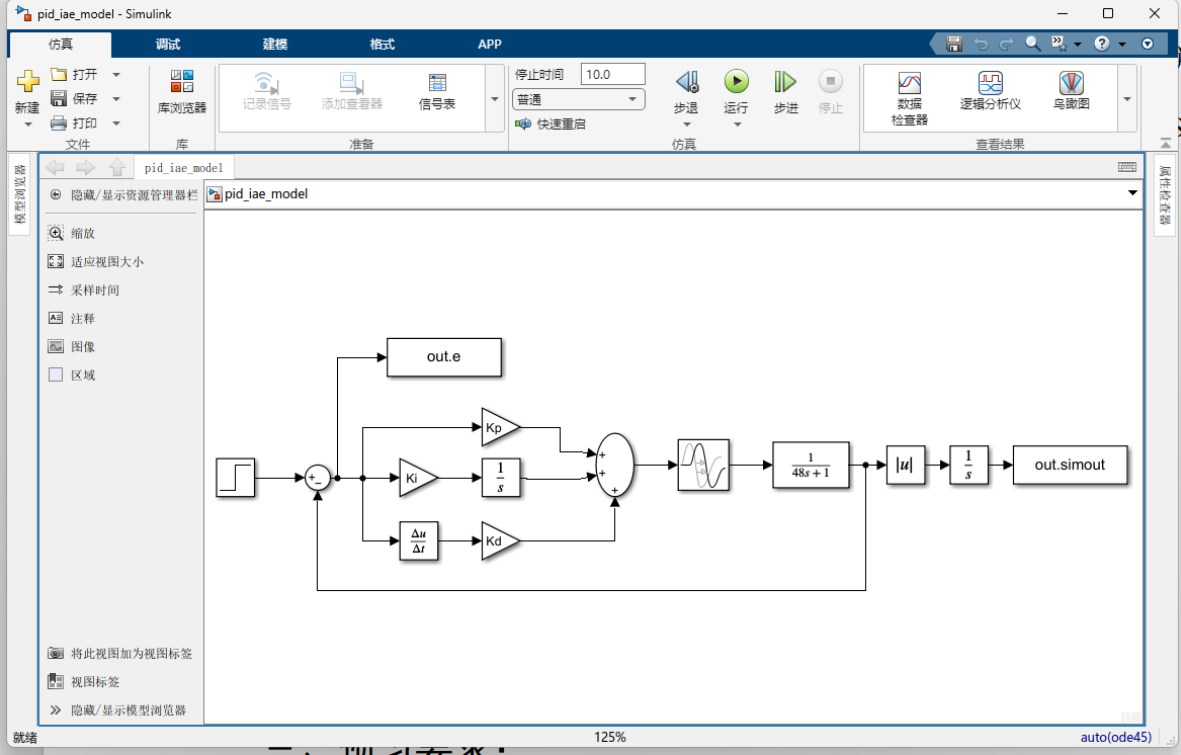
首先,我们要在Simulink里面搭建我们的题目条件以及底层的PID控制器:
一、模型整体功能概述
这个模型的核心目标有两个:
- 实现 PID 闭环控制:通过比例(P)、积分(I)、微分(D)三环节,对被控对象(一阶惯性环节)进行跟踪控制。
- 评估控制性能:计算 IAE(Integral of Absolute Error,绝对误差积分)指标,量化系统的跟踪精度与动态响应品质。
二、核心模块逐一拆解
我们从左到右、从上到下解析每个功能模块:
1. 输入与误差计算
- 阶跃信号模块 :作为系统的参考输入(Setpoint),模拟实际场景中"让系统从稳态切换到新目标值"的需求(比如让电机转速从0提升到1000rpm)。
- 求和模块(减法器) :计算误差信号 ( e(t) = r(t) - y(t) )(参考输入减去系统输出),这是 PID 控制器的输入信号。
out.e输出端口:导出误差信号,方便后续分析或在 Scope 中观察误差随时间的变化曲线。
2. PID 控制器核心环节
PID 控制器的输出是三个环节的叠加:
u(t)=Kpe(t)+Ki∫0te(τ)dτ+Kdde(t)dtu(t) = K_p e(t) + K_i \int_0^t e(\tau) d\tau + K_d \frac{de(t)}{dt}u(t)=Kpe(t)+Ki∫0te(τ)dτ+Kddtde(t)
对应图中的三个分支:
- 比例(P)环节 :直接对误差信号乘以比例系数 KpK_pKp,快速响应误差,但过大的 KpK_pKp 会导致系统振荡。
- 积分(I)环节 :误差信号先经过积分器(
1/s模块,代表积分运算∫e(t)dt\int e(t)dt∫e(t)dt,再乘以积分系数 KiK_iKi,用于消除稳态误差,但会增加系统超调。 - 微分(D)环节 :误差信号先经过微分器(
Δu/Δt模块,代表微分运算 de(t)dt\frac{de(t)}{dt}dtde(t),再乘以微分系数 KdK_dKd,用于抑制超调、加快响应,但对噪声敏感。 - 求和模块(加法器):将 P、I、D 三个环节的输出叠加,得到 PID 控制器的总输出 u(t) 。
3. 非线性环节(饱和模块)
在 PID 输出之后,可以串联一个饱和模块,这是工业场景的典型设计:
- 模拟执行器的"输出能力限制"(比如阀门的最大开度、电机的最大扭矩)。
- 防止控制器输出超出硬件极限,避免系统进入非线性失控状态。
4. 被控对象
模型中的被控对象是一个一阶惯性环节,传递函数为:
G(s)=148s+1G(s) = \frac{1}{48s + 1}G(s)=48s+11
- 一阶惯性环节是工业中最常见的近似模型(比如温度、液位等慢响应过程),
48s+1表示系统的时间常数为48秒,反映了系统响应的快慢。 - 输入是 PID 控制器的输出 u(t)u(t)u(t),输出是系统的实际响应y(t)y(t)y(t)。
5. IAE 性能指标计算
IAE 是控制系统常用的性能指标,定义为:
IAE=∫0∞∣e(t)∣dt\text{IAE} = \int_0^\infty |e(t)| dtIAE=∫0∞∣e(t)∣dt
对应图中的两个模块:
- 绝对值模块(
|u|) :对系统输出 y(t)y(t)y(t)与参考输入 r(t)r(t)r(t)的误差取绝对值,得到 ∣e(t)∣|e(t)|∣e(t)∣。 - 积分器(
1/s模块) :对 ∣e(t)∣|e(t)|∣e(t)∣进行积分运算,最终输出就是 IAE 指标值(out.simout端口导出)。 - 物理意义:IAE 越小,说明系统跟踪误差的累积越小,控制精度越高。
三、模型工作流程闭环逻辑
- 输入触发:阶跃信号产生参考输入 ( r(t) )。
- 误差生成:减法器计算误差 ( e(t) = r(t) - y(t) )。
- PID 运算:P/I/D 环节分别处理误差,叠加得到控制输出 ( u(t) )。
- 输出限幅:饱和模块限制 ( u(t) ) 的范围,模拟执行器约束。
- 对象响应:被控对象接收 ( u(t) ),输出实际响应 ( y(t) )。
- 反馈闭环:( y(t) ) 反馈到减法器,更新误差信号,形成闭环控制。
- 性能评估:绝对值+积分模块计算 IAE,量化控制效果。
三、 编程部分(MATLAB)
你希望我详细讲解这段名为 pid_iae_cost 的 MATLAB 函数代码,我会从功能、逐行逻辑、使用场景三个维度拆解,让你彻底理解它的作用和实现原理。
MATLAB代码一:pid_iae_cost函数
一、函数整体功能总结
这个函数是 PID 参数优化的代价函数(Cost Function) ,核心作用是:
输入一组 PID 参数(Kp/Ki/Kd),自动运行指定的 Simulink 模型,计算该参数下系统的 IAE(绝对误差积分) 值并返回;若参数非法或仿真出错,返回一个极大的惩罚值(1e6),避免优化算法选择无效参数。
简单来说,它是"自动调参"的核心:优化算法(如 fmincon/遗传算法)会反复调用这个函数,尝试不同的 PID 参数,最终找到使 IAE 最小的最优参数。
二、逐行代码解析
matlab
function J = pid_iae_cost(x, modelName, T_end)
% 1. 提取PID参数:x是优化算法传入的参数向量,格式为[Kp, Ki, Kd]
Kp = x(1); Ki = x(2); Kd = x(3);
% 2. 参数合法性校验:PID参数通常非负(工程上极少用负数)
if any(x < 0)
J = 1e6; % 若有负数参数,返回极大惩罚值(让优化算法放弃该参数)
return; % 直接退出函数,不执行后续仿真
end
% 3. 将参数赋值到MATLAB基础工作区
assignin('base','Kp',Kp);
assignin('base','Ki',Ki);
assignin('base','Kd',Kd);
% 4. 执行Simulink仿真并计算IAE(带异常处理,避免程序崩溃)
try
% 运行指定的Simulink模型,设置仿真结束时间,保存输出和时间数据
simOut = sim(modelName, 'StopTime', num2str(T_end), ...
'SaveOutput', 'on', 'SaveTime', 'on');
e = simOut.e.Data; % 提取仿真输出的误差信号e(对应Simulink的out.e端口)
t = simOut.tout; % 提取仿真的时间向量(横轴)
J = trapz(t, abs(e)); % 核心:用梯形积分法计算IAE(绝对误差积分)
catch ME % 捕获仿真过程中的错误(如模型不存在、参数非法等)
disp(['仿真错误: ' ME.message]); % 打印错误信息,方便调试
J = 1e6; % 返回惩罚值,保证优化算法能继续运行
end
end关键代码解释
-
参数提取与校验
x是优化算法(如fmincon)传入的参数向量,必须是[Kp, Ki, Kd]顺序;any(x < 0)检查是否有参数为负,工程上 PID 参数几乎都是非负的(负数会导致控制逻辑混乱),因此用1e6作为"惩罚值"------优化算法的目标是最小化J,会自动避开这类参数。
-
assignin函数的作用- 上面的Simulink 模型中,PID 模块的参数(Kp/Ki/Kd)引用了 MATLAB 基础工作区 的变量(而非固定值);
assignin('base','Kp',Kp)把函数内的 Kp 值"传递"到基础工作区,让 Simulink 模型能实时使用新的参数,这是"动态调参"的关键。
-
仿真与 IAE 计算
sim()函数:自动运行 Simulink 模型,StopTime设置仿真结束时间,SaveOutput开启输出保存;simOut.e.Data:提取你之前 Simulink 模型中out.e端口的误差信号数据(即e(t)=参考输入−系统输出e(t) = 参考输入 - 系统输出e(t)=参考输入−系统输出);trapz(t, abs(e)):用 梯形积分法 计算 IAE=∫0Tend∣e(t)∣dt\text{IAE} = \int_0^{T_{end}} |e(t)| dtIAE=∫0Tend∣e(t)∣dt,这是数值积分中最常用、最稳定的方法,比简单求和更精准。
-
异常处理(try-catch)
- 仿真可能出错(比如模型路径写错、参数超出执行器极限导致模型报错);
catch块会捕获错误,打印提示信息,并返回惩罚值1e6,避免优化算法因单次仿真失败而终止。
MATLAB代码二:主函数
你希望我详细讲解这段完整的 MATLAB 脚本,它是一套"PID 参数自动寻优 + 结果验证 + 可视化"的完整工作流,核心是用 fminsearch 算法找到使 IAE 最小的最优 PID 参数,并直观展示最优参数下的误差曲线。我会逐行拆解逻辑,同时说明关键函数的用法和注意事项。
一、脚本整体功能总结
这段脚本的核心目标是:
- 清空工作区、命令行和图表,初始化仿真参数;
- 用
fminsearch无约束优化算法,调用pid_iae_cost代价函数,自动迭代寻找最优 PID 参数(Kp/Ki/Kd); - 输出最优参数和对应的最小 IAE 值;
- 用最优参数重新运行 Simulink 模型,绘制误差曲线,直观验证控制效果。
二、逐行代码解析
matlab
% ===================== 第一步:环境初始化与参数设置 =====================
clear; clc; close all; % 清理工作区变量、清空命令行、关闭所有绘图窗口(避免干扰)
modelName = 'pid_iae_model'; % 你的Simulink模型名(必须和.slx文件名一致)
T_end = 300; % 仿真结束时间(300秒,足够系统达到稳态)
assignin('base','T_end',T_end); % (可选)将T_end传递到基础工作区,供Simulink模型调用(若模型用到)
% 第二步:设置优化初始值和算法参数
x0 = [0.5, 0.1, 0.01]; % PID参数初始猜测值 [Kp, Ki, Kd],可根据经验调整
options = optimset('Display','iter',... % 优化选项配置:显示迭代过程(方便看寻优进度)
'TolX',1e-3,... % 参数收敛精度:参数变化小于1e-3时停止迭代
'TolFun',1e-3,... % 代价函数收敛精度:IAE变化小于1e-3时停止迭代
'MaxIter',60,... % 最大迭代次数:最多迭代60次
'MaxFunEvals',120); % 最大函数调用次数:最多调用120次pid_iae_cost
% 第三步:调用fminsearch寻找最优PID参数
[x_opt,J_opt] = fminsearch( ...
@(x) pid_iae_cost(x,modelName,T_end), x0, options);
% 解释:@(x)是匿名函数,把x(PID参数)、modelName、T_end传给pid_iae_cost;
% x_opt:返回的最优PID参数 [Kp_opt, Ki_opt, Kd_opt];
% J_opt:返回最优参数下的最小IAE值。
% 第四步:输出最优结果(格式化打印,更易读)
fprintf('\n 最优 PID 参数:\nKp = %.4f\nKi = %.4f\nKd = %.4f\n', ...
x_opt(1),x_opt(2),x_opt(3)); % %.4f表示保留4位小数
fprintf('最小 IAE = %.6f\n',J_opt); % 保留6位小数,更精准
% 第五步:用最优参数更新工作区,重新运行仿真
assignin('base','Kp',x_opt(1)); % 把最优Kp传给基础工作区
assignin('base','Ki',x_opt(2)); % 最优Ki
assignin('base','Kd',x_opt(3)); % 最优Kd
simOut = sim(modelName, 'StopTime', num2str(T_end)); % 用最优参数运行Simulink模型
% 第六步:提取仿真数据,绘制误差曲线
t = simOut.tout; % 提取仿真时间向量
e = simOut.e.Data; % 提取误差信号e(t)的数据
figure; % 新建绘图窗口
plot(t, e, 'LineWidth', 1.5); % 绘制误差曲线,线宽1.5(更清晰)
xlabel('时间 t (s)'); % x轴标签
ylabel('误差 e(t)'); % y轴标签
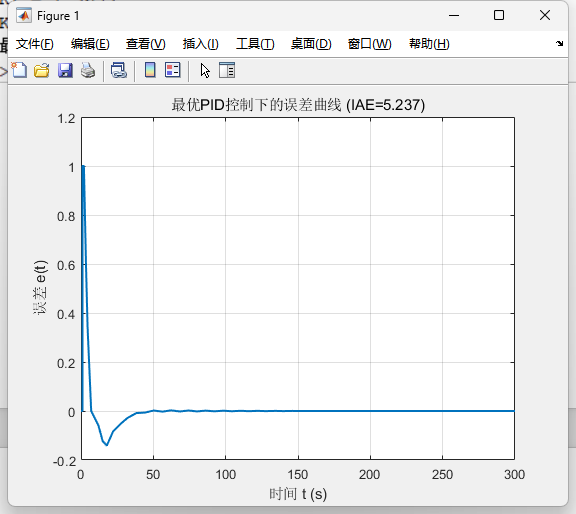
title(['最优PID控制下的误差曲线 (IAE=' num2str(J_opt) ')']); % 标题包含IAE值
grid on; % 显示网格,方便读取数值三、关键知识点补充
1. fminsearch vs fmincon(优化算法选择)
fminsearch:无约束优化算法(基于单纯形法),优点是无需安装优化工具箱 (MATLAB基础版就有)、用法简单;缺点是无法直接设置参数上下限(但你的pid_iae_cost里已经用any(x<0)限制了非负,间接实现约束)。fmincon:有约束优化算法(需优化工具箱),可直接设置参数上下限(如lb=[0,0,0], ub=[10,2,1]),寻优更精准,但依赖工具箱。- 你这段脚本用
fminsearch更轻量化,适合新手入门。
2. optimset 参数的含义(新手必懂)
| 参数名 | 作用 |
|---|---|
Display','iter |
显示迭代过程(打印每一步的参数和IAE值),方便调试;若设为'off'则不显示 |
TolX |
参数收敛阈值:两次迭代的PID参数变化小于1e-3时,认为参数收敛,停止迭代 |
TolFun |
代价函数收敛阈值:两次迭代的IAE值变化小于1e-3时,认为IAE收敛 |
MaxIter |
最大迭代次数:防止算法无限迭代(60次足够PID寻优) |
MaxFunEvals |
最大函数调用次数:限制pid_iae_cost的调用次数(避免仿真耗时过久) |
3. 常见问题与避坑点
- 报错:找不到模型/变量 :确保
modelName和Simulink模型文件名完全一致,且模型文件在MATLAB当前工作目录下; - 迭代次数用完仍未收敛 :可适当增大
MaxIter(如改为100)或放宽TolX/TolFun(如改为1e-2); - 误差曲线为空 :检查Simulink模型的
out.e端口是否正确命名,且SaveOutput是否开启(pid_iae_cost里的sim函数已设置SaveOutput='on',无需额外设置); - 最优参数为0 :初始值
x0设置不合理(如太小),可调整x0(比如[1,0.2,0.05]),或增大参数上限(若用fmincon)。
总结
- 这段脚本是完整的PID参数自动寻优工作流:初始化→参数寻优→结果输出→仿真验证→可视化,覆盖了工程中PID整定的核心环节;
- 核心逻辑是用
fminsearch调用pid_iae_cost,通过最小化IAE找到最优PID参数,fminsearch无需工具箱,适合新手; - 最后绘制误差曲线是关键验证步骤:最优参数下的误差曲线应快速收敛到0,且无明显振荡,直观体现控制效果。
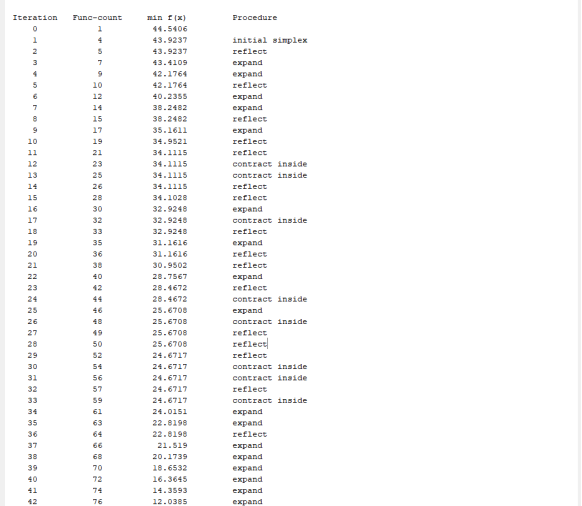
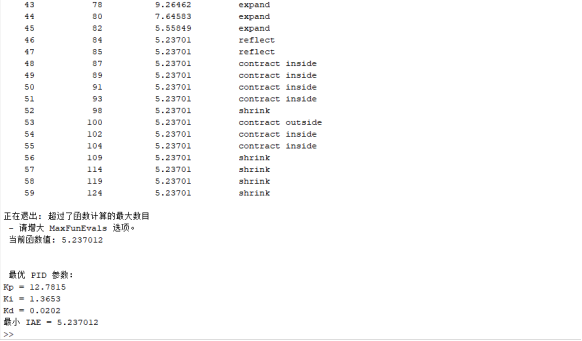
四、运行结果