习题与总结 - 技术栈

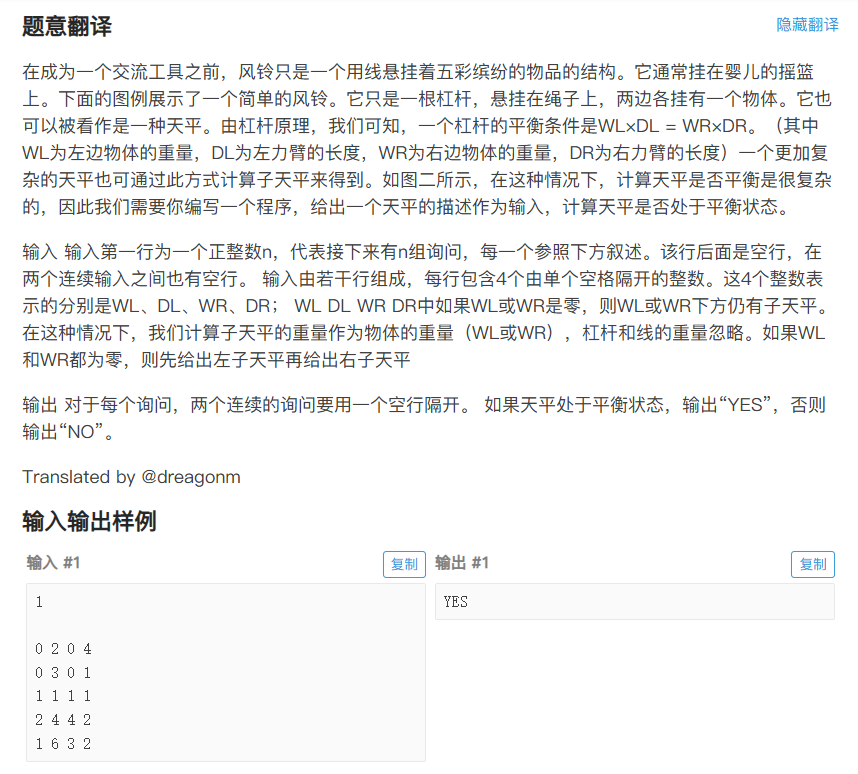
天平（UVa 839 Not so Mobile）

递归向下：遇到重量为 0 就深入子树
回溯向上：子树返回自己的总重量和平衡状态
自底向上计算：叶子节点先计算，父节点依赖子节点的结果

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;

// 递归函数：返回该天平是否平衡，并通过引用返回总重量
bool solve(int& totalWeight) {
    int wl, dl, wr, dr;
    cin >> wl >> dl >> wr >> dr;
    
    bool leftBalanced = true;
    bool rightBalanced = true;
    int leftWeight = wl;
    int rightWeight = wr;
    
    // 如果左边是子天平，递归处理
    if (leftWeight == 0) {
        leftBalanced = solve(leftWeight);
    }
    
    // 如果右边是子天平，递归处理
    if (rightWeight == 0) {
        rightBalanced = solve(rightWeight);
    }
    
    // 计算当前天平的总重量
    totalWeight = leftWeight + rightWeight;
    
    // 检查是否平衡：力矩相等且左右子树都平衡
    return (leftWeight * dl == rightWeight * dr) && leftBalanced && rightBalanced;
}

int main() {
    int t;
    cin >> t;
    
    for (int i = 0; i < t; i++) {
        int totalWeight; // 存储总重量，但这里主要用不到
        if (solve(totalWeight)) {
            cout << "YES" << endl;
        } else {
            cout << "NO" << endl;
        }
        
        // 测试用例之间用空行分隔，这里只是输出时处理
        if (i < t - 1) {
            cout << endl; // 题目要求输出用例间空行
        }
    }
    
    return 0;
}

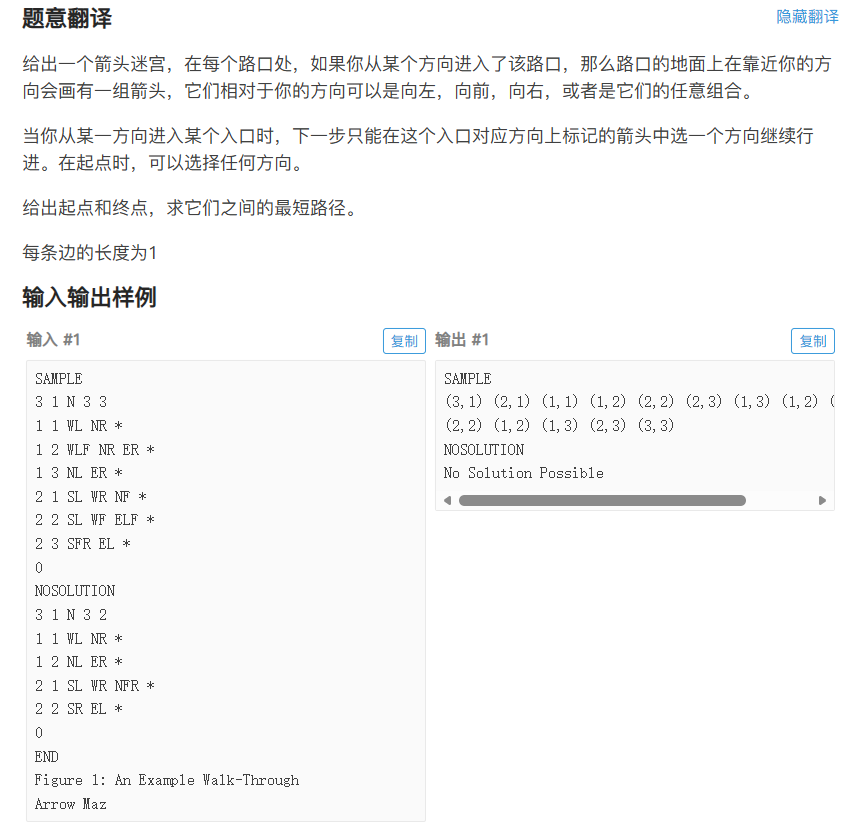
Abbott的复仇（UVA816 Abbott's Revenge）

详解

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;

struct Node {
    int r, c, dir;  // 行，列，方向
    Node(int r=0, int c=0, int dir=0): r(r), c(c), dir(dir) {}
};

// 方向：N,E,S,W
const int dr[] = {-1, 0, 1, 0};
const int dc[] = {0, 1, 0, -1};
const char* dir_name = "NESW";
const char* turn_name = "FLR";

int dir_id(char c) {
    for (int i = 0; i < 4; i++)
        if (dir_name[i] == c) return i;
    return 0;
}

int turn_id(char c) {
    for (int i = 0; i < 3; i++)
        if (turn_name[i] == c) return i;
    return 0;
}

// 主要函数
void solve() {
    string name;
    int r0, c0, r2, c2;
    char dir0;
    
    cin >> name;
    cin >> r0 >> c0 >> dir0 >> r2 >> c2;
    
    // 实际起点是进入的第一个位置
    int dir = dir_id(dir0);
    int r1 = r0 + dr[dir];
    int c1 = c0 + dc[dir];
    
    // 存储规则：has_rule[r][c][dir][turn]
    bool rule[10][10][4][3] = {false};
    
    // 读入规则
    int r, c;
    while (cin >> r && r) {
        cin >> c;
        string s;
        while (cin >> s && s != "*") {
            int dir = dir_id(s[0]);
            for (int i = 1; i < s.length(); i++) {
                int turn = turn_id(s[i]);
                rule[r][c][dir][turn] = true;
            }
        }
    }
    
    // BFS
    int dist[10][10][4];
    Node parent[10][10][4];
    memset(dist, -1, sizeof(dist));
    
    queue<Node> q;
    Node start(r1, c1, dir);
    dist[r1][c1][dir] = 0;
    q.push(start);
    
    Node end_node(-1, -1, -1);  // 记录终点
    
    while (!q.empty()) {
        Node u = q.front(); q.pop();
        
        // 到达终点
        if (u.r == r2 && u.c == c2) {
            end_node = u;
            break;
        }
        
        // 尝试三种转向
        for (int turn = 0; turn < 3; turn++) {
            if (rule[u.r][u.c][u.dir][turn]) {
                int new_dir = u.dir;
                if (turn == 0);       // 直行，方向不变
                else if (turn == 1)   // 左转
                    new_dir = (u.dir + 3) % 4;
                else if (turn == 2)   // 右转
                    new_dir = (u.dir + 1) % 4;
                
                int nr = u.r + dr[new_dir];
                int nc = u.c + dc[new_dir];
                
                // 检查是否在迷宫内且未访问
                if (nr >= 1 && nr <= 9 && nc >= 1 && nc <= 9) {
                    if (dist[nr][nc][new_dir] < 0) {
                        dist[nr][nc][new_dir] = dist[u.r][u.c][u.dir] + 1;
                        parent[nr][nc][new_dir] = u;
                        q.push(Node(nr, nc, new_dir));
                    }
                }
            }
        }
    }
    
    // 输出结果
    cout << name << endl;
    
    if (end_node.r == -1) {
        cout << "  No Solution Possible" << endl;
    } else {
        // 重建路径
        vector<Node> path;
        Node cur = end_node;
        
        // 回溯到起点
        while (true) {
            path.push_back(cur);
            if (cur.r == r1 && cur.c == c1 && cur.dir == dir) break;
            cur = parent[cur.r][cur.c][cur.dir];
        }
        
        // 添加起点
        path.push_back(Node(r0, c0));
        
        // 反向输出
        for (int i = path.size()-1, cnt = 0; i >= 0; i--) {
            if (cnt % 10 == 0) cout << " ";
            cout << " (" << path[i].r << "," << path[i].c << ")";
            if (++cnt % 10 == 0) cout << endl;
        }
        if (path.size() % 10 != 0) cout << endl;
    }
}

int main() {
    while (true) {
        solve();
        string end_check;
        if (!(cin >> end_check) || end_check == "END") break;
    }
    return 0;
}

Petri网模拟（UVA804 Petri Net Simulation）

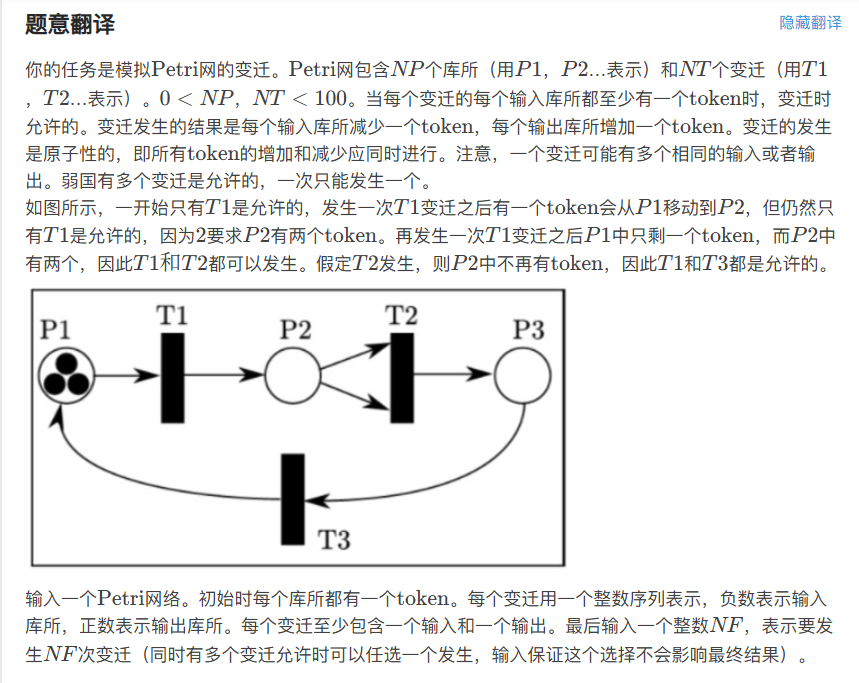
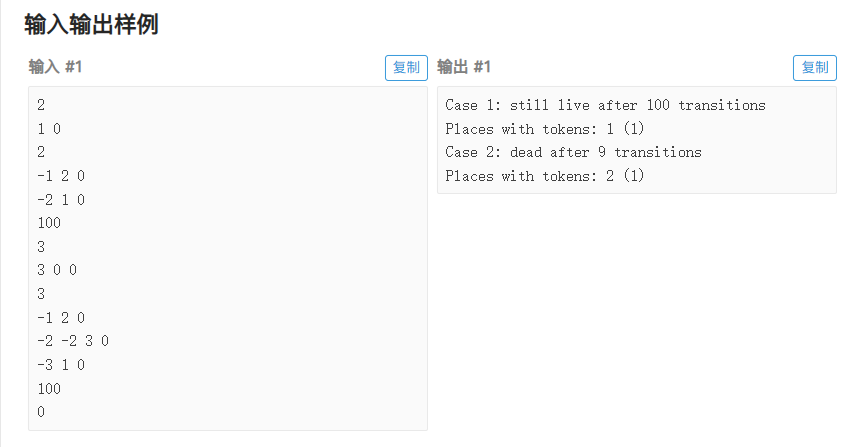
任务是模拟Petri网的运转。在这个网中会有N个P（Place），即"仓库"。还会有N个T（Transitions），即"中转站"。仓库中会有一些token（图中的小黑球），他们需要通过管道（例图中的箭头）在Petri网中移动。

运转规则是：对于一个中转站，它的运转要求他的输入端（指向他的箭头）至少满足每个输入端有一个token。例如例图中的T2需要P2中至少有两个token才能发生运转。运转发生后，中转站的每个输入端减少一个token，它的每个输出端增加一个token。

例如例图中，当P2有两个token，T2发生运转，则P2清空，P3增加一个token。注意！当有同时多个中转站满足运转要求，则可以任选一个运转，输入会保证结果唯一.

请问输入的Petri网是否能运转到指定次数？

理解题面后，解题十分容易，直接按照题意处理即可。循环遍历每个中转站，如果可以运转，则运转，即检查一个Trans的输入端的Place中的token数量是否满足要求，运转后并将运转次数++，然后把一个Trans输出端的Place相应增加一些token。如果所有中转站都无法运转，则运转结束。

需要注意一下，每个Transition的输入当中可能有多个不一样序号的Place，同一个Place也可能会有多次输入同一个Transition中。输出也是类似的。所以我的解题代码当中，一个Trans的结构用map存放了序号对应的个数，并用vector记录了有哪些Place。

其次注意一下，每组数据的输出需要和下组输出之间多空一行。

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;

struct Transition {
    vector<pair<int, int>> input;   // (place, weight)
    vector<pair<int, int>> output;  // (place, weight)
};

int main() {
    int NP, NT, NF;
    int caseNum = 1;
    
    while (cin >> NP && NP) {
        // 读取初始令牌
        vector<int> tokens(NP + 1);
        for (int i = 1; i <= NP; i++) {
            cin >> tokens[i];
        }
        
        // 读取变迁
        cin >> NT;
        vector<Transition> trans(NT + 1);
        
        for (int i = 1; i <= NT; i++) {
            int k, p, w;
            
            // 输入弧
            cin >> k;
            for (int j = 0; j < k; j++) {
                cin >> p >> w;
                trans[i].input.push_back({p, w});
            }
            
            // 输出弧
            cin >> k;
            for (int j = 0; j < k; j++) {
                cin >> p >> w;
                trans[i].output.push_back({p, w});
            }
        }
        
        // 模拟
        cin >> NF;
        int step;
        bool dead = false;
        
        for (step = 1; step <= NF; step++) {
            // 寻找第一个使能的变迁
            int fire_trans = 0;
            for (int t = 1; t <= NT; t++) {
                bool can_fire = true;
                
                // 检查所有输入弧
                for (auto &in : trans[t].input) {
                    if (tokens[in.first] < in.second) {
                        can_fire = false;
                        break;
                    }
                }
                
                if (can_fire) {
                    fire_trans = t;
                    break;
                }
            }
            
            // 如果没有使能的变迁
            if (fire_trans == 0) {
                dead = true;
                break;
            }
            
            // 执行变迁
            for (auto &in : trans[fire_trans].input) {
                tokens[in.first] -= in.second;
            }
            for (auto &out : trans[fire_trans].output) {
                tokens[out.first] += out.second;
            }
        }
        
        // 输出结果
        cout << "Case " << caseNum++ << ": ";
        if (dead) {
            cout << "dead after " << step - 1 << " transitions" << endl;
        } else {
            cout << "still live after " << NF << " transitions" << endl;
        }
        
        cout << "Places with tokens:";
        for (int i = 1; i <= NP; i++) {
            if (tokens[i] > 0) {
                cout << " " << i << " (" << tokens[i] << ")";
            }
        }
        cout << endl << endl;
    }
    
    return 0;
}

总结

主要学习目标

STL容器：vector、set和map这三个容器；string 和 stringstream；排序和检索相关函数。

栈、队列和优先队列的概念，并能用STL实现他们。

完全二叉树的数组实现，完全二叉树的链式表示法和数组表示法。

了解动态内存分配和释放方法及其注意事项。

掌握二叉树的先、中、后序遍历和层次遍历。

掌握图的DFS及连通块计数和 BFS及最短路的输出

掌握拓扑排序算法与欧拉回路算法