2026.1.25日周报

2026.01.25 周报

文献阅读
- 摘要
- 创新点
- 网络框架
- 结果
- 结论
- 不足与展望
二、实验
三、量子计算学习笔记
- [量子测量 ------Quantum Measurement](#量子测量 ——Quantum Measurement)
- 多寄存器系统坍缩
- 编码与隐形传态协议
- 量子态编码传输及单量子比特门操作
- 量子操作实现信息传递
- 量子线路与受控门

文献阅读

题目： 《Spatiotemporal Predictive Learning for Radar-Based Precipitation Nowcasting》
期刊： Atmosphere
作者： Xiaoying Wang, Haixiang Zhao, Guojing Zhang, Qin Guan, and Yu Zhu
发表时间： 2024
文章链接： https://www.google.com/search?q=https://doi.org/10.3390/atmos15080914

摘要

本文针对短临降水预报（0-2小时）中捕捉中小尺度天气系统复杂变化的难题，基于2017-2020年银川贺兰山地区的C波段天气雷达和地面降水数据，评估了近年来主流的15种深度学习模型的预报性能。研究发现，虽然无循环模型在参数量和计算效率上具有显著优势，但在捕捉雷达回波图像的复杂物理变化和强降水区域方面存在不足。为此，作者提出了一种改进模型 SimVP-GMA。该模型保留了SimVP的整体架构，但利用 Group-Mix Attention机制替换了原有的Inception时间预测模块，并引入 SCConv 空间编码器。实验结果表明，SimVP-GMA 在 MSE 和 LPIPS 指标上分别比 SimVP 提升了 0.55 和 0.0193，且在强降水（dBZ > 20）的预报细节和准确性上表现更为优异。

创新点

针对现有轻量级模型在复杂时空特征提取上的不足，创新性地融合了 Group-Mix Attention 机制。该机制通过分组注意力并行处理时空信息，增强了模型对长期时间演变的捕捉能力，弥补了CNN在长程依赖上的短板。
在空间编码器部分引入了 Spatial and Channel reconstruction Convolution。通过空间重构单元和通道重构单元，有效减少了特征图中的空间和通道冗余，在降低计算成本的同时提升了特征表示能力。

网络框架

本文提出的 SimVP-GMA 模型建立在 SimVP 的通用架构之上，主要由空间编码器、时间转换器和空间解码器三部分组成。

编码器负责从输入的雷达回波序列中提取空间特征；转换器负责在潜在空间中进行时间演化预测；解码器则将预测的潜在特征重构回雷达回波图像。

SimVP-GMA 的核心改进在于将原转换器中的 Inception 模块替换为 GMA 模块，并在编码器中集成了 SCConv。

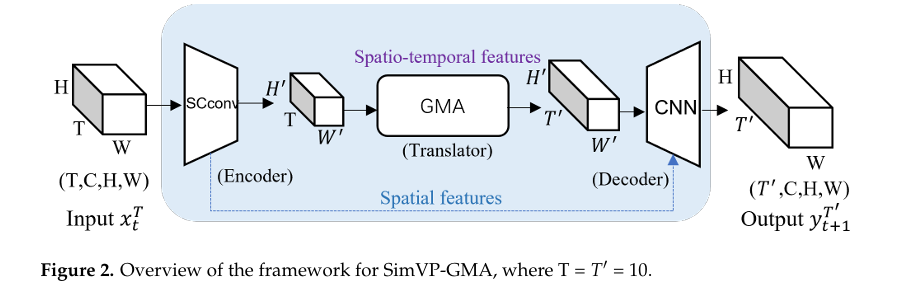
Group-Mix Attention（GMA）

GMA 模块旨在捕捉长期的时空依赖关系。它将输入的特征图分割成多个组，利用组混合注意力机制同时聚合空间和通道信息。这种设计使得模型能够在不显著增加计算量的情况下，通过注意力机制有效地关注到强降水区域的演变。

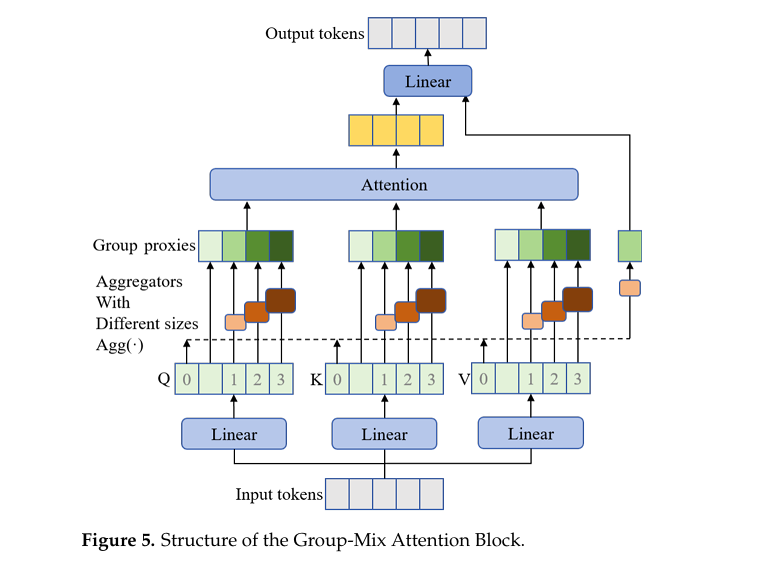
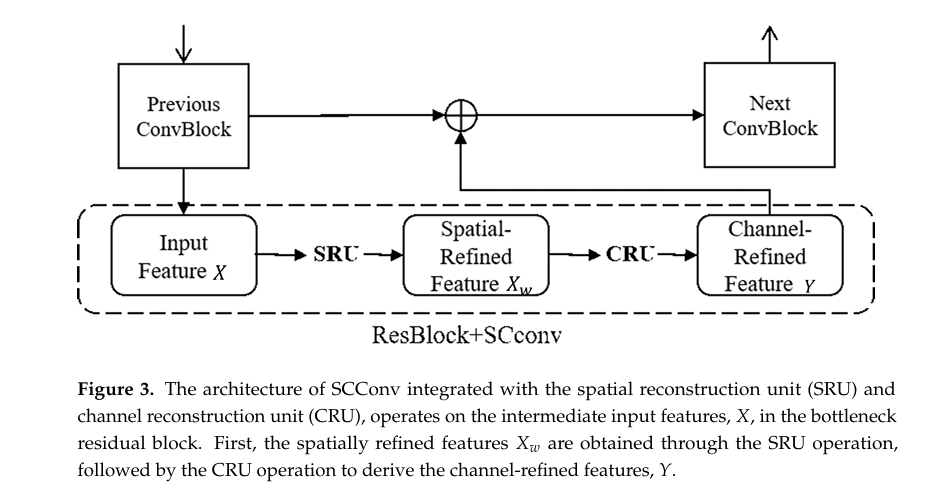
空间与通道重构卷积

为了解决特征冗余问题，模型在编码阶段使用了 SCConv。

SCConv 包含两个单元：Spatial Reconstruction Unit（SRU）利用分离-重构的方法来抑制空间上的冗余特征。

Channel Reconstruction Unit(CRU)利用分割-变换-融合的策略来减少通道维度上的冗余。

结果

研究使用了银川地区 2017-2020 年的雷达回波数据进行训练和测试，采用 CSI, POD, FAR, MSE, MAE, LPIPS 等多项指标进行评估。
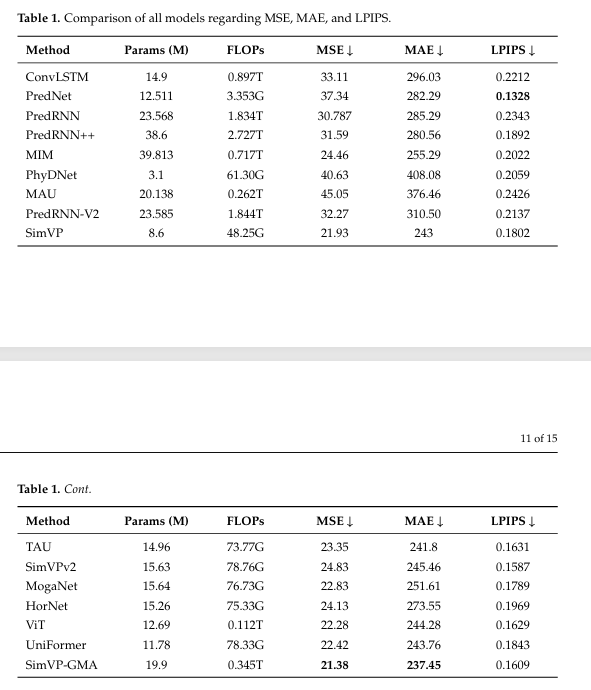
模型性能综合对比

作者对比了包括 ConvLSTM, PredRNN, MIM, SimVP 等在内的 15 种模型。

无循环模型如 SimVP 在计算效率上远超循环模型。改进后的 SimVP-GMA 在综合指标上表现最佳。与基础模型 SimVP 相比，SimVP-GMA 将 MSE 降低了 0.55，LPIPS降低了 0.0193，说明预测图像不仅数值误差更小，而且在视觉纹理上更接近真实雷达图。

强降水预报能力分析

针对不同强度的降水，分析了各模型的 CSI 和 POD 指标。SimVP-GMA 在中强降水的预报中展现出显著优势。

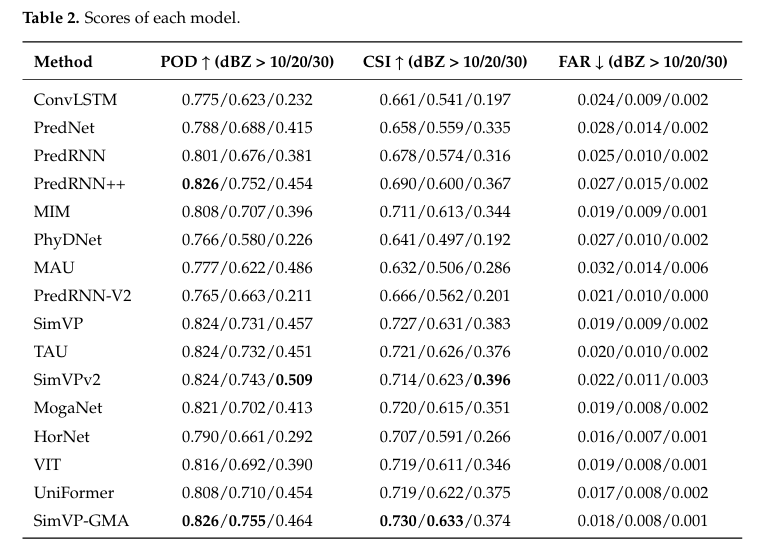
可视化结果显示，该模型能更清晰地预测出高回波区域的形状和位置，而其他轻量级模型往往会产生模糊的预测结果。

结论

本文提出了一种结合了 Group-Mix Attention 和 SCConv 的新型时空预测模型 SimVP-GMA，专门用于雷达回波短临预报。通过在银川地区真实数据集上的广泛测试，证明了该模型成功解决了传统 CNN 模型感受野受限和特征冗余的问题，为区域性精准短临预报提供了一种高效且可靠的深度学习解决方案。

不足与展望

目前的研究仅基于银川贺兰山地区的雷达数据，不同地区的地形和气候特征可能对模型泛化能力提出挑战，未来需在更多样化的数据集上验证；虽然引入了注意力机制，但模型本质上仍是纯数据驱动的，缺乏对大气动力学物理过程的显式建模。未来可探索将物理约束融入网络设计。且目前仅使用了雷达和地面降水数据，未来可以考虑融合卫星云图、数值模式预报等多源数据，以进一步提升预报时效和准确率。

二、实验

本周复现了《A quantum neural network model for short term wind speed forecasting using weather data》，该项目是一个基于量子神经网络(QNN)的风速预测系统，使用气象数据预测未来1-6小时的风速。项目采用了PennyLane量子机器学习框架和PyTorch深度学习框架，然后并用在了自己的数据集中，用做降雨预测但是整体效果一般般，后面需要转变实验思路。

量子电路模块 (circuits.py)

定义了两种具有不同拓扑结构的变分量子电路：

一种是圆形纠缠结构，即量子比特首尾相接形成环状；

qnode_circular_entangling() - 圆形纠缠量子节点
另一种是并行纠缠结构，通过交替的偶数位和奇数位 CNOT 门实现纠缠。
qnode_parallel_entangling() - 并行纠缠量子节点
这两个函数都包含特征映射层：利用 Hadamard 门和 Y 轴角度嵌入
变分层：包含可训练的旋转门参数。
测量层：返回每个量子比特的 PauliZ 期望值。

python 复制代码

import pennylane as qml

def qnode_circular_entangling(inputs, weights):
    """
    圆形纠缠量子节点
    
    Args:
        inputs: 输入特征向量
        weights: 可训练权重参数，形状为(n_layers,n_qubits,3)
    
    Returns:
        每个量子比特的PauliZ期望值列表
    """
    n_layers = len(weights)
    n_qubits = len(weights[0])
    
    ###############
    # 特征映射层 #
    ###############
    for idx in range(n_qubits):
        qml.Hadamard(wires=idx)  # 对每个量子比特应用Hadamard门
    qml.templates.AngleEmbedding(inputs, rotation='Y', wires=range(n_qubits))  # 使用Y轴旋转编码输入特征
    
    ##########
    # 变分层 #
    ##########
    for k in range(n_layers):
        # 纠缠层 - 圆形拓扑结构
        for i in range(n_qubits-1):
            qml.CNOT(wires=[i,i+1])  # 相邻量子比特间的CNOT门
        qml.CNOT(wires=[n_qubits-1,0])  # 最后一个量子比特与第一个量子比特纠缠，形成圆形
        
        # 变分层 - 可训练参数
        for i in range(len(weights[k])):
            qml.Rot(*weights[k][i],wires=i)  # 三参数旋转门(Rx,Ry,Rz)
    
    ###############
    # 测量层 #
    ###############
    return [qml.expval(qml.PauliZ(wires=i)) for i in range(n_qubits)]  # 测量每个量子比特的PauliZ算子期望值

def qnode_parallel_entangling(inputs, weights):
    """
    并行纠缠量子节点
    
    Args:
        inputs: 输入特征向量
        weights: 可训练权重参数，形状为(n_layers,n_qubits,3)
    
    Returns:
        每个量子比特的PauliZ期望值列表
    """
    n_layers = len(weights)
    n_qubits = len(weights[0])
    
    ###############
    # 特征映射层 #
    ###############
    for idx in range(n_qubits):
        qml.Hadamard(wires=idx)  # 对每个量子比特应用Hadamard门
    qml.templates.AngleEmbedding(inputs, rotation='Y', wires=range(n_qubits))  # 使用Y轴旋转编码输入特征
    
    ##########
    # 变分层 #
    ##########
    for k in range(n_layers):
        # 纠缠层 - 并行拓扑结构
        for i in range(0, n_qubits - 1, 2): 
            qml.CNOT(wires=[i, i + 1])  # 偶数索引量子比特与下一个量子比特纠缠
        for i in range(1, n_qubits - 1, 2):  
            qml.CNOT(wires=[i, i + 1])  # 奇数索引量子比特与下一个量子比特纠缠
        
        # 变分层 - 可训练参数
        for i in range(len(weights[k])):
            qml.Rot(*weights[k][i],wires=i)  # 三参数旋转门(Rx,Ry,Rz)
    
    ###############
    # 测量层 #
    ###############
    return [qml.expval(qml.PauliZ(wires=i)) for i in range(n_qubits)]  # 测量每个量子比特的PauliZ算子期望值

量子神经网络模型（utils/models.py）

该类封装了一个量子层 TorchLayer 和一个经典线性输出层，支持在前向传播中处理批次数据，并将量子电路的输出映射到指定的预测窗口大小。通过使用 EarlyStopper ，通过监控验证集损失的变化来自动控制训练轮数，从而防止模型过拟合。

python 复制代码

import torch
import torch.nn as nn
import pennylane as qml

def quantum_circuit(inputs, weights):
    """
    量子电路函数，用于量子神经网络
    
    Args:
        inputs: 输入特征向量
        weights: 可训练权重参数
    
    Returns:
        每个量子比特的PauliZ期望值列表
    """
    # 解包权重参数
    qdepth = weights.size(dim=0)  # 量子电路深度
    nqubits = weights.size(dim=1)  # 量子比特数量
    
    #############
    # 嵌入层 #
    #############
    for i in range(nqubits):
        qml.Hadamard(wires=i)  # 创建叠加态
        qml.RY(inputs[i], wires=i)  # 将输入特征编码到Y轴旋转

    ##########
    # 变分层 #
    ##########
    for k in range(qdepth):
        # 纠缠层 - 并行纠缠模式
        for i in range(0, nqubits - 1, 2): 
            qml.CNOT(wires=[i, i + 1])  # 偶数位量子比特纠缠
        for i in range(1, nqubits - 1, 2):  
            qml.CNOT(wires=[i, i + 1])  # 奇数位量子比特纠缠
        # 旋转层 - 可训练参数
        for y in range(nqubits):
            qml.Rot(*weights[k][y], wires=y)  # 三参数旋转门(Rx,Ry,Rz)

    return [qml.expval(qml.PauliZ(wires=i)) for i in range(nqubits)]  # 返回PauliZ测量期望值

class QuantumNeuralNetwork(nn.Module):
    """
    量子神经网络类，结合量子电路和经典神经网络
    
    Args:
        forecast_window_size: 预测时间窗口大小
        num_qubits: 量子比特数量
        QML_device: 量子机器学习设备类型
        num_layers: 量子电路层数
        torch_device: PyTorch设备(CPU/GPU)
    """
    def __init__(self, forecast_window_size, num_qubits, QML_device, num_layers, torch_device): 
        super(QuantumNeuralNetwork, self).__init__() 
        self.forecast_window_size = forecast_window_size  # 预测窗口大小
        
        self.device = torch_device  # 计算设备
        penny_dev = qml.device(QML_device, wires = num_qubits)  # 创建量子设备
        
        # 创建量子节点，使用PyTorch接口和最佳微分方法
        qnode = qml.QNode(quantum_circuit, penny_dev, interface='torch', diff_method="best")
        self._quantum_circuit = qnode  # 量子电路节点

        # 定义量子层权重形状
        q_weights_shape = {'weights':(num_layers, num_qubits, 3)}
        self.hidden_quantum_layer = qml.qnn.TorchLayer(self._quantum_circuit, q_weights_shape)        
        
        # 输出层：经典线性层，将量子输出映射到预测结果
        self.output_classical_layer = torch.nn.Linear(num_qubits, forecast_window_size) 
    
    def forward(self, batch):
        """
        前向传播
        
        Args:
            batch: 输入批次数据
        
        Returns:
            批次预测结果，形状为[Batch, Output length]
        """
        batch_output = []
        for y in batch:
            y = self.hidden_quantum_layer(y).to(self.device)  # 量子层前向传播
            y = self.output_classical_layer(y)  # 经典输出层
            batch_output.append(y)

        return torch.vstack(batch_output)  # 堆叠批次输出
    
class EarlyStopper:
    """
    早停类，用于防止模型过拟合
    
    Args:
        patience: 容忍轮数，验证损失不改善的最大轮数
        min_delta: 最小改善阈值，只有超过此阈值才认为是改善
    """
    def __init__(self, patience=1, min_delta=0):
        self.patience = patience  # 容忍轮数
        self.min_delta = min_delta  # 最小改善阈值
        self.counter = 0  # 当前计数器
        self.min_validation_loss = float('inf')  # 最小验证损失

    def early_stop(self, validation_loss):
        """
        判断是否应该早停
        
        Args:
            validation_loss: 当前验证损失
        
        Returns:
            bool: 是否应该停止训练
        """
        if validation_loss < self.min_validation_loss:
            self.min_validation_loss = validation_loss  # 更新最小损失
            self.counter = 0  # 重置计数器
        elif validation_loss > (self.min_validation_loss + self.min_delta):
            self.counter += 1  # 增加计数器
            if self.counter >= self.patience:
                return True  # 达到容忍上限，停止训练
        return False  # 继续训练

将上述代码修改，然后改成了我自己用的降雨数据集，实验，结果如下：
当depth为7的时候，验证损失是最低的：

模型深度	验证损失	排名
Depth 3	0.06595	5
Depth 4	0.06449	4
Depth 5	0.06288	3
Depth 6	0.06169	2
Depth 7	0.06094	1

关于Depth的补充如下：

每一层是一个Depth，都由两个核心算子组成：

纠缠算子（ U e n t U_{ent} Uent）：使用控制非门（CNOT）在相邻量子比特之间建立关联，使模型能够捕捉特征间的相互依赖性。
变分算子（ U v a r U_{var} Uvar）：包含一系列可训练的旋转门（如 R z , R y R_z, R_y Rz,Ry），这些门的旋转角度 θ \theta θ 是模型在训练过程中不断优化的参数。

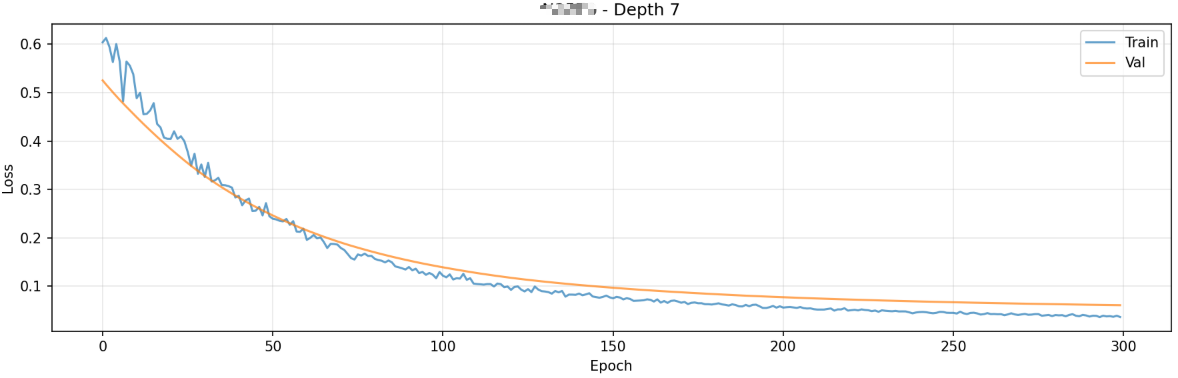
因此Depth 7，就是包含了7层这个结构，Depth7的训练损失与验证损失的下降如图所示：

用Depth7的模型进行预测，得到的结果如下，R方基本上都是负数

预测时效	MAE (mm)	MSE	RMSE (mm)	NRMSE	R	R²
H1 (t+1h)	0.166	0.0373	0.193	3.041	0.253	-8.39
H2 (t+2h)	0.156	0.0416	0.204	3.208	-0.264	-9.46
H3 (t+3h)	0.097	0.0146	0.121	1.903	0.125	-2.68

时序预测图如下：

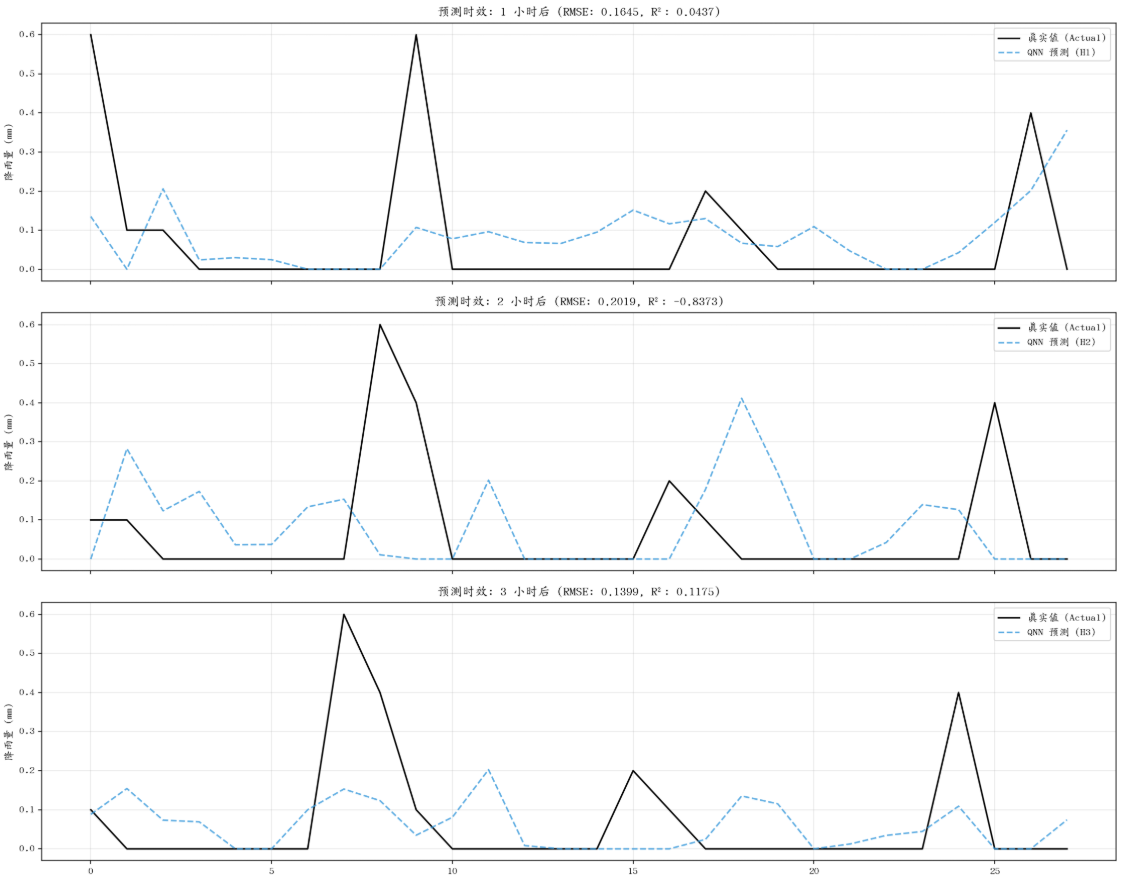
总结

经过这周的实验，发现用时序数据做降雨预测其实是不实际的。因为降雨属于稀疏事件，如果不是针对某种汛期或者雨季去做预测的话，即使时序数据集再大，降雨量大多数都是0，模型注定能学到的大多都是比较平坦的情况。所以后面要转变一下思路，还是要用雷达回波图去做降雨预测。

三、量子计算学习笔记

量子测量 ------Quantum Measurement

量子测量是从量子态中提取经典信息的唯一途径，是连接量子世界与经典世界的桥梁。其原理基于一套严格的数学假设。一次测量是针对一个特定的标准正交基 { ∣ v i ⟩ } \{|v_i\rangle\} {∣vi⟩} 来进行的，这组基向量张成了整个状态空间。对于一个待测量的量子态 ∣ ψ ⟩ |\psi\rangle ∣ψ⟩，首先需要将其在该测量基下进行展开： ∣ ψ ⟩ = ∑ i a i ∣ v i ⟩ |\psi\rangle = \sum_i a_i |v_i\rangle ∣ψ⟩=∑iai∣vi⟩。测量的结果是概率性的 。具体来说，测量到结果 i i i 的概率为 P ( i ) = ∣ a i ∣ 2 P(i) = |a_i|^2 P(i)=∣ai∣2。所有可能结果的概率之和为1，这由量子态的归一化性质保证。测量的另一个关键特征是状态坍缩 ，即一旦测量得到结果 i i i，量子系统将不可逆地坍缩到对应的基向量状态 ∣ v i ⟩ |v_i\rangle ∣vi⟩ 上。此外，量子态的全局相位 ，即一个整体的复数因子 e i α e^{i\alpha} eiα在物理上是不可测量的，因为它在计算概率时会被模平方抵消，不影响任何测量结果。

多寄存器系统坍缩

当一个量子系统由多个子系统或称为寄存器，如多个量子比特构成时，我们可以只对其中一部分进行测量。这种局部测量同样会影响整个系统的状态。

考虑一个双量子比特系统，其状态为 ∣ ψ ⟩ = 1 10 ∣ 00 ⟩ + 2 10 ∣ 01 ⟩ + 3 10 ∣ 10 ⟩ + 4 10 ∣ 11 ⟩ |\psi\rangle = \frac{1}{\sqrt{10}}|00\rangle + \sqrt{\frac{2}{10}}|01\rangle + \sqrt{\frac{3}{10}}|10\rangle + \sqrt{\frac{4}{10}}|11\rangle ∣ψ⟩=10 1∣00⟩+102 ∣01⟩+103 ∣10⟩+104 ∣11⟩

若我们只在计算基 { ∣ 0 ⟩ , ∣ 1 ⟩ } \{|0\rangle, |1\rangle\} {∣0⟩,∣1⟩} 下测量第一个量子比特

首先需要按第一个比特的状态对总状态进行重写：
∣ ψ ⟩ = ∣ 0 ⟩ ⊗ ( 1 10 ∣ 0 ⟩ + 2 10 ∣ 1 ⟩ ) + ∣ 1 ⟩ ⊗ ( 3 10 ∣ 0 ⟩ + 4 10 ∣ 1 ⟩ ) |\psi\rangle = |0\rangle \otimes \left(\sqrt{\frac{1}{10}}|0\rangle + \sqrt{\frac{2}{10}}|1\rangle\right) + |1\rangle \otimes \left(\sqrt{\frac{3}{10}}|0\rangle + \sqrt{\frac{4}{10}}|1\rangle\right) \text{} ∣ψ⟩=∣0⟩⊗(101 ∣0⟩+102 ∣1⟩)+∣1⟩⊗(103 ∣0⟩+104 ∣1⟩)

测量第一个比特得到 0 的概率，等于其系数向量,即与 ∣ 0 ⟩ |0\rangle ∣0⟩ 发生张量积的部分的范数平方。

计算可得：
P ( 0 ) = ∥ 1 10 ∣ 0 ⟩ + 2 10 ∣ 1 ⟩ ∥ 2 = 1 10 + 2 10 = 3 10 P(0) = \|\sqrt{\frac{1}{10}}|0\rangle + \sqrt{\frac{2}{10}}|1\rangle\|^2 = \frac{1}{10} + \frac{2}{10} = \frac{3}{10} P(0)=∥101 ∣0⟩+102 ∣1⟩∥2=101+102=103。

同理，测得 1 的概率为 P ( 1 ) = 7 10 P(1) = \frac{7}{10} P(1)=107。

如果测量结果为 0，整个系统将坍缩，第一个比特确定为 ∣ 0 ⟩ |0\rangle ∣0⟩，而第二个比特的状态则坍缩为对应系数向量归一化后的新状态：
∣ ψ s u b ′ ⟩ = 1 10 ∣ 0 ⟩ + 2 10 ∣ 1 ⟩ 3 / 10 = 1 3 ∣ 0 ⟩ + 2 3 ∣ 1 ⟩ |\psi'_{sub}\rangle = \frac{\sqrt{\frac{1}{10}}|0\rangle + \sqrt{\frac{2}{10}}|1\rangle}{\sqrt{3/10}} = \frac{1}{\sqrt{3}}|0\rangle + \sqrt{\frac{2}{3}}|1\rangle \text{} ∣ψsub′⟩=3/10 101 ∣0⟩+102 ∣1⟩=3 1∣0⟩+32 ∣1⟩

编码与隐形传态协议

量子测量与量子纠缠的结合，催生了两种著名的量子信息协议。超密编码 利用量子信道高效传输经典信息，而量子隐形传态 则利用经典信道和纠缠来传输一个未知的量子态。这两种协议的核心都依赖于对贝尔基的测量。

贝尔基 是由四个两量子比特的最大纠缠态构成的标准正交基，它们是进行双比特联合测量的基础。这四个贝尔态分别是：

∣ β 00 ⟩ = 1 2 ( ∣ 00 ⟩ + ∣ 11 ⟩ ) |\beta_{00}\rangle = \frac{1}{\sqrt{2}}(|00\rangle + |11\rangle) ∣β00⟩=2 1(∣00⟩+∣11⟩)
∣ β 01 ⟩ = 1 2 ( ∣ 10 ⟩ + ∣ 01 ⟩ ) |\beta_{01}\rangle = \frac{1}{\sqrt{2}}(|10\rangle + |01\rangle) ∣β01⟩=2 1(∣10⟩+∣01⟩)
∣ β 10 ⟩ = 1 2 ( ∣ 00 ⟩ − ∣ 11 ⟩ ) |\beta_{10}\rangle = \frac{1}{\sqrt{2}}(|00\rangle - |11\rangle) ∣β10⟩=2 1(∣00⟩−∣11⟩)
∣ β 11 ⟩ = 1 2 ( ∣ 01 ⟩ − ∣ 10 ⟩ ) |\beta_{11}\rangle = \frac{1}{\sqrt{2}}(|01\rangle - |10\rangle) ∣β11⟩=2 1(∣01⟩−∣10⟩)

由于这四个态是两两正交的，因此可以作为一组测量基。在协议中，执行一次贝尔基测量，系统会以特定概率坍缩到这四个状态之一，从而获得两位经典信息（00, 01, 10, 或 11）。

量子态编码传输及单量子比特门操作

具有个例子来协议详细展示了如何通过单量子比特门操作来编码并传输信息。
初始资源 ：比如A和B预先共享一个处于 ∣ β 00 ⟩ |\beta_{00}\rangle ∣β00⟩ 态的纠缠对，A持有第一个Qubit，B持有第二个。
编码：A希望发送两位经典信息 zx。她对自己持有的Qubit施加一个相应的单比特Pauli门操作，从而将整个系统的状态转换为对应的贝尔态。

发送00：施加 I I I 门，系统态仍为 ∣ β 00 ⟩ |\beta_{00}\rangle ∣β00⟩。

发送01：施加 X X X 门，系统态变为 ∣ β 01 ⟩ |\beta_{01}\rangle ∣β01⟩。

发送10：施加 Z Z Z 门，系统态变为 ∣ β 10 ⟩ |\beta_{10}\rangle ∣β10⟩。

发送11：施加 Z X ZX ZX 门，系统态变为 ∣ β 11 ⟩ |\beta_{11}\rangle ∣β11⟩。
传输：A将她操作过的单个Qubit 发送给B。
解码：B收到Qubit后，对他拥有的两个Qubit执行一次贝尔基测量 。测量结果将唯一确定系统的状态是四个贝尔态中的哪一个，从而解码出Alice发送的两位经典比特 zx。

该协议的核心是利用一个纠缠比特和一个量子比特的传输，完成了两个经典比特的信息传递，因此被称为"超密"。

量子操作实现信息传递

量子隐形传态 是另一个经典协议，它展示了如何利用纠缠和经典通信来传输一个未知的量子态。

目标与资源 ：A有一个未知量子态 ∣ ψ ⟩ = a ∣ 0 ⟩ + b ∣ 1 ⟩ |\psi\rangle = a|0\rangle + b|1\rangle ∣ψ⟩=a∣0⟩+b∣1⟩ 希望传给B。A和B同样预共享一个 ∣ β 00 ⟩ |\beta_{00}\rangle ∣β00⟩ 纠缠对，并且可以使用一个双向的经典信道。
A的操作 ：A对她手中的两个Qubit（未知态 ∣ ψ ⟩ |\psi\rangle ∣ψ⟩和纠缠对的一半）进行一次贝尔基测量 。系统的总状态可以被重新展开为以A的贝尔基为基础的叠加形式。A的测量将使系统坍缩，并获得一个两位经典结果（00, 01, 10, 或 11）。与此同时，B的Qubit也相应地坍缩到了一个与原始态 ∣ ψ ⟩ |\psi\rangle ∣ψ⟩相关的特定状态。

经典通信 ：A通过经典信道将她的两位测量结果发送给B。
B的重构 ：B根据收到的经典信息，对自己手中的Qubit施加一个对应的幺正操作（ I , X , Z , I, X, Z, I,X,Z, 或 Z X ZX ZX）来修正其状态，从而精确地恢复出原始的未知量子态 ∣ ψ ⟩ |\psi\rangle ∣ψ⟩。

这个过程实现了量子态的传输，而没有物理地移动粒子本身，并且整个过程中 ∣ ψ ⟩ |\psi\rangle ∣ψ⟩的具体信息（系数a, b）对于A和B来说都是未知的。

量子线路与受控门

为了形式化地描述这些协议和算法，引入量子线路 的概念。
基本元素 ：量子线路从左到右读取。水平的实线代表一个量子比特 ，而双实线则代表一个经典比特 。线路上的方框代表作用在该比特上的量子门 或操作。线路末端的"仪表盘"符号代表在该基下的测量。

受控门 ：这是多比特操作的核心，其中一个或多个Qubit作为控制位，决定是否在目标位上施加一个操作。
CNOT (受控非门) ：用一个实心圆点表示控制位，一个 ⊕ \oplus ⊕符号表示目标位。当且仅当控制位为 ∣ 1 ⟩ |1\rangle ∣1⟩时，目标位执行 X X X操作。
Controlled-U ：用实心圆点连接到目标位上的 U U U门方框，表示当控制位为 ∣ 1 ⟩ |1\rangle ∣1⟩时，在目标位上执行 U U U操作。
在 ∣ 0 ⟩ |0\rangle ∣0⟩上受控 *：如果控制条件是控制位为 ∣ 0 ⟩ |0\rangle ∣0⟩，则在线路上用一个空心圆点表示。