UWB 雷达综述精读:应用、标准、信号处理、数据集、芯片与未来方向
M. Cheraghinia et al., "A Comprehensive Overview on UWB Radar: Applications, Standards, Signal Processing Techniques, Datasets, Radio Chips, Trends and Future Research Directions," in IEEE Communications Surveys & Tutorials, vol. 27, no. 4, pp. 2283-2324, Aug. 2025, doi: 10.1109/COMST.2024.3488173.
1. 这篇综述到底在解决什么问题
这篇文章的定位很明确:把 UWB 雷达作为一个完整系统来梳理:从基础定义、信道/回波表示(CIR)、系统形态与标准约束(频谱、信道、PHY),一路到五大应用域(presence detection、device-free localization、activity/gesture、vital signs、ISAC),并进一步整理了可用数据集、商用芯片与模块,以及未来研究挑战与路线图。文章强调其贡献在于"只聚焦 UWB 雷达",并覆盖硬件、软件、数据集、标准与未来方向等"全栈视角"。
为了让后面每一类算法与应用"落地",需要先抓住本文隐含的一条主线:
UWB 雷达的核心数据形态是 CIR(Channel Impulse Response),而所有应用几乎都可被看成:在慢时间(slow-time)上观测 CIR 的变化,并在快时间(fast-time)上做距离维/到达时延维的定位与分离。
2. 文章结构图(图 2)与阅读地图
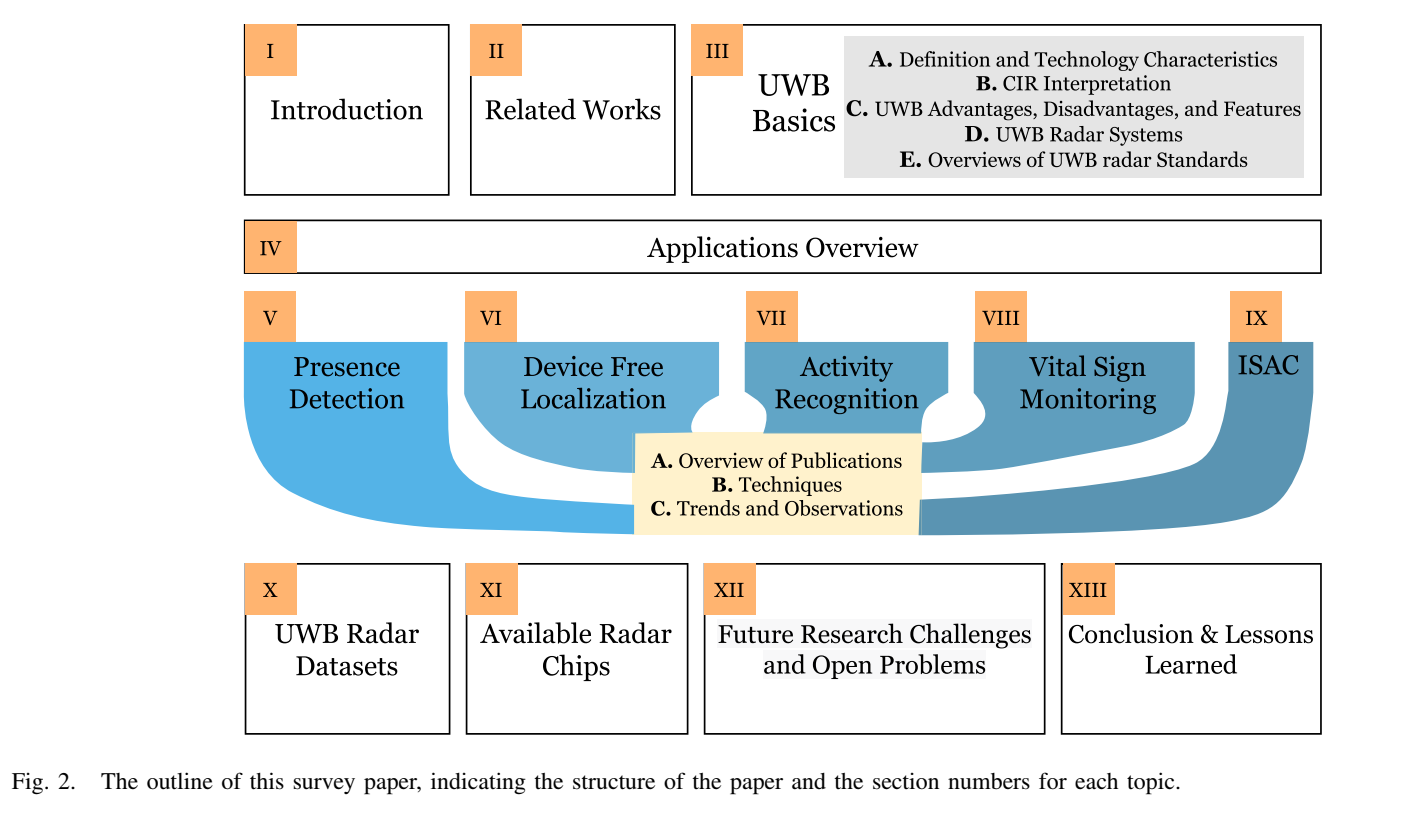
图 2 是作者给出的"路线图":先给基础(UWB basics、系统与标准),再给应用总览,然后分别深挖四个传统应用域,最后讨论 ISAC(集成感知与通信),再接数据集、芯片、未来挑战与结论。
3. UWB 的定义、脉冲宽度与"为什么它天生适合雷达"
3.1 两种定义方式:绝对带宽与分数带宽
文章给出 UWB 的两个判据:绝对带宽大于 500 MHz,或分数带宽不小于 0.2。
即:
BW>500 MHz,BF≥0.2 BW > 500\,\mathrm{MHz}, \qquad BF \ge 0.2 BW>500MHz,BF≥0.2
其中分数带宽按文中(-10 dB 发射点)定义为:
BF=BWfC=fH−fL(fH+fL)/2. BF = \frac{BW}{f_C} = \frac{f_H - f_L}{(f_H + f_L)/2}. BF=fCBW=(fH+fL)/2fH−fL.
这里 f_H,f_Lf\_H,f\_Lf_H,f_L 是上/下 -10 dB 频点,f_Cf\_Cf_C 是算术中心频率。
3.2 "带宽越大,时域脉冲越窄":文中给出 BW⋅T≥4/πBW\cdot T\ge 4/\piBW⋅T≥4/π
作者在引言里用一个非常关键的关系:
BW×T≥4πBW\times T \ge \frac{4}{\pi}BW×T≥π4
并给了对比:WiFi 典型 20MHz20 \mathrm{MHz}20MHz 带宽导致脉冲宽度大于 4ns4 \mathrm{ns}4ns;而 500MHz500\mathrm{MHz}500MHz 的 UWB 可把时域脉冲压到约 0.16ns0.16\mathrm{ns}0.16ns 量级,从而足以区分直达径与反射径,使其非常适合雷达。
为了后文严谨,我们把它稍微"推导化"理解:若把 TTT 当作有效脉冲宽度(例如主瓣宽度或等效时间扩展),则宽带信号的频谱扩展 BWBWBW 越大,时域集中程度越强,形成一种"时间-频率不确定性"的工程形式。附录里会给出一个从矩形谱/高斯脉冲出发的推导,解释为什么会出现常数 4π\frac{4}{\pi}π4 这一类界。
4. 图 1:带宽、距离分辨率、最大探测距离之间的"硬约束三角形"
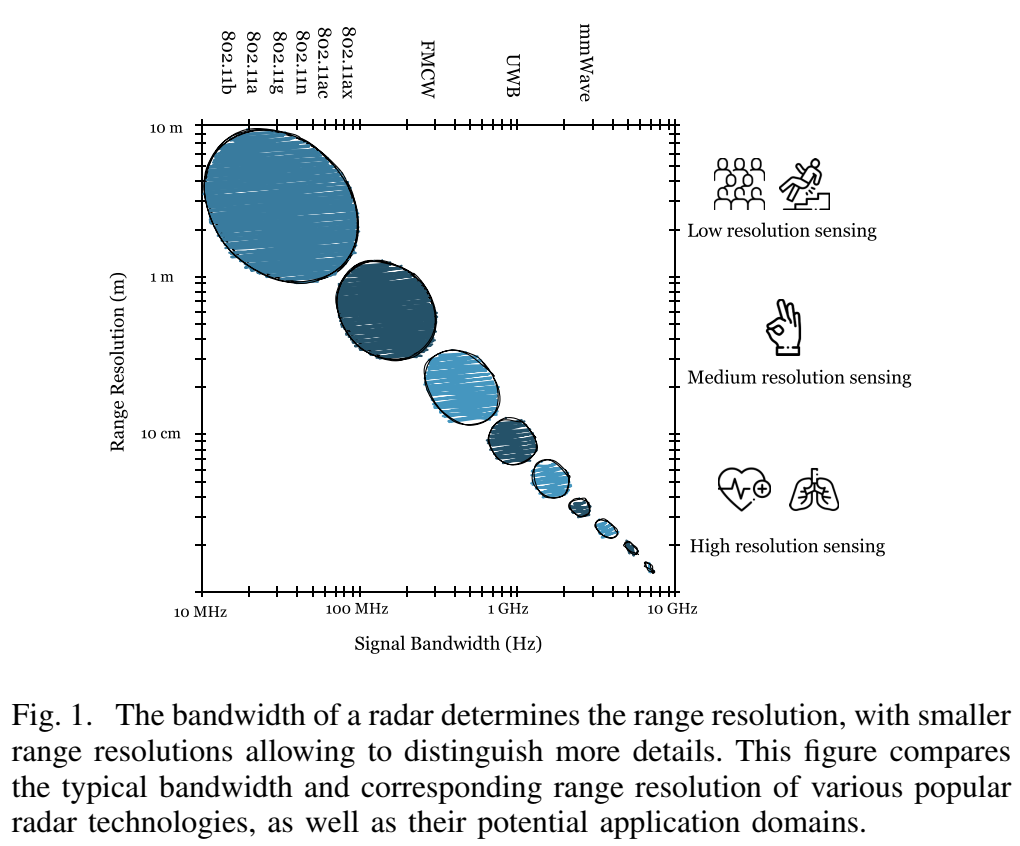
图 1 的横轴是带宽(对数尺度),纵轴是距离分辨率(同样对数尺度),还标了多类雷达/无线技术所在区间。这部分想表达的核心不是"UWB 比 WiFi 强",而是一个更接近系统设计的结论:
-
距离分辨率随带宽提升而改善,典型公式为
Dres=c2BW, D_{\mathrm{res}} = \frac{c}{2BW}, Dres=2BWc,
其中 ccc 为光速。
-
但在采样率固定时,带宽越大反而会压缩"可观测的最大距离窗",作者给出
Rmax=Fs c2BW, R_{\max} = \frac{F_s\,c}{2BW}, Rmax=2BWFsc,
其中 F_sF\_sF_s 是采样率(更准确说是快时间采样率或等效采样能力)。如果想要更"细"的距离像素,就得付出"距离窗变短/最大距离变小"的代价(在硬件采样资源不变时)。
-
文中还提醒:除了加大 BWBWBW,还可以用更长的观测时间(更多帧/更多 CIR 样本)做"分辨率上采样",这在 UWB 雷达中很常用。
这句话背后对应的是"相干/非相干积累"与"超分辨估计"的思想:在噪声可积累平均、目标结构稳定的前提下,慢时间堆叠能提升等效 SNR,从而让更精细的时延估计成为可能。
此外,原文作者也从中心频率与调制角度对比了 WiFi/UWB/mmWave:较低中心频率通常传播更远、更易穿透;UWB 处于 3.1--10.6 GHz 频段,并具有较强抗干扰与较好穿透特性(相较 mmWave)。
5. 从"通信信道"到"雷达回波":CIR 模型
5.1 CIR 的基本模型:离散多径 + 噪声
文章采用经典 UWB 信道冲激响应模型:
h(t)=∑i=1NAi δ(t−τi)+ν(t). h(t) = \sum_{i=1}^{N} A_i\,\delta(t-\tau_i) + \nu(t). h(t)=i=1∑NAiδ(t−τi)+ν(t).
第一项是确定性多径:每条路径用幅度 A_iA\_iA_i 与时延 τ_i\tau\_iτ_i 表征;第二项 ν(t)\nu(t)ν(t) 是弥散多径/随机扰动,近似为加性白高斯噪声(AWGN)。文中也给了噪声自相关形式:
E{ν(t)ν∗(τ)}=S(t)δ(t−τ). \mathbb{E}\{\nu(t)\nu^*(\tau)\}=S(t)\delta(t-\tau). E{ν(t)ν∗(τ)}=S(t)δ(t−τ).
这里 S(t)S(t)S(t) 可理解为噪声强度(或功率谱密度映射到时域的形式),用 δ(⋅)\delta(\cdot)δ(⋅) 表达"不同时间不相关"。
在后面所有"背景扣除、目标检测、定位追踪、呼吸心跳提取"几乎都可以写成"在 h(t)h(t)h(t) 或其离散采样上做分解与估计"。
5.2 频域响应:H(f)H(f)H(f) 是 h(t)h(t)h(t) 的傅里叶变换
给出:
H(f)=∫−∞∞h(t)e−j2πft dt. H(f)=\int_{-\infty}^{\infty} h(t)e^{-j2\pi f t}\,dt. H(f)=∫−∞∞h(t)e−j2πftdt.
把上式代入 h(t)h(t)h(t) 的冲激串结构,立即得到一个很"雷达化"的表达:
H(f)=∑i=1NAie−j2πfτi+N(f), H(f)=\sum_{i=1}^{N} A_i e^{-j2\pi f \tau_i}+N(f), H(f)=i=1∑NAie−j2πfτi+N(f),
其中 N(f)N(f)N(f) 是噪声项的频域表示。多径在频域表现为一堆相位随频率线性旋转的复指数叠加,频率选择性衰落本质上就是这些相量在不同 fff 上相互抵消/叠加导致的幅度波动。UWB 因为带宽极宽,H(f)H(f)H(f) 的"波纹"更复杂,也更需要算法去做鲁棒处理。
6. 图 3 与图 4:单帧 CIR(快时间)与慢时间堆叠(slow-fast 表示)
6.1 图 3:同一系统在"无目标/有目标"两种场景下的 CIR
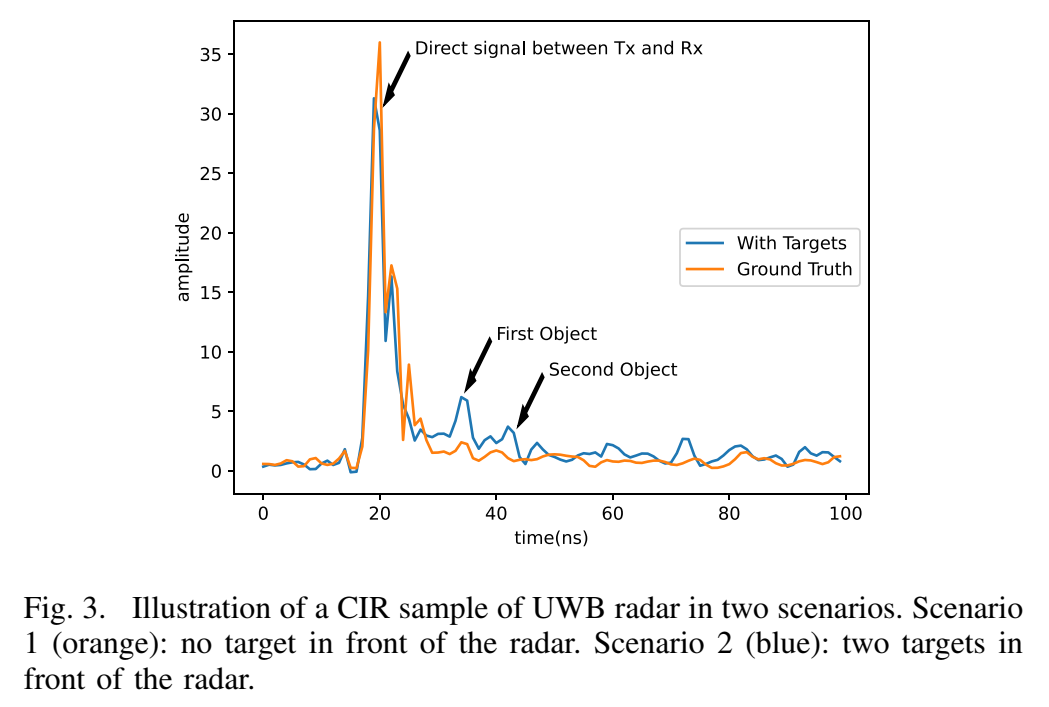
作者解释图 3 时强调了 CIR 的几个关键部件:最早到达且通常最强的是 TX→RX 的直达分量;随后出现的是目标反射;再往后是墙壁、家具等产生的多径杂波,这会干扰目标检测。
用数学语言描述:若把每次发射得到的一条离散 CIR 记为向量 h[k]∈RM\mathbf{h}[k]\in\mathbb{R}^Mh[k]∈RM(kkk 是慢时间帧号,MMM 是快时间采样点数),那么"有目标/无目标"的差别,往往并不是整条向量都变化,而是某个时延区间(对应某个距离区间)出现系统性偏差或微小扰动。图 3 里蓝色曲线相对橙色曲线多出两个明显反射峰,对应"两个人/两个物体"的回波。
把"时延差→距离"写出来,单基地(monostatic)情形下最常用的是:
R=c Δt2. R = \frac{c\,\Delta t}{2}. R=2cΔt.
文中在 IR-UWB 部分也使用了这一类 ToF 关系来做距离估计。
6.2 图 4:slow-fast index 热力图如何"把呼吸从噪声里显出来"
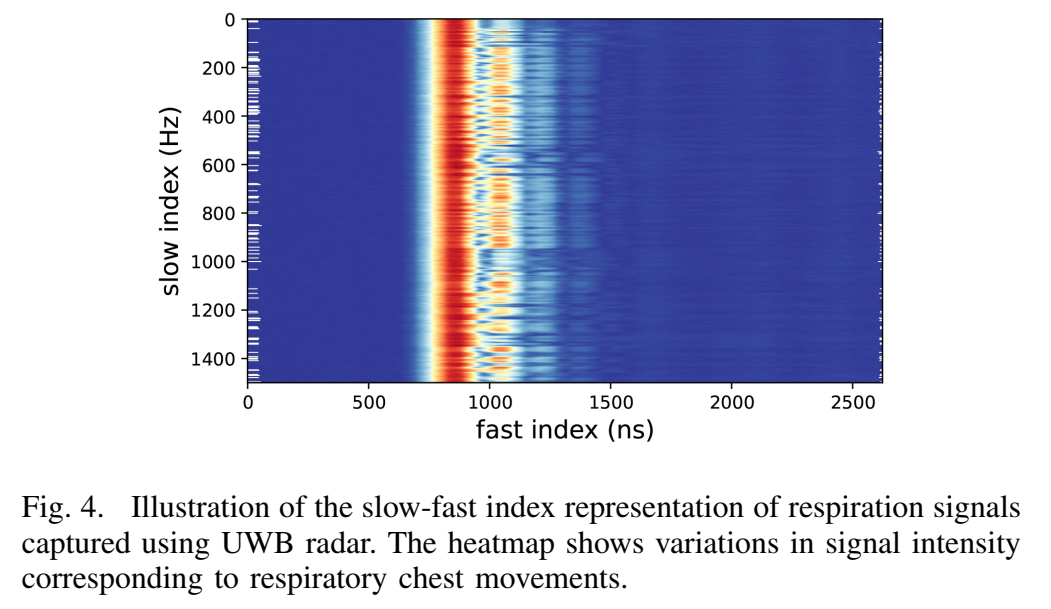
作者给出的解释是:快时间轴(x 轴)表示单次接收 CIR 的时间(ns 或 μs),慢时间轴(y 轴)表示发包/重复发射的时间序列索引或发包频率维度;将每帧 CIR 按时间堆叠成二维矩阵,得到所谓 slow-fast 表示。图 4 的热力图亮带随慢时间呈周期性变化,对应胸廓起伏引起的微小距离变化,从而在某一段时延区间内形成强烈的"周期纹理"。
形式化地,令第 kkk 帧 CIR 为 KaTeX parse error: Undefined control sequence: \[ at position 11: \mathbf{h}\̲[̲k]=\[h\_1\[k],\...,则 slow-fast 矩阵为:
H=[h[1]⊤h[2]⊤⋮h[K]⊤]∈RK×M. \mathbf{H}= \begin{bmatrix} \mathbf{h}[1]^\top\\ \mathbf{h}[2]^\top\\ \vdots\\ \mathbf{h}[K]^\top \end{bmatrix} \in\mathbb{R}^{K\times M}. H= h[1]⊤h[2]⊤⋮h[K]⊤ ∈RK×M.
快时间索引 mmm 与距离门(range bin)一一对应,慢时间索引 kkk 与目标的微运动(呼吸、手势、走动)对应。于是呼吸检测很多时候就变成:在某个 mmm(或一段 ROI)上取慢时间序列 KaTeX parse error: Undefined control sequence: \[ at position 5: h\_m\̲[̲k],再做带通滤波与频谱峰值检测,或做更复杂的解混/去噪。
7. UWB 雷达系统形态:DS-UWB vs IR-UWB 与三种雷达拓扑(图 5)
7.1 DS-UWB 与 IR-UWB:信号模型与复杂度差别
文章将 UWB 雷达分成 DS-UWB 与 IR-UWB,并给出 DS-UWB 的典型发射信号:
s(t)=2ETcos(2πfct+θ)∑n=−∞∞cn p(t−nTc). s(t)=\sqrt{\frac{2E}{T}}\cos(2\pi f_c t+\theta)\sum_{n=-\infty}^{\infty} c_n\,p(t-nT_c). s(t)=T2E cos(2πfct+θ)n=−∞∑∞cnp(t−nTc).
这里 c_nc\_nc_n 是 PN 码片序列,p(t)p(t)p(t) 是码片波形,T_cT\_cT_c 是 chip duration。DS-UWB 的关键是"扩频":把能量摊到更宽频带,提高抗干扰与隐蔽性,但系统需要载波、同步、解扩等复杂模块。
相对地,IR-UWB 更接近"发窄脉冲---测往返时延"的雷达直觉,其实现更简单、功耗更低、对多径更鲁棒,因此在雷达应用更常见。
7.2 图 5:mono-static / bi-static / multi-static 的几何意义
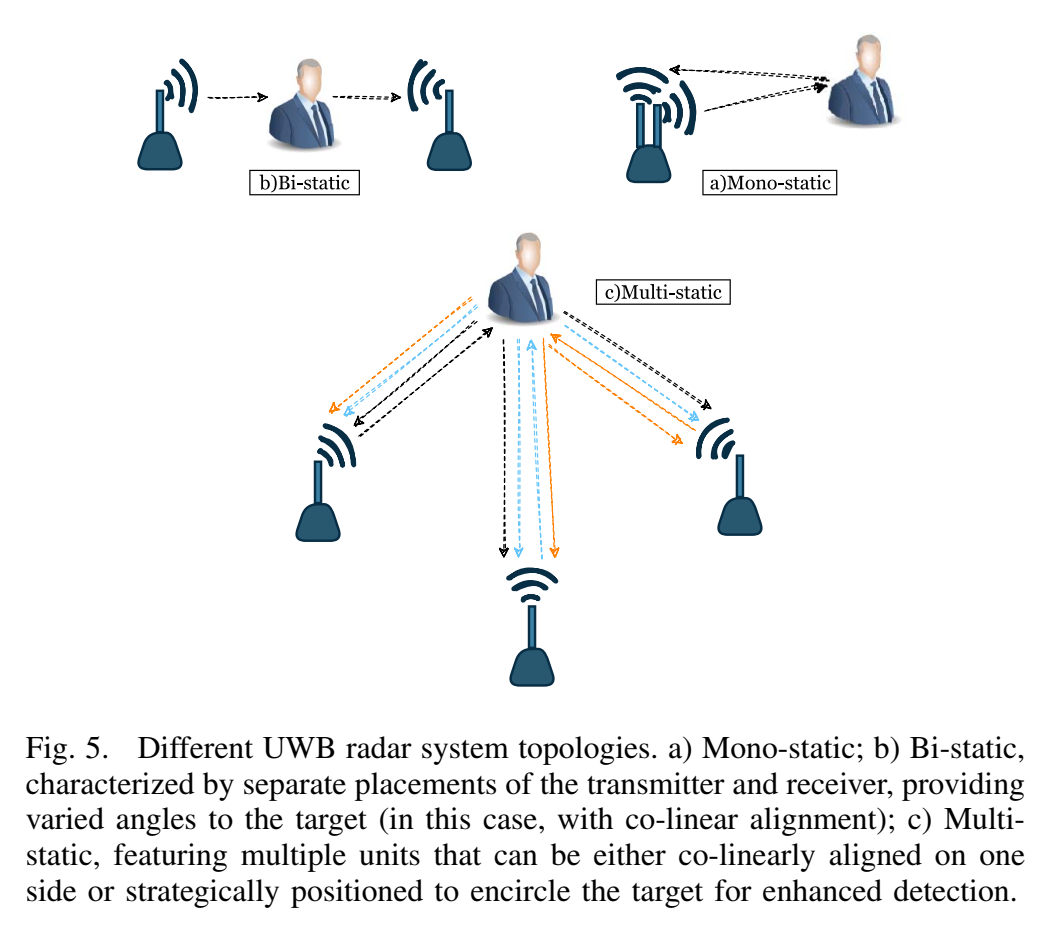
单基地(mono-static)可以抽象成同一设备发射与接收,目标距离 RRR 通过往返时延估计,最直接:
Δt≈2Rc. \Delta t \approx \frac{2R}{c}. Δt≈c2R.
双基地(bi-static)或多基地(multi-static)则更像定位问题:目标到不同 TX/RX 组合的路径长度不同,形成双曲线/多双曲线约束。比如一个 TX 与一个 RX 分离时,若目标位置为 x\mathbf{x}x,TX/RX 位置为 x_T,x_R\mathbf{x}\_T,\mathbf{x}\_Rx_T,x_R,则传播距离是:
d(x)=∥x−xT∥+∥x−xR∥, d(\mathbf{x})=\|\mathbf{x}-\mathbf{x}_T\|+\|\mathbf{x}-\mathbf{x}_R\|, d(x)=∥x−xT∥+∥x−xR∥,
对应到达时延
τ(x)=d(x)c. \tau(\mathbf{x})=\frac{d(\mathbf{x})}{c}. τ(x)=cd(x).
多基地时会得到多条这样的约束,理论上可显著提升定位与分离多目标的能力,但付出的代价是同步、时钟偏差、节点间协同与通信成本。文中在结论"经验教训"里多次强调 multi-static 能增强能力但同步是硬问题。
8. 图 6:频谱与监管约束不是"背景知识",而是算法边界条件
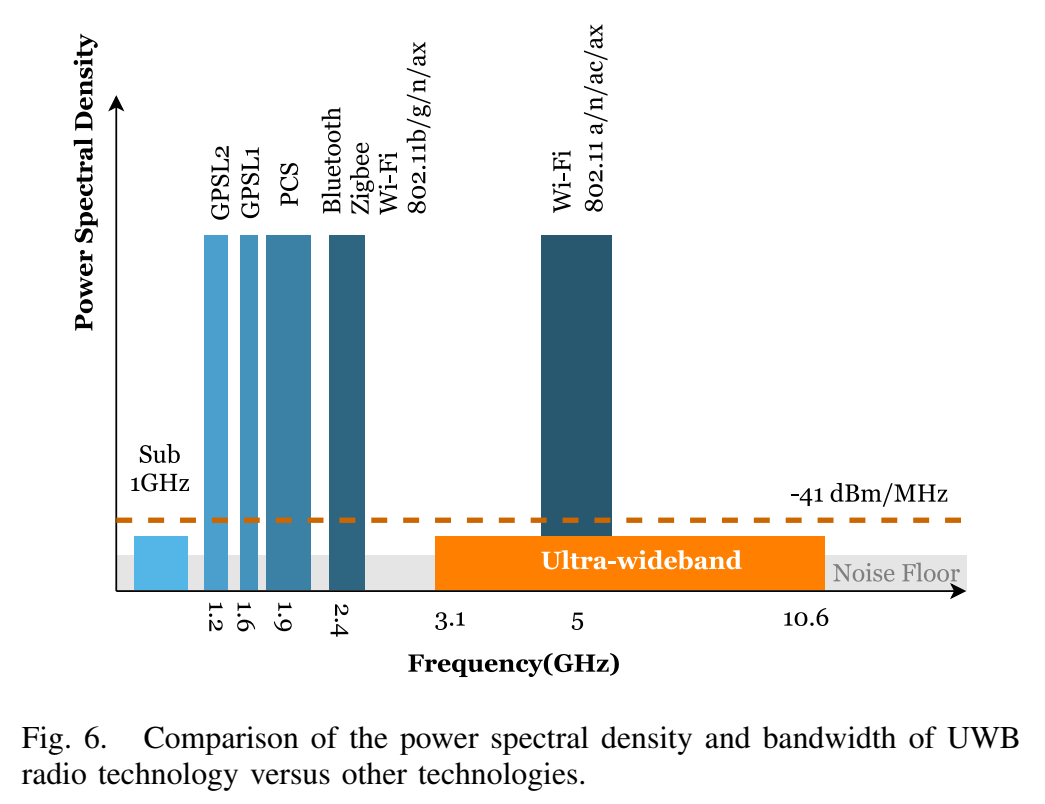
图 6 的直觉是:UWB 能在很宽的频带上工作(典型 3.1--10.6 GHz),但每 MHz 的发射功率受到严格限制(常见说法是"低功率谱密度"),因此不会像窄带系统那样"很大声地喊",而是"很宽地铺开"。
这件事对信号处理意味着什么?至少有三点:
第一,低 PSD 直接导致单次回波 SNR 不高,因此需要依赖匹配滤波、累积、去杂波与统计检测等方法把目标从噪声里抠出来。第二,频谱受限意味着无法随意选择波形与带宽,一些算法假设的"理想白谱"或"任意带宽"在标准里可能根本不允许。第三,频谱共存会成为越来越现实的问题:作者在趋势与未来挑战中明确指出 Wi-Fi 6E 在 6 GHz 频段与部分 UWB 信道重叠,会影响 UWB 性能,需要研究共存与干扰抑制;同时标准与产业界正在倾向使用 UWB channel 9(约 7.99 GHz)以获得更高监管清晰度并避开潜在 Wi-Fi 干扰。
9. 五大应用域的"共同技术链路":从 H\mathbf{H}H 中分离"人"与"环境"
在进入每个应用之前,先把它们共同的数学形式抽出来,会更容易理解为什么很多方法反复出现。令 slow-fast 矩阵为 H∈RK×M\mathbf{H}\in\mathbb{R}^{K\times M}H∈RK×M。一个非常通用的建模方式是:
H=B+S+N. \mathbf{H}=\mathbf{B}+\mathbf{S}+\mathbf{N}. H=B+S+N.
- B\mathbf{B}B 是背景(静态环境、固定反射、多径结构、天线耦合残留等),通常在慢时间上变化缓慢或近似不变;
- S\mathbf{S}S 是我们关心的"信号"(人的运动、呼吸、手势、位移导致的时延/幅度微扰);
- N\mathbf{N}N 是测量噪声与随机扰动。
几乎所有"背景扣除 / 杂波抑制 / ROI / 去噪 / 分离"都在想办法把 S\mathbf{S}S 从 B\mathbf{B}B 与 N\mathbf{N}N 中分离出来。
文中明确指出:背景扣除(background subtraction)是许多应用中的常见操作,其思路是用一段"无目标"的 CIR 估计时间不变背景,并从实时 CIR 中减掉;也有人用自适应方式更新背景,或用参数模型/机器学习/PCA 等方法做更鲁棒的背景建模。
10. Presence Detection:在低采样、低带宽约束下做"可靠存在性判决"
文末总结"经验教训"时,作者对 presence detection 的判断很尖锐:为了低功耗与可普及部署,presence detection 往往希望低采样率、低带宽;但这会导致数据分辨率不足,从而需要更聪明的检测算法(包括 ML 与异常检测)来区分人、物体与各种微动,同时 multi-static 虽能增强能力但同步难题必须解决。
如果把 presence detection 抽象成统计检测,它常见的基本形式是:
{H0:h[k]=b+n[k],无人/无目标变化H1:h[k]=b+s[k]+n[k],有人/有目标变化 \begin{cases} \mathcal{H}_0: \mathbf{h}[k]=\mathbf{b}+\mathbf{n}[k], & \text{无人/无目标变化}\\ \mathcal{H}_1: \mathbf{h}[k]=\mathbf{b}+\mathbf{s}[k]+\mathbf{n}[k], & \text{有人/有目标变化} \end{cases} {H0:h[k]=b+n[k],H1:h[k]=b+s[k]+n[k],无人/无目标变化有人/有目标变化
其中 b\mathbf{b}b 是背景 CIR。背景扣除后得到残差:
r[k]=h[k]−b^. \mathbf{r}[k]=\mathbf{h}[k]-\hat{\mathbf{b}}. r[k]=h[k]−b^.
接下来必须要设计一个检验统计量 KaTeX parse error: Undefined control sequence: \[ at position 13: T(\mathbf{r}\̲[̲k]),例如能量、方差、熵、变化率等,并设阈值 γ\gammaγ:
T(r[k])≷H0H1γ. T(\mathbf{r}[k]) \mathop{\gtrless}_{\mathcal{H}_0}^{\mathcal{H}_1} \gamma. T(r[k])≷H0H1γ.
presence detection 的难点恰恰在于:人的存在未必导致"大能量峰",尤其在静止、呼吸微动、遮挡或强多径环境下,s[k]\mathbf{s}[k]s[k] 可能是结构化且很弱的扰动;此时仅靠能量阈值容易误报/漏报,于是异常检测、时序建模与学习方法(尤其能跨环境自适应的)就变得关键。
11. Device-Free Localization:从"检测到有人"走向"人在何处、如何移动"
作者在结论中强调,device-free localization 往往依赖 multi-static、低采样与低带宽配置,通过杂波扣除、目标检测、定位与追踪等链路实现定位;同时指出 AoA 在 UWB 雷达中的研究相对不足,限制了更高精度定位,且复杂环境下多目标追踪仍是难题。用一个"由易到难"的数学视角来看:
先在每条链路上做目标检测,得到一组候选回波时延(或距离门)τ^ℓ{\hat{\tau}\{\ell}}τ^_ℓ;再把这些观测映射到几何约束;最后在时间序列上追踪。
如果是单基地,观测往往就是一维距离估计:
R^k=c τ^k2. \hat{R}_k=\frac{c\,\hat{\tau}_k}{2}. R^k=2cτ^k.
若有多基地,多条链路给出多条约束:
τ^p,k≈∥xk−xT,p∥+∥xk−xR,p∥c,p=1,...,P. \hat{\tau}_{p,k}\approx \frac{\|\mathbf{x}k-\mathbf{x}{T,p}\|+\|\mathbf{x}k-\mathbf{x}{R,p}\|}{c}, \qquad p=1,\ldots,P. τ^p,k≈c∥xk−xT,p∥+∥xk−xR,p∥,p=1,...,P.
于是定位可写成最小二乘(或加权最小二乘):
x^k=argminx∑p=1Pwp(τ^p,k−τp(x))2. \hat{\mathbf{x}}k =\arg\min{\mathbf{x}} \sum_{p=1}^{P} w_p\left(\hat{\tau}{p,k}-\tau{p}(\mathbf{x})\right)^2. x^k=argxminp=1∑Pwp(τ^p,k−τp(x))2.
而追踪则引入状态空间模型,例如常速度模型:
xk=[xkykx˙ky˙k],xk=Fxk−1+qk−1,zk=h(xk)+vk. \mathbf{x}k= \begin{bmatrix} x_k\\y_k\\\dot{x}k\\\dot{y}k \end{bmatrix}, \qquad \mathbf{x}{k}=\mathbf{F}\mathbf{x}{k-1}+\mathbf{q}{k-1}, \qquad \mathbf{z}_k=\mathbf{h}(\mathbf{x}_k)+\mathbf{v}_k. xk= xkykx˙ky˙k ,xk=Fxk−1+qk−1,zk=h(xk)+vk.
其中 z_k\mathbf{z}\_kz_k 可以是距离观测或到达时延观测。随后自然用到 KF/EKF/UKF/粒子滤波。
12. Activity / Gesture Recognition:ROI、去噪与"时频特征 + 分类器"
在 activity/gesture 章节,作者把技术归为三块:预处理(ROI、背景/噪声去除)、特征提取(统计特征、PCA、STFT、VMD 等)、分类算法(从传统模式识别到神经网络)。
这里最值得精读的是"ROI"这个概念:UWB 的 CIR 很长,但与手势/动作真正相关的信息常集中在某段快时间区间(某个距离门附近),因此很多工作会先选定 ROI 以降低计算量并提高实时性。
设 ROI 对应快时间索引集合 M\mathcal{M}M,则 ROI 截取相当于:
hROI[k]={hm[k]}m∈M. \mathbf{h}{\mathrm{ROI}}[k] = \{h_m[k]\}{m\in\mathcal{M}}. hROI[k]={hm[k]}m∈M.
进一步,如果做 slow-fast 表示,就得到子矩阵 H_ROI∈RK×∣M∣\mathbf{H}\_{\mathrm{ROI}}\in\mathbb{R}^{K\times |\mathcal{M}|}H_ROI∈RK×∣M∣。后续无论做 PCA 降维还是 STFT 提时频图,计算量都会大幅降低。
而特征提取方面,STFT 是动作/手势类任务的"常用武器",因为动作具有时间变化结构。若对某个距离门的慢时间序列 KaTeX parse error: Undefined control sequence: \[ at position 2: x\̲[̲k] 做 STFT:
X(n,ω)=∑k=−∞∞x[k] w[k−n] e−jωk, X(n,\omega)=\sum_{k=-\infty}^{\infty} x[k]\,w[k-n]\,e^{-j\omega k}, X(n,ω)=k=−∞∑∞x[k]w[k−n]e−jωk,
其谱图(spectrogram)为:
S(n,ω)=∣X(n,ω)∣2. S(n,\omega)=|X(n,\omega)|^2. S(n,ω)=∣X(n,ω)∣2.
把 S(n,ω)S(n,\omega)S(n,ω) 当作二维"图像",就自然能用 CNN 处理;把它当作序列,就能用 LSTM/Transformer 处理。这就是为什么很多雷达动作识别论文会向"视觉网络结构"借鉴。
结论部分对 activity recognition 的经验总结也点出:这类系统往往需要更高采样率与带宽,并依赖杂波/噪声去除、ROI 与高级特征提取;而在复杂场景中区分相似动作、应对密集多人环境仍很难,持续学习/增量学习等方向值得探索。
13. Vital Sign Monitoring:把"毫米级胸廓微动"变成可测的频率峰(式 13)
13.1 关键建模:距离随时间的双正弦微扰
文章用一个凝练的模型表达呼吸与心跳共同导致的距离变化:
d(t)=d0+m(t)=d0+mbsin(2πfbt)+mhsin(2πfht). d(t)=d_0+m(t)=d_0+m_b\sin(2\pi f_b t)+m_h\sin(2\pi f_h t). d(t)=d0+m(t)=d0+mbsin(2πfbt)+mhsin(2πfht).
其中 d_0d\_0d_0 是名义距离,m_b,m_hm\_b,m\_hm_b,m_h 分别是呼吸/心跳位移幅度,f_b,f_hf\_b,f\_hf_b,f_h 是对应频率。
这条式子看起来简单,但它其实把 vital sign 监测的关键难点全写进去了:m_hm\_hm_h 往往比 m_bm\_bm_b 小得多,且人体姿态、衣物、遮挡、墙体穿透都会导致回波结构变化;同时环境多径会把"纯正弦位移"映射成幅度与相位都变化的复杂观测。
13.2 从 d(t)d(t)d(t) 到"可检测的雷达观测":相位/时延调制视角
如果把目标回波在某个距离门附近近似为一个复数观测(或某个相关输出)y(t)y(t)y(t),其相位会随传播距离变化。最粗略的单频 CW 模型是:
y(t)≈A e−j4πλd(t)+n(t), y(t)\approx A\,e^{-j\frac{4\pi}{\lambda}d(t)} + n(t), y(t)≈Ae−jλ4πd(t)+n(t),
但 UWB 是宽带脉冲,真实情况更复杂:我们往往不是直接拿"单一相位",而是在 CIR 里选定某段 ROI 后,跟踪峰值位置的微小漂移或跟踪复相关输出的相位变化。无论哪一种,其本质都是把 d(t)d(t)d(t) 的微小变化映射为可观测的时间序列,再通过滤波、分离与频谱估计得到 f_b,f_hf\_b,f\_hf_b,f_h。
文末"经验教训"也指出:vital sign 监测通常采用"正前方 mono-static + 高采样率/高带宽",并结合滤波、信号分离与 ML;常用设备之一是 Novelda XeThru 系列;主要挑战包括实时性、多人体同时监测、人体朝向/位置变化,以及隐私与健康数据安全问题;同步 multi-static 可能进一步提升适用性。
14. ISAC:当 UWB 同时承担"通信 + 感知",最难的不是想法而是系统闭环
文章认为 UWB 的 ISAC 研究还很新,挑战尚未被充分覆盖;要做出有效 ISAC 系统,需要物理层、芯片、天线与算法协同设计,且目前缺乏实验研究与统一 benchmark;同时自干扰消除、宽带隔离、射频路由等硬件问题是关键难点之一。可以用一个数学"底线"来理解 ISAC 的 trade-off:当把同一波形用于通信和雷达,设计目标就变成一个多目标优化,例如同时最大化通信速率并最小化感知参数(时延、角度、多普勒)的估计误差。典型地,估计误差的理论下界可用 Fisher 信息矩阵与 Cramér--Rao Bound(CRB)刻画。
附录会给一个"已知发射波形 + AWGN"的时延估计 CRB 推导,说明为什么更宽带宽会带来更小的时延方差下界,从而解释"带宽就是感知分辨率"。
15. 数据集、芯片与趋势:为什么作者反复强调"缺数据、缺标准、要共存"
原文作者在未来挑战中明确提出:开放 UWB 雷达数据集很稀缺,研究社区需要更丰富、贴近真实场景(车内、住宅、工业)的数据集,也需要竞赛来推动公平对比与快速迭代。
并且温度、振动、湿度、衣物、墙体材质、人体姿态与朝向等都会影响 UWB 雷达性能,而目前大多数论文还停留在控制变量较少的实验室环境,需要发展外部噪声抑制、姿态估计、非相关频段抑制等方法来提高鲁棒性。
在频谱趋势上,作者指出 2007 年 IEEE 802.15.4a 之后分配了标准化信道(带宽约 500 MHz、1.1 GHz、1.35 GHz 等),但商用非标准方案也出现过极宽带(例如带宽可到 8.7 GHz 的模块)以获得高精度测距;整体趋势是往更高频(尤其 channel 9,约 7.99 GHz)迁移以获得更强监管清晰度并规避 Wi-Fi 6E 重叠干扰。
此外,当大量 UWB 雷达同时部署时,同频并发会导致 CIR 质量下降,作者提到近期标准中的 scrambled time sequences(STS)可显著提升抗干扰鲁棒性,但仍需要更深入研究干扰影响与动态自适应的 PHY/信道/功率选择策略。
16. 结论"Lessons Learned"的再解读:五个应用域对应五种系统设计哲学
原文最后把五大应用域的经验浓缩成 Table XII 的"教训总结":
presence detection 的哲学是"低成本、低功耗、可规模化",因此低采样/低带宽是主旋律,但算法必须更聪明以弥补信息不足,同时 multi-static 能增强能力但同步难题要面对。
device-free localization 的哲学是"多视角几何约束",因此 multi-static 很关键;链路上杂波扣除、检测、定位、追踪缺一不可;AoA 等角度信息在 UWB 雷达中仍缺研究,限制了精定位与多目标能力。
activity recognition 的哲学是"信息尽量多再交给模型",因此高采样/高带宽与较重预处理是常态;复杂场景的相似动作区分与多人密集仍是痛点,持续学习/增量学习等值得推进。
vital sign monitoring 的哲学是"抓住微弱而结构化的周期",因此多用正前方 mono-static + 高采样/高带宽,并用滤波、分离与 ML 把呼吸/心跳从复杂回波里剥离;多人体与隐私是系统级挑战。
ISAC 的哲学是"同一硬件频谱做两件事",因此 trade-off 与系统协同设计是本质;当前缺实验与 benchmark,未来要补齐天线/射频/算法共同优化,尤其自干扰消除与宽带隔离等硬件难点。
附录:部分关键数学推导补齐
A1. 从带宽到脉冲宽度:解释 BW⋅T≥4πBW\cdot T\ge \frac{4}{\pi}BW⋅T≥π4 的一个推导路径
原文在引言给出 BW×T≥4/πBW\times T \ge 4/\piBW×T≥4/π 并用来解释"UWB 脉冲很窄"。
要看到 4π\frac{4}{\pi}π4 这种常数,一个常见做法是选取"等效脉冲宽度"与"等效带宽"的定义方式(工程里并不唯一)。这里给一个典型推导:假设信号频谱在 KaTeX parse error: Undefined control sequence: \[ at position 1: \̲[̲-BW/2,BW/2] 内近似平坦,其他频率为 0,即
X(f)={1,∣f∣≤BW20,else X(f)= \begin{cases} 1, & |f|\le \frac{BW}{2}\\ 0, & \text{else} \end{cases} X(f)={1,0,∣f∣≤2BWelse
则其时域为 sinc:
x(t)=∫−BW/2BW/2ej2πft df=BW sinc(BWt), x(t)=\int_{-BW/2}^{BW/2} e^{j2\pi f t}\,df = BW\,\mathrm{sinc}(BW t), x(t)=∫−BW/2BW/2ej2πftdf=BWsinc(BWt),
其中 sinc(u)=sin(πu)πu\mathrm{sinc}(u)=\frac{\sin(\pi u)}{\pi u}sinc(u)=πusin(πu)。
sinc 的主瓣零点在 t=±1/BWt=\pm 1/BWt=±1/BW,因此"零到零主瓣宽度"可定义为
Tzz=2BW. T_{\mathrm{zz}}=\frac{2}{BW}. Tzz=BW2.
如果用"半功率宽度"或"等效宽度"来定义 TTT,会得到不同常数。另一条能出现 4π\frac{4}{\pi}π4 的路线是用"有效脉冲宽度"定义为主瓣面积与峰值之比,或用 autocorrelation 的主瓣宽度。以自相关为例,sinc 信号的自相关与三角函数相关,最终会给出一个与 π\piπ 有关的常数界。更一般地,从时间-频率不确定性原理可得
σtσf≥14π, \sigma_t \sigma_f \ge \frac{1}{4\pi}, σtσf≥4π1,
若把有效带宽取为 BW≈2σ_fBW\approx 2\sigma\_fBW≈2σ_f,有效时宽取为 T≈2σ_tT\approx 2\sigma\_tT≈2σ_t,则
BW⋅T≳1π. BW\cdot T \gtrsim \frac{1}{\pi}. BW⋅T≳π1.
不同"等效"定义会把常数从 1/π1/\pi1/π 推到 4/π4/\pi4/π 这类形式;原文采用的常数可以理解为一种偏保守(更严格)的工程界,强调"要做到很窄脉冲,就必须真的很宽带"。
结论不变:BWBWBW 每增大一倍,时间分辨率(脉冲宽度尺度)就可压缩约一倍,这就是 UWB 适合 ToF/雷达的根本。
A2. 距离分辨率公式 D_res=c2BWD\_{\mathrm{res}}=\frac{c}{2BW}D_res=2BWc 的推导(匹配滤波视角)
原文直接给出:
Dres=c2BW. D_{\mathrm{res}}=\frac{c}{2BW}. Dres=2BWc.
推导从匹配滤波/相关输出的主瓣宽度出发最自然。设发射基带脉冲 s(t)s(t)s(t) 的自相关函数为
Rss(τ)=∫s(t)s∗(t−τ) dt. R_{ss}(\tau)=\int s(t)s^*(t-\tau)\,dt. Rss(τ)=∫s(t)s∗(t−τ)dt.
匹配滤波输出本质上就是 R_ss(τ)R\{ss}(\tau)R_ss(τ)(在噪声下的估计)。自相关主瓣宽度决定了区分两条相邻回波(时延差 Δτ\Delta\tauΔτ)的能力。对"带宽近似为 BWBWBW"的信号,R_ss(τ)R\{ss}(\tau)R_ss(τ) 的主瓣宽度尺度约为
Δτres≈1BW. \Delta\tau_{\mathrm{res}} \approx \frac{1}{BW}. Δτres≈BW1.
单基地雷达中,距离与往返时延关系为 Δτ=2ΔR/c\Delta\tau = 2\Delta R / cΔτ=2ΔR/c,因此两目标可分辨条件近似为
2ΔRc≳1BW⇒ΔR≳c2BW. \frac{2\Delta R}{c}\gtrsim \frac{1}{BW} \quad\Rightarrow\quad \Delta R \gtrsim \frac{c}{2BW}. c2ΔR≳BW1⇒ΔR≳2BWc.
这就是 D_resD\_{\mathrm{res}}D_res 的来源。它不是"定理",而是匹配滤波主瓣宽度量级推导,适用于常见宽带脉冲或扩频信号。
A3. "带宽越大最大距离越小":R_max=F_sc2BWR\_{\max}=\frac{F\_s c}{2BW}R_max=2BWF_sc 的推导(采样窗口视角)
原文给出:
Rmax=Fsc2BW. R_{\max}=\frac{F_s c}{2BW}. Rmax=2BWFsc.
理解它的关键是:快时间轴需要覆盖一定的"时间窗"来观察回波,时间窗越长就越能看更远的距离。但在硬件层面,"快时间采样点数"往往受限(ADC 速度、等效采样结构、CIR 输出长度等)。若我们假设每帧最多能拿到 NNN 个快时间采样点,那么快时间窗长为
Twin=NFs. T_{\mathrm{win}}=\frac{N}{F_s}. Twin=FsN.
而最大可观测往返时延近似是 T_winT\_{\mathrm{win}}T_win,对应最大距离
Rmax≈c Twin2=c2⋅NFs. R_{\max}\approx \frac{c\,T_{\mathrm{win}}}{2} =\frac{c}{2}\cdot\frac{N}{F_s}. Rmax≈2cTwin=2c⋅FsN.
那为什么原文是 F_s/BWF\_s/BWF_s/BW 形式?因为在很多 UWB 雷达实现里,NNN 与 BWBWBW 存在"等效采样密度"耦合:为了不失真地刻画宽带脉冲,等效采样点数往往要随 BWBWBW 增大而增大,或者在固定采样资源下,增大 BWBWBW 会压缩等效可观测时延长度。用一种简化工程等价写法,就是把 NNN 看成与 F_s/BWF\_s/BWF_s/BW 成比例,从而把上式化到原文形式。可以把它当作"固定采样资源预算下的带宽---距离窗 trade-off"的经验公式。
A4. 背景扣除的数学形式:滑动平均与指数遗忘
原文提到背景扣除、以及用自适应方法更新背景模型。
最常见的两种背景估计是:
(1)固定窗口平均(适合静态环境标定):
b^=1K0∑k=1K0h[k]. \hat{\mathbf{b}}=\frac{1}{K_0}\sum_{k=1}^{K_0}\mathbf{h}[k]. b^=K01k=1∑K0h[k].
(2)指数滑动平均(适合缓慢变化环境):
b^[k]=αb^[k−1]+(1−α)h[k],0<α<1. \hat{\mathbf{b}}[k]=\alpha \hat{\mathbf{b}}[k-1]+(1-\alpha)\mathbf{h}[k], \qquad 0<\alpha<1. b^[k]=αb^[k−1]+(1−α)h[k],0<α<1.
对应残差:
r[k]=h[k]−b^[k]. \mathbf{r}[k]=\mathbf{h}[k]-\hat{\mathbf{b}}[k]. r[k]=h[k]−b^[k].
指数平均相当于对历史赋予指数衰减权重:
b^[k]=(1−α)∑i=0∞αih[k−i]. \hat{\mathbf{b}}[k]=(1-\alpha)\sum_{i=0}^{\infty}\alpha^i \mathbf{h}[k-i]. b^[k]=(1−α)i=0∑∞αih[k−i].
这给了一个可解释的"时间常数":
Tmem≈11−α. T_{\mathrm{mem}}\approx \frac{1}{1-\alpha}. Tmem≈1−α1.
如果人慢慢进入场景,α\alphaα 过小会把"人"也吸收进背景导致漏检;α\alphaα 过大又会对环境变化太敏感导致误检。presence detection 与 DFL 的很多工程调参,本质上就在调这个时间常数。
A5. CA-CFAR 阈值推导(指数杂波模型)
很多雷达检测会用 CFAR(恒虚警率)思路。虽然原文在我们摘取片段中没有展开推导,但它是理解"阈值如何随虚警率变化"的关键工具。
设在纯噪声/杂波假设下,每个距离门的能量 ZZZ 近似服从指数分布:
Z∼Exp(λ),fZ(z)=λe−λz, z≥0. Z\sim \mathrm{Exp}(\lambda), \qquad f_Z(z)=\lambda e^{-\lambda z},\ z\ge 0. Z∼Exp(λ),fZ(z)=λe−λz, z≥0.
假设用 NNN 个参考单元估计背景功率:
μ^=1N∑i=1NZi. \hat{\mu}=\frac{1}{N}\sum_{i=1}^{N} Z_i. μ^=N1i=1∑NZi.
CA-CFAR 用阈值 γ=αμ^\gamma = \alpha \hat{\mu}γ=αμ^,其中 α\alphaα 选取使虚警率 P_FAP\_{\mathrm{FA}}P_FA 恒定。推导思路是先条件化:给定 μ^\hat{\mu}μ^,虚警事件为 Z_0>αμ^Z\_0>\alpha \hat{\mu}Z_0>αμ^。
在指数模型下(更严格地在 Gamma 分布推导下),最终可得到经典结果:
PFA=(1+α)−N⇒α=PFA−1/N−1. P_{\mathrm{FA}}=\left(1+\alpha\right)^{-N} \quad\Rightarrow\quad \alpha = P_{\mathrm{FA}}^{-1/N}-1. PFA=(1+α)−N⇒α=PFA−1/N−1.
这条式子非常有用:当我们希望更低虚警率时,α\alphaα 会非线性增大;当参考单元数 NNN 增加时,阈值因子对 P_FAP\_{\mathrm{FA}}P_FA 的敏感性降低。
A6. EKF / UKF 的完整更新公式(用于 UWB 多基地追踪)
当观测模型 z_k=h(x_k)+v_k\mathbf{z}\_k=\mathbf{h}(\mathbf{x}\_k)+\mathbf{v}\_kz_k=h(x_k)+v_k 非线性时,EKF/UKF 常用。
A6.1 EKF
预测:
x^k∣k−1=Fx^k−1∣k−1,Pk∣k−1=FPk−1∣k−1F⊤+Q. \hat{\mathbf{x}}{k|k-1}=\mathbf{F}\hat{\mathbf{x}}{k-1|k-1}, \qquad \mathbf{P}{k|k-1}=\mathbf{F}\mathbf{P}{k-1|k-1}\mathbf{F}^\top+\mathbf{Q}. x^k∣k−1=Fx^k−1∣k−1,Pk∣k−1=FPk−1∣k−1F⊤+Q.
线性化:
Hk=∂h∂x∣x^k∣k−1. \mathbf{H}k = \left.\frac{\partial \mathbf{h}}{\partial \mathbf{x}}\right|{\hat{\mathbf{x}}_{k|k-1}}. Hk=∂x∂h x^k∣k−1.
更新:
Kk=Pk∣k−1Hk⊤(HkPk∣k−1Hk⊤+R)−1, \mathbf{K}k=\mathbf{P}{k|k-1}\mathbf{H}_k^\top(\mathbf{H}k\mathbf{P}{k|k-1}\mathbf{H}_k^\top+\mathbf{R})^{-1}, Kk=Pk∣k−1Hk⊤(HkPk∣k−1Hk⊤+R)−1,
x^k∣k=x^k∣k−1+Kk(zk−h(x^k∣k−1)), \hat{\mathbf{x}}{k|k}=\hat{\mathbf{x}}{k|k-1}+\mathbf{K}_k(\mathbf{z}k-\mathbf{h}(\hat{\mathbf{x}}{k|k-1})), x^k∣k=x^k∣k−1+Kk(zk−h(x^k∣k−1)),
Pk∣k=(I−KkHk)Pk∣k−1. \mathbf{P}_{k|k}=(\mathbf{I}-\mathbf{K}_k\mathbf{H}k)\mathbf{P}{k|k-1}. Pk∣k=(I−KkHk)Pk∣k−1.
A6.2 UKF(Sigma 点)
设状态维度为 LLL,选参数 α,β,κ\alpha,\beta,\kappaα,β,κ,定义
λ=α2(L+κ)−L. \lambda=\alpha^2(L+\kappa)-L. λ=α2(L+κ)−L.
构造 Sigma 点:
χ0=x^, \chi_{0}=\hat{\mathbf{x}}, χ0=x^,
χi=x^+[(L+λ)P]i,i=1,...,L, \chi_{i}=\hat{\mathbf{x}}+\left[\sqrt{(L+\lambda)\mathbf{P}}\right]_i,\quad i=1,\ldots,L, χi=x^+[(L+λ)P ]i,i=1,...,L,
χi+L=x^−[(L+λ)P]i,i=1,...,L. \chi_{i+L}=\hat{\mathbf{x}}-\left[\sqrt{(L+\lambda)\mathbf{P}}\right]_i,\quad i=1,\ldots,L. χi+L=x^−[(L+λ)P ]i,i=1,...,L.
权重:
W0(m)=λL+λ,W0(c)=λL+λ+(1−α2+β), W_0^{(m)}=\frac{\lambda}{L+\lambda},\quad W_0^{(c)}=\frac{\lambda}{L+\lambda}+(1-\alpha^2+\beta), W0(m)=L+λλ,W0(c)=L+λλ+(1−α2+β),
Wi(m)=Wi(c)=12(L+λ). W_i^{(m)}=W_i^{(c)}=\frac{1}{2(L+\lambda)}. Wi(m)=Wi(c)=2(L+λ)1.
预测时把 Sigma 点过状态转移,更新时把 Sigma 点过观测函数 h(⋅)\mathbf{h}(\cdot)h(⋅),再计算均值、协方差、互协方差并得到 Kalman 增益。UKF 的价值在于:不用求雅可比,非线性较强时往往比 EKF 更稳。
A7. 粒子滤波 PF(多目标与非高斯环境常用)
粒子滤波用样本近似后验:
p(xk∣z1:k)≈∑i=1Npwk(i)δ(xk−xk(i)). p(\mathbf{x}k|\mathbf{z}{1:k})\approx \sum_{i=1}^{N_p} w_k^{(i)}\delta(\mathbf{x}_k-\mathbf{x}_k^{(i)}). p(xk∣z1:k)≈i=1∑Npwk(i)δ(xk−xk(i)).
预测用状态模型采样:
xk(i)∼p(xk∣xk−1(i)). \mathbf{x}_k^{(i)}\sim p(\mathbf{x}k|\mathbf{x}{k-1}^{(i)}). xk(i)∼p(xk∣xk−1(i)).
权重更新(重要性采样):
w~k(i)=wk−1(i) p(zk∣xk(i)),wk(i)=w~k(i)∑jw~k(j). \tilde{w}k^{(i)} = w{k-1}^{(i)}\,p(\mathbf{z}_k|\mathbf{x}_k^{(i)}), \qquad w_k^{(i)}=\frac{\tilde{w}k^{(i)}}{\sum{j}\tilde{w}_k^{(j)}}. w~k(i)=wk−1(i)p(zk∣xk(i)),wk(i)=∑jw~k(j)w~k(i).
为避免退化,定义有效样本数:
Neff=1∑i(wk(i))2. N_{\mathrm{eff}}=\frac{1}{\sum_{i}(w_k^{(i)})^2}. Neff=∑i(wk(i))21.
当 N_effN\_{\mathrm{eff}}N_eff 过小就重采样。多基地、多目标、遮挡导致的非线性/多峰后验场景下,PF 往往是更"保险"的选择,但计算开销也更大。
A8. 时延估计的 Fisher 信息与 CRB:解释"带宽越大,下界越小"
ISAC 与定位/测距都关心 ToA/ToF 的估计精度。考虑最简模型:接收信号为已知波形的时移版本 + AWGN:
r(t)=αs(t−τ)+n(t),n(t)∼N(0,N02). r(t)=\alpha s(t-\tau)+n(t), \qquad n(t)\sim \mathcal{N}(0,\frac{N_0}{2}). r(t)=αs(t−τ)+n(t),n(t)∼N(0,2N0).
对参数 τ\tauτ 的 Fisher 信息(忽略 α\alphaα 或假定已知)为:
I(τ)=2N0∫∣∂∂ταs(t−τ)∣2dt=2α2N0∫∣s′(t−τ)∣2dt=2α2N0∫∣s′(t)∣2dt. \mathcal{I}(\tau)=\frac{2}{N_0}\int \left|\frac{\partial}{\partial\tau}\alpha s(t-\tau)\right|^2dt = \frac{2\alpha^2}{N_0}\int |s'(t-\tau)|^2dt = \frac{2\alpha^2}{N_0}\int |s'(t)|^2dt. I(τ)=N02∫ ∂τ∂αs(t−τ) 2dt=N02α2∫∣s′(t−τ)∣2dt=N02α2∫∣s′(t)∣2dt.
因此 CRB 为
Var(τ^)≥1I(τ)=N02α2∫∣s′(t)∣2dt. \mathrm{Var}(\hat{\tau})\ge \frac{1}{\mathcal{I}(\tau)} = \frac{N_0}{2\alpha^2\int |s'(t)|^2dt}. Var(τ^)≥I(τ)1=2α2∫∣s′(t)∣2dtN0.
把它转到频域更能看到带宽的作用。由 Parseval 定理:
∫∣s′(t)∣2dt=∫(2πf)2∣S(f)∣2df. \int |s'(t)|^2dt= \int (2\pi f)^2 |S(f)|^2 df. ∫∣s′(t)∣2dt=∫(2πf)2∣S(f)∣2df.
于是
Var(τ^)≥N04α2π2∫f2∣S(f)∣2df. \mathrm{Var}(\hat{\tau}) \ge \frac{N_0}{4\alpha^2\pi^2\int f^2|S(f)|^2df}. Var(τ^)≥4α2π2∫f2∣S(f)∣2dfN0.
如果 ∣S(f)∣2|S(f)|^2∣S(f)∣2 在 [−BW/2,BW/2][-BW/2,BW/2][−BW/2,BW/2] 内"分布得更宽",∫f2∣S(f)∣2df\int f^2|S(f)|^2df∫f2∣S(f)∣2df 会更大,从而时延方差下界更小。这就是"带宽提高→ToA 精度提高"的信息论/估计论解释,也是 ISAC 里常说"感知分辨率与带宽强相关"的数学根源。
若进一步把时延方差换算为距离方差(单基地):
R^=cτ^2⇒Var(R^)=(c2)2Var(τ^). \hat{R}=\frac{c\hat{\tau}}{2} \quad\Rightarrow\quad \mathrm{Var}(\hat{R})=\left(\frac{c}{2}\right)^2\mathrm{Var}(\hat{\tau}). R^=2cτ^⇒Var(R^)=(2c)2Var(τ^).
A9. "观测时间越长分辨率越好":相干积累提升 SNR 的定量关系
原文提到"通过捕获更多样本(更长观测时间)可进一步提升雷达分辨率"。
设每帧匹配滤波输出在目标时延处为
yk=A+nk,nk∼N(0,σ2). y_k = A + n_k,\qquad n_k\sim \mathcal{N}(0,\sigma^2). yk=A+nk,nk∼N(0,σ2).
若对 KKK 帧做相干累积(假设相位对齐):
yˉ=1K∑k=1Kyk=A+1K∑k=1Knk. \bar{y}=\frac{1}{K}\sum_{k=1}^{K} y_k = A + \frac{1}{K}\sum_{k=1}^{K} n_k. yˉ=K1k=1∑Kyk=A+K1k=1∑Knk.
则噪声方差变为 σ2/K\sigma^2/Kσ2/K,因此 SNR 提升因子为 KKK:
SNRcoh=A2σ2/K=K⋅A2σ2. \mathrm{SNR}_{\mathrm{coh}} = \frac{A^2}{\sigma^2/K}=K\cdot \frac{A^2}{\sigma^2}. SNRcoh=σ2/KA2=K⋅σ2A2.
当相位无法对齐时用非相干累积(能量累积)也能提升检测性能,但增益弱一些(典型近似为 K\sqrt{K}K 级别)。这解释了为什么 presence/vital sign 等"信号弱但可重复观测"的任务,会天然依赖慢时间堆叠与长时间窗口。