【1】349. 两个数组的交集
日期:1.16
https://leetcode.cn/problems/intersection-of-two-arrays/description/?envType=problem-list-v2&envId=sorting2.类型：哈希表，双指针，排序
3.方法：两个集合（半解）
计算两个数组的交集，直观的方法是遍历数组 nums1，对于其中的每个元素，遍历数组 nums2 判断该元素是否在数组 nums2 中，如果存在，则将该元素添加到返回值。
核心思想：使用哈希集合去重和查找
去重：使用unordered_set存储数组元素，自动去除重复元素
快速查找：unordered_set基于哈希表实现，查找操作平均O(1)时间复杂度
优化：总是遍历较小的集合，减少比较次数
关键代码：
cpp
vector<int> intersection(vector<int>& nums1, vector<int>& nums2){
// 使用两个unordered_set分别存储两个数组的元素
unordered_set<int> set1, set2;
// 将nums1中的元素插入set1中
for(auto& num:nums1){
set1.insert(num);
}
// 将nums2中的元素插入set2中
for(auto& num:nums2){
set2.insert(num);
}
return getIntersection(set1, set2);
}日期:1.17
2.类型：哈希表，双指针，排序
3.方法：两个集合（半解）
记录频率：使用unordered_map记录较小数组中每个数字出现的次数
匹配删除：遍历第二个数组，如果数字在哈希映射中存在且计数大于0，则加入结果，并减少计数
优化：总是用较小的数组构建哈希映射，减少内存使用
与交集I的区别：
交集I：结果中每个元素只出现一次（去重）
交集II：结果中元素出现的次数等于两个数组中该元素出现次数的最小值
关键代码：
cpp
if(nums1.size()>nums2.size()){
return intersect(nums2,nums1);
}
unordered_map<int,int>m;
// 遍历第一个数组，记录每个数字的出现次数
for(int num:nums1){
++m[num];
}
vector<int> intersection;
for(int num:nums2){
// 如果当前数字在哈希映射中存在且计数大于0
if(m.count(num)){
intersection.push_back(num);
--m[num];
// 如果计数减为0，则从哈希映射中删除该键，以避免后续重复判断
if(m[num]==0){
m.erase(num);
}
}
}日期:1.18
2.类型：动态规划，排序
3.方法：动态规划（官方题解）
核心思路：
降维处理：将二维问题转换为一维问题
排序技巧：先按宽度升序，宽度相同则按高度降序
动态规划：转换为高度序列的最长递增子序列问题
状态定义：f[i]：以第i个信封为结尾的最长递增子序列的长度
状态转移方程：
f[i] = max(f[j] + 1) 对于所有 j < i 且 envelopes[j][1] < envelopes[i][1]
初始值：f[i] = 1（每个信封自身形成一个序列）
关键代码:
cpp
// 排序规则：先按宽度升序，如果宽度相同，则按高度降序
sort(envelopes.begin(), envelopes.end(), [](const auto& e1, const auto& e2){
return e1[0]<e2[0]||(e1[0]==e2[0]&&e1[1]>e2[1]);
});
// f[i] 表示以第i个信封为结尾的最长递增子序列的长度
vector<int> f(n, 1);
for(int i=1;i<n;++i){
for(int j=0;j<i;++j){
// 因为已经按宽度排序，所以只需要检查高度
// 如果信封j的高度小于信封i的高度，且可以形成更长的序列
if(envelopes[j][1]<envelopes[i][1]){
f[i]=max(f[i],f[j]+1);
}
}
}
return *max_element(f.begin(),f.end());将这个二维数组转成一维数组，并对该一维数组进行排序。最后这个一维数组中的第 k 个数即为答案。
关键代码：
cpp
for(auto& row:matrix){
for(int it:row){
rec.push_back(it);
}
}
// 对一维数组进行排序（升序）
sort(rec.begin(),rec.end());
return rec[k - 1];4.方法二：归并排序（半解）
最小堆存储候选元素：将每行的第一个元素（最小值）加入堆中
逐步弹出最小元素：每次从堆中弹出当前最小的元素
补充后续元素：当弹出一个元素后，将其所在行的下一个元素加入堆中
重复k-1次：弹出前k-1个最小元素后，堆顶就是第k小的元素
关键代码：
cpp
struct point{
int val,x,y;
point(int val,int x,int y):val(val),x(x),y(y){}
// 重载大于运算符，用于构建最小堆
bool operator>(const point& a)const{
return this->val>a.val;
}
};
// 创建最小堆（优先队列），存储point对象
priority_queue<point, vector<point>, greater<point>> que;
int n=matrix.size(); // 矩阵的大小（n×n）
for(int i=0;i<n;i++){
que.emplace(matrix[i][0],i,0);
}
// 执行k-1次弹出操作
// 因为我们要找第k小的元素，所以需要弹出前k-1个最小的元素
for(int i=0;i<k-1;i++){
point now=que.top();
que.pop();
// 如果当前元素不是它所在行的最后一个元素
if(now.y!=n-1){
// 将同一行的下一个元素（右侧元素）加入堆中
que.emplace(matrix[now.x][now.y + 1], now.x, now.y + 1);
}
}
return que.top().val;日期:1.20
2.类型：排序
3.方法一：从低到高考虑（半解）
每个人由一对整数 (h, k) 表示，其中：
h：这个人的身高
k：排在这个人前面且身高大于或等于 h 的人数
需要重新排列这些人，使得排列后的队列满足每个人的 k 值条件。
核心思想：贪心算法 + 从低到高插入
排序策略：先按身高升序，身高相同则按k值降序
插入策略：从最矮的人开始，按照k值找到合适的空位插入
官方题解：
cpp
sort(people.begin(),people.end(),[](const vector<int>& u,const vector<int>& v){
return u[0] < v[0] || (u[0] == v[0] && u[1] > v[1]);
});
int n=people.size();
vector<vector<int>> ans(n);
// 按照排序后的顺序，将每个人插入到正确的位置
for(const vector<int>& person:people){
int spaces=person[1]+1;
for(int i=0;i<n;++i){
// 如果当前位置为空，说明可以放置（或为空位）
if(ans[i].empty()){
--spaces;
// 当空位减少到0时，说明找到了插入位置
if(!spaces){
ans[i]=person;
break;
}
}
}
}【6】435. 无重叠区间
日期:1.21
2.类型：排序，贪心，动态规划
3.方法一：动态规划（官方题解）
核心思想：转化为最长不重叠区间序列问题
问题：移除最少的区间使剩余区间互不重叠
等价于：找到最多的互不重叠区间
所以：最少移除数 = 总区间数 - 最大不重叠区间数
动态规划定义：
先按左端点排序，这样我们可以按顺序考虑区间
f[i]：以第i个区间结尾的最长不重叠区间序列的长度
初始值：每个区间自身就是一个序列，所以f[i] = 1
状态转移：
对于第i个区间，检查所有j < i的区间：
如果区间j与区间i不重叠（即intervals[j][1] <= intervals[i][0]）
那么可以将区间i接在区间j后面，形成更长的序列
更新：f[i] = max(f[i], f[j] + 1)
关键代码：
cpp
sort(intervals.begin(),intervals.end(),[](const auto& u,const auto& v){
return u[0]<v[0];
});
int n=intervals.size();
// 动态规划数组，f[i]表示以第i个区间结尾的最长不重叠区间序列的长度
vector<int> f(n,1);
for(int i=1;i<n;++i){
for(int j=0;j<i;++j){
// 如果区间j与区间i不重叠（即区间j的右端点 <= 区间i的左端点）
if(intervals[j][1]<=intervals[i][0]){
// 更新f[i]为f[j] + 1和当前f[i]的较大值
f[i]=max(f[i],f[j]+1);
}
}
}
// 需要移除的区间数量 = 总区间数 - 最长不重叠区间序列的长度
return n-*max_element(f.begin(),f.end());【7】436. 寻找右区间
日期:1.22
2.类型：字符串，贪心，哈希表
3.方法一：按照出现频率排序（半解）
核心思想：统计 → 排序 → 重建
统计频率：使用哈希表统计每个字符出现的次数
排序：将哈希表转换为可排序的vector，按频率降序排序
重建字符串：按照排序结果重建字符串
cpp
unordered_map<char, int> mp;
int length=s.length();
for(auto &ch:s){
mp[ch]++; // 如果字符不存在，会自动创建并初始化为0，然后加1
}
vector<pair<char, int>> vec; // 存储(字符, 频率)对
for(auto &it:mp){
// emplace_back直接构造pair，避免创建临时对象
vec.emplace_back(it);
}
sort(vec.begin(),vec.end(),[](const pair<char,int> &a,const pair<char,int> &b){
// 按频率降序排序（a.second > b.second）
return a.second>b.second;
});
string ret;
for(auto &[ch,num]:vec){
for(int i=0;i<num;i++){
ret.push_back(ch);
}
}
return ret;日期:1.23
2.类型：排序，贪心
3.方法一：排序 + 贪心（官方题解）
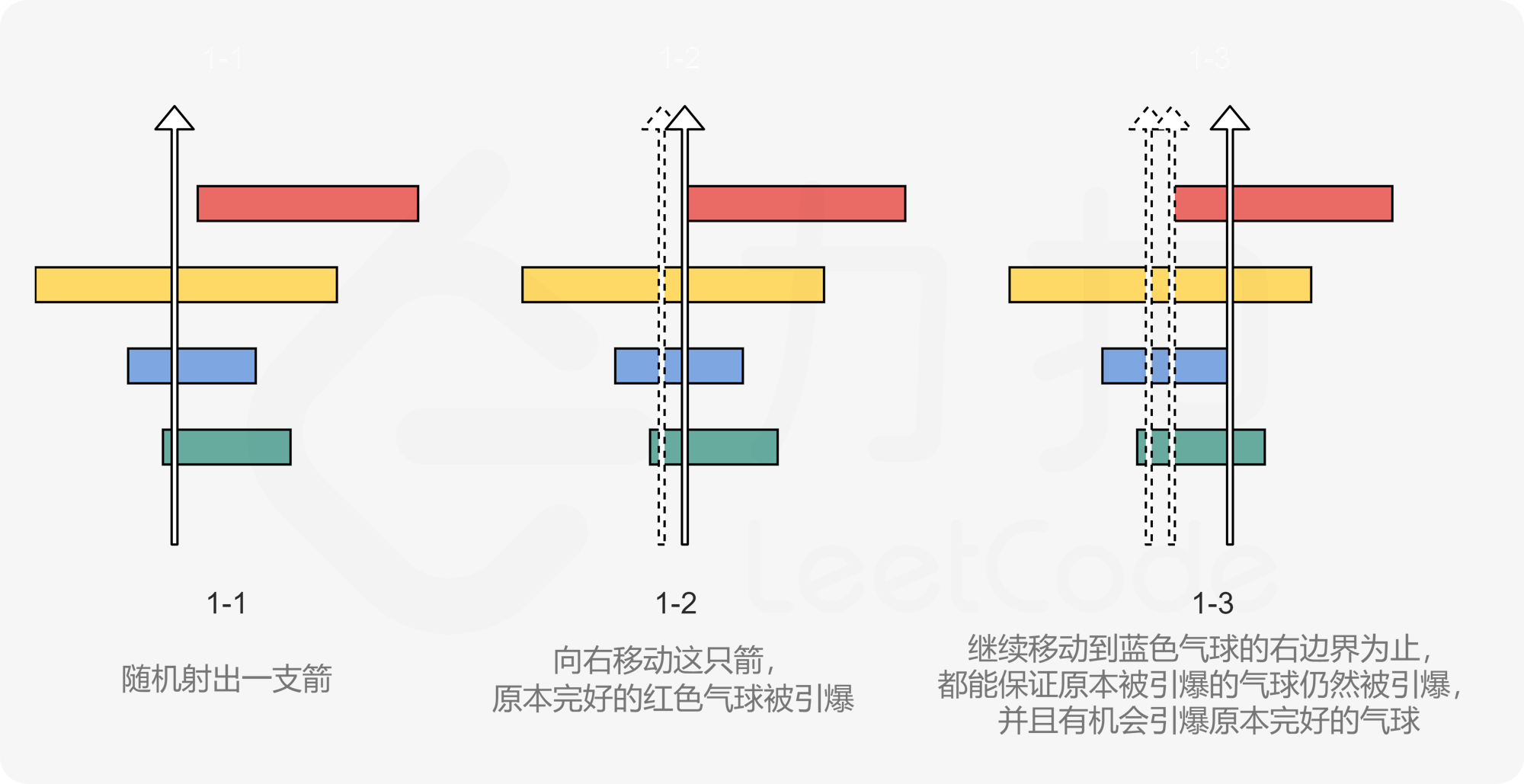
核心思想：贪心算法
排序：按照气球的结束位置升序排序
贪心选择：总是把箭射在第一个气球的结束位置，这样可以射中尽可能多的气球
跳过已覆盖：如果一个气球已经被当前的箭射中，跳过它
关键点：
一支箭可以射中所有开始位置 ≤ 箭的位置 ≤ 结束位置的气球
为了用最少的箭，每支箭应该射中尽可能多的气球
把箭射在一个气球的结束位置，可以保证射中这个气球，同时尽可能多地射中其他气球
关键代码：
cpp
// 按照气球的结束坐标升序排序
// 即按照每个区间的右端点（结束位置）从小到大排序
sort(points.begin(), points.end(), [](const vector<int>& u, const vector<int>& v){
return u[1]<v[1];
});
int pos=points[0][1];
int ans=1;
for (const vector<int>& balloon:points){
// 如果当前气球的开始位置大于箭的位置，说明当前箭无法射中这个气球
// 需要一支新箭，射在当前气球的结束位置
if(balloon[0]>pos){
pos=balloon[1];
++ans;
}
// 如果当前气球的开始位置 ≤ 箭的位置，说明当前箭可以射中这个气球
// 不需要增加新箭，继续检查下一个气球
}【9】506. 相对名次
日期:1.24
2.类型：排序，数组
3.方法一：排序（一次题解）
题目要求找到每个运动员的相对名次，并同时给前三名标记为 "Gold Medal", "Silver Medal", "Bronze Medal"，其余的运动员则标记为其相对名次。
将所有的运动员按照成绩的高低进行排序，然后将按照名次进行标记即可。
关键代码:
cpp
for(int i=0;i<n;++i){
arr.emplace_back(make_pair(-score[i],i));
}
sort(arr.begin(),arr.end());
vector<string> ans(n);
for(int i=0;i<n;++i){
if(i>=3){
ans[arr[i].second]=to_string(i + 1);
}else{
ans[arr[i].second]=desc[i];
}
}【10】561. 数组拆分
日期:1.25
2.类型：排序，数学
3.方法一：排序（一次题解）
核心思想：排序 + 贪心
排序：将数组按升序排序
贪心选择：将相邻的两个数配对，取每对中的较小值
求和：所有配对中较小值的和就是最大可能和
数学原理：
假设排序后的数组为：a₁ ≤ a₂ ≤ a₃ ≤ a₄ ≤ ... ≤ a₂ₙ
最优配对方式为：(a₁, a₂), (a₃, a₄), ..., (a₂ₙ₋₁, a₂ₙ)
此时，每对的最小值分别是：a₁, a₃, a₅, ..., a₂ₙ₋₁
总和 = a₁ + a₃ + a₅ + ... + a₂ₙ₋₁
关键代码：
cpp
sort(nums.begin(),nums.end());
int ans=0;
for(int i=0;i<nums.size();i+=2){
ans+=nums[i];
}
return ans;