用于汽车应用的数字码调制(DCM)雷达白皮书精读
DIGITAL CODE MODULATION(DCM) RADAR FOR AUTOMOTIVE APPLICATION,Wayne Stark
https://www.uhnder.com/images/data/DCM_Radar_for_Automotive_Application_Final.pdf
1. 文章主旨与问题背景:车载雷达走向"高分辨 + 高对比 + 抗干扰"
这篇白皮书从车载自动化等级提升带来的感知需求增长展开:雷达在夜间、雨雾等条件下仍可工作,同时可直接测径向速度(多普勒),因此是 ADAS/自动驾驶的关键传感器。但是随着车辆上雷达数量增加,互扰会变得突出,从而逼迫雷达体制在"分辨率、判别力、干扰鲁棒性"方面一起升级。
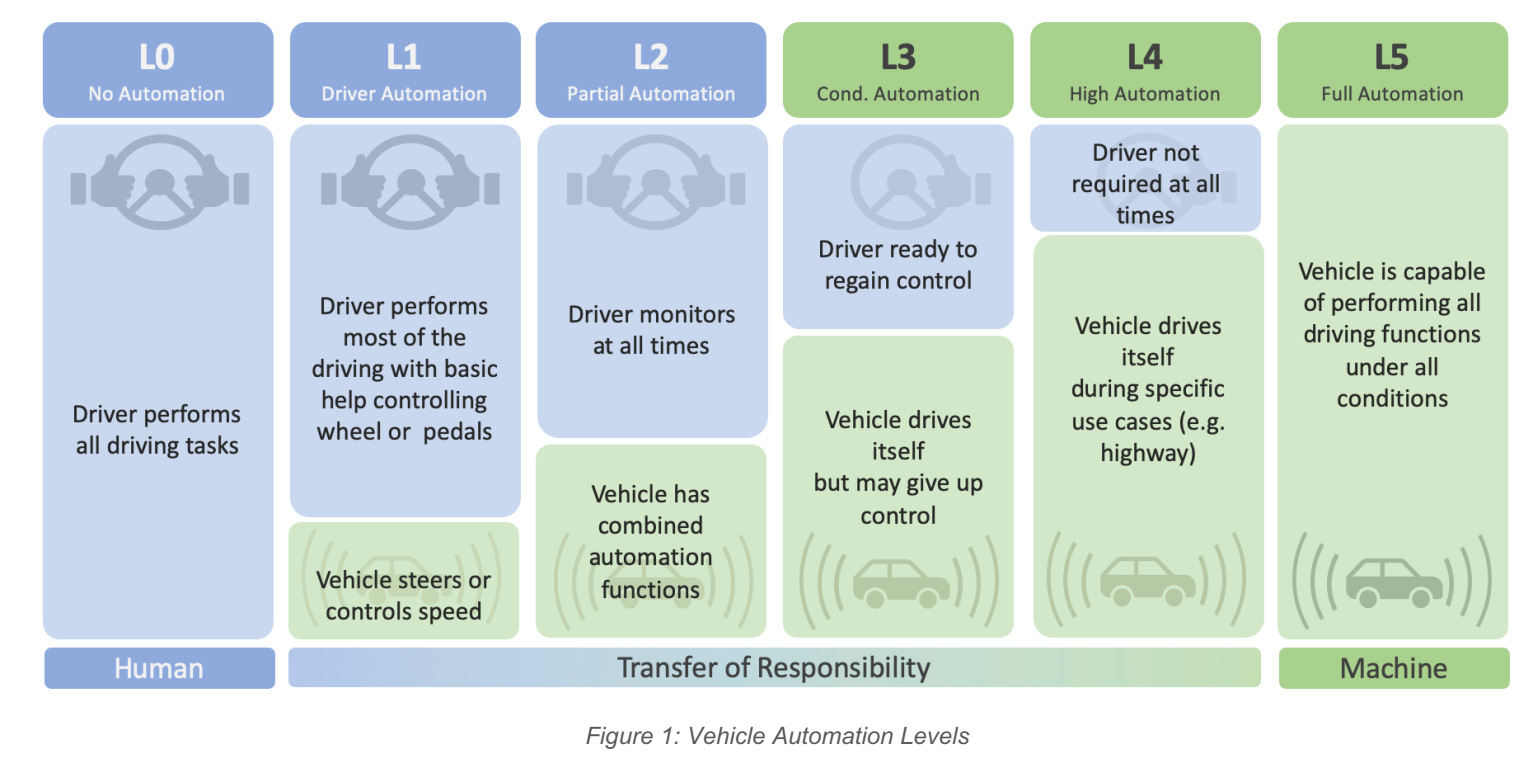
Figure 1: 越往高阶走,系统需要更可靠地识别更远、更小、更密集、更复杂的目标集合(特别是弱目标贴近强反射体时),并且要在更短的刷新周期内完成感知闭环。

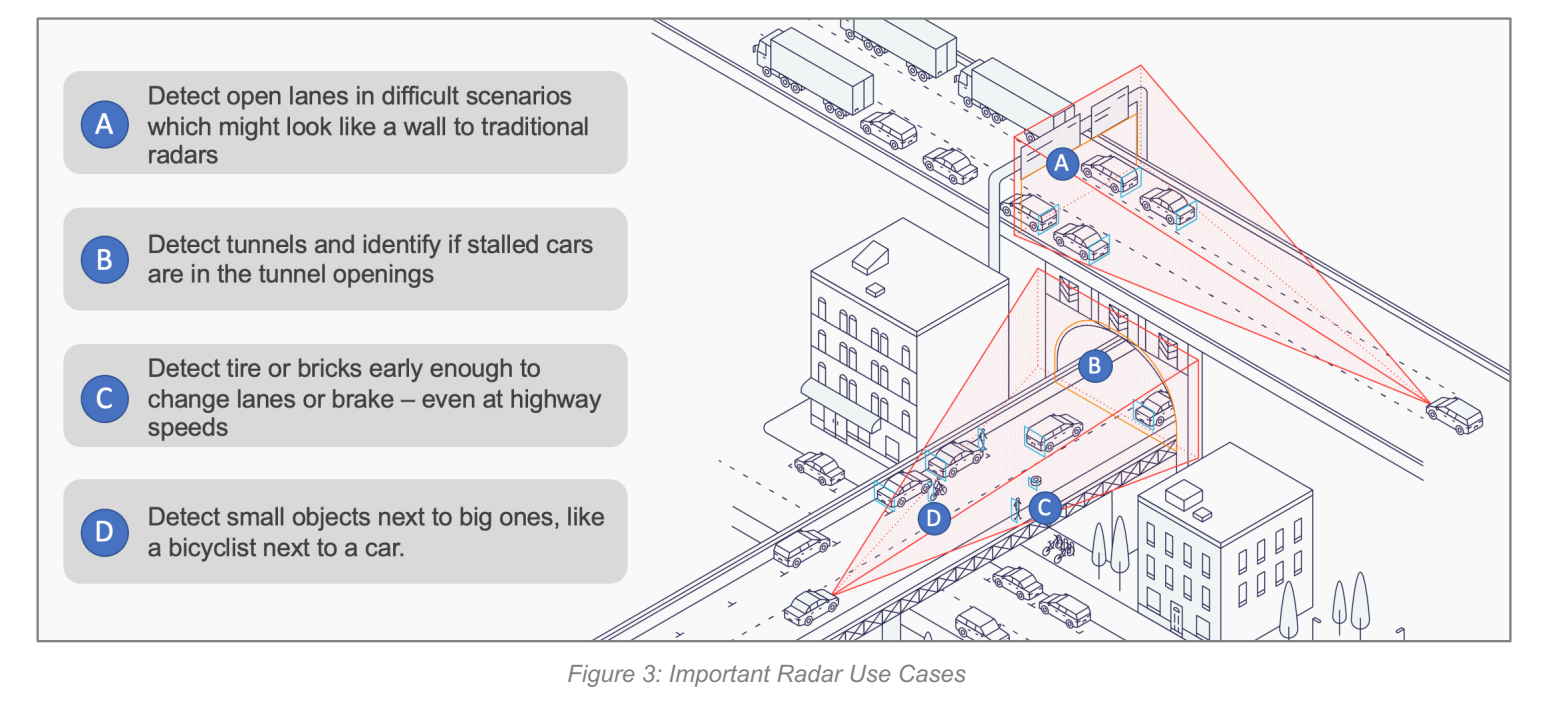
Figure 2 与 Figure 3: 这部分展示典型车辆多雷达布置(前向长距、角雷达、后向等)以及关键用例(如 ACC、AEB、盲区、交叉路口等)。图面展示了"同一时间同一频段会有更多雷达在发射",这会把互扰从偶发问题变成系统级瓶颈。
2. 雷达要测什么:距离、速度、角度与阵列带来的"虚拟孔径"
雷达的核心测量维度归纳为距离 RRR、径向速度 vvv、方向(方位/俯仰)。单发单收(SISO)能较直接地完成距离与速度估计;测角通常要靠扫描或多天线阵列。多发多收(MIMO)通过把不同发射通道与不同接收通道配对,构造出更多"虚拟接收通道",等价于把阵列孔径做大,从而提升角分辨率。
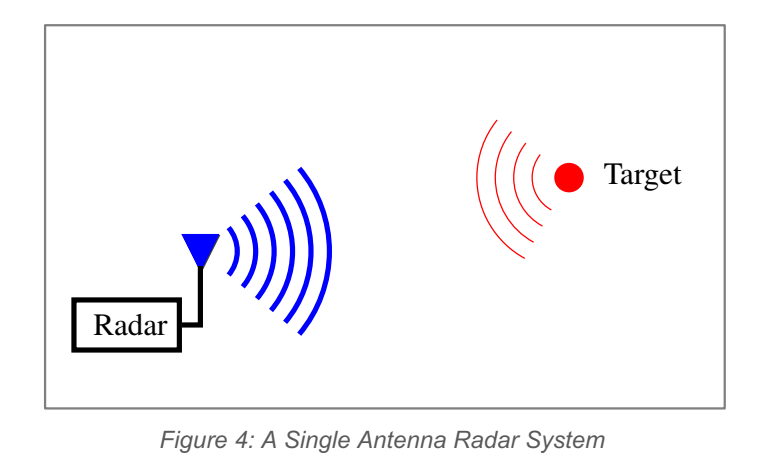
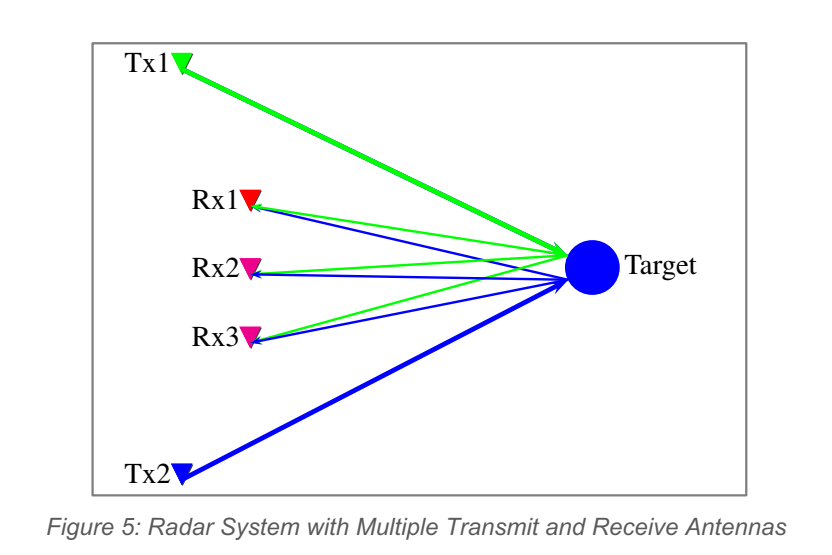
对应 Figure 4 与 Figure 5: 左侧 SISO 示意强调"单通道也能测距测速";右侧以 2Tx×3Rx2\text{Tx}\times 3\text{Rx}2Tx×3Rx 的例子说明可以形成 666 个虚拟阵元。角分辨率与等效孔径近似成反比,虚拟阵列把孔径拉大后,同样视场中能分开的角间隔更小。

表 1 中把性能指标组织为覆盖范围、精度、分辨率与扫描时间;并特别点明传统"分辨率"定义常默认两目标 RCS 相同,但车载更关心强弱目标紧邻时能否分开,因此引出 HCR(High Contrast Resolution)。
3. FMCW/FCM 的数学骨架:从线性调频到拍频,再到 R_maxR\_{\max}R_max、R_uR\_uR_u 与 ΔR\Delta RΔR
先给出 FMCW/FCM 的发射信号模型:中心频率 f_cf\_cf_c,瞬时调制 f_m(t)f\_m(t)f_m(t),发射功率 PPP:
sT(t)=2Pcos (2π(fc+fm(t))t). s_T(t)=\sqrt{2P}\cos\!\bigl(2\pi(f_c+f_m(t))t\bigr). sT(t)=2P cos(2π(fc+fm(t))t).
对静止目标,回波相当于延时 τ\tauτ 的版本,且距离与延时关系为
R=cτ2,τ=2Rc. R=\frac{c\tau}{2},\qquad \tau=\frac{2R}{c}. R=2cτ,τ=c2R.
关键机制 在于:线性调频的瞬时频率随时间变化,延时后的回波在任意时刻对应的是"过去某一时刻的频率",因此同一时刻发射与接收频率不同,混频后出现拍频 f_bf\_bf_b,并且 f_bf\_bf_b 与 τ\tauτ(进而与 RRR)成正比。
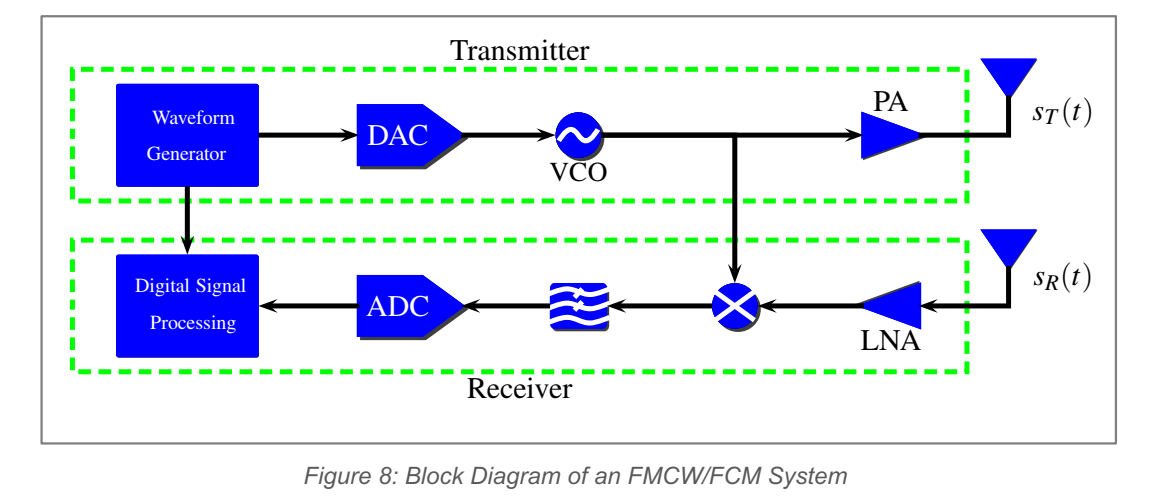
Figure 8: 这是典型 FMCW/FCM 收发链路:VCO 产生线性斜坡(或分段斜坡),一方面送至功放和天线发射,另一方面作为本振参与下变频;接收端混频、低通、ADC 后进入数字域。图面突出的是"模拟域完成频率差提取",数字域主要做 FFT 与后端检测。
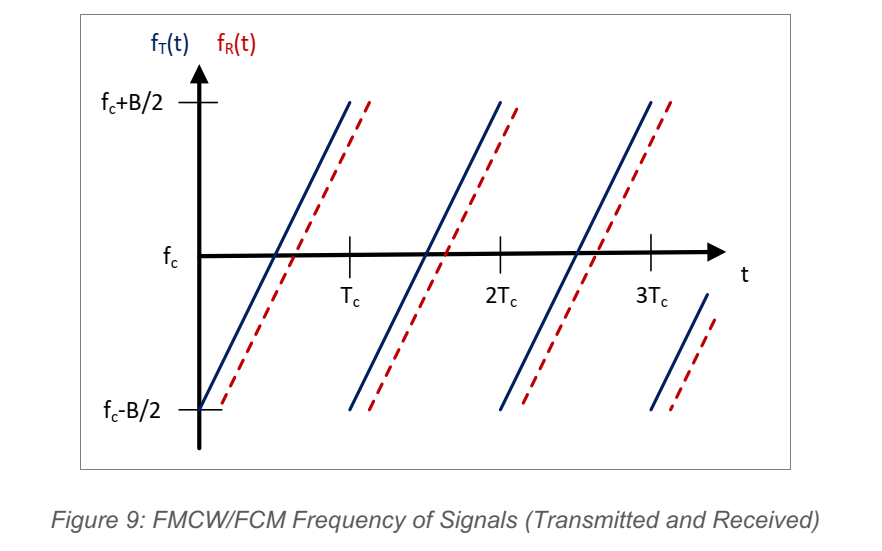
对应 Figure 9: 该图用频率---时间图展示:发射 chirp 是一条斜线,回波是延时后的平行斜线;在同一时刻,两条线的垂直差就是频率差,经混频转成拍频。图的视觉重点是:延时越大,垂直差越大,拍频越高。在此基础上,文章给出最大可探测距离与接收低通带宽 B_rB\_rB_r 的关系:若最大拍频不超过 B_rB\_rB_r,则最大距离为
Rmax=c Tc Br2B, R_{\max}=\frac{c\,T_c\,B_r}{2B}, Rmax=2BcTcBr,
并进一步指出采样率 f_sf\_sf_s(Nyquist)会决定最大无歧义距离:若拍频超过 f_s/2f\_s/2f_s/2 会折叠,导致远距离"映射成"近距离,从而最大无歧义距离为
Ru=c Tc fs2B. R_u=\frac{c\,T_c\,f_s}{2B}. Ru=2BcTcfs.
距离分辨率方面,原文通过"两目标拍频差"与 FFT 频率分辨率的关系推到经典结论:
ΔR=c2B. \Delta R=\frac{c}{2B}. ΔR=2Bc.
这里需要强调文章隐含的要点:ΔR\Delta RΔR 虽然只由 BBB 决定,但 FFT 形成的距离响应(主瓣与旁瓣形状)会直接影响强弱目标相邻可分性,也就是后面的 HCR。
4. DMR/DCM 的数学骨架:相位码、匹配滤波与"拇指钉"距离响应
文章把 DCM 视作数字调制雷达(DMR)的一类:载波仍是 f_cf\_cf_c,但相位 ϕ(t)\phi(t)ϕ(t) 按 chip 间隔离散跳变,发射信号写为
s(t)=2Pcos (2πfct+ϕ(t)), s(t)=\sqrt{2P}\cos\!\bigl(2\pi f_c t+\phi(t)\bigr), s(t)=2P cos(2πfct+ϕ(t)),
并规定在每个 chip 内相位保持常值:对整数 ℓ\ellℓ,当 KaTeX parse error: Undefined control sequence: \< at position 10: \ell T\c\̲<̲t\le(\ell+1)T\... 时,ϕ(t)=ϕ_ℓ\phi(t)=\phi\_\ellϕ(t)=ϕ_ℓ。
二相(BPSK)情形可写成 a(t)∈+1,−1a(t)\in{+1,-1}a(t)∈+1,−1 的符号序列乘载波,文章指出这种相位/符号变化会把频谱扩展到与 chip 速率同阶的带宽,从而仍能用大带宽获得高距离分辨率。
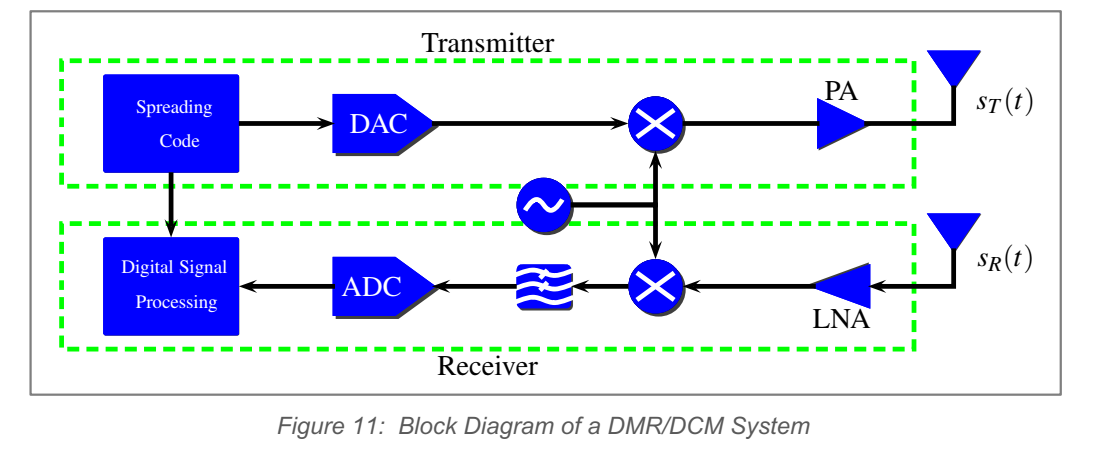
DCM 的"距离成像"不靠拍频,而靠匹配滤波(相关):把接收到的基带信号与本地码做相关,输出近似是码的自相关函数随延时的扫描。于是只要码的自相关"主峰尖、旁瓣低",距离响应就呈"针尖"形状(thumbtack-like),强目标的能量更难在距离上拖尾覆盖弱目标,这直接提升 HCR。
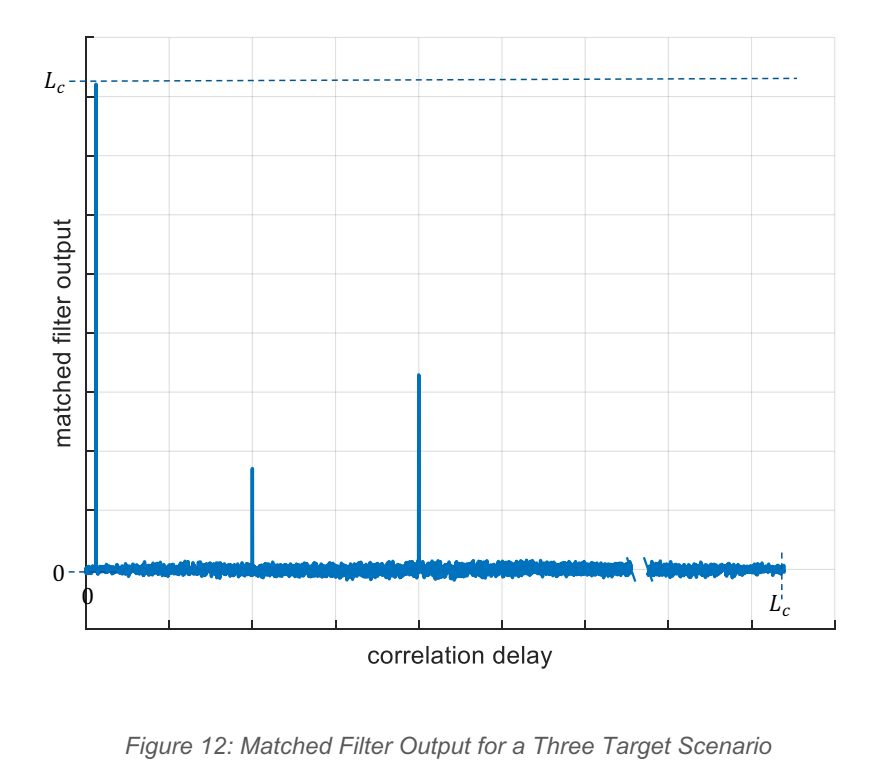
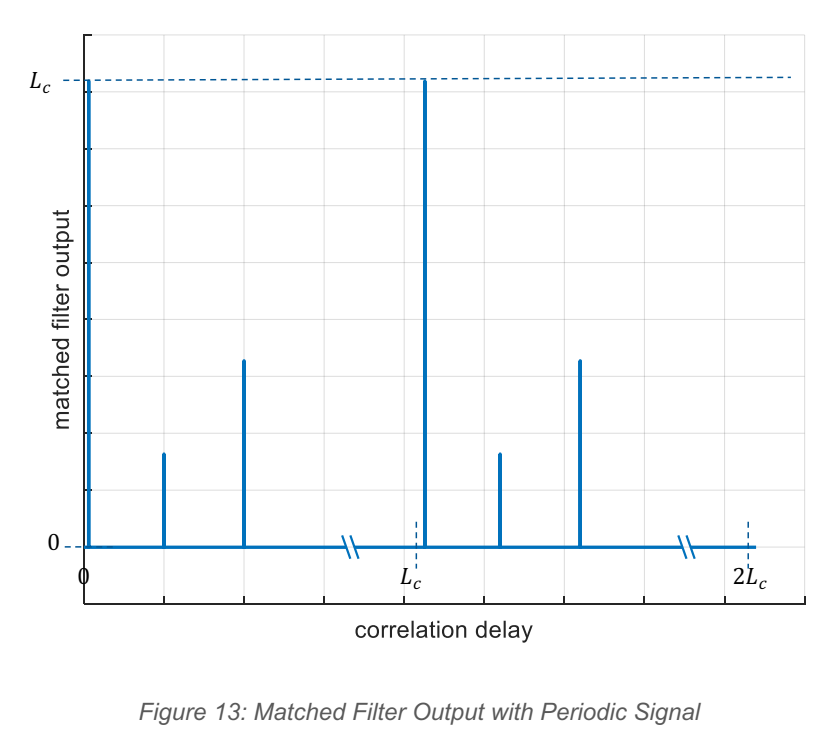
Figure 12 与 Figure 13: 图中给出三目标时匹配滤波输出随延时的曲线:三个尖峰对应三个目标距离;对比"非周期发送"与"周期发送",可以看到周期情况下背景更均匀、非峰值更低(或者更可控)。DCM 的距离响应更像一根根"针",而不是一团"宽主瓣 + 明显旁瓣"的能量堆。
文章直接给出 DCM 距离分辨率与 chip 宽度的关系:两个目标若其往返时延差小于一个 chip,相关主峰会重叠而不可分,因此
ΔR=cTc2. \Delta R=\frac{cT_c}{2}. ΔR=2cTc.
又因为通常 T_c≈1/BT\_c\approx 1/BT_c≈1/B,于是得到同样的形式
ΔR=c2B. \Delta R=\frac{c}{2B}. ΔR=2Bc.
但与 FMCW 的差别在于距离响应形态:FMCW 的 FFT 距离谱旁瓣结构与窗函数、泄漏等高度相关;DCM 由码自相关主导,天然更接近"尖峰 + 低旁瓣"的理想形状,从而在高动态场景(强弱目标共存)更有优势。
5. 多普勒与速度:从 IQ 旋转到无歧义速度与速度分辨率
经典多普勒关系:往返传播导致频移与速度满足
fD=2vfcc,v=fDc2fc. f_D=\frac{2vf_c}{c},\qquad v=\frac{f_Dc}{2f_c}. fD=c2vfc,v=2fcfDc.
速度估计的核心不是"单次测量",而是"重复观测":在 DCM 中,每次匹配滤波可以得到某个距离单元的复数输出(I/Q),重复 NNN 次后,这些复数点会以与 f_Df\_Df_D 成正比的角速度在复平面旋转。
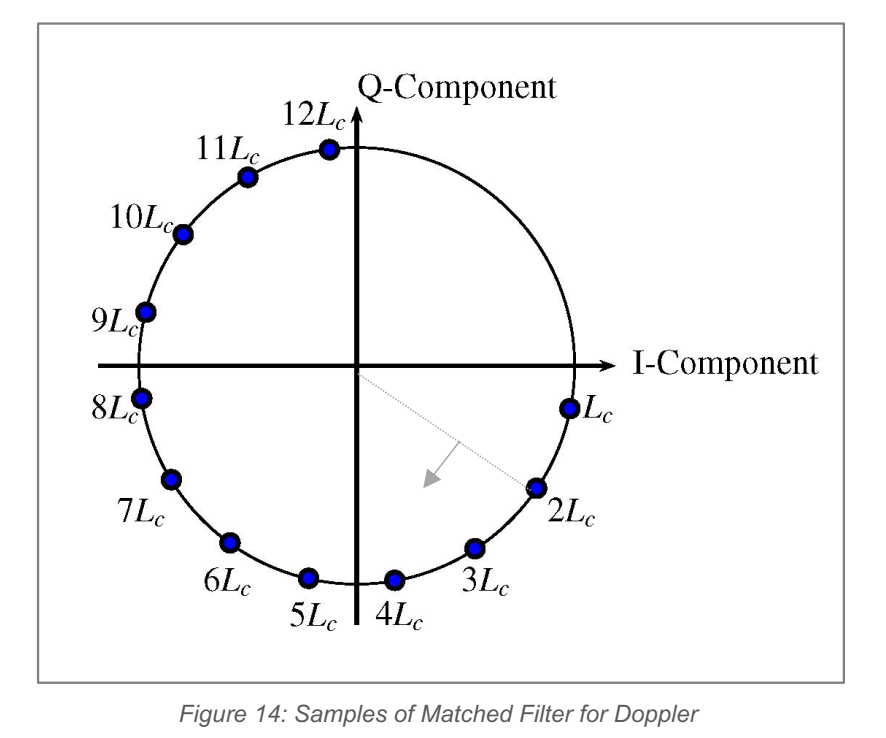
**Figure 14:**图中把每次相关输出画在 IQ 平面上形成近圆形轨迹:旋转方向代表接近或远离,旋转速度代表多普勒大小。对车载处理而言,这意味着在"慢时间"维度做 FFT,就能把不同速度的目标分离出来。
进一步给出无歧义速度的概念:若在一个码周期(或等效重复间隔)内相位转过 2π2\pi2π,会发生速度混叠。用这一物理直观推导出无歧义速度边界,并给出速度分辨率为"无歧义窗口宽度除以 NNN"的结果:
Δv=c2fc N Tc L. \Delta v=\frac{c}{2f_c\,N\,T_c\,L}. Δv=2fcNTcLc.
注意这里出现的 LT_cLT\_cLT_c 其实是"每次相关输出之间的等效重复周期"(码周期),因此 N⋅LT_cN\cdot LT\_cN⋅LT_c 就是总相干观测时间;观测越久速度越细,但刷新率(扫描时间)会变长,这是车载雷达无法回避的系统折中。
6. MIMO 复用方式与 DCM 的"天然 CDM":通道隔离为什么靠码长
文章对比 TDM/CDM/FDM MIMO(表 2),强调 TDM 会让扫描时间随 Tx 数增长,同时最大无歧义速度随 Tx 数下降;CDM 允许多个 Tx 同时发射,通过不同码分离,代价是数字处理更重,但能保持速度性能并缩短扫描时间。同时也明确指出:DCM 天然采用 CDM MIMO------不同 Tx 使用不同扩频码。

表 2: 三种复用方式的优缺点:TDM 的优势是分离简单,但时间代价高;FDM 需要更大带宽与更复杂滤波;CDM 在同频同时间并发发射,通过码的相关性实现分离,强调"并发"对车载短刷新周期的意义。
多 Tx 的关键问题是"通道隔离":若 Tx1 与 Tx2 的码互相关不够低,那么 Tx2 的能量会泄漏进 Tx1 的匹配滤波输出,表现为底噪/旁瓣抬升,从而吞噬弱目标。文章指出隔离主要靠更长码长提升。
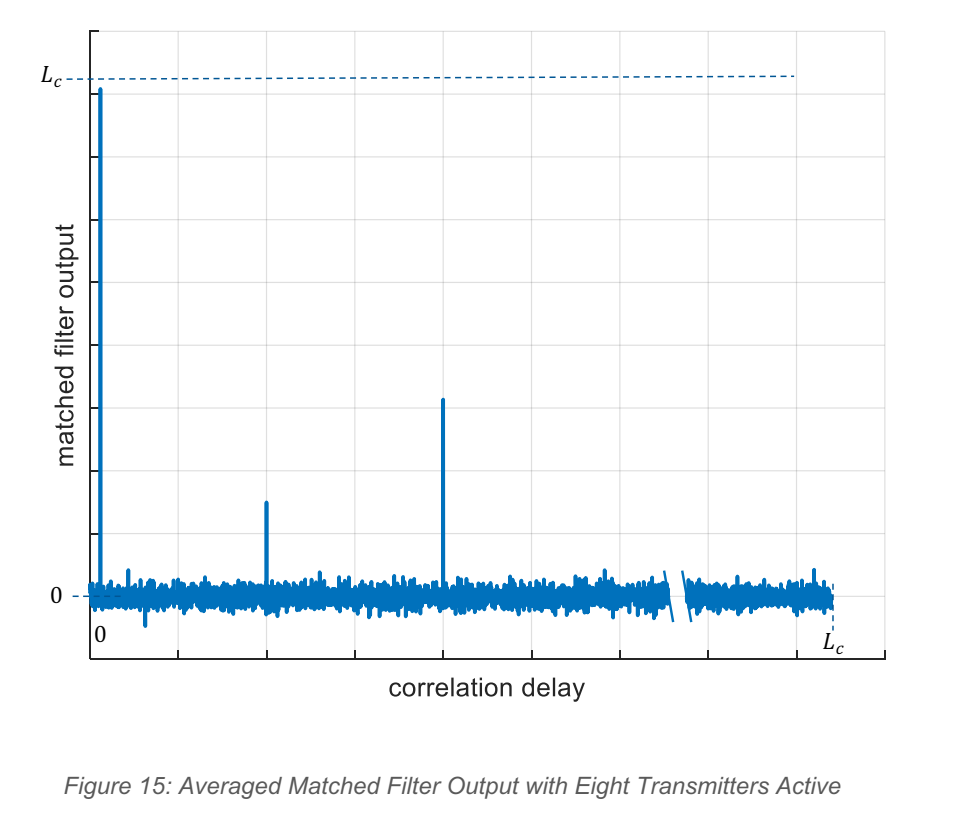
Figure 15: 示例为 8Tx 同时工作且各自使用不同码时的平均匹配滤波输出:相比单 Tx(三目标)情形,非峰值能量整体抬升,直观体现互相关泄漏;据此强调通过增大码长降低互相关可改善隔离度。
除此之外,原文还用"相位编码 FMCW(chirp 间 PRBS)"与 DCM 的对比说明:在同样扫描时长(如 5ms)下,DCM 能利用更高 chip 率获得更长序列,从而为更多 Tx 并发和更高隔离提供空间。
7. HCR(高对比度分辨率):从需求到"旁瓣结构决定弱目标生存空间"
文章提出 HCR 的动机是车载场景里强弱目标 RCS 差异巨大,且经常贴近:例如小孩在卡车前、行人贴近护栏等。HCR 衡量在给定 RCS 对比度下,目标在距离/角度/速度维度上最小可分离间隔。
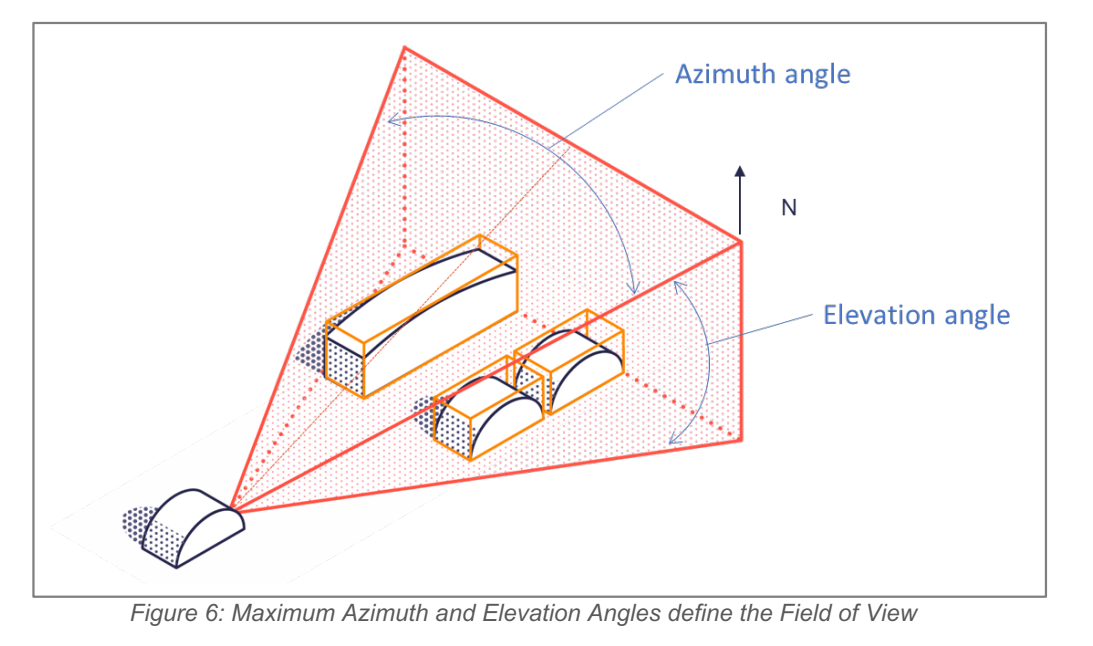
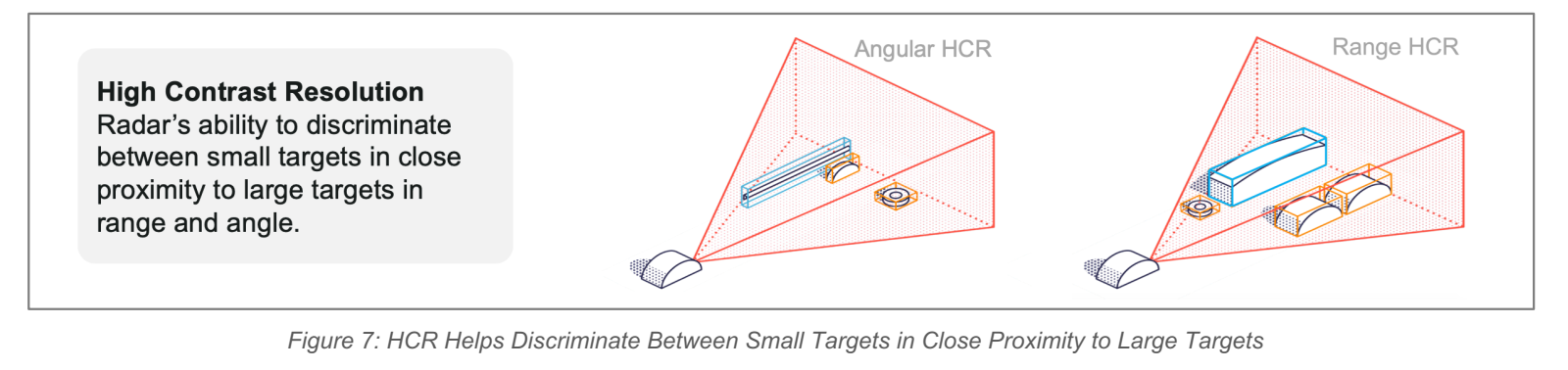
Figure 6 与 Figure 7: Figure 6 是雷达视场(FOV)示意;Figure 7 用小图强调:传统"分辨率"只看两个点能否分开,而 HCR 关心强目标旁边的弱目标是否会被强目标的泄漏(旁瓣/谱泄漏)压住。图上强目标的"扩散尾巴"覆盖弱目标时,即便名义分辨率足够,系统仍可能检测不到弱目标。
把 FMCW 与 DCM 放在同一框架下,文章实际上在暗示一种更"系统"的理解:分辨率 ΔR=c2B\Delta R=\frac{c}{2B}ΔR=2Bc 只是主瓣宽度的量级指标;真正影响 HCR 的是距离响应 h(R)h(R)h(R) 在主瓣附近的衰减速度与旁瓣高度。DCM 由于相关输出更接近理想自相关主峰(thumbtack-like),因此更不容易出现强目标能量在距离维度大范围拖尾,从而 HCR 更好。
8. 干扰机理:INR 与 ISF(KKK)把"体制差异"变成可算指标
文章指出车载互干扰之所以麻烦,一个直接原因是 LOS 干扰只经历单程传播损耗,而目标回波经历双程损耗,因此干扰在受害雷达处往往天然更强。
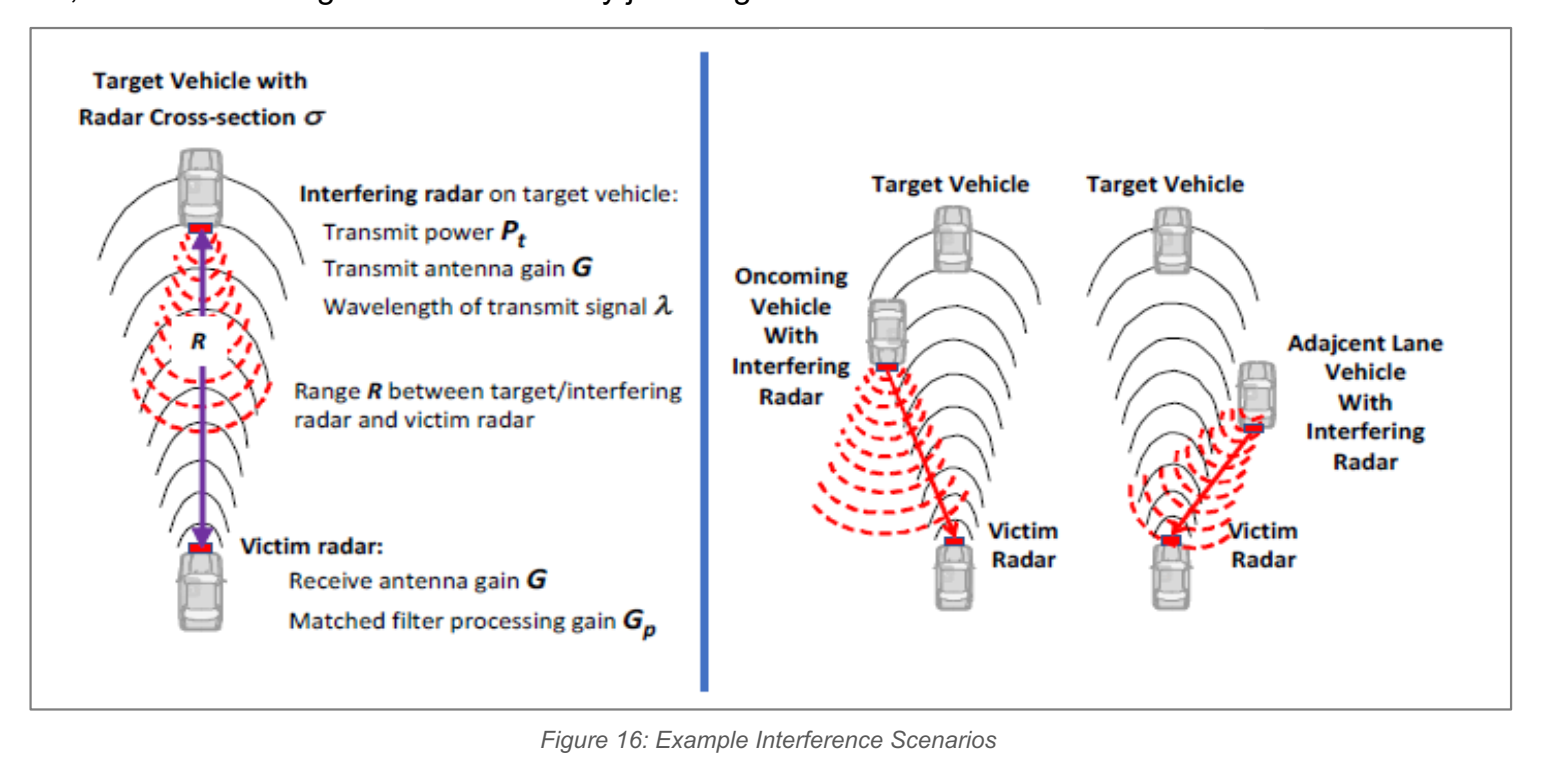
Figure 16: 图中一辆车的雷达信号直接进入另一辆车的雷达接收机(LOS),同时受害雷达还要接收来自目标的反射回波。即"同一接收机里同时存在目标回波与外来雷达信号",这会把干扰表现为噪声底抬升、虚警、漏检,甚至造成距离/速度假目标。
文章用 INR(interference-to-noise ratio)来量化"干扰相对噪声的强弱",定义为
INR=PSDintPSDnoise. \mathrm{INR}=\frac{\mathrm{PSD}{\mathrm{int}}}{\mathrm{PSD}{\mathrm{noise}}}. INR=PSDnoisePSDint.
接着引入 ISF(interference susceptibility factor),记为 KKK,在 FMCW-to-FMCW 的讨论中把它定义成"下变频后干扰 PSD 与 RF 端干扰 PSD 的比例",也可写为带宽比:
K=PSDBBPSDRF=ΔFRFΔFBB. K=\frac{\mathrm{PSD}{\mathrm{BB}}}{\mathrm{PSD}{\mathrm{RF}}} =\frac{\Delta F_{\mathrm{RF}}}{\Delta F_{\mathrm{BB}}}. K=PSDRFPSDBB=ΔFBBΔFRF.
直观解释是:如果干扰经过下变频后被"压缩"到更窄的 ΔF_BB\Delta F\_{\mathrm{BB}}ΔF_BB,它的 PSD 会升高,从而 INR 增大;相反,如果干扰仍保持宽带噪声样分布,PSD 不会被显著抬高。
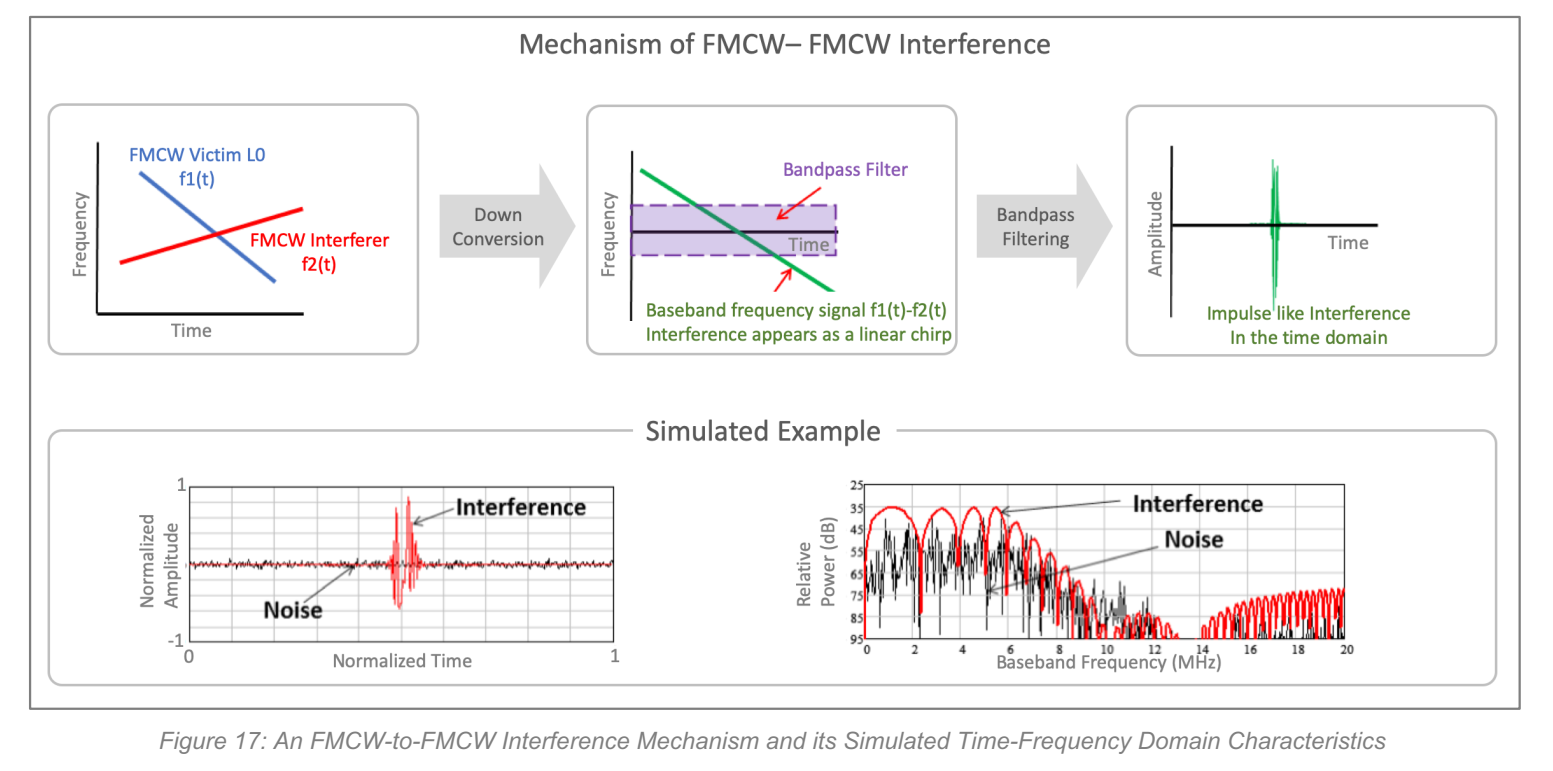
Figure 17: 图中展示两条 FMCW chirp 在时频平面相交时,受害雷达下变频后看到的干扰在其 IF/BB 通带内扫过;经过带通后,时域像一段短脉冲,频域表现为噪声底抬升。并且需要强调"干扰并不是整段时间都落在通带内,而是与两 chirp 的相对斜率有关"。
进一步指出:当两雷达斜率更相似时,交叉更慢,干扰持续时间变长,等效 ΔF_BB\Delta F\_{\mathrm{BB}}ΔF_BB 变小,导致 KKK 变大、INR 更严重。
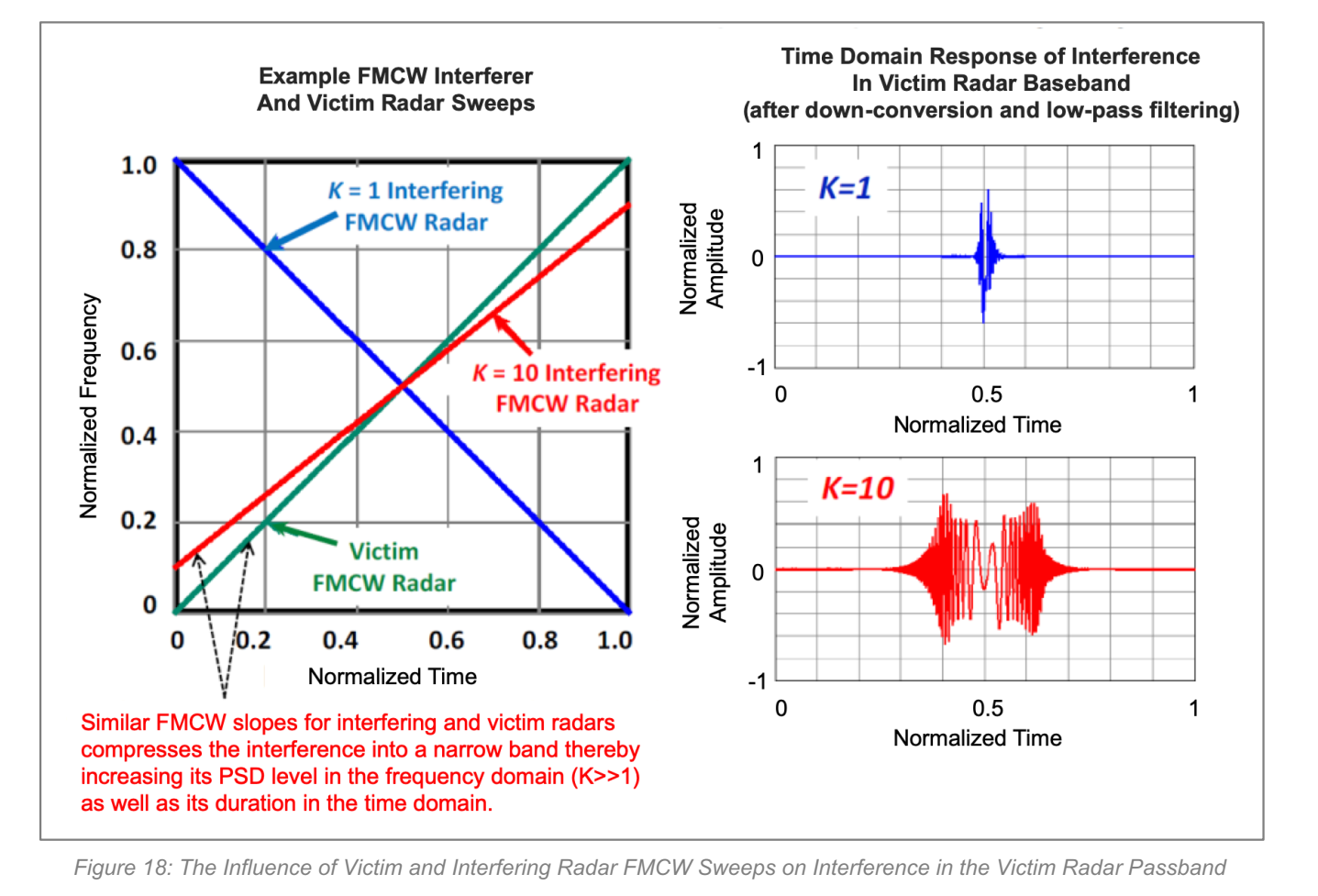
Figure 18: 给出 K=1K=1K=1 与 K=10K=10K=10 两种示意:当相对斜率使得交叉很快时,干扰在 BB 中更"分散",KKK 小;当交叉慢时,干扰能量集中度提升,KKK 可达 10,意味着 PSD/INR 约放大 10 倍。而对于 DCM,原文指出只要涉及 DCM(DCM-to-DCM 或 DCM-to-FMCW/反向),干扰往往更像扩频噪声,通常 KKK 接近 1,因而干扰敏感度更低且更稳定;并指出 DCM↔FMCW 两种互扰在 INR 上对称。
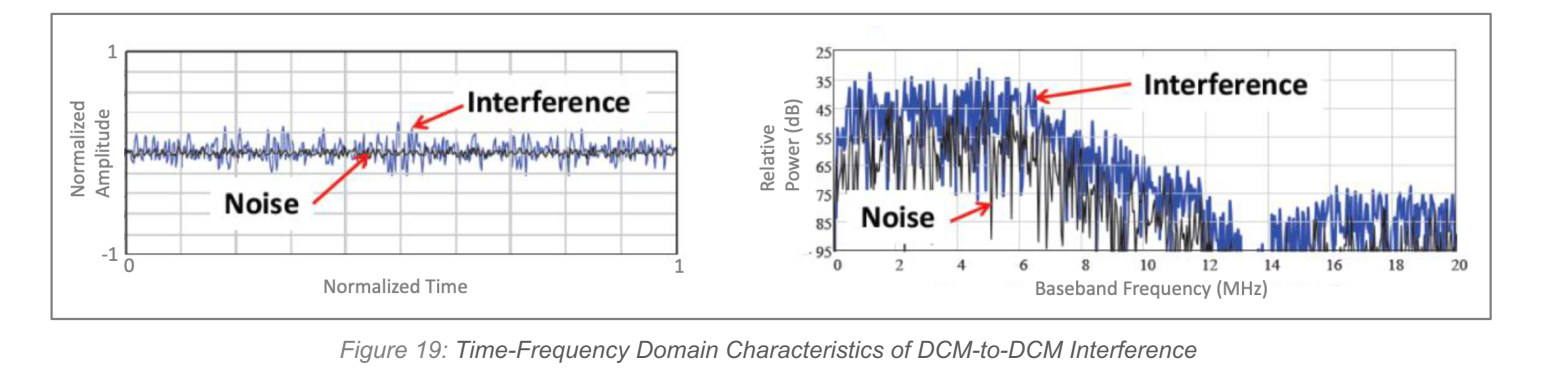
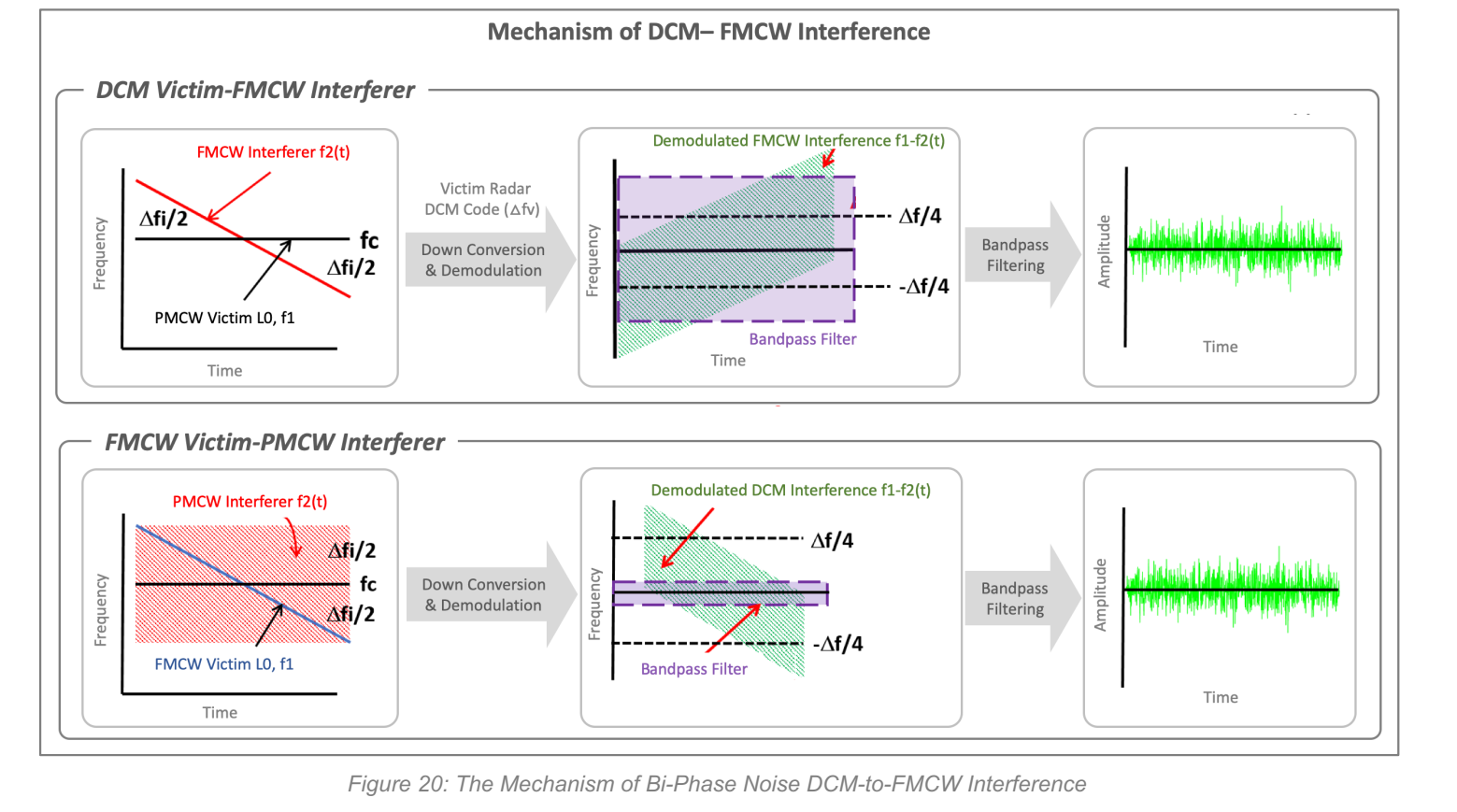
Figure 19 与 Figure 20: Figure 19 描绘 DCM-to-DCM:时频上更接近"随机噪声样能量铺展",下变频后不会被强烈压窄;Figure 20 描绘 DCM-to-FMCW(以及反向):干扰在受害链路里仍更像宽带噪声,因而 KKK 更接近 1。结论是:FMCW↔FMCW 的 KKK 对几何与斜率高度敏感,而 DCM 相关情形更不敏感。
9. 工程落地:DCM 从"成本障碍"到"可上车"的技术条件
文章指出 DCM 的关键处理(匹配滤波/相关)主要在数字域完成,因此需要高速 ADC 与强数字算力,这曾经成本过高;而 CMOS 工艺与高速低功耗 ADC 的进步使"雷达射频 + 数字处理"单芯片集成成为可能。

Figure 21: 展示 CMOS DCM radar-on-chip 架构:前端采集高速数据后,通过专用加速器把原始数据做匹配滤波与降维,输出更接近"目标级信息",再交给通用处理器完成跟踪与应用逻辑。图面想强调的是:DCM 的"数字重"并非不可行,而是依赖硬件加速把吞吐量问题解决。
附录:补全被省略的推导
A.1 FMCW 拍频 f_b=Sτf\_b=S\tauf_b=Sτ 的推导(线性调频近似)
设发射为线性调频(上扫):
fT(t)=f0+St,S=BTc. f_T(t)=f_0+St,\qquad S=\frac{B}{T_c}. fT(t)=f0+St,S=TcB.
对应的瞬时相位(忽略常数项)为
θT(t)=2π∫0tfT(u) du=2π(f0t+S2t2). \theta_T(t)=2\pi\int_0^t f_T(u)\,du =2\pi\left(f_0 t+\frac{S}{2}t^2\right). θT(t)=2π∫0tfT(u)du=2π(f0t+2St2).
发射信号(取复包络表示更清晰):
xT(t)=exp (jθT(t)). x_T(t)=\exp\!\bigl(j\theta_T(t)\bigr). xT(t)=exp(jθT(t)).
静止目标回波(仅延时):
xR(t)=α xT(t−τ)=αexp (j2π(f0(t−τ)+S2(t−τ)2)). x_R(t)=\alpha\,x_T(t-\tau) =\alpha\exp\!\Bigl(j2\pi\left(f_0(t-\tau)+\frac{S}{2}(t-\tau)^2\right)\Bigr). xR(t)=αxT(t−τ)=αexp(j2π(f0(t−τ)+2S(t−τ)2)).
与本振(取发射的共轭)混频:
y(t)=xR(t) xT∗(t)=αexp (j2π[−f0τ+S2((t−τ)2−t2)]). y(t)=x_R(t)\,x_T^*(t) =\alpha\exp\!\Bigl(j2\pi\left[-f_0\tau+\frac{S}{2}\bigl((t-\tau)^2-t^2\bigr)\right]\Bigr). y(t)=xR(t)xT∗(t)=αexp(j2π[−f0τ+2S((t−τ)2−t2)]).
展开平方项:
(t−τ)2−t2=t2−2tτ+τ2−t2=−2tτ+τ2. (t-\tau)^2-t^2=t^2-2t\tau+\tau^2-t^2=-2t\tau+\tau^2. (t−τ)2−t2=t2−2tτ+τ2−t2=−2tτ+τ2.
代回:
y(t)=αexp (j2π[−f0τ+S2(−2tτ+τ2)])=αexp (j2π[−f0τ−Stτ+S2τ2]). y(t)=\alpha\exp\!\Bigl(j2\pi\left[-f_0\tau+\frac{S}{2}(-2t\tau+\tau^2)\right]\Bigr) =\alpha\exp\!\Bigl(j2\pi\left[-f_0\tau-S t\tau+\frac{S}{2}\tau^2\right]\Bigr). y(t)=αexp(j2π[−f0τ+2S(−2tτ+τ2)])=αexp(j2π[−f0τ−Stτ+2Sτ2]).
其中随时间 ttt 线性变化的相位项是 −2πSτ,t-2\pi S\tau,t−2πSτ,t,因此 y(t)y(t)y(t) 是一个频率为 SτS\tauSτ 的复正弦(外加常数相位):
fb=Sτ=BTcτ. f_b=S\tau=\frac{B}{T_c}\tau. fb=Sτ=TcBτ.
再用 τ=2Rc\tau=\frac{2R}{c}τ=c2R 得
fb=2BRcTc. f_b=\frac{2BR}{cT_c}. fb=cTc2BR.
这与正文中的直觉推导一致,也是文中"拍频与距离成正比"的数学根基。
A.2 距离分辨率 ΔR=c2B\Delta R=\frac{c}{2B}ΔR=2Bc 的 FFT 推导(从频率栅格到距离栅格)
对单个 chirp 的混频输出 y(t)y(t)y(t),理想情况下是若干个拍频分量之和:
y(t)=∑kAkej2πfb,kt,t∈[0,Tc). y(t)=\sum_k A_k e^{j2\pi f_{b,k} t},\qquad t\in[0,T_c). y(t)=k∑Akej2πfb,kt,t∈[0,Tc).
对区间 KaTeX parse error: Undefined control sequence: \[ at position 1: \̲[̲0,T\_c) 做 NNN 点 FFT(采样率 f_sf\_sf_s),其频率栅格间隔为
Δf=fsN≈1Tc, \Delta f=\frac{f_s}{N}\approx \frac{1}{T_c}, Δf=Nfs≈Tc1,
(当 N=f_sT_cN=f\_sT\_cN=f_sT_c 时为严格等号)。当两目标拍频差小于一个栅格时,就难以分辨,因此取
Δfb≈1Tc. \Delta f_b\approx \frac{1}{T_c}. Δfb≈Tc1.
而由拍频与距离关系 f_b=2BcT_cRf\_b=\frac{2B}{cT\_c}Rf_b=cT_c2BR,两目标距离差 ΔR\Delta RΔR 产生的拍频差为
Δfb=2BcTcΔR. \Delta f_b=\frac{2B}{cT_c}\Delta R. Δfb=cTc2BΔR.
令 Δf_b=1T_c\Delta f\_b=\frac{1}{T\_c}Δf_b=T_c1,解得
ΔR=c2B. \Delta R=\frac{c}{2B}. ΔR=2Bc.
这就是的距离分辨率。
A.3 DCM 匹配滤波输出为何是自相关:从离散码到"针尖主峰"
用离散 BPSK 码 KaTeX parse error: Undefined control sequence: \[ at position 2: a\̲[̲\ell]\in{\pm1} 表示 chip 序列,chip 波形为矩形脉冲 p(t)p(t)p(t)(宽度 T_cT\_cT_c,幅度 1):
a(t)=∑ℓ=0L−1a[ℓ] p(t−ℓTc). a(t)=\sum_{\ell=0}^{L-1} a[\ell]\,p(t-\ell T_c). a(t)=ℓ=0∑L−1a[ℓ]p(t−ℓTc).
忽略载波并假设已下变频到基带,则回波为延时版本:
r(t)=α a(t−τ)+n(t). r(t)=\alpha\,a(t-\tau)+n(t). r(t)=αa(t−τ)+n(t).
匹配滤波器(对 a(t)a(t)a(t) 的匹配)为 h(t)=a∗(−t)h(t)=a^*(-t)h(t)=a∗(−t),输出为卷积:
y(τ′)=(r∗h)(τ′)=∫r(t) a∗(t−τ′) dt≈α∫a(t−τ) a(t−τ′) dt. y(\tau')=(r*h)(\tau')=\int r(t)\,a^*(t-\tau')\,dt \approx \alpha\int a(t-\tau)\,a(t-\tau')\,dt. y(τ′)=(r∗h)(τ′)=∫r(t)a∗(t−τ′)dt≈α∫a(t−τ)a(t−τ′)dt.
令 u=t−τ′u=t-\tau'u=t−τ′,则
y(τ′)≈α∫a(u+τ′−τ) a(u) du=α Raa(τ′−τ), y(\tau')\approx \alpha\int a(u+\tau'-\tau)\,a(u)\,du =\alpha\,R_{aa}(\tau'-\tau), y(τ′)≈α∫a(u+τ′−τ)a(u)du=αRaa(τ′−τ),
也就是码的自相关函数在 τ′=τ\tau'=\tauτ′=τ 处取主峰。若码设计使 R_aa(Δ)R\_{aa}(\Delta)R_aa(Δ) 在 Δ≠0\Delta\neq 0Δ=0 时足够小(低旁瓣),则输出呈现"一个尖主峰 + 很低背景",这就是文中所谓 thumbtack-like 的数学表达。
A.4 DCM 距离分辨率 ΔR=cT_c2\Delta R=\frac{cT\_c}{2}ΔR=2cT_c 的由来:相关主峰宽度与 chip 宽度同阶
对矩形 chip 波形 p(t)p(t)p(t),其自相关 R_pp(Δ)R\_{pp}(\Delta)R_pp(Δ) 是一个底宽为 2T_c2T\_c2T_c 的三角形;码序列的自相关主峰实际上是各 chip 自相关叠加的结果,因此主峰"有效宽度"与 T_cT\_cT_c 同阶。于是若两目标时延差 KaTeX parse error: Undefined control sequence: \< at position 13: |\Delta\tau|\̲<̲T\_c,两者主峰会显著重叠而难区分,取
Δτ≈Tc⇒ΔR=cΔτ2≈cTc2. \Delta\tau\approx T_c \quad\Rightarrow\quad \Delta R=\frac{c\Delta\tau}{2}\approx \frac{cT_c}{2}. Δτ≈Tc⇒ΔR=2cΔτ≈2cTc.
这与原文给出的结果一致,并进一步用 T_c≈1/BT\_c\approx 1/BT_c≈1/B 得到 ΔR=c2B\Delta R=\frac{c}{2B}ΔR=2Bc。
A.5 速度 FFT:为何 Δv\Delta vΔv 与总相干时间成反比
对某个距离单元,设第 nnn 次重复(间隔为 T_rT\_rT_r,在原文语境中常取 T_r=LT_cT\_r=LT\_cT_r=LT_c)的匹配滤波输出为
z[n]=Aej(2πfDnTr+ϕ0). z[n]=A e^{j(2\pi f_D nT_r+\phi_0)}. z[n]=Aej(2πfDnTr+ϕ0).
这就是离散时间复指数,做 NNN 点 FFT 时可分辨的最小频差为
ΔfD=1NTr. \Delta f_D=\frac{1}{NT_r}. ΔfD=NTr1.
由 f_D=2vf_ccf\_D=\frac{2vf\_c}{c}f_D=c2vf_c,速度分辨率为
Δv=c2fcΔfD=c2fc⋅1NTr=c2fc N LTc, \Delta v=\frac{c}{2f_c}\Delta f_D =\frac{c}{2f_c}\cdot\frac{1}{NT_r} =\frac{c}{2f_c\,N\,LT_c}, Δv=2fccΔfD=2fcc⋅NTr1=2fcNLTcc,
与原文一致。
A.6 ISF(KKK)为何可写成带宽比:从功率守恒到 PSD 变换
设 RF 端干扰在频域内近似均匀铺展在带宽 ΔF_RF\Delta F\{\mathrm{RF}}ΔF_RF 上,总功率为 P_intP\{\mathrm{int}}P_int,则其 RF 端 PSD 近似为
PSDRF≈PintΔFRF. \mathrm{PSD}{\mathrm{RF}}\approx \frac{P{\mathrm{int}}}{\Delta F_{\mathrm{RF}}}. PSDRF≈ΔFRFPint.
经过受害雷达的下变频与滤波后,干扰能量被映射到基带的有效带宽 ΔF_BB\Delta F\{\mathrm{BB}}ΔF_BB。在不考虑额外增益/损耗(或把其并入 P_intP\{\mathrm{int}}P_int)的前提下,总功率仍约为 P_intP\_{\mathrm{int}}P_int,因此基带 PSD 近似为
PSDBB≈PintΔFBB. \mathrm{PSD}{\mathrm{BB}}\approx \frac{P{\mathrm{int}}}{\Delta F_{\mathrm{BB}}}. PSDBB≈ΔFBBPint.
二者比值为
K=PSDBBPSDRF≈Pint/ΔFBBPint/ΔFRF=ΔFRFΔFBB, K=\frac{\mathrm{PSD}{\mathrm{BB}}}{\mathrm{PSD}{\mathrm{RF}}} \approx \frac{P_{\mathrm{int}}/\Delta F_{\mathrm{BB}}}{P_{\mathrm{int}}/\Delta F_{\mathrm{RF}}} =\frac{\Delta F_{\mathrm{RF}}}{\Delta F_{\mathrm{BB}}}, K=PSDRFPSDBB≈Pint/ΔFRFPint/ΔFBB=ΔFBBΔFRF,
这就是原文给出的 ISF 表达式。
在 FMCW↔FMCW 中,ΔF_BB\Delta F\{\mathrm{BB}}ΔF_BB 与两 chirp 的相对斜率(交叉快慢)有关:交叉越慢,干扰在通带内停留越久,等效 ΔF_BB\Delta F\{\mathrm{BB}}ΔF_BB 越小,KKK 越大;原文用 K=1K=1K=1 与 K=10K=10K=10 的示意说明这一点。而涉及 DCM 时,干扰更接近扩频噪声样分布,通常不会被显著压窄,因此 KKK 往往接近 1,这也是原文强调 DCM 更抗互扰的核心之一。
B.1 FMCW:考虑多普勒后的"解调(dechirp)"基带信号推导
为避免三角函数干扰推导,使用复包络。设发射 chirp 的瞬时频率为
fT(t)=f0+St,S=BTc, f_T(t)=f_0+St,\qquad S=\frac{B}{T_c}, fT(t)=f0+St,S=TcB,
其相位为
θT(t)=2π∫0tfT(u) du=2π(f0t+S2t2), \theta_T(t)=2\pi\int_0^t f_T(u)\,du =2\pi\left(f_0 t+\frac{S}{2}t^2\right), θT(t)=2π∫0tfT(u)du=2π(f0t+2St2),
发射复信号
xT(t)=ejθT(t). x_T(t)=e^{j\theta_T(t)}. xT(t)=ejθT(t).
对一个以径向速度 vvv 运动的点目标,回波除了往返延时 τ\tauτ 外,还会引入多普勒频移 f_Df\_Df_D。原文给出多普勒关系
fD=2vfcc. f_D=\frac{2vf_c}{c}. fD=c2vfc.
常用近似模型是:回波为延时并叠加多普勒调制(把多普勒视为基带频移):
xR(t)=α ej2πfDt xT(t−τ). x_R(t)=\alpha\,e^{j2\pi f_D t}\,x_T(t-\tau). xR(t)=αej2πfDtxT(t−τ).
代入 x_T(t−τ)x\_T(t-\tau)x_T(t−τ):
xR(t)=α ej2πfDtexp (j2π[f0(t−τ)+S2(t−τ)2]). x_R(t)=\alpha\,e^{j2\pi f_D t}\exp\!\Bigl(j2\pi\left[f_0(t-\tau)+\frac{S}{2}(t-\tau)^2\right]\Bigr). xR(t)=αej2πfDtexp(j2π[f0(t−τ)+2S(t−τ)2]).
dechirp(与本振 x_T∗(t)x\_T^*(t)x_T∗(t) 相乘):
y(t)=xR(t)xT∗(t)=α ej2πfDtexp (j2π[f0(t−τ)+S2(t−τ)2−f0t−S2t2]). y(t)=x_R(t)x_T^*(t) =\alpha\,e^{j2\pi f_D t}\exp\!\Bigl(j2\pi\left[f_0(t-\tau)+\frac{S}{2}(t-\tau)^2-f_0t-\frac{S}{2}t^2\right]\Bigr). y(t)=xR(t)xT∗(t)=αej2πfDtexp(j2π[f0(t−τ)+2S(t−τ)2−f0t−2St2]).
整理括号内项:
f0(t−τ)−f0t=−f0τ, f_0(t-\tau)-f_0t=-f_0\tau, f0(t−τ)−f0t=−f0τ,
S2((t−τ)2−t2)=S2(−2tτ+τ2)=−Stτ+S2τ2. \frac{S}{2}\bigl((t-\tau)^2-t^2\bigr)=\frac{S}{2}\bigl(-2t\tau+\tau^2\bigr)=-S t\tau+\frac{S}{2}\tau^2. 2S((t−τ)2−t2)=2S(−2tτ+τ2)=−Stτ+2Sτ2.
因此
y(t)=αexp (j2π[(fD−Sτ)t+(−f0τ+S2τ2)⏟常相位]). y(t)=\alpha \exp\!\Bigl(j2\pi\bigl[(f_D-S\tau)t + \underbrace{(-f_0\tau+\tfrac{S}{2}\tau^2)}_{\text{常相位}}\bigr]\Bigr). y(t)=αexp(j2π[(fD−Sτ)t+常相位 (−f0τ+2Sτ2)]).
这表明基带(慢时间内)是一个频率为
fb=Sτ−fD f_b = S\tau - f_D fb=Sτ−fD
的复指数(符号正负视具体混频定义而定,幅度与常相位无关距离估计)。若忽略多普勒或 f_D≪Sτf\_D\ll S\tauf_D≪Sτ,就退化回静止目标 f_b≈Sτf\_b\approx S\tauf_b≈Sτ 的常见结论。
把 τ=2Rc\tau=\frac{2R}{c}τ=c2R 代入得
fb(R,v)=2SRc−2vfcc=2RcBTc−2vfcc. f_b(R,v)=\frac{2SR}{c}-\frac{2vf_c}{c} =\frac{2R}{c}\frac{B}{T_c}-\frac{2vf_c}{c}. fb(R,v)=c2SR−c2vfc=c2RTcB−c2vfc.
这条式子的含义是:单次 chirp 的拍频同时包含距离项与速度项,因此会出现距离-速度耦合,工程上通常用多 chirp 形成二维 FFT(Range-Doppler)来分离。
B.2 FMCW:上下扫(up/down chirp)如何消除距离-速度耦合
如果再发一个下扫 chirp(斜率 −S-S−S),则同样推导会得到
- 上扫拍频:
fb(+)=Sτ−fD, f_b^{(+)} = S\tau - f_D, fb(+)=Sτ−fD,
- 下扫拍频:
fb(−)=−Sτ−fD. f_b^{(-)} = -S\tau - f_D. fb(−)=−Sτ−fD.
将两者线性组合:
距离项(由差得到):
fb(+)−fb(−)=2Sτ⇒τ=fb(+)−fb(−)2S, f_b^{(+)}-f_b^{(-)} = 2S\tau \quad\Rightarrow\quad \tau=\frac{f_b^{(+)}-f_b^{(-)}}{2S}, fb(+)−fb(−)=2Sτ⇒τ=2Sfb(+)−fb(−),
因此距离估计为
R=cτ2=c4S(fb(+)−fb(−)). R=\frac{c\tau}{2}=\frac{c}{4S}\bigl(f_b^{(+)}-f_b^{(-)}\bigr). R=2cτ=4Sc(fb(+)−fb(−)).
速度项(由和得到):
fb(+)+fb(−)=−2fD⇒fD=−12(fb(+)+fb(−)), f_b^{(+)}+f_b^{(-)} = -2f_D \quad\Rightarrow\quad f_D=-\frac{1}{2}\bigl(f_b^{(+)}+f_b^{(-)}\bigr), fb(+)+fb(−)=−2fD⇒fD=−21(fb(+)+fb(−)),
因此速度估计为
v=cfD2fc=−c4fc(fb(+)+fb(−)). v=\frac{cf_D}{2f_c} =-\frac{c}{4f_c}\bigl(f_b^{(+)}+f_b^{(-)}\bigr). v=2fccfD=−4fcc(fb(+)+fb(−)).
这给出一种"单帧内靠上下扫解耦"的经典路径;若只用同斜率多 chirp,则改为二维 FFT 解耦(见下一节)。
B.3 FMCW:二维 FFT(Range-Doppler)与栅格分辨率公式
设一帧包含 MMM 个 chirp,每个 chirp 内采 NNN 个快时间样本。将 dechirp 后信号记为 KaTeX parse error: Undefined control sequence: \[ at position 2: y\̲[̲m,n],其中 mmm 是 chirp 索引(慢时间),nnn 是快时间采样点。对单目标,在理想离散模型下可写为
y[m,n]=Aexp (j2π(kRNn+kDMm)), y[m,n]=A \exp\!\left(j2\pi\left(\frac{k_R}{N}n+\frac{k_D}{M}m\right)\right), y[m,n]=Aexp(j2π(NkRn+MkDm)),
其中 k_Rk\_Rk_R 与拍频有关,k_Dk\_Dk_D 与多普勒有关。对 nnn 做 NNN 点 FFT 得距离谱,对 mmm 做 MMM 点 FFT 得多普勒谱。
快时间频率分辨率(每个 chirp 内)为
Δfb=1Tc, \Delta f_b = \frac{1}{T_c}, Δfb=Tc1,
由 f_b≈Sτ=2SRcf\_b\approx S\tau=\frac{2SR}{c}f_b≈Sτ=c2SR 得距离分辨率
ΔR=c2SΔfb=c2S⋅1Tc=c2(B/Tc)⋅1Tc=c2B, \Delta R=\frac{c}{2S}\Delta f_b =\frac{c}{2S}\cdot\frac{1}{T_c} =\frac{c}{2(B/T_c)}\cdot\frac{1}{T_c} =\frac{c}{2B}, ΔR=2ScΔfb=2Sc⋅Tc1=2(B/Tc)c⋅Tc1=2Bc,
与原文一致。
慢时间多普勒分辨率由总相干观测时间 T_coh=MT_rT\_{\text{coh}}=M T\_rT_coh=MT_r(T_rT\_rT_r 是 chirp 重复周期,常近似 T_r≈T_cT\_r\approx T\_cT_r≈T_c 或含空隙)决定:
ΔfD=1MTr. \Delta f_D=\frac{1}{M T_r}. ΔfD=MTr1.
速度分辨率因此为
Δv=c2fcΔfD=c2fcMTr. \Delta v=\frac{c}{2f_c}\Delta f_D =\frac{c}{2f_c M T_r}. Δv=2fccΔfD=2fcMTrc.
这与 DCM 的结论结构完全同构:都是"速度分辨率 ∝\propto∝ 总相干时间的倒数"。原文给出了 DCM 形式 Δv=c2f_cNT_cL\Delta v=\frac{c}{2f\_c N T\_c L}Δv=2f_cNT_cLc(其中 NNN 对应重复次数,LT_cLT\_cLT_c 对应重复周期)。
B.4 FMCW:最大无歧义距离与采样率的更完整表达
对单 chirp,dechirp 后的拍频最大不应超过 Nyquist:
∣fb∣≤fs2. |f_b| \le \frac{f_s}{2}. ∣fb∣≤2fs.
忽略多普勒项时 f_b=Sτf\_b=S\tauf_b=Sτ,故
Sτmax=fs2⇒τmax=fs2S. S\tau_{\max}=\frac{f_s}{2} \quad\Rightarrow\quad \tau_{\max}=\frac{f_s}{2S}. Sτmax=2fs⇒τmax=2Sfs.
距离上限(无歧义)为
Ru=cτmax2=c2⋅fs2S=cfs4S=cfs4(B/Tc)=cTcfs4B. R_u=\frac{c\tau_{\max}}{2} =\frac{c}{2}\cdot\frac{f_s}{2S} =\frac{c f_s}{4S} =\frac{c f_s}{4(B/T_c)} =\frac{cT_c f_s}{4B}. Ru=2cτmax=2c⋅2Sfs=4Scfs=4(B/Tc)cfs=4BcTcfs.
会发现这比原文的 R_u=cT_cf_s2BR\_u=\frac{cT\_c f\_s}{2B}R_u=2BcT_cf_s 少一个系数 2。差异来自"Nyquist 用 f_sf\_sf_s 还是 f_s/2f\_s/2f_s/2 以及带宽定义"习惯:有些推导把可用拍频带宽视为 KaTeX parse error: Undefined control sequence: \[ at position 1: \̲[̲0,f\_s) 或把实信号与复采样的等效带宽不同处理。原文给出
Ru=cTcfs2B, R_u=\frac{cT_c f_s}{2B}, Ru=2BcTcfs,
我们可理解为它取了更宽的"可用 IF 带宽"定义(或按实采样、双边谱折算)。
工程实践里你只要记住:R_uR\_uR_u 与 T_cT\_cT_c、f_sf\_sf_s 成正比,与 BBB 成反比,常数因子由实现细节决定。
B.5 DCM:离散匹配滤波的"处理增益(processing gain)"与输出 SNR
令长度为 LLL 的 BPSK 码为 KaTeX parse error: Undefined control sequence: \[ at position 2: a\̲[̲\ell]\in{\pm1}。假设在某距离单元、某一次重复中,相关器输入采样(对齐到 chip 率)为
r[ℓ]=αa[ℓ]+n[ℓ], r[\ell] = \alpha a[\ell] + n[\ell], r[ℓ]=αa[ℓ]+n[ℓ],
其中 KaTeX parse error: Undefined control sequence: \[ at position 2: n\̲[̲\ell] 为零均值白噪声,方差 σ2\sigma^2σ2。
匹配滤波(相关)输出取
y=∑ℓ=0L−1r[ℓ]a[ℓ]. y = \sum_{\ell=0}^{L-1} r[\ell] a[\ell]. y=ℓ=0∑L−1r[ℓ]a[ℓ].
代入 KaTeX parse error: Undefined control sequence: \[ at position 2: r\̲[̲\ell]:
y=∑ℓ=0L−1(αa[ℓ]+n[ℓ])a[ℓ]=α∑ℓ=0L−1a2[ℓ]+∑ℓ=0L−1n[ℓ]a[ℓ]. y=\sum_{\ell=0}^{L-1} (\alpha a[\ell] + n[\ell])a[\ell] =\alpha\sum_{\ell=0}^{L-1} a^2[\ell]+\sum_{\ell=0}^{L-1} n[\ell]a[\ell]. y=ℓ=0∑L−1(αa[ℓ]+n[ℓ])a[ℓ]=αℓ=0∑L−1a2[ℓ]+ℓ=0∑L−1n[ℓ]a[ℓ].
因为 KaTeX parse error: Undefined control sequence: \[ at position 4: a^2\̲[̲\ell]=1,
y=αL+n~,n~=∑ℓ=0L−1n[ℓ]a[ℓ]. y = \alpha L + \tilde n, \qquad \tilde n = \sum_{\ell=0}^{L-1} n[\ell]a[\ell]. y=αL+n~,n~=ℓ=0∑L−1n[ℓ]a[ℓ].
由于 KaTeX parse error: Undefined control sequence: \[ at position 2: a\̲[̲\ell] 只是 ±1\pm1±1 的符号翻转,噪声统计不变:
E[n~]=0,Var(n~)=∑ℓ=0L−1Var(n[ℓ]a[ℓ])=Lσ2. \mathbb{E}[\tilde n]=0, \qquad \mathrm{Var}(\tilde n)=\sum_{\ell=0}^{L-1}\mathrm{Var}(n[\ell]a[\ell])=L\sigma^2. E[n~]=0,Var(n~)=ℓ=0∑L−1Var(n[ℓ]a[ℓ])=Lσ2.
因此输出 SNR(幅度平方比)为
SNRout=∣αL∣2Lσ2=∣α∣2σ2 L. \mathrm{SNR}_{\text{out}} =\frac{|\alpha L|^2}{L\sigma^2} =\frac{|\alpha|^2}{\sigma^2}\,L. SNRout=Lσ2∣αL∣2=σ2∣α∣2L.
这给出典型的处理增益:
Gp=L. G_p = L. Gp=L.
它解释了为什么 DCM 能在很低瞬时功率密度下通过长码相关把目标"拉出来",同时也解释了为什么码长对 MIMO CDM 的隔离很关键:码越长,相关峰越尖、互相关泄漏相对越小(见后续)。原文在讨论多 Tx 码隔离时强调"主要靠更长码长提升通道隔离"。
B.6 DCM:周期码的距离歧义与"循环相关"形式
若发送的是周期重复码(周期 LT_cLT\_cLT_c),则接收的延时若超过一个周期,会"折回"到同一相关峰附近,从而出现距离歧义。原文给出最大无歧义距离
Ru=cTcL2. R_u=\frac{cT_cL}{2}. Ru=2cTcL.
用离散形式可更清楚地看到:周期相关相当于循环相关
Raacirc[k]=∑ℓ=0L−1a[ℓ] a[(ℓ−k) mod L]. R_{aa}^{\text{circ}}[k]=\sum_{\ell=0}^{L-1} a[\ell]\,a[(\ell-k)\bmod L]. Raacirc[k]=ℓ=0∑L−1a[ℓ]a[(ℓ−k)modL].
当回波延时对应的 chip 偏移为 k_0k\_0k_0,相关输出将在 k=k_0k=k\_0k=k_0 与所有 k_0+mLk\_0+mLk_0+mL 的等价类上重复出现,这正对应距离轴上每隔 R_uR\_uR_u 周期性重复。
B.7 旁瓣、HCR 与模糊函数:为什么 DCM 更"拇指钉(thumbtack-like)"
原文用"thumbtack-like range response"来描述 DCM,并把它与更好的 HCR 关联。
这个说法在雷达理论里通常由 模糊函数(Ambiguity Function, AF) 精确刻画。对基带信号 s(t)s(t)s(t),AF 定义为
χ(τ,f)=∫−∞∞s(t) s∗(t−τ) e−j2πft dt. \chi(\tau,f)=\int_{-\infty}^{\infty} s(t)\,s^*(t-\tau)\,e^{-j2\pi f t}\,dt. χ(τ,f)=∫−∞∞s(t)s∗(t−τ)e−j2πftdt.
它表示:当匹配滤波器假设延时为 τ\tauτ、多普勒为 fff 时,对真实回波的响应强度。理想的"拇指钉"意味着:在 (τ,f)=(0,0)(\tau,f)=(0,0)(τ,f)=(0,0) 有一个尖峰,而离开原点后迅速衰减,旁瓣低且局部化。
1)相位编码(DCM/PSK)近似 AF 形态
把 s(t)=a(t)ej2πf_cts(t)=a(t)e^{j2\pi f\_c t}s(t)=a(t)ej2πf_ct 视为载波乘码包络 a(t)a(t)a(t)(BPSK 时 a(t)=±1a(t)=\pm1a(t)=±1)。在下变频后,AF 主要由 a(t)a(t)a(t) 决定:
χ(τ,f)≈∫a(t) a∗(t−τ) e−j2πft dt. \chi(\tau,f)\approx \int a(t)\,a^*(t-\tau)\,e^{-j2\pi f t}\,dt. χ(τ,f)≈∫a(t)a∗(t−τ)e−j2πftdt.
若 a(t)a(t)a(t) 是伪随机码,其自相关在 τ≠0\tau\neq 0τ=0 时接近零(旁瓣接近噪声地板),并且由于相位随机化,多普勒维度的能量也不形成长条纹,从而 χ(τ,f)\chi(\tau,f)χ(τ,f) 在二维上更像"点状主峰"。
2)FMCW 的 AF 为什么更容易形成耦合"条纹"
对 FMCW 的 s(t)=ej2π(f_0t+S2t2)s(t)=e^{j2\pi(f\_0 t+\frac{S}{2}t^2)}s(t)=ej2π(f_0t+2St2),代入 AF 定义会出现平方项导致的耦合,直观上会产生沿某些斜率方向拉长的能量脊线,这对应工程上常说的 range-Doppler coupling(需要二维处理去分离),也意味着强目标能量在某个维度更容易"拖尾",从而压制近邻弱目标。
把"拖尾"与 HCR 联系起来,可以用一个抽象但很实用的检测条件来写:设距离响应(或二维响应在某切片上)为 KaTeX parse error: Undefined control sequence: \[ at position 2: h\̲[̲k],强目标幅度为 A_sA\_sA_s,弱目标幅度为 A_wA\wA_w,强目标旁瓣在弱目标位置的相对高度为 ∣h_sl∣|h\{\text{sl}}|∣h_sl∣,噪声标准差为 σ\sigmaσ,弱目标能被可靠检测的大致条件可写成
Aw≳γσ+As∣hsl∣, A_w \gtrsim \gamma\sigma + A_s |h_{\text{sl}}|, Aw≳γσ+As∣hsl∣,
其中 γ\gammaγ 与虚警概率门限有关。对同样的 ΔR=c2B\Delta R=\frac{c}{2B}ΔR=2Bc ,若某体制让 ∣h_sl∣|h\_{\text{sl}}|∣h_sl∣ 更小、衰减更快,则在同样 A_s/A_wA\_s/A\_wA_s/A_w 下弱目标更容易满足不等式,这就是 HCR 的数学影子。
B.8 CDM MIMO:码间互相关泄漏功率与"通道隔离"近似
原文指出 DCM 天然支持 CDM MIMO:不同 Tx 用不同码,同时发射,靠相关分离;通道隔离主要靠码长提升。设 Txiii 使用码 KaTeX parse error: Undefined control sequence: \[ at position 5: a\_i\̲[̲\ell],Txjjj 使用码 KaTeX parse error: Undefined control sequence: \[ at position 5: a\_j\̲[̲\ell]。在 Rx 端对 Txiii 做匹配滤波(相关):
yi=∑ℓ=0L−1r[ℓ]ai[ℓ]. y_i = \sum_{\ell=0}^{L-1} r[\ell] a_i[\ell]. yi=ℓ=0∑L−1r[ℓ]ai[ℓ].
而接收信号包含多 Tx 叠加(忽略噪声与不同延时以突出码分离):
r[ℓ]=∑j=1NTxαjaj[ℓ]+n[ℓ]. r[\ell]=\sum_{j=1}^{N_{\text{Tx}}} \alpha_j a_j[\ell] + n[\ell]. r[ℓ]=j=1∑NTxαjaj[ℓ]+n[ℓ].
代入得
yi=∑jαj∑ℓ=0L−1aj[ℓ]ai[ℓ]+∑ℓn[ℓ]ai[ℓ]=αiL+∑j≠iαjCji+n~, y_i=\sum_{j}\alpha_j\sum_{\ell=0}^{L-1} a_j[\ell]a_i[\ell] + \sum_{\ell} n[\ell]a_i[\ell] =\alpha_i L + \sum_{j\ne i}\alpha_j C_{ji} + \tilde n, yi=j∑αjℓ=0∑L−1aj[ℓ]ai[ℓ]+ℓ∑n[ℓ]ai[ℓ]=αiL+j=i∑αjCji+n~,
其中
Cji=∑ℓ=0L−1aj[ℓ]ai[ℓ] C_{ji}=\sum_{\ell=0}^{L-1} a_j[\ell]a_i[\ell] Cji=ℓ=0∑L−1aj[ℓ]ai[ℓ]
是零延时互相关值(严格来说还应考虑非零延时互相关,但对同时对齐的码分离这是主要项)。
定义归一化互相关系数
ρji=1LCji, \rho_{ji}=\frac{1}{L}C_{ji}, ρji=L1Cji,
则泄漏项为
∑j≠iαjCji=L∑j≠iαjρji. \sum_{j\ne i}\alpha_j C_{ji}=L\sum_{j\ne i}\alpha_j \rho_{ji}. j=i∑αjCji=Lj=i∑αjρji.
如果码设计使 ρ_ji\rho\_{ji}ρ_ji 近似零均值、方差约为 1/L1/L1/L(伪随机码常见量级),则单个干扰 Tx 的泄漏幅度的均方根(RMS)尺度约为
∣αj∣LE[ρji2]∼∣αj∣L⋅1L=∣αj∣L. |\alpha_j| L \sqrt{\mathbb{E}[\rho_{ji}^2]} \sim |\alpha_j| L \cdot \frac{1}{\sqrt{L}} =|\alpha_j|\sqrt{L}. ∣αj∣LE[ρji2] ∼∣αj∣L⋅L 1=∣αj∣L .
而主信号幅度是 ∣α_i∣L|\alpha\_i|L∣α_i∣L,因此"主峰与泄漏的幅度比"尺度大致为
∣αi∣L∣αj∣L=∣αi∣∣αj∣L. \frac{|\alpha_i|L}{|\alpha_j|\sqrt{L}} = \frac{|\alpha_i|}{|\alpha_j|}\sqrt{L}. ∣αj∣L ∣αi∣L=∣αj∣∣αi∣L .
这揭示了:在同功率同路径损耗下(∣α_i∣≈∣α_j∣|\alpha\_i|\approx|\alpha\_j|∣α_i∣≈∣α_j∣),通道隔离的"典型尺度"随 L\sqrt{L}L 提升;若看功率比则随 LLL 提升。这与原文"主要靠更长码长提升隔离"的叙述在数学上吻合。
B.9 FMCW↔FMCW 干扰:KKK 与相对斜率差的近似关系(从几何到带宽比)
原文定义 ISF 为
K=PSDBBPSDRF=ΔFRFΔFBB, K=\frac{\mathrm{PSD}{\mathrm{BB}}}{\mathrm{PSD}{\mathrm{RF}}} =\frac{\Delta F_{\mathrm{RF}}}{\Delta F_{\mathrm{BB}}}, K=PSDRFPSDBB=ΔFBBΔFRF,
并指出当两雷达斜率更相似时 KKK 会更大(例如可到 10)。
下面给出一个常用的一阶近似推导框架,说明为什么 ΔF_BB\Delta F\_{\mathrm{BB}}ΔF_BB 会与"斜率差"相关。
设受害雷达(victim)发射/本振 chirp 的瞬时频率为
fv(t)=fv0+Svt, f_v(t)=f_{v0}+S_v t, fv(t)=fv0+Svt,
干扰雷达(interferer)发射 chirp 的瞬时频率为
fi(t)=fi0+Sit. f_i(t)=f_{i0}+S_i t. fi(t)=fi0+Sit.
忽略传播时延差(只关注相对斜率效应),干扰信号进入受害雷达并与 f_v(t)f\_v(t)f_v(t) dechirp 后,得到的瞬时差频近似为
fΔ(t)=fi(t)−fv(t)=(fi0−fv0)+(Si−Sv)t. f_{\Delta}(t)=f_i(t)-f_v(t)=(f_{i0}-f_{v0})+(S_i-S_v)t. fΔ(t)=fi(t)−fv(t)=(fi0−fv0)+(Si−Sv)t.
定义斜率差
ΔS=Si−Sv, \Delta S = S_i-S_v, ΔS=Si−Sv,
则
fΔ(t)=Δf0+ΔS t,Δf0=fi0−fv0. f_{\Delta}(t)=\Delta f_0 + \Delta S\,t, \qquad \Delta f_0=f_{i0}-f_{v0}. fΔ(t)=Δf0+ΔSt,Δf0=fi0−fv0.
受害雷达的基带/中频链路通常只允许 ∣f_Δ(t)∣≤B_IF/2|f\{\Delta}(t)|\le B\{\mathrm{IF}}/2∣f_Δ(t)∣≤B_IF/2(或 B_IFB\_{\mathrm{IF}}B_IF 的某种定义),也就是说干扰"落入通带"的时间区间满足
∣Δf0+ΔS t∣≤BIF2. | \Delta f_0+\Delta S\,t| \le \frac{B_{\mathrm{IF}}}{2}. ∣Δf0+ΔSt∣≤2BIF.
这是一个关于 ttt 的区间,其长度(干扰持续时间)近似为
Tint≈BIF∣ΔS∣. T_{\mathrm{int}}\approx \frac{B_{\mathrm{IF}}}{|\Delta S|}. Tint≈∣ΔS∣BIF.
从频域看,干扰在基带被"扫过"的频率跨度大致就是 B_IFB\_{\mathrm{IF}}B_IF,但它的等效"谱集中程度"与持续时间有关:持续时间越长,频谱主瓣越窄,等效占用带宽越小。用时频不确定性做粗略估计,可取
ΔFBB∼1Tint≈∣ΔS∣BIF. \Delta F_{\mathrm{BB}} \sim \frac{1}{T_{\mathrm{int}}} \approx \frac{|\Delta S|}{B_{\mathrm{IF}}}. ΔFBB∼Tint1≈BIF∣ΔS∣.
于是带宽比形式的 KKK 变为
K=ΔFRFΔFBB∼ΔFRF⋅BIF∣ΔS∣. K=\frac{\Delta F_{\mathrm{RF}}}{\Delta F_{\mathrm{BB}}} \sim \Delta F_{\mathrm{RF}} \cdot \frac{B_{\mathrm{IF}}}{|\Delta S|}. K=ΔFBBΔFRF∼ΔFRF⋅∣ΔS∣BIF.
这给出一个与原文叙述一致的方向性结论:当两雷达斜率越接近(∣ΔS∣|\Delta S|∣ΔS∣ 越小),则 ΔF_BB\Delta F\_{\mathrm{BB}}ΔF_BB 越小,KKK 越大,干扰 PSD 越高,INR 越糟。原文用图示对比 K=1K=1K=1 与 K=10K=10K=10 来表达这种敏感性。同时,这也解释了为什么涉及 DCM 时往往 K≈1K\approx 1K≈1:扩频相位码使干扰在解调后更像宽带噪声,不容易被"扫过通带的几何关系"压缩成窄带集中能量。原文明确指出 DCM 情形通常 KKK 接近 1。
B.10 INR 与检测门限:把 KKK、噪声底抬升与虚警/漏检连起来
原文用
INR=PSDintPSDnoise \mathrm{INR}=\frac{\mathrm{PSD}{\mathrm{int}}}{\mathrm{PSD}{\mathrm{noise}}} INR=PSDnoisePSDint
刻画干扰相对噪声的程度。
若系统噪声(热噪声+接收机噪声)等效 PSD 为 N_0N\_0N_0,干扰等效 PSD 为 I_0I\_0I_0,则
INR=I0N0. \mathrm{INR}=\frac{I_0}{N_0}. INR=N0I0.
在功率域,对某个处理带宽 B_pB\_pB_p(例如 FFT 一个 bin 的等效带宽或匹配滤波输出的噪声等效带宽),噪声功率与干扰功率为
PN=N0Bp,PI=I0Bp, P_N = N_0 B_p,\qquad P_I = I_0 B_p, PN=N0Bp,PI=I0Bp,
因此总背景功率
PN+I=(N0+I0)Bp=N0(1+INR)Bp. P_{N+I}=(N_0+I_0)B_p = N_0(1+\mathrm{INR})B_p. PN+I=(N0+I0)Bp=N0(1+INR)Bp.
若检测器采用恒虚警率(CFAR)思想,门限通常与背景功率成比例,即
T∝PN+I∝(1+INR). T \propto P_{N+I}\propto (1+\mathrm{INR}). T∝PN+I∝(1+INR).
这意味着 INR 上升会抬高门限,导致弱目标更难超过门限而漏检;反过来若门限不变则虚警会上升。把 ISF 写入 INR:若 RF 端干扰 PSD 为 I_RFI\{\mathrm{RF}}I_RF,基带 PSD 为 I_BB=KI_RFI\{\mathrm{BB}}=K I\_{\mathrm{RF}}I_BB=KI_RF,则
INR=KIRFN0. \mathrm{INR}=\frac{K I_{\mathrm{RF}}}{N_0}. INR=N0KIRF.
因此在 FMCW↔FMCW 中,当 KKK 因斜率接近而变大时,检测性能会以近似线性的方式恶化,这正是原文引入 KKK 的工程动机。
B.11 把"距离分辨率相同但 HCR 不同"写成可计算的旁瓣指标
原文强调 HCR 是车载更关心的指标:强弱目标相邻时能否分开。
用一维距离响应来刻画,设系统对点目标的归一化脉冲响应为 KaTeX parse error: Undefined control sequence: \[ at position 2: h\̲[̲k](距离 bin 的离散响应),强目标在 bin k_sk\_sk_s,弱目标在 k_wk\_wk_w。则强目标在弱目标位置贡献幅度为 KaTeX parse error: Undefined control sequence: \[ at position 7: A\_s h\̲[̲k\_w-k\_s]。弱目标可检测的粗条件可写为
Aw≥T+As∣h[kw−ks]∣. A_w \ge T + A_s |h[k_w-k_s]|. Aw≥T+As∣h[kw−ks]∣.
把对比度定义为
CR=AsAw, \mathrm{CR}=\frac{A_s}{A_w}, CR=AwAs,
则需要满足
1CR≥TAs+∣h[Δk]∣,Δk=kw−ks. \frac{1}{\mathrm{CR}} \ge \frac{T}{A_s} + |h[\Delta k]|,\qquad \Delta k=k_w-k_s. CR1≥AsT+∣h[Δk]∣,Δk=kw−ks.
当 CR\mathrm{CR}CR 很大时,主导项是 KaTeX parse error: Undefined control sequence: \[ at position 3: |h\̲[̲\Delta k]|,即旁瓣/泄漏高度。因此对固定对比度 CR\mathrm{CR}CR,HCR 的"最小可分距离"本质上是解下面的不等式得到的最小 Δk\Delta kΔk:
∣h[Δk]∣≤1CR−TAs. |h[\Delta k]| \le \frac{1}{\mathrm{CR}} - \frac{T}{A_s}. ∣h[Δk]∣≤CR1−AsT.
如果 DCM 的 KaTeX parse error: Undefined control sequence: \[ at position 3: |h\̲[̲\Delta k]| 衰减更快、更低旁瓣(接近理想自相关),则满足不等式的最小 Δk\Delta kΔk 更小,于是 HCR 更好;这与原文"thumbtack-like range response → better HCR"的论断一致。