为了更好的帮助大家备赛。我们预计在未来的每一天都针对一道去年美赛题目以及其对应的5篇O奖论文进行赏析,具体包含题目介绍、每篇论文获O奖原因介绍等。
具体而言,针对每一个问,将每一篇O奖论文进行横向的对比,进行拆解分析,分析正常的思路与O奖思路的区别,如何学习O奖思路的建立。最后,将5篇论文放在一起,赏析各自论文的绘图、排版以及非技术性文章等等
2025年ICM F题
国家网络安全政策的有效性分析
核心任务:建立一个理论来解释"什么构成强有力的国家网络安全政策",并用数据驱动的分析来支持你的理论。
需要探索的问题:
l网络犯罪的全球分布:哪些国家是网络犯罪的高发目标?哪里的网络犯罪成功率高/被阻止?哪里有报告和起诉?有什么规律?
l政策与犯罪分布的关联:对比各国公开的网络安全政策与网络犯罪分布,找出哪些政策条款特别有效(或无效)------包括预防、起诉和其他减缓措施。
l国家人口统计特征的相关性:互联网普及率、财富、教育水平等与网络犯罪分布有什么关联?
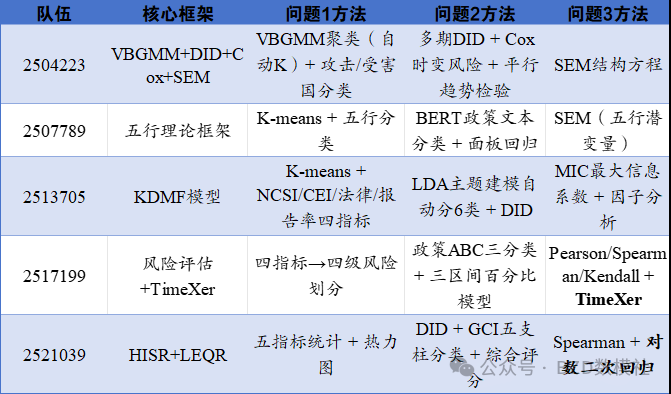
问题1方法对比
l网络犯罪的全球分布:哪些国家是网络犯罪的高发目标?哪里的网络犯罪成功率高/被阻止?哪里有报告和起诉?有什么规律?
|------------|-------------------------------------------------|---------------------|--------------|
| 队伍 | 聚类 / 分类方法 | 指标体系 | 验证方式 |
| 2504223 | VBGMM (自动确定 K ) | 攻击国/受害国双视角 | 与GCI对比 |
| 2507789 | K-means + 五行分类 | 金木水火土五类 | 理论推演 |
| 2513705 | K-means + 肘部法则 | NCSI/CEI/法律/报告率 | 轮廓系数 |
| 2517199 | 阈值划分四级风险 | 发现率/阻止率/损失率/严重性 | 与GCI对比 |
| 2521039 | 统计描述+热力图 | 目标数/成功率/阻止率/报告率/起诉率 | 可视化验证 |
从GMM到VBGMM的演进
- 传统GMM(高斯混合模型)
GMM假设数据由K个高斯分布混合生成,使用EM算法估计参数:
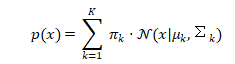
问题:必须预先指定K值(聚类数),选错K会导致过拟合或欠拟合。
- VBGMM(变分贝叶斯高斯混合模型)
VBGMM在GMM基础上引入贝叶斯推断,核心改进:
|-------|-----------|--------------|
| 特性 | GMM | VBGMM |
| 聚类数K | 需预先指定 | 自动确定(设置上限即可) |
| 参数估计 | 点估计(EM算法) | 分布估计(变分推断) |
| 过拟合风险 | 较高 | 较低(贝叶斯正则化) |
自动确定K的原理:
l设置一个较大的K上限(如K=10)
l模型训练过程中,不需要的聚类簇的混合权重会自动趋近于0
l最终只保留有效的聚类数
问题2方法对比
政策与犯罪分布的关联:对比各国公开的网络安全政策与网络犯罪分布,找出哪些政策条款特别有效(或无效)------包括预防、起诉和其他减缓措施。
|------------|----------------|----------------|----------------|--------------|
| 队伍 | 因果推断方法 | 政策分类方式 | 时间效应分析 | 验证检验 |
| 2504223 | 多期DID | GCI五维度 | Cox生存分析 | 平行趋势+安慰剂 |
| 2507789 | 面板回归 | BERT文本分类 | 无 | 无 |
| 2513705 | DID | LDA主题建模自动分6类 | 无 | 平行趋势 |
| 2517199 | 百分比变化分析 | 人工ABC三分类 | 三区间分析 | 无 |
| 2521039 | DID | GCI五支柱 | 无 | 平行趋势 |
DID = (实验组政策后 - 实验组政策前) - (对照组政策后 - 对照组政策前)
基本模型

问题3方法对比
l国家人口统计特征的相关性:互联网普及率、财富、教育水平等与网络犯罪分布有什么关联?
|------------|--------------------------|-----------------|---------------|
| 队伍 | 相关分析方法 | 回归/预测模型 | 处理非线性 |
| 2504223 | Pearson | SEM结构方程 | 潜变量路径 |
| 2507789 | - | SEM(五行潜变量) | 潜变量 |
| 2513705 | MIC最大信息系数 | 因子分析 | MIC捕捉非线性 |
| 2517199 | Pearson/Spearman/Kendall | TimeXer深度学习 | 注意力机制 |
| 2521039 | Spearman | LEQR对数二次回归 | log²项 |