目录
(一)常见排序
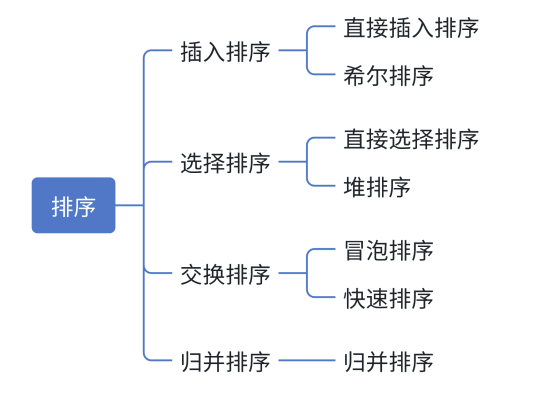
(二)实现各排序
(1)插入排序
①直接插入排序
cpp
void insertSort(int* arr,int size)
{
int end = 0;
int tmp = 0;
for (int i = 0;i < size - 1;++i)
{
end = i;
tmp = end + 1;
while (end >= 0)
{
if (arr[end] > arr[tmp])
{
sort_Swap(&arr[end], &arr[tmp]);
--end;
--tmp;
}
else
{
break;
}
}
}
}思路:每次给一个数找合适位置。
时间复杂度:平均小于O(N^2)。
②希尔排序
cpp
void shellSort(int* arr, int size)
{
int gap = size;
while (gap > 1)
{
gap = gap / 3 + 1;
for (int j = 0; j < size - gap;++j)
{
int end = j;
int tmp = j + gap;
while (end >= 0)
{
if (arr[end] > arr[tmp])
{
sort_Swap(&arr[end], &arr[tmp]);
end -= gap;
tmp -= gap;
}
else
{
break;
}
}
}
}
}思路:每次和gap步后的数比较。
时间复杂度:大概是O(N^1.3)。
(2)选择排序
①直接选择排序
cpp
void selectSort(int arr[],int size)
{
int begin = 0;
int end = size - 1;
while (begin < end)
{
int maxi = begin;
int mini = begin;
for (int i = begin + 1;i <= end;++i)
{
if (arr[maxi] < arr[i])
{
maxi = i;
}
if (arr[mini] > arr[i])
{
mini = i;
}
}
sort_Swap(&arr[mini], &arr[begin]);
if (maxi == begin)
{
maxi = mini;
}
if (maxi != end)
{
sort_Swap(&arr[maxi], &arr[end]);
}
++begin;
--end;
}
}思路:找最小值放最前面,找最大值放最后面。
易错:maxi,mini指向的数字会发生变化。
时间复杂度:O(N^2)
②堆排序
(3)交换排序
①冒泡排序
冒泡排序也是老生常谈了,这里不再赘述。
②快速排序
Ⅰ.hoare版本
findKey函数
cpp
int findKey1(int arr[], int left, int right)
{
int keyi = left;
++left;
while (left <= right)
{
// the left pointer searches for elements greater than the poninter
while (left <= right && arr[left] < arr[keyi])
{
++left;
}
// the right poninter searches for elements smaller than the pointer
while(left <= right && arr[right] > arr[keyi])
{
--right;
}
if (left <= right)
{
sort_Swap(&arr[left], &arr[right]);
}
}
if (right != keyi)
{
sort_Swap(&arr[right], &arr[keyi]);
}
return right;
}quickSort函数
cpp
void quickSort(int arr[],int left,int right)
{
if (left >= right)
{
return;
}
int keyi = findKey1(arr,left,right);
quickSort(arr,left,keyi - 1);
quickSort(arr,keyi+1,right);
}思路:每次给一个基准数找位置,基准数左右各递归。
难点:findKey整个循环在left==right的时候还不能退出。
时间复杂度:NlogN
Ⅱ.挖坑法
(此处代码省略n行)
思路:给基准值挖坑,right找到比基准值小的后和坑交换,left找到比基准值大的后和坑交换,最后基准值填入坑内。
Ⅲ.lomuto前后指针法
findKey函数
cpp
int findKey3(int arr[], int left, int right)
{
int keyi = left;
int prev = left;
int cur = prev + 1;
while(cur <= right)
{
if (arr[cur] < arr[keyi] && ++prev != cur)
{
sort_Swap(&arr[prev], &arr[cur]);
}
++cur;
}
if (prev != keyi)
{
sort_Swap(&arr[prev], &arr[keyi]);
}
return prev;
}思路:prev是cur前一个指针,cur找比基准值小的数,找到后++prev,俩指针交换位置,最后cur遍历完毕,keyi和prev指向的数交换位置。
Ⅳ.非递归版本
cpp
void quickSortNotR(int arr[], int left, int right)
{
ST stack;
STInit(&stack);
STPush(&stack, right);
STPush(&stack, left);
while (!STEmpty(&stack))
{
int left = STTop(&stack);
STPop(&stack);
int right = STTop(&stack);
STPop(&stack);
int keyi = left;
int prev = left;
int cur = prev + 1;
while(cur <= right)
{
if (arr[cur] < arr[keyi] && ++prev != cur)
{
sort_Swap(&arr[cur],&arr[prev]);
}
++cur;
}
if (keyi != prev)
{
sort_Swap(&arr[keyi], &arr[prev]);
}
keyi = prev;
if(keyi + 1 < right)
{
STPush(&stack, right);
STPush(&stack, keyi + 1);
}
if (left < keyi - 1)
{
STPush(&stack, keyi - 1);
STPush(&stack, left);
}
}
}思路:借助栈存放分出来的序列。
(三)归并排序
(1)递归版本
_mergeSort函数
cpp
void _mergeSort(int* arr, int* tmp, int left, int right)
{
if (left >= right)
{
return;
}
int mid = (left + right) / 2;
_mergeSort(arr, tmp, left, mid);
_mergeSort(arr, tmp, mid + 1, right);
int begin1 = left;
int begin2 = mid + 1;
int index = left;
while (begin1 <= mid && begin2 <= right)
{
if (arr[begin1] < arr[begin2])
{
tmp[index++] = arr[begin1++];
}
else
{
tmp[index++] = arr[begin2++];
}
}
while (begin1 <= mid)
{
tmp[index++] = arr[begin1++];
}
while (begin2 <= right)
{
tmp[index++] = arr[begin2++];
}
for (int i = left;i <= right;++i)
{
arr[i] = tmp[i];
}
}mergeSort函数
cpp
void mergeSort(int* arr, int size)
{
int* tmp = (int*)malloc(sizeof(int) * size);
_mergeSort(arr, tmp, 0, size - 1);
free(tmp);
tmp = NULL;
}思路:不断分组,再给最小数量的两个组排序合并,知道合并成原来数组大小。
时间复杂度:NlogN
(四)计数排序
cpp
void countSort(int* arr, int size)
{
int max = arr[0];
int min = arr[0];
for (int i = 1;i < size;++i)
{
if (arr[i] > max)
{
max = arr[i];
}
if (arr[i] < min)
{
min = arr[i];
}
}
int length = max - min + 1;
int* count = (int*)calloc(length,sizeof(int));
if (count == NULL)
{
perror("malloc failed");
exit(1);
}
for (int i = 0;i < size;++i)
{
++count[arr[i] - min];
}
int index = 0;
for (int i = 0;i < length;++i)
{
while(count[i]--)
{
arr[index++] = i + min;
}
}
free(count);
count = NULL;
}思路:计数数组,下标代表要排序的数。
时间复杂度:O(N+range)
(五)稳定性总结
稳定:排序后,重复数据的相对位置不变。
|--------|---------------------|-----------|----------|---------------|-----|
| 排序方法 | 平均情况 | 最好情况 | 最坏情况 | 辅助空间 | 稳定性 |
| 冒泡排序 | O(N^2) | O(N) | O(N^2) | O(1) | 稳定 |
| 直接选择排序 | O(N^2) | O(N^2) | O(N^2) | O(1) | 不稳定 |
| 直接插入排序 | O(N^2) | O(N) | O(N^2) | O(1) | 稳定 |
| 希尔排序 | O(NlogN) ~ O(N^2) | O(N^1.3) | O(N^2) | O(1) | 不稳定 |
| 堆排序 | O(NlogN) | O(N) | O(NlogN) | O(1) | 不稳定 |
| 归并排序 | O(NlogN) | O(NlogN) | O(NlogN) | O(N) | 稳定 |
| 快速排序 | O(NlogN) | O(NlogN) | O(N^2) | O(logN)~O(N) | 不稳定 |