【算法设计与分析】算法概述

hrrrrb2026-01-28 8:19

算法概述

算法概述

本章学习目标

  • 理解算法的定义和五个基本特征
  • 掌握算法复杂度分析方法（时间复杂度和空间复杂度）
  • 了解P类与NP类问题的基本概念
  • 认识常见的NP完全问题

目录

  • [1.1 算法与程序](#1.1 算法与程序)
  • [1.2 算法复杂性分析](#1.2 算法复杂性分析)
  • [1.3 NP完全性理论](#1.3 NP完全性理论)
  • 练习题
  • 本章小结

1.1 算法与程序

1.1.1 什么是算法

算法定义：算法是解决特定问题的一系列明确步骤，具有以下五个基本特征：

特征 英文 说明
有穷性 Finiteness 算法必须在有限步骤内执行完毕
确定性 Definiteness 每一步指令必须明确无歧义
可行性 Effectiveness 每一步操作都可以在有限时间内完成
输入 Input 算法有零个或多个输入
输出 Output 算法产生一个或多个输出

1.1.2 算法与程序的区别

算法和程序是相关但不同的概念：

python 复制代码 
# 示例1：这是一个算法（满足五个特征）
def sum_array(arr: list[int]) -> int:
    """计算数组元素的和"""
    total = 0
    for num in arr:
        total += num
    return total

# 示例2：这不是算法（不满足有穷性）
def infinite_server():
    """无限运行的服务器程序"""
    while True:  # 永不终止！
        handle_request()

# 示例3：这不是算法（不满足确定性）
def ambiguous_algorithm(x):
    """步骤不明确的代码"""
    # 处理数据...（具体步骤不清晰）
    return some_result  # 从哪里来？

关键区别：

  • 所有算法都可以用程序实现，但并非所有程序都是算法
  • 算法强调解决问题的方法和步骤 ，程序强调具体的实现
  • 算法必须在有限步内终止，程序可以是持续运行的（如操作系统）

1.1.3 算法设计原则

评价算法质量的四个标准：

标准 说明 Python体现
正确性 对所有合法输入产生正确输出 单元测试覆盖各种边界情况
可读性 代码易于理解和维护 有意义的变量名、清晰的注释
健壮性 对非法输入有合理的处理 异常处理、输入验证
效率 合理的时间和空间复杂度 选择合适的数据结构和算法
python 复制代码 
# 好的算法示例：二分查找
def binary_search(arr: list[int], target: int) -> int | None:
    """
    在有序数组中二分查找目标值

    Args:
        arr: 升序排列的整数数组
        target: 要查找的目标值

    Returns:
        目标值的索引，如果不存在则返回None
    """
    left, right = 0, len(arr) - 1

    while left <= right:
        mid = (left + right) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            left = mid + 1
        else:
            right = mid - 1

    return None

# 使用示例
if __name__ == "__main__":
    data = [1, 3, 5, 7, 9, 11, 13]
    print(binary_search(data, 7))   # 输出: 3
    print(binary_search(data, 8))   # 输出: None
python 复制代码 
# 不好的算法示例：同一问题的糟糕实现
def f(a, x):
    i = 0
    j = len(a) - 1
    while i <= j:
        m = (i + j) // 2
        if a[m] == x:
            return m
        # 逻辑混乱，难以理解
        i = m + 1 if a[m] < x else i
        j = m - 1 if a[m] > x else j
    return -1  # 返回值不一致（None vs -1）

代码风格对比：

  • 使用有意义的变量名（arr, target vs a, x）
  • 添加清晰的docstring文档
  • 一致的返回值类型
  • 添加边界条件处理

1.2 算法复杂性分析

1.2.1 为什么需要复杂度分析

复杂度分析是算法设计的核心工具，它帮助我们在不实际运行代码的情况下评估算法效率。

问题：为什么不能只靠实际运行时间来评价算法？

  1. 硬件依赖：同样的代码在不同机器上运行时间不同
  2. 实现依赖：编程语言、编译器优化会影响结果
  3. 输入规模：算法效率随数据规模增长的变化趋势更重要

1.2.2 渐进记号

大O记号（上界）

定义：f(n) = O(g(n)) 当且仅当存在正常数 c 和 n₀，使得对所有 n ≥ n₀，有 f(n) ≤ c·g(n)

复制代码 
含义：g(n) 是 f(n) 的上界（增长率不超过 g(n)）
python 复制代码 
# 示例：分析函数的时间复杂度
def example1(n: int) -> int:
    """O(1): 常数时间"""
    return n * 2 + 1  # 固定数量的操作

def example2(arr: list[int]) -> None:
    """O(n): 线性时间，n = len(arr)"""
    for x in arr:          # 循环n次
        print(x)           # O(1)操作

def example3(n: int) -> None:
    """O(n²): 平方时间"""
    for i in range(n):          # 外层循环n次
        for j in range(n):      # 内层循环n次
            print(i, j)         # O(1)操作
    # 总操作数：n × n = n²

def example4(n: int) -> int:
    """O(log n): 对数时间"""
    while n > 1:
        n = n // 2      # 每次n减半
        # 循环次数：log₂n
    return 0
大Ω记号（下界）

定义：f(n) = Ω(g(n)) 当且仅当存在正常数 c 和 n₀，使得对所有 n ≥ n₀，有 f(n) ≥ c·g(n)

复制代码 
含义：g(n) 是 f(n) 的下界（增长率不低于 g(n)）
大θ记号（紧确界）

定义：f(n) = Θ(g(n)) 当且仅当 f(n) = O(g(n)) 且 f(n) = Ω(g(n))

复制代码 
含义：g(n) 是 f(n) 的紧确界（增长率既不高于也不低于 g(n)）
三者关系图

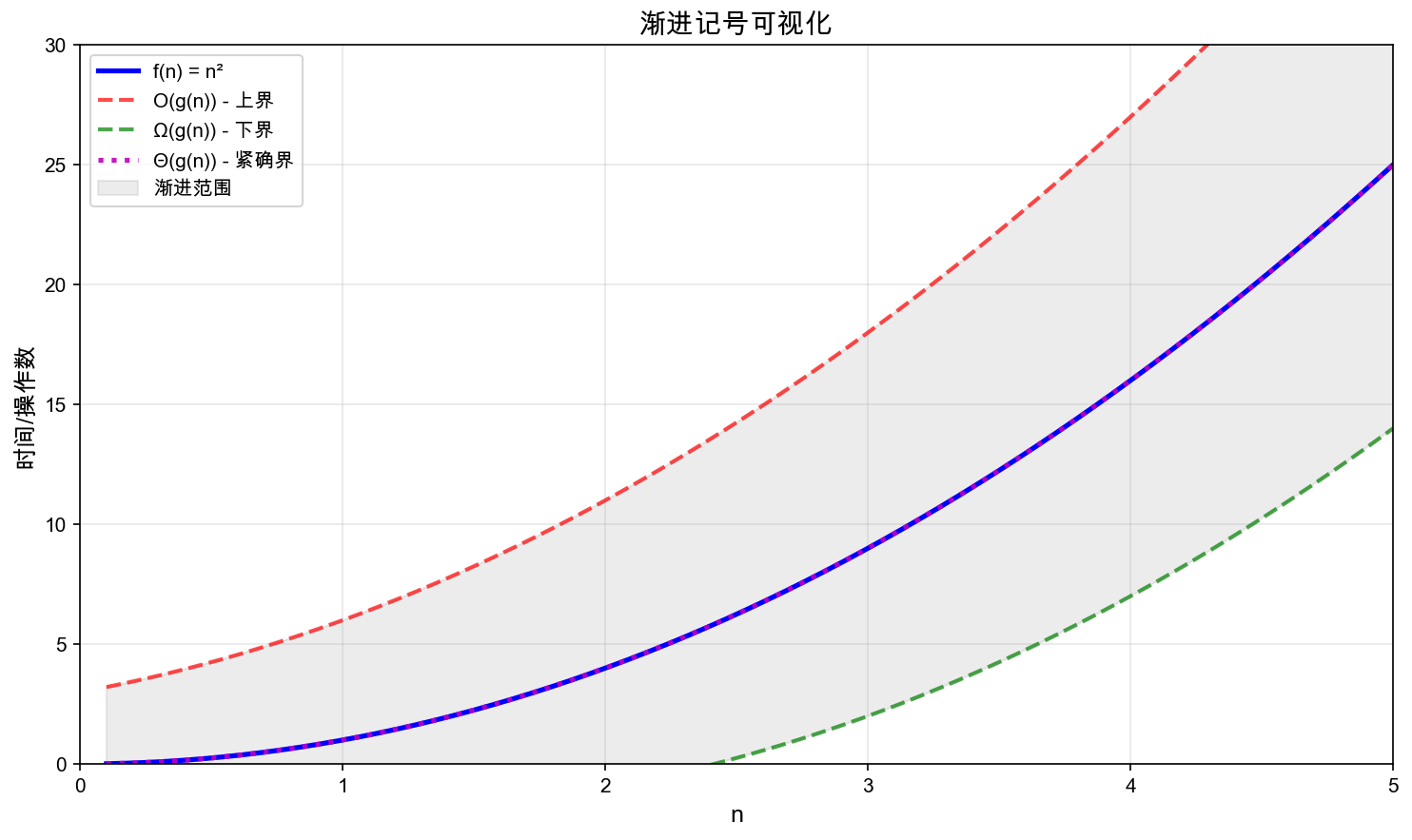
上图展示了渐进记号之间的关系：

  • 红色虚线：O(g(n)) 表示上界，f(n) 的增长率不超过这个
  • 绿色虚线：Ω(g(n)) 表示下界，f(n) 的增长率不低于这个
  • 紫色点线：Θ(g(n)) 表示紧确界，是上下界的交集

1.2.3 常见时间复杂度层次

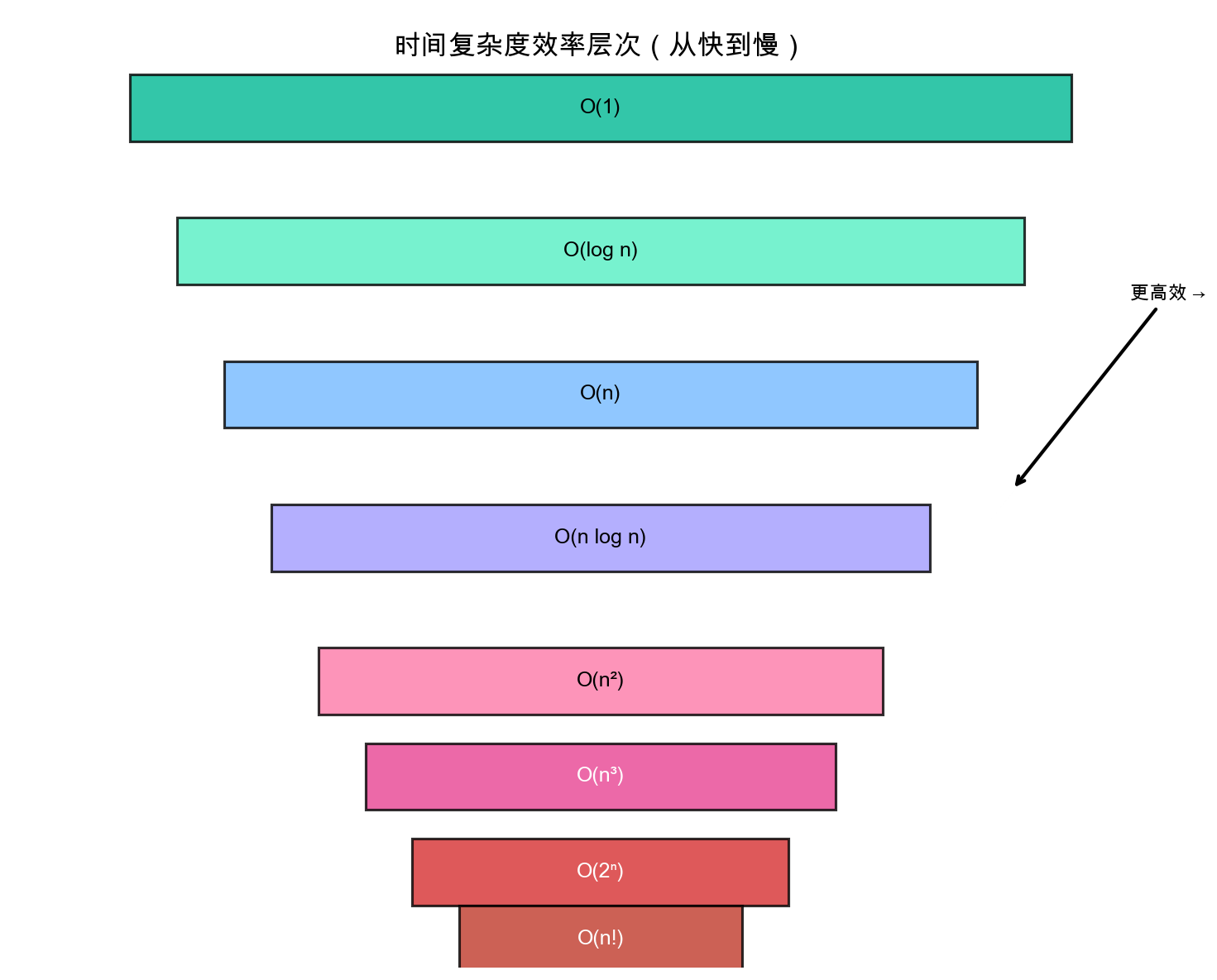
上图展示不同复杂度的效率层次：金字塔越高（操作数越少），算法效率越高。

按效率从高到低排序：

复杂度 符号 典型算法 n=100时操作数
常数 O(1) 数组访问、哈希查找 1
对数 O(log n) 二分搜索 ~7
线性 O(n) 顺序搜索 100
线性对数 O(n log n) 归并排序、快速排序 ~700
平方 O(n²) 冒泡排序、插入排序 10,000
立方 O(n³) 普通矩阵乘法 1,000,000
指数 O(2ⁿ) 汉诺塔、暴力搜索 1.27×10³⁰
阶乘 O(n!) 旅行商（暴力） 9.33×10¹⁵⁷
python 复制代码 
# 复杂度实验：对比不同复杂度的实际运行时间
import time

def constant_time(n: int) -> int:
    """O(1): 常数时间"""
    return n * 2

def linear_time(n: int) -> int:
    """O(n): 线性时间"""
    total = 0
    for i in range(n):
        total += 1
    return total

def quadratic_time(n: int) -> int:
    """O(n²): 平方时间"""
    count = 0
    for i in range(n):
        for j in range(n):
            count += 1
    return count

def measure_time(func, n, iterations=1000):
    """测量函数平均执行时间"""
    start = time.perf_counter()
    for _ in range(iterations):
        func(n)
    end = time.perf_counter()
    return (end - start) / iterations * 1000  # 毫秒

# 对比实验
if __name__ == "__main__":
    print(f"{'n':<10} {'O(1)(μs)':<12} {'O(n)(μs)':<12} {'O(n²)(μs)':<12}")
    print("-" * 50)

    for n in [100, 1000, 10000]:
        t1 = measure_time(constant_time, n)
        t2 = measure_time(linear_time, n)
        t3 = measure_time(quadratic_time, n)

        print(f"{n:<10} {t1:<12.4f} {t2:<12.4f} {t3:<12.4f}")

# 预期输出示例：
# n         O(1)(μs)     O(n)(μs)     O(n²)(μs)
# --------------------------------------------------
# 100       0.0005       0.0023       0.1234
# 1000      0.0004       0.0198       11.5678
# 10000     0.0006       0.1987       1245.6789

1.2.4 复杂度分析规则

python 复制代码 
# 规则1：顺序结构 - 取最大
def sequential(n: int) -> None:
    part1(n)      # O(n)
    part2(n)      # O(n²)
    part3(n)      # O(log n)
    # 总复杂度：O(n²) = max(O(n), O(n²), O(log n))

# 规则2：选择结构 - 取最大
def conditional(n: int) -> None:
    if condition:
        part1(n)      # O(n)
    else:
        part2(n)      # O(n²)
    # 总复杂度：O(n²) = max(O(n), O(n²))

# 规则3：循环结构 - 循环次数 × 循环体复杂度
def single_loop(n: int) -> None:
    for i in range(n):     # 循环n次
        O(1)_operation     # O(1)操作
    # 总复杂度：O(n) = n × O(1)

def nested_loops(n: int) -> None:
    for i in range(n):         # 外层：n次
        for j in range(n):     # 内层：n次
            O(1)_operation     # O(1)操作
    # 总复杂度：O(n²) = n × n × O(1)

# 规则4：函数调用 - 代入被调用函数的复杂度
def caller(n: int) -> None:
    for i in range(n):
        callee(n)      # callee的复杂度是O(n)
    # 总复杂度：O(n²) = n × O(n)

1.2.5 递归算法复杂度分析

递归树方法
python 复制代码 
# 示例1：归并排序的复杂度分析
def merge_sort(arr: list[int]) -> list[int]:
    """T(n) = 2T(n/2) + O(n) = O(n log n)"""
    if len(arr) <= 1:
        return arr

    mid = len(arr) // 2
    left = merge_sort(arr[:mid])      # T(n/2)
    right = merge_sort(arr[mid:])     # T(n/2)
    return merge(left, right)         # O(n) - 合并操作

# 递归树分析：
#              n                    <- 第1层：O(n)
#         n/2        n/2            <- 第2层：2 × O(n/2) = O(n)
#       n/4  n/4    n/4  n/4        <- 第3层：4 × O(n/4) = O(n)
#      ...  ...     ...  ...
#     1 1 1 1 1 1  1 1 1 1          <- 第log₂n层：n × O(1) = O(n)
#
# 总复杂度：(log₂n + 1) × O(n) = O(n log n)

# 示例2：二分搜索的复杂度分析
def binary_search(arr: list[int], target: int, left: int, right: int) -> int:
    """T(n) = T(n/2) + O(1) = O(log n)"""
    if left > right:
        return -1

    mid = (left + right) // 2
    if arr[mid] == target:
        return mid
    elif arr[mid] < target:
        return binary_search(arr, target, mid + 1, right)   # T(n/2)
    else:
        return binary_search(arr, target, left, mid - 1)    # T(n/2)

# 递归树分析：
#         n                    <- O(1)
#      n/2                    <- O(1)
#     n/4                     <- O(1)
#    ...                      <- ...
#    1                        <- O(1)
# 高度：log₂n，每层O(1)，总计：O(log n)
主定理（Master Theorem）

对于形如 T(n) = aT(n/b) + f(n) 的递归关系，其中 a ≥ 1, b > 1：

令 c = log_b(a)，比较 f(n) 与 n^c 的大小：

情况 条件 解
1 f(n) = O(n^(c-ε))，ε > 0 T(n) = Θ(n^c)
2 f(n) = Θ(n^c × log^k n)，k ≥ 0 T(n) = Θ(n^c × log^(k+1) n)
3 f(n) = Ω(n^(c+ε))，ε > 0，且满足正则条件 T(n) = Θ(f(n))
python 复制代码 
# 主定理应用示例

# 案例1：归并排序
# T(n) = 2T(n/2) + O(n)
# a=2, b=2, f(n)=n
# c = log₂(2) = 1
# f(n) = n = n^1 = Θ(n^c)，属于情况2（k=0）
# 解：T(n) = Θ(n log n)

# 案例2：二分搜索
# T(n) = T(n/2) + O(1)
# a=1, b=2, f(n)=1
# c = log₂(1) = 0
# f(n) = 1 = n^0 = Θ(n^c)，属于情况2（k=0）
# 解：T(n) = Θ(log n)

# 案例3：二叉树遍历
# T(n) = 2T(n/2) + O(1)
# a=2, b=2, f(n)=1
# c = log₂(2) = 1
# f(n) = 1 = O(n^(1-ε))，ε=1，属于情况1
# 解：T(n) = Θ(n)

1.2.6 空间复杂度分析

空间复杂度衡量算法执行过程中额外使用的存储空间。

python 复制代码 
# 空间复杂度示例

def example1(arr: list[int]) -> int:
    """空间复杂度：O(1) - 原地操作"""
    total = 0           # O(1)
    for x in arr:
        total += x      # 使用固定的额外空间
    return total

def example2(arr: list[int]) -> list[int]:
    """空间复杂度：O(n) - 创建新数组"""
    result = []                     # O(n)
    for x in arr:
        result.append(x * 2)        # 存储n个元素
    return result

def example3(n: int) -> int:
    """空间复杂度：O(n) - 递归调用栈"""
    if n <= 1:
        return 1
    return n * example3(n - 1)
    # 递归深度为n，每层栈帧O(1)，总计O(n)

def example4(matrix: list[list[int]]) -> list[list[int]]:
    """空间复杂度：O(n²) - 创建新矩阵"""
    n = len(matrix)
    result = [[0] * n for _ in range(n)]    # n × n 矩阵
    for i in range(n):
        for j in range(n):
            result[i][j] = matrix[i][j] * 2
    return result

原地算法（In-place Algorithm）：辅助空间为 O(1) 的算法

python 复制代码 
# 原地算法示例
def reverse_array_inplace(arr: list[int]) -> None:
    """原地反转数组 - O(1) 额外空间"""
    left, right = 0, len(arr) - 1
    while left < right:
        arr[left], arr[right] = arr[right], arr[left]
        left += 1
        right -= 1

# 非原地算法示例
def reverse_array_new(arr: list[int]) -> list[int]:
    """创建新数组存储反转结果 - O(n) 额外空间"""
    return arr[::-1]  # 创建新的反转数组

1.3 NP完全性理论

1.3.1 P类与NP类问题

计算复杂性理论将问题按照求解难度分类：

P类（Polynomial Time）

定义：可以在多项式时间内求解的判定问题

python 复制代码 
# P类问题示例：排序
def is_sorted(arr: list[int]) -> bool:
    """判断数组是否有序 - O(n) 多项式时间"""
    for i in range(len(arr) - 1):
        if arr[i] > arr[i + 1]:
            return False
    return True

def bubble_sort(arr: list[int]) -> list[int]:
    """冒泡排序 - O(n²) 多项式时间"""
    n = len(arr)
    result = arr.copy()
    for i in range(n):
        for j in range(n - 1 - i):
            if result[j] > result[j + 1]:
                result[j], result[j + 1] = result[j + 1], result[j]
    return result
NP类（Nondeterministic Polynomial Time）

定义 ：可以在多项式时间内验证解的判定问题

python 复制代码 
# NP问题示例：可满足性问题的验证
def verify_sat(
    formula: list[list[int]],
    assignment: list[bool]
) -> bool:
    """
    验证布尔公式是否被赋值满足 - 多项式时间O(m)

    Args:
        formula: CNF形式的布尔公式，每个子句是文字列表
                正数表示变量，负数表示变量的否定
        assignment: 变量赋值，True表示真，False表示假

    Returns:
        该赋值是否满足公式
    """
    for clause in formula:                # 遍历每个子句
        clause_satisfied = False
        for var in clause:
            if var > 0 and assignment[var - 1]:      # 正变量
                clause_satisfied = True
                break
            elif var < 0 and not assignment[-var - 1]:  # 负变量
                clause_satisfied = True
                break
        if not clause_satisfied:             # 有子句不满足
            return False
    return True

# 求解SAT问题 - 需要指数时间
def solve_sat_bruteforce(formula: list[list[int]]) -> list[bool] | None:
    """
    暴力求解SAT问题 - 指数时间 O(2^n × m)

    注意：验证是多项式时间，但求解是指数时间！
    这正是NP问题的关键特征。
    """
    if not formula:
        return []

    n_vars = max(abs(var) for clause in formula for var in clause)

    # 枚举所有可能的赋值：2^n 种
    for i in range(2 ** n_vars):
        assignment = [(i >> j) & 1 == 1 for j in range(n_vars)]
        if verify_sat(formula, assignment):
            return assignment
    return None

关键区别：

  • P类 ：多项式时间求解
  • NP类 ：多项式时间验证
  • P ⊆ NP（能快速求解的问题，肯定也能快速验证）

1.3.2 判定问题 vs 最优化问题

python 复制代码 
# 最优化问题：求最优解
def tsp_optimal(cities: list[tuple[float, float]]) -> tuple[list[int], float]:
    """
    旅行商问题（最优化版本）：找最短路径
    指数时间复杂度
    """
    from itertools import permutations

    n = len(cities)
    min_distance = float('inf')
    best_tour = list(range(n))

    for tour in permutations(range(n)):  # n! 种排列
        total = calculate_distance(cities, tour)
        if total < min_distance:
            min_distance = total
            best_tour = list(tour)

    return best_tour, min_distance

# 判定问题：是/否答案
def tsp_decision(
    cities: list[tuple[float, float]],
    max_distance: float
) -> bool:
    """
    旅行商问题（判定版本）：是否存在长度 ≤ max_distance 的路径？
    仍然是NP完全问题
    """
    from itertools import permutations

    for tour in permutations(range(len(cities))):
        if calculate_distance(cities, tour) <= max_distance:
            return True
    return False

# 最优化问题可以转化为判定问题（二分搜索答案）
def tsp_via_decision(cities: list[tuple[float, float]]) -> float:
    """通过判定问题求解最优化问题"""
    # 使用二分搜索 + 判定问题来找最优距离
    low, high = 0, float('inf')
    while high - low > 1e-6:
        mid = (low + high) / 2
        if tsp_decision(cities, mid):
            high = mid
        else:
            low = mid
    return high

1.3.3 NP完全性概念

规约（Reduction）

直观含义：如果问题A可以规约到问题B，那么"会解B就会解A"

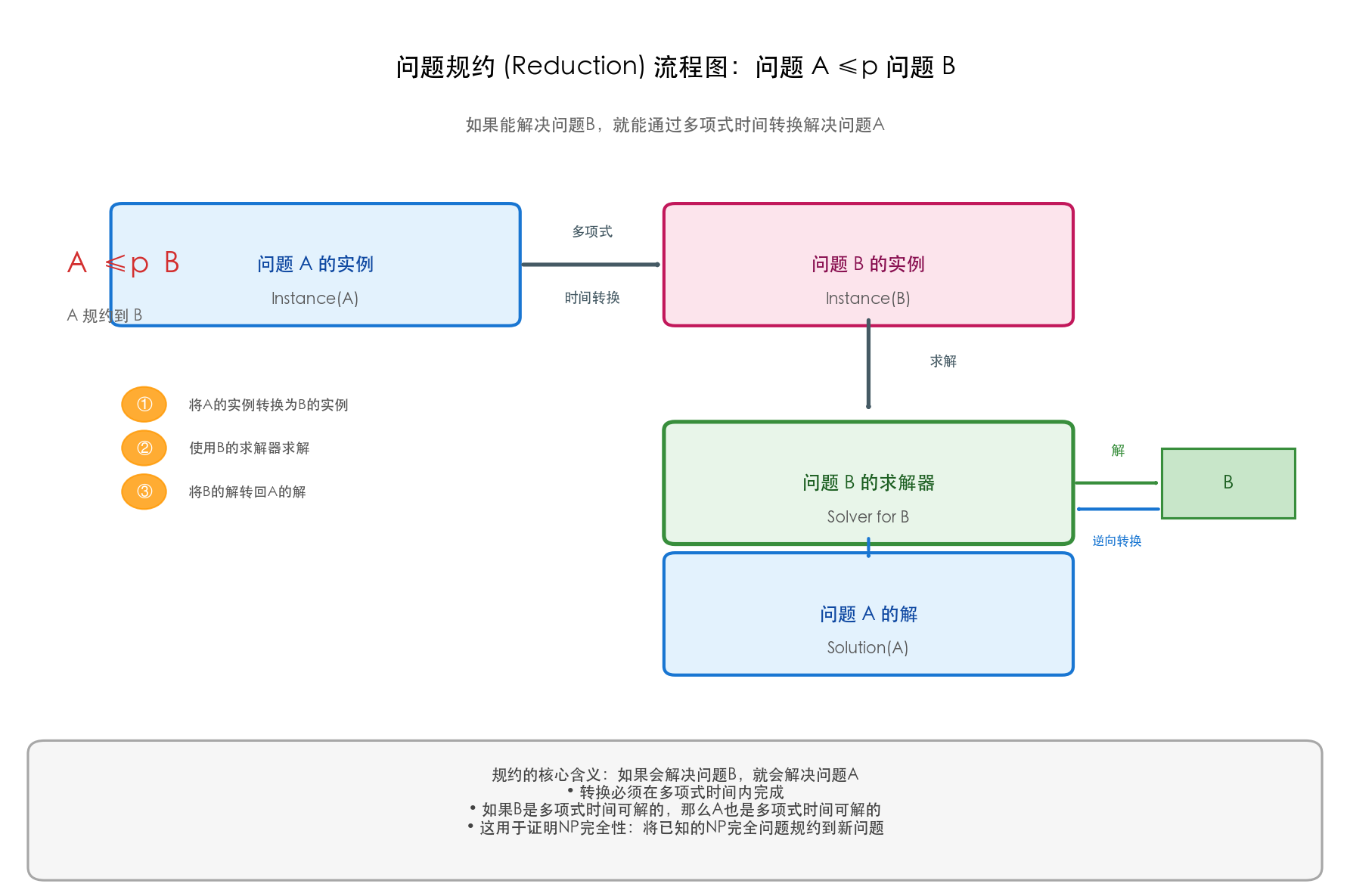
上图展示了规约的完整流程：

  1. 将问题A的实例转换为问题B的实例（多项式时间）
  2. 使用问题B的求解器得到B的解
  3. 将B的解转换回A的解

规约的传递性：如果 A ≤p B 且 B ≤p C，则 A ≤p C

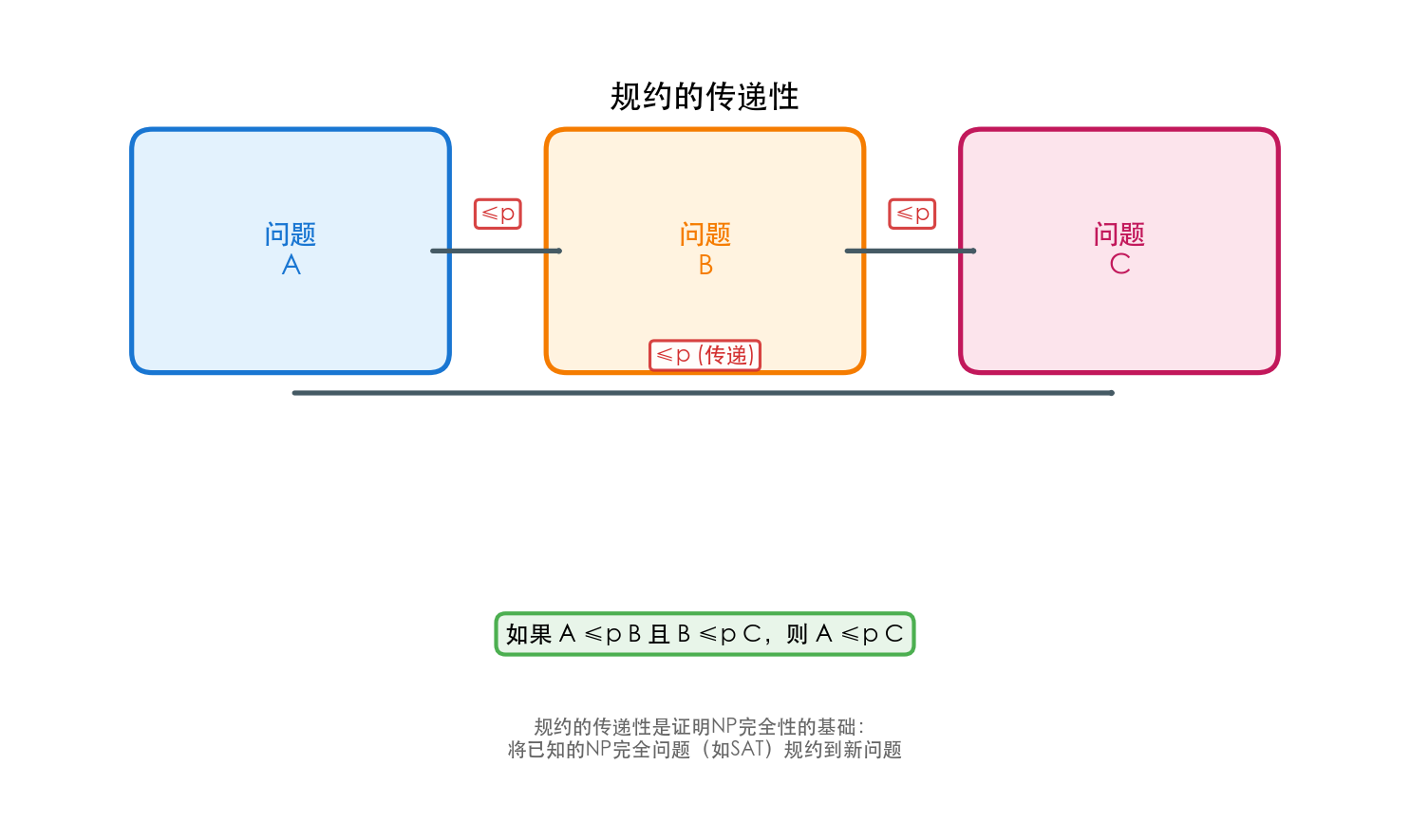
规约的传递性是证明NP完全性的基础：通过将已知的NP完全问题（如SAT）规约到新问题，可以证明新问题也是NP完全的。

NP完全、NP困难、NP的关系

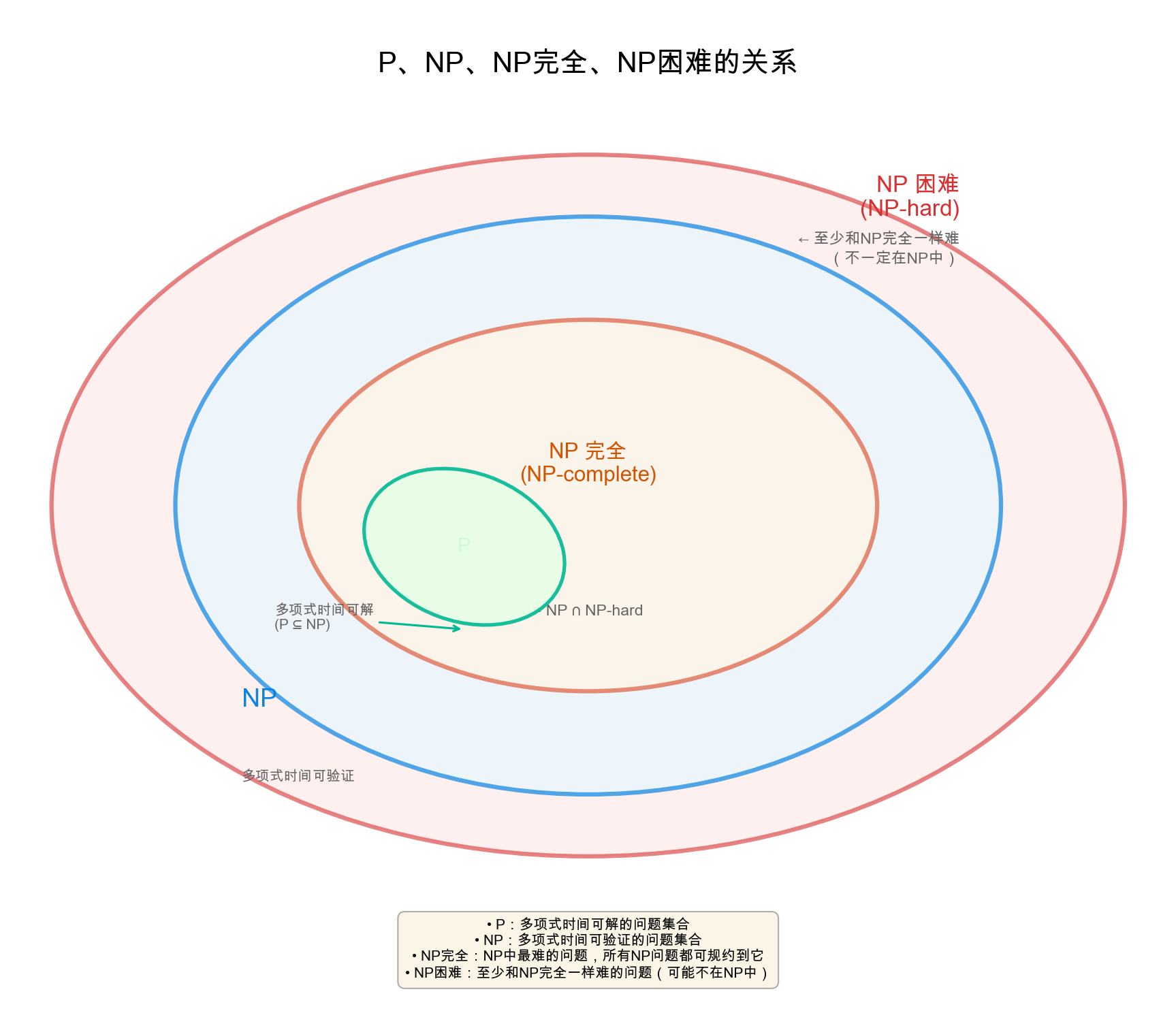
上图清晰地展示了P、NP、NP完全、NP困难之间的包含关系：

类别 定义 例子
P 多项式时间可解 排序、最短路径
NP 多项式时间可验证 SAT、TSP
NP完全 NP中最难的问题，所有NP问题都可规约到它 SAT、TSP、背包问题
NP困难 至少和NP完全一样难（可能不在NP中） 停机问题、TSP的最优化版本

关键关系：

  • P ⊆ NP（能快速求解的问题，肯定也能快速验证）
  • NP完全 = NP ∩ NP-hard（既在NP中，又是NP-hard）
  • P = NP? 是计算机科学中最重要的未解决问题之一
Cook-Levin定理

内容：SAT（布尔可满足性）问题是第一个NP完全问题

意义：

  • 证明了NP完全问题的存在
  • 提供了证明其他问题NP完全性的方法：通过从SAT规约
  • 不需要掌握证明，但需要理解其重要性

1.3.4 常见NP完全问题

1. SAT问题（Boolean Satisfiability）
python 复制代码 
def sat_example():
    """SAT问题示例"""
    # 公式：(x₁ ∨ ¬x₃) ∧ (¬x₁ ∨ x₂ ∨ x₃) ∧ (x₂)
    # 用列表表示子句，正数表示变量，负数表示其否定
    formula = [
        [1, -3],      # (x₁ ∨ ¬x₃)
        [-1, 2, 3],   # (¬x₁ ∨ x₂ ∨ x₃)
        [2]           # (x₂)
    ]

    # 验证赋值 x₁=True, x₂=True, x₃=False 是否满足
    assignment = [True, True, False]  # x₁, x₂, x₃
    result = verify_sat(formula, assignment)
    print(f"赋值 {assignment} 满足公式: {result}")  # True
2. 旅行商问题（TSP）
python 复制代码 
def tsp_example():
    """旅行商问题示例"""
    import math

    cities = [
        (0, 0),    # 城市0
        (1, 1),    # 城市1
        (2, 0),    # 城市2
        (1, -1)    # 城市3
    ]

    def distance(a, b):
        return math.sqrt((a[0] - b[0])**2 + (a[1] - b[1])**2)

    # 判定问题：是否存在长度 ≤ 6 的路径？
    max_dist = 6.0
    exists = tsp_decision(cities, max_dist)
    print(f"存在长度 ≤ {max_dist} 的路径: {exists}")

    # 验证给定路径的长度
    tour = [0, 1, 2, 3]  # 一个可能的路径
    tour_distance = calculate_distance(cities, tour)
    print(f"路径 {tour} 的长度: {tour_distance:.2f}")
3. 0-1背包问题
python 复制代码 
def knapsack_verify(
    weights: list[int],
    values: list[int],
    capacity: int,
    min_value: int,
    selection: list[bool]
) -> bool:
    """
    验证背包问题的解

    Args:
        weights: 物品重量
        values: 物品价值
        capacity: 背包容量
        min_value: 要求的最小价值
        selection: 物品选择列表

    Returns:
        该选择是否满足约束且达到最小价值
    """
    total_weight = sum(w for w, s in zip(weights, selection) if s)
    total_value = sum(v for v, s in zip(values, selection) if s)

    return total_weight <= capacity and total_value >= min_value

# 示例
weights = [2, 3, 4, 5]
values = [3, 4, 5, 6]
capacity = 5
min_value = 6

selection = [True, True, False, False]  # 选前两个物品
is_valid = knapsack_verify(weights, values, capacity, min_value, selection)
print(f"选择 {selection} 有效: {is_valid}")  # True（重量5，价值7）
4. 图着色问题
python 复制代码 
def graph_coloring_verify(
    edges: list[tuple[int, int]],
    colors: list[int],
    num_colors: int
) -> bool:
    """
    验证图着色问题的解

    Args:
        edges: 边列表
        colors: 每个顶点的颜色
        num_colors: 使用的颜色数量

    Returns:
        是否是合法的着色（相邻顶点不同色）
    """
    # 检查颜色范围
    if max(colors) >= num_colors:
        return False

    # 检查所有边
    for u, v in edges:
        if colors[u] == colors[v]:
            return False  # 相邻顶点同色！

    return True

# 示例：3个顶点的三角形图，需要3种颜色
edges = [(0, 1), (1, 2), (2, 0)]
colors = [0, 1, 2]  # 每个顶点不同颜色
is_valid = graph_coloring_verify(edges, colors, 3)
print(f"着色 {colors} 有效: {is_valid}")  # True

1.3.5 NP完全性的实际意义

面对NP完全问题的策略
python 复制代码 
"""
策略1：接受近似解
使用贪心算法或启发式算法，找到接近最优的解
"""

def tsp_greedy(cities: list[tuple[float, float]]) -> list[int]:
    """TSP的贪心近似算法 - O(n²)"""
    import math

    n = len(cities)
    unvisited = set(range(1, n))
    tour = [0]  # 从城市0开始

    while unvisited:
        current = tour[-1]
        # 选择最近的未访问城市
        nearest = min(unvisited,
                      key=lambda j: math.dist(cities[current], cities[j]))
        tour.append(nearest)
        unvisited.remove(nearest)

    return tour  # 不保证最优，但快速


"""
策略2：特殊结构利用
针对特定输入结构设计高效算法
"""

def knapsack_dp(weights: list[int], values: list[int], capacity: int) -> int:
    """
    背包问题的动态规划解法 - O(n × capacity)
    当容量较小时是多项式时间（伪多项式时间）
    """
    n = len(weights)
    dp = [[0] * (capacity + 1) for _ in range(n + 1)]

    for i in range(1, n + 1):
        for w in range(capacity + 1):
            if weights[i-1] <= w:
                dp[i][w] = max(
                    dp[i-1][w],
                    dp[i-1][w-weights[i-1]] + values[i-1]
                )
            else:
                dp[i][w] = dp[i-1][w]

    return dp[n][capacity]


"""
策略3：参数化算法
固定某个参数，使算法在该参数上高效
"""

def vertex_cover_parameterized(
    edges: list[tuple[int, int]],
    k: int
) -> list[int] | None:
    """
    顶点覆盖问题的参数化算法 - O(2^k × n)
    当k较小时实用
    """
    from itertools import combinations

    vertices = set()
    for u, v in edges:
        vertices.add(u)
        vertices.add(v)

    # 尝试所有大小为k的顶点组合
    for cover in combinations(vertices, k):
        cover_set = set(cover)
        # 检查是否覆盖所有边
        if all(u in cover_set or v in cover_set for u, v in edges):
            return list(cover)

    return None

1.3.6 P vs NP 问题

P = NP? 是计算机科学中最重要的未解决问题之一。

复制代码 
P = NP?
├── 如果 P = NP：
│   └── 所有可快速验证的问题都可快速求解
│       → 密码学体系崩溃
│       → 许多优化问题变得易解
│       → 人工智能可能达到人类水平
│
└── 如果 P ≠ NP（主流观点）：
    └── 存在本质上难求解的问题
        → 密码学安全有保障
        → 需要近似算法和启发式方法
        → 解释了为什么某些问题 inherently hard

当前状态：

  • 克雷数学研究所千禧年七大难题之一，悬赏100万美元
  • 学界普遍认为 P ≠ NP，但尚未证明
  • 自1971年提出以来，50多年仍未解决

练习题

概念题

  1. 算法的五个基本特征是什么？ 请举例说明一个不满足"有穷性"特征的程序。

  2. 判断以下函数的时间复杂度：

    python 复制代码 
    def func1(n):
    for i in range(n):
        for j in range(10):
            print(i, j)

def func2(n):
    i = 1
    while i < n:
        i *= 2

def func3(n):
    if n <= 1:
        return 1
    return func3(n-1) + func3(n-2)

  3. 什么是原地算法？ 以下哪个函数是原地算法？

    python 复制代码 
    def A(arr):
    return arr[::-1]

def B(arr):
    left, right = 0, len(arr)-1
    while left < right:
        arr[left], arr[right] = arr[right], arr[left]
        left += 1
        right -= 1

  4. 解释P类、NP类、NP完全、NP困难的区别，并画图说明它们的关系。

  5. 为什么说"验证容易，求解难"是NP问题的核心特征？ 请举例说明。

代码分析题

  1. 分析以下递归函数的时间复杂度，并画出递归树：

    python 复制代码 
    def recursive_func(n):
    if n <= 1:
        return 1
    return recursive_func(n//2) + recursive_func(n//2) + n

    提示：使用主定理。

  2. 以下函数用于计算斐波那契数列，分析其时间复杂度和空间复杂度：

    python 复制代码 
    def fib(n):
    if n <= 1:
        return n
    return fib(n-1) + fib(n-2)

    如何改进使其时间复杂度降到 O(n)？

  3. 判断以下说法是否正确，并说明理由：

    • "如果一个算法是O(n²)的，那么它一定不是O(n)的"
    • "如果一个算法是O(n)的，那么它也可能是O(n²)的"
    • "O(n)和O(n+1)是不同的复杂度"

编程题

  1. 实现一个函数判断数组是否有序，要求：

    • 时间复杂度 O(n)
    • 空间复杂度 O(1)
    • 同时支持升序和降序判断

  2. 实现SAT问题的暴力求解器：

    • 输入：CNF形式的布尔公式
    • 输出：满足的赋值，或None（无解）
    • 分析你的算法的时间复杂度

答案

概念题答案

  1. 算法的五个基本特征：

    • 有穷性：有限步骤内终止
    • 确定性：每步明确无歧义
    • 可行性：每步可执行
    • 输入：零个或多个输入
    • 输出：一个或多个输出

    不满足有穷性的程序示例：

    python 复制代码 
    def infinite_loop():
    while True:
        pass  # 永不终止

  2. 时间复杂度分析：

    • func1: O(n) - 外层n次，内层固定10次
    • func2: O(log n) - 每次i翻倍
    • func3: O(2^n) - 递归树有2^n个节点

  3. 原地算法：

    • 函数B是原地算法（O(1)额外空间）
    • 函数A不是（O(n)额外空间创建新数组）

  4. P/NP关系图：

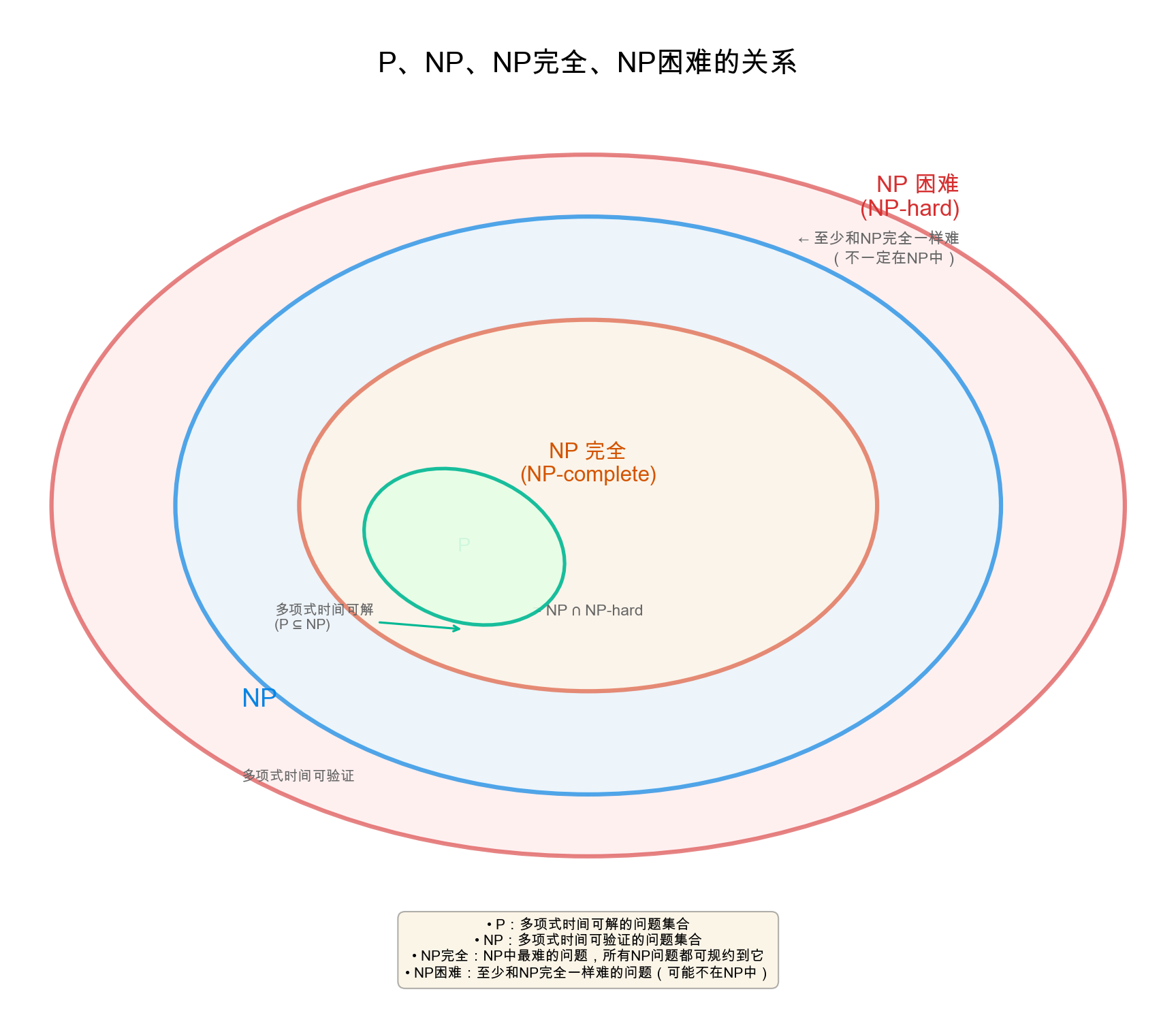
  5. 验证容易，求解难：

    • NP问题可以在多项式时间内验证解的正确性
    • 但找到解可能需要指数时间
    • 例如：SAT问题验证是O(m)，但求解是O(2^n)

代码分析题答案

  1. 递归函数分析：

    • 递归关系：T(n) = 2T(n/2) + O(n)
    • a=2, b=2, f(n)=n
    • c = log₂(2) = 1
    • f(n) = Θ(n^c)，属于主定理情况2
    • 答案：T(n) = Θ(n log n)

  2. 斐波那契数列分析：

    • 时间复杂度：O(2^n) - 每次调用产生两个新调用
    • 空间复杂度：O(n) - 递归深度

    改进版本（动态规划）：

    python 复制代码 
    def fib_improved(n):
    if n <= 1:
        return n
    a, b = 0, 1
    for _ in range(2, n + 1):
        a, b = b, a + b
    return b
# 时间复杂度：O(n)
# 空间复杂度：O(1)

  3. 判断正误：

    • "如果一个算法是O(n²)的，那么它一定不是O(n)的"

      • 错误：O(n²)是上界，算法可能同时是O(n)和O(n²)
      • 正确说法：如果一个算法是Θ(n²)的，那么它不是Θ(n)的

    • "如果一个算法是O(n)的，那么它也可能是O(n²)的"

      • 正确：O(n) ⊆ O(n²)

    • "O(n)和O(n+1)是不同的复杂度"

      • 错误：渐进记号忽略常数，O(n) = O(n+1)

编程题答案

  1. 判断数组是否有序：

    python 复制代码 
    def is_sorted(arr: list[int]) -> str:
    """
    判断数组是否有序

    Returns:
        "ascending" - 升序
        "descending" - 降序
        "unsorted" - 无序
    """
    if len(arr) <= 1:
        return "ascending"  # 单元素数组视为升序

    # 检查升序
    is_asc = all(arr[i] <= arr[i+1] for i in range(len(arr)-1))
    # 检查降序
    is_desc = all(arr[i] >= arr[i+1] for i in range(len(arr)-1))

    if is_asc:
        return "ascending"
    elif is_desc:
        return "descending"
    else:
        return "unsorted"

# 测试
print(is_sorted([1, 2, 3, 4]))      # ascending
print(is_sorted([4, 3, 2, 1]))      # descending
print(is_sorted([1, 3, 2, 4]))      # unsorted

  2. SAT问题暴力求解器：

    python 复制代码 
    def solve_sat(formula: list[list[int]]) -> list[bool] | None:
    """
    SAT问题暴力求解器

    时间复杂度：O(2^n × m)，n是变量数，m是子句数
    空间复杂度：O(n)
    """
    if not formula:
        return []

    # 确定变量数量
    n_vars = max(abs(var) for clause in formula for var in clause)

    # 枚举所有可能的赋值
    for i in range(2 ** n_vars):
        assignment = [(i >> j) & 1 == 1 for j in range(n_vars)]

        if verify_sat(formula, assignment):
            return assignment

    return None  # 无解

# 测试
formula = [[1, 2], [-1, 2], [-1, -2]]  # 可满足
result = solve_sat(formula)
print(f"解: {result}")  # 可能输出 [False, True] 或其他满足的赋值

本章小结

核心知识点回顾

  1. 算法定义：算法是满足五个基本特征（有穷性、确定性、可行性、输入、输出）的问题求解步骤

  2. 复杂度分析：

    • 时间复杂度：大O、大Ω、大θ记号
    • 常见层次：O(1) < O(log n) < O(n) < O(n log n) < O(n²) < O(2ⁿ)
    • 递归分析：递归树方法、主定理
    • 空间复杂度：区分输入空间和辅助空间

  3. NP完全性理论：

    • P类：多项式时间可解
    • NP类：多项式时间可验证
    • NP完全：NP中最难的问题
    • 面对NP完全问题的策略：近似、特殊结构、参数化

与后续章节的关联

本章内容 后续章节
算法特征 所有章节的算法设计
复杂度分析 每个算法都会分析其复杂度
递归分析 第2章递归与分治策略
NP完全性 第5、6章回溯法和分支限界法

学习建议

  1. 掌握复杂度分析是后续学习的基础，务必多做练习
  2. 不要死记硬背主定理公式，理解递归树分析方法更重要
  3. NP完全性理论偏重概念，重点在直观理解而非严格证明
  4. 动手实践：实现每个算法并实际测量其运行时间

下一章预告：递归与分治策略将学习如何将问题分解为更小的子问题，是递归算法和高效算法设计的核心技术。

相关推荐
SNAKEpc121382 小时前
快速了解PyQtGraph中的重要概念及核心类
python·qt·pyqt
xqqxqxxq2 小时前
认识数据结构之——图 构建图与应用
数据结构·python·算法
1candobetter2 小时前
JAVA后端开发——Spring Boot 多环境配置与实践
java·开发语言·spring boot
FMRbpm2 小时前
邻接矩阵练习1--------LCP 07.传递信息
数据结构·c++·算法·leetcode·深度优先·新手入门
啊阿狸不会拉杆2 小时前
《数字信号处理》第 1 章 离散时间信号与系统
人工智能·算法·机器学习·信号处理·数字信号处理·dsp
ʚB҉L҉A҉C҉K҉.҉基҉德҉^҉大2 小时前
C++安全编程指南
开发语言·c++·算法
沛沛老爹2 小时前
Web开发者实战:多模态Agent技能开发——语音交互与合成技能集成指南
java·开发语言·前端·人工智能·交互·skills
tianyuanwo2 小时前
Python RPM打包的基石：深入理解 python3.x-rpm-macros 组件
开发语言·python·xx-rpm-macros
啊阿狸不会拉杆2 小时前
《数字信号处理》第 2 章 - z 变换与离散时间傅里叶变换（DTFT）
人工智能·算法·机器学习·信号处理·数字信号处理·dsp
热门推荐
01GitHub 镜像站点02【网络安全测试】Burp Suite工具使用说明、配置及常见问题（有关必回）03OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)04Claude Code Skills 实用使用手册05UV安装并设置国内源06struts2 XML外部实体注入漏洞复现（CVE-2025-68493）07Open Code教程（四）| 高级配置与集成08在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）09AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南10Linux下V2Ray安装配置指南