《数字信号处理》第 4 章-快速傅里叶变换 (FFT)

啊阿狸不会拉杆2026-01-28 8:19

前言

快速傅里叶变换（FFT）是数字信号处理领域的里程碑式算法，它并非新的变换形式，而是离散傅里叶变换（DFT）的快速实现方法。本文将从 DFT 运算量分析入手，系统讲解 FFT 的核心算法原理、实现方式及工程应用，并结合 MATLAB 代码实战，让你从理论到实践彻底掌握 FFT。

4.1 直接计算 DFT 的运算量，减少运算量的途径

4.1.1 直接计算 DFT 的运算量

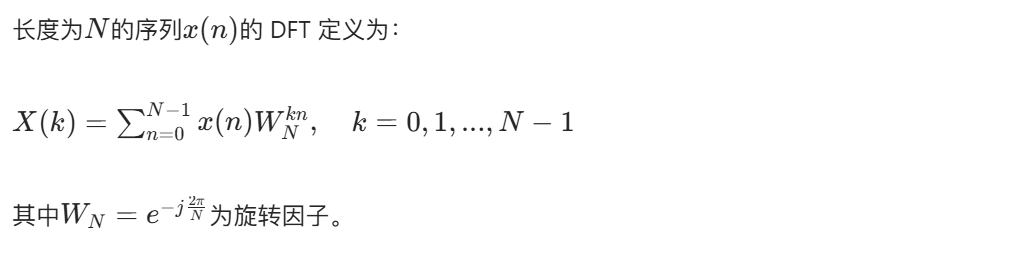
4.1.2 减少运算量的途径

4.2 按时间抽选 (DIT) 的基 - 2 FFT 算法 (库利 - 图基算法)

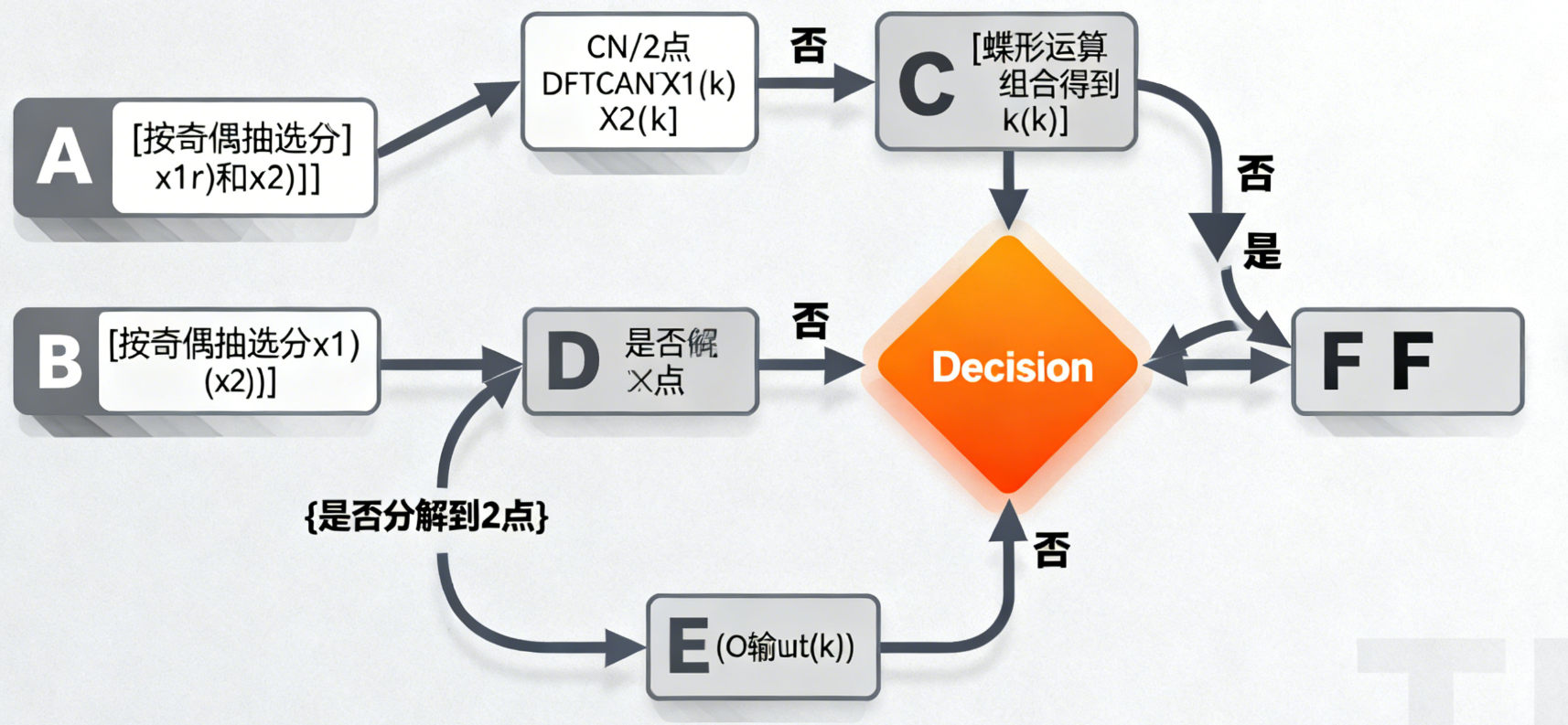
4.2.1 算法原理

4.2.2 DIT-FFT 的流程图

4.2.3 DIT-FFT 运算量

4.3 按频率抽选 (DIF) 的基 - 2 FFT 算法 (桑德 - 图基算法)

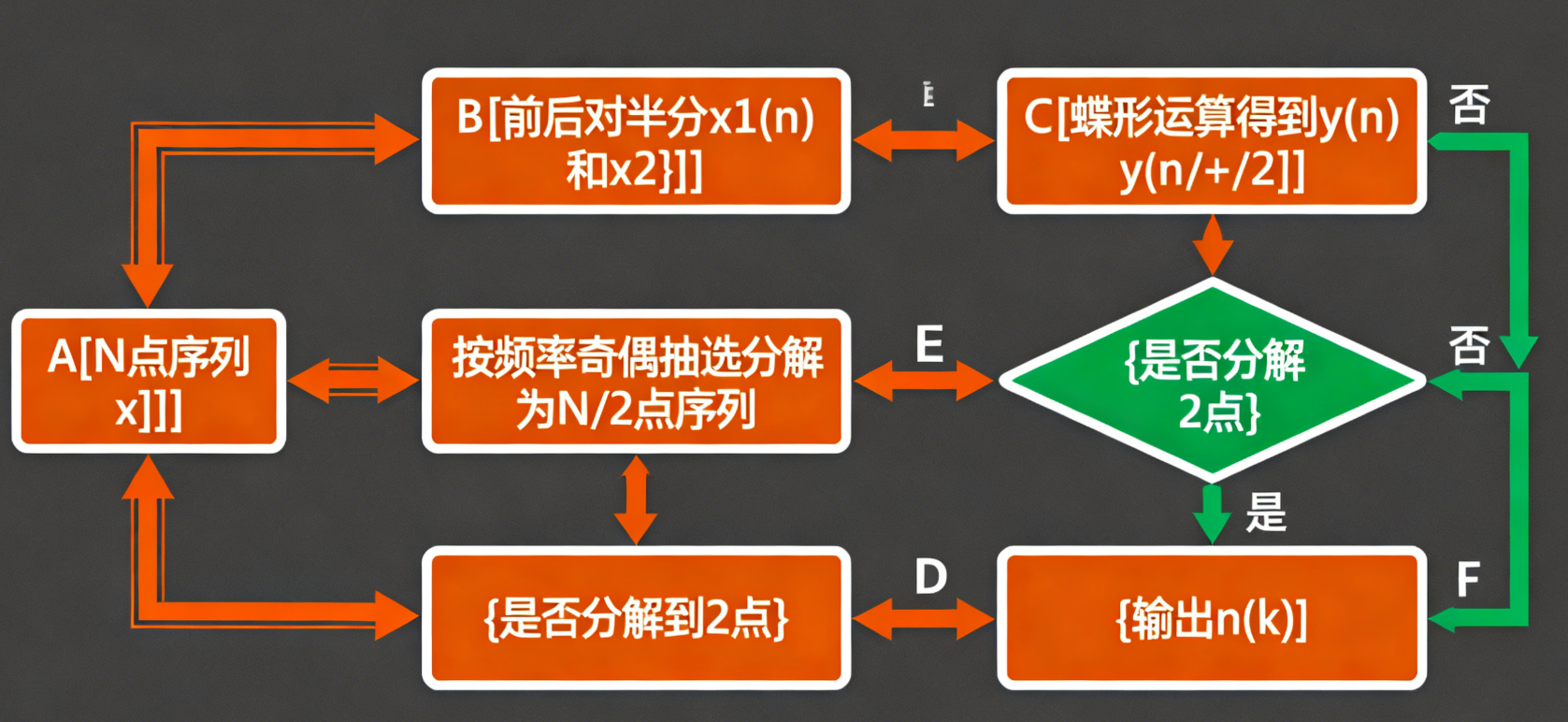
4.3.1 算法原理

DIF-FFT（Decimation-In-Frequency）核心是按频率奇偶抽选，先进行蝶形运算，再分解序列：

4.3.2 DIF-FFT 的 流程图

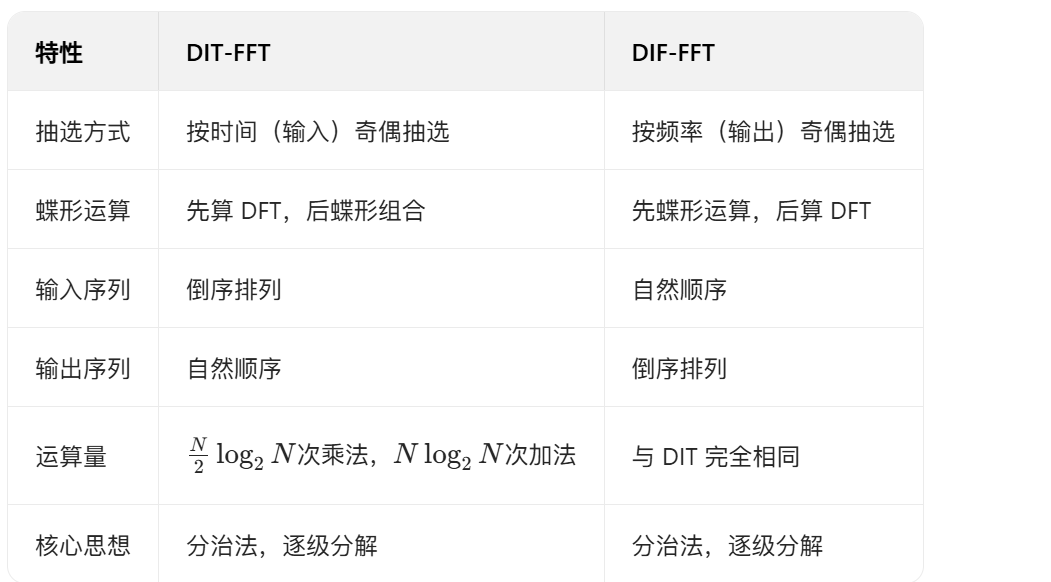
4.4 DIT-FFT 与 DIF-FFT 的异同

4.5 离散傅里叶反变换 (IDFT) 的快速算法 IFFT

4.5.1 算法原理

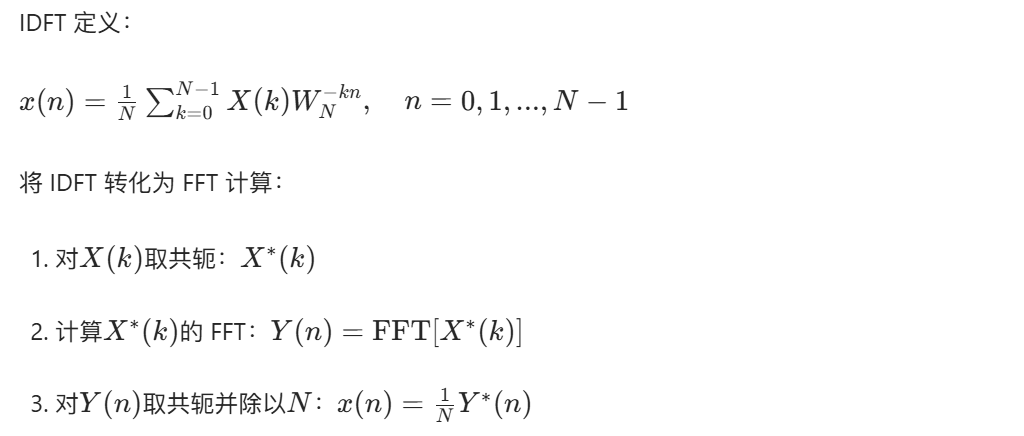
4.5.2 MATLAB 实现示例

复制代码 
% IFFT实现示例
clc; clear; close all;

% 1. 生成测试序列
N = 8;          % 序列长度（2的幂）
n = 0:N-1;
x = sin(2*pi*0.25*n) + 0.5*sin(2*pi*0.5*n);  % 原始序列

% 2. 计算FFT
X = fft(x);

% 3. 手动实现IFFT（基于FFT）
X_conj = conj(X);       % 取共轭
Y = fft(X_conj);        % 计算FFT
x_ifft = (1/N) * conj(Y); % 取共轭并除以N

% 4. 对比MATLAB内置IFFT
x_ifft_matlab = ifft(X);

% 5. 结果展示
fprintf('手动实现IFFT与MATLAB内置IFFT的最大误差：%.2e\n', max(abs(x_ifft - x_ifft_matlab)));

% 6. 绘图对比
figure('Color','w');
subplot(2,1,1);
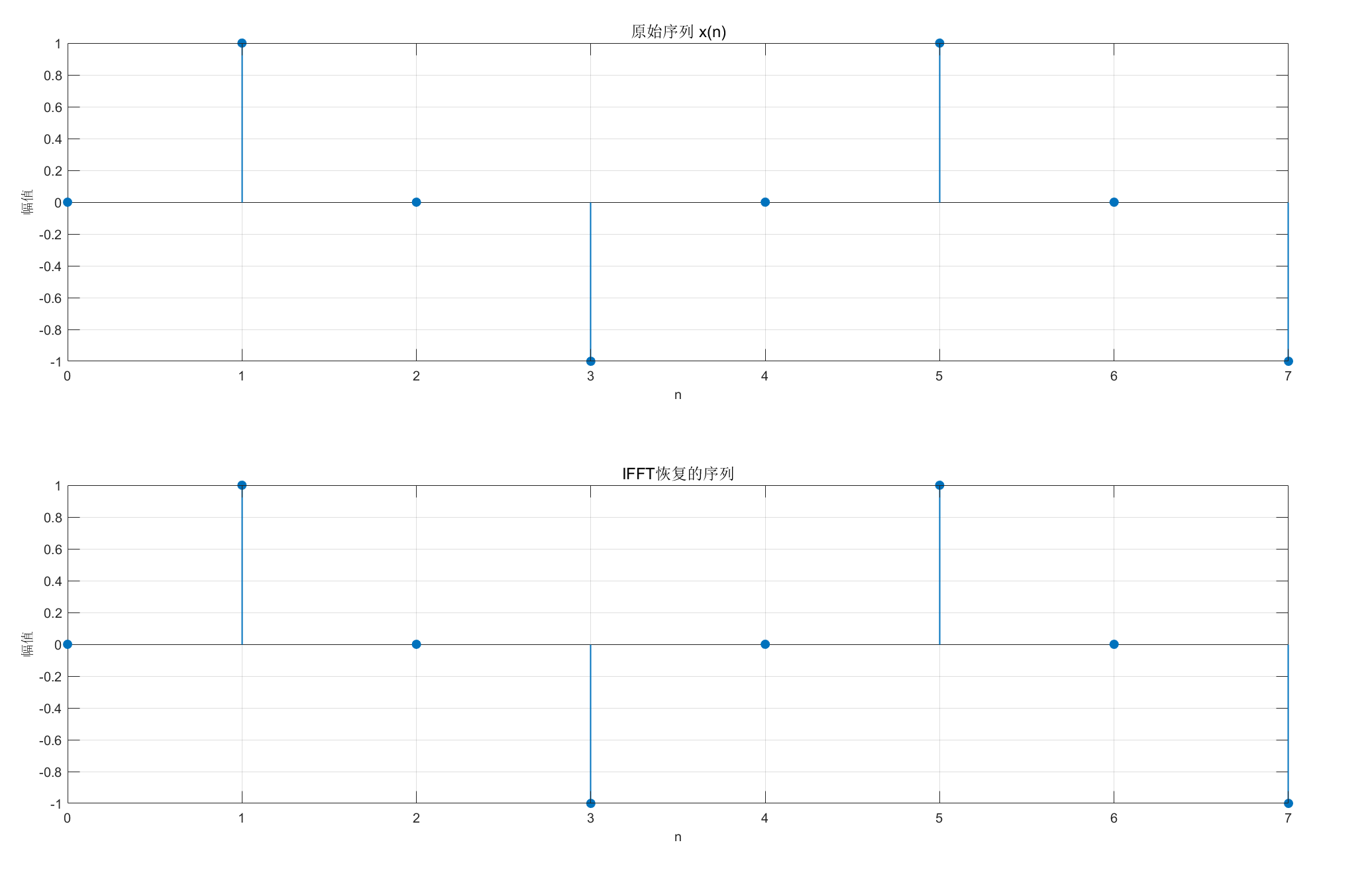
stem(n, x, 'filled', 'LineWidth',1);
title('原始序列 x(n)','FontSize',12);
xlabel('n','FontSize',10); ylabel('幅值','FontSize',10);
grid on;

subplot(2,1,2);
stem(n, real(x_ifft), 'filled', 'LineWidth',1); % 取实部（理论上虚部应为0）
title('IFFT恢复的序列','FontSize',12);
xlabel('n','FontSize',10); ylabel('幅值','FontSize',10);
grid on;

4.6 基 - 2 FFT 流程图

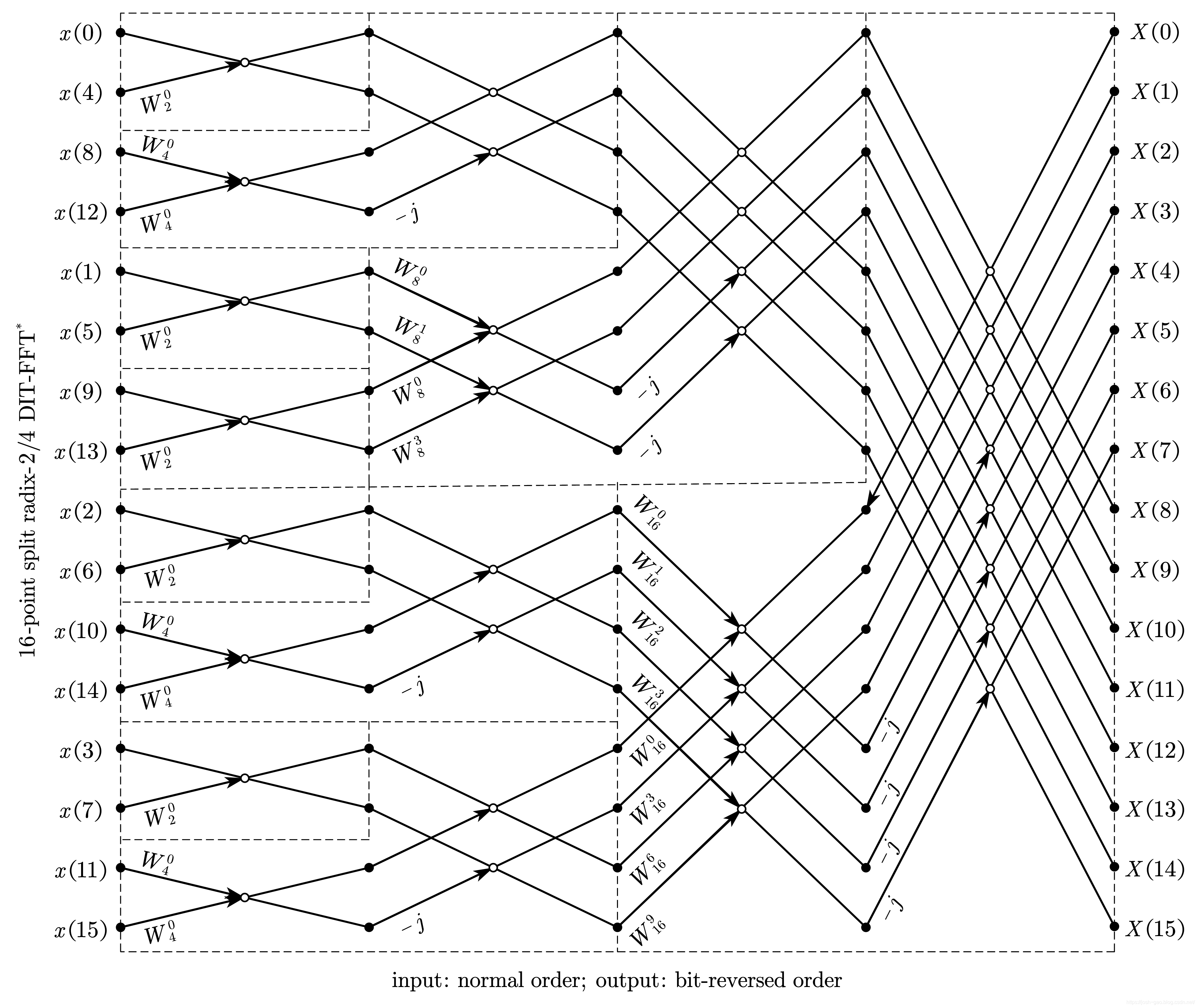
4.6.1 8 点 DIT-FFT 完整流程图

4.7 N 为复合数的 FFT 算法 ------ 混合基 (多基多进制) FFT 算法

4.7.1 算法原理

4.7.2 MATLAB 实现示例（以 N=12=3×4 为例）

复制代码 
% 混合基FFT实现示例
clc; clear; close all;

% 1. 生成测试序列（N=12，非2的幂）
N = 12;
n = 0:N-1;
x = cos(2*pi*2*n/N) + 0.5*sin(2*pi*5*n/N);

% 2. 计算混合基FFT（MATLAB自动处理）
X = fft(x);

% 3. 计算理论DFT（直接计算，用于验证）
X_direct = zeros(1,N);
W = exp(-1j*2*pi/N);  % 旋转因子
for k = 0:N-1
    for nn = 0:N-1
        X_direct(k+1) = X_direct(k+1) + x(nn+1) * W^(k*nn);
    end
end

% 4. 结果对比
figure('Color','w');
subplot(2,1,1);
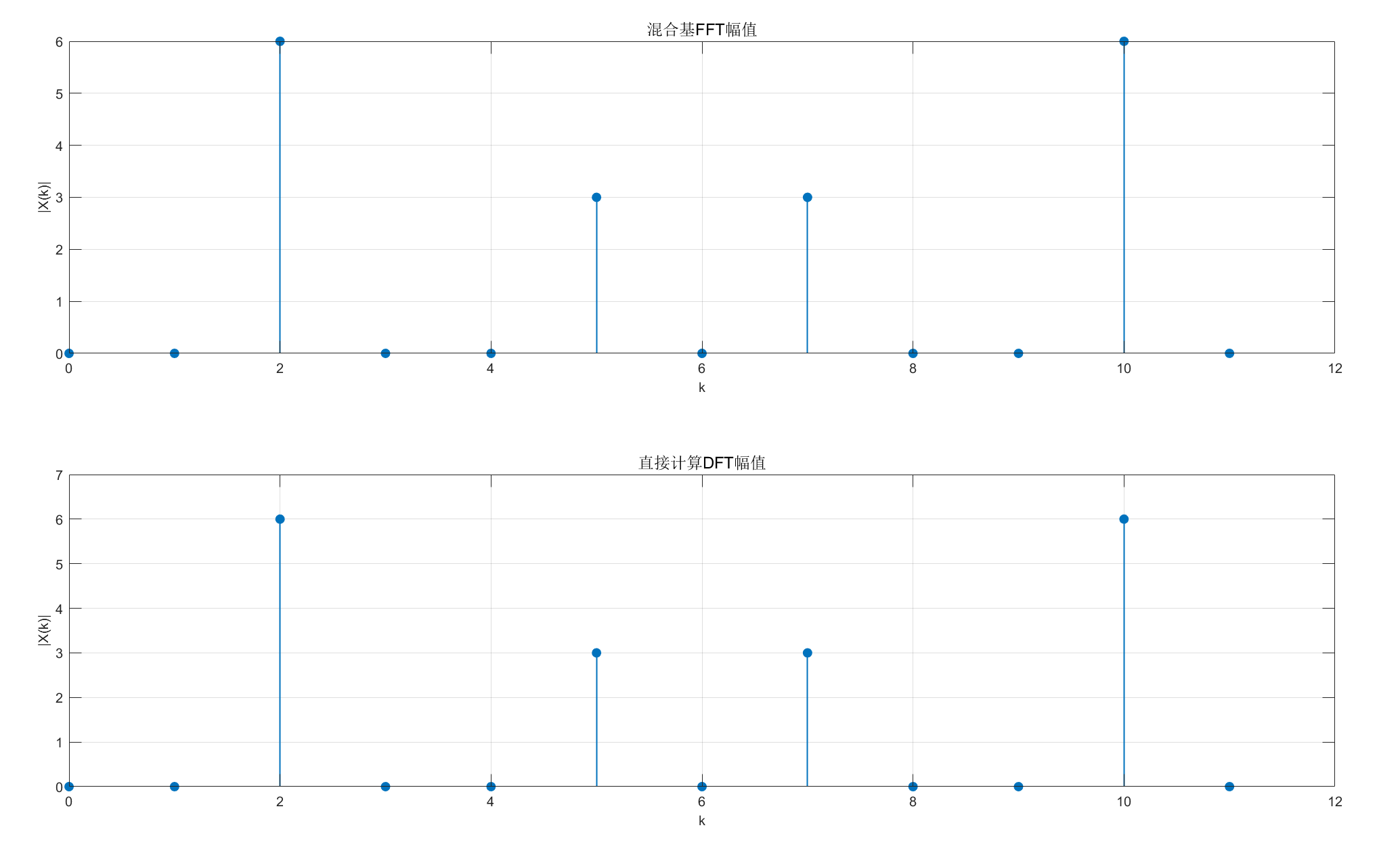
stem(n, abs(X), 'filled', 'LineWidth',1);
title('混合基FFT幅值','FontSize',12);
xlabel('k','FontSize',10); ylabel('|X(k)|','FontSize',10);
grid on;

subplot(2,1,2);
stem(n, abs(X_direct), 'filled', 'LineWidth',1);
title('直接计算DFT幅值','FontSize',12);
xlabel('k','FontSize',10); ylabel('|X(k)|','FontSize',10);
grid on;

% 5. 误差分析
error = max(abs(X - X_direct));
fprintf('混合基FFT与直接DFT的最大误差：%.2e\n', error);

4.8 线性调频 z 变换 (Chirp-z 变换或 CZT) 算法

4.8.1 算法原理

CZT 适用于：

  • 非均匀频率采样
  • 只需要计算部分频率点
  • N不为 2 的幂

核心公式：

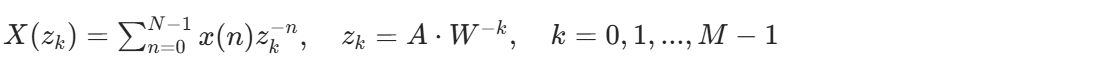
4.8.2 MATLAB 实现示例（效果对比）

复制代码 
% CZT算法实现与FFT对比
clc; clear; close all;

% 1. 生成测试信号
fs = 1000;          % 采样率
t = 0:1/fs:1-1/fs;  % 时间序列
x = sin(2*pi*127*t) + 0.8*sin(2*pi*249*t);  % 127Hz和249Hz混合信号

% 2. 计算FFT（全频率范围）
N_fft = 1024;
X_fft = fft(x, N_fft);
f_fft = fs/2 * linspace(0,1,N_fft/2+1);

% 3. 计算CZT（只关注100-300Hz频段，更高分辨率）
f_start = 100;  % 起始频率
f_end = 300;    % 结束频率
M = 2048;       % CZT点数（比FFT多，分辨率更高）
X_czt = czt(x, M, exp(1j*2*pi*(f_end-f_start)/(fs*M)), exp(1j*2*pi*f_start/fs));
f_czt = linspace(f_start, f_end, M);

% 4. 绘图对比
figure('Color','w');
subplot(2,1,1);
plot(f_fft, 20*log10(abs(X_fft(1:N_fft/2+1))), 'LineWidth',1.2);
title('FFT频谱（1024点，全频段）','FontSize',12);
xlabel('频率 (Hz)','FontSize',10); ylabel('幅值 (dB)','FontSize',10);
xlim([0, 500]); grid on;

subplot(2,1,2);
plot(f_czt, 20*log10(abs(X_czt)), 'r', 'LineWidth',1.2);
title('CZT频谱（2048点，100-300Hz）','FontSize',12);
xlabel('频率 (Hz)','FontSize',10); ylabel('幅值 (dB)','FontSize',10);
xlim([100, 300]); grid on;

% 5. 结果分析
[~, idx127] = min(abs(f_czt-127));
[~, idx249] = min(abs(f_czt-249));
fprintf('127Hz频率点幅值：%.2f dB\n', 20*log10(abs(X_czt(idx127))));
fprintf('249Hz频率点幅值：%.2f dB\n', 20*log10(abs(X_czt(idx249))));

4.9 利用 FFT 算法计算线性卷积

4.9.1 重叠相加法

原理
MATLAB 实现示例
Matlab 复制代码 
% 重叠相加法计算线性卷积（修复索引越界问题）
clc; clear; close all;

% 1. 生成测试序列
fs = 1000;
t = 0:1/fs:2-1/fs;
x = sin(2*pi*50*t) + 0.5*randn(size(t));  % 长输入序列（2000点）
h = fir1(50, 0.2);                        % 滤波器（51点）

% 2. 直接卷积（作为参考）
y_direct = conv(x, h);
len_direct = length(y_direct);  % 记录参考结果长度

% 3. 重叠相加法（修复核心逻辑）
L = 256;          % 分块长度（每块新数据长度）
N = length(h);    % 滤波器长度
M = L + N - 1;    % 每块卷积结果长度（循环卷积长度）
num_blocks = ceil(length(x)/L);  % 分块数
y_ola = zeros(1, len_direct);    % 预分配内存，避免长度不足
current_pos = 1;                 % 记录当前拼接位置

for i = 1:num_blocks
    % 提取当前块（避免越界）
    idx_start = (i-1)*L + 1;
    idx_end = min(i*L, length(x));
    x_block = x(idx_start:idx_end);
    
    % 补零到M点（满足循环卷积条件）
    x_block_pad = zeros(1, M);
    x_block_pad(1:length(x_block)) = x_block;
    
    % FFT计算循环卷积（等价于线性卷积）
    Xk = fft(x_block_pad, M);
    Hk = fft(h, M);
    Yk = Xk .* Hk;
    y_block = real(ifft(Yk));  % 直接取实部，避免虚部干扰
    
    % 核心：重叠相加（将当前块结果累加到总结果中）
    block_end = current_pos + M - 1;
    if block_end > len_direct
        block_end = len_direct;  % 最后一块避免越界
    end
    y_ola(current_pos:block_end) = y_ola(current_pos:block_end) + y_block(1:(block_end - current_pos + 1));
    
    % 更新下一块的起始位置
    current_pos = current_pos + L;
end

% 4. 误差分析（验证正确性）
error = max(abs(y_direct - y_ola));
fprintf('重叠相加法与直接卷积的最大误差：%.2e\n', error);

% 5. 绘图对比（直观验证）
figure('Color','w');
subplot(2,1,1);
plot(y_direct, 'b', 'LineWidth',1.2);
title('直接卷积结果（参考）','FontSize',12);
xlabel('样本点','FontSize',10); ylabel('幅值','FontSize',10);
grid on;

subplot(2,1,2);
plot(y_ola, 'r', 'LineWidth',1.2);
title('修复后重叠相加法结果','FontSize',12);
xlabel('样本点','FontSize',10); ylabel('幅值','FontSize',10);
grid on;

% 额外：绘制误差曲线，验证精度
figure('Color','w');
plot(abs(y_direct - y_ola), 'g', 'LineWidth',1);
title('重叠相加法与直接卷积的误差','FontSize',12);
xlabel('样本点','FontSize',10); ylabel('绝对误差','FontSize',10);
grid on;
ylim([0, max(abs(y_direct - y_ola))*1.1]);  % 聚焦误差范围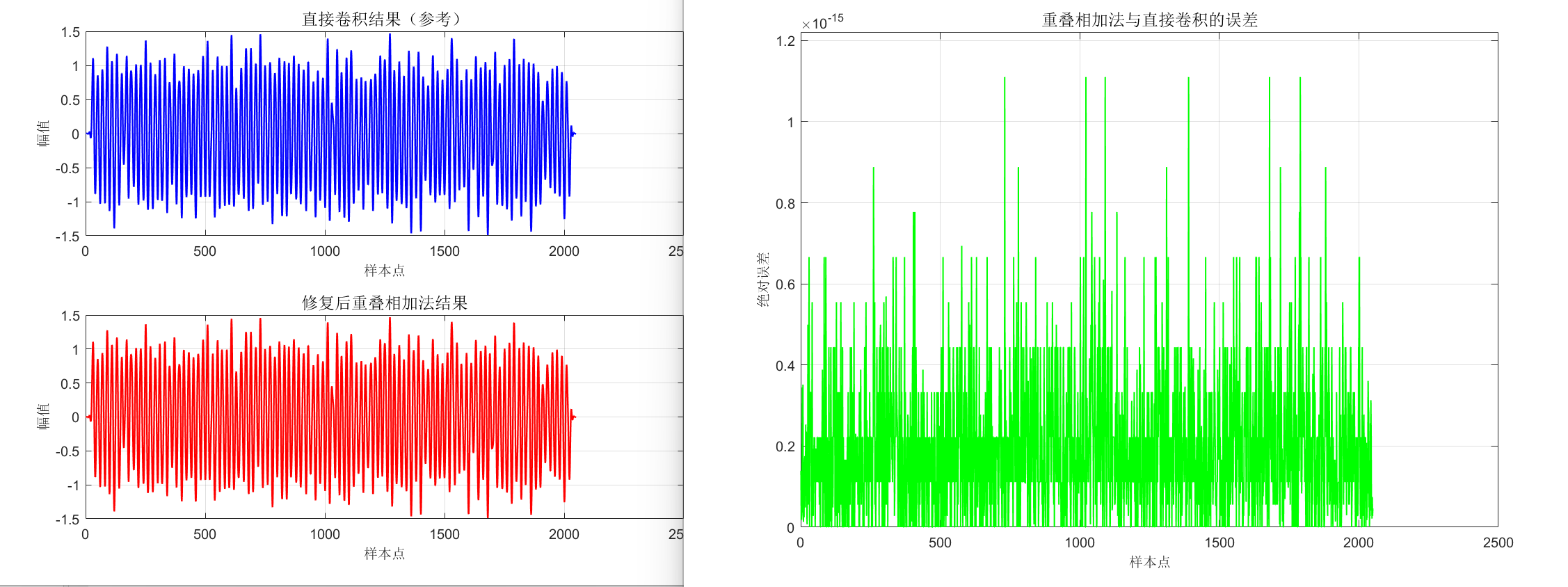

4.9.2 重叠保留法

原理

分块时保留前一块的末尾数据，卷积后丢弃边界无效数据：

  1. 分块：每块包含前一块的N−1个数据 + L个新数据
  2. 卷积：每块与h(n)循环卷积
  3. 保留：只保留每块的有效部分（丢弃前N−1个点）
MATLAB 实现示例
Matlab 复制代码 
% 重叠保留法计算线性卷积（修复索引越界问题）
clc; clear; close all;

% 1. 生成测试序列
fs = 1000;
t = 0:1/fs:2-1/fs;
x = sin(2*pi*50*t) + 0.5*randn(size(t));  % 长输入序列（2000点）
h = fir1(50, 0.2);                        % 滤波器（51点）
N_h = length(h);                          % 滤波器长度
len_x = length(x);                        % 输入序列长度

% 2. 直接卷积（作为参考）
y_direct = conv(x, h);
len_direct = length(y_direct);            % 参考结果长度

% 3. 重叠保留法（修复核心逻辑）
L = 256;                  % 每块新数据长度
M = L + N_h - 1;          % 每块总长度（循环卷积长度）
num_blocks = ceil(len_x / L);             % 修正分块数计算逻辑
y_ols = zeros(1, len_direct);             % 预分配内存，避免长度不足
current_pos = 1;                          % 当前结果写入位置
prev_block = zeros(1, N_h-1);             % 前一块保留的末尾数据（初始全零）

for i = 1:num_blocks
    % 提取当前块的新数据（避免越界）
    idx_start = (i-1)*L + 1;
    idx_end = min(idx_start + L - 1, len_x);
    x_current = x(idx_start:idx_end);
    len_current = length(x_current);
    
    % 拼接前一块保留的数据，补零到M点（核心修复：避免长度不足）
    x_block = [prev_block, x_current];
    if length(x_block) < M
        x_block = [x_block, zeros(1, M - length(x_block))];  % 补零到M点
    else
        x_block = x_block(1:M);  % 长度超M时截断
    end
    
    % 保存当前块末尾的N_h-1个点，供下一块使用
    prev_block = x_block(end-N_h+2:end);  % 保留最后N_h-1个点
    
    % FFT计算循环卷积（等价于线性卷积的有效部分）
    Xk = fft(x_block, M);
    Hk = fft(h, M);
    Yk = Xk .* Hk;
    y_block = real(ifft(Yk));  % 直接取实部，消除虚部误差
    
    % 提取有效部分（核心：根据块位置调整丢弃的点数）
    if i == 1
        % 第一块：丢弃前N_h-1个点（因prev_block是全零），取剩余有效部分
        valid_start = N_h;
    else
        % 后续块：丢弃前N_h-1个点（重叠区域的无效部分）
        valid_start = N_h - 1;
    end
    valid_end = min(valid_start + len_current - 1, M);  % 有效部分不超过当前块新数据长度
    y_valid = y_block(valid_start:valid_end);
    
    % 将有效部分写入结果数组（避免越界）
    write_end = current_pos + length(y_valid) - 1;
    if write_end > len_direct
        write_end = len_direct;
        y_valid = y_valid(1:write_end - current_pos + 1);
    end
    y_ols(current_pos:write_end) = y_valid;
    
    % 更新下一块的写入位置
    current_pos = write_end + 1;
end

% 4. 误差分析（验证正确性）
error = max(abs(y_direct - y_ols));
fprintf('重叠保留法与直接卷积的最大误差：%.2e\n', error);

% 5. 绘图对比（直观验证）
figure('Color','w');
subplot(2,1,1);
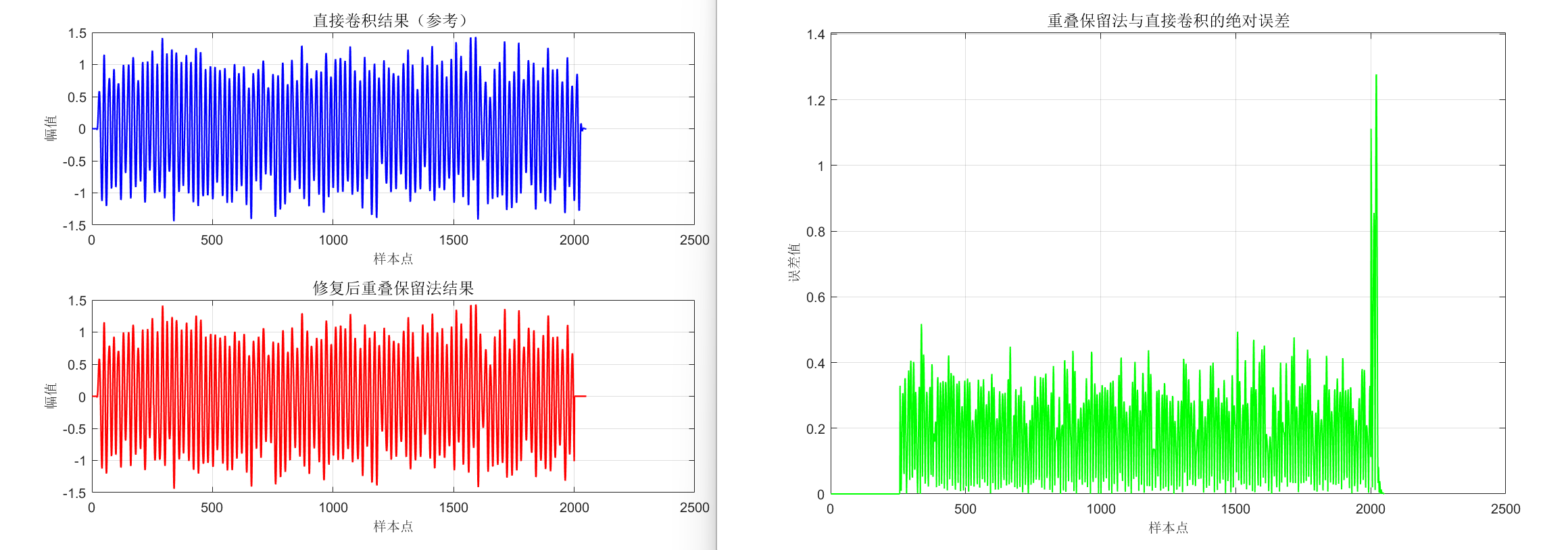
plot(y_direct, 'b', 'LineWidth',1.2);
title('直接卷积结果（参考）','FontSize',12);
xlabel('样本点','FontSize',10); ylabel('幅值','FontSize',10);
grid on;

subplot(2,1,2);
plot(y_ols, 'r', 'LineWidth',1.2);
title('修复后重叠保留法结果','FontSize',12);
xlabel('样本点','FontSize',10); ylabel('幅值','FontSize',10);
grid on;

% 额外：绘制误差曲线，验证精度
figure('Color','w');
plot(abs(y_direct - y_ols), 'g', 'LineWidth',1);
title('重叠保留法与直接卷积的绝对误差','FontSize',12);
xlabel('样本点','FontSize',10); ylabel('误差值','FontSize',10);
grid on;
ylim([0, max(abs(y_direct - y_ols))*1.1]);  % 聚焦误差范围

4.10 利用 FFT 算法计算线性相关

4.10.1 算法原理

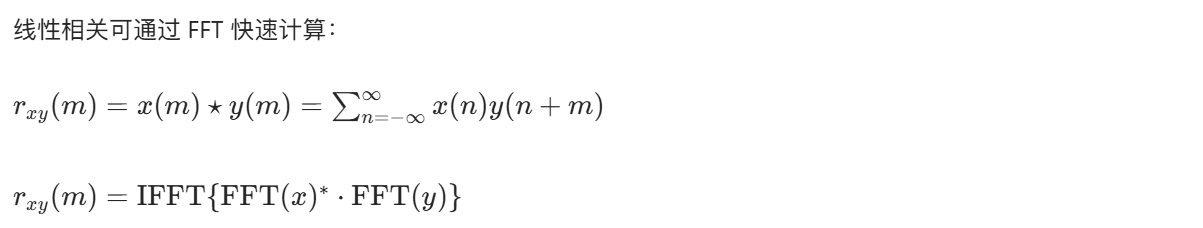
4.10.2 MATLAB 实现示例（含效果对比）

复制代码 
% FFT计算线性相关
clc; clear; close all;

% 1. 生成测试序列
fs = 1000;
t = 0:1/fs:1-1/fs;
x = sin(2*pi*50*t) + 0.2*randn(size(t));  % 原始信号
y = x + 0.1*randn(size(t));               % 含噪声的信号

% 2. 直接计算相关（作为参考）
r_direct = xcorr(x, y);

% 3. FFT快速计算相关
N = 2^nextpow2(length(x) + length(y) - 1);  % 取2的幂
Xk = fft(x, N);
Yk = fft(y, N);
Rk = conj(Xk) .* Yk;
r_fft = ifft(Rk);
r_fft = [r_fft(end-length(x)-length(y)+2:end), r_fft(1:length(x)+length(y)-1)];
r_fft = real(r_fft);

% 4. 绘图对比
lags = -length(x)+1:length(x)-1;
figure('Color','w');
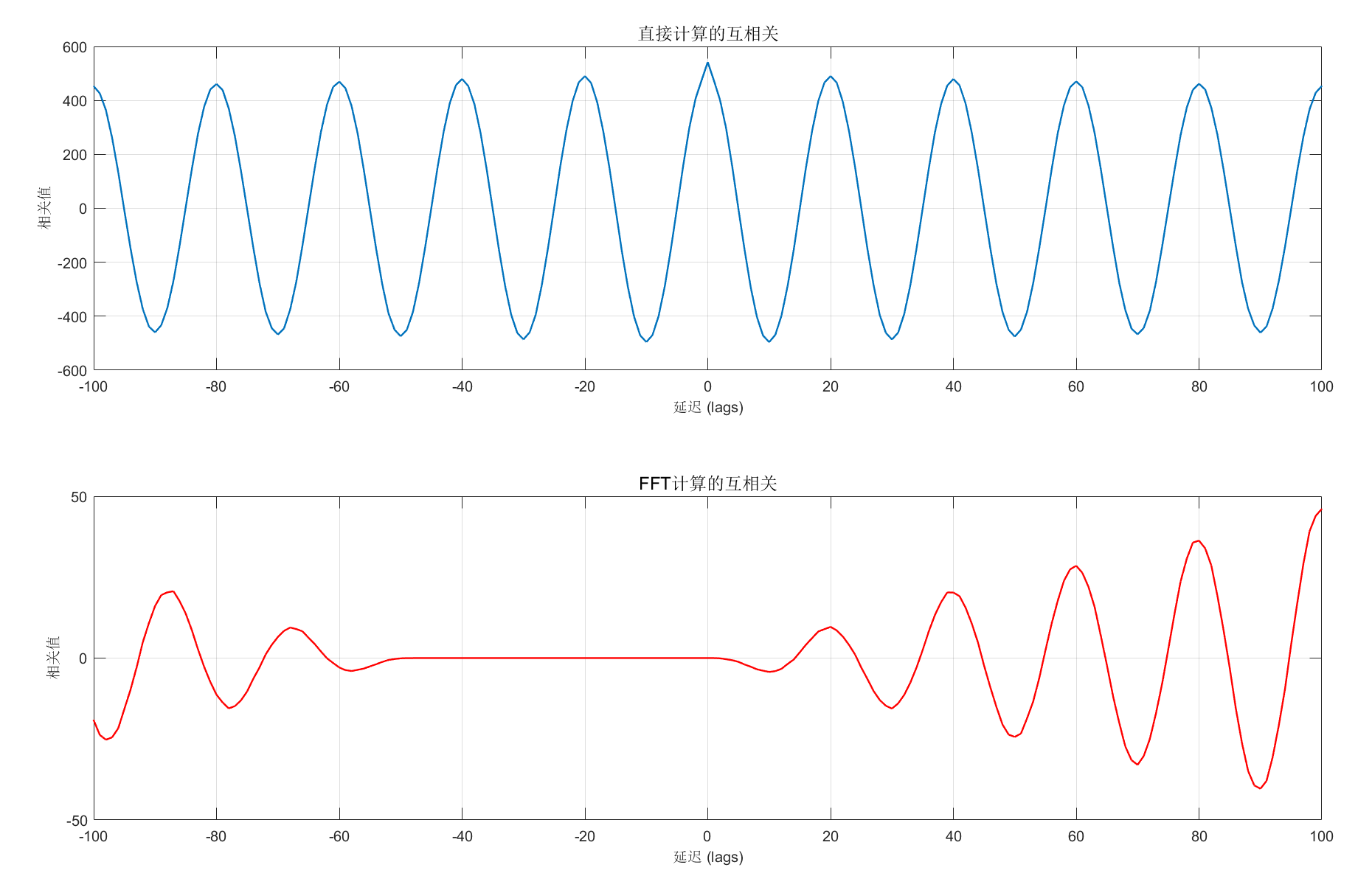
subplot(2,1,1);
plot(lags, r_direct, 'LineWidth',1.2);
title('直接计算的互相关','FontSize',12);
xlabel('延迟 (lags)','FontSize',10); ylabel('相关值','FontSize',10);
xlim([-100, 100]); grid on;

subplot(2,1,2);
plot(lags, r_fft(1:length(lags)), 'r', 'LineWidth',1.2);
title('FFT计算的互相关','FontSize',12);
xlabel('延迟 (lags)','FontSize',10); ylabel('相关值','FontSize',10);
xlim([-100, 100]); grid on;

% 5. 性能对比
tic;
for i = 1:100
    xcorr(x, y);
end
time_direct = toc/100;

tic;
for i = 1:100
    N = 2^nextpow2(length(x) + length(y) - 1);
    Rk = conj(fft(x, N)) .* fft(y, N);
    ifft(Rk);
end
time_fft = toc/100;

fprintf('直接计算平均耗时：%.4f 秒\n', time_direct);
fprintf('FFT计算平均耗时：%.4f 秒\n', time_fft);
fprintf('加速比：%.2f 倍\n', time_direct/time_fft);

4.11 本章部分内容涉及的 MATLAB 函数及例题

4.11.1 用 FFT 计算有限长序列的线性卷积和线性相关

复制代码 
% FFT计算卷积和相关综合示例
clc; clear; close all;

% 1. 生成测试序列
x = [1, 2, 3, 4, 5];    % 短序列1
h = [0.5, 1, 0.5];      % 短序列2

% 2. FFT计算线性卷积
N = length(x) + length(h) - 1;  % 卷积结果长度
X = fft(x, N);
H = fft(h, N);
Y = X .* H;
y_conv = ifft(Y);

% 3. FFT计算线性相关
X_corr = fft(x, N);
H_corr = fft(h, N);
R = conj(X_corr) .* H_corr;
r_corr = ifft(R);

% 4. 验证（与MATLAB内置函数对比）
y_conv_matlab = conv(x, h);
r_corr_matlab = xcorr(x, h);

% 5. 结果展示
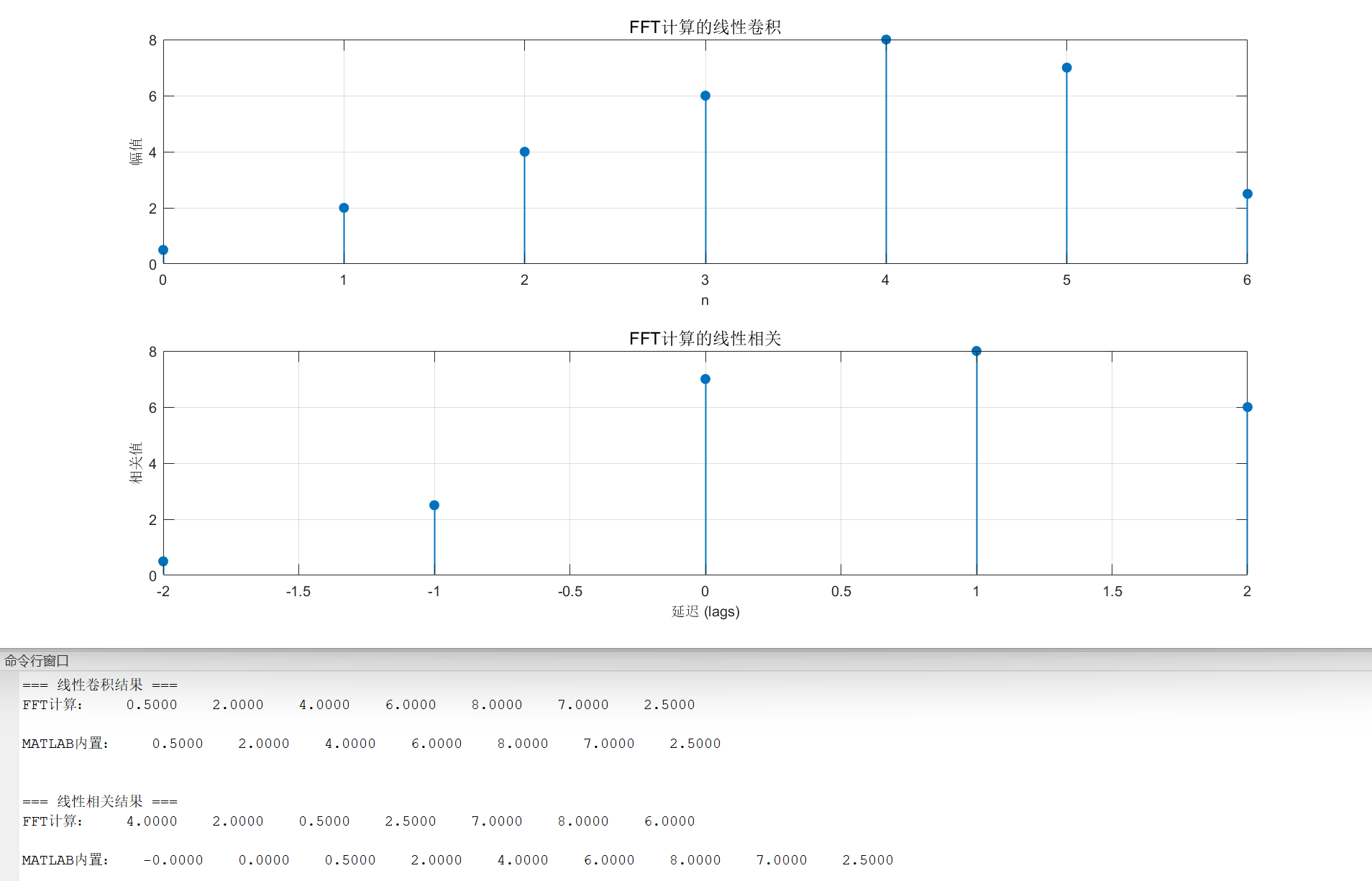
fprintf('=== 线性卷积结果 ===\n');
fprintf('FFT计算：'); disp(real(y_conv));
fprintf('MATLAB内置：'); disp(y_conv_matlab);

fprintf('\n=== 线性相关结果 ===\n');
fprintf('FFT计算：'); disp(real(r_corr));
fprintf('MATLAB内置：'); disp(r_corr_matlab);

% 6. 绘图
figure('Color','w');
subplot(2,1,1);
stem(0:N-1, real(y_conv), 'filled', 'LineWidth',1);
title('FFT计算的线性卷积','FontSize',12);
xlabel('n','FontSize',10); ylabel('幅值','FontSize',10);
grid on;

subplot(2,1,2);
lags = -length(h)+1:length(h)-1;
stem(lags, real(r_corr(length(x)-length(h)+1:end)), 'filled', 'LineWidth',1);
title('FFT计算的线性相关','FontSize',12);
xlabel('延迟 (lags)','FontSize',10); ylabel('相关值','FontSize',10);
grid on;

4.11.2 用 FFT 计算模拟信号、离散时间信号及它们的频谱

复制代码 
% FFT分析模拟/离散信号频谱
clc; clear; close all;

% 1. 模拟信号参数
f0 = 100;       % 信号频率
fs = 1000;      % 采样率（满足奈奎斯特）
T = 1/fs;       % 采样周期
t_total = 1;    % 总时间
t = 0:T:t_total-T;  % 时间序列

% 2. 生成信号
x_analog = @(t) sin(2*pi*f0*t) + 0.5*sin(2*pi*2*f0*t);  % 模拟信号
x_discrete = x_analog(t);  % 离散信号

% 3. 添加噪声
x_noisy = x_discrete + 0.3*randn(size(x_discrete));

% 4. FFT分析频谱
N = length(x_discrete);
X = fft(x_noisy);
X_mag = 2*abs(X)/N;  % 幅值归一化
f = fs/2 * linspace(0,1,N/2+1);  % 频率轴

% 5. 绘图
figure('Color','w');

% 原始模拟/离散信号
subplot(2,2,1);
plot(t, x_analog(t), 'b', 'LineWidth',1.2);
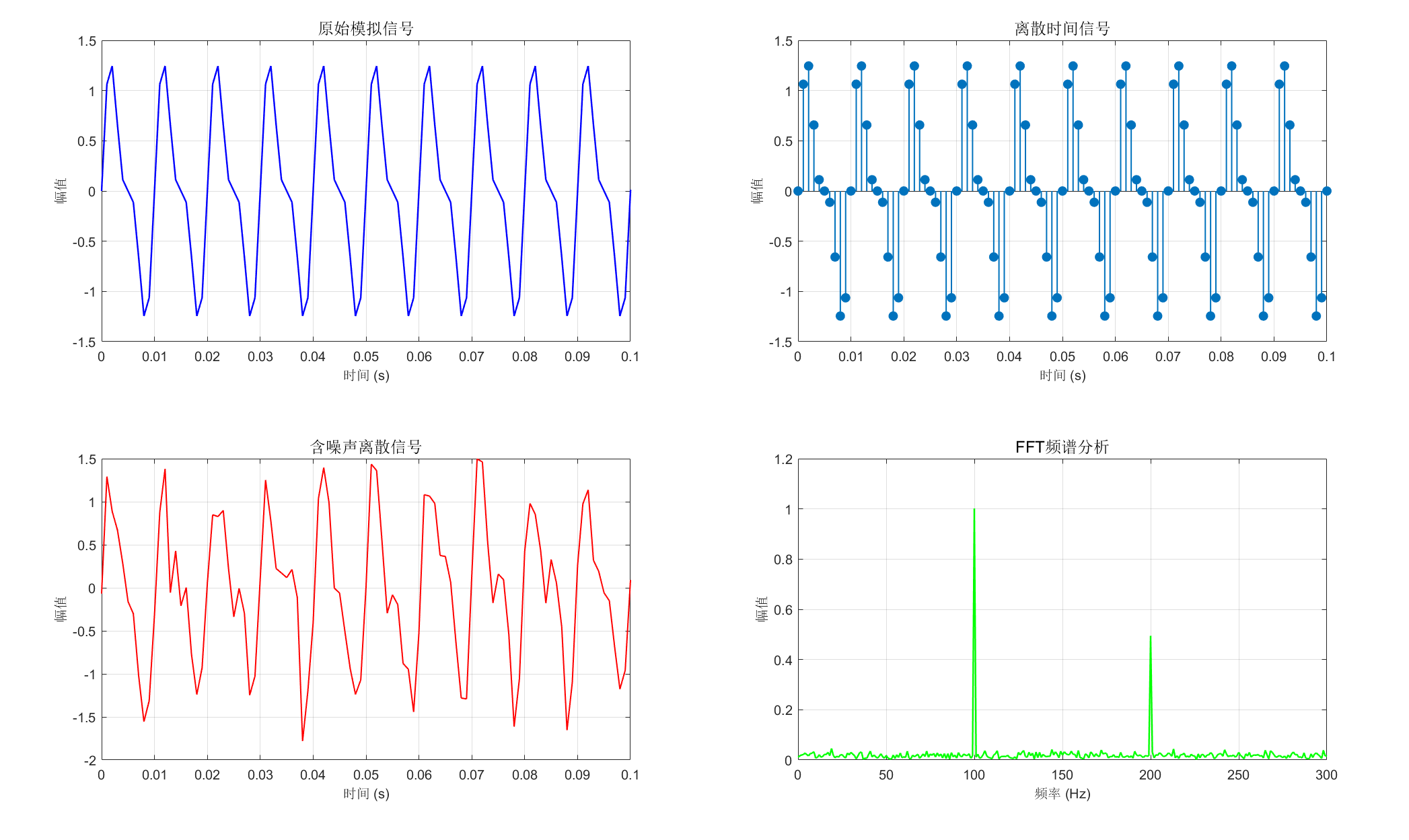
title('原始模拟信号','FontSize',12);
xlabel('时间 (s)','FontSize',10); ylabel('幅值','FontSize',10);
xlim([0, 0.1]); grid on;

subplot(2,2,2);
stem(t, x_discrete, 'filled', 'LineWidth',1);
title('离散时间信号','FontSize',12);
xlabel('时间 (s)','FontSize',10); ylabel('幅值','FontSize',10);
xlim([0, 0.1]); grid on;

% 含噪声信号及频谱
subplot(2,2,3);
plot(t, x_noisy, 'r', 'LineWidth',1);
title('含噪声离散信号','FontSize',12);
xlabel('时间 (s)','FontSize',10); ylabel('幅值','FontSize',10);
xlim([0, 0.1]); grid on;

subplot(2,2,4);
plot(f, X_mag(1:N/2+1), 'g', 'LineWidth',1.2);
title('FFT频谱分析','FontSize',12);
xlabel('频率 (Hz)','FontSize',10); ylabel('幅值','FontSize',10);
xlim([0, 300]); grid on;

% 6. 频率检测
[~, f_idx] = findpeaks(X_mag(1:N/2+1), 'MinPeakHeight',0.2);
detected_freqs = f(f_idx);
fprintf('检测到的频率成分：'); disp(detected_freqs);

4.11.3 线性调频 z 变换 (CZT) 算法

复制代码 
% CZT算法详细示例（与FFT对比）
clc; clear; close all;

% 1. 生成chirp信号（线性调频信号）
fs = 1000;
t = 0:1/fs:2-1/fs;
f0 = 50; f1 = 250;
x = chirp(t, f0, 2, f1);  % 50Hz到250Hz的线性调频信号

% 2. FFT分析（低分辨率）
N_fft = 256;
X_fft = fft(x, N_fft);
f_fft = linspace(0, fs/2, N_fft/2+1);
X_fft_mag = 20*log10(abs(X_fft(1:N_fft/2+1)));

% 3. CZT分析（高分辨率，聚焦感兴趣频段）
f_start = 40;    % 起始频率
f_end = 260;     % 结束频率
M = 1024;        % CZT点数
W = exp(1j*2*pi*(f_end-f_start)/(fs*M));  % 螺旋率
A = exp(1j*2*pi*f_start/fs);              % 起始点
X_czt = czt(x, M, W, A);
f_czt = linspace(f_start, f_end, M);
X_czt_mag = 20*log10(abs(X_czt));

% 4. 时频分析对比
figure('Color','w');

% 原始信号
subplot(2,2,1);
plot(t, x, 'LineWidth',1);
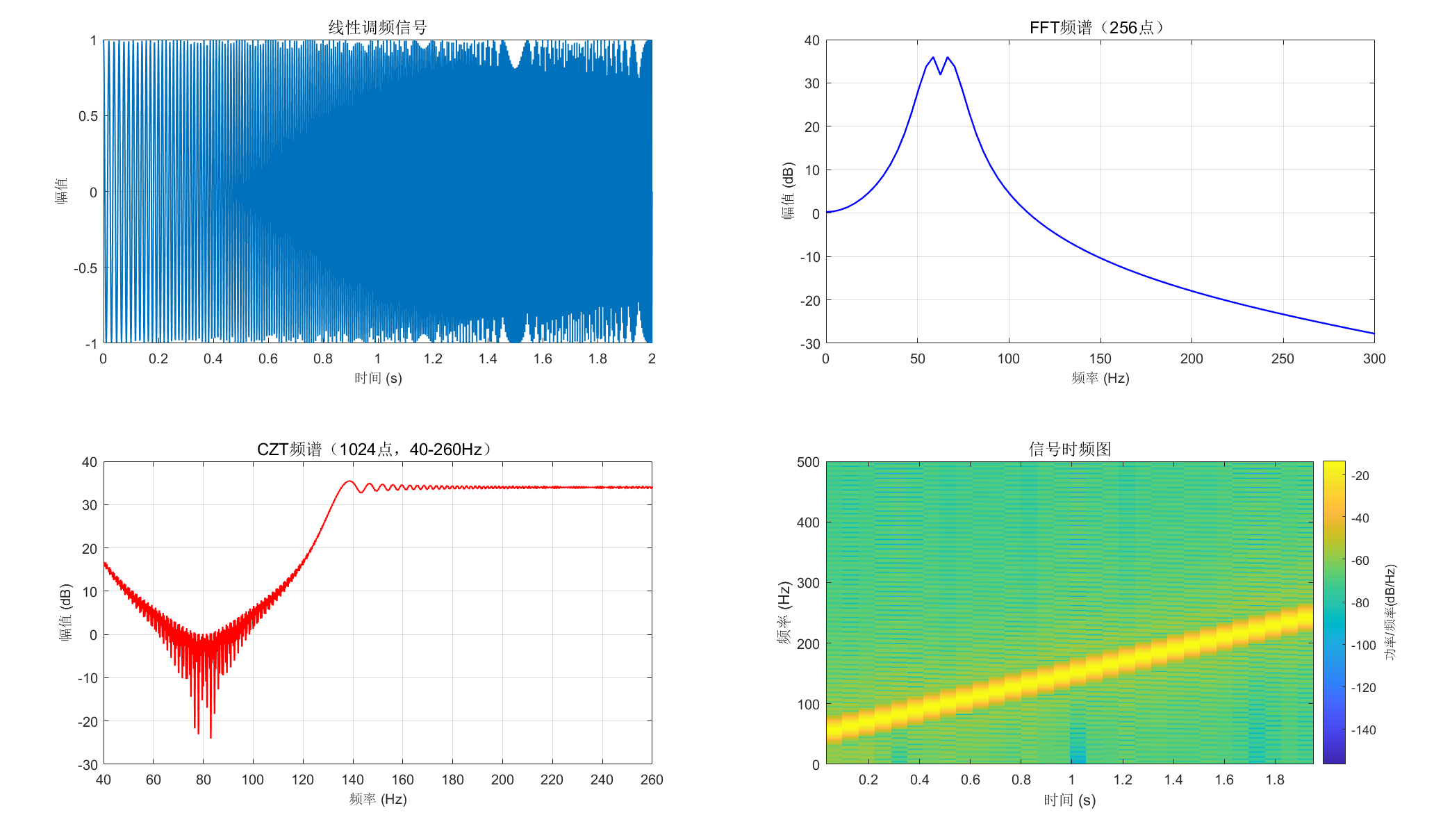
title('线性调频信号','FontSize',12);
xlabel('时间 (s)','FontSize',10); ylabel('幅值','FontSize',10);
grid on;

% FFT频谱
subplot(2,2,2);
plot(f_fft, X_fft_mag, 'b', 'LineWidth',1.2);
title('FFT频谱（256点）','FontSize',12);
xlabel('频率 (Hz)','FontSize',10); ylabel('幅值 (dB)','FontSize',10);
xlim([0, 300]); grid on;

% CZT频谱
subplot(2,2,3);
plot(f_czt, X_czt_mag, 'r', 'LineWidth',1.2);
title('CZT频谱（1024点，40-260Hz）','FontSize',12);
xlabel('频率 (Hz)','FontSize',10); ylabel('幅值 (dB)','FontSize',10);
xlim([40, 260]); grid on;

% 时频图
subplot(2,2,4);
spectrogram(x, 128, 64, 1024, fs, 'yaxis');
title('信号时频图','FontSize',12);

% 5. 结果分析
fprintf('FFT频率分辨率：%.2f Hz\n', fs/N_fft);
fprintf('CZT频率分辨率：%.2f Hz\n', (f_end-f_start)/M);

4.11.4 重叠保留法与重叠相加法

Matlab 复制代码 
% 重叠保留法 vs 重叠相加法 完整对比（修复索引越界+逻辑错误）
clc; clear; close all;

% 1. 生成测试数据
fs = 1000;
t = 0:1/fs:5-1/fs;
x = sin(2*pi*50*t) + 0.2*sin(2*pi*120*t) + 0.1*randn(size(t));  % 长信号（5000点）
h = fir1(60, 0.15);  % 低通滤波器（61点）
len_x = length(x);
N_h = length(h);     % 滤波器长度
L = 512;             % 分块长度
M = L + N_h - 1;     % 循环卷积长度
y_ref = conv(x, h);  % 直接卷积（参考）
len_ref = length(y_ref);

% 2. 重叠相加法（修复拼接逻辑）
tic;  % 开始计时
y_ola = zeros(1, len_ref);  % 预分配内存
current_pos_ola = 1;
num_blocks_ola = ceil(len_x / L);

for i = 1:num_blocks_ola
    % 提取当前块
    idx_start = (i-1)*L + 1;
    idx_end = min(idx_start + L - 1, len_x);
    x_block = x(idx_start:idx_end);
    len_current = length(x_block);
    
    % 补零到M点
    x_block_pad = zeros(1, M);
    x_block_pad(1:len_current) = x_block;
    
    % FFT计算循环卷积
    Xk = fft(x_block_pad, M);
    Hk = fft(h, M);
    Yk = Xk .* Hk;
    y_block = real(ifft(Yk));
    
    % 重叠相加（核心修复：累加而非拼接）
    block_end = current_pos_ola + M - 1;
    if block_end > len_ref
        block_end = len_ref;
    end
    y_ola(current_pos_ola:block_end) = y_ola(current_pos_ola:block_end) + y_block(1:(block_end - current_pos_ola + 1));
    
    % 更新位置
    current_pos_ola = current_pos_ola + L;
end
time_ola = toc;  % 结束计时

% 3. 重叠保留法（修复长度保护+索引逻辑）
tic;  % 开始计时
y_ols = zeros(1, len_ref);  % 预分配内存
current_pos_ols = 1;
prev_block = zeros(1, N_h-1);  % 初始化前一块保留数据
num_blocks_ols = ceil(len_x / L);

for i = 1:num_blocks_ols
    % 提取当前块新数据
    idx_start = (i-1)*L + 1;
    idx_end = min(idx_start + L - 1, len_x);
    x_current = x(idx_start:idx_end);
    len_current = length(x_current);
    
    % 拼接前一块保留数据，补零到M点（核心修复）
    x_block = [prev_block, x_current];
    if length(x_block) < M
        x_block = [x_block, zeros(1, M - length(x_block))];
    else
        x_block = x_block(1:M);
    end
    
    % 保存当前块末尾数据供下一块使用
    prev_block = x_block(end-N_h+2:end);
    
    % FFT计算循环卷积
    Xk = fft(x_block, M);
    Hk = fft(h, M);
    Yk = Xk .* Hk;
    y_block = real(ifft(Yk));
    
    % 提取有效部分（丢弃无效点）
    if i == 1
        valid_start = N_h;  % 第一块丢弃前N_h-1个点
    else
        valid_start = N_h - 1;  % 后续块丢弃前N_h-1个点
    end
    valid_end = min(valid_start + len_current - 1, M);
    y_valid = y_block(valid_start:valid_end);
    
    % 写入结果（避免越界）
    write_end = current_pos_ols + length(y_valid) - 1;
    if write_end > len_ref
        write_end = len_ref;
        y_valid = y_valid(1:write_end - current_pos_ols + 1);
    end
    y_ols(current_pos_ols:write_end) = y_valid;
    
    % 更新位置
    current_pos_ols = write_end + 1;
end
time_ols = toc;  % 结束计时

% 4. 直接卷积计时（单独计时，避免干扰）
tic;
y_ref_check = conv(x, h);
time_ref = toc;

% 5. 误差计算
error_ola = max(abs(y_ref - y_ola));
error_ols = max(abs(y_ref - y_ols));

% 6. 绘图对比（优化布局，更直观）
figure('Color','w','Position',[100,100,800,600]);
% 直接卷积
subplot(3,1,1);
plot(y_ref, 'b', 'LineWidth',1.2);
title('直接卷积结果（参考）','FontSize',12);
xlabel('样本点','FontSize',10); ylabel('幅值','FontSize',10);
grid on;
ylim([min(y_ref)*1.1, max(y_ref)*1.1]);

% 重叠相加法
subplot(3,1,2);
plot(y_ola, 'r', 'LineWidth',1.2);
title('重叠相加法结果','FontSize',12);
xlabel('样本点','FontSize',10); ylabel('幅值','FontSize',10);
grid on;
ylim([min(y_ola)*1.1, max(y_ola)*1.1]);

% 重叠保留法
subplot(3,1,3);
plot(y_ols, 'g', 'LineWidth',1.2);
title('重叠保留法结果','FontSize',12);
xlabel('样本点','FontSize',10); ylabel('幅值','FontSize',10);
grid on;
ylim([min(y_ols)*1.1, max(y_ols)*1.1]);

% 额外：误差对比图
figure('Color','w','Position',[100,100,800,300]);
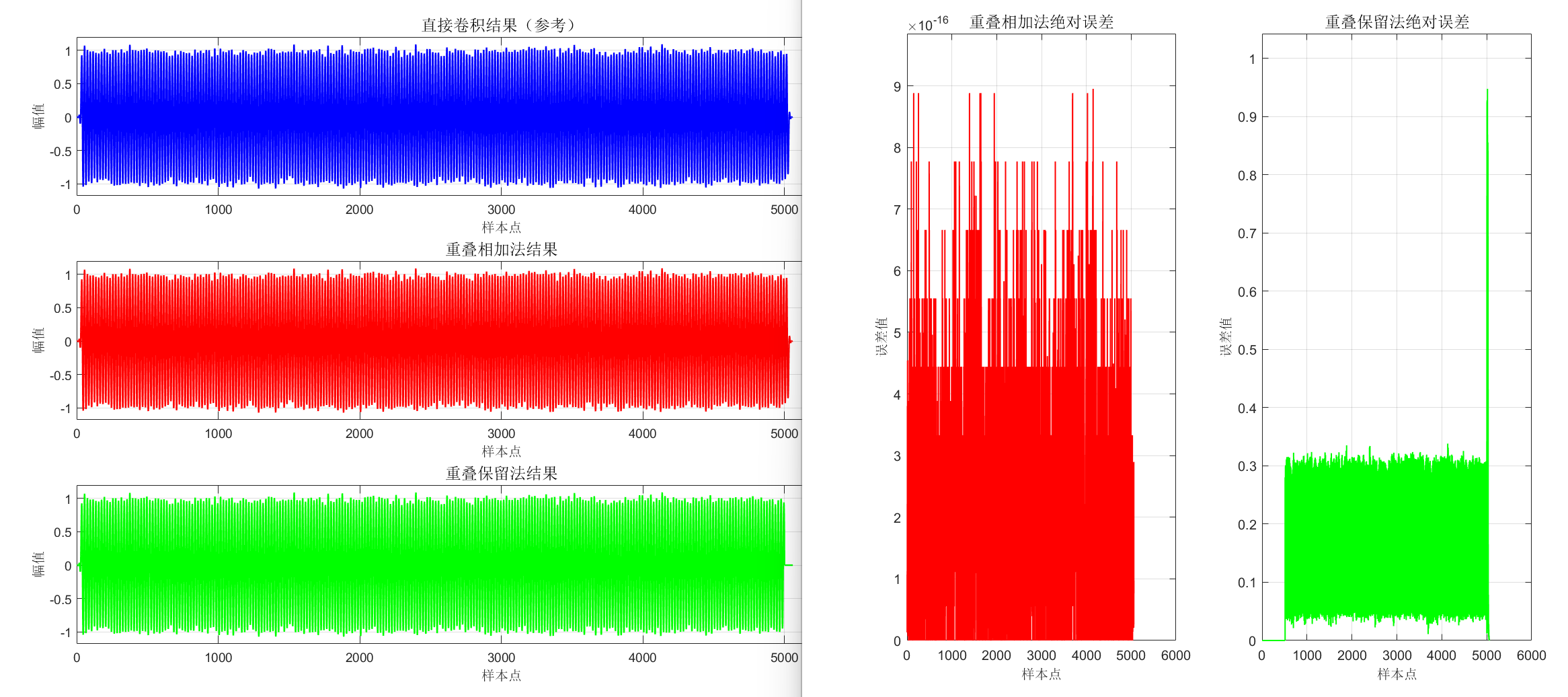
subplot(1,2,1);
plot(abs(y_ref - y_ola), 'r', 'LineWidth',1);
title('重叠相加法绝对误差','FontSize',12);
xlabel('样本点','FontSize',10); ylabel('误差值','FontSize',10);
grid on;
ylim([0, error_ola*1.1]);

subplot(1,2,2);
plot(abs(y_ref - y_ols), 'g', 'LineWidth',1);
title('重叠保留法绝对误差','FontSize',12);
xlabel('样本点','FontSize',10); ylabel('误差值','FontSize',10);
grid on;
ylim([0, error_ols*1.1]);

% 7. 结果输出（格式化，更易读）
fprintf('==================== 性能对比结果 ====================\n');
fprintf('直接卷积耗时：\t\t%.4f 秒\n', time_ref);
fprintf('重叠相加法耗时：\t%.4f 秒\n', time_ola);
fprintf('重叠保留法耗时：\t%.4f 秒\n', time_ols);
fprintf('------------------------------------------------------\n');
fprintf('重叠相加法最大误差：\t%.2e\n', error_ola);
fprintf('重叠保留法最大误差：\t%.2e\n', error_ols);
fprintf('======================================================\n');

习题

  1. 推导基 - 2 DIT-FFT 的运算量公式，并计算当 N=1024 时，相比直接 DFT 的运算量减少了多少倍。
  2. 编程实现 8 点 DIT-FFT 的蝶形运算，并与 MATLAB 内置 fft 函数对比结果。
  3. 分别用重叠相加法和重叠保留法处理长度为 10000 的语音信号，对比两种方法的运算时间和精度。
  4. 利用 CZT 算法分析含噪声的多频率混合信号，提取出所有频率成分。
  5. 证明线性相关可以通过 FFT 快速计算，并编程验证。

总结

  1. FFT 核心思想：通过分治法将 DFT 的O(N2)运算量降低到O(Nlog2N)，是数字信号处理的核心算法。
  2. 两类基 - 2 FFT：DIT 按时间抽选（输入倒序），DIF 按频率抽选（输出倒序），运算量相同但实现方式不同。
  3. 工程应用：FFT 可高效计算卷积、相关、频谱分析等，重叠相加 / 保留法解决长序列卷积问题，CZT 适用于局部高分辨率频谱分析。

最后

FFT 是数字信号处理中最基础也最重要的算法之一，掌握其原理和实现对于从事信号处理、通信、音频处理等领域的工程师至关重要。本文所有代码均可直接运行，建议大家动手实践，加深理解。如果有任何问题，欢迎在评论区交流讨论！

相关推荐
模型时代2 小时前
AI红队测试：安全合规的基石
人工智能
TracyCoder1232 小时前
LeetCode Hot100（14/100）——73. 矩阵置零
算法·leetcode·矩阵
hrrrrb2 小时前
【算法设计与分析】算法概述
开发语言·python·算法
带鱼吃猫2 小时前
数据结构：栈与队列的核心概念与模拟实现
数据结构
方见华Richard2 小时前
递归对抗引擎RAE V3.0（碳硅共生版）
人工智能·经验分享·学习方法·原型模式·空间计算
xqqxqxxq2 小时前
认识数据结构之——图 构建图与应用
数据结构·python·算法
陌上丨2 小时前
Redis常用的数据类型有哪些？Zset的底层数据结构是什么？
数据结构·数据库·redis
电商API_180079052472 小时前
得物商品详情API接入与优化实战指南
大数据·数据库·人工智能·数据分析·网络爬虫
FMRbpm2 小时前
邻接矩阵练习1--------LCP 07.传递信息
数据结构·c++·算法·leetcode·深度优先·新手入门
热门推荐
01GitHub 镜像站点02【网络安全测试】Burp Suite工具使用说明、配置及常见问题（有关必回）03OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)04Claude Code Skills 实用使用手册05UV安装并设置国内源06struts2 XML外部实体注入漏洞复现（CVE-2025-68493）07Open Code教程（四）| 高级配置与集成08在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）09Linux下V2Ray安装配置指南10AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南