【算法训练营 · 二刷总结篇】二叉树、栈与队列部分

文章目录

二叉树部分
- 核心知识点
- ★如何思考递归★
- 技巧方法
- - [✅ 技巧一：递归遍历（★★★★★ 占比50%+）](#✅ 技巧一：递归遍历（★★★★★ 占比50%+）)
  - [✅ 技巧二：迭代遍历（★★★★★ 占比20%+）](#✅ 技巧二：迭代遍历（★★★★★ 占比20%+）)
  - [✅ 技巧三：层序遍历（BFS，★★★★ 占比15%+）](#✅ 技巧三：层序遍历（BFS，★★★★ 占比15%+）)
  - [✅ 技巧四：BST专属技巧（★★★★ 占比10%+）](#✅ 技巧四：BST专属技巧（★★★★ 占比10%+）)
  - [✅ 技巧五：二叉树构造类技巧（★★★ 占比5%+）](#✅ 技巧五：二叉树构造类技巧（★★★ 占比5%+）)
  - [✅ 技巧六：路径问题技巧（★★★ 占比5%+）](#✅ 技巧六：路径问题技巧（★★★ 占比5%+）)
  - [✅ 技巧七：二叉树对称相同判断技巧（★★★ 占比5%+）](#✅ 技巧七：二叉树对称相同判断技巧（★★★ 占比5%+）)
- 通用代码模板
- - [✔ 模板1：递归遍历（前中后序通用）](#✔ 模板1：递归遍历（前中后序通用）)
  - [✔ 模板2：迭代遍历（统一标记法，前中后序通用）](#✔ 模板2：迭代遍历（统一标记法，前中后序通用）)
  - [✔ 模板3：层序遍历（BFS）](#✔ 模板3：层序遍历（BFS）)
  - [✔ 模板4：BST核心操作（验证+搜索+插入+删除）](#✔ 模板4：BST核心操作（验证+搜索+插入+删除）)
  - [✔ 模板5：构造二叉树（前序+中序）](#✔ 模板5：构造二叉树（前序+中序）)
  - [✔ 模板6：路径求和问题（递归+回溯）](#✔ 模板6：路径求和问题（递归+回溯）)
栈与队列部分
- 核心知识点
- 技巧方法
- - [✅ 技巧一：单调栈（★★★★★ 占比40%+，核心中的核心）](#✅ 技巧一：单调栈（★★★★★ 占比40%+，核心中的核心）)
  - [✅ 技巧二：栈与队列互模拟（★★★★ 占比20%+，基础必背）](#✅ 技巧二：栈与队列互模拟（★★★★ 占比20%+，基础必背）)
  - [✅ 技巧三：括号匹配（★★★★ 占比15%+，送分题）](#✅ 技巧三：括号匹配（★★★★ 占比15%+，送分题）)
  - [✅ 技巧四：层序遍历/滑动窗口/单调队列（队列/BFS，★★★★ 占比10%+）](#✅ 技巧四：层序遍历/滑动窗口/单调队列（队列/BFS，★★★★ 占比10%+）)
  - [✅ 技巧五：最小栈（★★★ 占比8%+，常数时间最值）](#✅ 技巧五：最小栈（★★★ 占比8%+，常数时间最值）)
  - [✅ 技巧六：表达式求值（栈，★★★ 占比7%+）](#✅ 技巧六：表达式求值（栈，★★★ 占比7%+）)
- 通用代码模板
- - [✔ 模板1：单调栈（找下一个更大元素，LeetCode 496）](#✔ 模板1：单调栈（找下一个更大元素，LeetCode 496）)
  - [✔ 模板2：栈模拟队列（LeetCode 232）](#✔ 模板2：栈模拟队列（LeetCode 232）)
  - [✔ 模板3：队列模拟栈（LeetCode 225）](#✔ 模板3：队列模拟栈（LeetCode 225）)
  - [✔ 模板4：括号匹配（LeetCode 20）](#✔ 模板4：括号匹配（LeetCode 20）)
  - [✔ 模板5：每日温度（单调栈经典题，LeetCode 739）](#✔ 模板5：每日温度（单调栈经典题，LeetCode 739）)
  - [✔ 模板6：最小栈（LeetCode 155）](#✔ 模板6：最小栈（LeetCode 155）)
  - [✔ 模板7：滑动窗口最大值（单调队列，LeetCode 239）](#✔ 模板7：滑动窗口最大值（单调队列，LeetCode 239）)
  - [✔ 模板8：逆波兰表达式求值（LeetCode 150）](#✔ 模板8：逆波兰表达式求值（LeetCode 150）)

二叉树部分

核心知识点

二叉树的核心分类（后端面试常问区别）

类型	核心特征	后端工程应用场景
普通二叉树	每个节点最多2个子节点，无其他约束	算法题基础载体
二叉搜索树（BST）	① 左子树所有节点值 < 根节点值；② 右子树所有节点值 > 根节点值；③ 左右子树也是BST	数据库索引（B+树基础）、有序数据查询
完全二叉树	除最后一层外每层满，最后一层节点靠左排列	堆（PriorityQueue）、数组高效存储
满二叉树	所有层节点数满，节点总数 = 2 h − 1 2^h - 1 2h−1（h为高度）	二叉树性质推导、完美平衡场景
平衡二叉树（AVL）	左右子树高度差 ≤ 1，插入/删除需旋转平衡	高性能查询场景（红黑树简化版）
红黑树	近似平衡，满足5条核心性质（根黑、叶黑、红父必黑、路径黑节点数相同）	HashMap/JDK1.8、ConcurrentHashMap

二叉树的存储方式（后端工程实现）
- 链式存储（算法题首选） ：Java中用类定义节点，包含val、left、right指针，灵活但占内存稍多：
  java 复制代码
```
public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode() {}
    TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}
```
- 数组存储（完全二叉树高效） ：索引i的左孩子 = 2i+1，右孩子 = 2i+2，父节点 = (i-1)/2（Java堆的底层实现方式）。

遍历方式（算法题核心，递归+迭代都要会）

遍历类型	顺序	核心用途	递归难度	迭代难度
前序DFS	根→左→右	构造二叉树、复制树、序列化	简单	中等
中序DFS	左→根→右	BST验证（升序）、找BST第k小	简单	中等
后序DFS	左→右→根	删除树、计算子树和、路径回溯	简单	较难
层序BFS	按层从上到下	层级输出、最小深度、层最大值	中等	简单

核心属性计算（高频小题）
- 高度 vs 深度 ：
  - 深度：从根节点到当前节点的边数/节点数（算法题多按节点数算）；
  - 高度：从当前节点到叶子节点的边数/节点数（空节点高度记为-1或0，需统一标准）；
- 直径：二叉树中任意两节点的最长路径长度，核心逻辑是「每个节点的左右子树高度和的最大值」；
- 完全二叉树节点数 ：优化解法O( l o g 2 n log^2n log2n)（普通遍历O(n)），利用完全二叉树"左/右子树必为满二叉树"的特性。
BST的核心特性（必背，关联数据库索引）
- 中序遍历结果是严格升序（含重复值的BST需额外约定，如右子树≥根）；
- 搜索/插入/删除的平均时间复杂度O(logn)，最坏O(n)（退化为链表）；
- 数据库B+树是BST的多叉扩展，所有数据在叶子节点，非叶子节点仅存索引，提升磁盘IO效率。
红黑树的核心（HashMap底层追问）
- 5条核心性质：① 节点是红/黑；② 根是黑；③ 叶子（NIL）是黑；④ 红节点的子节点必为黑；⑤ 任一节点到其叶子的所有路径含相同数目的黑节点；
- 对比AVL：红黑树牺牲"严格平衡"换"插入/删除效率"（旋转次数少），更适合高频修改的场景（如HashMap）。
二叉树序列化/反序列化（中等题高频）
- 核心：将树转为字符串（便于传输/存储），再还原为树；
- 常用方式：前序遍历+空节点标记（如null用#表示）、层序遍历+空节点标记。

★如何思考递归★

递归的使用场景：可以用数学归纳法总结的相同子问题嵌套的问题。与动态规划的区别在于：递归是自顶向下的 "暴力拆解"，天然会重复计算子问题；动态规划是针对有重叠子问题 + 最优子结构的问题，通过记录子问题答案彻底消除重复计算。

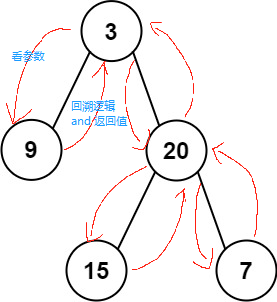
从单层逻辑来说（也是思考的维度），其结构大致是：

该层的参数（参数列表决定每层可以使用的东西）
递归的终止条件：递归的终止条件一般是要优先考虑的，没有特殊情况，一般是放在方法体的开头
该层的处理逻辑，一定要分配明确，其中一定会包含：
- 递之前
- 递出去：也就是再次调用该方法，进入下一层逻辑
- 归回来：调用的方法执行完毕，可能会有返回值返回到该层进行使用
- 归之后：回溯的逻辑部分
- 递和归决定走向，而真正的逻辑在于递之前以及归之后的逻辑
思考的方式：方法虽然是递归的，但是思考不要递归，在确定了递归终止条件的情况下，推演一到两层符合逻辑即可。
解决问题的途径：我们可以将解决问题的逻辑大致放在两个位置，一个是递之前（递归方法前），还有一个是归之后（递归方法之后，本质就是回溯）。这两种方式的选择在于，是否需要借助下层递归返回值的帮助。

技巧方法

二叉树95%的高频题可被以下6个技巧覆盖，记牢这些能快速匹配最优解法。

优先级：递归遍历 > 迭代遍历 > 层序遍历 > BST专属 > 构造类 > 路径问题

✅ 技巧一：递归遍历（★★★★★ 占比50%+）

✔ 核心定位

二叉树解题的"万能钥匙"，后端面试中「优先写递归解法」（代码简洁、易理解，面试官默认基础解法），后续可根据追问补迭代写法，是二刷必须固化的核心技巧。

✔ 核心原理

基于二叉树"左子树+右子树+根节点"的天然分治结构，利用函数调用栈模拟"深度优先"遍历，将大问题（遍历整棵树）拆解为小问题（遍历左子树、遍历右子树），符合"分治思想"。

Java中递归的本质是JVM调用栈的压栈/弹栈：每次递归调用压入函数上下文（参数、局部变量、返回地址），递归终止时弹栈并回溯结果。

✔ 适用场景

基础遍历：前序（根→左→右）、中序（左→根→右）、后序（左→右→根）遍历；
属性计算：二叉树高度/深度、直径、节点数、路径和、对称判断；
BST操作：验证BST、BST搜索/插入（简单版）、找BST第k小节点。

✔ 核心思路（三步法，必背）

确定递归终止条件：处理空节点边界（避免空指针），明确终止时的返回值（如求高度时空节点返回-1/0，遍历时空节点返回）；
确定单层递归逻辑：按遍历顺序/问题需求，处理"根节点"，再递归处理左子树、右子树（顺序决定前/中/后序）；
确定返回值：需向上传递结果（如高度、路径和）则返回具体值（int/TreeNode），仅遍历无返回值则用void。

补充：递归的两种核心模式------

「自顶向下」：根节点先处理，再将参数传递给左右子树（如路径和、前序遍历记录）；
「自底向上」：先递归左右子树获取结果，再用子树结果处理根节点（如高度、直径、平衡判断）。

✔ 高频经典题

LeetCode 144. 二叉树的前序遍历（基础递归，二刷速过）；
LeetCode 104. 二叉树的最大深度（自底向上递归，入门必刷）；
LeetCode 543. 二叉树的直径（核心：直径=左右子树高度和的最大值，自底向上）；
LeetCode 101. 对称二叉树（递归判断左右子树镜像，需传递两个节点）；
LeetCode 98. 验证二叉搜索树（递归传递上下界，避免仅比较根节点）。

✔ 避坑点

遗漏递归终止条件：如未判断root==null直接操作left/right，导致空指针异常（NPE）；
返回值设计错误：自底向上问题（如高度）未接收左右子树结果，直接返回固定值；
单层逻辑顺序颠倒：如中序遍历先处理根再遍历左子树，导致结果错误；
递归深度溢出：二叉树退化为链表时（如链长1e4），递归会触发StackOverflowError（二刷需知道"递归转迭代"是解决方案）；
验证BST仅比较根与左右子节点：忽略"左子树所有节点<根，右子树所有节点>根"，误判[1,3,2]为有效BST。

✅ 技巧二：迭代遍历（★★★★★ 占比20%+）

✔ 核心定位

递归的"底层实现补充"，考察代码功底与对栈的理解，后端面试中常问"递归解法有什么问题？请写迭代版"，二刷需掌握「统一标记法」（一套模板适配前/中/后序）。

✔ 核心原理

用Java的Deque（替代遗留类Stack）模拟JVM调用栈，通过"手动压栈/弹栈"复刻递归逻辑；统一标记法的核心是「用null标记已处理节点」，未标记节点先压子节点，标记节点直接处理值，实现三种遍历的代码统一。

✔ 适用场景

递归深度溢出场景（如长链表式二叉树）；
面试官明确要求"非递归解法"；
需要手动控制遍历顺序的问题（如前序遍历序列化二叉树）。

✔ 核心思路（统一标记法，三步法）

初始化：Deque存储TreeNode，若根节点非空则压入栈；
遍历栈：
- 弹出节点，若为非null（未处理）：按"反遍历顺序"压入子节点+当前节点+null标记（如前序遍历"根→左→右"，反序压"右→左→根+null"）；
- 若为null（已标记）：弹出栈顶节点（已处理节点），将值加入结果集。
终止：栈为空时遍历结束。

补充：三种遍历的压栈顺序差异（仅调整非null节点的压入顺序）------

前序：右子树 → 左子树 → 根节点+null；
中序：右子树 → 根节点+null → 左子树；
后序：根节点+null → 右子树 → 左子树。

✔ 高频经典题

LeetCode 94. 二叉树的中序遍历（迭代版高频追问，BST相关题基础）；
LeetCode 145. 二叉树的后序遍历（统一标记法核心练习，后序遍历最难手动实现）；
LeetCode 173. 二叉搜索树迭代器（中序迭代的进阶应用，后端迭代器设计场景）。

✔ 避坑点

用Stack类而非Deque：Java官方不推荐Stack（继承Vector，线程安全但低效），二刷统一用Deque stack = new ArrayDeque()；
压栈顺序错误：如前序遍历漏压右子树，导致右子树无法遍历；
未用null标记：手动区分"待处理"和"已处理"节点，导致逻辑混乱（如中序遍历提前处理根节点）；
栈空时未终止：导致循环死循环（需判断stack.isEmpty()作为终止条件）。

✅ 技巧三：层序遍历（BFS，★★★★ 占比15%+）

✔ 核心定位

二叉树"广度优先"遍历的标准实现，代码模板固定、逻辑简单，是后端面试中的"送分题"，二刷需做到"提笔就写，零错误"。

✔ 核心原理

用队列（Java用LinkedList实现Queue）存储当前层节点，利用队列"先进先出（FIFO）"特性，每次遍历前记录队列大小（当前层节点数），确保仅遍历当前层节点，逐层向下遍历。

✔ 适用场景

按层输出节点（如逐层打印二叉树）；
层级相关计算：最小深度、每层最大值/平均值、最底层最左节点值；
二叉树序列化/反序列化（层序方式，便于传输存储）。

✔ 核心思路（四步法）

初始化：Queue存储TreeNode，根节点非空则入队；
遍历队列：循环条件为队列非空；
处理当前层：记录队列大小levelSize，循环levelSize次，依次出队节点、处理值，再将左/右子节点（判空）入队；
终止：队列空时遍历结束，若为计算类问题（如最小深度），可提前终止（如遇到叶子节点直接返回深度）。

✔ 高频经典题

LeetCode 102. 二叉树的层序遍历（基础模板题，二刷速过）；
LeetCode 111. 二叉树的最小深度（层序优化，遇到叶子节点直接返回深度）；
LeetCode 103. 二叉树的锯齿形层序遍历（层序+奇偶层反转，进阶练习）；
LeetCode 297. 二叉树的序列化与反序列化（层序方式，后端数据传输场景）。

✔ 避坑点

未记录levelSize：导致无法区分层级，只能输出所有节点，无法按层返回结果；
最小深度误判：未判断叶子节点，直接返回队列遍历次数（如非叶子节点提前终止，导致深度偏小）；
子节点未判空入队：将null入队，导致后续遍历处理时空指针异常；
序列化时遗漏空节点：如未用#标记null，导致反序列化时无法唯一构造二叉树。

✅ 技巧四：BST专属技巧（★★★★ 占比10%+）

✔ 核心定位

二叉搜索树（BST）是后端面试的"算法+工程"结合点（关联数据库索引B+树、红黑树），技巧性强且考察频率高，二刷需吃透"特性复用"思路。

✔ 核心原理

基于BST的两大核心特性：① 中序遍历结果为严格升序（含重复值需额外约定）；② 左子树所有节点值<根节点值，右子树所有节点值>根节点值，可实现O(logn)的搜索/插入/删除操作。

✔ 适用场景

BST验证与修复；
BST的搜索、插入、删除操作；
BST的特殊查询：第k小节点、众数、最近公共祖先。

✔ 核心思路（分场景）

验证BST：两种方案------
- 方案1（递归传递上下界）：左子树以上界为当前根值，右子树以下界为当前根值，避免仅比较根与左右子节点；
- 方案2（中序遍历升序）：记录前一个节点值，中序遍历中判断当前值是否大于前值，不满足则非BST。
BST搜索/插入：
- 搜索：值小于根则找左子树，大于则找右子树，等于则返回节点；
- 插入：递归找到叶子节点位置，小于根插左，大于插右（无需旋转，保持BST特性即可）。
BST删除：分三种情况------
- 叶子节点：直接删除（返回null）；
- 单孩子节点：用子节点替代当前节点（返回子节点）；
- 双孩子节点：找中序后继（右子树最小节点）或前驱（左子树最大节点）替代当前节点值，再删除后继/前驱节点。

✔ 高频经典题

LeetCode 98. 验证二叉搜索树（两种方案都需掌握，后端面试必问）；
LeetCode 700. 二叉搜索树中的搜索（基础操作，O(logn)思路）；
LeetCode 450. 删除二叉搜索树中的节点（核心难点，三种删除场景全覆盖）；
LeetCode 230. 二叉搜索树中第K小的元素（中序遍历特性，后端有序查询场景）。

✔ 避坑点

验证BST用int存储上下界：当节点值为Integer.MAX_VALUE/Integer.MIN_VALUE时溢出，二刷用long类型（如lower=Long.MIN_VALUE）；
BST删除双孩子节点时仅替换值，未删除后继/前驱：导致树结构异常，出现重复节点；
认为BST插入需要旋转：普通BST无需旋转（红黑树/AVL树才需要），插入仅需找叶子节点位置；
中序遍历找第k小节点未提前终止：遍历到第k个节点即可返回，无需遍历完整棵树（优化效率）。

✅ 技巧五：二叉树构造类技巧（★★★ 占比5%+）

✔ 核心定位

考察"树的结构还原能力"，结合哈希表优化，是二刷中"中等难度性价比题"（代码模板固定，掌握后可快速得分）。

✔ 核心原理

利用"遍历序列的唯一性"构造二叉树：前序/后序序列确定根节点位置，中序序列通过根节点分割左右子树，递归构造左右子树；用哈希表存储中序"值→索引"，将根节点查找时间从O(n)优化到O(1)。

核心前提：树中所有节点值唯一（题目默认保证，否则无法唯一构造）。

✔ 适用场景

前序、后序用来确认根

中序用来确认左右子树的节点数量

以此来对两个数组进行递归切割

前序+中序构造二叉树；
后序+中序构造二叉树；
层序+中序构造二叉树（进阶，大厂难题偶考）。

✔ 核心思路（前序+中序为例，四步法）

初始化哈希表：存储中序数组"值→索引"，便于快速定位根节点；
确定根节点：前序数组的第一个元素为当前树的根节点；
分割左右子树：通过中序数组中根节点的索引，分割出左子树中序序列（左）和右子树中序序列（右），计算左子树节点数leftSize；
递归构造：前序数组中，左子树范围为[1, leftSize]，右子树范围为[leftSize+1, 末尾]，分别构造左右子树并挂载到根节点。

注意：

树的递归构造有两种方式：

从上向下构造（递之前造）：传入根节点，无需返回值
从下向上构造（归之后造）：无需传入根节点，返回节点，该方法更加常用，且代码更加简洁（下面的BST树构造有两种方法的例子）。

✔ 高频经典题

LeetCode 105. 从前序与中序遍历序列构造二叉树（模板题，二刷必背）；
LeetCode 106. 从后序与中序遍历序列构造二叉树（仅根节点位置和前序不同，思路复用）。

✔ 避坑点

递归索引范围越界：未严格定义前序/中序的左右边界（如preL、preR、inL、inR），导致数组下标异常；
未用哈希表优化：直接遍历中序数组找根节点，时间复杂度从O(n)升至O(n²)，二刷必须加优化；
忽略"节点值唯一"前提：若存在重复值，哈希表会覆盖索引，导致构造错误（题目一般明确说明无重复值）；
后序构造时根节点位置错误：后序数组的最后一个元素为根节点，而非第一个（易与前序混淆）。

✔ BST树的构造

核心也是一样，二叉树的构造怎么都离不开，确认根节点，分割左右子树，递归构造这几个步骤。

代码如下（LeetCode108）：

从下往上造：

java 复制代码

class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        return buildTree(nums,0,nums.length - 1);
    }

    public TreeNode buildTree(int[] nums, int left, int right) {
        if(right < left) return null;
        int middle = (left + right) / 2;
        TreeNode node = new TreeNode(nums[middle]);
        node.left = buildTree(nums,left,middle - 1);
        node.right = buildTree(nums,middle + 1,right);
        return node;
    }
}

从上往下造：

java 复制代码

class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        TreeNode root = new TreeNode(nums[(nums.length - 1) / 2]);
        buildTree(root, nums, 0, nums.length - 1);
        return root;
    }

    public void buildTree(TreeNode node,int[] nums,int left,int right) {
        if(node == null) return;
        int middle = (left + right) / 2;
        TreeNode leftNode;
        if(middle - 1 < left) leftNode = null;
        else leftNode = new TreeNode(nums[(middle + left - 1) / 2]);
        TreeNode rightNode;
        if(middle + 1 > right) rightNode = null;
        else rightNode = new TreeNode(nums[(middle + right + 1) / 2]);
        node.left = leftNode;
        node.right = rightNode;
        buildTree(node.left,nums,left,middle - 1);
        buildTree(node.right,nums,middle + 1,right);
    }
}

✅ 技巧六：路径问题技巧（★★★ 占比5%+）

✔ 核心定位

递归+回溯的典型应用，考察"路径追踪与回溯"能力，后端场景中对应"配置项遍历、路径规划"，是二刷中"思路迁移性强"的技巧。

✔ 核心原理

基于"自顶向下"递归，用容器（如List、StringBuilder）记录当前路径，遍历到叶子节点时验证条件（如路径和是否达标）；回溯的核心是"撤销选择"（如从路径中移除当前节点），避免影响其他路径的遍历。

✔ 适用场景

路径和问题（是否存在、所有路径和、最小路径和）；
路径记录问题（所有根到叶子路径、路径中是否含目标序列）；
路径最值问题（最长同值路径、二叉树中的最大路径和）。

✔ 核心思路（三步法）

路径追踪：递归进入左右子树前，将当前节点加入路径，更新路径状态（如路径和）；
条件验证：遍历到叶子节点时，判断是否满足目标条件（如路径和==target），满足则记录结果；
回溯撤销：递归返回前，将当前节点从路径中移除，恢复路径状态（避免污染其他分支）。

✔ 高频经典题

LeetCode 112. 路径总和（基础路径题，无需回溯，仅验证存在性）；
LeetCode 257. 二叉树的所有路径（递归+回溯，路径记录核心练习）；
LeetCode 124. 二叉树中的最大路径和（进阶，需结合自底向上递归，非根到叶子路径）。

✔ 避坑点

回溯时未撤销选择：如用StringBuilder记录路径，未调用setLength()恢复长度，导致路径包含无关节点；
路径和验证未判断叶子节点：非叶子节点提前终止，导致漏解（如路径和达标但未到叶子，误判为有效路径）；
最大路径和忽略"非根到叶子"路径：如节点的左右子树路径和大于根节点路径，需单独计算（自底向上思路）；
路径记录用String拼接：String不可变，每次拼接生成新对象，效率低，二刷用StringBuilder+回溯。

✅ 技巧七：二叉树对称相同判断技巧（★★★ 占比5%+）

也是递归判断的一种。区别在于有两个树节点的传入。同时递归的终止条件也会发生变化。

例如判断两棵树是否对称：

java 复制代码

class Solution {
    public boolean isSymmetric(TreeNode root) {
        return isSymmetricTree(root.left,root.right);
    }

    public boolean isSymmetricTree(TreeNode node1, TreeNode node2) {
        if (node1 == null || node2 == null) {
            return node1 == node2;
        }
        //如果都不为null，值是否相同
        boolean result1 = node1.val == node2.val;
        //继续判断子节点
        boolean result2 = isSymmetricTree(node1.left,node2.right);
        boolean result3 = isSymmetricTree(node1.right,node2.left);
        return result1 && result2 && result3;
    }
}

通用代码模板

✔ 模板1：递归遍历（前中后序通用）

java 复制代码

// 1. 前序遍历（根→左→右）
class Preorder {
    List<Integer> res = new ArrayList<>();
    public List<Integer> preorderTraversal(TreeNode root) {
        if (root == null) return res;
        res.add(root.val); // 根
        preorderTraversal(root.left); // 左
        preorderTraversal(root.right); // 右
        return res;
    }
}

// 2. 中序遍历（左→根→右）
class Inorder {
    List<Integer> res = new ArrayList<>();
    public List<Integer> inorderTraversal(TreeNode root) {
        if (root == null) return res;
        inorderTraversal(root.left); // 左
        res.add(root.val); // 根
        inorderTraversal(root.right); // 右
        return res;
    }
}

// 3. 后序遍历（左→右→根）
class Postorder {
    List<Integer> res = new ArrayList<>();
    public List<Integer> postorderTraversal(TreeNode root) {
        if (root == null) return res;
        postorderTraversal(root.left); // 左
        postorderTraversal(root.right); // 右
        res.add(root.val); // 根
        return res;
    }
}

✔ 模板2：迭代遍历（统一标记法，前中后序通用）

java 复制代码

// 统一标记法：null标记已处理节点
class UnifiedIteration {
    // 前序遍历（根→左→右）
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        if (root != null) stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            if (node != null) {
                // 未标记：先压右→再压左→最后压根+null（前序）
                if (node.right != null) stack.push(node.right);
                if (node.left != null) stack.push(node.left);
                stack.push(node);
                stack.push(null); // 标记已处理
            } else {
                // 标记节点：弹出并处理
                res.add(stack.pop().val);
            }
        }
        return res;
    }

    // 中序遍历（左→根→右）：仅调整压栈顺序
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        if (root != null) stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            if (node != null) {
                // 未标记：先压右→再压根+null→最后压左（中序）
                if (node.right != null) stack.push(node.right);
                stack.push(node);
                stack.push(null);
                if (node.left != null) stack.push(node.left);
            } else {
                res.add(stack.pop().val);
            }
        }
        return res;
    }

    // 后序遍历（左→右→根）：仅调整压栈顺序
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        if (root != null) stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            if (node != null) {
                // 未标记：先压根+null→再压右→最后压左（后序）
                stack.push(node);
                stack.push(null);
                if (node.right != null) stack.push(node.right);
                if (node.left != null) stack.push(node.left);
            } else {
                res.add(stack.pop().val);
            }
        }
        return res;
    }
}

✔ 模板3：层序遍历（BFS）

java 复制代码

class LevelOrder {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        if (root == null) return res;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            int levelSize = queue.size(); // 关键：记录当前层节点数
            List<Integer> levelList = new ArrayList<>();
            for (int i = 0; i < levelSize; i++) {
                TreeNode node = queue.poll();
                levelList.add(node.val);
                // 左子节点入队（判空）
                if (node.left != null) queue.offer(node.left);
                // 右子节点入队（判空）
                if (node.right != null) queue.offer(node.right);
            }
            res.add(levelList);
        }
        return res;
    }

    // 扩展：二叉树最小深度（层序遍历优化版）
    public int minDepth(TreeNode root) {
        if (root == null) return 0;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int depth = 1;
        while (!queue.isEmpty()) {
            int levelSize = queue.size();
            for (int i = 0; i < levelSize; i++) {
                TreeNode node = queue.poll();
                // 叶子节点直接返回当前深度（核心优化）
                if (node.left == null && node.right == null) return depth;
                if (node.left != null) queue.offer(node.left);
                if (node.right != null) queue.offer(node.right);
            }
            depth++;
        }
        return depth;
    }
}

✔ 模板4：BST核心操作（验证+搜索+插入+删除）

java 复制代码

class BSTOperations {
    // 1. 验证BST（最优解：递归传递上下界）
    public boolean isValidBST(TreeNode root) {
        return isValidBST(root, Long.MIN_VALUE, Long.MAX_VALUE);
    }
    private boolean isValidBST(TreeNode root, long lower, long upper) {
        if (root == null) return true;
        // 超出上下界则无效
        if (root.val <= lower || root.val >= upper) return false;
        // 左子树：上界为当前根值；右子树：下界为当前根值
        return isValidBST(root.left, lower, root.val) && isValidBST(root.right, root.val, upper);
    }

    // 2. BST搜索
    public TreeNode searchBST(TreeNode root, int val) {
        if (root == null || root.val == val) return root;
        // 利用BST性质：小于根找左，大于找右
        return root.val > val ? searchBST(root.left, val) : searchBST(root.right, val);
    }

    // 3. BST插入（递归版）
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if (root == null) return new TreeNode(val); // 找到叶子节点，插入
        if (root.val > val) {
            root.left = insertIntoBST(root.left, val);
        } else {
            root.right = insertIntoBST(root.right, val);
        }
        return root;
    }

    // 4. BST删除（核心难点）
    public TreeNode deleteNode(TreeNode root, int key) {
        if (root == null) return null;
        // 1. 找到要删除的节点
        if (root.val > key) {
            root.left = deleteNode(root.left, key);
        } else if (root.val < key) {
            root.right = deleteNode(root.right, key);
        } else {
            // 2. 处理删除逻辑
            // 情况1：叶子节点/单孩子节点
            if (root.left == null) return root.right;
            if (root.right == null) return root.left;
            // 情况2：双孩子节点→找中序后继（右子树最小节点）
            TreeNode successor = getSuccessor(root.right);
            root.val = successor.val; // 替换值
            root.right = deleteNode(root.right, successor.val); // 删除后继
        }
        return root;
    }
    // 找右子树最小节点（中序后继）
    private TreeNode getSuccessor(TreeNode node) {
        while (node.left != null) {
            node = node.left;
        }
        return node;
    }
}

✔ 模板5：构造二叉树（前序+中序）

java 复制代码

class BuildTree {
    // 哈希表存储中序值→索引，优化查找根位置
    Map<Integer, Integer> inorderMap = new HashMap<>();
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        // 初始化哈希表
        for (int i = 0; i < inorder.length; i++) {
            inorderMap.put(inorder[i], i);
        }
        // 递归构造：前序[preL,preR]，中序[inL,inR]
        return build(preorder, 0, preorder.length-1, inorder, 0, inorder.length-1);
    }
    private TreeNode build(int[] preorder, int preL, int preR, int[] inorder, int inL, int inR) {
        if (preL > preR || inL > inR) return null;
        // 前序首元素是根
        int rootVal = preorder[preL];
        TreeNode root = new TreeNode(rootVal);
        // 中序中根的位置
        int rootIdx = inorderMap.get(rootVal);
        // 左子树节点数
        int leftSize = rootIdx - inL;
        // 递归构造左子树：前序[preL+1, preL+leftSize]，中序[inL, rootIdx-1]
        root.left = build(preorder, preL+1, preL+leftSize, inorder, inL, rootIdx-1);
        // 递归构造右子树：前序[preL+leftSize+1, preR]，中序[rootIdx+1, inR]
        root.right = build(preorder, preL+leftSize+1, preR, inorder, rootIdx+1, inR);
        return root;
    }
}

✔ 模板6：路径求和问题（递归+回溯）

java 复制代码

class PathSum {
    // 1. 路径总和（是否存在从根到叶子的路径和为target）
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if (root == null) return false;
        // 叶子节点：判断剩余和是否为0
        if (root.left == null && root.right == null) {
            return targetSum - root.val == 0;
        }
        // 递归左/右子树，传递剩余目标值
        return hasPathSum(root.left, targetSum - root.val) || hasPathSum(root.right, targetSum - root.val);
    }

    // 2. 二叉树的所有路径（递归+回溯）
    List<String> res = new ArrayList<>();
    public List<String> binaryTreePaths(TreeNode root) {
        if (root == null) return res;
        backtrack(root, new StringBuilder());
        return res;
    }
    private void backtrack(TreeNode root, StringBuilder path) {
        if (root == null) return;
        int len = path.length();
        path.append(root.val);
        // 叶子节点：添加路径到结果
        if (root.left == null && root.right == null) {
            res.add(path.toString());
        } else {
            path.append("->");
            backtrack(root.left, path);
            backtrack(root.right, path);
        }
        // 回溯：撤销选择（恢复StringBuilder长度）
        path.setLength(len);
    }
}

栈与队列部分

核心知识点

核心定义与特性

数据结构	核心特性	核心操作	时间复杂度（核心操作）
栈（Stack）	后进先出（LIFO），仅栈顶可操作	入栈（push）、出栈（pop）、查看栈顶（peek）	O(1)
队列（Queue）	先进先出（FIFO），队尾入、队头出	入队（offer）、出队（poll）、查看队头（peek）	O(1)
双端队列（Deque）	两端均可入/出，兼容栈+队列特性	栈模式：push/pop/peek；队列模式：offer/poll/peek	O(1)
单调栈	维护栈内元素「递增/递减」的特殊栈	入栈前弹出破坏单调性的元素，再入栈	O(n)（每个元素仅入栈出栈1次）
单调队列	维护队列内元素「递增/递减」的特殊队列	入队前移除比当前元素小/大的队尾元素	O(n)

Java中栈/队列的实现（工程级重点，面试高频追问）

实现类	核心特点	适用场景	避坑点
`Stack`（遗留类）	继承`Vector`，线程安全（加锁），效率低，允许`null`	不推荐使用（Java官方已标记过时）	线程安全但性能差，底层数组扩容成本高
`Deque`（接口）+ `ArrayDeque`	基于循环数组实现，无锁，效率最高，不允许`null`	刷题/开发首选（替代Stack/Queue）	扩容时复制数组（O(n)），但平均O(1)
`Deque` + `LinkedList`	基于链表实现，支持`null`，灵活但效率略低	需要存储`null`或频繁增删场景	节点对象占用额外内存
`Queue` + `BlockingQueue`（如`ArrayBlockingQueue`/`LinkedBlockingQueue`）	线程安全，提供阻塞`put()`/`take()`	后端并发场景（线程池、生产者消费者模型）	`put()`满时阻塞，`take()`空时阻塞
`PriorityQueue`	优先级队列（堆实现），非FIFO，按元素优先级出队	任务调度、TopK问题	底层是完全二叉树，入队/出队O(logn)

核心API（刷题高频，按使用频率排序）

（1）Deque（推荐，替代Stack/Queue）

java 复制代码

Deque<Integer> deque = new ArrayDeque<>();
// 栈模式（操作队首）
deque.push(1); // 入栈（等价于addFirst()，满时抛异常）
deque.pop();   // 出栈（等价于removeFirst()，空时抛异常）
deque.peek();  // 查看栈顶（等价于peekFirst()，空时返回null）
// 队列模式（操作队尾入、队首出）
deque.offer(2); // 入队（等价于addLast()，满时返回false）
deque.poll();   // 出队（等价于removeFirst()，空时返回null）
deque.peek();   // 查看队头（空时返回null）
// 通用方法
deque.isEmpty(); // 判断是否为空
deque.size();    // 获取元素数量

（2）BlockingQueue（后端并发场景）

java 复制代码

BlockingQueue<String> queue = new ArrayBlockingQueue<>(10);
queue.put("task1"); // 阻塞：队列满时等待
queue.take();       // 阻塞：队列空时等待
queue.offer("task2", 1, TimeUnit.SECONDS); // 超时阻塞：1秒后仍满则返回false

高频考点

单调栈/队列的核心价值：将暴力O(n²)的"找下一个更大/更小元素""滑动窗口最值"问题优化为O(n)，是后端高性能数据处理的核心思想（如热点数据筛选、流量峰值统计）。
线程池的工作队列 ：ThreadPoolExecutor的workQueue参数默认用LinkedBlockingQueue，核心线程满时任务入队，队列满时创建非核心线程（后端面试必问）。
JVM调用栈 ：方法执行时压栈（存储局部变量、操作数栈、返回地址），方法结束时出栈，栈溢出（StackOverflowError）的常见原因是递归深度过大。
消息队列的底层思想：RabbitMQ/Kafka的队列模型本质是FIFO，保证消息有序消费，对应算法题中的"队列模拟任务调度"。

技巧方法

栈队列90%的高频题可被以下6个技巧覆盖，记牢这些能快速匹配最优解法。

优先级：单调栈 > 栈队列互模拟 > 括号匹配 > 层序遍历/滑动窗口 > 最小栈 > 表达式求值

✅ 技巧一：单调栈（★★★★★ 占比40%+，核心中的核心）

✔ 核心定位

解决"下一个更大/更小元素""距离最近的更大/更小元素"类问题的最优解，后端面试中等题高频（如每日温度、接雨水）。

✔ 核心原理

基于栈 "后进先出（LIFO）" 特性，手动维护栈内元素（存储索引而非值）的「递增 / 递减」单调性：

遍历数组时，若当前元素破坏栈的单调性（如递减栈中当前元素＞栈顶值），则弹出栈顶元素，此时当前元素就是栈顶元素的 "目标值"（如下一个更大元素）；
每个元素仅入栈、出栈 1 次，整体时间复杂度 O (n)，空间复杂度 O (n)；

✔ 适用场景

下一个更大元素（LeetCode 496）、每日温度（LeetCode 739）；
接雨水（LeetCode 42）、柱状图中最大的矩形（LeetCode 84）；
去除重复字母（LeetCode 316，最小字典序）。

✔ 核心思路（三步法）

初始化 ：用Deque存储数组索引（而非值，方便计算距离/区间），维护栈内索引对应值的单调性（递增/递减）；
遍历数组 ：
- 若当前元素（i）破坏栈的单调性（如递减栈中当前元素>栈顶值），则弹出栈顶索引，一直弹，直到栈中元素符合单调性；
- 当前元素（i）就是这些弹出来的栈顶索引的"目标值"（如下一个更大元素=当前元素，距离=当前索引-栈顶索引）；
收尾：遍历结束后，栈内剩余索引的"目标值"为-1（无更大/更小元素）。

✔ 关键规则

找下一个更大元素 → 用递减栈（栈顶到栈底递减，遇到更大元素则弹栈）；
找下一个更小元素 → 用递增栈（栈顶到栈底递增，遇到更小元素则弹栈）。

✔ 避坑点

混淆"递增栈"和"递减栈"（记反导致逻辑全错）；
栈中存储"值"而非"索引"（无法计算距离/区间）；
遍历结束后未处理栈内剩余元素（漏解）。

✅ 技巧二：栈与队列互模拟（★★★★ 占比20%+，基础必背）

✔ 核心原理

面试官"基础能力考察"必考点，检验对LIFO/FIFO特性的理解，代码模板固定。

利用"双栈/单队列调整元素顺序"，模拟对方的核心特性：

栈模拟队列：两个栈（入栈inStack、出栈outStack），仅当outStack为空时，将inStack所有元素弹出压入outStack（保证FIFO）；
队列模拟栈：单个队列，入队后将前n-1个元素弹出重新入队（让最新入队元素到队首，模拟LIFO）。

✔ 适用场景

用栈实现队列（LeetCode 232）；
用队列实现栈（LeetCode 225）。

✔ 核心思路

场景1：用栈实现队列（LeetCode 232）

初始化 ：定义两个Deque<Integer>（inStack负责入队，outStack负责出队）；
入队（push） ：直接将元素压入inStack；
出队（pop）/查看队头（peek） ：
- 核心：仅当outStack为空时，将inStack所有元素弹出并压入outStack（避免打乱顺序）；
- 出队：弹出outStack栈顶元素；
- 查看队头：返回outStack栈顶元素；
判空（empty） ：inStack和outStack都为空时，队列才为空。

场景2：用队列实现栈（LeetCode 225）

初始化 ：定义一个Queue<Integer>（LinkedList实现）；
入栈（push） ：
- 元素入队；
- 记录当前队列大小size，将前size个元素（旧元素）弹出并重新入队（让新元素到队首）；
出栈（pop）：直接出队（队首是最新入栈元素）；
查看栈顶（top）：返回队首元素；
判空（empty）：队列是否为空。 |

✔ 避坑点

栈模拟队列时，每次出队都转移元素（正确：仅outStack为空时转移）；
队列模拟栈时，忘记调整元素顺序（导致出栈顺序还是FIFO）。

✅ 技巧三：括号匹配（★★★★ 占比15%+，送分题）

✔ 核心定位

简单/中等题高频，考察栈的"匹配"特性，后端场景中用于接口参数校验、表达式解析。

✔ 适用场景

有效的括号（LeetCode 20）、最长有效括号（LeetCode 32）；
删除无效的括号（LeetCode 301，进阶）。

✔ 核心思路

简单匹配（单类型括号）：可用计数器（左括号+1，右括号-1，负数则无效）；
复杂匹配（多类型括号） ：用栈存储左括号索引/字符：
- 可借用map结构存储对应关系，简化判断，但是时间会增加
- 遇到左括号（(/{/[）→ 入栈；
- 遇到右括号 → 若栈顶是匹配的左括号则弹栈，否则标记为无效；
- 最终栈为空则括号有效（最长有效括号需计算索引差）。

✔ 避坑点

多类型括号仅判断数量相等（未判断类型匹配，如([)]误判为有效）；
忘记处理栈中剩余的左括号（导致误判有效）。

✅ 技巧四：层序遍历/滑动窗口/单调队列（队列/BFS，★★★★ 占比10%+）

✔ 核心定位

队列的经典应用，后端场景中用于任务调度、滑动窗口限流（如接口QPS统计）。

层序遍历（BFS）：用普通队列存储当前层节点，利用FIFO特性逐层遍历，记录每层节点数（levelSize）保证按层输出；
滑动窗口最大值：用递减单调队列维护窗口内元素，队首为窗口最大值，入队前移除比当前元素小的队尾元素（这些元素无法成为后续窗口最大值），出队时移除超出窗口的队首元素。

✔ 适用场景

二叉树层序遍历（LeetCode 102，队列）；
滑动窗口最大值（LeetCode 239，单调队列）；
任务调度（LeetCode 621，队列）。

✔ 核心思路

（1）层序遍历

队列存储当前层节点；
每次遍历前记录队列大小（当前层节点数），保证只遍历当前层；
遍历当前层节点，将子节点入队（判空）。

（2）滑动窗口最大值（单调队列）

和单调栈类似，单调队列中维护的是元素的索引。
用递减队列维护窗口内元素（队首是窗口最大值）；
入队前：移除所有比当前元素小的队尾元素（这些元素不可能成为后续窗口的最大值）；
出队时：若队首元素超出窗口范围（索引<当前窗口左边界），则移除；
窗口形成后（索引≥k-1），记录队首为当前窗口最大值。

✔ 避坑点

层序遍历未记录当前层节点数（无法按层输出）；
滑动窗口最大值未移除超出窗口的队首元素（导致最大值错误）。

✅ 技巧五：最小栈（★★★ 占比8%+，常数时间最值）

✔ 核心定位

考察栈的"辅助结构"设计思想，后端场景中用于监控系统的实时最值统计。

与单调栈的区别在于：

维度	最小栈	单调栈
核心约束	无顺序约束，仅需记录最小值	栈内元素必须保持单调顺序
核心能力	O(1) 获取最小值	高效找"下一个极值元素"
实现方式	主栈 + 辅助栈（存最小值）	普通栈 + 入栈出栈规则控制
应用场景	频繁查最小值的栈操作	数组/序列的极值位置查询

✔ 适用场景

最小栈（LeetCode 155，常数时间获取最小值）；
最大栈（同理，仅辅助栈存储最大值）。

✔ 核心思路

主栈存储所有元素；
辅助栈存储"当前栈内的最小值"：
- 入栈：若当前元素≤辅助栈顶，则同步入辅助栈（注意不要忽略等于的情况）；
- 出栈：若主栈弹出元素=辅助栈顶，则辅助栈同步弹出；
- 获取最小值：直接返回辅助栈顶。

✔ 避坑点

辅助栈仅存储"更小值"（未处理"等于"的情况，导致最小值丢失）；
出栈时未同步辅助栈（导致最小值错误）。

✅ 技巧六：表达式求值（栈，★★★ 占比7%+）

✔ 核心定位

考察栈的"运算优先级"处理能力，后端场景中用于公式引擎、计算器功能。

✔ 适用场景

逆波兰表达式求值（LeetCode 150）；
基本计算器（LeetCode 224，带括号/加减乘除）。

✔ 核心思路

（1）逆波兰表达式（后缀表达式）

数字入栈；
遇到运算符：弹出栈顶两个数（先弹的是右操作数，后弹的是左操作数），计算后结果入栈；
遍历结束后，栈顶为最终结果。

（2）基本计算器

两个栈：数字栈存储操作数，运算符栈存储运算符；
处理括号：遇到(入栈，遇到)则计算到(为止；
处理优先级：高优先级运算符（×/÷）优先计算，低优先级（+/-）延后。

✔ 避坑点

逆波兰表达式中数字弹出顺序错误（左操作数在后，右操作数在前）；
基本计算器中运算符优先级处理错误（如先算+再算×）。

通用代码模板

✔ 模板1：单调栈（找下一个更大元素，LeetCode 496）

java 复制代码

class NextGreaterElement {
    public int[] nextGreaterElement(int[] nums1, int[] nums2) {
        // 步骤1：先遍历nums2，用单调栈找每个元素的下一个更大元素，存入map
        Map<Integer, Integer> greaterMap = new HashMap<>();
        Deque<Integer> monoStack = new ArrayDeque<>(); // 递减栈，存储nums2的索引
        for (int i = 0; i < nums2.length; i++) {
            // 步骤2：破坏递减性则弹栈，计算下一个更大元素
            while (!monoStack.isEmpty() && nums2[i] > nums2[monoStack.peek()]) {
                int idx = monoStack.pop();
                greaterMap.put(nums2[idx], nums2[i]);
            }
            monoStack.push(i); // 步骤3：当前索引入栈
        }
        // 步骤4：处理栈内剩余元素（无更大元素，值为-1）
        while (!monoStack.isEmpty()) {
            greaterMap.put(nums2[monoStack.pop()], -1);
        }
        // 步骤5：遍历nums1，从map中取值
        int[] res = new int[nums1.length];
        for (int i = 0; i < nums1.length; i++) {
            res[i] = greaterMap.get(nums1[i]);
        }
        return res;
    }
}

✔ 模板2：栈模拟队列（LeetCode 232）

java 复制代码

class MyQueue {
    private final Deque<Integer> inStack;  // 入栈专用
    private final Deque<Integer> outStack; // 出栈专用

    public MyQueue() {
        inStack = new ArrayDeque<>();
        outStack = new ArrayDeque<>();
    }

    // 入队：直接入inStack
    public void push(int x) {
        inStack.push(x);
    }

    // 出队：outStack为空时，将inStack所有元素转移到outStack，再出栈
    public int pop() {
        transfer();
        return outStack.pop();
    }

    // 查看队头：逻辑同pop
    public int peek() {
        transfer();
        return outStack.peek();
    }

    // 判断为空：两个栈都为空才是空
    public boolean empty() {
        return inStack.isEmpty() && outStack.isEmpty();
    }

    // 核心：仅当outStack为空时转移元素（避免打乱顺序）
    private void transfer() {
        if (outStack.isEmpty()) {
            while (!inStack.isEmpty()) {
                outStack.push(inStack.pop());
            }
        }
    }
}

✔ 模板3：队列模拟栈（LeetCode 225）

java 复制代码

class MyStack {
    private final Queue<Integer> queue;

    public MyStack() {
        queue = new LinkedList<>();
    }

    // 入栈：入队后将前n-1个元素弹出重新入队，保证队首是最新元素
    public void push(int x) {
        int size = queue.size();
        queue.offer(x);
        // 调整顺序：前size个元素（旧元素）弹出并重新入队
        for (int i = 0; i < size; i++) {
            queue.offer(queue.poll());
        }
    }

    // 出栈：直接出队（队首是最新入栈的元素）
    public int pop() {
        return queue.poll();
    }

    // 查看栈顶：直接查看队首
    public int top() {
        return queue.peek();
    }

    // 判断为空：队列是否为空
    public boolean empty() {
        return queue.isEmpty();
    }
}

✔ 模板4：括号匹配（LeetCode 20）

java 复制代码

class ValidParentheses {
    public boolean isValid(String s) {
        Deque<Character> stack = new ArrayDeque<>();
        // 步骤1：建立括号匹配映射（简化判断）
        Map<Character, Character> map = new HashMap<>();
        map.put(')', '(');
        map.put('}', '{');
        map.put(']', '[');

        for (char c : s.toCharArray()) {
            // 步骤2：左括号入栈
            if (map.containsValue(c)) {
                stack.push(c);
            } else {
                // 步骤3：右括号匹配
                if (stack.isEmpty() || stack.peek() != map.get(c)) {
                    return false; // 无匹配的左括号
                }
                stack.pop(); // 匹配成功，弹栈
            }
        }
        // 步骤4：栈为空才是有效（无剩余左括号）
        return stack.isEmpty();
    }
}

✔ 模板5：每日温度（单调栈经典题，LeetCode 739）

java 复制代码

class DailyTemperatures {
    public int[] dailyTemperatures(int[] temperatures) {
        int n = temperatures.length;
        int[] res = new int[n];
        Deque<Integer> monoStack = new ArrayDeque<>(); // 递减栈，存储索引

        for (int i = 0; i < n; i++) {
            // 破坏递减性：弹出栈顶，计算天数差
            while (!monoStack.isEmpty() && temperatures[i] > temperatures[monoStack.peek()]) {
                int idx = monoStack.pop();
                res[idx] = i - idx; // 核心：索引差=天数差
            }
            monoStack.push(i);
        }
        // 剩余元素res默认0，无需处理
        return res;
    }
}

✔ 模板6：最小栈（LeetCode 155）

java 复制代码

class MinStack {
    private final Deque<Integer> mainStack; // 主栈：存储所有元素
    private final Deque<Integer> minStack;  // 辅助栈：存储当前最小值

    public MinStack() {
        mainStack = new ArrayDeque<>();
        minStack = new ArrayDeque<>();
        // 初始化辅助栈（避免空指针）
        minStack.push(Integer.MAX_VALUE);
    }

    // 入栈：当前元素≤辅助栈顶则同步入辅助栈
    public void push(int val) {
        mainStack.push(val);
        if (val <= minStack.peek()) {
            minStack.push(val);
        }
    }

    // 出栈：主栈弹出元素=辅助栈顶则同步弹出
    public void pop() {
        if (mainStack.pop().equals(minStack.peek())) {
            minStack.pop();
        }
    }

    // 获取栈顶：主栈顶
    public int top() {
        return mainStack.peek();
    }

    // 获取最小值：辅助栈顶
    public int getMin() {
        return minStack.peek();
    }
}

✔ 模板7：滑动窗口最大值（单调队列，LeetCode 239）

java 复制代码

class SlidingWindowMax {
    public int[] maxSlidingWindow(int[] nums, int k) {
        int n = nums.length;
        int[] res = new int[n - k + 1];
        Deque<Integer> monoQueue = new ArrayDeque<>(); // 递减队列，存储索引

        for (int i = 0; i < n; i++) {
            // 步骤1：移除超出窗口的队首元素（索引<当前窗口左边界）
            while (!monoQueue.isEmpty() && monoQueue.peek() < i - k + 1) {
                monoQueue.poll();
            }
            // 步骤2：移除队尾比当前元素小的元素（无法成为后续窗口最大值）
            while (!monoQueue.isEmpty() && nums[i] > nums[monoQueue.peekLast()]) {
                monoQueue.pollLast();
            }
            // 步骤3：当前索引入队
            monoQueue.offer(i);
            // 步骤4：窗口形成后，记录队首为最大值
            if (i >= k - 1) {
                res[i - k + 1] = nums[monoQueue.peek()];
            }
        }
        return res;
    }
}

✔ 模板8：逆波兰表达式求值（LeetCode 150）

java 复制代码

class EvalRPN {
    public int evalRPN(String[] tokens) {
        Deque<Integer> stack = new ArrayDeque<>();
        for (String token : tokens) {
            // 步骤1：数字入栈
            if (isNumber(token)) {
                stack.push(Integer.parseInt(token));
            } else {
                // 步骤2：运算符计算（注意弹出顺序：右操作数先出）
                int num2 = stack.pop();
                int num1 = stack.pop();
                int res = calculate(num1, num2, token);
                stack.push(res);
            }
        }
        // 步骤3：栈顶为最终结果
        return stack.pop();
    }

    // 判断是否为数字（处理负数）
    private boolean isNumber(String s) {
        return !("+".equals(s) || "-".equals(s) || "*".equals(s) || "/".equals(s));
    }

    // 计算逻辑
    private int calculate(int num1, int num2, String op) {
        return switch (op) {
            case "+" -> num1 + num2;
            case "-" -> num1 - num2;
            case "*" -> num1 * num2;
            case "/" -> num1 / num2; // 题目保证除数不为0
            default -> 0;
        };
    }
}