这篇博客是为了区分机器人里面的几何雅可比与解析雅可比矩阵,以及他们的计算代码。在下面的推导与叙述中我们是以基坐标为参考系。
一. 几何雅可比矩阵与解析雅可比矩阵的区别
几何雅可比 描述的是末端执行器的空间运动速度(线速度和角速度) 与关节速度之间的关系。
解析雅可比 描述的是末端执行器的位姿参数(如位置和欧拉角)的时间导数 与关节速度之间的关系。
它们的根本区别源于对"末端姿态变化率"的不同描述方式。
二. 几何雅可比矩阵
2.1 几何雅可比矩阵的定义
几何雅可比矩阵直接建立在机器人末端执行器的瞬时运动旋量概念上。
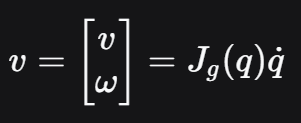

关键特征:
-
角速度 ω:这是一个直接存在于三维空间中的物理量,不依赖于任何特定的姿态参数化方式(如欧拉角)。它描述了末端坐标系旋转的瞬时轴和速率。
-
物理直观性强:每一列对应一个关节运动引起的末端线速度和角速度。
-
无奇异(在定义域内) :只要机器人构型不在自身的运动学奇异点,
就良好定义。角速度 ω 本身不会因为姿态表示方法而产生奇异。
-
用于速度级控制:是设计基于速度的机器人控制器(如逆运动学求解、阻抗控制)的自然选择。
2.2 几何雅可比矩阵公式
几何雅可比矩阵的分解

几何雅可比矩阵的计算公式
对于具有 n 个旋转关节的机械臂,几何雅可比矩阵的第 i 列计算公式如下:

矩阵形式的完整表达式
将各列组合,得到完整的几何雅可比矩阵:
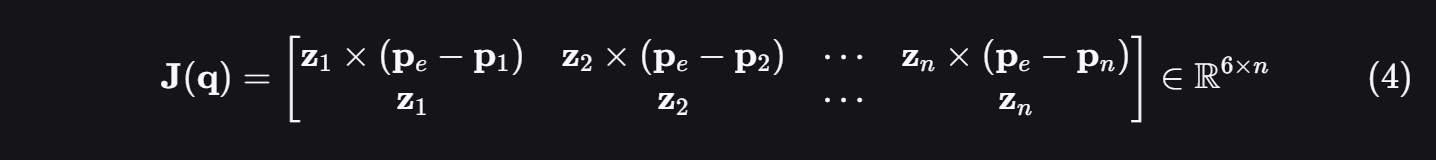
2.3 几何雅可比矩阵计算代码
Matlab
function J_geo = geometric_jacobian(q, use_default_tool, extra_length, euler_seq)
% 计算几何雅可比矩阵,支持工具配置和欧拉角顺序检查
%
% 输入参数:
% q - 7×1关节角向量 [rad]
% use_default_tool - 布尔值:true表示使用Franka默认工具,false表示不使用默认工具
% extra_length - 额外工具长度 [m],当use_default_tool=true时,总长度=0.1034+extra_length
% 当use_default_tool=false时,总长度=extra_length
% euler_seq - 字符串:指定欧拉角顺序,目前仅支持'ZYX'(不区分大小写)
%
% 输出:
% J_geo - 6×7几何雅可比矩阵(MATLAB顺序:前3行角速度,后3行线速度)
%
% 示例:
% J1 = geometric_jacobian(q, true, 0, 'ZYX') % 使用默认工具,无额外长度
% J2 = geometric_jacobian(q, true, 0.05, 'zyx') % 默认工具+50mm额外长度
% J3 = geometric_jacobian(q, false, 0.15, 'ZYX') % 自定义150mm工具
% 参数检查和默认值处理
if nargin < 4
euler_seq = 'ZYX'; % 默认欧拉角顺序
end
% 检查欧拉角顺序
if ~ischar(euler_seq) || ~strcmpi(euler_seq, 'ZYX')
error(['目前仅支持ZYX欧拉角顺序。您输入的欧拉角顺序为: ', euler_seq, ...
'。请使用''ZYX''作为euler_seq参数。']);
end
% 设置默认工具长度
franka_default_tool_length = 0.1034; % Franka Panda默认末端执行器长度 [m]
% 计算总工具长度
if use_default_tool
if extra_length < 0
error('额外长度不能为负数');
end
total_EE_length = franka_default_tool_length + extra_length;
fprintf('几何雅可比计算:使用默认Franka工具 (0.1034m) + 额外长度 %.4fm = 总长度 %.4fm\n', ...
extra_length, total_EE_length);
else
if extra_length < 0
error('自定义工具长度不能为负数');
end
total_EE_length = extra_length;
if total_EE_length == 0
fprintf('几何雅可比计算:不使用任何工具\n');
else
fprintf('几何雅可比计算:使用自定义工具长度: %.4fm\n', total_EE_length);
end
end
% 调用内部函数计算几何雅可比
J_geo = geometric_jacobian_core(q, total_EE_length);
end
function J_geo = geometric_jacobian_core(q, total_EE_length)
% 内部核心函数:根据关节角度和工具长度计算几何雅可比矩阵
% 匹配MATLAB工具箱的顺序(前3行:角速度,后3行:线速度)
% 输入: q - 7×1关节角向量 (弧度)
% total_EE_length - 末端执行器总长度 [m]
% 输出: J_geo - 6×7几何雅可比矩阵
% Franka Panda的DH参数 (Modified DH)
% 格式: [alpha, a, d, theta]
MDH = [0, 0, 0.333, q(1);
-pi/2, 0, 0, q(2);
pi/2, 0, 0.316, q(3);
pi/2, 0.0825, 0, q(4);
-pi/2, -0.0825,0.384, q(5);
pi/2, 0, 0, q(6);
pi/2, 0.088, 0.107, q(7)];
% 计算每个关节的变换矩阵和位置
n = 7;
T = eye(4);
p_all = zeros(3, n);
z_all = zeros(3, n);
for i = 1:n
alpha = MDH(i, 1);
a = MDH(i, 2);
d = MDH(i, 3);
theta = MDH(i, 4);
% 改进DH变换矩阵
Ti = [cos(theta), -sin(theta), 0, a;
sin(theta)*cos(alpha), cos(theta)*cos(alpha), -sin(alpha), -d*sin(alpha);
sin(theta)*sin(alpha), cos(theta)*sin(alpha), cos(alpha), d*cos(alpha);
0, 0, 0, 1];
T = T * Ti;
p_all(:, i) = T(1:3, 4);
z_all(:, i) = T(1:3, 3);
end
% 末端执行器位置(考虑工具长度)
% 工具沿最后一个关节的z轴方向偏移
p_ee = p_all(:, end) + total_EE_length * z_all(:, end);
% 计算几何雅可比 - 修正关节编号对应关系
J_geo = zeros(6, n);
for i = 1:n
if i == 1
% 关节1:使用基坐标系
p_i = [0; 0; 0];
z_i = [0; 0; 1];
else
% 关节i:使用连杆i-1的坐标系
p_i = p_all(:, i); % 改进DH:使用i
z_i = z_all(:, i); % 改进DH:使用i
end
% 线速度在前,角速度在后
J_geo(1:3, i) = cross(z_i, p_ee - p_i); % 线速度部分
J_geo(4:6, i) = z_i; % 角速度部分
end
end
function T = forward_kinematics_mdh(q, total_EE_length)
% 改进DH正运动学,支持工具长度参数
%
% 输入参数:
% q - 7×1关节角向量 [rad]
% total_EE_length - 可选,末端执行器总长度 [m],默认0.1034
%
% 输出:
% T - 4×4齐次变换矩阵
% 设置默认参数
if nargin < 2
total_EE_length = 0.1034; % Franka Panda默认末端执行器长度
end
MDH = [0, 0, 0.333, q(1);
-pi/2, 0, 0, q(2);
pi/2, 0, 0.316, q(3);
pi/2, 0.0825, 0, q(4);
-pi/2, -0.0825,0.384, q(5);
pi/2, 0, 0, q(6);
pi/2, 0.088, 0.107, q(7)];
T = eye(4);
for i = 1:7
alpha = MDH(i, 1);
a = MDH(i, 2);
d = MDH(i, 3);
theta = MDH(i, 4);
Ti = [cos(theta), -sin(theta), 0, a;
sin(theta)*cos(alpha), cos(theta)*cos(alpha), -sin(alpha), -d*sin(alpha);
sin(theta)*sin(alpha), cos(theta)*sin(alpha), cos(alpha), d*cos(alpha);
0, 0, 0, 1];
T = T * Ti;
end
% 添加工具偏移(沿最后一个关节的z轴方向)
if total_EE_length ~= 0
T_ee = [1, 0, 0, 0;
0, 1, 0, 0;
0, 0, 1, total_EE_length;
0, 0, 0, 1];
T = T * T_ee;
end
end- 测试代码,将我们自定义的几何雅可比矩阵与matlab自带的Robotics System Toolbox(机器人系统工具箱)里面的函数geometricJacobian对比看看有没有计算错
Matlab
clc; close all; clear all;
% 创建机器人模型
robot = loadrobot('frankaEmikaPanda', 'DataFormat', 'row');
% 测试关节角度
q_full = [0.1, 0.2, 0.3, -pi/2, 0, pi/2, 0, 0, 0];
% 1. MATLAB工具箱的雅可比
J_matlab1 = geometricJacobian(robot, q_full, 'panda_link8');
J_matlab1 = J_matlab1(:, 1:7); % 只取前7列(手臂关节)
J_matlab(1:3,:) = J_matlab1(4:6,:);
J_matlab(4:6,:) = J_matlab1(1:3,:);
disp('MATLAB工具箱几何雅可比 (6×7):');
disp('前3行: 角速度 (ω_x, ω_y, ω_z)');
disp('后3行: 线速度 (v_x, v_y, v_z)');
disp(J_matlab);
disp(['矩阵维度: ', num2str(size(J_matlab))]);
% 2. 自定义函数(已修正关节编号对应关系)
q_arm = q_full(1:7)';
J_custom = geometric_jacobian(q_arm, false, 0);
disp('自定义几何雅可比 (6×7):');
disp('前3行: 角速度 (ω_x, ω_y, ω_z) - 匹配MATLAB');
disp('后3行: 线速度 (v_x, v_y, v_z) - 匹配MATLAB');
disp(J_custom);
disp(['矩阵维度: ', num2str(size(J_custom))]);
% 3. 比较结果
disp('MATLAB工具箱与自定义函数的差异:');
error_matrix = J_matlab - J_custom;
disp('误差矩阵范数:');
disp(norm(error_matrix, 'fro'));
% 4. 逐列比较
disp('逐列比较:');
for i = 1:7
col_error = norm(J_matlab(:, i) - J_custom(:, i));
fprintf('第%d列误差范数: %.6e\n', i, col_error);
end
% 5. 验证正运动学
T_matlab = getTransform(robot, q_full, 'panda_link8');
T_custom = forward_kinematics_mdh(q_arm, 0);
disp('位置误差:');
pos_error = norm(T_matlab(1:3,4) - T_custom(1:3,4));
disp(pos_error);
% 6. 可视化比较
figure('Position', [100, 100, 1200, 800]);
% 子图1: MATLAB雅可比
subplot(2,3,1);
imagesc(J_matlab);
colorbar; title('MATLAB工具箱雅可比');
xlabel('关节 (1-7)'); ylabel('行(1-3:角速度, 4-6:线速度)');
set(gca, 'XTick', 1:7, 'YTick', 1:6, 'YTickLabel', {'ω_x','ω_y','ω_z','v_x','v_y','v_z'});
% 子图2: 自定义雅可比
subplot(2,3,2);
imagesc(J_custom);
colorbar; title('自定义雅可比');
xlabel('关节 (1-7)'); ylabel('行(1-3:角速度, 4-6:线速度)');
set(gca, 'XTick', 1:7, 'YTick', 1:6, 'YTickLabel', {'ω_x','ω_y','ω_z','v_x','v_y','v_z'});
% 子图3: 绝对误差
subplot(2,3,3);
imagesc(abs(J_matlab - J_custom));
colorbar; title('绝对误差');
xlabel('关节 (1-7)'); ylabel('行');
set(gca, 'XTick', 1:7, 'YTick', 1:6);
% 子图4: 每列的误差范数
subplot(2,3,4);
bar(1:7, sqrt(sum((J_matlab - J_custom).^2, 1)));
xlabel('关节'); ylabel('列误差范数');
title('每列误差范数'); grid on;
% 子图5: 误差分布直方图
subplot(2,3,5);
errors = J_matlab(:) - J_custom(:);
histogram(errors, 50);
xlabel('误差值'); ylabel('频数');
title('误差分布直方图'); grid on;
% 子图6: 位置误差验证
subplot(2,3,6);
p_matlab = T_matlab(1:3,4);
p_custom = T_custom(1:3,4);
bar(1:3, abs(p_matlab - p_custom));
xlabel('坐标轴'); ylabel('位置误差 (m)');
title(['位置误差: ', num2str(pos_error, '%.2e'), ' m']);
set(gca, 'XTickLabel', {'X','Y','Z'}); grid on;
% ====================== 函数定义 ======================
function J_geo = geometric_jacobian(q, use_default_tool, extra_length, euler_seq)
% 计算几何雅可比矩阵,支持工具配置和欧拉角顺序检查
%
% 输入参数:
% q - 7×1关节角向量 [rad]
% use_default_tool - 布尔值:true表示使用Franka默认工具,false表示不使用默认工具
% extra_length - 额外工具长度 [m],当use_default_tool=true时,总长度=0.1034+extra_length
% 当use_default_tool=false时,总长度=extra_length
% euler_seq - 字符串:指定欧拉角顺序,目前仅支持'ZYX'(不区分大小写)
%
% 输出:
% J_geo - 6×7几何雅可比矩阵(MATLAB顺序:前3行角速度,后3行线速度)
%
% 示例:
% J1 = geometric_jacobian(q, true, 0, 'ZYX') % 使用默认工具,无额外长度
% J2 = geometric_jacobian(q, true, 0.05, 'zyx') % 默认工具+50mm额外长度
% J3 = geometric_jacobian(q, false, 0.15, 'ZYX') % 自定义150mm工具
% 参数检查和默认值处理
if nargin < 4
euler_seq = 'ZYX'; % 默认欧拉角顺序
end
% 检查欧拉角顺序
if ~ischar(euler_seq) || ~strcmpi(euler_seq, 'ZYX')
error(['目前仅支持ZYX欧拉角顺序。您输入的欧拉角顺序为: ', euler_seq, ...
'。请使用''ZYX''作为euler_seq参数。']);
end
% 设置默认工具长度
franka_default_tool_length = 0.1034; % Franka Panda默认末端执行器长度 [m]
% 计算总工具长度
if use_default_tool
if extra_length < 0
error('额外长度不能为负数');
end
total_EE_length = franka_default_tool_length + extra_length;
fprintf('几何雅可比计算:使用默认Franka工具 (0.1034m) + 额外长度 %.4fm = 总长度 %.4fm\n', ...
extra_length, total_EE_length);
else
if extra_length < 0
error('自定义工具长度不能为负数');
end
total_EE_length = extra_length;
if total_EE_length == 0
fprintf('几何雅可比计算:不使用任何工具\n');
else
fprintf('几何雅可比计算:使用自定义工具长度: %.4fm\n', total_EE_length);
end
end
% 调用内部函数计算几何雅可比
J_geo = geometric_jacobian_core(q, total_EE_length);
end
function J_geo = geometric_jacobian_core(q, total_EE_length)
% 内部核心函数:根据关节角度和工具长度计算几何雅可比矩阵
% 匹配MATLAB工具箱的顺序(前3行:角速度,后3行:线速度)
% 输入: q - 7×1关节角向量 (弧度)
% total_EE_length - 末端执行器总长度 [m]
% 输出: J_geo - 6×7几何雅可比矩阵
% Franka Panda的DH参数 (Modified DH)
% 格式: [alpha, a, d, theta]
MDH = [0, 0, 0.333, q(1);
-pi/2, 0, 0, q(2);
pi/2, 0, 0.316, q(3);
pi/2, 0.0825, 0, q(4);
-pi/2, -0.0825,0.384, q(5);
pi/2, 0, 0, q(6);
pi/2, 0.088, 0.107, q(7)];
% 计算每个关节的变换矩阵和位置
n = 7;
T = eye(4);
p_all = zeros(3, n);
z_all = zeros(3, n);
for i = 1:n
alpha = MDH(i, 1);
a = MDH(i, 2);
d = MDH(i, 3);
theta = MDH(i, 4);
% 改进DH变换矩阵
Ti = [cos(theta), -sin(theta), 0, a;
sin(theta)*cos(alpha), cos(theta)*cos(alpha), -sin(alpha), -d*sin(alpha);
sin(theta)*sin(alpha), cos(theta)*sin(alpha), cos(alpha), d*cos(alpha);
0, 0, 0, 1];
T = T * Ti;
p_all(:, i) = T(1:3, 4);
z_all(:, i) = T(1:3, 3);
end
% 末端执行器位置(考虑工具长度)
% 工具沿最后一个关节的z轴方向偏移
p_ee = p_all(:, end) + total_EE_length * z_all(:, end);
% 计算几何雅可比 - 修正关节编号对应关系
J_geo = zeros(6, n);
for i = 1:n
if i == 1
% 关节1:使用基坐标系
p_i = [0; 0; 0];
z_i = [0; 0; 1];
else
% 关节i:使用连杆i-1的坐标系
p_i = p_all(:, i); % 改进DH:使用i
z_i = z_all(:, i); % 改进DH:使用i
end
% 线速度在前,角速度在后
J_geo(1:3, i) = cross(z_i, p_ee - p_i); % 线速度部分
J_geo(4:6, i) = z_i; % 角速度部分
end
end
function T = forward_kinematics_mdh(q, total_EE_length)
% 改进DH正运动学,支持工具长度参数
%
% 输入参数:
% q - 7×1关节角向量 [rad]
% total_EE_length - 可选,末端执行器总长度 [m],默认0.1034
%
% 输出:
% T - 4×4齐次变换矩阵
% 设置默认参数
if nargin < 2
total_EE_length = 0.1034; % Franka Panda默认末端执行器长度
end
MDH = [0, 0, 0.333, q(1);
-pi/2, 0, 0, q(2);
pi/2, 0, 0.316, q(3);
pi/2, 0.0825, 0, q(4);
-pi/2, -0.0825,0.384, q(5);
pi/2, 0, 0, q(6);
pi/2, 0.088, 0.107, q(7)];
T = eye(4);
for i = 1:7
alpha = MDH(i, 1);
a = MDH(i, 2);
d = MDH(i, 3);
theta = MDH(i, 4);
Ti = [cos(theta), -sin(theta), 0, a;
sin(theta)*cos(alpha), cos(theta)*cos(alpha), -sin(alpha), -d*sin(alpha);
sin(theta)*sin(alpha), cos(theta)*sin(alpha), cos(alpha), d*cos(alpha);
0, 0, 0, 1];
T = T * Ti;
end
% 添加工具偏移(沿最后一个关节的z轴方向)
if total_EE_length ~= 0
T_ee = [1, 0, 0, 0;
0, 1, 0, 0;
0, 0, 1, total_EE_length;
0, 0, 0, 1];
T = T * T_ee;
end
end三. 解析雅可比矩阵
3.1 解析雅可比矩阵的定义

3.2 解析雅可比与几何雅可比的关系

3.3 基于ZYX欧拉角的解析雅可比公式

3.4 解析雅可比矩阵的完整公式


3.2 解析雅可比矩阵的代码实现
Matlab
% J_analytical = analytical_jacobian(q_arm, false, 0.00, 'zyx');
function J_ana = analytical_jacobian(q, use_default_tool, extra_length, euler_seq)
% 计算解析雅可比矩阵(支持不同工具配置和欧拉角顺序检查)
%
% 输入参数:
% q - 7×1关节角向量 [rad]
% use_default_tool - 布尔值:true表示使用Franka默认工具,false表示不使用默认工具
% extra_length - 额外工具长度 [m],当use_default_tool=true时,总长度=0.1034+extra_length
% 当use_default_tool=false时,总长度=extra_length
% euler_seq - 字符串:指定欧拉角顺序,目前仅支持'ZYX'(不区分大小写)
%
% 输出:
% J_ana - 6×7解析雅可比矩阵
%
% 示例:
% J1 = analytical_jacobian(q, true, 0, 'ZYX') % 使用默认工具,无额外长度
% J2 = analytical_jacobian(q, true, 0.05, 'zyx') % 默认工具+50mm额外长度
% J3 = analytical_jacobian(q, false, 0.15, 'ZYX') % 自定义150mm工具
% 参数检查
if nargin < 4
euler_seq = 'ZYX'; % 默认欧拉角顺序
end
% 检查欧拉角顺序
if ~ischar(euler_seq) || ~strcmpi(euler_seq, 'ZYX')
error(['目前仅支持ZYX欧拉角顺序。您输入的欧拉角顺序为: ', euler_seq, ...
'。请使用''ZYX''作为euler_seq参数。']);
end
% 设置默认工具长度
franka_default_tool_length = 0.1034; % Franka Panda默认末端执行器长度 [m]
% 计算总工具长度
if use_default_tool
if extra_length < 0
error('额外长度不能为负数');
end
total_EE_length = franka_default_tool_length + extra_length;
% fprintf('使用默认Franka工具 (0.1034m) + 额外长度 %.4fm = 总长度 %.4fm\n', ...
% extra_length, total_EE_length);
else
if extra_length < 0
error('自定义工具长度不能为负数');
end
total_EE_length = extra_length;
if total_EE_length == 0
fprintf('不使用任何工具\n');
else
fprintf('使用自定义工具长度: %.4fm\n', total_EE_length);
end
end
% 计算解析雅可比(调用内部函数)
J_ana = analytical_jacobian_zyx_core(q, total_EE_length);
end
% 内部核心函数(只处理ZYX欧拉角)
function J_ana = analytical_jacobian_zyx_core(q, total_EE_length)
% 计算基于ZYX欧拉角的解析雅可比(内部函数)
% 输入: q - 关节角度,total_EE_length - 总工具长度
% 计算正运动学(包含工具)
T = forward_kinematics_mdh(q, total_EE_length);
R = T(1:3, 1:3);
p = T(1:3, 4);
% 提取ZYX欧拉角
eul_zyx = rotm2eul(R, 'ZYX'); % [偏航(yaw), 俯仰(pitch), 横滚(roll)]
% 为了与常见文献一致,重新排序为[φ, θ, ψ] = [横滚, 俯仰, 偏航]
phi = eul_zyx(3); % 横滚 (roll)
theta = eul_zyx(2); % 俯仰 (pitch)
psi = eul_zyx(1); % 偏航 (yaw)
% 计算几何雅可比(包含工具)
J_geo = geometric_jacobian(q, total_EE_length);
% 分离几何雅可比的位置和姿态部分
J_v = J_geo(1:3, :); % 线速度部分
J_w = J_geo(4:6, :); % 角速度部分
% 计算B矩阵(从欧拉角导数到角速度的转换矩阵)
% 对于ZYX欧拉角,当角速度在基坐标系中时:
B = [cos(psi)*cos(theta), -sin(psi), 0;
sin(psi)*cos(theta), cos(psi), 0;
-sin(theta), 0, 1];
% 检查奇异性(万向锁)
if abs(cos(theta)) < 1e-6
warning('接近万向锁奇点 (俯仰角θ≈±90°),B矩阵接近奇异');
B_inv = pinv(B);
else
B_inv = inv(B);
end
% 解析雅可比
J_ana = zeros(6, 7);
J_ana(1:3, :) = J_v; % 位置导数部分
J_ana(4:6, :) = B_inv * J_w; % 欧拉角导数部分
end
% 几何雅可比函数(与之前相同,但添加了total_EE_length参数)
function J_geo = geometric_jacobian(q, total_EE_length)
% 设置默认参数
if nargin < 2
total_EE_length = 0.1034; % Franka Panda默认末端执行器长度
end
MDH = [0, 0, 0.333, q(1);
-pi/2, 0, 0, q(2);
pi/2, 0, 0.316, q(3);
pi/2, 0.0825, 0, q(4);
-pi/2, -0.0825,0.384, q(5);
pi/2, 0, 0, q(6);
pi/2, 0.088, 0.107, q(7)];
n = 7;
T = eye(4);
p_all = zeros(3, n);
z_all = zeros(3, n);
for i = 1:n
alpha = MDH(i, 1);
a = MDH(i, 2);
d = MDH(i, 3);
theta = MDH(i, 4);
Ti = [cos(theta), -sin(theta), 0, a;
sin(theta)*cos(alpha), cos(theta)*cos(alpha), -sin(alpha), -d*sin(alpha);
sin(theta)*sin(alpha), cos(theta)*sin(alpha), cos(alpha), d*cos(alpha);
0, 0, 0, 1];
T = T * Ti;
p_all(:, i) = T(1:3, 4);
z_all(:, i) = T(1:3, 3);
end
% 计算包含工具的末端位置
p_ee = p_all(:, end) + total_EE_length * z_all(:, end);
J_geo = zeros(6, n);
for i = 1:n
if i == 1
p_i = [0; 0; 0];
z_i = [0; 0; 1];
else
p_i = p_all(:, i);
z_i = z_all(:, i);
end
J_geo(1:3, i) = cross(z_i, p_ee - p_i);
J_geo(4:6, i) = z_i;
end
end
% 正运动学函数(与之前相同,但添加了total_EE_length参数)
function T = forward_kinematics_mdh(q, total_EE_length)
% 设置默认参数
if nargin < 2
total_EE_length = 0.1034; % Franka Panda默认末端执行器长度
end
MDH = [0, 0, 0.333, q(1);
-pi/2, 0, 0, q(2);
pi/2, 0, 0.316, q(3);
pi/2, 0.0825, 0, q(4);
-pi/2, -0.0825,0.384, q(5);
pi/2, 0, 0, q(6);
pi/2, 0.088, 0.107, q(7)];
T = eye(4);
for i = 1:7
alpha = MDH(i, 1);
a = MDH(i, 2);
d = MDH(i, 3);
theta = MDH(i, 4);
Ti = [cos(theta), -sin(theta), 0, a;
sin(theta)*cos(alpha), cos(theta)*cos(alpha), -sin(alpha), -d*sin(alpha);
sin(theta)*sin(alpha), cos(theta)*sin(alpha), cos(alpha), d*cos(alpha);
0, 0, 0, 1];
T = T * Ti;
end
% 添加工具偏移
if total_EE_length ~= 0
T_ee = [1, 0, 0, 0;
0, 1, 0, 0;
0, 0, 1, total_EE_length;
0, 0, 0, 1];
T = T * T_ee;
end
end- 测试代码,将我们自定义的解析雅可比矩阵与基于欧拉角差分的方法对比看看有没有计算错
Matlab
clc; close all; clear all;
% 创建机器人模型
robot = loadrobot('frankaEmikaPanda', 'DataFormat', 'row');
% 测试关节角度
q_full = [0.1, 0.2, 0.3, -pi/2, 0, pi/2, 0, 0, 0];
q_arm = q_full(1:7)';
% 1. 首先计算几何雅可比(作为参考)
J_geo_matlab = geometricJacobian(robot, q_full, 'panda_link8');
J_geo_matlab = J_geo_matlab(:, 1:7); % 只取前7列
% 2. 计算解析雅可比(使用ZYX欧拉角)
% 注意:MATLAB没有直接的解析雅可比函数,但我们可以通过符号或数值方法验证
disp('=== 解析雅可比计算与验证 ===');
% 方法1: 使用我们的解析雅可比函数
J_analytical_custom = analytical_jacobian_zyx(q_arm);
disp('自定义解析雅可比 (6×7):');
disp('前3行: 位置对关节角度的导数');
disp('后3行: ZYX欧拉角对关节角度的导数');
disp(J_analytical_custom);
% 方法2: 使用有限差分法验证(数值基准)
J_analytical_fd = analytical_jacobian_finite_difference(q_arm);
disp('有限差分法计算的解析雅可比 (6×7):');
disp(J_analytical_fd);
% 3. 比较两种方法
disp('自定义解析雅可比 vs 有限差分法差异:');
error_fd = norm(J_analytical_custom - J_analytical_fd, 'fro');
fprintf('误差范数: %.6e\n', error_fd);
% 4. 验证几何雅可比与解析雅可比的关系
% 几何雅可比 -> 解析雅可比的转换
J_analytical_from_geo = convert_geometric_to_analytical(q_arm, J_geo_matlab);
disp('从几何雅可比转换得到的解析雅可比:');
disp(J_analytical_from_geo);
disp('自定义解析雅可比 vs 几何雅可比转换的差异:');
error_convert = norm(J_analytical_custom - J_analytical_from_geo, 'fro');
fprintf('误差范数: %.6e\n', error_convert);
% ====================== 函数定义 ======================
function J_ana = analytical_jacobian_zyx(q)
% 计算基于ZYX欧拉角的解析雅可比
% 输入: q - 7×1关节角向量
% 输出: J_ana - 6×7解析雅可比矩阵
% 计算正运动学
T = forward_kinematics_mdh(q);
R = T(1:3, 1:3);
p = T(1:3, 4);
% 提取ZYX欧拉角 (Z-Y-X,即横滚-俯仰-偏航)
% MATLAB的rotm2eul函数默认是ZYX顺序
eul_zyx = rotm2eul(R, 'ZYX'); % [偏航(yaw), 俯仰(pitch), 横滚(roll)]
% 为了与常见文献一致,我们重新排序为[φ, θ, ψ] = [横滚, 俯仰, 偏航]
phi = eul_zyx(3); % 横滚 (roll)
theta = eul_zyx(2); % 俯仰 (pitch)
psi = eul_zyx(1); % 偏航 (yaw)
% 计算几何雅可比(使用之前修正的函数)
J_geo = geometric_jacobian_from_q_corrected(q);
% 分离几何雅可比的位置和姿态部分
J_v = J_geo(1:3, :); % 线速度部分
J_w = J_geo(4:6, :); % 角速度部分
% 计算B矩阵(从欧拉角导数到角速度的转换矩阵)
% 对于ZYX欧拉角 (φ, θ, ψ) = (横滚, 俯仰, 偏航)
% ω = B(φ, θ) * [φ̇; θ̇; ψ̇]
% B = [1, 0, sin(theta);
% 0, cos(phi), -cos(theta)*sin(phi);
% 0, sin(phi), cos(theta)*cos(phi)];
B = [cos(psi)*cos(theta), -sin(psi), 0;
sin(psi)*cos(theta), cos(psi), 0;
-sin(theta), 0, 1];
% 检查奇异性(当θ = ±π/2时)
if abs(abs(theta) - pi/2) < 1e-6
warning('接近万向锁奇点 (θ ≈ ±90°),B矩阵接近奇异');
end
% 解析雅可比
% 位置部分:与几何雅可比的线速度部分相同
% 姿态部分:B^{-1} * J_w
J_ana = zeros(6, 7);
J_ana(1:3, :) = J_v; % 位置导数部分
J_ana(4:6, :) = B \ J_w; % 欧拉角导数部分
end
function J_ana_fd = analytical_jacobian_finite_difference(q)
% 使用有限差分法计算解析雅可比(数值基准)
% 输入: q - 7×1关节角向量
% 输出: J_ana_fd - 6×7解析雅可比矩阵
n = length(q);
J_ana_fd = zeros(6, n);
% 计算基准位姿
T0 = forward_kinematics_mdh(q);
p0 = T0(1:3, 4);
R0 = T0(1:3, 1:3);
eul0 = rotm2eul(R0, 'ZYX');
eul0 = [eul0(3), eul0(2), eul0(1)]; % [φ, θ, ψ]
% 扰动大小
delta = 1e-6;
for i = 1:n
% 创建扰动向量
q_plus = q;
q_plus(i) = q_plus(i) + delta;
% 计算扰动后的位姿
T_plus = forward_kinematics_mdh(q_plus);
p_plus = T_plus(1:3, 4);
R_plus = T_plus(1:3, 1:3);
eul_plus = rotm2eul(R_plus, 'ZYX');
eul_plus = [eul_plus(3), eul_plus(2), eul_plus(1)]; % [φ, θ, ψ]
% 计算有限差分导数
J_ana_fd(1:3, i) = (p_plus - p0) / delta; % 位置导数
J_ana_fd(4:6, i) = (eul_plus - eul0)' / delta; % 欧拉角导数
% 可选:使用中心差分提高精度
q_minus = q;
q_minus(i) = q_minus(i) - delta;
T_minus = forward_kinematics_mdh(q_minus);
p_minus = T_minus(1:3, 4);
R_minus = T_minus(1:3, 1:3);
eul_minus = rotm2eul(R_minus, 'ZYX');
eul_minus = [eul_minus(3), eul_minus(2), eul_minus(1)];
% 中心差分
J_ana_fd(1:3, i) = (p_plus - p_minus) / (2*delta);
J_ana_fd(4:6, i) = (eul_plus - eul_minus)' / (2*delta);
end
end
function J_ana_from_geo = convert_geometric_to_analytical(q, J_geo)
% 从几何雅可比转换到解析雅可比
% 输入: q - 关节角度, J_geo - 几何雅可比矩阵
% 输出: 解析雅可比矩阵
% 计算正运动学
T = forward_kinematics_mdh(q);
R = T(1:3, 1:3);
% 提取ZYX欧拉角
eul_zyx = rotm2eul(R, 'ZYX');
phi = eul_zyx(3); % 横滚
theta = eul_zyx(2); % 俯仰
psi = eul_zyx(1); % 偏航
% 计算B矩阵
B = [cos(psi)*cos(theta), -sin(psi), 0;
sin(psi)*cos(theta), cos(psi), 0;
-sin(theta), 0, 1];
% 分离几何雅可比
J_w = J_geo(1:3, :); % 角速度部分
J_v = J_geo(4:6, :); % 线速度部分
% 转换
J_ana_from_geo = zeros(6, 7);
J_ana_from_geo(1:3, :) = J_v; % 位置部分相同
J_ana_from_geo(4:6, :) = B \ J_w; % 姿态部分转换
end
function J_ana_sym = analytical_jacobian_symbolic(q)
% 使用符号计算验证解析雅可比(如果符号工具箱可用)
% 注意:这会比较慢,但精度高
syms q1 q2 q3 q4 q5 q6 q7 real
q_sym = [q1; q2; q3; q4; q5; q6; q7];
% 将数值q代入符号变量
q_sym_val = subs(q_sym, [q1 q2 q3 q4 q5 q6 q7], q');
% 计算正运动学(符号)
T_sym = forward_kinematics_mdh_symbolic(q_sym);
p_sym = T_sym(1:3, 4);
% 计算旋转矩阵和欧拉角
R_sym = T_sym(1:3, 1:3);
% 从旋转矩阵提取ZYX欧拉角
% 公式:φ = atan2(r32, r33), θ = -asin(r31), ψ = atan2(r21, r11)
phi_sym = atan2(R_sym(3,2), R_sym(3,3));
theta_sym = -asin(R_sym(3,1));
psi_sym = atan2(R_sym(2,1), R_sym(1,1));
% 组合位姿向量
x_sym = [p_sym; phi_sym; theta_sym; psi_sym];
% 计算解析雅可比(符号偏导数)
J_ana_sym_s = jacobian(x_sym, q_sym);
% 代入数值
J_ana_sym = double(subs(J_ana_sym_s, q_sym, q_sym_val));
end
function T = forward_kinematics_mdh_symbolic(q_sym)
% 符号版本的正运动学函数
% Franka Panda的改进DH参数
MDH = [0, 0, 0.333, q_sym(1);
-sym(pi)/2, 0, 0, q_sym(2);
sym(pi)/2, 0, 0.316, q_sym(3);
sym(pi)/2, 0.0825, 0, q_sym(4);
-sym(pi)/2, -0.0825,0.384, q_sym(5);
sym(pi)/2, 0, 0, q_sym(6);
sym(pi)/2, 0.088, 0.107, q_sym(7)];
T = sym(eye(4));
for i = 1:7
alpha = MDH(i, 1);
a = MDH(i, 2);
d = MDH(i, 3);
theta = MDH(i, 4);
Ti = [cos(theta), -sin(theta), 0, a;
sin(theta)*cos(alpha), cos(theta)*cos(alpha), -sin(alpha), -d*sin(alpha);
sin(theta)*sin(alpha), cos(theta)*sin(alpha), cos(alpha), d*cos(alpha);
0, 0, 0, 1];
T = T * Ti;
end
end
function J_geo = geometric_jacobian_from_q_corrected(q)
% 你之前修正的几何雅可比函数
MDH = [0, 0, 0.333, q(1);
-pi/2, 0, 0, q(2);
pi/2, 0, 0.316, q(3);
pi/2, 0.0825, 0, q(4);
-pi/2, -0.0825,0.384, q(5);
pi/2, 0, 0, q(6);
pi/2, 0.088, 0.107, q(7)];
n = 7;
T = eye(4);
p_all = zeros(3, n);
z_all = zeros(3, n);
for i = 1:n
alpha = MDH(i, 1);
a = MDH(i, 2);
d = MDH(i, 3);
theta = MDH(i, 4);
Ti = [cos(theta), -sin(theta), 0, a;
sin(theta)*cos(alpha), cos(theta)*cos(alpha), -sin(alpha), -d*sin(alpha);
sin(theta)*sin(alpha), cos(theta)*sin(alpha), cos(alpha), d*cos(alpha);
0, 0, 0, 1];
T = T * Ti;
p_all(:, i) = T(1:3, 4);
z_all(:, i) = T(1:3, 3);
end
p_ee = p_all(:, end);
J_geo = zeros(6, n);
for i = 1:n
if i == 1
p_i = [0; 0; 0];
z_i = [0; 0; 1];
else
p_i = p_all(:, i);
z_i = z_all(:, i);
end
J_geo(1:3, i) = cross(z_i, p_ee - p_i);
J_geo(4:6, i) = z_i;
end
end
function T = forward_kinematics_mdh(q)
% 正运动学函数
MDH = [0, 0, 0.333, q(1);
-pi/2, 0, 0, q(2);
pi/2, 0, 0.316, q(3);
pi/2, 0.0825, 0, q(4);
-pi/2, -0.0825,0.384, q(5);
pi/2, 0, 0, q(6);
pi/2, 0.088, 0.107, q(7)];
T = eye(4);
for i = 1:7
alpha = MDH(i, 1);
a = MDH(i, 2);
d = MDH(i, 3);
theta = MDH(i, 4);
Ti = [cos(theta), -sin(theta), 0, a;
sin(theta)*cos(alpha), cos(theta)*cos(alpha), -sin(alpha), -d*sin(alpha);
sin(theta)*sin(alpha), cos(theta)*sin(alpha), cos(alpha), d*cos(alpha);
0, 0, 0, 1];
T = T * Ti;
end
end
function J=my_analytical_jacobian(q)
%1~3行为线速度,4~6行为ZYZ欧拉角变化率,7~9行为ZYX欧拉角变化率,10行为x3导数
J=zeros(6,7);
J1=zeros(3,7);
T=[cos(q(1)) -sin(q(1)) 0 0;sin(q(1)) cos(q(1)) 0 0;0 0 1 0.333;0 0 0 1];
p1=T(1:3,4);
J1(:,1)=T(1:3,3);
T=T*[cos(q(2)) -sin(q(2)) 0 0;0 0 1 0;-sin(q(2)) -cos(q(2)) 0 0;0 0 0 1];
p2=T(1:3,4);
J1(:,2)=T(1:3,3);
T=T*[cos(q(3)) -sin(q(3)) 0 0;0 0 -1 -0.316;sin(q(3)) cos(q(3)) 0 0;0 0 0 1];
p3=T(1:3,4);
J1(:,3)=T(1:3,3);
T=T*[cos(q(4)) -sin(q(4)) 0 0.0825;0 0 -1 0;sin(q(4)) cos(q(4)) 0 0;0 0 0 1];
p4=T(1:3,4);
J1(:,4)=T(1:3,3);
T=T*[cos(q(5)) -sin(q(5)) 0 -0.0825;0 0 1 0.384;-sin(q(5)) -cos(q(5)) 0 0;0 0 0 1];
p5=T(1:3,4);
J1(:,5)=T(1:3,3);
T=T*[cos(q(6)) -sin(q(6)) 0 0;0 0 -1 0;sin(q(6)) cos(q(6)) 0 0;0 0 0 1];
p6=T(1:3,4);
J1(:,6)=T(1:3,3);
T=T*[cos(q(7)) -sin(q(7)) 0 0.088;0 0 -1 0;sin(q(7)) cos(q(7)) 0 0;0 0 0 1];
%p7=T(1:3,4);
J1(:,7)=T(1:3,3);
% T=T*[1 0 0 0;0 1 0 0;0 0 1 0.107;0 0 0 1]; % 不带末端执行器
Re=T(1:3,1:3);
pe=T(1:3,4);
%ZYX
alpha=atan2(Re(2,1),Re(1,1));
beta=atan2(-Re(3,1),sqrt(Re(1,1)^2+Re(2,1)^2));
a=-sin(alpha);
c=cos(alpha);
b=c*cos(beta);
d=-a*cos(beta);
e=-sin(beta);
temp=a*d-b*c;
transform2=[c*e/temp -a*e/temp 1;d/temp -b/temp 0;-c/temp a/temp 0];
J(4:6,1)=skew(J1(:,1))*(pe-p1);
J(4:6,2)=skew(J1(:,2))*(pe-p2);
J(4:6,3)=skew(J1(:,3))*(pe-p3);
J(4:6,4)=skew(J1(:,4))*(pe-p4);
J(4:6,5)=skew(J1(:,5))*(pe-p5);
J(4:6,6)=skew(J1(:,6))*(pe-p6);
J(4:6,7)=[0;0;0];
% 求解的是解析雅克比矩阵 J_A = inv(T_A)*J
% ZYX欧拉角 T_A = [0 -sin(alpha) cos(beta)*cos(alpha);
% 0 cos(alpha) cos(beta)*sin(alpha);
% 1 0 -sin(beta) ]
J(1:3,:)=transform2*J1;
end