即插即用系列 | AAAI 2026 WaveFormer: 当视觉建模遇上波动方程，频率-时间解耦的新SOTA

论文题目：WaveFormer: Frequency-Time Decoupled Vision Modeling with Wave Equation

论文作者：Zishan Shu, Juntong Wu, et al. (Peking University, Tsinghua University)

论文链接 (Paper)：https://arxiv.org/abs/2601.08602

代码链接(code)：https://github.com/ZishanShu/WaveFormer

哔哩哔哩视频讲解 ：https://space.bilibili.com/57394501?spm_id_from=333.337.0.0

- - [1. 核心思想](#1. 核心思想)
  - [2. 背景与动机](#2. 背景与动机)
  - - [2.1 文本背景与痛点](#2.1 文本背景与痛点)
    - [2.2 动机图解分析](#2.2 动机图解分析)
  - [3. 主要创新点](#3. 主要创新点)
  - [4. 方法细节](#4. 方法细节)
  - - [4.1 整体网络架构](#4.1 整体网络架构)
    - [4.2 核心创新模块详解](#4.2 核心创新模块详解)
    - [4.3 理念与机制总结](#4.3 理念与机制总结)
  - [5. 即插即用模块的作用](#5. 即插即用模块的作用)
  - [6. 实验分析](#6. 实验分析)
  - [7. 获取即插即用代码关注【AI即插即用】](#7. 获取即插即用代码关注【AI即插即用】)

1. 核心思想

本文提出了一种名为 WaveFormer 的全新视觉骨干网络，旨在解决现有 Transformer 计算复杂度高以及基于"热传导"物理模型容易导致特征过度平滑的问题。核心思想是将特征图视为一种空间信号，利用欠阻尼波动方程（Underdamped Wave Equation）来建模其随网络深度的演化过程。通过推导该方程在频域的闭式解，作者设计了波传播算子（WPO），实现了频率与时间的解耦，使得模型既能以 O ( N log ⁡ N ) O(N \log N) O(NlogN) 的线性复杂度进行全局建模，又能有效保留高频细节（如边缘、纹理），在图像分类、检测和分割任务上均取得了优于 Swin Transformer 和 Vision Mamba 的性能。

2. 背景与动机

2.1 文本背景与痛点

视觉基础模型（Foundation Models）目前面临两个主要流派的局限：

Transformer 流派 ：虽然通过 Self-Attention 实现了全局建模，但 O ( N 2 ) O(N^2) O(N2) 的计算复杂度限制了高分辨率图像的处理，且缺乏物理可解释性。
物理启发流派（如 vHeat） ：近期出现了一些基于热传导方程（Heat Equation）的模型。然而，热传导本质上是一种低通滤波器 ，高频信号（细节）会随着传播时间（网络深度）的增加而迅速衰减，导致特征过度平滑（Over-smoothing），丢失了视觉任务中至关重要的边缘和纹理信息。

本文动机 ：能否找到一种物理机制，既能像波一样传播很远（全局建模），又能保持高频能量不被迅速耗散（保留细节）？答案就是波动方程。

2.2 动机图解分析

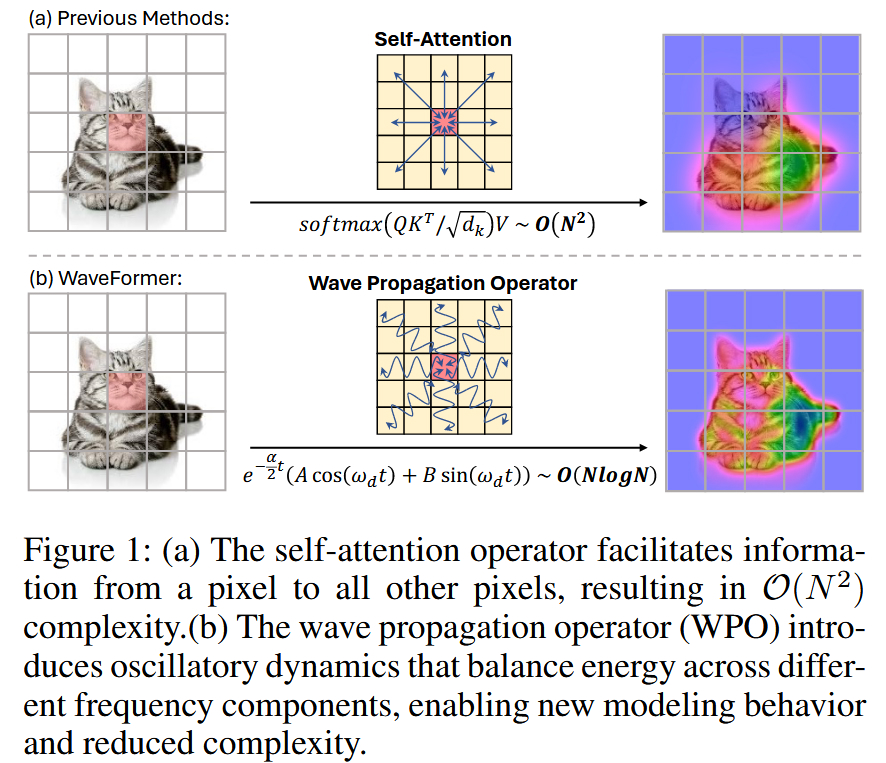
看图说话（动机分析）：

左图 (Previous Methods - Attention) ：展示了 Self-Attention 的机制。可以看到，一个像素点需要与全图中所有其他像素点建立连接（密集的红色箭头）。这意味着计算量是像素数 N N N 的平方 ( O ( N 2 ) O(N^2) O(N2))，效率极低，且缺乏对空间传播规律的显式建模。
右图 (WaveFormer - WPO) ：展示了本文提出的波传播机制。
- 形态：特征像水波纹（Ripple）一样向外扩散，呈现出振荡（Oscillatory）特性。
- 公式：图中给出的核心公式 e − α t / 2 ( A cos ⁡ ω t + B sin ⁡ ω t ) e^{-\alpha t/2}(A \cos \omega t + B \sin \omega t) e−αt/2(Acosωt+Bsinωt) 揭示了其本质------振荡传播。
- 优势：这种机制的复杂度仅为 O ( N log ⁡ N ) O(N \log N) O(NlogN)（借助 FFT），且通过振荡，能量可以在不同频率间平衡，不会像热传导那样"闷死"高频细节。

3. 主要创新点

物理启发的波动视角 ：首次将视觉特征图的演化建模为欠阻尼波动方程的物理过程，打破了传统的注意力机制或热传导范式。
频率-时间解耦 (Frequency-Time Decoupling) ：推导出了波动方程的频域闭式解，使得信号的衰减（Damping, α \alpha α）与空间频率（ ω \omega ω）解耦。这意味着我们可以让高频边缘传播得很远，而不受低通滤波限制。
波传播算子 (WPO) ：设计了一个基于快速傅里叶变换（FFT）的高效算子，将复杂的微分方程求解转化为频域的逐元素乘法，实现了 O ( N log ⁡ N ) O(N \log N) O(NlogN) 的极低复杂度。
WaveFormer 架构：构建了一个通用的分层视觉骨干网络，作为即插即用的模块替代标准 ViT 或 CNN，在各项任务上实现了精度与效率的双赢。

4. 方法细节

4.1 整体网络架构

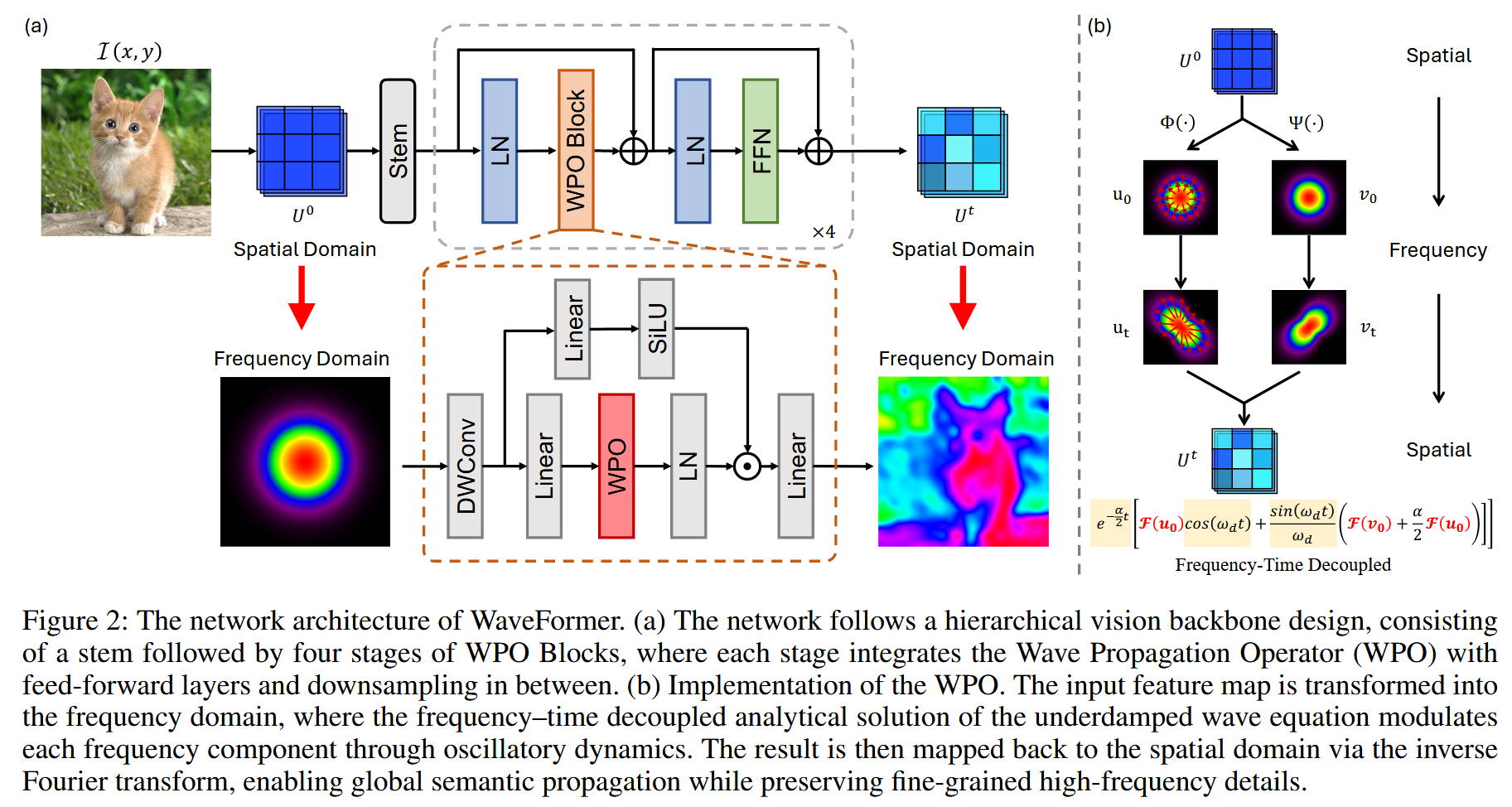
数据流详解：

输入 (Input) ：输入图像（ H × W × 3 H \times W \times 3 H×W×3）。
分层结构 (Hierarchical Stages) ：
- 网络分为 4 个阶段（Stage 1 ~ Stage 4），类似于 Swin Transformer 或 ResNet。
- Downsampling：每个阶段开始前，使用重叠的 Patch Embedding 进行下采样，降低分辨率并增加通道数。
核心路径 (Main Path) ：
- 在每个阶段内部，堆叠多个 WaveFormer Block。
- 每个 Block 包含两个主要部分：WPO (Wave Propagation Operator) 负责空间混合，FFN (Feed-Forward Network) 负责通道混合。
- 残差连接（Residual Connection）贯穿始终，保证梯度流动。
输出 (Output)：经过全局平均池化和分类头（或直接输出特征图给检测头）。

4.2 核心创新模块详解

模块 A：波传播算子 (Wave Propagation Operator, WPO)

内部结构与数据流 ：
1. 频域变换 (FFT) ：输入特征 X X X 经过二维 FFT 变换到频域 F ( X ) \mathcal{F}(X) F(X)。
2. 波核调制 (Modulation) ：这是核心步骤。在频域中，特征与一个物理推导出的波传播核 (Green's Function) 进行逐元素相乘。
  - 核心公式 ： U t = F − 1 { e − α t / 2 [ F ( U 0 ) cos ⁡ ( ω d t ) + ... ω d sin ⁡ ( ω d t ) ] } U_t = \mathcal{F}^{-1} \{ e^{-\alpha t/2} [\mathcal{F}(U_0) \cos(\omega_d t) + \frac{\dots}{\omega_d} \sin(\omega_d t)] \} Ut=F−1{e−αt/2[F(U0)cos(ωdt)+ωd...sin(ωdt)]}
  - 物理含义 ：
    - e − α t / 2 e^{-\alpha t/2} e−αt/2：阻尼项 。控制信息的整体衰减速度，但它是独立于频率的。
    - cos ⁡ ( ω d t ) / sin ⁡ ( ω d t ) \cos(\omega_d t) / \sin(\omega_d t) cos(ωdt)/sin(ωdt)：振荡项。负责将信息以波的形式传播出去。
    - ω d \omega_d ωd：频率项 。由空间频率 ( k x , k y ) (k_x, k_y) (kx,ky) 决定。
3. 逆变换 (IFFT)：将调制后的频域特征变换回空域，得到传播后的特征。
4. 参数学习 ：其中的阻尼系数 α \alpha α 和波速 v v v 是可学习的参数，让网络自适应地决定"波"传多快、衰减多慢。

模块 B：自适应参数机制

设计理念：不同图像、不同层级需要的感受野和细节保留程度不同。
工作机制 ：作者并没有把波速 v v v 和阻尼 α \alpha α 设为固定常数，而是设为可学习参数（甚至可以设计为 Input-dependent 的）。这使得 WaveFormer 能够针对特定语义（如物体边界）进行定向的波传播，增强了灵活性。

4.3 理念与机制总结

WaveFormer 的核心理念是**"用振荡对抗平滑"**：

传统的热传导 （Heat-based）是耗散的，时间越长，细节越少（低通滤波）。
本文的波动方程 （Wave-based）是守恒/振荡 的。通过引入频率-时间解耦，它允许高频信息（细节）在传播过程中"存活"下来，同时利用波的衍射特性实现全局覆盖。这在数学上保证了模型既有 ViT 的全局视野，又有 CNN 的细节捕捉能力。

5. 即插即用模块的作用

WPO (Wave Propagation Operator) 模块是一个高度通用的组件：

替代 Self-Attention ：
- 适用场景：任何使用 ViT 的场景，特别是对计算资源敏感或输入分辨率极高（如遥感、医疗影像）的任务。
- 应用：直接替换 Transformer Block 中的 MHSA（多头自注意力），可以将复杂度从 O ( N 2 ) O(N^2) O(N2) 降为 O ( N log ⁡ N ) O(N \log N) O(NlogN)，同时显著提升推理速度（Throughput）。
增强 CNN 的全局感知 ：
- 适用场景：纯 CNN 架构（如 ConvNeXt）。
- 应用：可以在 CNN 的深层插入 WPO 模块，作为一种高效的 Global Context Block，帮助 CNN 突破感受野限制。

6. 实验分析

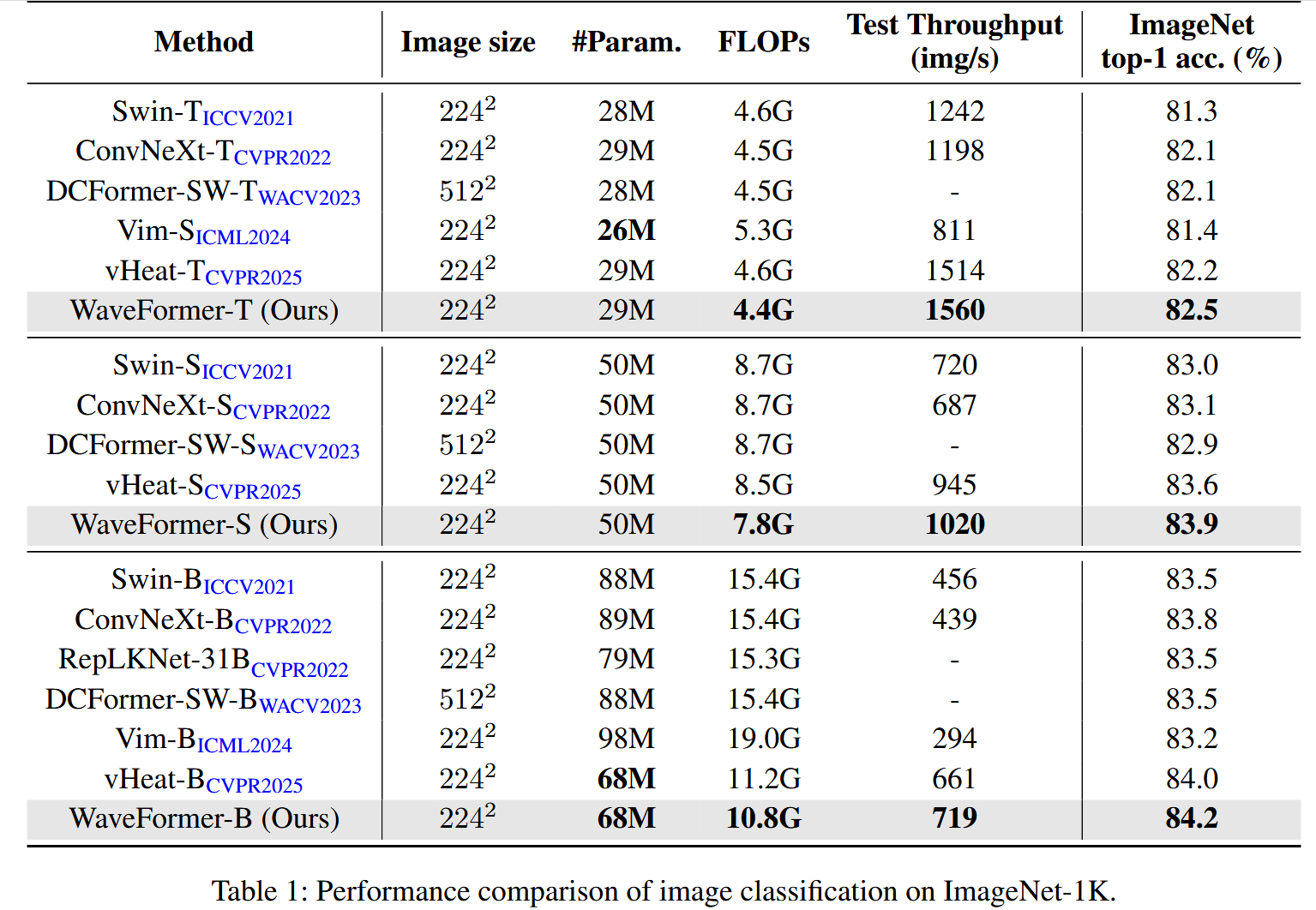
ImageNet 分类 ：
- 精度：WaveFormer-Base 达到 84.2% Top-1，超越了 Swin-B (83.5%) 和最近的 Vision Mamba (Vim-B, 83.2%)。
- 效率：在同等精度下，WaveFormer 的吞吐量（Throughput）显著更高。例如，WaveFormer-T 比 ConvNeXt-T 快 26% ，比 Vim-S 快 92%。
下游任务 (COCO 检测 & ADE20K 分割) ：
- 在 Mask R-CNN 框架下，WaveFormer-T 的 AP_box 达到 45.8 ，比 Swin-T 高出 3.1 个点。
- 这证明了保留高频细节（波的特性）对于定位密集型任务（检测、分割）具有巨大优势。
物理模型对比 ：
- 相比于基于热传导的 vHeat (CVPR 2025)，WaveFormer 在各项指标上均有提升，直接验证了"波动优于热传导"的理论假设------即避免过度平滑对于视觉表征至关重要。

总结：WaveFormer 是一篇非常硬核的"AI + Physics"论文。它不仅仅是借用了物理名词，而是真正从微分方程的解的性质出发，设计了对应的算子，解决了视觉建模中本质的"全局 vs 细节"矛盾。对于关注高效主干网络 和物理启发深度学习的研究者来说，这是一篇不容错过的佳作。

到此，所有的内容就基本讲完了。如果觉得这篇文章对你有用，记得点赞、收藏并分享给你的小伙伴们哦😄。