1、为什么引入 S神经元(Sigmoid neurons)
请先参考 神经网络之感知机(Perceptron)
假设在 手写数字识别 网络,若网络将一张本应是数字 "9" 的图像误识别为 "8",找到对应的方式微调权重和偏置,让网络对这张图像的识别结果更接近正确的 "9"。之后不断重复这一操作,反复调整权重与偏置以实现输出效果的持续优化 。 这一过程,就是神经网络的学习。
倘若权重(或偏置)的微小调整只会让输出产生相应的小幅变化,我们便可利用这一特性调整权重与偏置,让网络的表现更贴合预期。
当网络由感知机构成时 ,实际情况是即便只是对网络中某一个感知机的权重或偏置做微小调整,都有可能导致该感知器的输出发生彻底反转,比如从 0 直接变为 1。这种输出反转,又可能以某种极为复杂的方式,让网络其余部分的表现发生全局性的彻底改变。如此一来,即便这张数字 "9" 的图像此刻能被正确识别,网络对其他所有图像的识别表现,却很可能以一种难以控制的方式完全改变。这就让我们无从找到逐步调整权重与偏置的方法,来让网络的表现逐步趋近预期效果。
因此,对网络中的某一个权重(或偏置)做出微小调整,这样的权重微调,仅会让网络输出产生相应的小幅变化。具备这一特性,才让网络学习成为可能。
此时引入一种名为S 型神经元的新型人工神经元来解决这一问题。S 型神经元与感知机原理相近,但其结构经过改进,使得权重和偏置的微小调整,仅会让自身输出产生相应的小幅变化。也正是这一关键特性,让由 S 型神经元构成的网络具备了学习的可能。
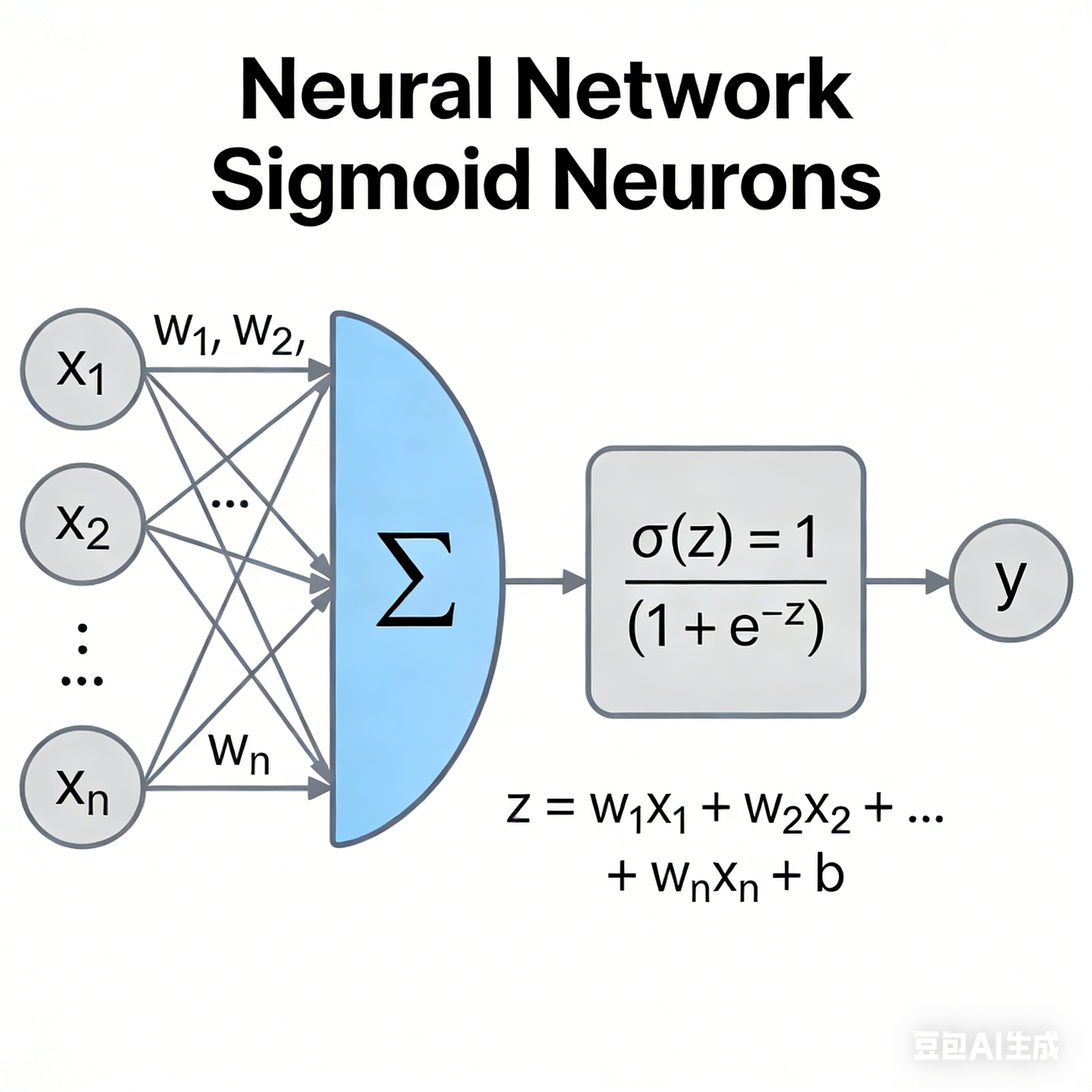
2、S神经元(Sigmoid neurons)
Sigmoid神经元是一种人工神经元模型,其核心特征是使用Sigmoid函数作为激活函数。它接收多个输入信号,加权求和后通过Sigmoid函数进行非线性变换,输出一个介于0到1之间的连续值。
Sigmoid是早期神经网络中最常用的激活函数之一,公式简洁,数学性质良好,适合教学和初学者入门。
数学表达式:
设输入为 x 1 , x 2 , ... , x n x_1, x_2, \dots, x_n x1,x2,...,xn,对应的权重为 w 1 , w 2 , ... , w n w_1, w_2, \dots, w_n w1,w2,...,wn,偏置为 b b b,则Sigmoid神经元的输出为:
a = σ ( z ) = 1 1 + e − z , 其中 z = w 1 x 1 + w 2 x 2 + ⋯ + w n x n + b a = \sigma(z) = \frac{1}{1 + e^{-z}}, \quad \text{其中} \quad z = w_1x_1 + w_2x_2 + \cdots + w_nx_n + b a=σ(z)=1+e−z1,其中z=w1x1+w2x2+⋯+wnxn+b
这里的 σ ( z ) \sigma(z) σ(z) 就是Sigmoid函数。
当 z = w ⋅ x + b z=w⋅x+b z=w⋅x+b为一个较大的正数,此时 e − z ≈ 0 e^{-z} ≈0 e−z≈0,因此 σ ( z ) ≈ 1 σ(z)≈1 σ(z)≈1。也就是说,当 z = w ⋅ x + b z=w⋅x+b z=w⋅x+b取较大正值时,S 型神经元的输出近似为 1,这与感知机的输出表现一致。
反之,若 z = w ⋅ x + b z=w⋅x+b z=w⋅x+b为一个绝对值很大的负数,那么 σ ( z ) → ∞ σ(z)→∞ σ(z)→∞,进而 σ ( z ) ≈ 0 σ(z)≈0 σ(z)≈0。可见,当 z = w ⋅ x + b z=w⋅x+b z=w⋅x+b取绝对值很大的负值时,S 型神经元的行为也与感知机高度近似。
只有当 w ⋅ x + b w⋅x+b w⋅x+b的取值处于中间范围时,S 型神经元的表现才会与感知机模型出现较明显的偏差。
特征
- 输出范围:(0,1)
- 平滑可导:在整个定义域内连续且可导,便于使用梯度下降法进行训练
- 图像 :呈"S"形曲线
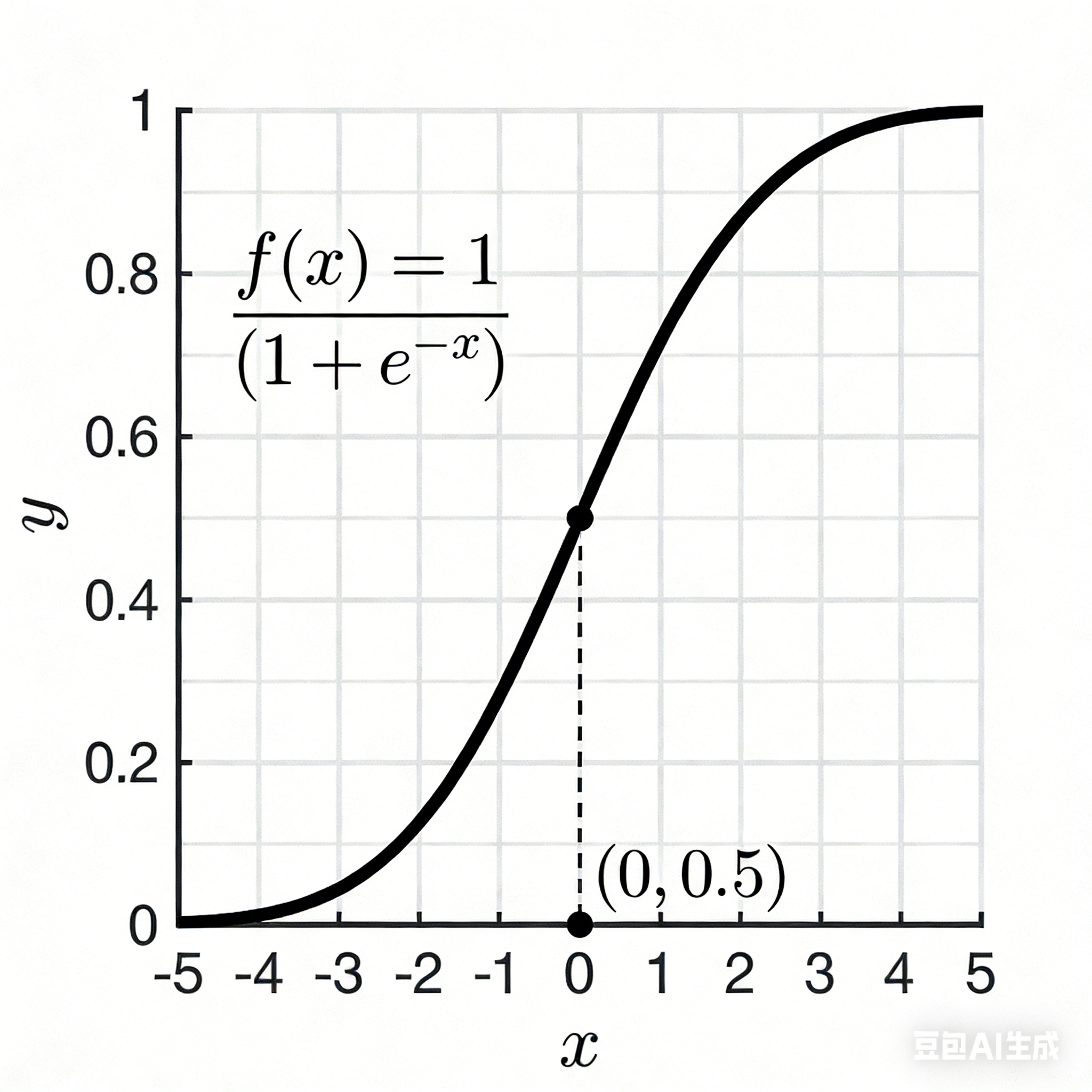
σ 函数实现了感知器的平滑化,权重的微小变化Δwj和偏置的微小变化Δb,只会让神经元的输出产生微小的变化Δoutput
Δ o u t p u t ≈ ∑ j σ o u t p u t σ w j + σ o u t p u t σ b Δ b Δoutput≈ \sum_{j} \frac{\sigma output}{\sigma w_j} + \frac{\sigma output}{\sigma b}Δb Δoutput≈j∑σwjσoutput+σbσoutputΔb
局限性
Sigmoid 神经元是早期神经网络的核心激活神经元,凭借连续可微、输出值映射到 (0,1) 区间的特性,解决了感知机不可微、无法做梯度下降训练的问题,成为 BP(反向传播)算法的基础,但随着深度学习的发展,其暴露的多重核心局限性,使其逐渐被 ReLU 等激活函数对应的神经元替代,尤其在深层神经网络中几乎不再作为核心激活单元。
梯度消失问题
Sigmoid 函数的导数范围为 (0, 0.25],深层网络反向传播时,梯度经多层连乘后快速衰减,浅层权重几乎无法更新,模型难以收敛
非零中心输出
输出恒为 (0,1) 的正数,梯度更新方向持续单向,出现 "之字形" 震荡,降低收敛效率。
计算效率低
包含指数运算,相比 ReLU 等分段函数,计算与反向传播耗时更高。
饱和后难以恢复学习
进入饱和区(输入过大或过小),梯度几乎为 0,权重几乎不再更新。