Leecode热题100：螺旋矩阵（矩阵）

给你一个 m 行 n 列的矩阵 matrix ，请按照顺时针螺旋顺序，返回矩阵中的所有元素。

示例：

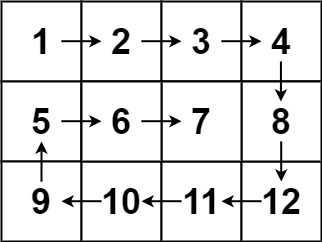
输入：matrix = $\[1,2,3,4$ , $5,6,7,8$ , $9,10,11,12$ ]

输出： $1,2,3,4,8,12,11,10,9,5,6,7$

（来源：Leecode）

第一步：回归本质------什么是"螺旋"？

从物理空间来看，螺旋遍历实际上是**不断"剥洋葱"**的过程。

每当你走完最上面的一行，这一行就从矩阵中"消失"了。
每当你走完最右边的一列，这一列也"消失"了。
本质事实 ：每一步操作都在缩小下一次可活动的矩形范围。

与其去判断"是否访问过"，不如去定义这个**"动态缩小的矩形"**。

第二步：定义逻辑模型（四个边界）

我们可以用四个变量来锁定这个动态的矩形：

up: 当前矩形的上边界
down: 下边界
left: 左边界
right: 右边界

动作逻辑：

从左往右走 ：走完后，up（上边界）向下移一行。
从上往下走 ：走完后，right（右边界）向左移一列。
从右往左走 ：走完后，down（下边界）向上移一行。
从下往上走 ：走完后，left（左边界）向右移一列。

临界点判断 ：每缩小一次边界，就判断一下：上边界是否超过了下边界？左边界是否超过了右边界？ 如果超过了，说明"洋葱"剥完了。

第三步：C++ 代码实现

让我们一步步写出代码。

1. 初始化边界

cpp 复制代码

vector<int> spiralOrder(vector<vector<int>>& matrix) {
    if (matrix.empty()) return {};
    int m = matrix.size(), n = matrix[0].size();
    
    // 物理边界的初始化
    int up = 0, down = m - 1, left = 0, right = n - 1;
    vector<int> res;

2. 开始螺旋循环

我们按照顺时针的四个方向依次循环。

cpp 复制代码

while (true) {
        // 第一步：从左向右
        for (int i = left; i <= right; ++i) res.push_back(matrix[up][i]);
        if (++up > down) break; // 上边界下移，如果越过下边界，结束

        // 第二步：从上向下
        for (int i = up; i <= down; ++i) res.push_back(matrix[i][right]);
        if (--right < left) break; // 右边界左移

        // 第三步：从右向左
        for (int i = right; i >= left; --i) res.push_back(matrix[down][i]);
        if (--down < up) break; // 下边界上移

        // 第四步：从下向上
        for (int i = down; i >= up; --i) res.push_back(matrix[i][left]);
        if (++left > right) break; // 左边界右移
    }
    return res;
}

为什么是if (++up > down)？

在矩阵（二维数组）中，行索引 i 是从上往下增长的：

第 0 行：在最顶端。
第 1 行：在第 0 行下面。
第 m-1 行：在最底端。

所以，当你说"上边界向下移动（缩小范围）"时：

如果原来的上边界 up 是 0。
我们遍历完了第 0 行，现在上边界应该变成第 1 行。
从 0 到 1，是增加，所以是 up++（或者写成 ++up）。

我们可以把这四个边界想象成四面向内推的墙：

up 墙 ：往下推索引变大 (++)
down 墙 ：往上推索引变小 (--)
left 墙 ：往右推索引变大 (++)
right 墙 ：往左推索引变小 (--)

总结疑问

如果你写 up--：你会试图去访问 matrix[-1]，这会导致程序崩溃。
如果你不判断 > down：你可能会在同一个地方"原地踏步"或者反复打转。

第一性原理带给我们的启示： 当我们觉得"判断条件"很复杂时（比如你要判断东南西北四个方向、还要看周围有没有走过），往往是因为我们还停留在微观个体 的视角。当我们跳出来，看整个空间容器的变化，复杂的判断逻辑就变成了简单的四个边界变量的增减。