单向链表的常用操作方法---嵌入式入门---Linux

在上一次为大家讲解了什么是数据结构，以及讲述了一些单向链表的操作，今天将把单向链表剩下的一些常见操作为大家讲述清楚。

1、链表的中间节点

cpp 复制代码

ListNode *FindMidNode(ListNode *dummy) {
    if(!dummy->next) return NULL;
    
    ListNode *slow = head->next;
    ListNode *fast = head->next;

    while(fast && fast->next) {
        fast = fast->next->next;
        slow = slow->next;
    }

    return slow;
}

这里我们采用的方法是快慢指针法，这个快慢指针对于好多情况下都实用，什么意思呢，就是说每次让快指针走两步，慢指针走一步，这样每次快指针都比慢指针多走一步，也就是一倍，那么快指针走到末尾，慢指针就走了整个的一半，是不是很巧妙呢。

2、链表的倒数第K个节点

同样的，对于倒数第K个节点，我们同样可以使用快慢指针完成，这次就让快指针先走K步，在让两指针同时走，是不是二者差值就为K了呢，当快指针到达NULL时，减去K,也就是慢指针的位置，即为我们所求的节点了。

cpp 复制代码

ListNode *FindKthFromEnd(ListNode *dummy, int K) {
    ListNode *slow = dummy->next;
    ListNode *fast = dummy->next;
    
    for(int i = 0; i < K; i++) {
        if(fast == NULL) {
            return NULL;
        }
        fast = fast->next;
    }

    while(fast) {
        fast = fast->next;
        slow = slow->next;
    }
    
    return slow;
}

3、链表的反转

链表的反转，我们又怎么去做呢，还记得头插法吗？我们也采用这个方法进行反转，那如何实现呢，先将我们的哑节点断开，也就是dummy->next = NULL即可，然后每次断一个节点，通过头插法在插到dummy的后面，就可以实现反转了。

cpp 复制代码

int ReverseLinkList(ListNode *dummy) {
    if(!dummy->next) return -1;
    ListNode *cur = NULL;
    ListNode *next = NULL;
    cur = next = dummy->next;
    
    dummy->next = NULL;
    while(next) {
        next = next->next;
        cur->next = dummy->next;
        dummy->next = cur;
        cur = next;
    }
    
    return 0;
}

4、链表的排序

4.1 冒泡排序

冒泡排序大家还记得吗？我们如果用链表又怎么去做呢，该怎么去操作呢，先给大家画个图吧。

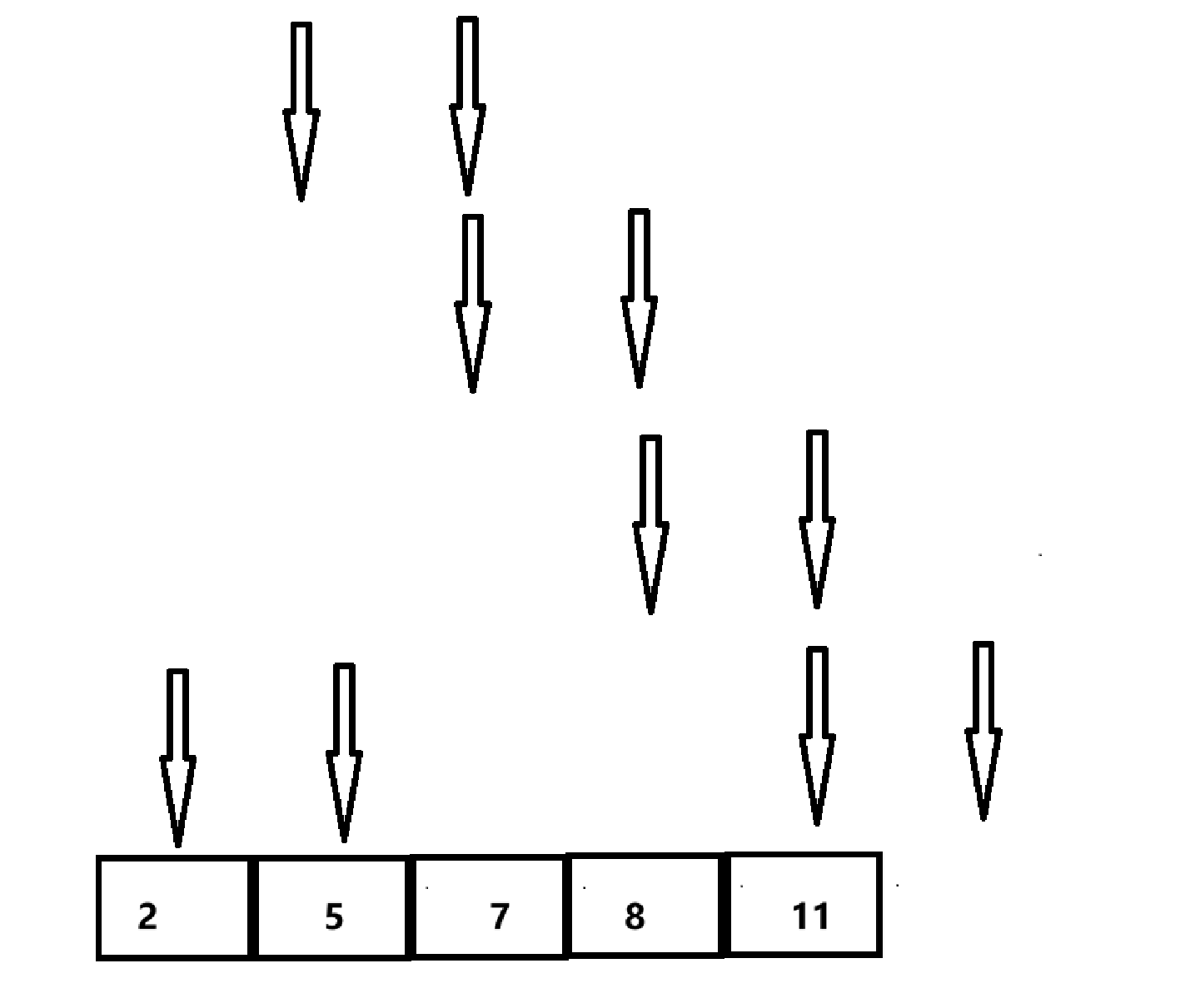
从上图可以看到什么规律吗？定义两个指针，每次遍历完，末指针的结束位置是不是上一次遍历的前指针的位置呢，外循环结束的条件呢，是不是也是后一个指针不等于上一次前指针的位置呢，还有内循环没遍历一次，就得将两个指针指回最开始的位置，那我们开始编码吧：

cpp 复制代码

int BubbleSortLinkList(ListNode *dummy) {
    if(!dummy->next || !dummy->next->next) return 0;
    
    ListNode *tmpNode1 = dummy->next;
    ListNode *tmpNode2 = dummy->next->next;
    ListNode *endNode = NULL;
    
    while(tmpNode2 != endNode) {
        while(tmpNode2 != endNode) {
            if(tmpNode1->val > tmpNode2->val) {
                DataType tmp_val = tmpNode1->val;
                tmpNode1->val = tmpNode2->val;
                tmpNode2->val = tmp_val;
            }
            tmpNode1 = tmpNode1->next;
            tmpNode2 = tmpNode2->next;
        }
        endNode = tmpNode1;
        tmpNode1 = dummy->next;
        tmpNode2 = dummy->next->next;
    }
    
    return 0;
}

4.2 选择排序

学习完冒泡排序，我们在来学学选择排序，同样的需要三个指针进行遍历，那该怎么做呢，还是看看图吧：

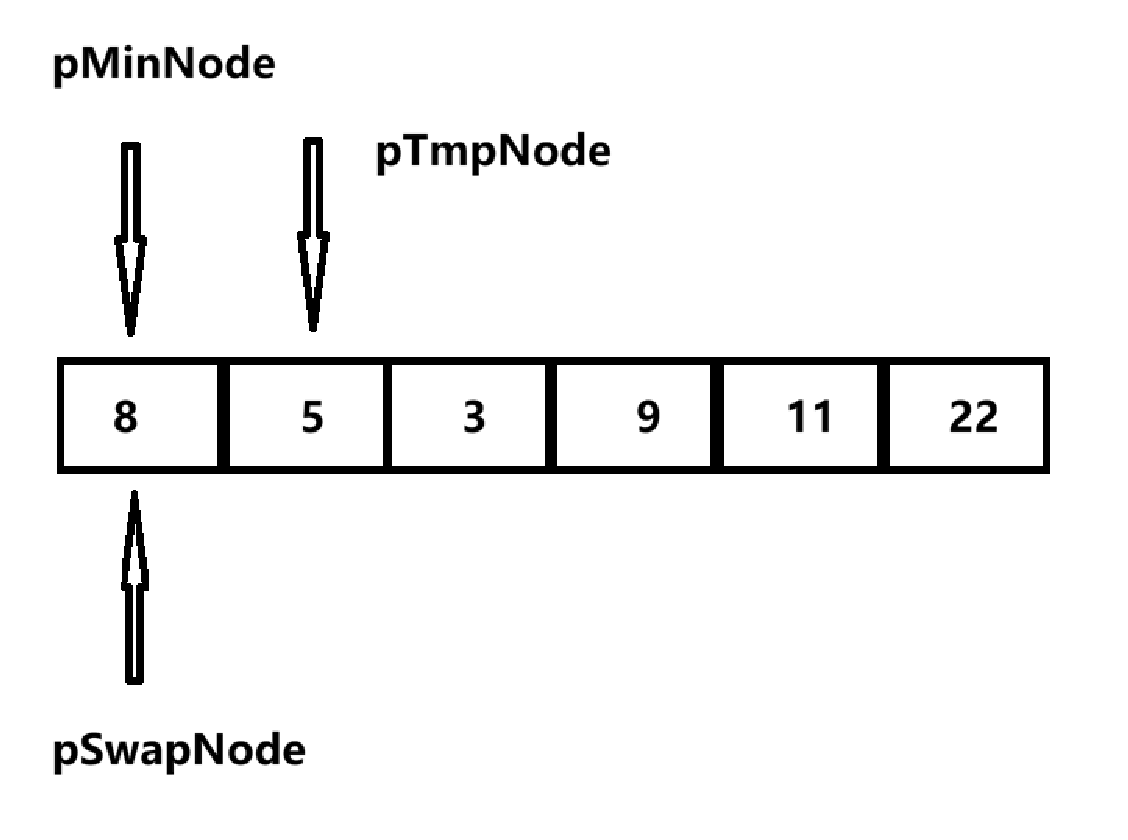
每次我们通过一个指针定义需要交换的节点，然后初始定义最小值也为它，然后在定义一个指针，从它的后面开始遍历，每次如果比初始还小，就把最小值的节点指向新的小的节点，遍历一次后，判断需要交换的节点和最小值的节点是否相同，相同则不需要改，不同则交换两节点的值，然后向后移动，继续下次遍历。

cpp 复制代码

int SelectSortLinkList(LinstNode *dummy) {
    if(!dummy->next || !dummy->next->next) {
        return 0;
    }
    
    ListNode *swapNode = dummy->next;
    ListNode *tmpNode = NULL;
    ListNode *minNode = NULL;
    
    while(swap->next) {
        minNode = swapNode;
        tmpNode = swapNode->next;
        while(tmpNode) {
            if(tmpNode->val < minNode_val) {
                minNode = tmpNode;
            }
            tmpNode = tmpNode->next;
        }
        if(swapNode != mi}nNode) {
            DataType tmp_val = swapNode->val;
            swapNode->val = minNode->val;
            minNode->val = tmp_val;
        }
        swapNode = swapNode->next;
    }
    
    return 0;
}

5、判断链表是否有环

对于这个题目，我们依旧可以用快慢指针，也就是说快指针每次走两步，慢指针每次走一步，如果有环它们将会相遇，那是为什么呢，想像一下，如果是在环形操场跑步，一直跑的两个人，是不是总会有快的人会与慢的人相遇，不管它们差多少，总会在某一刻相遇，对于这道题目而言，也是一样的。

那么如果有环，那环长又怎么去算呢，是不是可以从相遇的点开始，走一圈就会回到这个点，很好理解对吧，那最后入环的起点又怎么去求呢，我们来推到一下吧：

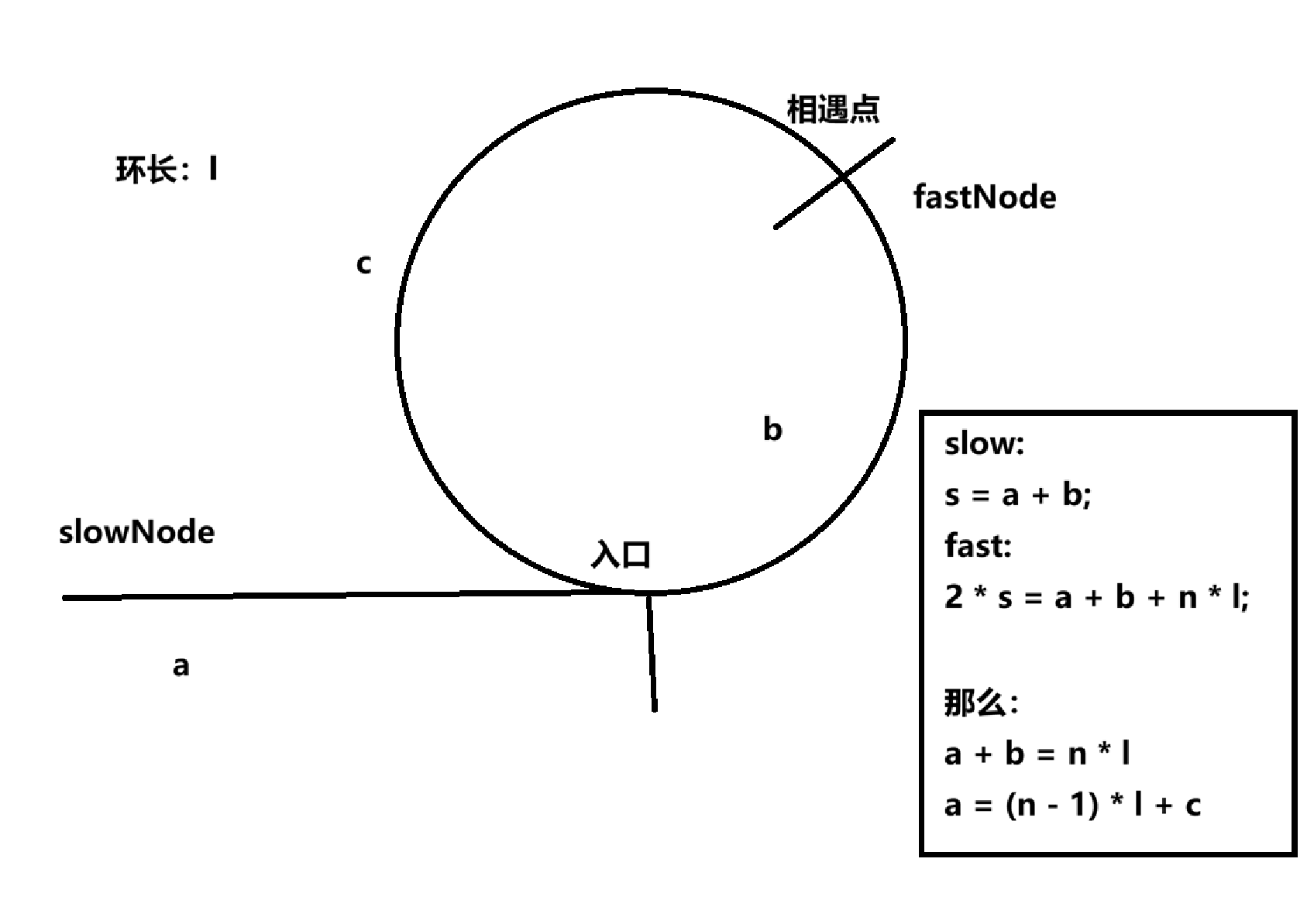
通过推到我们可以看到a和c的关系，那推导这个有什么用呢，这个就可以让我们知道入口点在哪里，因为定义两个指针，一个从起点，一个从相遇点，以相同的速度一起走，总会在入口相遇，假设这个n = 1,是不是就好理解了，此时： a = c，两者的路程就是一样的，是不是就会相遇在此呢。

那我们就开始编写代码吧：

cpp 复制代码

int FloydCycle(ListNode *dummy, int *pLen, ListNode **firstCycleNode) {
    if(!dummy->next) return 0;
    
    ListNode *slow = dummy->next;
    ListNode *fast = dummy->next;
    
    int isCycle = 0;
    
    while(fast && fast->next) {
        slow = slow->next;
        fast = fast->next->next;
        if(slow == fast) {
            isCycle = 1;
            break;
        }
    }
    
    if(!isCycle) return 0;
    
    int len = 0;
    slow = slow->next;
    len++;
    while(slow != fast) {
        slow = slow->next;
        len++;
    }
    
    *pLen = len;
    slow = dummy->next;
    while(slow != fast) {
        slow = slow->next;
        fast = fast->next;
    }
    *firstCycleNode = fast;
    
    return 1;
}

这种解法就是经典的龟兔赛跑算法，也叫做Floyd判圈算法，你们可以自己动手来试试。

好了，到此，单向链表的内容就到这里结束了，下次我们将开始学习双向链表，和单向链表有一点点区别。敬请期待！！！