
| 🔭 个人主页: 散峰而望 |
|---|
《C语言:从基础到进阶》《编程工具的下载和使用》《C语言刷题》《算法竞赛从入门到获奖》《人工智能》《AI Agent》
愿为出海月,不做归山云
🎬博主简介



【基础算法】算法的"预谋":前缀和如何改变游戏规则
- 前言
- 前缀和
-
- [1.1 一维前缀和](#1.1 一维前缀和)
-
- [1.1.1 前缀和](#1.1.1 前缀和)
- [1.1.2 最大子段和](#1.1.2 最大子段和)
- [1.2 二维前缀和](#1.2 二维前缀和)
-
- [1.2.1 二维前缀和](#1.2.1 二维前缀和)
- [1.2.2 激光炸弹](#1.2.2 激光炸弹)
- 结语
前言
在算法设计与优化中,前缀和是一种简单却强大的技巧,能够将复杂问题转化为高效计算。无论是处理一维数组的区间求和,还是解决二维矩阵的子矩阵问题,前缀和都能通过预处理将时间复杂度从线性降低到常数级别,彻底改变问题的解决方式。
从经典的最大子段和问题到实际应用中的"激光炸弹"场景,前缀和不仅展现了数学的优雅,更体现了算法思维的灵活性。本文将深入探讨一维和二维前缀和的原理与应用,揭示其如何通过"预谋"式的预处理,在竞赛与工程中成为改变游戏规则的关键。
前缀和
前缀和与差分的核心思想是预处理,可以在暴力枚举的过程中,快速给出查询的结果,从而优化时间复杂度。
是经典的用空间替换时间的做法。
前缀和: 快速求出数组中某一段区间和,时间复杂度为 O(1)。
1.1 一维前缀和
1.1.1 前缀和
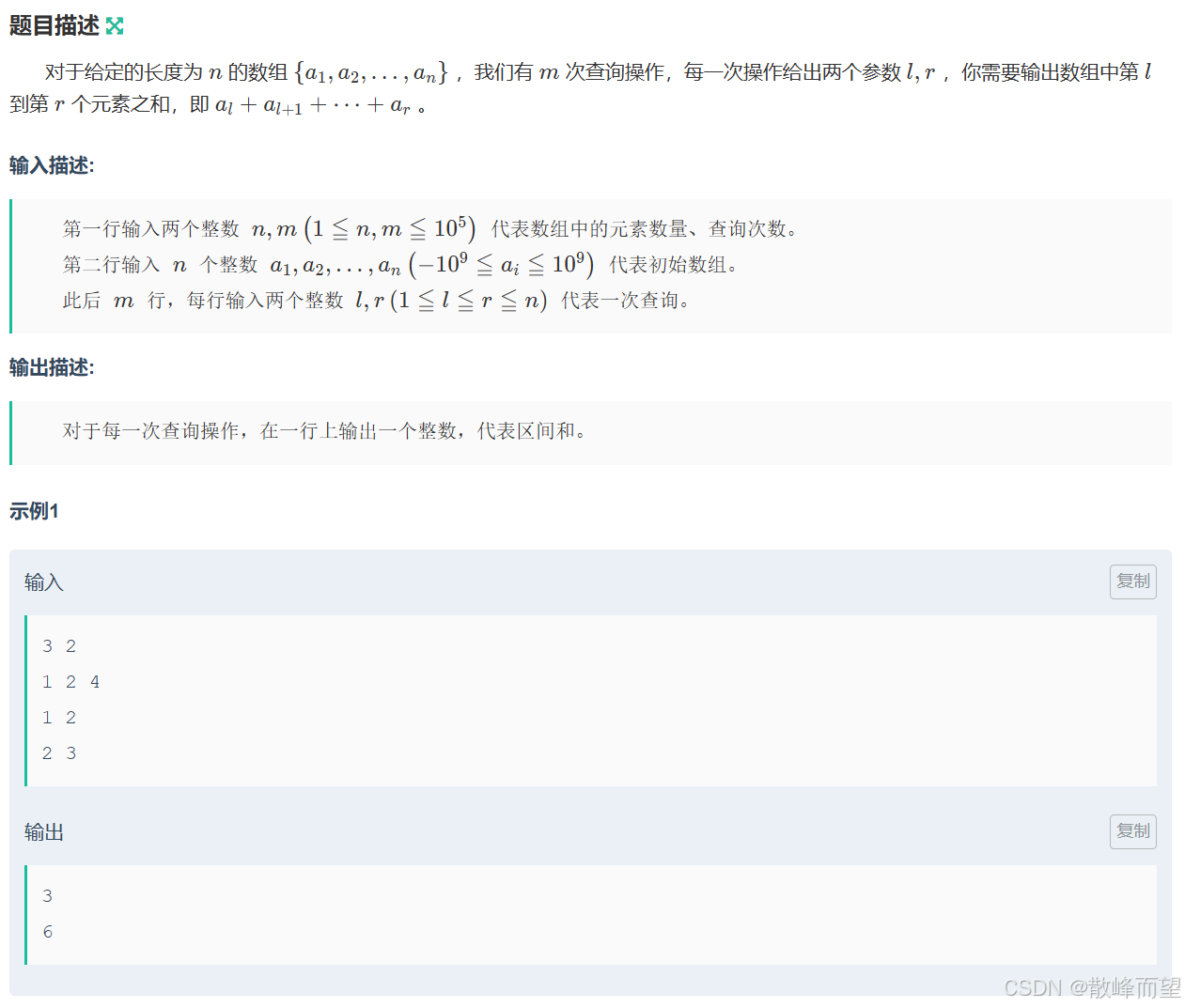
算法原理:
- 暴力模拟实现,从指定的下标进行循环,时间复杂度为 O(n * q) 会超时
- 前缀和:
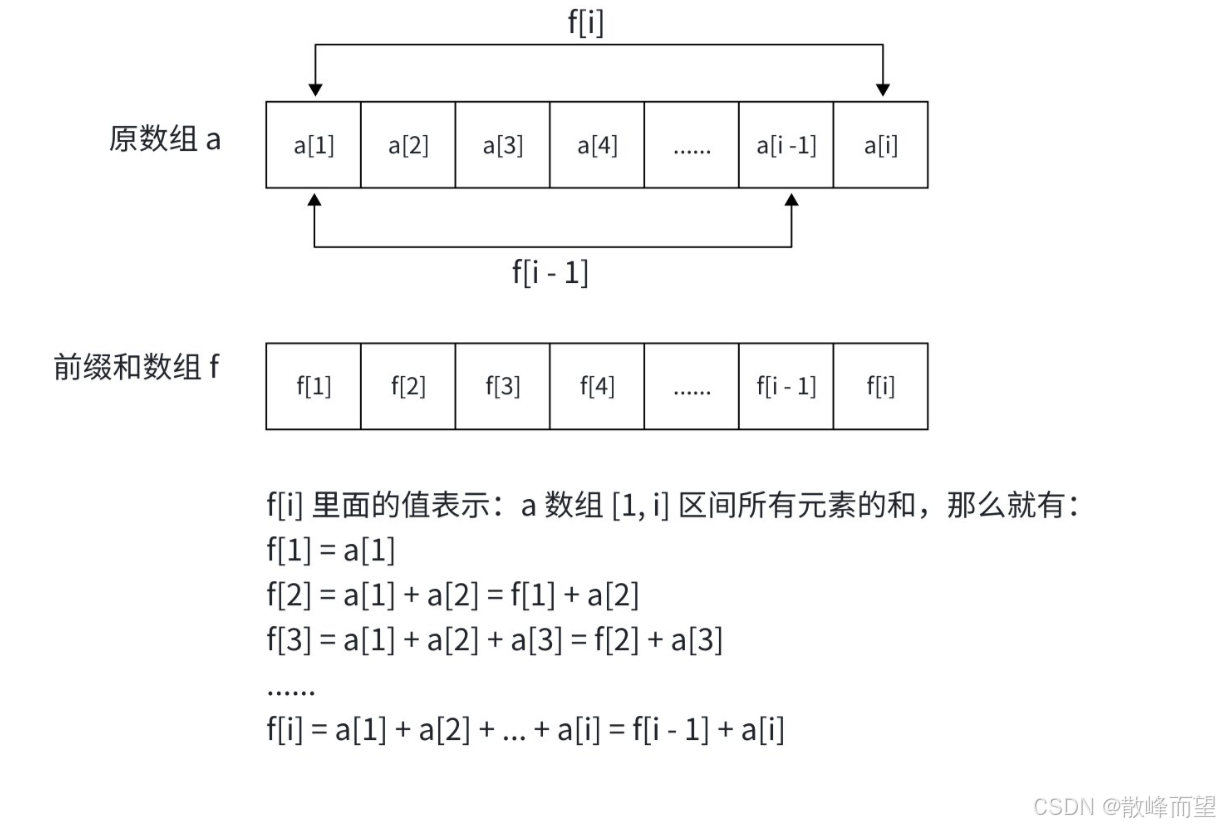
a. 先预处理出来一个前缀和数组
f[i] 表示:区间 [1, i] 中所有元素和
则f[i] = f[i - 1] + a[i]
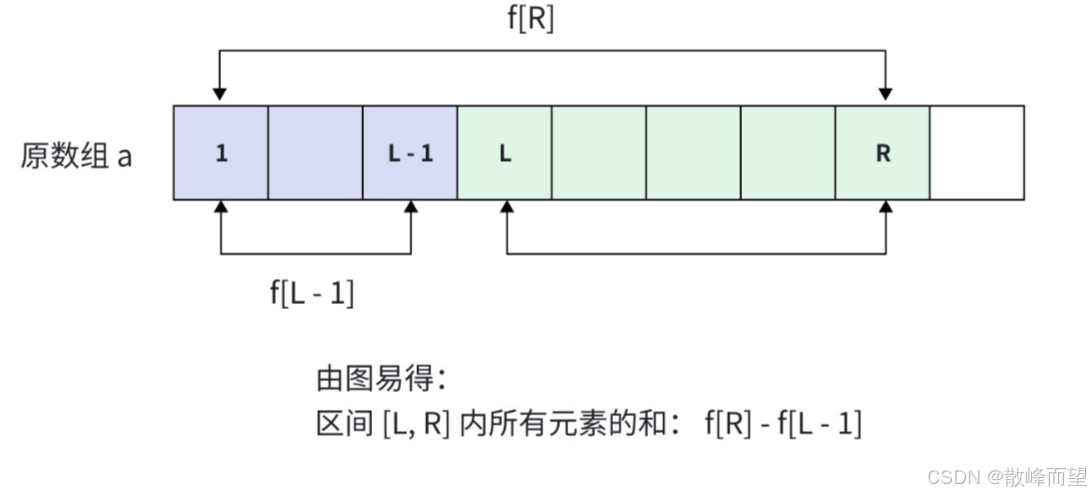
b. 查询 [l, r] 区间和,则f[r] - f[l - 1]
参考代码:
cpp
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
typedef long long LL;
int n, q;
LL a[N];
LL f[N];//前缀和数组
int main()
{
cin >> n >> q;
for(int i = 1; i <= n; i++) cin >> a[i];
//处理前缀和
for(int i = 1; i <= n; i++)
{
f[i] = f[i - 1] + a[i];
}
//处理q次询问
while(q--)
{
int l, r; cin >> l >> r;
cout << f[r] - f[l - 1] << endl;
}
return 0;
} 1.1.2 最大子段和
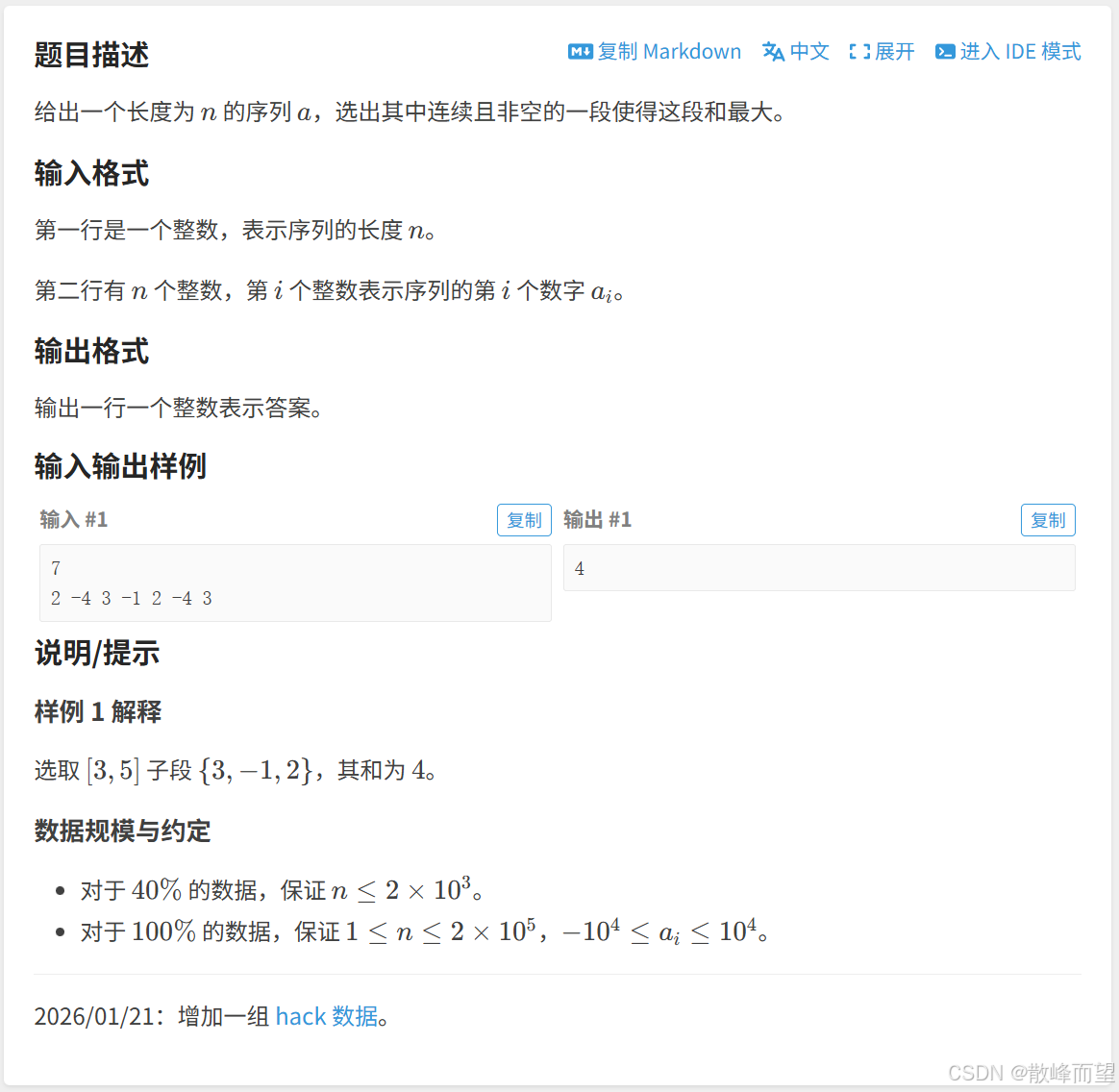
算法竞赛:
关于这道题的解法有很多种,我们先介绍利用「前缀和」的解法。
考虑以 i 位置的元素 a[i]「为结尾」的最大子段和:
- 在求「区间和」时,相当于是用 f[i] 减去 i 位置前面的某一个 f[x]
- 如果想要「最大子段和」,也就是「最大区间和」,那么用 f[i] 减去一个「前驱最小值」即可
参考代码:
cpp
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 2e5 + 10;
int n;
LL f[N];//前缀和数组
int main()
{
cin >> n;
for(int i = 1; i <= n; i++)
{
LL x; cin >> x;
f[i] = f[i - 1] + x;
}
LL ret = -1e20;
LL prevmin = 0;
for(int i = 1; i <= n; i++)
{
ret = max(ret, f[i] - prevmin);
prevmin = min(prevmin, f[i]);
}
cout << ret << endl;
} 1.2 二维前缀和
1.2.1 二维前缀和
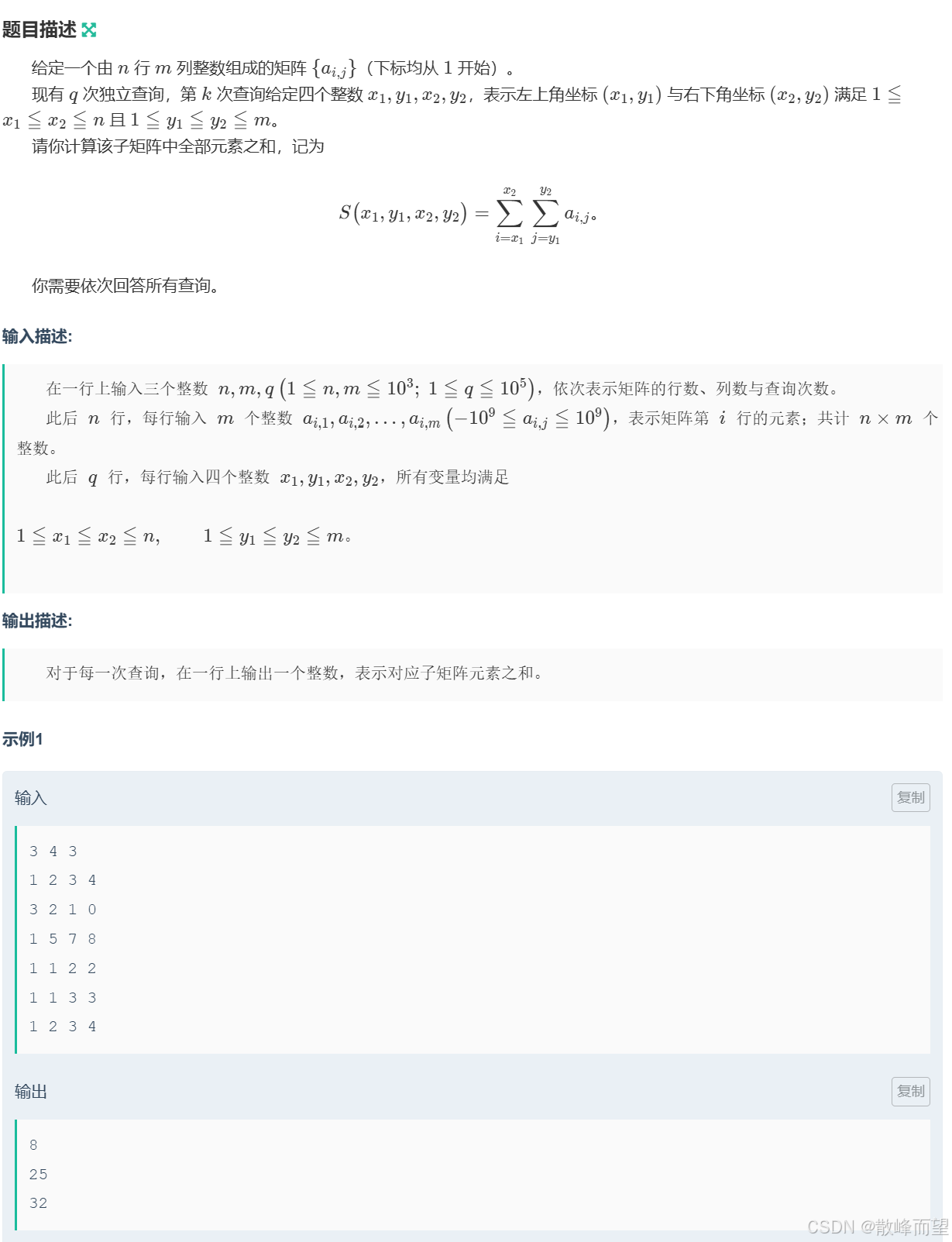
根据题目要求,我们知道题目的求和情况如下:

算法原理:
- 暴力模拟
查询哪个子区间,用两层 for 循环,累加。时间复杂度高 O(q * n * m) - 二维前缀和
快速查询二维数组中的某个子矩阵所有元素和,时间复杂度 O(n * m) + O(q)
a.预处理出二维前缀和矩阵 f[i][j] 表示从 [1, 1] 到 [i, j] 区域内所有的元素和。
b.用二维前缀和的矩阵解决问题。
- 创建前缀和矩阵:
f[i][j]=f[i−1][j]+f[i][j−1]−f[i−1][j−1]+a[i][j]
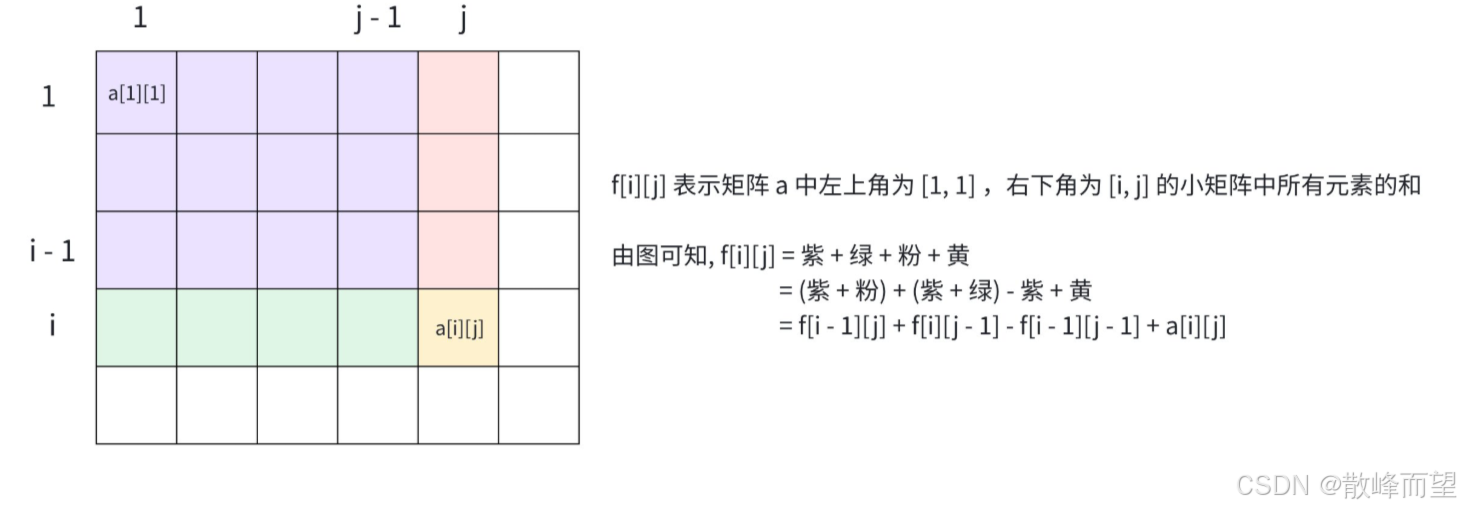
- 查询以 (x1, y1) 为左上角 (x2, y2) 为右下角的子矩阵的和
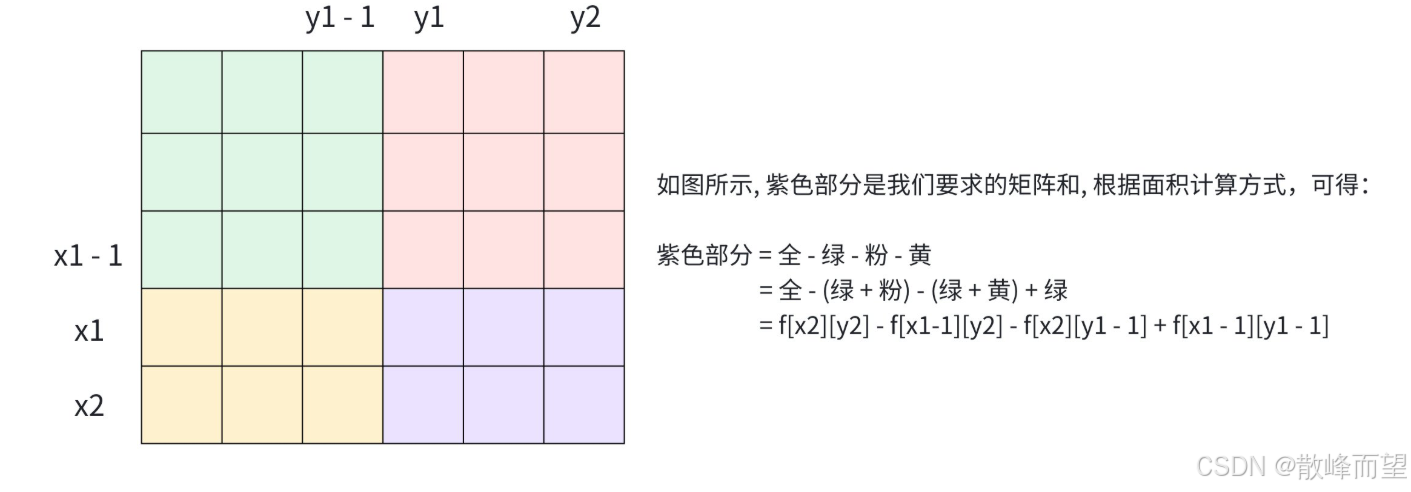
cpp
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 1010;
int n, m, q;
LL f[N][N];
int main()
{
cin >> n >> m >> q;
//预处理前缀和矩阵
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
LL x; cin >> x;
f[i][j] = f[i -1][j] + f[i][j - 1] - f[i - 1][j - 1] + x;
}
}
//处理q查询
while(q--)
{
int x1, y1, x2, y2; cin >> x1 >> y1 >> x2 >> y2;
cout << f[x2][y2] - f[x1 - 1][y2] - f[x2][y1 - 1] + f[x1 - 1][y1 - 1] << endl;
}
return 0;
} 1.2.2 激光炸弹
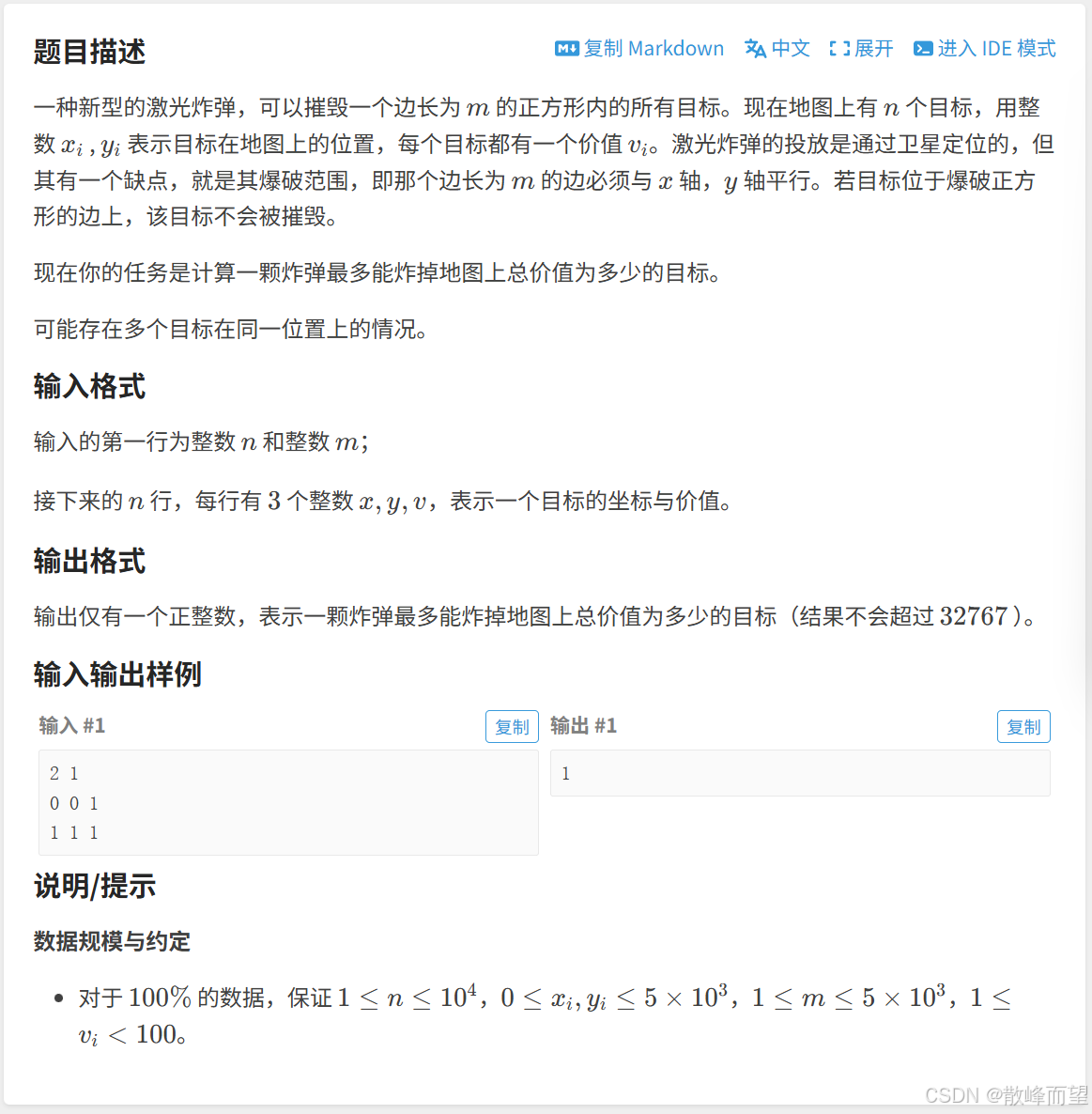
因为题目要求若目标位于爆破正方形的边上,该目标不会被摧毁,则以下这些情况炸弹威力会减弱
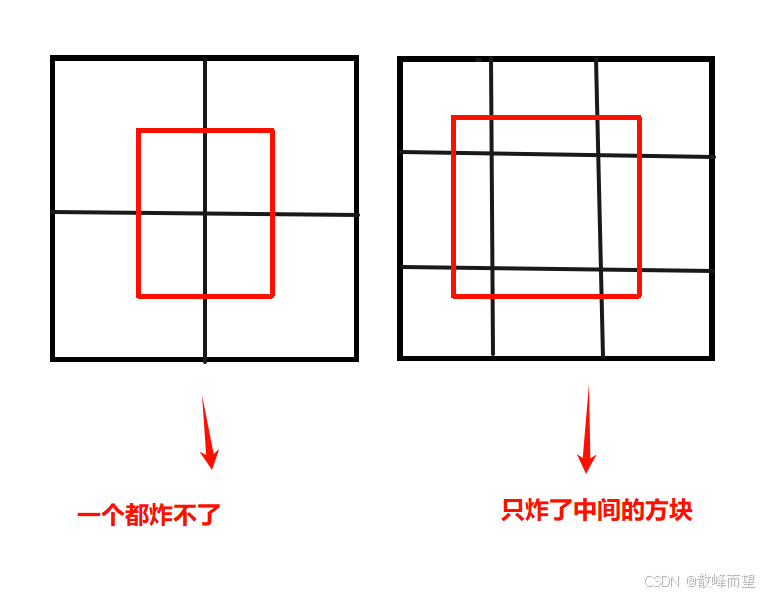
即如果想尽可能炸更多目标,炸弹边和矩阵边重叠。
算法原理:
暴力枚举坐标系中所有边长为 R 的正方形,找出正方形内目标价值最大的目标即可。
枚举右下角 [x2, y2] 从而得到整个正方形,用一个二维矩阵将所有目标的价值存起来,其中 a[i][j] 就表示 [i, j] 位置的目标价值之和。
cpp
#include <iostream>
using namespace std;
const int N = 5010;
int n, m;
int a[N][N];
int f[N][N];//前缀和
int main()
{
cin >> n >> m;
while(n--)
{
int x, y, v; cin >> x >> y >> v;
x++, y++;//下标从1开始
a[x][y] += v;//同一个位置可能有多个目标
}
//预处理
n = 5001;
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= n; j++)
{
f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + a[i][j];
}
}
int ret = 0;
m = min(m, n); // 如果 m 很大,相当于就是把整个区域全部摧毁
// 枚举所有边?为 m 的正方形
for(int x2 = m; x2 <= n; x2++)
{
for(int y2 = m; y2 <= n; y2++)
{
int x1 = x2 - m + 1, y1 = y2 - m + 1;
ret = max(ret, f[x2][y2] - f[x1 - 1][y2] - f[x2][y1 - 1] + f[x1 - 1][y1 - 1]);
}
}
cout << ret << endl;
return 0;
} 结语
前缀和作为一种基础而强大的算法技巧,通过预处理数据将复杂度从线性降至常数级别,彻底改变了处理区间问题的游戏规则。从一维数组的快速求和、最大子段和优化,到二维矩阵的区域统计、激光炸弹效果模拟,前缀和以空间换时间的策略展现了极高的效率。
掌握前缀和不仅能够解决经典问题,更能为复杂场景(如动态规划、数据结构优化)提供关键思路。其思想可以延伸到更高维度的数据处理中,成为算法设计中不可或缺的"预谋"手段。理解并灵活运用前缀和,是提升算法问题解决能力的重要一步。
愿诸君能一起共渡重重浪,终见缛彩遥分地,繁光远缀天。
