文章目录
-
-
- 一、机器学习的基本流程(3个步骤)
- 二、数据集的概念与划分
-
- [2.1 数据集划分](#2.1 数据集划分)
- [2.2 开发集(验证集)](#2.2 开发集(验证集))
- 三、过拟合与泛化能力
-
- [3.1 核心概念](#3.1 核心概念)
- [3.2 为什么会过拟合?](#3.2 为什么会过拟合?)
- 四、问题设定:线性回归问题
-
- [4.1 问题描述](#4.1 问题描述)
- [4.2 机器学习的过程](#4.2 机器学习的过程)
- 五、线性模型的设定
-
- [5.1 模型选择](#5.1 模型选择)
- [5.2 简化模型(本讲使用)](#5.2 简化模型(本讲使用))
- [六、损失函数(Loss Function)](#六、损失函数(Loss Function))
-
- [6.1 为什么需要损失函数?](#6.1 为什么需要损失函数?)
- [6.2 损失函数的定义](#6.2 损失函数的定义)
- [6.3 均方误差(MSE)](#6.3 均方误差(MSE))
- [6.4 具体计算示例](#6.4 具体计算示例)
- 七、穷举法找最优权重
-
- [7.1 穷举法的思路](#7.1 穷举法的思路)
- [7.2 损失曲线](#7.2 损失曲线)
- 八、完整线性模型代码详解(含w和b两个参数)
- 九、可视化与训练监控
-
- [9.1 为什么要可视化?](#9.1 为什么要可视化?)
- [9.2 常见的可视化方式](#9.2 常见的可视化方式)
- [9.3 重要的观察指标](#9.3 重要的观察指标)
- [9.4 断点续训](#9.4 断点续训)
- 十、本讲核心要点总结
-
一、机器学习的基本流程(3个步骤)
刘二大人开篇就介绍了做机器学习的三个核心步骤:
| 步骤 | 内容 | 说明 |
|---|---|---|
| 第1步 | 准备数据集 | 收集、整理数据 |
| 第2步 | 模型选择/设计 | 选择浅层模型还是复杂模型(神经网络、决策树、朴素贝叶斯等),根据数据集情况决定 |
| 第3步 | 训练(Training) | 确定模型权重,大部分模型都需要训练 |
关于训练的特殊说明:
- 大部分模型都需要训练(Training)
- 少数模型如 KNN(K近邻) 不需要训练,只是把数据存起来,有新数据时找特征值最接近的样本决定类别
- 训练完成后,模型权重确定,就可以进行推理(Inference)------用新数据进行预测
二、数据集的概念与划分
2.1 数据集划分
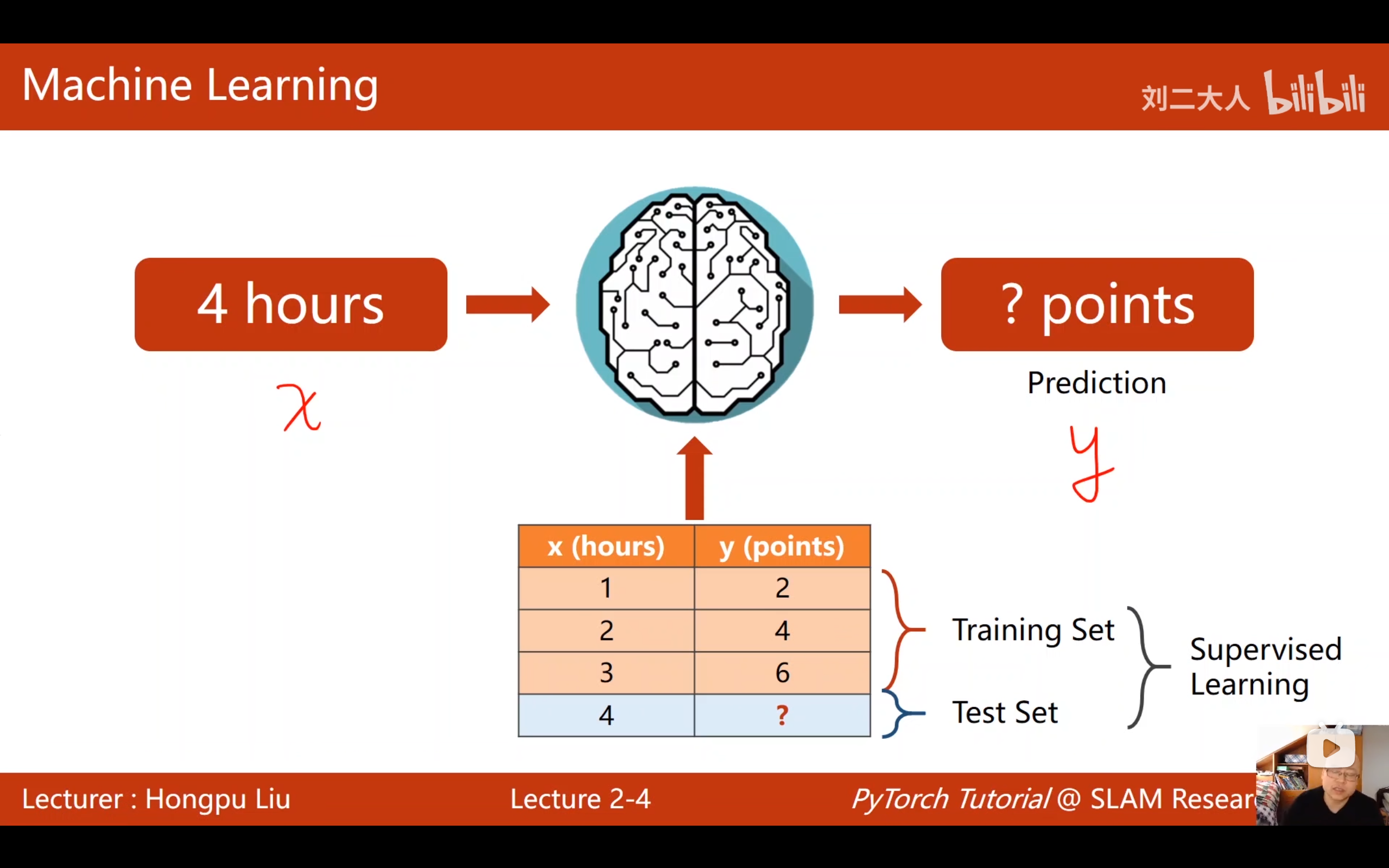
在实际应用中,数据集通常要分成两部分:
| 数据集类型 | 英文 | 用途 | 是否能看到y值 |
|---|---|---|---|
| 训练集 | Training Set | 用来训练模型 | ✅ 能看到x和y |
| 测试集 | Test Set | 训练好后测试模型性能 | ❌ 通常只能看到x |
关键原则: 训练过程中绝对不能偷看测试集 ,否则无法真实评估模型的泛化能力。
2.2 开发集(验证集)
问题: 如果测试集看不到y,怎么在训练时评估模型好坏?
解决方案: 把训练集再分成两份:
- 一部分用来训练
- 另一部分用来评估 (称为开发集/验证集)
如果开发集评估效果好,最后再把全部训练集数据扔进模型训练一次,然后面对测试集。
三、过拟合与泛化能力
3.1 核心概念
| 概念 | 定义 |
|---|---|
| 过拟合(Overfitting) | 模型在训练集上表现极好,但没见过的新数据上表现差 |
| 泛化能力(Generalization) | 模型对没见过的数据也能正确识别的能力 |
3.2 为什么会过拟合?
原因1:训练集无法完全代表真实分布
- 根据概率论,要用采样方法接近真实分布,需要满足大数定律(样本量足够多)
- 但现实中由于"维度诅咒",数据量再大也很难精确表示真实分布
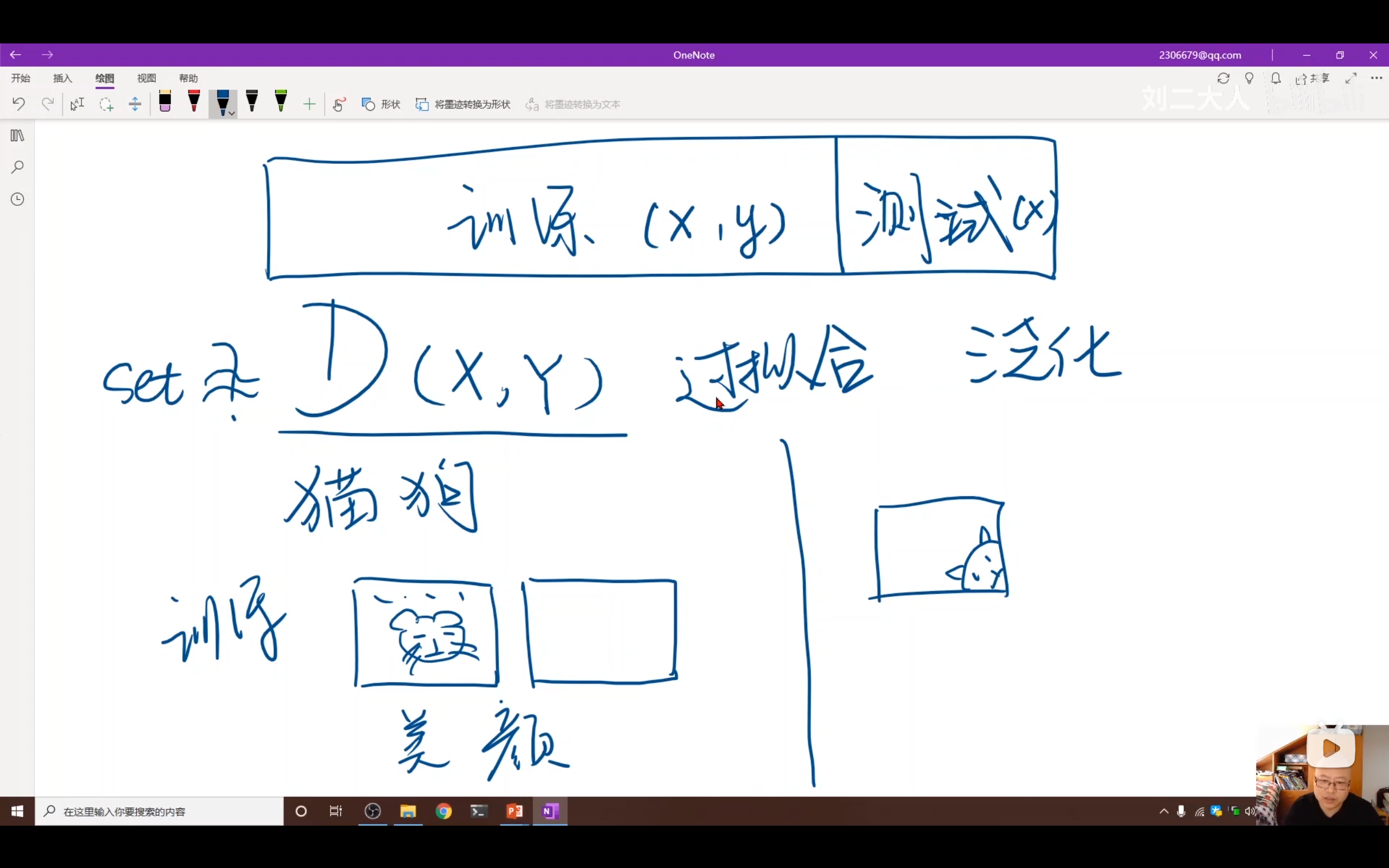
原因2:训练集与真实场景分布不一致(举例说明)
刘二大人举了一个猫狗识别的例子:
- 训练集:艺术照片、美颜过的漂亮图片,动物脸都在图像中间
- 真实场景:用户随手一拍,动物脸可能在任意位置
如果只在训练集上训练,模型可能只学会了"识别图像中间的动物",上线后性能会很差。
结论: 要让模型上线后表现好,训练集必须尽可能与真实场景的数据分布一致。
四、问题设定:线性回归问题
4.1 问题描述
场景: 预测学生期末考试成绩
| 每周学习时长(x) | 期末成绩(y) |
|---|---|
| 1小时 | 2分 |
| 2小时 | 4分 |
| 3小时 | 6分 |
目标: 给定一个新的学习时长x,预测期末成绩y
4.2 机器学习的过程
数据集(x,y) → 交给算法训练 → 获得新输入x → 模型计算出预测结果ŷ注意符号:
- x:输入特征(学习时长)
- y:真实输出(实际成绩)
- ŷ(y hat):模型预测的值
五、线性模型的设定
5.1 模型选择
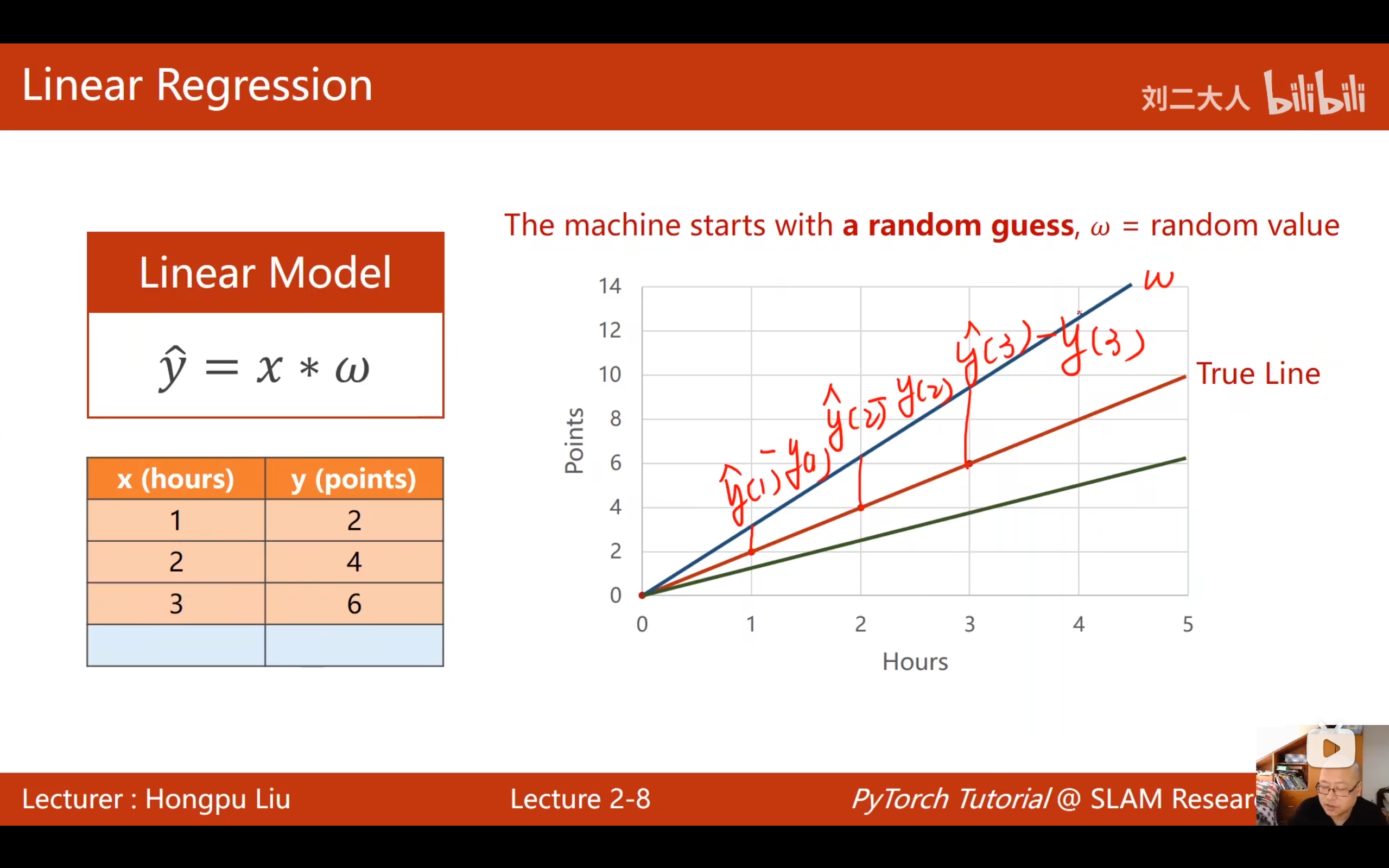
最简单的模型选择是线性模型:
ŷ = wx + b- w:权重(weight)
- b:偏置/截距(bias)
5.2 简化模型(本讲使用)
为了简化问题,先去掉截距b,模型变为:
ŷ = wx问题转化为: 找到最优的权重w,使得模型预测ŷ与真实值y尽可能接近。
六、损失函数(Loss Function)
6.1 为什么需要损失函数?
随机猜测一个w值,不一定正好是最优值。需要一种方法来评估 当前w的好坏------即模型预测与真实数据之间的误差有多大。
6.2 损失函数的定义
对于单个样本:
loss = (ŷ - y)² = (wx - y)²为什么用平方?
- 误差可能是正的也可能是负的
- 平方可以消除符号影响,只关心误差大小
6.3 均方误差(MSE)
对于整个训练集(n个样本),计算平均损失:
cost = (1/n) * Σ(ŷᵢ - yᵢ)² = (1/n) * Σ(wxᵢ - yᵢ)²这个函数叫做 MSE(Mean Squared Error,均方误差),是深度学习中最常用的损失函数之一。
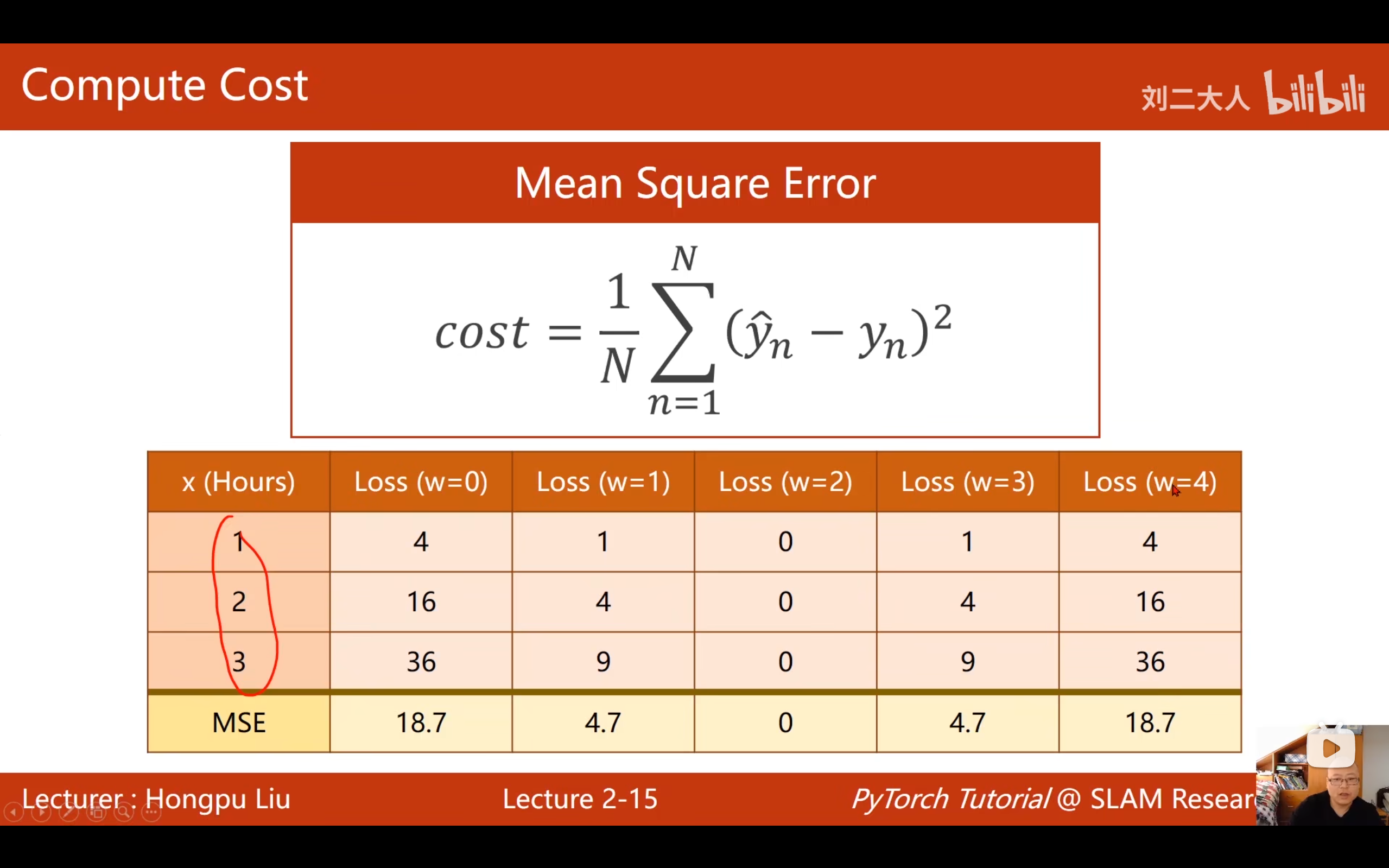
6.4 具体计算示例
数据集: (1,2), (2,4), (3,6)
当w=3时:
| x | y | ŷ=3x | 误差(ŷ-y) | 平方误差 |
|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 1 |
| 2 | 4 | 6 | 2 | 4 |
| 3 | 6 | 9 | 3 | 9 |
| 总和 | 14 | |||
| 平均(MSE) | 14/3 ≈ 4.67 |
当w=4时:
| x | y | ŷ=4x | 误差 | 平方 |
|---|---|---|---|---|
| 1 | 2 | 4 | 2 | 4 |
| 2 | 4 | 8 | 4 | 16 |
| 3 | 6 | 12 | 6 | 36 |
| 平均MSE | 56/3 ≈ 18.67 |
当w=2时:
| x | y | ŷ=2x | 误差 | 平方 |
|---|---|---|---|---|
| 1 | 2 | 2 | 0 | 0 |
| 2 | 4 | 4 | 0 | 0 |
| 3 | 6 | 6 | 0 | 0 |
| 平均MSE | 0 |
结论: w=2时,MSE=0,是最优解。
七、穷举法找最优权重
7.1 穷举法的思路
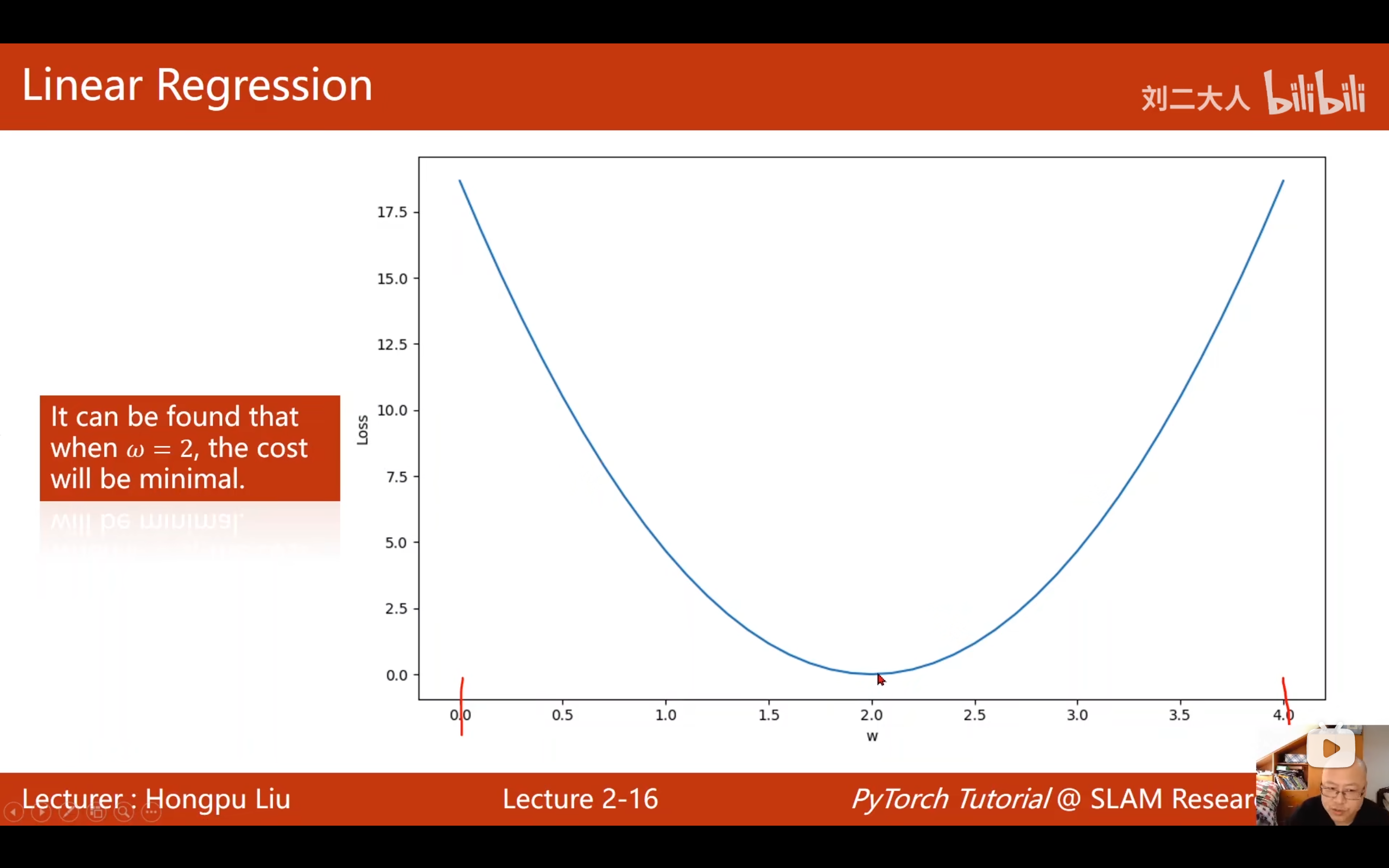
假设权重w在04之间存在最优值,把04之间所有可能的取值都计算一遍损失,然后找最低点。
注意: 实数域有无穷多个值,实际只能进行采样(如每隔0.1取一个值)。
7.2 损失曲线
将不同w值对应的MSE画成曲线:
- w=0时,MSE=56/3
- w=1时,MSE=14/3
- w=2时,MSE=0(最低点)
- w=3时,MSE=14/3
- w=4时,MSE=56/3
曲线呈抛物线形状,最低点在w=2处。
八、完整线性模型代码详解(含w和b两个参数)
这是本讲作业的实现代码,同时学习w和b两个参数,并绘制三维损失曲面。

python
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
x_data = [1.0, 2.0, 3.0]
y_data = [3.0, 4.0, 6.0]
def forward(x, w, b):
return x * w + b
def loss(x, y, w, b):
y_pred = forward(x, w, b)
loss = (y_pred - y) ** 2
return loss
w_list = np.arange(0.0, 4.1, 0.1)
b_list = np.arange(-2.0, 2.1, 0.1)
# mse_matrix用于存储不同 w,b 组合下的均方误差损失
mse_matrix = np.zeros((len(w_list), len(b_list)))
for i, w in enumerate(w_list):
for j, b in enumerate(b_list):
l_sum = 0
for x_val, y_val in zip(x_data, y_data):
l_sum += loss(x_val, y_val, w, b)
mse_matrix[i, j]= l_sum/len(x_data)
W, B = np.meshgrid(w_list, b_list)
fig = plt.figure('Linear Model Cost Value')
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(W, B, mse_matrix.T, cmap='viridis')
ax.set_xlabel('w')
ax.set_ylabel('b')
ax.set_zlabel('loss')
plt.show()8.1 导入库
python
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D| 库 | 作用 |
|---|---|
numpy |
数值计算,提供数组操作和数学函数 |
matplotlib.pyplot |
绘图库,用于绘制2D/3D图形 |
mpl_toolkits.mplot3d.Axes3D |
专门用于绘制3D图形的工具包 |
8.2 准备数据
python
x_data = [1.0, 2.0, 3.0] # 输入特征:每周学习时长
y_data = [3.0, 4.0, 6.0] # 输出标签:期末成绩注意: 这里的y_data和视频中不同:
- 视频原版 :
[2.0, 4.0, 6.0]→ 严格满足 y = 2x,不需要b - 本版本 :
[3.0, 4.0, 6.0]→ 不是严格的y=2x,需要同时学习w和b两个参数
验证:
- 如果只用w=2,预测值是[2, 4, 6],与真实值[3, 4, 6]有误差
- 需要用w和b配合才能拟合更好
8.3 定义模型(前向传播)
python
def forward(x, w, b):
return x * w + b| 参数 | 含义 |
|---|---|
x |
输入特征(学习时长) |
w |
权重(weight) |
b |
偏置/截距(bias) |
功能: 计算预测值 ŷ = wx + b
与视频的区别: 视频中的简化版是 return x * w(没有b),这里是完整版。
8.4 定义损失函数
python
def loss(x, y, w, b):
y_pred = forward(x, w, b) # 调用forward计算预测值ŷ
loss = (y_pred - y) ** 2 # 计算平方误差
return loss| 参数 | 含义 |
|---|---|
x |
输入特征 |
y |
真实标签 |
w, b |
模型参数 |
返回: 单个样本的平方误差 (ŷ - y)²
8.5 定义搜索范围
python
w_list = np.arange(0.0, 4.1, 0.1) # w从0到4,步长0.1,共41个值
b_list = np.arange(-2.0, 2.1, 0.1) # b从-2到2,步长0.1,共41个值np.arange(start, stop, step) 详解:
| 参数 | 说明 |
|---|---|
start |
起始值(包含) |
stop |
结束值(不包含,所以写4.1才能包含4.0) |
step |
步长 |
结果:
w_list= [0.0, 0.1, 0.2, ..., 4.0] 共41个值b_list= [-2.0, -1.9, -1.8, ..., 2.0] 共41个值
8.6 创建存储矩阵
python
# mse_matrix用于存储不同 w,b 组合下的均方误差损失
mse_matrix = np.zeros((len(w_list), len(b_list)))作用: 创建一个 41×41 的零矩阵,用于存储每种 (w, b) 组合对应的MSE值。
矩阵结构:
- 行数 = w的取值个数(41)
- 列数 = b的取值个数(41)
mse_matrix[i, j]= 第i个w值、第j个b值对应的MSE
8.7 核心计算------穷举所有组合
python
for i, w in enumerate(w_list): # 遍历所有w值,i是索引,w是值
for j, b in enumerate(b_list): # 遍历所有b值,j是索引,b是值
l_sum = 0 # 累计损失,每次新组合要清零
for x_val, y_val in zip(x_data, y_data): # 遍历所有训练样本
l_sum += loss(x_val, y_val, w, b) # 累加每个样本的损失
mse_matrix[i, j] = l_sum / len(x_data) # 计算平均损失,存入矩阵三层循环详解:
| 循环层 | 作用 |
|---|---|
外层 for i, w in enumerate(w_list) |
遍历41个w值 |
中层 for j, b in enumerate(b_list) |
遍历41个b值 |
内层 for x_val, y_val in zip(x_data, y_data) |
遍历3个训练样本 |
enumerate() 函数: 同时返回索引和值
i= 0, 1, 2, ..., 40(w的索引)w= 0.0, 0.1, 0.2, ..., 4.0(w的具体值)
zip(x_data, y_data) 函数: 将两个列表配对
- 第1次:(1.0, 3.0)
- 第2次:(2.0, 4.0)
- 第3次:(3.0, 6.0)
计算流程示例(w=1.0, b=1.0时):
| x | y | ŷ=1·x+1 | 损失(ŷ-y)² |
|---|---|---|---|
| 1.0 | 3.0 | 2.0 | (2-3)² = 1 |
| 2.0 | 4.0 | 3.0 | (3-4)² = 1 |
| 3.0 | 6.0 | 4.0 | (4-6)² = 4 |
| 总和 | 6 | ||
| MSE | 6/3 = 2 |
所以 mse_matrix[10, 30](假设w=1.0是第10个,b=1.0是第30个)= 2.0
8.8 生成网格坐标
python
W, B = np.meshgrid(w_list, b_list)这是最关键也最难以理解的一步!
为什么要用meshgrid?
3D绘图需要三个都是二维矩阵的输入:
- X坐标矩阵:每个点的w值
- Y坐标矩阵:每个点的b值
- Z坐标矩阵:每个点的loss值
meshgrid的作用: 把一维数组转换成二维网格矩阵
具体转换:
假设 w_list = [0, 1, 2], b_list = [0, 1](简化版)
w_list(横向): [0, 1, 2]
b_list(纵向): [0]
[1]np.meshgrid(w_list, b_list) 结果:
W = [[0, 1, 2], # 第0行:w值横向复制
[0, 1, 2]] # 第1行:w值横向复制
B = [[0, 0, 0], # 第0列:b值纵向复制
[1, 1, 1]] # 第1列:b值纵向复制这样W和B的对应位置就组成了所有(w,b)组合:
| 位置 | W | B | 组合 |
|---|---|---|---|
| (0,0) | 0 | 0 | (0, 0) |
| (0,1) | 1 | 0 | (1, 0) |
| (0,2) | 2 | 0 | (2, 0) |
| (1,0) | 0 | 1 | (0, 1) |
| (1,1) | 1 | 1 | (1, 1) |
| (1,2) | 2 | 1 | (2, 1) |
可视化理解:
w=0 w=1 w=2
┌─────┬─────┬─────┐
b=0 │(0,0)│(1,0)│(2,0)│
├─────┼─────┼─────┤
b=1 │(0,1)│(1,1)│(2,1)│
└─────┴─────┴─────┘8.9 绘制3D图形
python
fig = plt.figure('Linear Model Cost Value') # 创建画布,设置窗口标题
ax = fig.add_subplot(111, projection='3d') # 添加3D子图| 代码 | 含义 |
|---|---|
plt.figure('...') |
创建新画布,标题为"Linear Model Cost Value" |
fig.add_subplot(111) |
创建1×1网格的第1个子图(即整个画布) |
projection='3d' |
指定为3D投影 |
python
ax.plot_surface(W, B, mse_matrix.T, cmap='viridis')| 参数 | 含义 |
|---|---|
W |
x轴数据(w值网格) |
B |
y轴数据(b值网格) |
mse_matrix.T |
z轴数据(损失值),需要转置! |
cmap='viridis' |
颜色映射方案,从紫到黄 |
为什么需要.T(转置)?
meshgrid生成的W和B形状是 (len(b_list), len(w_list)),即 (41, 41)
但mse_matrix的形状是 (len(w_list), len(b_list)),即 (41, 41)
两者是转置关系,所以需要转置才能对应。
如果不转置会怎样? w和b的轴会互换,图形看起来"旋转"了90度。
python
ax.set_xlabel('w') # 设置x轴标签
ax.set_ylabel('b') # 设置y轴标签
ax.set_zlabel('loss') # 设置z轴标签
plt.show() # 显示图形8.10 图形解读
运行后会看到一个三维曲面,形状像一个"碗":
loss (z轴,向上)
↑
│ ╱╲
│ ╱ ╲
│ ╱ ╲
│ ╱ 最低点 ╲
│╱____________╲
w → b (x,y平面)- 最低点:最优的(w, b)组合,损失最小
- 从任意方向往中心走,损失都会下降
- 曲面越平缓的地方,参数越不敏感;越陡峭的地方,参数越敏感
完整流程图
┌─────────────────────────────────────────┐
│ 1. 准备数据: x=[1,2,3], y=[3,4,6] │
├─────────────────────────────────────────┤
│ 2. 定义模型: ŷ = wx + b │
├─────────────────────────────────────────┤
│ 3. 定义损失: loss = (ŷ-y)² │
├─────────────────────────────────────────┤
│ 4. 穷举搜索: w∈[0,4], b∈[-2,2] │
│ 共 41×41 = 1681 种组合 │
├─────────────────────────────────────────┤
│ 5. 计算MSE: 每种组合算3个样本的平均损失 │
├─────────────────────────────────────────┤
│ 6. 存储结果: 41×41的mse_matrix │
├─────────────────────────────────────────┤
│ 7. 生成网格: meshgrid转一维为二维 │
├─────────────────────────────────────────┤
│ 8. 3D绘图: plot_surface画曲面 │
└─────────────────────────────────────────┘关键要点总结
| 要点 | 说明 |
|---|---|
| 穷举法 | 在参数空间内采样,计算每种组合的损失 |
| meshgrid | 将一维数组扩展为二维网格,用于3D绘图 |
| 转置.T | 保证矩阵维度与网格坐标对应 |
| 3D曲面 | 直观展示损失函数在参数空间的形状 |
| 碗形曲面 | 线性回归的损失函数是凸函数,有唯一全局最优 |
九、可视化与训练监控
9.1 为什么要可视化?
实际训练中,模型可能需要训练几天甚至几周,需要实时监控训练状态。
9.2 常见的可视化方式
| 方式 | 说明 |
|---|---|
| 打印日志 | 输出训练过程中的损失值 |
| 绘图 | 画损失曲线观察收敛情况 |
| 实时绘图(Visdom) | 创建web服务,远程查看训练状态 |
9.3 重要的观察指标
横坐标不是权重w,而是训练轮数(Epoch)
实际训练中画的是:
- 训练集损失:通常持续下降
- 开发集损失:先下降后上升(上升时说明开始过拟合)
找最优停止点: 开发集损失最低的点就是最优模型,继续训练会导致过拟合。
9.4 断点续训
训练时间长时需要考虑:
- 定期存盘(持久化):防止程序崩溃导致训练白费
- 断点重开:从上次保存的模型继续训练
十、本讲核心要点总结
机器学习流程 :准备数据 → 选择模型 → 训练 → 推理
数据 : 训练集(训练集+验证集)、测试集(最终评估)
模型 :先选择简单的线性模型(ŷ = wx + b)
训练 :根据穷举法找出损失函数最小的wb,就是模型。
缺点:然而,当考虑参数数量增加时,穷举法的搜索空间会呈指数级增长。例如:
- 单参数w:100种可能
- 双参数w1,w2:100²=10,000种组合
- 10个参数:100¹⁰种组合
这种指数爆炸现象使得穷举法在实际应用中极不高效,难以找到最优解。