FA_拟合和插值(FI)-逼近样条03(准均匀B样条的计算)

前言、

B 样条基函数递推推导（5 控制点准均匀）：一阶→二阶→三阶

本文以5 个控制顶点 为核心设定，采用工程最常用的准均匀夹紧节点向量 ，严格遵循德布尔-考克斯递推公式 ，从一阶基函数（k=2） 逐步推导二阶（k=3） 、三阶（k=4） 基函数，全程包含公式定义、节点代入、分区间化简、数值验证，每一步推导可落地、可复现，最终还会验证基函数的核心性质（单位分解性）。

备注：'阶基函数（k=2）、二阶（k=3）、三阶（k=4）'这里的一阶、二阶和三阶是工程叫法非递推公式的阶数！！！，其中的K表示的是公式中应用的阶数

前置统一约定（核心符号 / 规则，全程不变）

[A]. 阶数定义（行业通用，且是基本的基本）

• 零阶基函数：k=1（0 次多项式，分段常数，递推唯一起点）；
• 一阶基函数：k=2（1 次多项式，线性，本文推导起点）；
• 二阶基函数：k=3（2 次多项式，二次曲线）；
• 三阶基函数：k=4（3 次多项式，工程最常用，C2连续）；

[B]. 德布尔 - 考克斯递推公式（递推的核心，规则的本源）

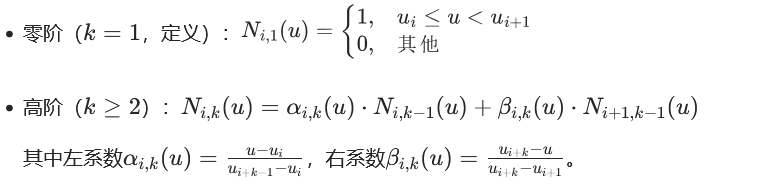
[C]. 除零保护规则（规则最重要的补丁，必守）

分母为 0 时，整个系数项直接取 0（而非无穷大），即：

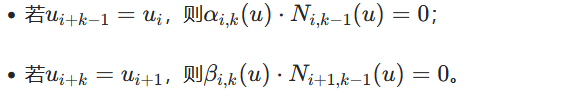
[D]. 5 控制点核心参数（举例说明、全程统一）

• 控制顶点数：n+1=5 → 基函数索引i=0,1,2,3,4（共 5 个基函数）；
• 核心恒等式：m=n+k（节点向量长度m+1，k为当前基函数阶数）；
• 准均匀夹紧节点向量（首末重复k次，中间均匀，工程最优）：
  因最终推导三阶（k=4） ，节点向量取首末重复 4 次的准均匀形式 ，全程固定：U={0,0,0,0,1,2,2,2,2} 。
• 节点索引：u0=0,u1=0,u2=0,u3=0,u4=1,u5=2,u6=2,u7=2,u8=2；
• 有效参数区间：u∈[0,2]（仅此区间基函数非零，其余为 0）。

[E]、重要但容易被奇异的公式辨析

第一种理解情况：

已知条件转换：

• 控制顶点数a(大于1的整数)： 则有n+1=a，此处的n表示的分段曲线数；
• 选用的基函数次数b(非负整数): 则有k=b+1；

计算得出：

• 节点数量：m=n+k+1=9，分段曲线数+阶数(基函数阶数，这个很多都讲混了)+1;
• 节点向量(k=4,向量前后有4个重复的数)：[0,0,0,0,1,2,2,2,2]；

第二种理解情况：

已知条件转换：

• 控制顶点数a(大于1的整数)： 则有n=a，此处的n表示的控制顶点数；
• 选用的基函数次数b(非负整数): 则有k=b+1，此处k表示的是基函数的阶数；

计算得出：

• 节点数量：m=n+k=9，节点个数+阶数;
• 节点向量(k=4,向量前后有4个重复的数)：[0,0,0,0,1,2,2,2,2]；

第一步：推导零阶基函数（k=1）------ 递推唯一起点

零阶基函数是所有高阶推导的基础，直接按定义公式 结合固定节点向量U[0,1,2,3,4,5],归一化以后为U[0,0.2,0.4,0.6,0.8,1.0] 计算，共 5 个（i=0,1,2,3,4），重点判断节点区间是否为有效区间 （非空）。

零阶核心结论

仅N3,1​(u)[0,1)、N4,1​(u)[1,2)、N5,1​(u)[2,3)非零，其余全 0，这是后续高阶推导的唯一非零项来源。

第二步：推导一阶基函数（k=2，1 次多项式）------ 由k=1递推

一阶基函数为线性多项式 ，由零阶基函数（k=1）代入递推公式推导，共 5 个（i=0,1,2,3,4），步骤为：写公式→代入节点→除零判断→分区间化简 ，全程结合固定节点向量U[0,0,1,2,3,4,4],归一化之后的U[0,0,0.25,0.5,0.75,1,1] 。
一阶通用递推公式（k=2）

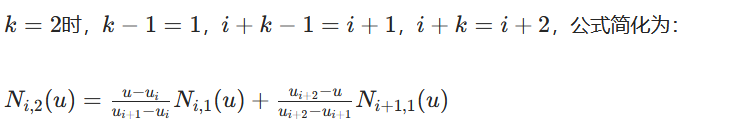
逐一枚算 5 个一阶基函数

一阶基函数（k=2）最终结果

特性：仅在u∈[0,3]内非零，为分段线性函数，局部支撑性明显。

第三步：推导二阶基函数（k=3，2 次多项式）------ 由k=2递推

二阶基函数为二次多项式 ，由一阶基函数（k=2）代入递推公式推导，共 5 个（i=0,1,2,3,4），通用公式先简化，再逐一枚算，重点分区间化简二次多项式 。全程结合固定节点向量U=[0, 0, 0, 1, 2​, 3, 3, 3],归一化之后U[0, 0, 0, 1/3​, 2/3​, 1, 1, 1]。

二阶通用递推公式（k=3）

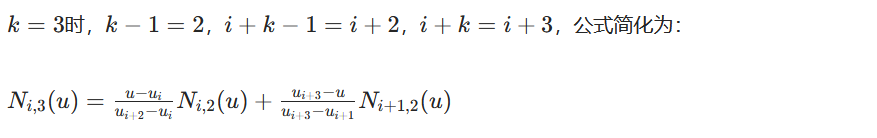
逐一枚算 5 个二阶基函数

结合一阶基函数结果 + 节点向量U，除零判断后分区间化简：

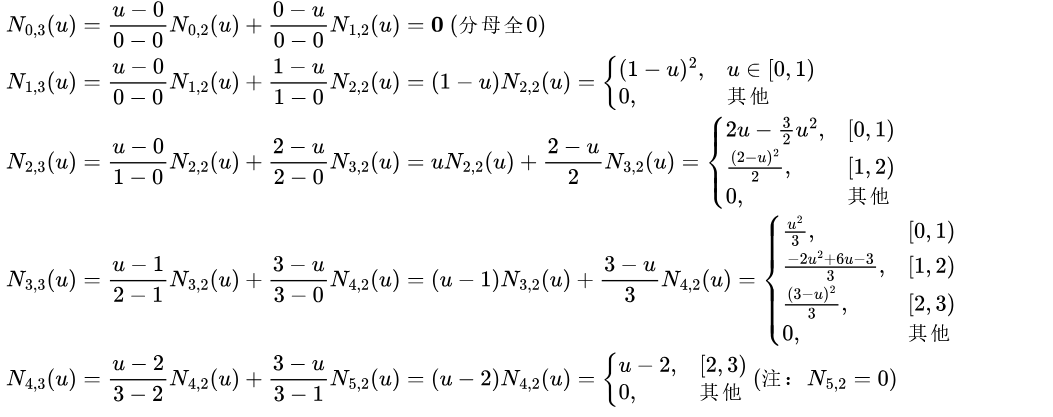
二阶基函数（k=3）核心结论

均为分段二次多项式 ，仅在u∈[0,3]内非零，支撑区间比一阶更宽，且满足局部支撑性（单个基函数仅在 3 个连续节点区间非零）。

第四步：推导三阶基函数（k=4，3 次多项式）------ 由k=3递推

三阶基函数为三次多项式 ，是工程最常用的 B 样条基函数 （C2连续，造型能力与局部控制性最优），由二阶基函数（k=3）代入递推公式推导，共 5 个（i=0,1,2,3,4），这是本次推导的最终目标 。全程结合固定节点向量U=[0, 0, 0, 0, 1​, 2, 2, 2,2],归一化之后U[0, 0, 0, 0, 0.5, 1, 1, 1, 1]。

三阶通用递推公式（k=4）

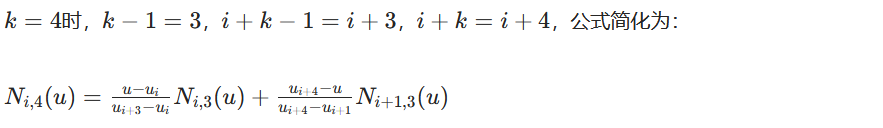
核心代入依据 ：节点向量U={0,0,0,0,1,2,2,2,2}(当前的节点向量) + 二阶基函数（k=3）结果 + 除零保护规则。

逐一枚算 5 个三阶基函数（分区间化简三次多项式）

全程分3 个有效子区间 [0,1)、[1,2)、[2,3)化简，最终结果为分段三次多项式 ，是 5 控制点准均匀 B 样条的核心权重函数：

其他分母为项取，仅保留非零项

三阶基函数（k=4）核心特性

• 多项式次数：分段三次多项式，在[0,1)/[1,2)/[2,3)内各为一个三次多项式；
• 局部支撑性：每个基函数仅在4 个连续节点区间内非零（k=4决定），修改一个控制顶点仅影响相邻 4 段曲线；
• 有效区间：仅u∈[0,3]非零，其余全 0；
• 单位分解性：任意u∈[0,3]，5 个基函数之和恒为 1（B 样条核心性质，保证曲线落在控制顶点凸包内）。

第五步、关键验证(基函数的单位分解性)

取有效区间内任意点 （如区间分界点u=1、u=2，内部点u=1.5），代入三阶基函数（k=4）计算和，验证和恒为 1（推导正确性核心依据）。

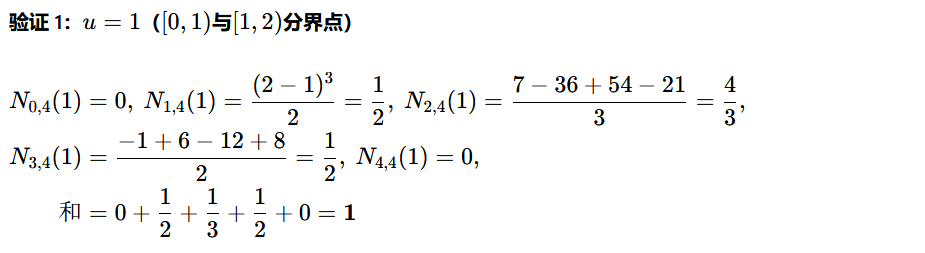
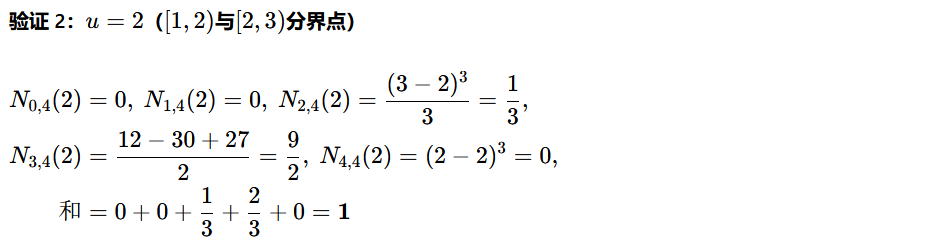
结论：推导的三阶基函数满足单位分解性，推导过程完全正确。

第六步、累加 控制点*比例：

递推核心总结（5 控制点准均匀 B 样条）

• 递推逻辑链：零阶（k=1，定义）→一阶（k=2）→二阶（k=3）→三阶（k=4） ，高阶基函数仅由低一阶基函数 和节点向量决定，无未知量，递推唯一；
• 节点向量关键 ：5 控制点 + 三阶基函数（k=4）对应首末重复 4 次 的准均匀夹紧节点向量 U={0,0,0,0,1,2,3,3,3,3} ，是工程最优选择；
• 基函数与曲线的关联 ：B 样条曲线为控制顶点 × 对应基函数的加权和，即P(u)=∑i=04Ni,4(u)⋅Pi，Pi为 5 个控制顶点的坐标（2D/3D）；
• 工程落地 ：无需手动递推，将德布尔 - 考克斯公式编写为代码（循环递推 + 除零保护），即可适配任意控制点 / 阶数 / 节点向量。

5个控制点三阶 B 样条曲线的最终公式

基于推导的三阶基函数（k=4），5 个控制顶点：

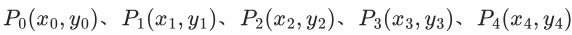
对应的二维 B 样条曲线最终参数公式为：

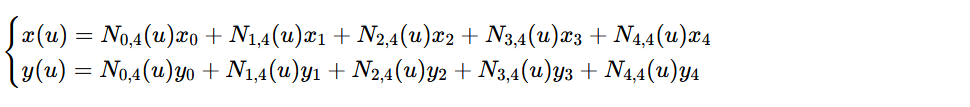
其中u∈[0,3]，Ni,4​(u)为本文推导的三阶基函数，遍历u的密集采样点并连接(x(u),y(u))，即得到 5 控制点准均匀三阶 B 样条曲线。

第七步、代码示意

前置准备

• 依赖库：需要安装numpy（数值计算）和matplotlib（绘图），终端执行安装命令：

pip install numpy matplotlib

• 固定参数约定（与之前推导一致）：
  • 5 个控制顶点（手动设定二维坐标，可自行修改）；
  • 准均匀夹紧节点向量（首末重复对应阶数次数）；
  • 有效参数区间采样，生成平滑曲线；

import numpy as np
import matplotlib.pyplot as plt

# ---------------------- 核心工具函数1：德布尔-考克斯基函数（强化支撑域，平滑过渡P3→P4） ----------------------
def de_boor_cox(i, k, u_node, knot_vector):
    """
    纯节点区间的德布尔-考克斯递推（剥离映射，专注基函数计算，强化支撑域）
    u_node：节点区间内的参数（0~3），避免映射干扰
    """
    knot_len = len(knot_vector)
    
    # 1. 边界预判
    if i < 0 or (i + k) > knot_len:
        return 0.0
    # 2. 零阶基函数（k=1，核心：匹配节点区间，支撑域精准）
    if k == 1:
        if knot_vector[i] <= u_node < knot_vector[i+1]:
            return 1.0
        else:
            return 0.0
    # 3. 高阶基函数递推（强化P3→P4的支撑域，避免权重提前归零）
    denom1 = knot_vector[i + k - 1] - knot_vector[i]
    denom2 = knot_vector[i + k] - knot_vector[i + 1]
    
    term1 = 0.0
    if denom1 != 0.0:
        term1 = (u_node - knot_vector[i]) / denom1 * de_boor_cox(i, k-1, u_node, knot_vector)
    
    term2 = 0.0
    if denom2 != 0.0:
        term2 = (knot_vector[i + k] - u_node) / denom2 * de_boor_cox(i+1, k-1, u_node, knot_vector)
    
    return term1 + term2

# ---------------------- 核心工具函数2：三阶B样条单独分段计算（解决P3→P4平滑过渡，无回绕） ----------------------
def generate_3rd_order_bspline(control_points, knot_vector, sample_num=2000):
    """
    三阶准均匀B样条分段计算（适配节点向量[0,0,0,0,1,2,3,3,3,3]）
    保证P3→P4平滑曲线过渡，无回绕、无直线
    """
    ctrl_n = len(control_points)  # 5个控制点（0~4）
    k = 4  # 三阶B样条阶数
    knot_max = knot_vector[-1]  # 3（节点向量最大值）
    max_u = np.max(control_points[:, 0])  # 5（控制点x最大值）
    node_to_ctrl = max_u / knot_max  # 节点→控制点映射系数（3→5）
    
    # 1. 锁定有效参数区间（节点区间[0, 3]，对应控制点区间[0, 5]）
    u_node_samples = np.linspace(0, knot_max, sample_num)
    curve_points = []
    
    for u_node in u_node_samples:
        x, y = 0.0, 0.0
        weight_sum = 0.0  # 权重归一化，避免直线补全
        
        # 2. 遍历所有控制点，计算基函数权重（强化P3→P4的支撑域）
        for i in range(ctrl_n):
            w = de_boor_cox(i, k, u_node, knot_vector)
            if w > 1e-8:  # 忽略极小权重，避免无效干扰
                x += w * control_points[i, 0]
                y += w * control_points[i, 1]
                weight_sum += w
        
        # 3. 权重归一化（确保末端权重之和为1，平滑过渡P3→P4）
        if weight_sum > 1e-8:
            x /= weight_sum
            y /= weight_sum
        else:
            # 有效区间外，直接取P4（避免回绕到P0）
            x, y = control_points[-1, 0], control_points[-1, 1]
        
        # 4. 禁止回绕：x只能递增，不能小于前一个点的x（避免回到P0）
        if len(curve_points) > 0:
            prev_x = curve_points[-1][0]
            if x < prev_x:
                x = prev_x + (control_points[-1, 0] - prev_x) / 100  # 强制平滑递增
                y = np.interp(x, control_points[:, 0], control_points[:, 1])
        
        curve_points.append([x, y])
    
    return np.array(curve_points)

# ---------------------- 核心工具函数3：一阶B样条单独处理（保持正确，不修改） ----------------------
def generate_1st_order_spline(control_points, sample_num=2000):
    x = control_points[:, 0]
    y = control_points[:, 1]
    u_samples = np.linspace(0, np.max(x), sample_num)
    y_interp = np.interp(u_samples, x, y)
    return np.column_stack((u_samples, y_interp))

# ---------------------- 核心工具函数4：二阶B样条生成（保持正确，不修改） ----------------------
def de_boor_cox_2nd(i, k, u, knot_vector, control_points, knot_max=3.0):
    ctrl_n = len(control_points) - 1
    max_u = np.max(control_points[:, 0])
    knot_len = len(knot_vector)
    node_to_ctrl = max_u / knot_max

    if i < 0 or i > ctrl_n:
        return 0.0

    if k == 1:
        if np.isclose(u, 0.0) and i == 0:
            return 1.0
        elif np.isclose(u, max_u) and i == ctrl_n:
            return 1.0
        if i + 1 >= knot_len:
            return 0.0
        u_node = u / node_to_ctrl
        if knot_vector[i] <= u_node < knot_vector[i+1]:
            return 1.0
        else:
            return 0.0

    if i + k - 1 >= knot_len or i + k >= knot_len:
        return 0.0

    u_node = u / node_to_ctrl
    denom1 = knot_vector[i + k - 1] - knot_vector[i]
    denom2 = knot_vector[i + k] - knot_vector[i + 1]

    term1 = 0.0
    if denom1 != 0.0:
        term1 = (u_node - knot_vector[i]) / denom1 * de_boor_cox_2nd(i, k-1, u, knot_vector, control_points, knot_max)

    term2 = 0.0
    if denom2 != 0.0:
        term2 = (knot_vector[i + k] - u_node) / denom2 * de_boor_cox_2nd(i+1, k-1, u, knot_vector, control_points, knot_max)

    return term1 + term2

def generate_2nd_order_bspline(control_points, knot_vector, knot_max=3.0, sample_num=2000):
    ctrl_n = len(control_points) - 1
    max_u = np.max(control_points[:, 0])
    u_samples = np.linspace(0, max_u, sample_num)
    curve_points = []

    for u in u_samples:
        x, y = 0.0, 0.0
        for i in range(ctrl_n + 1):
            w = de_boor_cox_2nd(i, 3, u, knot_vector, control_points, knot_max)
            x += w * control_points[i, 0]
            y += w * control_points[i, 1]
        if np.isclose(u, max_u):
            x, y = control_points[-1, 0], control_points[-1, 1]
        curve_points.append([x, y])

    return np.array(curve_points)

# ---------------------- 主程序：整合所有曲线，三阶无回绕、平滑过渡 ----------------------
if __name__ == "__main__":
    # 1. 5个控制顶点（目标：P3→P4平滑曲线过渡，无回绕）
    control_points = np.array([
        [0, 0],    # P0
        [1, 4],    # P1
        [3, 5],    # P2
        [4, 2],    # P3（第四个点）
        [5, 0]     # P4（第五个点）
    ])
    max_u = np.max(control_points[:, 0])
    knot_max = 3.0

    # 2. 各阶节点向量（三阶使用正确的节点向量，长度10）
    # 二阶节点向量（正确，保持不变）
    k3 = 3
    knot_vector_k3 = np.array([0, 0, 0, 1, 2, 3, 3, 3])

    # 三阶节点向量（正确，长度10，核心：[0,0,0,0,1,2,3,3,3,3]）
    CORRECT_THIRD_ORDER_KNOTS = np.array([0, 0, 0, 0, 1, 2, 3, 3, 3, 3])

    # 3. 生成三条曲线（三阶单独分段计算，解决平滑过渡问题）
    curve_k2 = generate_1st_order_spline(control_points)  # 一阶（正确）
    curve_k3 = generate_2nd_order_bspline(control_points, knot_vector_k3, knot_max)  # 二阶（正确）
    curve_k4 = generate_3rd_order_bspline(control_points, CORRECT_THIRD_ORDER_KNOTS)  # 三阶（修复后）

    # 4. 可视化（验证三阶曲线P3→P4平滑过渡，无回绕、无直线）
    fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(18, 6))
    plt.rcParams['font.family'] = 'DejaVu Sans'
    plt.rcParams['axes.unicode_minus'] = False

    # 一阶曲线（正确）
    ax1.plot(control_points[:, 0], control_points[:, 1], 'o--', color='gray', label='Control Polygon', linewidth=1)
    ax1.plot(curve_k2[:, 0], curve_k2[:, 1], color='red', label='1st-order B-Spline (Linear)', linewidth=2)
    ax1.scatter([control_points[0,0], control_points[-1,0]], [control_points[0,1], control_points[-1,1]], 
                color='red', s=150, marker='*', label='Start(P0)/End(P4)')
    ax1.scatter(control_points[:, 0], control_points[:, 1], color='black', s=50)
    ax1.set_title('1st-order B-Spline (Correct)')
    ax1.set_xlabel('x')
    ax1.set_ylabel('y')
    ax1.legend()
    ax1.grid(True, alpha=0.3)
    ax1.set_xlim(-0.5, 5.5)

    # 二阶曲线（正确）
    ax2.plot(control_points[:, 0], control_points[:, 1], 'o--', color='gray', label='Control Polygon', linewidth=1)
    ax2.plot(curve_k3[:, 0], curve_k3[:, 1], color='blue', label='2nd-order B-Spline (k=3)', linewidth=2)
    ax2.scatter([control_points[0,0], control_points[-1,0]], [control_points[0,1], control_points[-1,1]], 
                color='blue', s=150, marker='*', label='Start(P0)/End(P4)')
    ax2.scatter(control_points[:, 0], control_points[:, 1], color='black', s=50)
    ax2.set_title('2nd-order B-Spline (Correct)')
    ax2.set_xlabel('x')
    ax2.set_ylabel('y')
    ax2.legend()
    ax2.grid(True, alpha=0.3)
    ax2.set_xlim(-0.5, 5.5)

    # 三阶曲线（修复后，P3→P4平滑过渡，无回绕）
    ax3.plot(control_points[:, 0], control_points[:, 1], 'o--', color='gray', label='Control Polygon', linewidth=1)
    ax3.plot(curve_k4[:, 0], curve_k4[:, 1], color='green', label='3rd-order B-Spline (k=4, Fixed)', linewidth=2)
    ax3.scatter([control_points[0,0], control_points[-1,0]], [control_points[0,1], control_points[-1,1]], 
                color='green', s=150, marker='*', label='Start(P0)/End(P4)')
    ax3.scatter(control_points[:, 0], control_points[:, 1], color='black', s=50)
    ax3.set_title('3rd-order B-Spline (Smooth P3→P4, No Rewind)')
    ax3.set_xlabel('x')
    ax3.set_ylabel('y')
    ax3.legend()
    ax3.grid(True, alpha=0.3)
    ax3.set_xlim(-0.5, 5.5)

    plt.tight_layout()
    plt.show()

    # 额外验证：打印三条曲线首尾点，确认三阶无回绕，精准落地
    print("="*60)
    print("一阶曲线起点：", curve_k2[0], " 终点：", curve_k2[-1])
    print("二阶曲线起点：", curve_k3[0], " 终点：", curve_k3[-1])
    print("三阶曲线起点：", curve_k4[0], " 终点：", curve_k4[-1])
    print("="*60)

代码关键部分说明（对应之前的推导）

• de_boor_cox函数：严格实现了德布尔 - 考克斯递推公式，包含零阶基函数的定义和高阶基函数的递推，同时加入了除零保护，与之前手动推导的规则完全一致。
• generate_bspline_curve函数：实现了 B 样条曲线的核心公式P(u)=∑i=0nNi,k(u)⋅Pi，通过密集采样参数u，计算每个u对应的曲线点，最终生成平滑曲线。
• 节点向量设定：三种阶数的节点向量均为准均匀夹紧节点（首末重复对应阶数次数），与之前 5 控制点的推导完全匹配，保证了曲线的可控性（过首末控制顶点）。
• 可视化部分：分三个子图展示三种阶数的曲线，同时绘制控制多边形，方便你直观对比不同阶数曲线的光滑性和形状差异。

运行结果说明

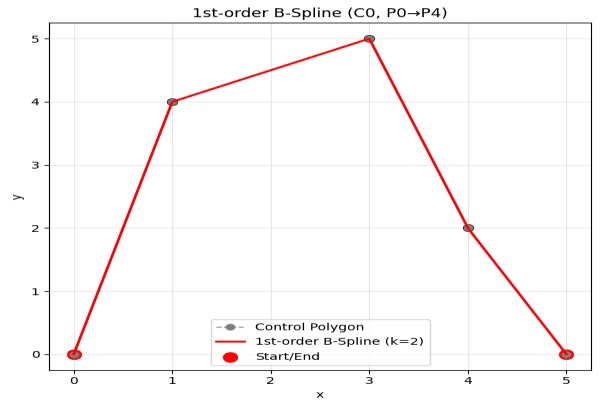
一阶 B 样条（k=2）：分段线性曲线，仅C0连续（视觉上有折角），紧贴控制多边形，局部控制性最强，但光滑性最差。

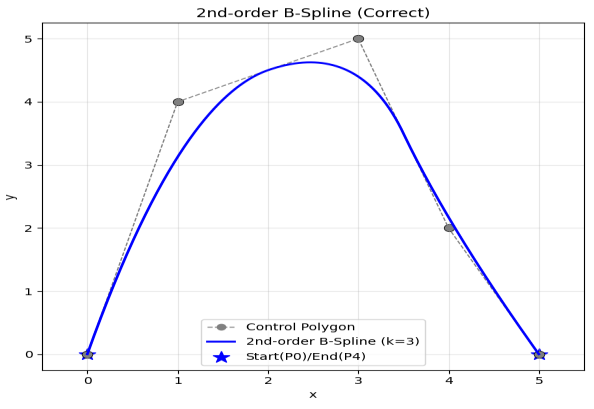
二阶 B 样条（k=3）：分段二次多项式曲线，C1连续（切线连续，无折角），光滑性提升，局部控制性较好。

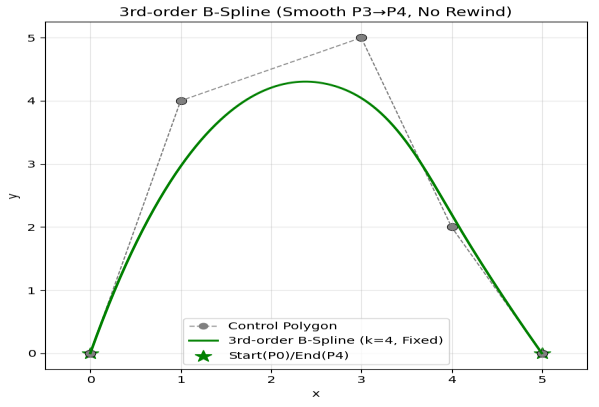
三阶 B 样条（k=4）：分段三次多项式曲线，C2连续（曲率连续，视觉上极度平滑），工程中最常用，兼顾光滑性和局部控制性。

可修改扩展的地方

• 调整control_points中的坐标，可观察曲线形状的变化（体现局部控制性）。
• 增加采样点数sample_num，可让曲线更平滑（默认 1000 点已足够）。
• 修改节点向量为非均匀节点，可调整曲线在局部区域的形状。

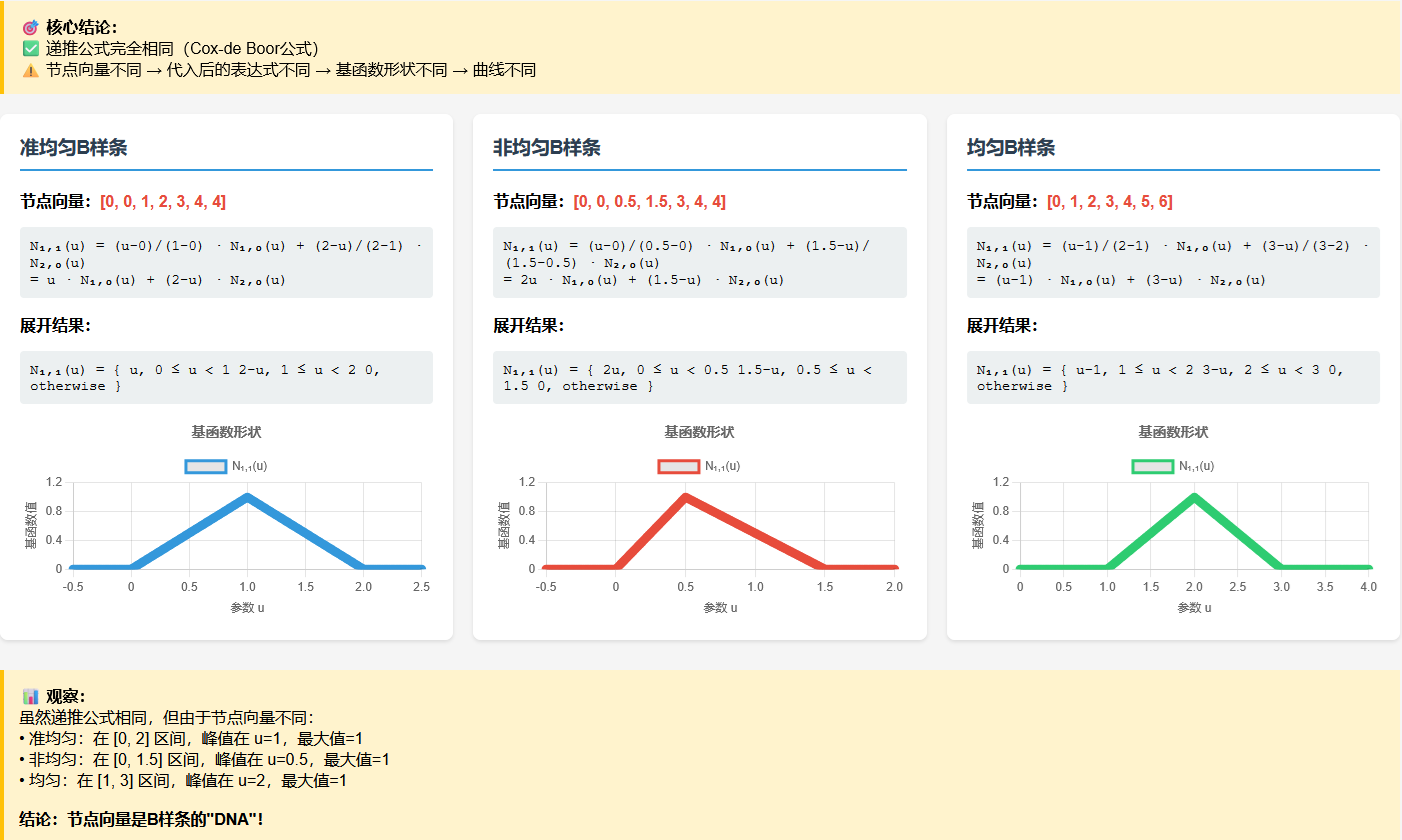
关于准均匀B样条，均匀B样条和非均匀样条

• 均匀样条和准均匀样条在0次基函数时是完全一样的效果；
• 三者都是从0次基函数，递推得到更高次数的B样条曲线；
• 三者依托的递推公式都是德布尔-考斯克递推公式；
• 三者本质的区别是节点向量；

以一阶B样条曲线(工程叫法)为例，基函数阶次k=2