梯度在神经网络中的实际应用:从"猜答案"到"学会思考"的旅程
作者:Weisian
日期:2026年2月3日

上一篇我们讲了梯度是AI优化的"导航仪"------它告诉模型该往哪个方向走,才能最快降低错误。但你可能会问:这个"导航仪"到底装在哪儿?又是怎么工作的?
答案就藏在现代AI的核心引擎里:神经网络。
本文将用一个贯穿始终的生活比喻------带你一步步理解:
- 神经网络到底是什么?
- 它如何通过"试错"学习?
- 损失函数、学习率、正向传播、反向传播分别扮演什么角色?
- 梯度又如何在其中精准指挥每一处调整?
- 以及,为什么训练大模型有时会"卡住"或"发疯"?
全程无公式轰炸,只有真实场景 + 直观类比,让你真正看懂"AI是怎么学会的"。
一、神经网络是什么?------就像一个"多层猜题小组"
想象你在辅导一个刚上小学的孩子做加法题,比如:"3 + 5 = ?"
孩子一开始不会,只能瞎猜:"8!"------碰巧对了。
但换成"7 + 9 = ?",他可能答:"15?"------错了。
于是你告诉他:"不对,正确答案是16。"
他点点头,下次再遇到类似题目,可能会更小心一点。
神经网络,本质上就是一个会"猜答案"的机器 。
但它不是一个人猜,而是一个由多层"小助手"组成的团队,每一层都负责处理一部分信息。
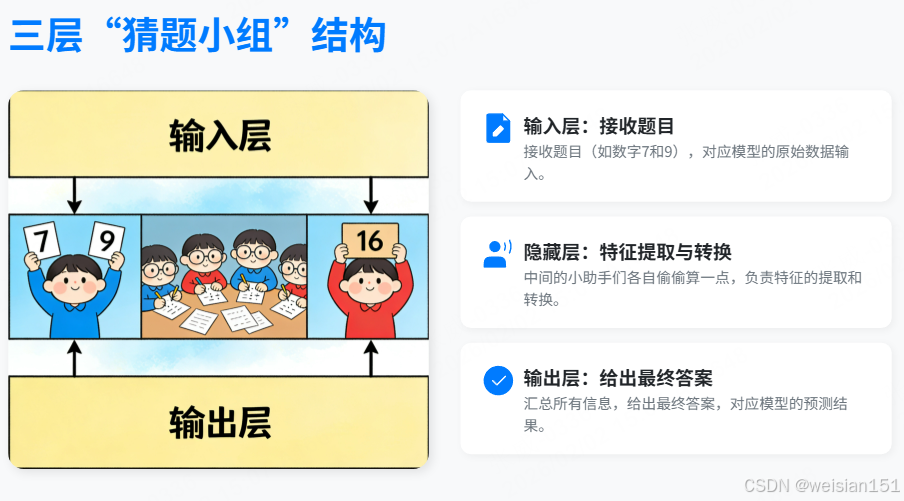
结构类比:三层"猜题小组"
- 输入层:接收题目(比如数字7和9)
- 隐藏层:中间的小助手们,各自偷偷算一点(比如有人算个位,有人估算大小)
- 输出层:汇总所有信息,给出最终答案(比如"15")
这些"小助手"之间通过权重(weights) 连接------你可以理解为他们之间的"信任程度"。
如果某个小助手经常说对,他的发言权(权重)就大;如果说错太多,大家就不太听他的(权重变小)。
✅ 关键点 :神经网络本身没有"知识",它只有一堆可调的"旋钮"(参数)。
学习的过程,就是不断调整这些旋钮,让猜的答案越来越准。
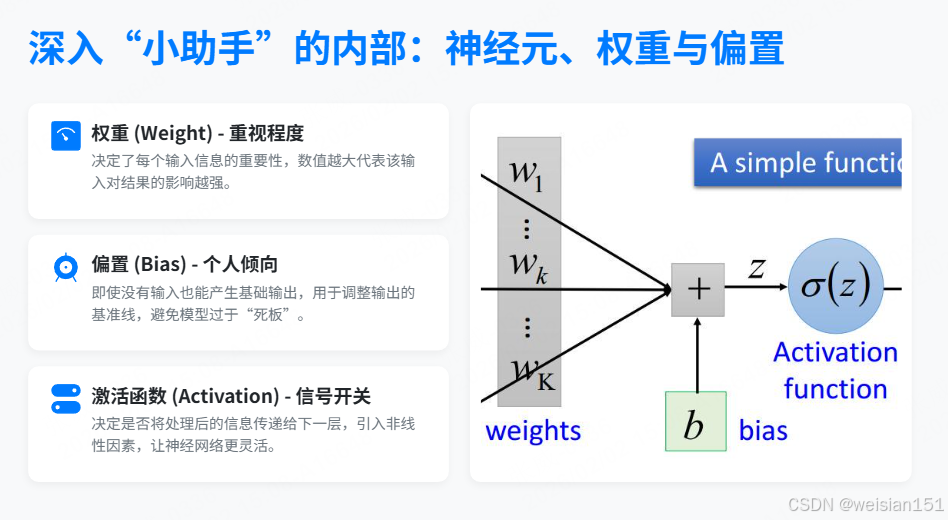
🔍 深入"小助手"的内部:神经元、权重与偏置
每个"小助手"其实就是一个神经元(Neuron)------它是神经网络的基本计算单元。
想象一个隐藏层的小助手,他的任务是判断:"这两个数加起来是不是接近20?"
他怎么判断?他有三个工具:
1. 权重(Weight)------"重视程度"
他先看输入的两个数:7 和 9。
但他不会平等对待它们------也许他更相信第一个数,于是给"7"打8分重视(权重=0.8),给"9"打9分重视(权重=0.9)。
这就像老师批改作文:内容占60%,字迹占10%------不同部分权重不同。
数学上,他会先做加权求和:
加权总和=7×0.8+9×0.9=5.6+8.1=13.7 \text{加权总和} = 7 \times 0.8 + 9 \times 0.9 = 5.6 + 8.1 = 13.7 加权总和=7×0.8+9×0.9=5.6+8.1=13.7
2. 偏置(Bias)------"个人倾向"
但这个小助手有点"乐观",总觉得结果会比计算值大一点。
于是他在总和上悄悄加一个固定值,比如 +2 ------这就是偏置(Bias)。
带偏置的总和=13.7+2=15.7 \text{带偏置的总和} = 13.7 + 2 = 15.7 带偏置的总和=13.7+2=15.7
💡 偏置的作用 :即使输入全是0,神经元也能输出非零值。
它就像人的"默认心态"------有人天生谨慎(偏置负),有人天生大胆(偏置正)。
3. 激活函数(Activation)------"要不要发言"
现在总和是15.7,但他不能直接把15.7传出去------他得决定"这个信号值不值得说"。
于是他用一个激活函数(比如 ReLU)做最后判断:
- 如果总和 > 0,就说出来(输出 = 15.7)
- 如果 ≤ 0,就闭嘴(输出 = 0)
这模拟了人脑神经元的"放电"机制:只有刺激足够强,才会传递信号。
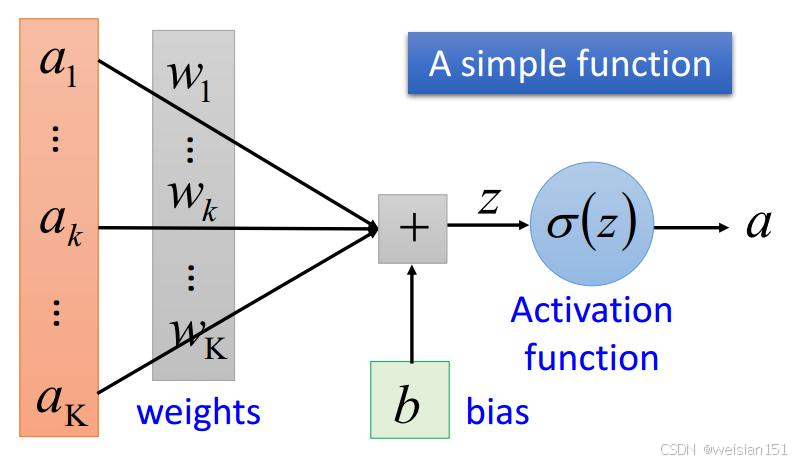
总结:一个神经元的工作流程
每个小助手(神经元)的完整思考过程是:
输入 → 乘以各自的权重 → 求和 → 加上偏置 → 经过激活函数 → 输出而整个神经网络,就是成千上万个这样的小助手层层串联,前一层的输出变成后一层的输入,最终从原始数据(如像素、文字)一步步提炼出高级判断。
🌟 关键洞察:
- 权重决定"听谁的"
- 偏置决定"自己怎么想"
- 激活函数决定"要不要说"
而学习,就是通过反复试错,自动调整所有权重和偏置,让最终答案越来越准。
二、正向传播:先大胆猜一次
继续用"教孩子做题"的场景。
当题目"7 + 9"出现时,孩子的大脑会经历一个从输入到输出的完整流程:
- 眼睛看到"7"和"9"
- 大脑里多个区域开始活动(回忆、估算、心算)
- 最终嘴巴说出一个答案:"15"
在神经网络中,这个过程叫 正向传播(Forward Propagation) ------
数据从输入层流经隐藏层,最终到达输出层,生成预测结果。
这一步不涉及学习,只是"当前状态下的一次猜测"。
🔍 就像考试时,你先凭现有知识作答,不管对错------这是正向传播。
但这个"猜"的过程其实非常有序:
- 第一层小助手(输入层)把"7"和"9"原样传给下一层;
- 第二层的小助手们各自拿出自己的"权重本"和"偏置笔记",算出加权总和,再决定要不要发言(激活函数);
- 第三层的小助手又基于上一层的发言,重复同样的计算......
- 直到最后,输出层的小助手综合所有信息,喊出最终答案:"15!"
整个过程就像一场接力赛 :
每一棒选手(神经元)只负责自己那一段计算,然后把结果传给下一棒。
没有人回头看,也没有人修正错误------他们只是忠实地执行当前的"操作手册"(即当前的权重和偏置)。
📌 正向传播的关键在于:它完全由当前参数决定,是一次"开环"的推理 。
只有等答案出来、老师批改后(计算损失),系统才会启动"反思模式"------那就是我们之后要讲的反向传播。
三、损失函数:老师批改试卷
孩子说了"15",但正确答案是"16"。
你怎么判断他错得多离谱?
- 如果他说"100",那显然完全没思路 → 大错
- 如果他说"15",只差1 → 小错
这个"衡量错误程度"的工具,在AI中叫 损失函数(Loss Function)。
常见的比如均方误差(MSE) :
Loss=(预测值−真实值)2 \text{Loss} = (预测值 - 真实值)^2 Loss=(预测值−真实值)2
- 预测15,真实16 → Loss = (15−16)² = 1
- 预测100,真实16 → Loss = (100−16)² = 7056
损失越大,说明模型越"懵";损失越小,说明越接近真相。
📝 损失函数就像老师的红笔------它不教你怎么改,只告诉你"错在哪、错多狠"。
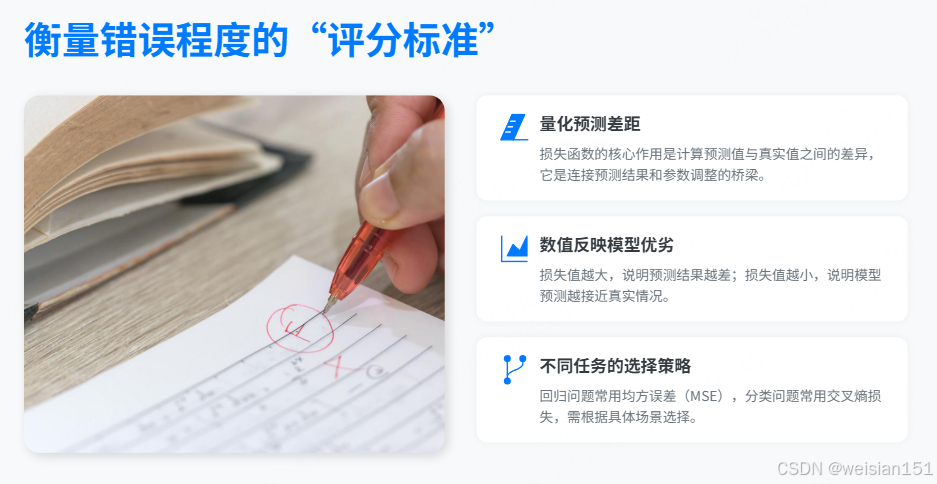
损失函数的作用不止于"打分"。
更重要的是:这个分数会变成后续调整的"指南针" 。
因为损失函数是可微的(数学上光滑连续),我们才能通过它计算出梯度------也就是"如果我想让分数变低,每个参数该往哪边调、调多少"。
而且,不同任务用的"评分标准"也不同:
- 做数学题、预测房价 (回归问题)→ 用均方误差(MSE),惩罚大错更狠
- 判断图片是猫还是狗 (分类问题)→ 用交叉熵损失(Cross-Entropy) ,关注"信心是否匹配事实"
- 比如模型说"99%是猫",结果真是猫 → 扣1分
- 说"99%是猫",结果是狗 → 扣100分!
💡 所以,损失函数不仅是"裁判",更是连接预测结果与参数调整的桥梁 。
没有它,模型就算猜错了,也不知道该怎么进步。
四、学习率:别改太猛,也别太怂
现在你知道孩子错了,下一步是教他怎么改。
但怎么改才合理?
- 如果他每次错一点,你就让他彻底推翻重来("以后别用脑子算了,直接背答案!")→ 改太猛,容易矫枉过正
- 如果他错了100分,你只让他微调0.001 → 改太轻,一辈子也学不会
这就引出了学习率(Learning Rate) ------
它控制每次参数调整的"步子有多大"。
- 学习率太大 → 像醉汉走路,左右摇摆,可能永远到不了终点(发散)
- 学习率太小 → 像蜗牛爬山,一年才挪一厘米(收敛太慢)
- 学习率适中 → 稳步逼近正确答案
⚖️ 学习率是AI训练中最关键的"手感"参数------它决定了模型是"激进改革"还是"温和改良"。

但现实中,最优步长并不是一成不变的 。
就像登山:
- 在陡峭山坡上(损失高、梯度大),可以迈大步快速下降;
- 靠近谷底时(损失低、梯度小),就要放慢脚步,避免冲过头来回震荡。
因此,工程师常使用学习率衰减 策略:
训练初期用大学习率快速靠近目标,后期逐渐减小,实现"先快后稳"的精细收敛。
此外,学习率还和梯度本身配合工作:
- 实际参数更新 = 学习率 × 梯度
- 即使梯度很大(错误明显),如果学习率很小,改动依然温和;
- 反之,梯度虽小,若学习率过大,也可能引发剧烈波动。
🌟 所以,学习率不是孤立的旋钮,而是与梯度协同工作的"油门踏板" ------
踩太深会失控,踩太浅没动力,唯有恰到好处,才能平稳驶向最优解。
五、反向传播:从错误倒推责任
最关键的来了:谁该为这次错误负责?
孩子答错"7 + 9 = 15",问题到底出在哪?
- 是他把"9"看成了"8"?(输入识别错了)
- 是他记得"7 + 8 = 15",但混淆了数字?(记忆/规则层有误)
- 还是心算时忘了进位?(计算逻辑出问题)
你不能只说"你错了",而要从结果往回捋 :
哪一步的判断偏差最大?哪个环节的"小助手"给出了误导性信息?
在神经网络中,这个"追责"过程就叫 反向传播(Backpropagation)。
它的核心思想是:
既然最终答案错了,那就把这份"错误责任"沿着信息流原路返回,一层一层拆解,精确分配给每个参与决策的神经元。
具体怎么做?靠的是微积分中的链式法则(Chain Rule) ------
就像拆解一根多米诺骨牌链:
- 最后一块倒了(输出错误),是因为前一块推得太猛或太弱;
- 而前一块的问题,又源于它前面那块......
- 于是,错误信号从输出层开始,逆向穿过隐藏层,一路传回输入层。
在这个过程中,每个神经元都会收到一个"责任分数"------这就是损失对它的参数的梯度。
- 梯度大 → 说明你的判断对错误"贡献巨大",必须重点调整;
- 梯度小 → 说明你基本没错,稍微微调即可。
🔁 正向传播是"猜答案",反向传播是"复盘错因"。
前者决定当前表现 ,后者决定未来进步。
而最终,所有这些梯度信息会被汇总起来,交给梯度下降算法 ,统一指挥每个权重和偏置该如何更新------
这才完成了一次真正意义上的"学习"。

六、梯度登场:精准定位"该调哪个旋钮"
还记得上一篇说的吗?梯度告诉我们:在当前位置,往哪个方向调参数,能让损失下降最快。
在神经网络中,这个抽象概念变得极其具体:
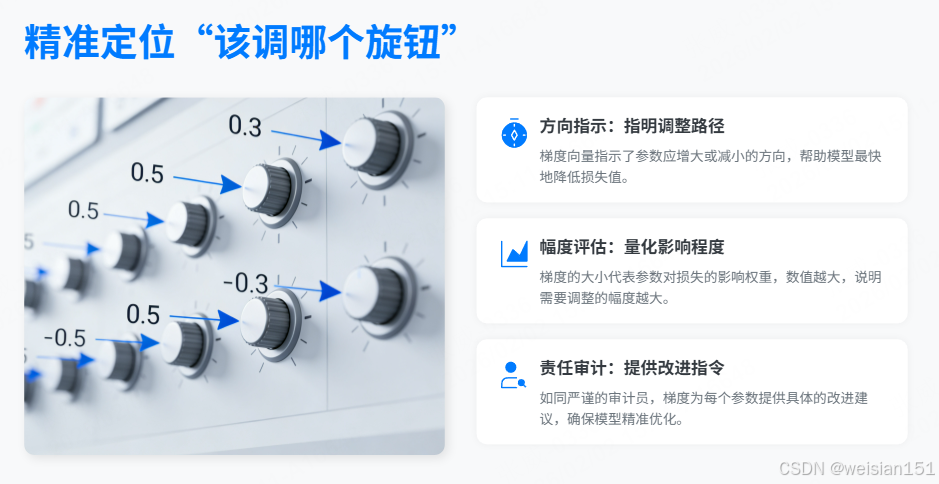
- 每一个权重 (连接两个神经元的线)和每一个偏置 (神经元的个人倾向),都对应一个专属的梯度值;
- 梯度的正负 告诉你:这个参数该增大还是减小;
- 梯度的大小 告诉你:该调多猛------贡献越大,改得越狠。
举个例子:
假设某个权重 w = 0.5 ,通过反向传播算出它的梯度为
∂Loss∂w=+2.0 \frac{\partial \text{Loss}}{\partial w} = +2.0 ∂w∂Loss=+2.0
→ 这意味着:如果我把 w 增大一点点,损失会明显上升;反之,减小 w ,损失会快速下降 。
→ 于是,在学习率 \\eta 的控制下,我们更新它:
wnew=0.5−η×2.0 w_{\text{new}} = 0.5 - \eta \times 2.0 wnew=0.5−η×2.0
🎯 梯度就像一个"责任审计员" :
它不靠猜测,而是用数学精确计算出------
"这个旋钮拧紧1格,错误会减少多少;那个旋钮松开半格,模型会更准一点。"
而且,这个审计是全网同步进行的 :
一次反向传播结束后,成千上万个权重和偏置同时拿到自己的梯度报告 ,然后集体微调。
这就像一场精密的交响乐排练------每个乐手(参数)根据指挥(梯度)调整自己的音高和力度,只为让整体演奏(预测结果)更和谐。
💡 正因如此,没有梯度,就没有真正的学习 。
正向传播只是"表演",反向传播是"复盘",而梯度,就是复盘后发给每个人的个性化改进清单。
七、梯度常遇到的问题:为什么AI也会"学傻"?
即使有了梯度这个精准的"导航仪",神经网络在训练途中仍可能"迷路""崩溃"甚至"躺平"。
这并非模型笨,而是梯度信号在复杂高维地形中传递时,容易失真、衰减或误导 。
以下是三个最经典的"学习陷阱":
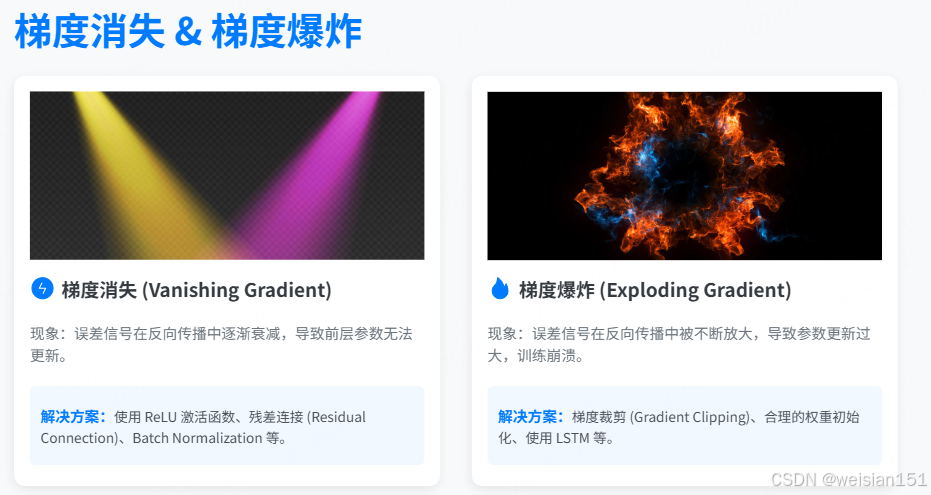
1. 梯度消失(Vanishing Gradient)
-
现象:在很深的网络中,误差信号从输出层往回传时,每过一层就"缩水"一次,到前面几层时几乎为零。
-
后果 :靠前的层(如负责识别边缘、基础特征的层)收不到有效反馈,参数几乎不更新------它们"学不动"了。
-
生活类比:
老师在教室前排怒吼:"这次考试全班不及格!"
但声音传到最后一排时只剩耳语,后排学生一脸茫然:"关我什么事?我又没考。"
于是他们继续睡觉,毫无改进。
-
解决方案:
- ReLU 激活函数:避免使用会压缩信号的 Sigmoid/Tanh,让梯度在正区间保持为1;
- 残差连接(ResNet):给信息开"高速公路",允许误差信号直接跳过多层,直达底层;
- 批归一化(BatchNorm):稳定每层输入的分布,防止信号在传递中逐渐"漂移"或"坍缩"。
2. 梯度爆炸(Exploding Gradient)
-
现象:与消失相反,某些层的梯度在反向传播中被不断放大,变得极大(如 10⁶、10⁹),导致参数更新一步跨出合理范围。
-
后果:权重变成无穷大或 NaN,loss 瞬间爆炸,训练直接崩溃。
-
生活类比:
孩子算错一道题,你暴跳如雷:"你这辈子都别碰数学了!你根本不配学!"
他吓得彻底放弃,连1+1都不敢算了------信心归零,系统宕机。
-
解决方案:
- 梯度裁剪(Gradient Clipping):设定一个阈值(如5.0),一旦梯度范数超过它,就按比例缩放回来;
- 合理的权重初始化(如 Xavier 或 He 初始化):确保信号在前向和反向传播中既不爆炸也不消失;
- 使用 LSTM/GRU 等门控机制(在 RNN 中):通过"遗忘门""输入门"控制信息流,抑制梯度失控。
3. 困在局部最优或鞍点(Local Minima & Saddle Points)
-
现象:
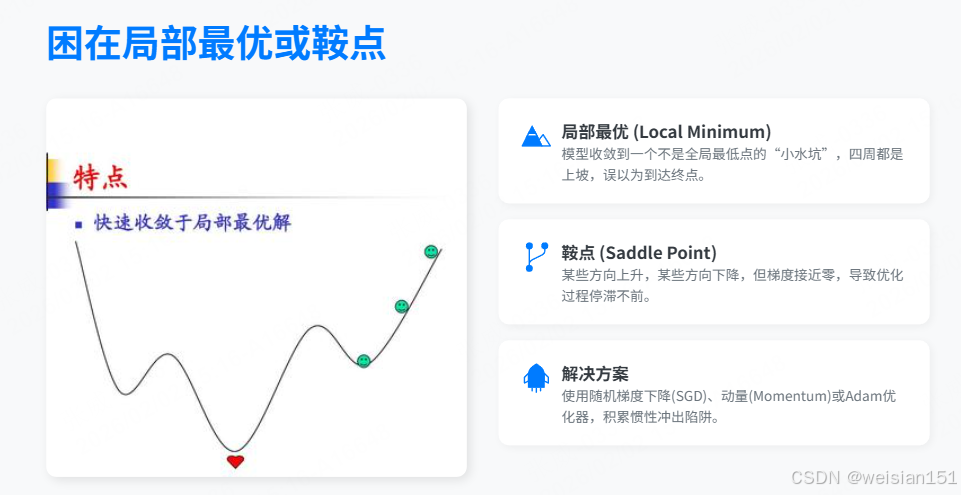
- 局部极小值:损失函数的一个"小水坑",周围都比它高,但不是全局最低点;
- 鞍点(更常见):某些方向上升、某些方向下降,但梯度≈0,模型误以为"到顶了"。
-
后果:训练提前收敛,模型性能卡在次优水平。
-
生活类比:
你在山里徒步,走到一个小山谷(海拔500米),四周都是上坡,你以为这就是"最低点"。
但其实翻过一座山,还有个真正的盆地(海拔100米)------你只是视野太窄,误判了地形。
-
解决方案:
- 随机梯度下降(SGD):每次只用一小批数据计算梯度,天然带"噪声",有助于跳出浅坑;
- 动量(Momentum):像滚球下山,积累速度惯性,即使遇到小凸起也能冲过去;
- Adam 优化器:结合动量 + 自适应学习率,对每个参数动态调整步长,既能稳又能快。
💡 本质洞察 :
这些问题的根源,都是梯度作为局部信息,在复杂非凸高维空间中无法完美代表全局趋势 。
而现代深度学习的几乎所有技巧------从激活函数、网络结构到优化器------
都在做同一件事:让梯度这个"信使",传得更远、更真、更稳。
八、总结:神经网络学习的完整闭环
让我们把整个流程串起来,用"教孩子做题"复盘一遍,看清AI是如何一步步"学会思考"的:
| 步骤 | AI术语 | 生活类比 |
|---|---|---|
| 1 | 输入数据 | 给孩子出题:"7 + 9 = ?" ------这是学习的起点 |
| 2 | 正向传播 | 孩子调动记忆、估算、心算,最终回答:"15" ------一次基于当前"知识"的预测 |
| 3 | 计算损失 | 老师批改:真实答案是16,所以 Loss = (15−16)² = 1 ------量化错误有多严重 |
| 4 | 反向传播 | 老师从结果倒推:是数字识别错了?进位漏了?还是加法规则记混了? ------追溯错误根源 |
| 5 | 计算梯度 | 精确算出每个"思维旋钮"的责任:• 数字"9"的识别权重该 −0.05 • 进位规则的偏置该 +0.1 ------为每个参数分配改进方向 |
| 6 | 梯度下降 | 微调这些权重和偏置,相当于悄悄修正孩子的"直觉"和"习惯" |
| 7 | 重复迭代 | 换新题目(如"6 + 8"),再猜、再错、再调......经过成千上万次循环,错误越来越小,反应越来越准 |

🔁 这是一个自我完善的闭环 :
预测 → 暴露错误 → 分析原因 → 精准修正 → 再预测 。没有死记硬背,没有外部灌输,只有在反馈中不断校准自己的内部机制。
这就是AI"学习"的本质 :
不是记住标准答案,而是通过海量试错,构建一套能泛化到新问题的推理系统 。
就像孩子最终不再依赖"7+9=16"这个孤立事实,而是真正理解了"个位相加满十要进一"的通用规则。
而驱动这一切的,正是那个看不见却无处不在的数学信使------梯度。
九、结语:梯度,也是人生的隐喻
其实,梯度下降不仅是AI的算法,也是人类成长的缩影。
- 我们犯错(高损失)→ 反思原因(计算梯度)→ 调整行为(参数更新)→ 再尝试(下一轮迭代)
- 有人改得太猛,反复横跳(学习率过大)
- 有人害怕犯错,不敢改变(学习率过小)
- 有人困在舒适区,以为这就是最好(局部最优)
- 但只要保持方向正确、步幅合理、持续迭代,终会走向更优的自己
🌟 梯度告诉我们:进步不需要一步登天,只需要每一次都朝着"减少错误"的方向,轻轻转动那个属于你的旋钮。
AI如此,人生亦如此。
记住 :
神经网络不是魔法,它只是一个会"从错误中学习"的数学系统;
梯度不是神秘力量,它只是微积分送给AI的一盏指路明灯。
而你,早已在不知不觉中,活成了一个最精妙的"神经网络"------
不断感知世界,做出预测,承受反馈,调整自我,走向更好的版本。
这才是真正的智能。