数据结构（初阶）笔记归纳10：二叉树

二叉树

目录

二叉树

一、二叉树的性质

二、二叉树的遍历

三、计算节点个数

四、计算叶子节点个数

五、计算树的高度

六、计算第k层节点个数

七、查找值为x的节点

八、二叉树的销毁

九、层序遍历

十、完全二叉树判断

十一、二叉树OJ

试题1：单值二叉树

试题2：相同的树

试题3：对称二叉树

试题4：二叉树的前序遍历

试题5：另一颗树的子树

试题6：二叉树的遍历

---

一、二叉树的性质

1.根节点层数为1，一颗非空二叉树的第i层上最多有2^(i-1)个节点

2.根节点层数为1，深度为h的二叉树的最大节点数是2^h - 1

3.任何二叉树，度为0的叶节点个数为n(0)，度为2的分支节点个数为n(2)，则有n(0) = n(2) + 1

4.根节点层数为1，有n个节点的满二叉树深度h = log(2)(n + 1)

二、二叉树的遍历

子树不断被拆解为根和子树

**前序遍历：**根 左子树 右子树

访问根节点的操作发送在遍历其左右子树之前

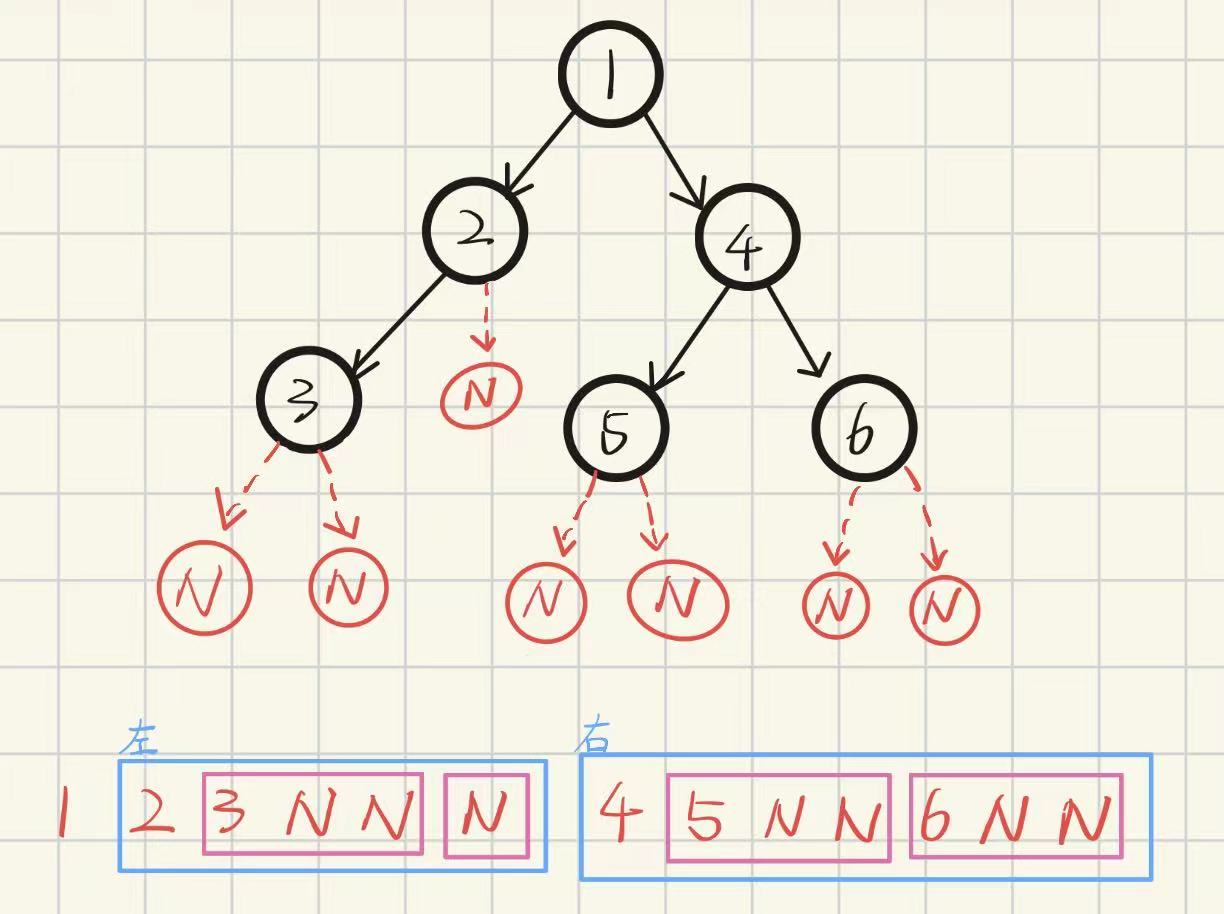
**中序遍历：**左子树 根 右子树

访问根节点的操作发送在遍历其左右子树之间

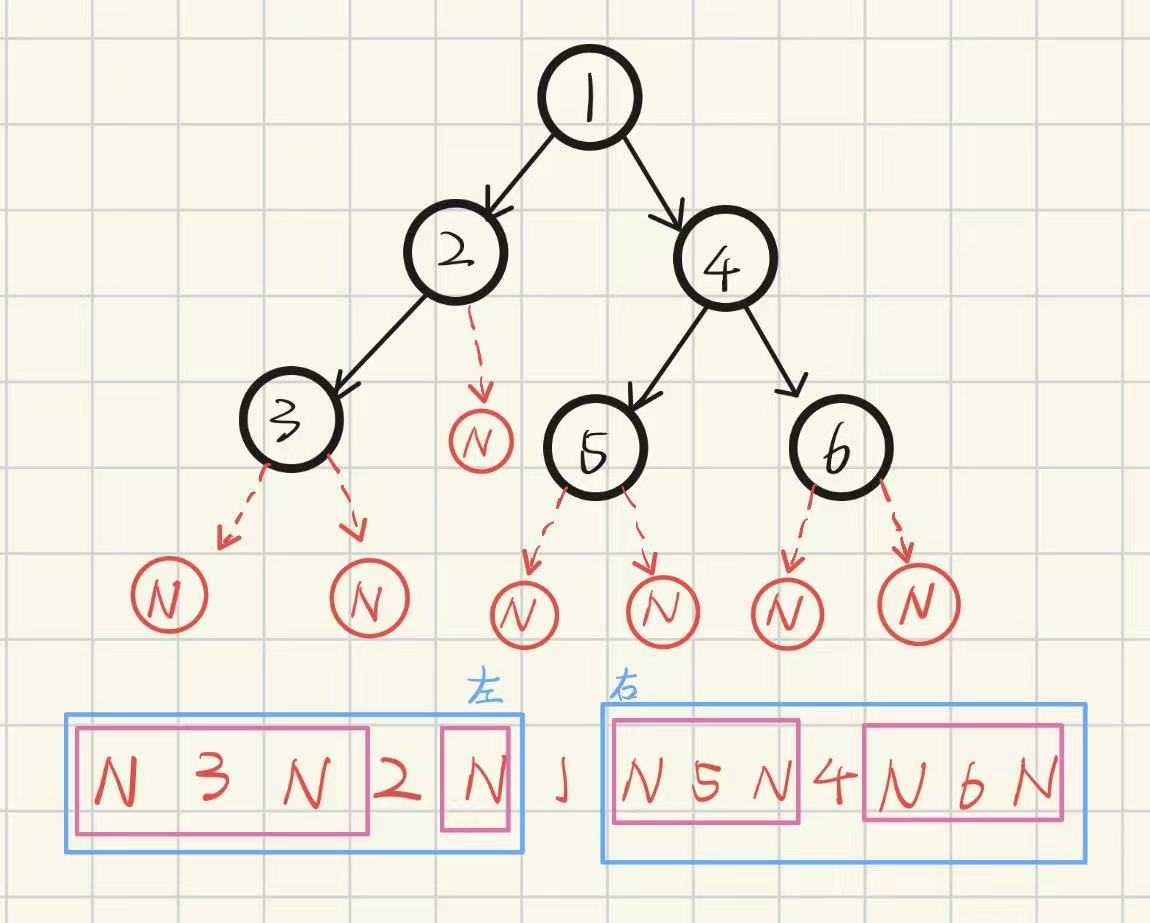
**后序遍历：**左子树 右子树 根

访问根节点的操作发送在遍历其左右子树之后

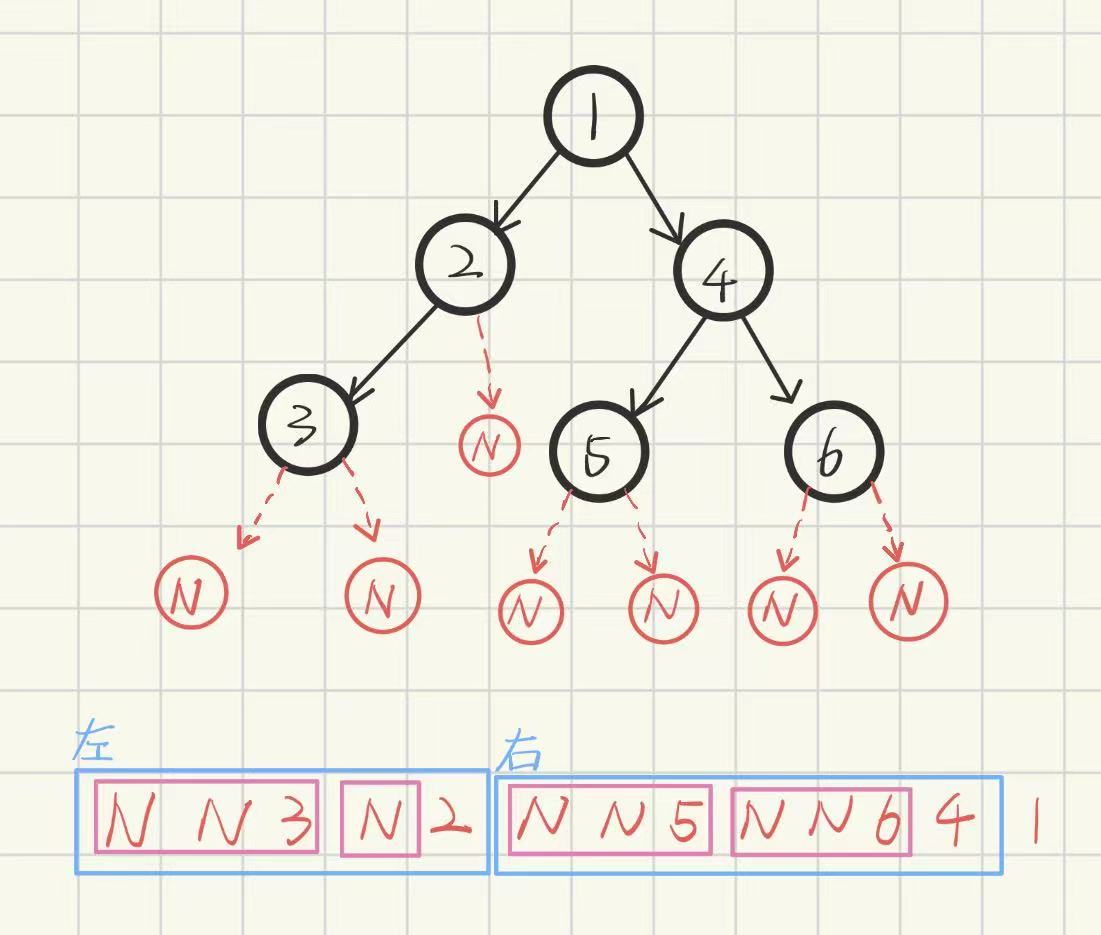
创建一颗二叉树，并且前序遍历

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>

typedef int BTDataType;

typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

BTNode* BuyNode(int x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		perror("malloc fail");
		return NULL;
	}

	node->data = x;
	node->left = NULL;
	node->right = NULL;
}

BTNode* CreatBinaryTree()
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);

	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;

	return node1;
}

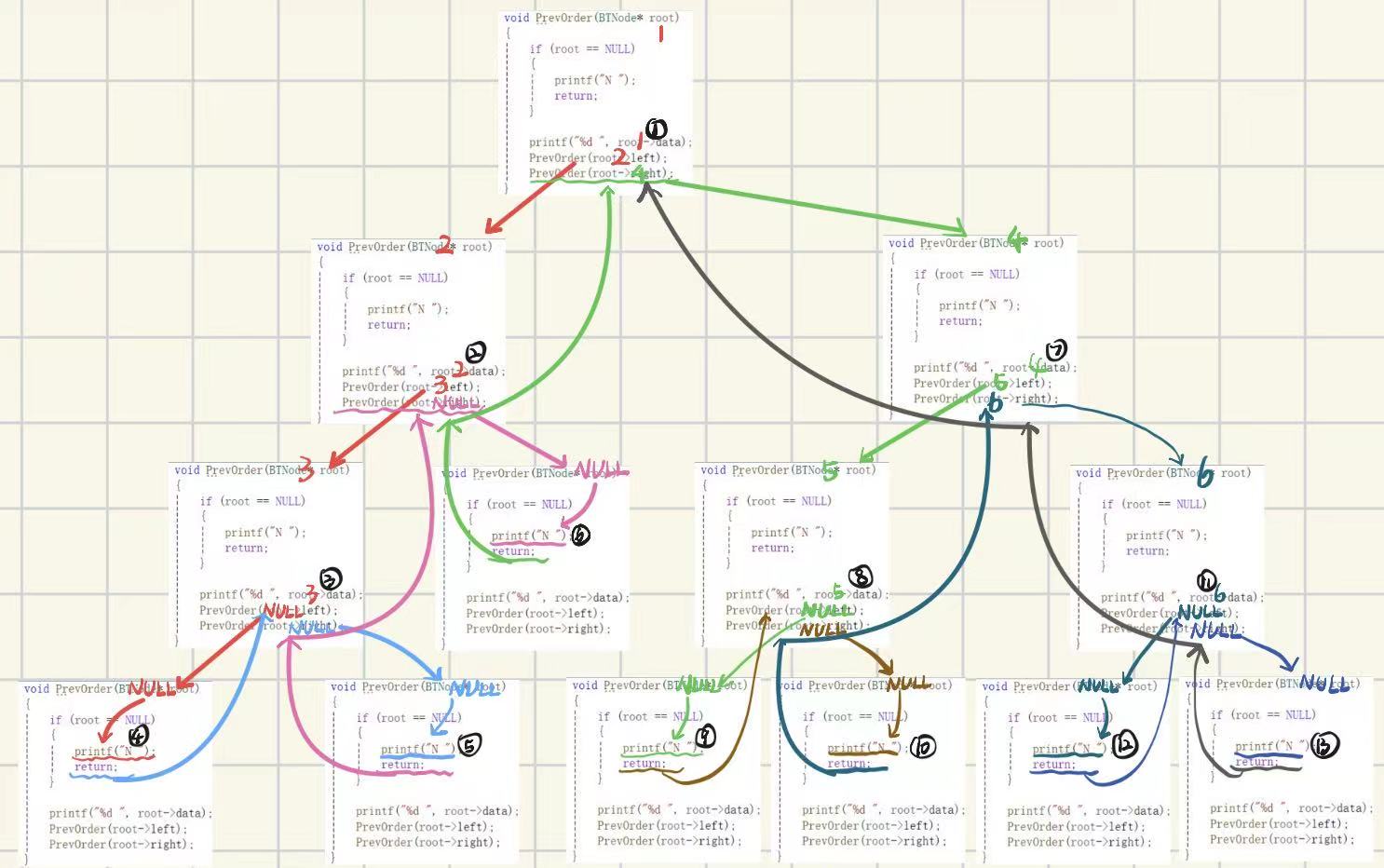
void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}

	printf("%d ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

int main()
{
	BTNode* root = CreatBinaryTree();
	PrevOrder(root);
	printf("\n");

	return 0;
}

创建一颗二叉树，并且中序遍历

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>

typedef int BTDataType;

typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

BTNode* BuyNode(int x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		perror("malloc fail");
		return NULL;
	}

	node->data = x;
	node->left = NULL;
	node->right = NULL;
}

BTNode* CreatBinaryTree()
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);

	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;

	return node1;
}

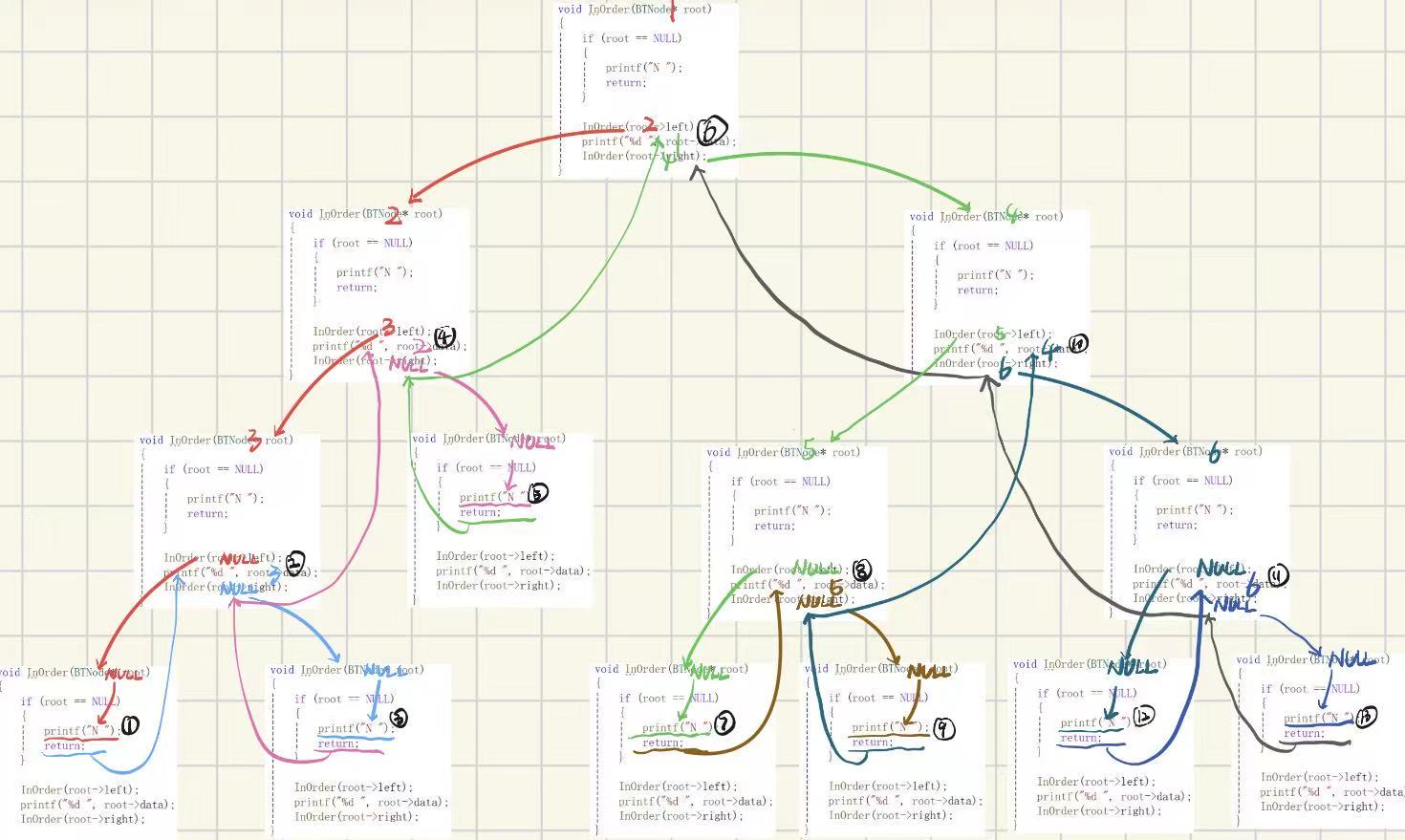
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}

	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}

int main()
{
	BTNode* root = CreatBinaryTree();
	InOrder(root);
	printf("\n");

	return 0;
}

三、计算节点个数

int TreeSize(BTNode* root)
{
	return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1
}

四、计算叶子节点个数

int TreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}

	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

五、计算树的高度

int TreeHeight(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}

	int leftHeight = TreeHeight(root->left);
	int rightHeight = TreeHeight(root->right);

	return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

六、计算第k层节点个数

int TreeLevelKSize(BTNode* root, int k)
{
	//如果当前节点是空的，说明这颗子树没有节点，返回0
	if (root == NULL)
	{
		return 0;
	}
	//如果k等于1，说明要找的就是根节点所在层，返回1
	if (k == 1)
	{
		return 1;
	}
	//子问题：第k层的节点数 = 左子树的第k-1层节点数 + 右子树的第k-1层节点数
	return TreeLevelKSize(root->left, k - 1) + TreeLevelKSize(root->right, k - 1);
}

七、查找值为x的节点

BTNode* TreeFind(BTNode* root, BTDataType x)
{
	//如果当前节点是空的，说明这条路径找不到，返回NULL
	if (root == NULL)
	{
		return NULL;
	}
	//如果当前节点的值就是x，找到了，直接返回这个节点
	if (root->data == x)
	{
		return root;
	}
	//去左子树里找
	BTNode* ret1 = TreeFind(root->left, x);
	//如果左子树找到了，就直接返回找到的节点
	if (ret1)
	{
		return ret1;
	}
	//左子树没找到，就去右子树里找
	BTNode* ret2 = TreeFind(root->right, x);
	//如果右子树找到了，也直接返回
	if (ret2)
	{
		return ret2;
	}
	//左右子树都没有找到，返回NULL
	return NULL;
}

八、二叉树的销毁

void TreeDestroy(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	TreeDestroy(root->left);
	TreeDestroy(root->right);
	free(root);
}

九、层序遍历

广度优先遍历（BFS）

#include "Queue.h"

void TreeLevelOrder()
{
	Queue q;
	QueueInit(&q);
	if (root)
	{
		QueuePush(&q, root);
	}
	while (!QueueEmty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%d ", front->data);
		if (front->left)
		{
			QueuePush(&q, front->left);
		}
		if (front->right)
		{
			QueuePush(&q, front->right);
		}
	}
	QueueDestroy(&q);
}

十、完全二叉树判断

层序遍历，空节点也入队

遇到第一个空节点时判断

后面全为空节点就是完全二叉树

int TreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
	{
		QueuePush(&q, root);
	}
	while (!QueueEmty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		//遇到第一个空，就判断队列中是否还有非空
		if (front == NULL)
		{
			break;
		}
		QueuePush(&q, front->left);
		QueuePush(&q, front->right);
	}
	while (!QueueEmty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		//如果有非空，就不是完全二叉树
		if (front)
		{
			QueueDestroy(&q);
			return false;
		}
	}
	QueueDestroy(&q);
}

十一、二叉树OJ

试题1：单值二叉树

题目内容：

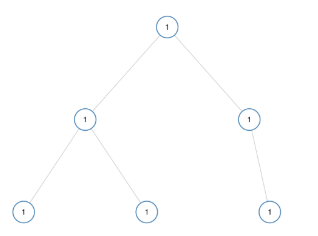
如果二叉树每个节点都具有相同的值，那么该二叉树就是单值二叉树

只有给定的树是单值二叉树时，才返回true；否则返回false

示例：

输入：[1,1,1,1,1,null,1]

输出：true

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool isUnivalTree(struct TreeNode* root) 
{
    if(root == NULL)
    {
        return true;
    }

    if(root->left && root->left->val != root->val)
    {
        return false;
    }

    if(root->right && root->right->val != root->val)
    {
        return false;
    }

    return isUnivalTree(root->left) &&  isUnivalTree(root->right);
}

试题2：相同的树

题目内容：

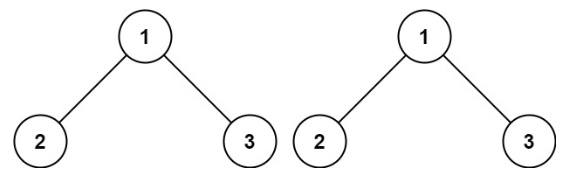
给你两棵二叉树的根节点p和q，编写一个函数来检验这两棵树是否相同

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的

示例：

输入：p = [1,2,3]，q = [1,2,3]

输出：true

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool isSameTree(struct TreeNode* p, struct TreeNode* q) 
{
    //两个都为空
    if(p == NULL && q == NULL)
    {
        return true;
    }
    //其中一个为空
    if(p == NULL || q == NULL)
    {
        return false;
    }
    if(p->val != q->val)
    {
        return false;
    }

    return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}

试题3：对称二叉树

题目内容：

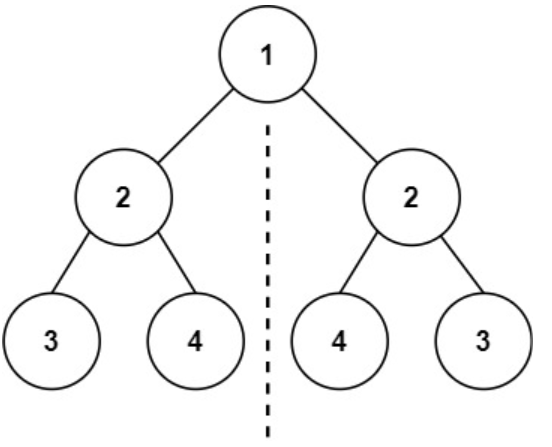
给你一个二叉树的根节点root，检查它是否轴对称

示例：

输入：root = [1,2,2,3,4,4,3]

输出：true

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool _isSymmetric(struct TreeNode* q,struct TreeNode* p)
{
    if(p == NULL && q == NULL)
    {
        return true;
    }
    if(p == NULL || q == NULL)
    {
        return false;
    }

    return (p->val == q->val) && _isSymmetric(p->left,q->right) && _isSymmetric(p->right,q->left);
}
bool isSymmetric(struct TreeNode* root) 
{
    if(root == NULL)
    {
        return true;
    }
    return _isSymmetric(root->left,root->right);
}

试题4：二叉树的前序遍历

题目内容：

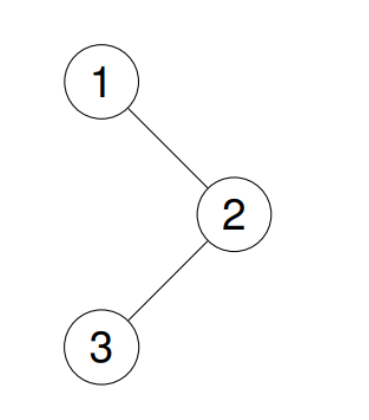
给你二叉树的根节点root，返回它节点值的前序遍历

示例：

输入：root = [1,null,2,3]

输出：[1,2,3]

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int TreeSize(struct TreeNode* root)
{
    return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

void preOrder(struct TreeNode* root,int* a,int* pi)
{
    if(root == NULL)
    {
        return;
    }
    a[(*pi)++] = root->val;
    preOrder(root->left,a,pi);
    preOrder(root->right,a,pi);
}

int* preorderTraversal(struct TreeNode* root, int* returnSize) 
{
    *returnSize = TreeSize(root);
    int* a = (int*)malloc(sizeof(int)*(*returnSize));
    int i = 0;
    preOrder(root,a,&i);
    return a;
}

试题5：另一颗树的子树

题目内容：

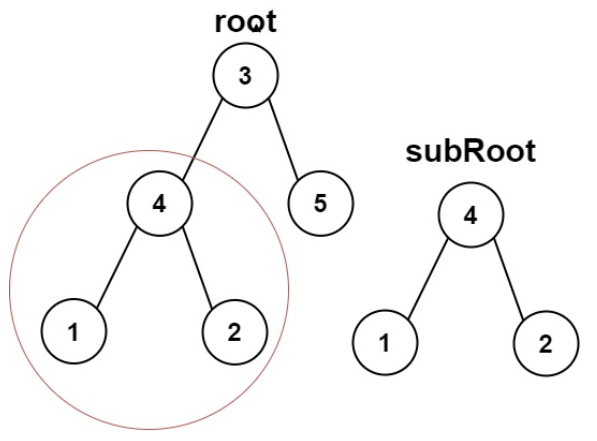
给你两棵二叉树root和subRoot，检验root中是否包含和subRoot具有相同结构和节点值的子树，如果存在，返回true，否则，返回false

二叉树tree的一棵子树包括tree的某个节点和这个节点的所有后代节点

tree也可以看做它自身的一棵子树

示例：

输入：root = [2,4,5,1,2]，subRoot = [4,1,2]

输出：true

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool isSameTree(struct TreeNode* p,struct TreeNode* q)
{
    if(p == NULL && q == NULL)
    {
        return true;
    }

    if(p == NULL || q == NULL)
    {
        return false;
    }

    if(p->val != q->val)
    {
        return false;
    }

    return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) 
{
    if(root == NULL)
    {
        return false;
    }
    if(root->val == subRoot->val && isSameTree(root,subRoot))
    {
        return true;
    }
    return isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
}

试题6：二叉树的遍历

题目内容：

读入输入的一串先序遍历字符串，用此字符串建立一个二叉树（以指针方式存储）

例如如下的先序遍历字符串： ABC##DE#G##F###

其中"#"表示的是空格，空格字符代表空树

建立起此二叉树以后，再对二叉树进行中序遍历，输出遍历结果

示例：

输入：abc##de#g##f###

输出：c b e g d f a

#include <stdio.h>
#include <stdlib.h>

typedef struct BinTreeNode
{
	char val;
	struct BinTreeNode* left;
	struct BinTreeNode* right;
}BTNode;

BTNode* CreateTree(char* a,int* pi)
{
    if(a[*pi] == '#')
    {
        (*pi)++;
        return NULL;
    }

    BTNode* root = (BTNode*)malloc(sizeof(BTNode));
    root->val = a[(*pi)++];
    root->left = CreateTree(a,pi);
    root->right = CreateTree(a,pi);
    return root;
}

void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}

	InOrder(root->left);
	printf("%c ", root->val);
	InOrder(root->right);
}

int main()
{
    char a[100];
    scanf("%s",a);
    int i = 0;
    BTNode* root = CreateTree(a,&i);
    InOrder(root);
    return 0;
}