【人工智能中的“智能”是如何实现的】从逻辑回归到神经网络（自用笔记整理）

前言

上文中我们介绍了线性回归，线性回归通过自变量的线性组合来预测一个连续的数值 📈（比如：根据面积预测房价）。然而，在现实中，我们经常面临"是非题"，即分类问题 🎯（比如：根据肿瘤大小判断是良性还是恶性）。因此就出现了逻辑回归以及进一步的神经网络。

1. 线性回归的本质

线性回归做的事情可以用一句话概括：

用一个线性函数去拟合"输入 → 连续输出"的关系

数学形式是： y = w x + b y = w x + b y=wx+b

或者多维情况： y = w 1 x 1 + w 2 x 2 + ⋯ + w n x n + b y = w_1 x_1 + w_2 x_2 + \dots + w_n x_n + b y=w1x1+w2x2+⋯+wnxn+b

• 输入 (x)：特征
• 输出 (y)：一个实数
• 目标：让预测值尽量接近真实值

---

2. 线性回归适合的场景

比如：

• 根据面积预测房价 → 3.2 万/㎡
• 根据气温预测用电量 → 1234 kWh
• 根据学习时长预测成绩 → 87.5 分

这些都有一个共同点：

👉 标签是连续的数

---

假设场景变了：

我想根据：

• 学习时长
• 平时成绩
• 出勤率

预测：

👉 能否通过考试？（通过 / 不通过）

这个标签还是连续数吗？

• 通过 = 1
• 不通过 = 0

如果你硬用线性回归：

y = w x + b y = w x + b y=wx+b

模型可能会预测出：

• 1.2
• -0.3
• 0.7
• 2.5

这些数在"通过/不通过"的语境下显然是无意义的。

---

这就是逻辑回归诞生的最核心矛盾 🎯

线性回归的输出是连续值，而分类问题需要的是"类别"

我们现在就顺着这条思路，一步步探索逻辑回归为什么会出现。

---

直接用线性回归做分类会发生什么

假设我们只有一个特征：

• (x)：学习时长
• (y)：是否通过考试（0 或 1）

真实数据可能是这样的：

学习时长 x	是否通过 y
1	0
2	0
3	0
4	1
5	1
6	1

你如果用线性回归：

y ^ = w x + b \hat y = w x + b y^=wx+b

模型可能学到一条直线：

y
1 |        *
  |      *
0 | *  *
  +------------
     x

问题 1：预测值不在 [0,1]

对一个新样本 x=10：

y ^ = 2.3 \hat y = 2.3 y^=2.3

👉 这在分类语义下毫无意义

---

问题 2：对异常点极其敏感

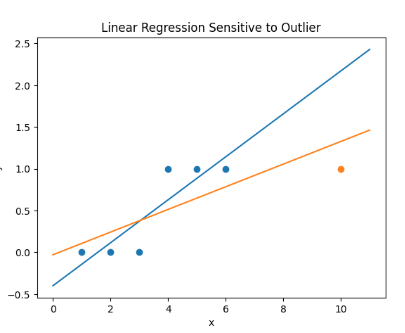
如图：

• 蓝色点：原本的正常样本

• 橙色那个孤立点：异常点 x=10

• 两条直线：

  • 一条是"没有异常点时"的回归线
  • 一条是"加入异常点后"的回归线

你可以明显看到：

只因为一个点

👉 整条直线的斜率和截距都被大幅拉偏

💥 一个极端样本，就能毁掉整个分类器

---

这暴露了线性回归的两个本质缺陷

（1）平方误差的锅

线性回归最小化：

∑ ( y − y ^ ) 2 \sum (y - \hat y)^2 ∑(y−y^)2

异常点的误差平方会巨大

模型会拼命去迎合它。

---

（2）输出空间不对

就算没有异常点：

• 直线输出是 − ∞ ∼ + ∞ -\infty \sim +\infty −∞∼+∞
• 而分类只需要"0 或 1 的概率"

---

我们真正想要的是什么？

对于分类问题，我们希望模型输出的是：

"属于某一类的概率"

也就是：

P ( y = 1 ∣ x ) P(y=1|x) P(y=1∣x)

这个值必须满足：

• 介于 0～1
• 能表示"置信度"
• 再通过阈值变成类别

因此我们需要：

把线性回归的输出

👉 压缩到 0～1 之间

👉 并解释为概率

这一步，就是：

✨ 逻辑回归 = 线性模型 + 一个非线性函数

---

这个非线性函数要满足：

1. 输入：任意实数（线性模型 (wx+b) 的结果）
2. 输出：必须在 0～1 之间
3. 单调、光滑，能表示"概率从小到大渐变"

线性回归 + 一个"压缩器"

线性回归给我们的是：

z = w x + b z = w x + b z=wx+b

但 z ∈ ( − ∞ , + ∞ ) z\in(-\infty,+\infty) z∈(−∞,+∞)，不适合当概率。

于是我们希望：

y ^ = f ( z ) \hat y = f(z) y^=f(z)

其中 (f(z)) 要满足你刚才说的 1、2、3 点。

---

最经典的选择：Sigmoid 函数

数学家们发现一个完美符合要求的函数：

σ ( z ) = 1 1 + e − z \sigma(z) = \frac{1}{1 + e^{-z}} σ(z)=1+e−z1

它的性质：

• 当 z → + ∞ z\to +\infty z→+∞， σ ( z ) → 1 \sigma(z)\to1 σ(z)→1
• 当 z → − ∞ z\to -\infty z→−∞， σ ( z ) → 0 \sigma(z)\to0 σ(z)→0
• 单调递增、光滑

图像：

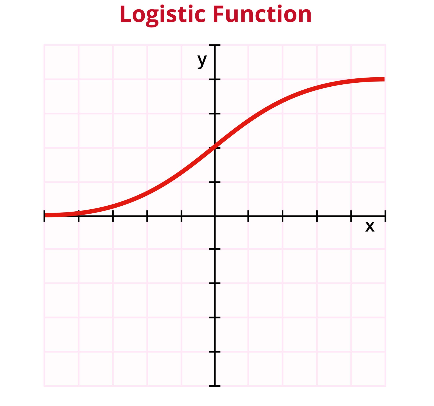
所以：

逻辑回归 = 线性模型 + Sigmoid

P ( y = 1 ∣ x ) = σ ( w x + b ) P(y=1|x) = \sigma(w x + b) P(y=1∣x)=σ(wx+b)

---

逻辑回归到底在解决什么问题？

现在可以给出更准确的答案了：

逻辑回归是为了解决

👉 "二分类问题 + 概率建模问题"

它要做的是：

• 不是直接预测 0/1

• 而是预测

  P ( y = 1 ∣ x ) P(y=1|x) P(y=1∣x)

再通过阈值：

• ≥ 0.5 → 判为 1
• < 0.5 → 判为 0

---

逻辑回归用什么损失函数？

我们现在的模型是：

p = σ ( w x + b ) p=\sigma(wx+b) p=σ(wx+b)

输出的是：

预测为 1 的概率

真实标签：

• y ∈ {0,1}

---

先用直觉想

我们希望模型：

• 当 y=1 时

  👉 p 越接近 1 越好

• 当 y=0 时

  👉 p 越接近 0 越好

---

逻辑回归真正的损失：交叉熵

损失函数是：

L = − [ y log ⁡ p + ( 1 − y ) log ⁡ ( 1 − p ) ] L = -[y\log p + (1-y)\log(1-p)] L=−[ylogp+(1−y)log(1−p)]

我们拆开看：

p定义为类别为 1 时的概率

当真实值 y=1：

L = − log ⁡ p L=-\log p L=−logp

• p=0.99 → 损失很小
• p=0.1 → 损失巨大

当真实值 y=0：

L = − log ⁡ ( 1 − p ) L=-\log(1-p) L=−log(1−p)

• p=0.01 → 损失很小
• p=0.9 → 损失巨大

---

它在干的事是：

最大化"真实类别的概率"，让损失尽可能小

也就是：

• 真实是 1，就拼命把 p 拉向 1
• 真实是 0，就拼命把 p 拉向 0

---

关键连接：通向神经网络

逻辑回归可以看作：

一个神经元！

• 输入：x
• 权重：w
• 激活函数：Sigmoid
• 损失：交叉熵

👉 这就是神经网络的最小单元

💡 神经网络 = 很多个逻辑回归的组合

---

从一个神经元到多个神经元

一个神经元太弱

只能学：

• 一条直线边界
• 线性可分问题

比如：

• 与门、或门 → 可以
• 异或 XOR → 不行

---

那就来多个神经元

假设两个：

x → [神经元1] → h1
x → [神经元2] → h2

再组合：

h1,h2 → 输出层

这就是：

单隐层神经网络！

---

为什么要多层？

关键一句话：

多层 = 自动构造特征

逻辑回归：

• 只能用"原始特征"的线性组合

神经网络：

• 第一层：学基础特征
• 第二层：学特征的特征
• 第三层：更抽象

---

举个直觉例子（图像）

• 第1层：边缘
• 第2层：形状
• 第3层：眼睛/轮廓
• 第4层：人脸

---

激活函数

如果没有激活函数：

多层 = 还是线性模型

为什么会等价？

假设两层"纯线性"：

h = W 1 x + b 1 h = W_1 x + b_1 h=W1x+b1
y = W 2 h + b 2 y = W_2 h + b_2 y=W2h+b2

代进去：

y = W 2 ( W 1 x + b 1 ) + b 2 y = W_2(W_1 x + b_1) + b_2 y=W2(W1x+b1)+b2

整理：

y = ( W 2 W 1 ) x + ( W 2 b 1 + b 2 ) y = (W_2W_1)x + (W_2b_1+b_2) y=(W2W1)x+(W2b1+b2)

👉 还是：

y = W x + b y = Wx + b y=Wx+b

再多层也逃不出线性！

---

所以神经网络的灵魂是：

✅ 非线性激活函数

没有它：

• 深度 = 0
• 表达能力 = 线性回归

---

常见激活函数的角色

1. Sigmoid

• 输出 0~1
• 适合概率
• 但有：梯度消失

2. ReLU（现在最主流）

ReLU ( x ) = max ⁡ ( 0 , x ) \text{ReLU}(x)=\max(0,x) ReLU(x)=max(0,x)

优点：

• 计算简单
• 梯度好
• 稀疏表示

3. Tanh

• -1~1
• 比 Sigmoid 对称

---

🎯 下一步：真正的分类网络

接下来必须解决：

多分类问题怎么办？

逻辑回归只能：

• 二分类
• 输出一个概率

如果是：

• 手写数字 0~9
• 10 类
• 100 类

👉 就要引出Softmax

---

假设三分类：

• 猫
• 狗
• 鸟

你觉得模型最后应该输出：

A. 一个数

B. 三个互斥概率，和为1

C. 三个互不相关的0~1

答案是B

必须输出一组"互斥且和为1"的概率。

非常漂亮！你现在的直觉已经完全是"深度学习路线"了 👍
多分类的本质：必须输出一组"互斥且和为1"的概率。

---

假设网络最后一层得到三个原始分数：

z = [ z 1 , z 2 , z 3 ] z=[z_1,z_2,z_3] z=[z1,z2,z3]

Softmax 做的事：

p i = e z i ∑ j e z j p_i=\frac{e^{z_i}}{\sum_j e^{z_j}} pi=∑jezjezi

特点：

• 每个 p i ∈ ( 0 , 1 ) p_i\in(0,1) pi∈(0,1)
• ∑ p i = 1 \sum p_i = 1 ∑pi=1
• 最大的就是预测类别

---

类比二分类

二分类时：

• Sigmoid
• 输出一个概率

多分类：

• Softmax
• 输出一组概率

Softmax = 多分类版 Sigmoid

---

一个完整神经网络结构

输入 x
 ↓
[线性层]
 ↓
ReLU
 ↓
[线性层]
 ↓
Softmax
 ↓
概率分布

训练目标：

交叉熵损失（多分类版）

---

现在我们知道：

1. 逻辑回归 = 单神经元
2. 多神经元 + 激活 = 神经网络
3. 二分类 → Sigmoid
4. 多分类 → Softmax

---

🎯 下一步最关键

只剩最后一个大问题：

这么多层参数

👉 怎么训练？

也就是：

💥 反向传播（Backprop）

假设：

• 预测是猫 0.2
• 真实是猫 1.0

我们希望：

让"对的类别"概率变大

让"错的"变小
通过误差 → 一层层反向调整权重

👉 这就是反向传播（Backpropagation）

一、先看整体流程

训练神经网络就三步循环：

1. 前向传播 → 得到预测
2. 计算损失 → 知道"错多少"
3. 反向传播 → 调整每层权重

---

1. 前向传播

x → 线性 → ReLU → 线性 → Softmax → p

得到：

• 预测概率 p
• 真实标签 y

这里的 ReLU 是为了制造非线性特征

因为我们前面提到 没有激活函数的多层 = 还是线性模型

线性 → ReLU → 线性 这个过程不是 经过ReLU后还是线性

线性 → ReLU

👉 已经实现了非线性变换

后面再接线性：

是在"非线性特征空间"里做线性

比如：

假设一维：

1. 先线性：
   z = w x + b z = wx+b z=wx+b

2. 再 ReLU：
   h = max ⁡ ( 0 , z ) h=\max(0,z) h=max(0,z)

这个 h 已经：

• 不再是 x 的线性函数
• 出现拐点！

再接：

y = w 2 h + b 2 y = w_2 h + b_2 y=w2h+b2

👉 整体绝不是直线

位置	目的
隐藏层 ReLU	构造非线性特征
最后一层 Sigmoid/Softmax	变成概率

---

ReLU 后再接线性"不是又变回线性"，

因为 ReLU 已经把数据映射到非线性空间，

后面的线性是在新特征上的组合。

---

2. 计算误差

用交叉熵：

L = − ∑ y i log ⁡ p i L = -\sum y_i \log p_i L=−∑yilogpi

衡量"有多不相信真实答案"

---

二、反向传播的直觉

核心问题：

输出层的一个错误

👉 应该怪谁？（找到主谋）

就像公司项目出问题：

• 是最后一层的锅？
• 还是前面特征提取不对？
• 每层各承担多少？

---

1. 责任分摊思想

误差会：

从后往前

一层层"分摊责任"

每个权重收到：

新权重 = 旧权重 − η ⋅ 梯度 \text{新权重} = \text{旧权重} - \eta \cdot \text{梯度} 新权重=旧权重−η⋅梯度

• η：学习率
• 梯度：这个参数对错误的贡献

---

2. 关键直觉

如果一个权重：

• 让正确类别概率变大

  👉 梯度会鼓励它

• 让错误类别变大

  👉 梯度会惩罚它

---

总结

1. 核心矛盾：连续 vs 离散

线性回归的局限： 输出空间是 ( − ∞ , + ∞ ) (-\infty, +\infty) (−∞,+∞)。在分类任务（如考试通过/不通过）中，线性回归会产生无意义的预测值（如 2.5 或 -0.3），且极易受到异常值的干扰。

需求： 我们需要一个能把预测值压缩在 [0, 1] 之间，并能解释为"概率"的模型。

2. 逻辑回归：分类的基石

公式： 逻辑回归 = 线性模型 ( w x + b ) + Sigmoid函数 \text{逻辑回归} = \text{线性模型} (wx + b) + \text{Sigmoid函数} 逻辑回归=线性模型(wx+b)+Sigmoid函数。

Sigmoid ：

它将任意实数映射到 ( 0 , 1 ) (0, 1) (0,1)。

损失函数：不再使用平方误差，而是使用交叉熵（Cross-Entropy）。其核心直觉是：如果真实标签是 1，模型预测概率越接近 0，惩罚就越大（趋于无穷）。

3. 从单神经元到神经网络

逻辑回归 = 最小单元：一个逻辑回归就是一个神经元。

多层网络：

隐藏层：通过多个神经元的组合，自动构造、提取特征（如从像素点提取到边缘，再到形状）。

激活函数（ReLU/Sigmoid）：赋予模型非线性能力。如果没有它，再深的网络也只是一个复杂的线性模型。

4. 多分类的跨越：Softmax

场景升级：当面对猫、狗、鸟等多个类别时，Sigmoid（输出单概率）不再适用。

Softmax 作用：将网络最后一层的得分（Logits）转化为一个互斥且和为 1 的概率分布。

p i = e z i ∑ e z j p_i = \frac{e^{z_i}}{\sum e^{z_j}} pi=∑ezjezi

最大概率对应的索引即为预测类别。

5. 训练的灵魂：反向传播 (Backpropagation)

前向传播：数据通过一层层计算，得到预测概率。

反向传播：

通过链式法则，将最后一层的误差（损失）从后往前分摊到每一个权重参数上。

更新规则： w n e w = w o l d − η ⋅ ∂ L ∂ w w_{new} = w_{old} - \eta \cdot \frac{\partial L}{\partial w} wnew=wold−η⋅∂w∂L（权重 = 原权重 - 学习率 × 梯度）。

目的：让正确类别的概率越来越大，错误类别的概率越来越小。