【C语言】 数组函数与排序算法

数组的输入输出函数

数组与函数参数传递

在C语言中，数组作为函数参数传递时，传递的是数组的首地址（指针），而不是整个数组的副本。因此，为了在函数中正确处理数组，通常需要两个参数：

• 数组的地址：即数组名，它代表数组第一个元素的地址。
• 数组的元素个数：因为函数内部无法直接获取数组长度。

数组输入函数设计

设计一个通用的数组输入函数，可以接收用户输入并为数组赋值。

void arrayInput(int *p, int num) {
    for (int i = 0; i < num; i++) {
        printf("请输入第 %d 个元素: ", i + 1);
        scanf("%d", &p[i]);  // 等价于 p + i 或 *(p + i)
    }
}

说明：

• p 是指向整型的指针，接收数组首地址。
• num 表示数组元素个数。
• p[i] 等价于 *(p + i)，都是访问数组第 i 个元素。

数组输出函数设计

设计一个通用的数组输出函数，用于打印数组的所有元素。

void arrayOutput(int *p, int num) {
    printf("数组元素为：");
    for (int i = 0; i < num; i++) {
        printf("%d ", p[i]);  // 也可用 *(p + i)
    }
    printf("\n");
}

示例

#include <stdio.h>
#pragma warning(disable : 4996)

void arrayInput(int *p, int num);
void arrayOutput(int *p, int num);
int main(void)
{
    int a[5] = {1, 2, 3, 4, 5};
    arrayInput(a, 5);
    arrayOutput(a, 5); // 此处a == &a[0],int *
    return 0;
}

void arrayInput(int *p, int num)
{
    // 当主函数第8行，调用函数后，int *p = a
    // 因此a[0] ~ a[4]可以用p[0] ~ p[4]替代
    for (int i = 0; i < num; i++)
    {
        scanf("%d", &p[i]); // p + i
        // p[i] == *(p+i)
        //&p[i] == &*(p+i) == p + i
    }
}

void arrayOutput(int *p, int num)
{
    // 当主函数第8行，调用函数后，int *p = a
    // 因此a[0] ~ a[4]可以用p[0] ~ p[4]替代
    for (int i = 0; i < num; i++)
    {
        printf("p[%d] = %d\n", i, p[i]); // 此处p[i]还可以用 *(p+i)代替
    }
}

注意：

• 数组名 a 即 &a[0]，类型为 int *。
• 在函数内部对数组元素的修改会影响原数组，因为传递的是地址。

排序问题

排序是将一组数据按照某种规则（升序或降序）重新排列的过程。排序的目的是提高数据的可读性、查询效率和数据处理速度。

排序的重要性与分类

重要性：

• 便于数据检索与分析
• 提高算法效率（如二分查找要求数据有序）
• 数据去重与统计

分类：

• 内部排序：数据全部加载到内存中进行排序（如冒泡、快速、希尔排序）。
• 外部排序：数据量过大，需借助外存进行排序（如归并排序的外部版本）。

冒泡排序

设计思想与名称由来

冒泡排序是一种简单的交换排序算法。其基本思想是：

重复遍历待排序序列，依次比较相邻两个元素，若顺序错误则交换。遍历直到没有元素需要交换为止。

名称由来：较小的元素会逐渐"浮"到序列顶端，如同气泡上浮。

流程演示与步骤解析

流程演示：

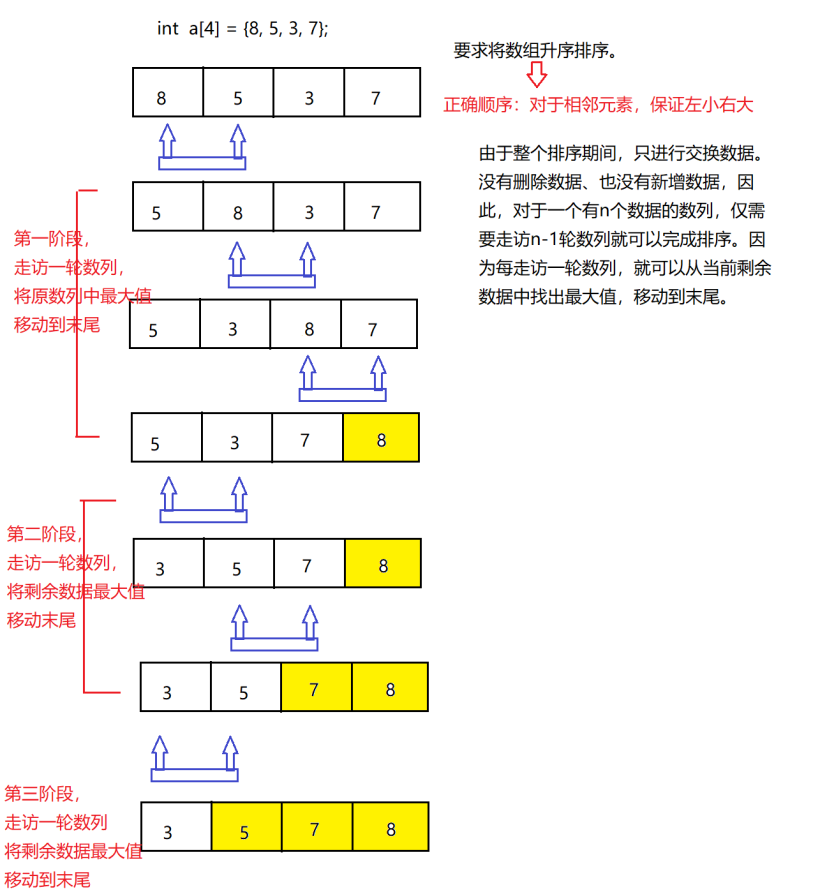
假设数组 arr = [5, 3, 8, 1, 2]，按升序排序：

第一轮：
5 3 8 1 2 → 3 5 8 1 2
3 5 8 1 2 → 3 5 8 1 2
3 5 8 1 2 → 3 5 1 8 2
3 5 1 8 2 → 3 5 1 2 8

第二轮：
3 5 1 2 8 → 3 5 1 2 8
3 5 1 2 8 → 3 1 5 2 8
3 1 5 2 8 → 3 1 2 5 8

第三轮：
3 1 2 5 8 → 1 3 2 5 8
1 3 2 5 8 → 1 2 3 5 8

第四轮：
1 2 3 5 8 → 已有序，结束

代码实现与优化

基础版本：

void bubbleSort(int arr[], int n) {
    for (int i = 0; i < n - 1; i++) {
        for (int j = 0; j < n - 1 - i; j++) {
            if (arr[j] > arr[j + 1]) {
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

优化版本（添加标志位判断是否已有序）：

void bubbleSortOptimized(int arr[], int n) {
    for (int i = 0; i < n - 1; i++) {
        int swapped = 0;  // 标记是否发生交换
        for (int j = 0; j < n - 1 - i; j++) {
            if (arr[j] > arr[j + 1]) {
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
                swapped = 1;
            }
        }
        if (swapped == 0) break;  // 若未交换，则已有序
    }
}

时间复杂度分析：

• 最优情况：数组已有序，时间复杂度为 O(n)。
• 最坏情况：数组完全逆序，时间复杂度为 O(n²)。
• 平均情况：时间复杂度为 O(n²)。

空间复杂度：O(1)，原地排序。

插入排序

设计思想

插入排序是一种简单直观的排序算法，其工作原理类似于整理扑克牌。它的基本思想是：

将数组分为已排序和未排序两部分，初始时已排序部分只包含第一个元素。然后依次将未排序部分的元素插入到已排序部分的正确位置，直到所有元素都插入完毕。

形象比喻：就像打扑克牌时，我们一张一张地拿起牌，并将每张新牌插入到手中已有牌的正确位置。

排序过程详解

初始状态

假设有数组：[5, 3, 8, 1, 2]

初始： [5] | 3, 8, 1, 2
已排序↑     ↑未排序

步骤1：处理第二个元素3

• 比较3和5，3<5，将3插入到5前面
• 结果：[3, 5] | 8, 1, 2

步骤2：处理第三个元素8

• 比较8和5，8>5，位置不变
• 结果：[3, 5, 8] | 1, 2

步骤3：处理第四个元素1

• 从右向左比较：1<8，右移8；1<5，右移5；1<3，右移3
• 将1插入到首位
• 结果：[1, 3, 5, 8] | 2

步骤4：处理第五个元素2

• 从右向左比较：2<8，右移8；2<5，右移5；2<3，右移3；2>1，停止
• 将2插入到1后面
• 结果：[1, 2, 3, 5, 8]

代码实现

void insertionSortWithSteps(int arr[], int n) {
    printf("初始数组: ");
    printArray(arr, n);
    printf("\n");
    
    for (int i = 1; i < n; i++) {
        int key = arr[i];
        printf("处理元素 arr[%d] = %d\n", i, key);
        
        int j = i - 1;
        while (j >= 0 && arr[j] > key) {
            printf("  将 arr[%d]=%d 移动到 arr[%d]\n", j, arr[j], j+1);
            arr[j + 1] = arr[j];
            j--;
        }
        
        if (j + 1 != i) {
            printf("  插入 %d 到 arr[%d]\n", key, j+1);
            arr[j + 1] = key;
        } else {
            printf("  %d 已在正确位置\n", key);
        }
        
        printf("当前状态: ");
        printArray(arr, n);
        printf("\n");
    }
}

希尔排序

设计思想与增量分组

希尔排序是插入排序的改进版本，也称为"缩小增量排序"。其核心思想是：

将整个序列按增量分组，对每组进行插入排序；随着增量逐渐减小，序列逐渐趋于有序，最后当增量为1时，进行最后一次插入排序。

特点与优势分析

特点：

1. 分组排序：减少大规模数据移动。
2. 多组同时进行：提高排序效率。
3. 不稳定排序：相等元素可能在排序后改变相对位置。

优势：

• 相较于直接插入排序，减少了数据移动次数。
• 适合中等规模数据排序。

流程示意图解析

初始序列：[9, 8, 7, 6, 5, 4, 3, 2, 1]

增量 h = 4：
分组：[9,5,1]、[8,4]、[7,3]、[6,2]
组内排序：[1,5,9]、[4,8]、[3,7]、[2,6]
合并：[1,4,3,2,5,8,7,6,9]

增量 h = 2：
分组：[1,3,5,7,9]、[4,2,8,6]
组内排序：[1,3,5,7,9]、[2,4,6,8]
合并：[1,2,3,4,5,6,7,8,9]

增量 h = 1：
直接插入排序，最终有序。

代码实现示例

void shellSort(int arr[], int n) {
    for (int gap = n / 2; gap > 0; gap /= 2) {
        for (int i = gap; i < n; i++) {
            int temp = arr[i];
            int j;
            for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {
                arr[j] = arr[j - gap];
            }
            arr[j] = temp;
        }
    }
}