欧氏内积（Euclidean Inner Product）是n维欧几里得空间（ℝ𝑛）中定义的一种基础运算，通常称为点积或数量积。它将两个向量映射为一个标量，计算规则为对应分量乘积之和，即
⟨𝑥,𝑦⟩=𝑛𝑖=1𝑥𝑖𝑦𝑖
。该内积满足对称、正定、数乘和可加性，用于定义向量的长度、角度和距离。
关键特性与定义
-
定义 ：对于向量
𝑥=(𝑥1,𝑥2,...,𝑥𝑛) 和𝑦=(𝑦1,𝑦2,...,𝑦𝑛)，欧氏内积即标准点积：
⟨𝑥,𝑦⟩=𝑥1𝑦1+𝑥2𝑦2+...+𝑥𝑛𝑦𝑛
-
物理/几何意义 ：内积
𝑥⋅𝑦 等于
𝑥 的模（长度）与 
𝑦 在 
𝑥 方向上投影的乘积，也可表示为 
𝑥⋅𝑦=‖𝑥‖‖𝑦‖cos𝜃，其中
𝜃 是向量间夹角。 -
性质 ：
-
对称性 ：
⟨𝑥,𝑦⟩=⟨𝑦,𝑥⟩
-
正定性 ：
⟨𝑥,𝑥⟩≥0，且
⟨𝑥,𝑥⟩=0 当且仅当𝑥=0 -
线性 ：
⟨𝑐𝑥+𝑦,𝑧⟩=𝑐⟨𝑥,𝑧⟩+⟨𝑦,𝑧⟩
-
-
几何应用 ：
-
长度（范数） ：
-
夹角 ：
cos𝜃=⟨𝑥,𝑦⟩‖𝑥‖‖𝑦‖
-
距离 ：
𝑑(𝑥,𝑦)=‖𝑥−𝑦‖=(𝑥𝑖−𝑦𝑖)2
-
欧氏内积在几何、物理及机器学习中的特征向量计算中起着基础性作用。
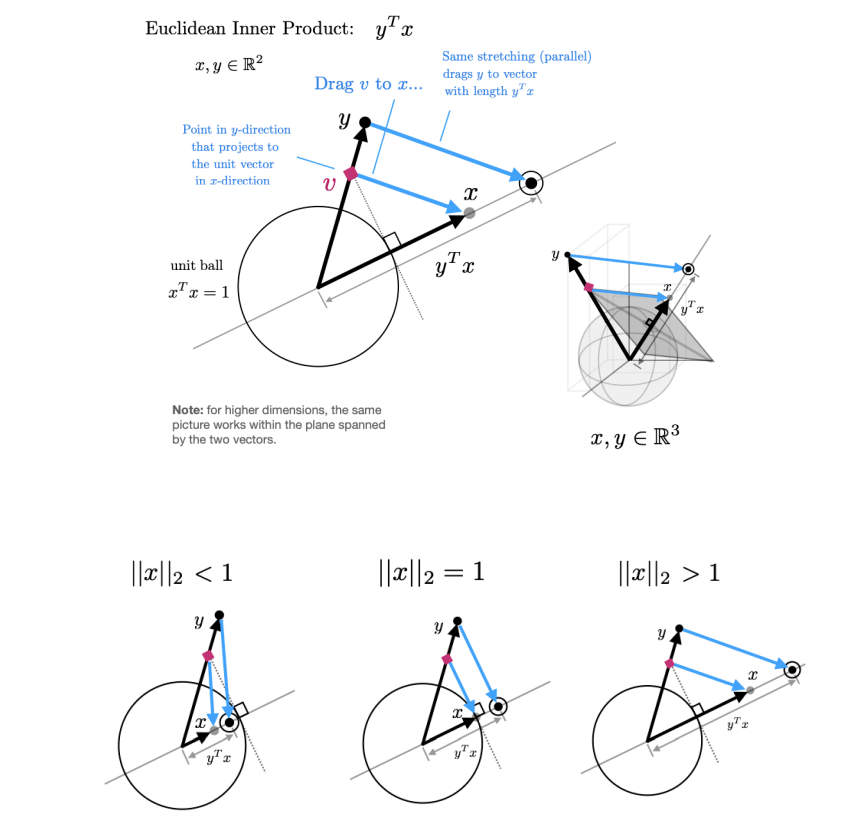
概述：
这张图片展示了欧几里得内积（Dot Product/Inner Product，即 或
）的一种非常巧妙的几何解释。
这里的蓝色箭头和线条并不是代表向量的移动，而是代表一种线性比例关系（Scaling） ，或者更直观地说，利用相似三角形原理来通过作图求解内积的数值。
以下是详细的步骤讲解：
1. 核心概念：相似与比例
这张图试图用几何作图的方式来计算 。
-
常规理解： 我们通常把内积理解为"
在
-
图中理解： 图中通过蓝色平行线构建了一个比例关系，把这个乘法运算变成了几何上的"拉伸"或"缩放"。
2. 关键元素解读
要看懂蓝色箭头，首先要看懂图中那个粉色的菱形点 ：
-
粉色点 v： 这是一个位于向量 y 方向上的辅助点。它的位置是特意选定的，使得它向 x 轴做垂线投影时，恰好落在单位圆（Unit Ball）与 x 轴的交点上（即长度为 1 的地方）。
- 数学含义：v 的投影长度为 1。
3. 蓝色箭头的具体意义
图中的两条蓝色带箭头的线段是平行 的（注意图中标注的平行符号 //）。这构成了相似三角形：
-
第一条蓝色线（基准线）： 连接粉色点 v 和向量 x 的顶点（灰色点）。
- 这就建立了一个"基准比例"：从"单位投影长度（1）"到"实际向量 x 长度"的映射关系。
-
第二条蓝色线（结果线）： 连接向量 y 的顶点和 x 轴上的空心圆点（结果点）。
- 因为这条线与第一条线平行，根据相似三角形定理（或截线定理），它将同样的比例应用到了 y 身上。
4. 总结：蓝色箭头表征的操作
蓝色箭头表征的是"同比例拉伸/缩放"的过程。
逻辑链条如下：
-
比例源头： 既然点 v（投影为1）通过蓝色连线对应到了向量 x（长度为
-
比例应用： 那么向量 y（是 v 的某个倍数）通过平行的蓝色连线，就会对应到结果点
-
数学验证：
-
根据相似三角形：
-
所以：
-
因为 v 的投影是 1，在直角三角形中
-
代入公式：
-
这正是内积的定义！
-
简单来说
蓝色箭头告诉你："你看，v 点和 x 点是怎么连线的？照着这个斜率，把 y 点也连一条平行线射到 x 轴上，那个落点就是内积的数值。"
底部的三个小图分别展示了当 x 的长度小于 1、等于 1、大于 1 时，这个"落点"（内积值）相对于 y 的原始投影是被"缩小"、"不变"还是"放大"了。
详述
我先按图里的几条"线索"把欧氏内积 讲清楚：它既是投影长度 ，也是"对齐程度×长度缩放"。
1) 欧氏内积是什么
对 ，欧氏内积（点积）定义为
它是一个标量（有正负号）。
2) 图中最核心的几何意义：投影
上半部分的大图，在 里画了两根向量 x（灰/黑）和 y（黑），并画了从 y 到 x 方向的垂足（那个直角符号）。
关键公式是：
其中 θ 是 x 与 y 的夹角。
当 x 是单位向量（∥x∥=1）时
这正是 y 在 x 方向上的"有符号投影长度"。
-
图里沿着 x 那条斜线标出来的那段长度就是
-
直角投影说明：你把 y 垂直"摁"到 x 所在直线上，落点到原点的距离（带符号）就是内积。
符号怎么理解：
-
θ<90∘：同向分量为正，
-
θ=90∘：正交，
-
θ>90∘：反向分量为负，
3) 图里蓝色"拖拽"在表达什么
蓝色箭头写着 "Same stretching (parallel) ... with length "（同样的伸缩/平移）。
它想强调两点：
-
向量可以平移不变形：把 y 平移到以 x 端点为起点的位置（图中蓝色平行移动），投影长度不变------内积只取决于方向与长度，不取决于你画在平面哪里。
-
内积对"沿 x 方向的分量"做测量：蓝色标出的最终那段长度就是"把 y 拉到 x 方向上能得到多少"。
图中的粉色点 v（在 y 的方向上）配合"unit ball "的圆，直观上是在告诉你：
用"单位长度"的 x 做尺子 ，去量 y 在 x 方向上到底有多长（就是
4) 下方三幅小图：∥x∥ 影响"缩放倍数"
下排分别画了：
-
∥x∥2<1
-
∥x∥2=1
-
∥x∥2>1
这是在强调：
(y 在 x 单位方向上的投影长度)
也就是：
- x 更短（∥x∥<1）：同样的对齐程度，内积数值更小（"尺子更短，量出来更小"）。
- x 在单位圆内部。
- y 的正交投影 v 落在 x 的延长线上，但因为 ||x|| < 1，v 可能落在 x 向量之外。
- 最终拖出的蓝色向量（长度 yᵀx）会比投影段短，体现内积的"收缩"效果。
- x 是单位向量（∥x∥=1）：内积就是纯投影长度。
- x 是单位向量（落在单位圆上）。
- y 的投影直接落在 x 上，粉红色点到原点的距离就是 |yᵀx|。
- 内积 yᵀx 等于 y 在 x 方向上的有向投影长度（带正负号，取决于角度是否锐角）。
- x 更长（∥x∥>1）：同样的对齐程度，内积被放大（"尺子更长，量出来更大"）
- x 在单位圆外部。
- 投影 v 落在 x 向量内部。
- 最终拖出的蓝色向量会比投影段长，体现内积的"放大"效果。
这三张图完美说明了：内积的大小不仅取决于 y 的投影长度，还取决于 x 的长度 ||x||。当 ||x|| ≠ 1 时，需要额外的伸缩。
5) 扩展到 / 更高维
右上角的小 3D 图写着：在更高维同样成立。原因是：
无论在几维里，x 和 y 张成的空间最多是一个二维平面 ；内积的几何关系（夹角、投影）都可以在这个平面里看，跟 完全同构。
一句话总结
-
欧氏内积
-
它衡量：两向量有多同向 （cosθ）以及各自有多长（∥x∥∥y∥）。
我们在这张图的基础上再"往下挖"三层：投影公式怎么从内积推出来 、为什么它能当"相似度" 、以及在机器学习/矩阵里它具体干什么用。
6) 从内积推出"投影向量"公式（不仅是投影长度）
图里标的是投影长度 （当 ∥x∥=1 时）。更一般地，我们关心的是：
y 在 x 方向上的那一整段"影子向量"到底是什么？
设投影向量是 ，它一定跟 x 同方向，所以可以写成
关键是找 α。
投影的定义是：误差 y−αx 与 x 正交（图里的直角符号就是这个意思）：
展开：
所以
-
如果 ∥x∥=1，那么
此时"投影长度"就是
7) 为什么内积能表示"对齐程度"？------把长度因素剥离出来
图里给了 ，但它同时受角度 和长度影响：
很多时候我们只想要"方向是否一致"，不想被长度干扰，于是用余弦相似度：
直观解释（跟图对上）：
-
内积 = "把 y 沿 x 方向的分量拿出来" × "∥x∥ 的缩放"
-
再除以 ∥y∥∥x∥，就只剩"纯对齐" cosθ
8) 正交（内积为 0）到底意味着什么
这在图上就是：投影点落在原点（投影长度 0）。
更"实用"的理解：
-
x 方向上完全没有 y 的分量
-
用 x 作为"测量尺"，测不到 y 在该方向上的任何成分
-
在数据里经常等价于"互不干扰/不相关"（注意：统计"零相关"是更强条件，和几何正交相关但不完全等同）
9) 一个超关键的不等式：内积不会"乱跑"（柯西-施瓦茨）
图里下方强调了 ∥x∥ 会放大/缩小内积。那它的上界是什么？
等号何时成立？------当且仅当 y 与 x 共线（完全同向或反向）。
这跟图的直觉一致：
-
**最"对齐"**时，投影长度达到最大（就是 ∥y∥∥x∥）
-
越偏离，cosθ 越小，内积越小
10) 跟"距离/平方长度"的关系：内积是最常用的展开工具
欧氏范数的平方可以用内积写：
两点距离平方：
这条在机器学习里非常常用：
-
最小二乘 、K-means 、SVM 的间隔计算...都离不开这类展开
-
你会反复看到
11) 内积的"线性"特性：为什么它像一个测量仪器
内积对每个输入都是线性的（准确说是双线性）：
这意味着：
把
所以图里"把 y 拖到 x 方向量长度"的直觉，其实对应了一个很深的观点：
- 固定 y，函数
12) 数值例子（把"投影长度/正负/缩放"一次看懂）
取
内积：
，投影长度（y 在 x 方向上的有符号长度）是：
投影向量是：
也就是说，这个例子里 y 在 x 方向上的"影子向量"刚好等于 x 本身（很直观：y 在 x 方向的分量挺大）。
如果把 y 换成 ，那么
投影长度变负，表示"主要沿 x 的反方向"。