队列和宽搜
N 叉树的层序遍历
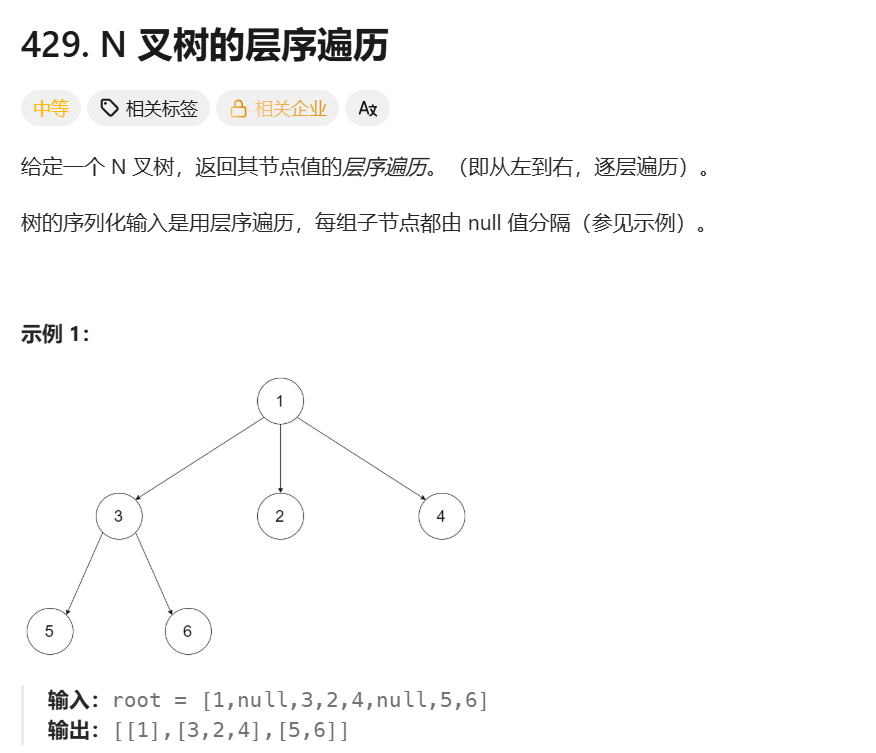
**思路:**借助队列,先将根节点放入队列中,然后将根节点从队列取出的时候将根节点的所有孩子加入队列中,依次类推,每个孩子从队列取出的时候,在将这个孩子的孩子节点放入队列中,直到队列为空,即所有元素都被取出且没有元素再进入,就完成了层序遍历。
代码:
cpp
/*
// Definition for a Node.
class Node {
public:
int val;
vector<Node*> children;
Node() {}
Node(int _val) {
val = _val;
}
Node(int _val, vector<Node*> _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public:
vector<vector<int>> levelOrder(Node* root) {
if(root == NULL)
return {};
queue<Node*> q;
vector<vector<int>> ret;
q.push(root);
while(!q.empty()){
int n = q.size();
vector<int> tmp;
for(int i = 0; i < n; i++){
Node* node = q.front();
q.pop();
tmp.push_back(node->val);
for(auto& child : node->children){
q.push(child);
}
}
ret.push_back(tmp);
}
return ret;
}
};二叉树的锯齿形层序遍历
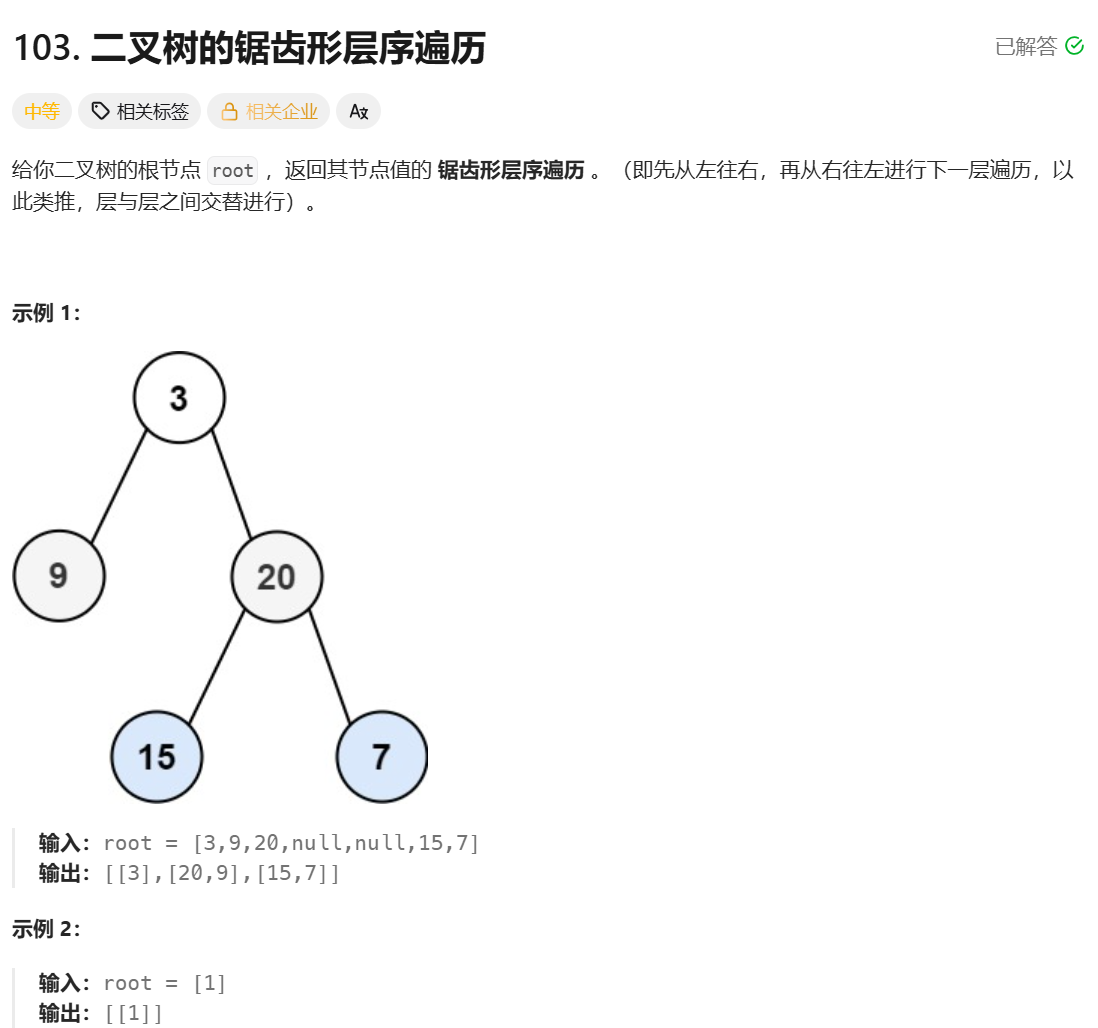
**思路:**借助队列,先将根节点放入队列中,然后将根节点从队列取出的时候将根节点的所有孩子加入队列中,依次类推,每个孩子从队列取出的时候,在将这个孩子的孩子节点放入队列中,直到队列为空,即所有元素都被取出且没有元素再进入,就完成了层序遍历。上面是正常的层序遍历方式,但是这道题要求锯齿形,其实就是偶数层元素需要逆序,例如第二层的 9,20,放入数组的顺序应该是 20,9,这个效果只需要一个标记变量就行,根据标记变量的值判断是否需要对这一层的元素进行逆序。
代码:
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
vector<vector<int>> ret;
if(root == NULL)
return ret;
queue<TreeNode*> q;
q.push(root);
int level = 1;
while(!q.empty()){
int n = q.size();
vector<int> tmp;
for(int i = 0; i < n; i++){
TreeNode* node = q.front();
q.pop();
tmp.push_back(node->val);
if(node->left)
q.push(node->left);
if(node->right)
q.push(node->right);
}
if(level % 2 == 0)
reverse(tmp.begin(), tmp.end());
ret.push_back(tmp);
level++;
}
return ret;
}
};二叉树最大宽度
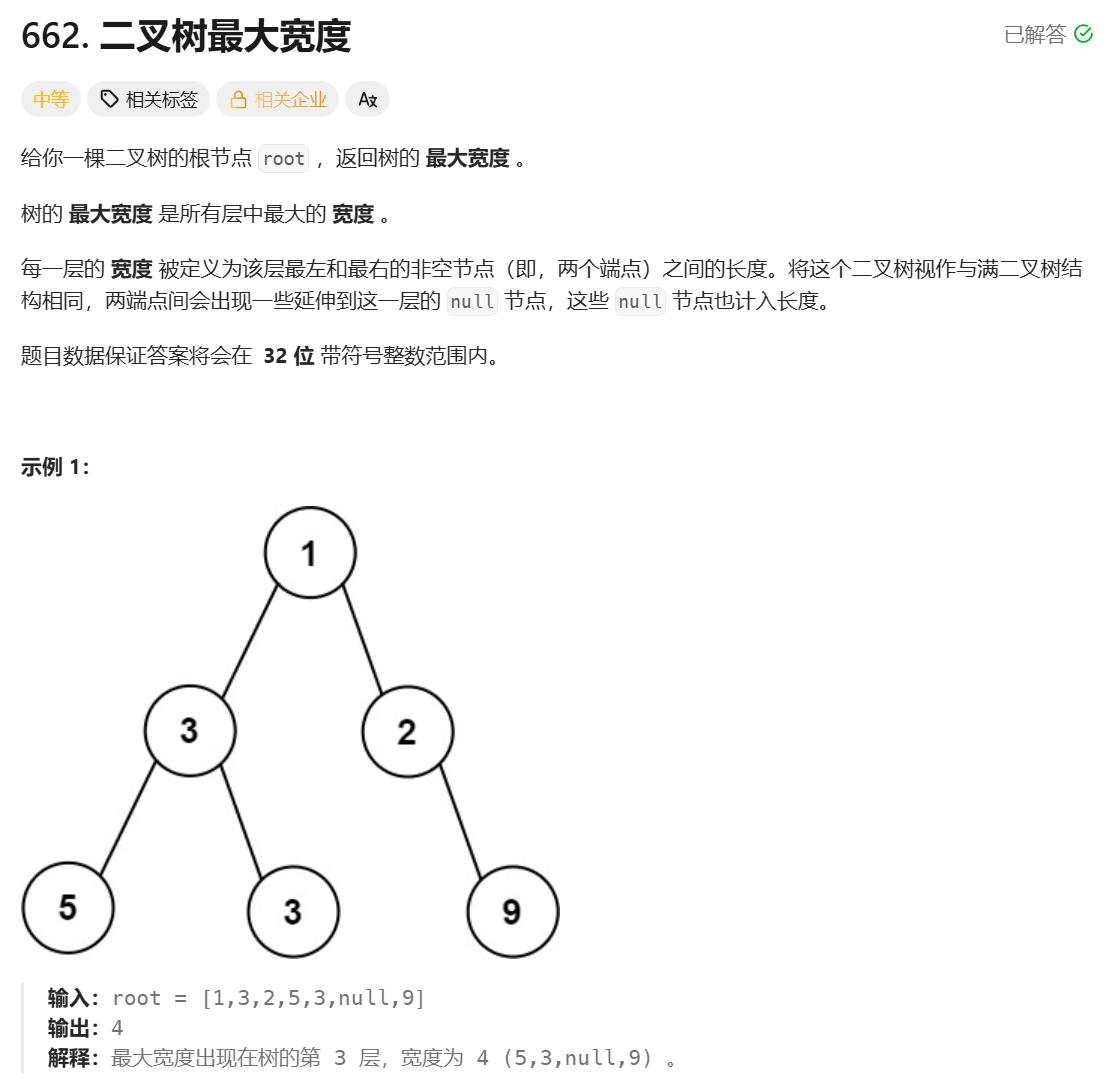
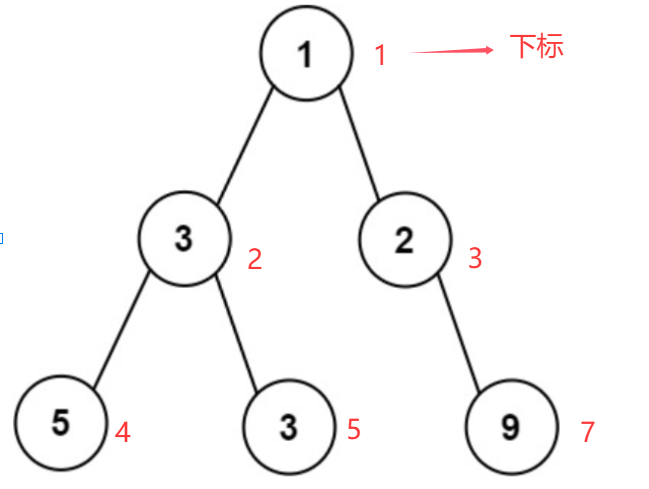
**思路:**还是借助栈遍历二叉树(下面代码使用数组模拟的栈),利用数组存储二叉树的方式(也就是堆),给每个节点编号,然后栈存储 pair<TreeNode*, int> 类型,其中 pair 中的 int 是用来存储编号的。我们设第一个节点编号是 1,然后设每个父节点编号为 x,那么每个孩子节点的编号就是 2x(左孩子),2x + 1(右孩子)。如果设第一个节点编号为0,那么每个孩子节点编号就是 2x + 1(左孩子),2x + 2(右孩子)。下面代码设第一个编号节点为 1(设成 0 也不影响,只是计算孩子编号的公式变化一下)。这样每层节点的数量其实就是这一层第一个节点的编号减去这一层最后一个节点的编号加 1(就是这两个编号中间的节点个数在加上这两个编号代表的节点),这样算出来的节点数量是计算了 null 的。所以只需要层序遍历,然后通过上述方式计算每层的节点个数,不断更新,最终得到最大的节点个数。
代码:
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution
{
public:
int widthOfBinaryTree(TreeNode* root)
{
vector<pair<TreeNode*, unsigned int>> q;
unsigned int ret = 0;
q.push_back({root, 1});
while(q.size())
{
auto& [x1, y1] = q[0];
auto& [x2, y2] = q.back();
ret = max(ret, y2 - y1 + 1);
vector<pair<TreeNode*, unsigned int>> tmp;
for(auto& [x, y] : q)
{
if(x->left)
tmp.push_back({x->left, 2 * y});
if(x->right)
tmp.push_back({x->right, 2 * y + 1});
}
q = tmp;
}
return ret;
}
};在每个树行中找最大值
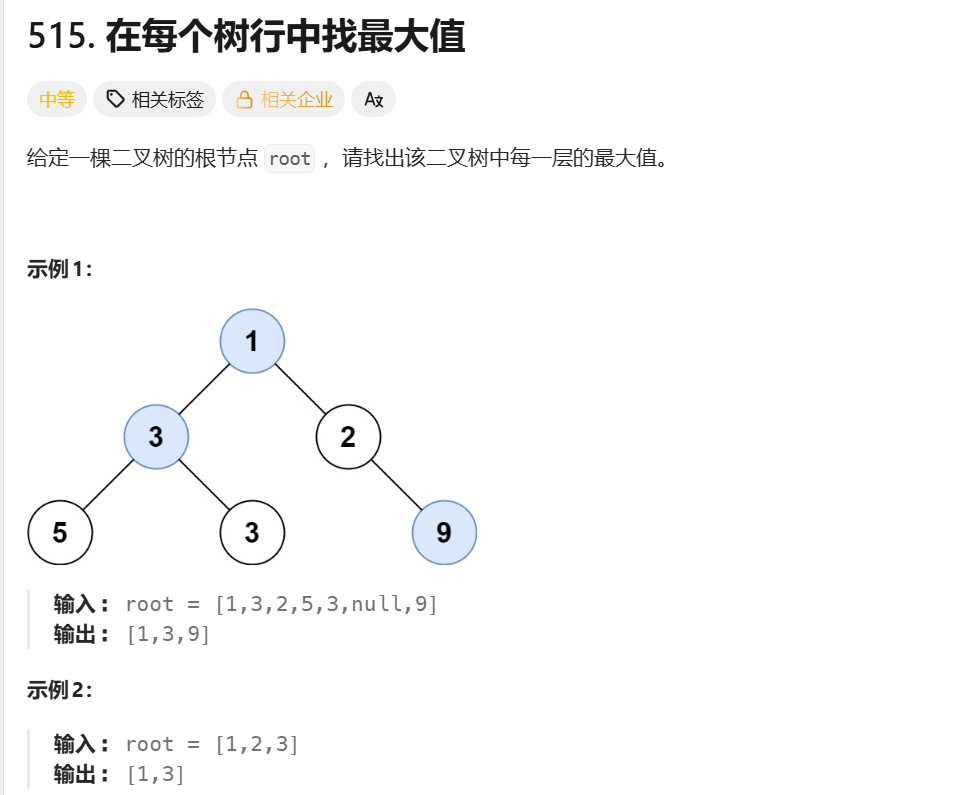
**思路:**借助栈,对二叉树进行层序遍历,遍历的时候用一个变量记录当前层最大值即可。
代码:
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> largestValues(TreeNode* root) {
vector<int> ret;
if(root == NULL)
return ret;
queue<TreeNode*> q;
q.push(root);
while(!q.empty()){
int n = q.size();
int m = INT_MIN;
for(int i = 0; i < n; i++){
TreeNode* node = q.front();
q.pop();
m = max(m, node->val);
if(node->left)
q.push(node->left);
if(node->right)
q.push(node->right);
}
ret.push_back(m);
}
return ret;
}
};堆
最后一块石头的重量

**思路:**创建一个大根堆,将数组所有元素放入大根堆中,然后每次取出两个元素模拟粉碎过程,直到堆中只剩一个元素,剩下的这个元素就是结果了。
代码:
cpp
class Solution {
public:
int lastStoneWeight(vector<int>& stones) {
priority_queue<int> heap;
for(auto n : stones)
heap.push(n);
while(heap.size() > 1){
int a = heap.top();
heap.pop();
int b = heap.top();
heap.pop();
if(a > b)
heap.push(a - b);
}
return heap.size() == 0 ? 0 : heap.top();
}
};数据流中的第 K 大元素

思路: 这道题是求第 K 大的元素,应该创建一个大小为 K 的小根堆,然后遍历数组,所有数据一次进堆,如果堆的大小超过 K,就将堆顶元素扔出。最后堆顶就是第K大的元素。
代码:
cpp
class KthLargest
{
priority_queue<int, vector<int>, greater<int>> q;
int _k;
public:
KthLargest(int k, vector<int>& nums)
{
_k = k;
for(auto& num : nums)
{
q.push(num);
}
while(q.size() > _k)
{
q.pop();
}
}
int add(int val)
{
q.push(val);
if(q.size() > _k)
q.pop();
return q.top();
}
};前K个高频单词

**思路:**首先使用一个哈希表,统计一下每个单词出现的次数,然后创建一个大小为 K 的堆,对于频次而言,需要小根堆,对于字典序而言(频次相同的时候),需要大根堆。遍历哈希表,让所有元素依次进堆,然后判断堆数据个数是否超过 K,如果超过就丢弃堆顶元素,直到个数小于等于 K。遍历结束后,堆中的数据就是结果了。
代码:
cpp
class Solution {
struct cmp{
bool operator()(pair<string, int> p1, pair<string, int> p2){
if(p1.second != p2.second)
return p1.second > p2.second;
else
return p1.first < p2.first;
}
};
public:
vector<string> topKFrequent(vector<string>& words, int k) {
unordered_map<string, int> hash;
for(auto& s : words)
hash[s]++;
priority_queue<pair<string, int>, vector<pair<string, int>>, cmp> heap;
for(auto& h : hash){
heap.push(h);
if(heap.size() > k)
heap.pop();
}
vector<string> ret;
while(!heap.empty()){
ret.push_back(heap.top().first);
heap.pop();
}
reverse(ret.begin(), ret.end());
return ret;
}
};数据流的中位数

**思路:**使用两个堆,一个大堆,一个小堆,当数组元素个数为偶数,两个堆各存一半,当数组元素个数为奇数时,大堆比小堆多存一个(小堆多存也可以,下面代码是让大堆多存一个)。存储规则如下图:
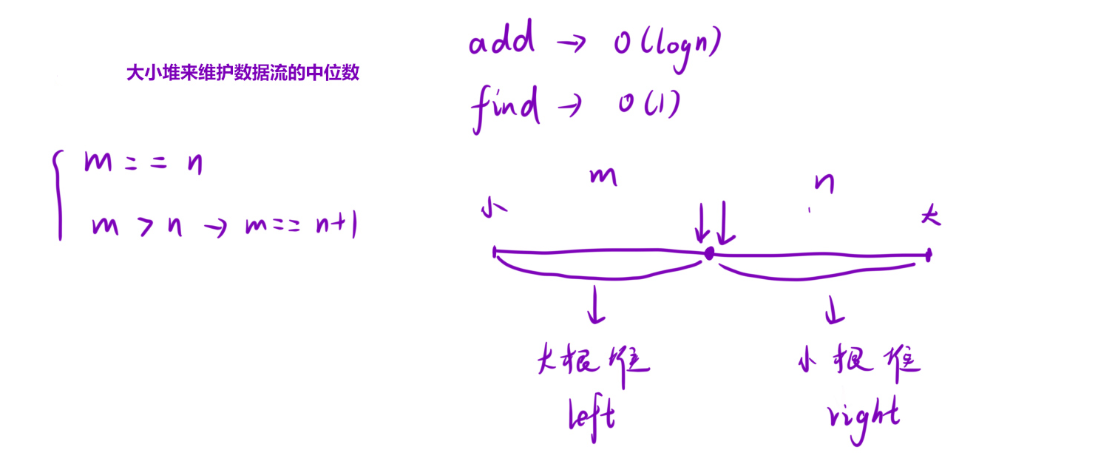
元素入堆情况如下:
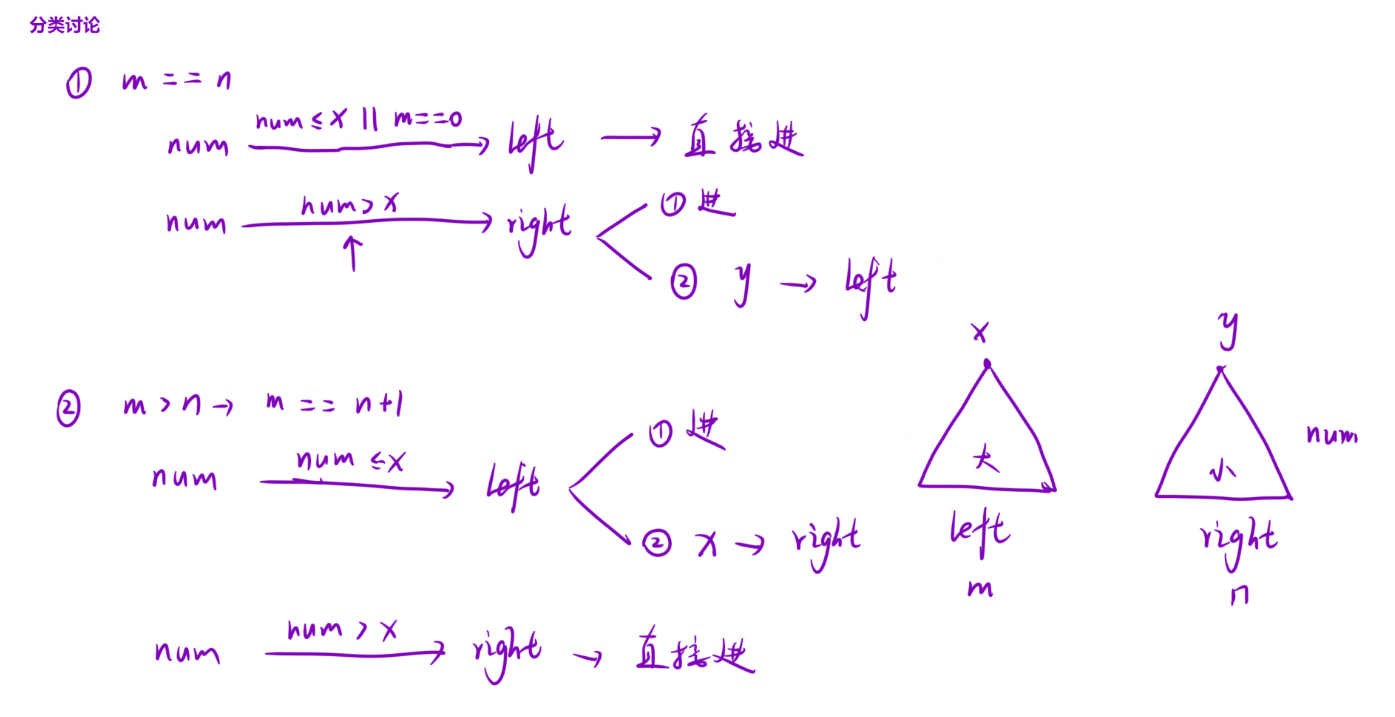
代码:
cpp
class MedianFinder
{
priority_queue<int> left;
priority_queue<int, vector<int>, greater<int>> right;
public:
MedianFinder()
{
}
void addNum(int num)
{
if(left.size() == right.size())
{
if(left.empty() || num <= left.top())
{
left.push(num);
}
else
{
right.push(num);
left.push(right.top());
right.pop();
}
}
else
{
if(num <= left.top())
{
left.push(num);
right.push(left.top());
left.pop();
}
else
{
right.push(num);
}
}
}
double findMedian()
{
if(left.size() == right.size())
return (left.top() + right.top()) / 2.0;
else
return left.top();
}
};