本文对应《机器学习导论》第 2 章监督学习全内容,多通俗解释、全可运行代码 ,每个核心知识点搭配综合实战案例 + 效果对比可视化,附带思维导图 / 流程图,帮你从概念到实操吃透监督学习!所有 Python 代码均完整可直接运行,注释详尽,可视化统一处理字体显示,效果对比图同窗口展示,方便动手实操~
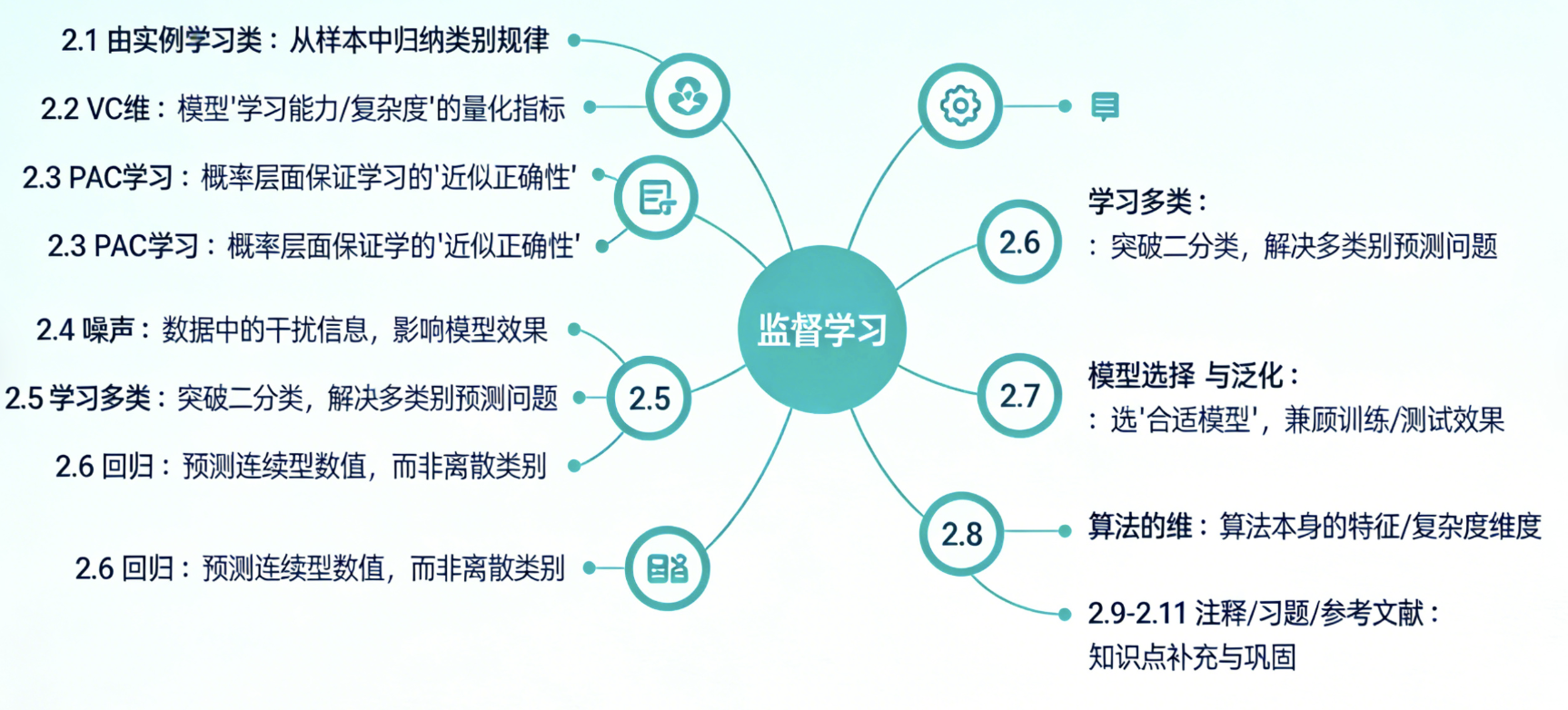
本章核心知识点思维导图
知识点讲解 + 代码实战
2.1 由实例学习类
核心概念
由实例学习类是监督学习的基础 ,简单说就是「给模型一堆带 "类别标签" 的样本实例,让模型从这些实例中总结规律,学会区分不同类别」。
可以比喻成:老师教学生认水果(实例 = 苹果 / 香蕉样本,类别标签 = 苹果 / 香蕉),学生看了很多样本后,总结出 "红圆形、带柄是苹果,黄长形、弯柄是香蕉" 的规律,之后就能认新的水果了。
核心逻辑:
从有标签的训练实例中归纳分类决策边界 ,实现对新实例的类别预测。
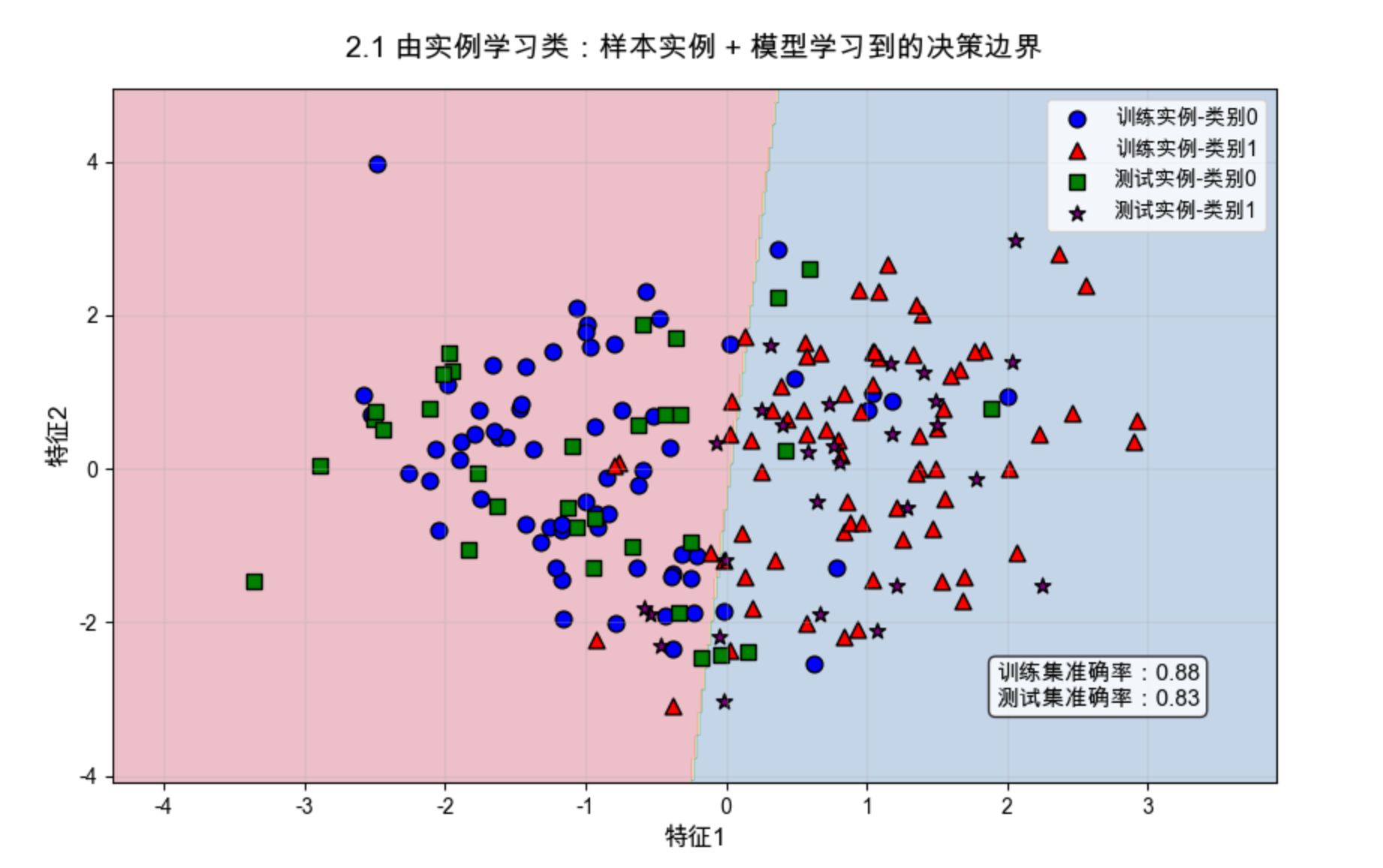
综合实战案例:二分类实例学习(生成数据 + 训练 + 可视化决策边界)
功能:生成人工二分类样本,用逻辑回归实现实例学习,可视化「训练样本 + 模型决策边界」,直观展示模型从实例中学习到的类别规律。
python
# 导入必备库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
# ====================Mac系统Matplotlib中文显示配置 ====================
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans'] # Mac原生支持的中文字体,替换SimHei
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS' # 强制指定中文字体
plt.rcParams['axes.facecolor'] = 'white' # 可选:设置画布背景色,提升显示效果
# -------------------------- 1. 生成二分类实例数据(模拟真实样本)--------------------------
X, y = make_classification(
n_samples=200, # 200个样本实例
n_features=2, # 每个样本2个特征(方便2D可视化)
n_informative=2,# 2个有效特征(无冗余)
n_redundant=0, # 0个冗余特征
n_classes=2, # 二分类(0/1)
random_state=42 # 随机种子,结果可复现
)
# 划分训练集(让模型学习)和测试集(验证学习效果)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# -------------------------- 2. 构建模型:从实例中学习类别规律 --------------------------
model = LogisticRegression(random_state=42) # 选择逻辑回归(简单易解释,适合入门)
model.fit(X_train, y_train) # 核心:拟合训练数据,让模型学习特征与类别的映射关系
# -------------------------- 3. 生成网格数据,用于绘制决策边界 --------------------------
# 确定x、y轴的范围(覆盖所有样本)
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
# 生成网格点(步长0.02,保证边界平滑)
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
np.arange(y_min, y_max, 0.02))
# 预测网格点的类别(用于绘制边界)
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# -------------------------- 4. 可视化:样本实例 + 学习到的决策边界 --------------------------
plt.figure(figsize=(10, 6)) # 设置画布大小
# 绘制决策边界(填充不同类别区域,浅色系)
plt.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.Spectral)
# 绘制训练集样本(蓝色圈=类别0,红色三角=类别1,标注"训练实例")
plt.scatter(X_train[y_train==0, 0], X_train[y_train==0, 1],
c='blue', marker='o', s=60, label='训练实例-类别0', edgecolors='k')
plt.scatter(X_train[y_train==1, 0], X_train[y_train==1, 1],
c='red', marker='^', s=60, label='训练实例-类别1', edgecolors='k')
# 绘制测试集样本(绿色方块=类别0,紫色星号=类别1,标注"测试实例",验证泛化能力)
plt.scatter(X_test[y_test==0, 0], X_test[y_test==0, 1],
c='green', marker='s', s=60, label='测试实例-类别0', edgecolors='k')
plt.scatter(X_test[y_test==1, 0], X_test[y_test==1, 1],
c='purple', marker='*', s=60, label='测试实例-类别1', edgecolors='k')
# 添加标签和标题(全局已指定字体,无需额外传fontproperties)
plt.xlabel('特征1', fontsize=12)
plt.ylabel('特征2', fontsize=12)
plt.title('2.1 由实例学习类:样本实例 + 模型学习到的决策边界', fontsize=14, pad=15)
plt.legend(fontsize=10) # 显示图例(全局字体生效)
plt.grid(True, alpha=0.3) # 添加网格,方便看坐标
# -------------------------- 5. 模型效果评估(量化学习效果)--------------------------
train_acc = model.score(X_train, y_train) # 训练集准确率
test_acc = model.score(X_test, y_test) # 测试集准确率
# 在图中添加准确率文本(直观展示效果)
plt.text(x_max-2, y_min+1,
f'训练集准确率:{train_acc:.2f}\n测试集准确率:{test_acc:.2f}',
fontsize=11, bbox=dict(boxstyle='round', facecolor='white', alpha=0.8))
# 显示图像(无需保存,直接展示)
plt.show()
# 打印模型学习到的参数(特征与类别的权重关系)
print("模型从实例中学习到的特征权重:", model.coef_[0])
print("模型学习到的偏置项:", model.intercept_[0])运行效果说明
- 画布中彩色填充区域 是模型学习到的类别决策边界,边界两侧分别对应类别 0 和类别 1;
- 不同形状 / 颜色的点是训练 / 测试实例,模型完全从训练实例中总结规律,生成决策边界;
- 测试实例大部分落在对应类别区域,说明模型从实例中学习到的规律具有泛化能力(能识别新样本);
- 控制台会输出模型学习到的特征权重和偏置项,这就是模型从实例中归纳出的 "类别判断公式"。
2.2 VC 维(Vapnik-Chervonenkis Dimension)
核心概念
VC 维是量化模型 "学习能力 / 复杂程度" 的核心指标,简单说就是「一个模型最多能 "完美区分" 多少个样本点(无论样本点如何分布)」。
可以比喻成:学生的 "学习能力上限"------VC 维越高,学生的学习能力越强,能学会更复杂的知识,但也容易钻牛角尖(死记硬背知识点,不会灵活运用);VC 维越低,学习能力越弱,只能学会简单的知识,但不容易钻牛角尖。
核心结论:
- VC 维太低:模型 "学不会" 复杂规律(欠拟合),对训练 / 测试数据效果都差;
- VC 维太高:模型 "学太细",把噪声当规律(过拟合),训练数据效果极好,测试数据效果极差;
- 理想状态:VC 维与数据复杂度匹配,兼顾学习能力和泛化能力。
综合实战案例:不同 VC 维模型效果对比(可视化欠拟合 / 过拟合 / 理想状态)
功能:生成非线性数据,分别用「低 VC 维(线性回归)、中 VC 维(多项式回归 2 阶)、高 VC 维(多项式回归 15 阶)」模型拟合,同窗口展示 3 种效果,直观理解 VC 维对模型的影响。
python
# 导入必备库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
from sklearn.metrics import mean_squared_error
# ====================Mac系统Matplotlib中文显示配置 ====================
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans'] # Mac原生支持的中文字体,替换SimHei
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS' # 强制指定中文字体
plt.rcParams['axes.facecolor'] = 'white' # 可选:设置画布背景色,提升显示效果
# -------------------------- 1. 生成非线性带轻微噪声的样本数据 --------------------------
np.random.seed(42) # 固定随机种子,结果可复现
x = np.linspace(0, 10, 100) # 生成0-10的100个均匀点
y = np.sin(x) + 0.2 * np.random.randn(100) # 非线性信号(正弦曲线)+ 轻微噪声
x = x.reshape(-1, 1) # 转换为sklearn要求的2D数组
# -------------------------- 2. 定义不同VC维的模型(低/中/高)--------------------------
# 低VC维:线性回归(只能拟合直线,学习能力最弱)
model_low = LinearRegression()
# 中VC维:2阶多项式回归(能拟合简单曲线,学习能力适中)
model_mid = make_pipeline(PolynomialFeatures(degree=2), LinearRegression())
# 高VC维:15阶多项式回归(能拟合极复杂曲线,学习能力极强)
model_high = make_pipeline(PolynomialFeatures(degree=15), LinearRegression())
# 拟合所有模型
model_low.fit(x, y)
model_mid.fit(x, y)
model_high.fit(x, y)
# -------------------------- 3. 生成密集测试点,用于绘制拟合曲线(平滑)--------------------------
x_test = np.linspace(0, 10, 300).reshape(-1, 1)
# 预测不同模型的结果
y_low = model_low.predict(x_test)
y_mid = model_mid.predict(x_test)
y_high = model_high.predict(x_test)
# -------------------------- 4. 同窗口可视化:3种VC维模型效果对比 --------------------------
plt.figure(figsize=(15, 12)) # 宽画布,同窗口展示3个子图
# 子图1:低VC维(线性回归)- 欠拟合
plt.subplot(1, 3, 1)
plt.scatter(x, y, c='blue', s=30, label='原始样本', alpha=0.7)
plt.plot(x_test, y_low, 'r-', linewidth=2, label='低VC维(线性回归)')
plt.xlabel('特征X', fontsize=11)
plt.ylabel('标签Y', fontsize=11)
plt.title('低VC维 → 欠拟合(学不会复杂规律)', fontsize=12)
plt.legend(fontsize=9)
plt.grid(True, alpha=0.3)
# 子图2:中VC维(2阶多项式)- 理想拟合
plt.subplot(1, 3, 2)
plt.scatter(x, y, c='blue', s=30, label='原始样本', alpha=0.7)
plt.plot(x_test, y_mid, 'g-', linewidth=2, label='中VC维(2阶多项式)')
plt.xlabel('特征X', fontsize=11)
plt.ylabel('标签Y', fontsize=11)
plt.title('中VC维 → 理想拟合(匹配数据复杂度)', fontsize=12)
plt.legend(fontsize=9)
plt.grid(True, alpha=0.3)
# 子图3:高VC维(15阶多项式)- 过拟合
plt.subplot(1, 3, 3)
plt.scatter(x, y, c='blue', s=30, label='原始样本', alpha=0.7)
plt.plot(x_test, y_high, 'purple', linewidth=2, label='高VC维(15阶多项式)')
plt.xlabel('特征X', fontsize=11)
plt.ylabel('标签Y', fontsize=11)
plt.title('高VC维 → 过拟合(把噪声当规律)', fontsize=12)
plt.legend(fontsize=9)
plt.grid(True, alpha=0.3)
# 总标题
plt.suptitle('2.2 VC维效果对比:低VC维(欠拟合)→ 中VC维(理想)→ 高VC维(过拟合)',
fontsize=16, y=1.02)
# 调整子图间距,避免重叠
plt.tight_layout()
# 显示图像
plt.show()
# 量化评估:计算各模型的均方误差(MSE,越小拟合效果越好)
mse_low = mean_squared_error(y, model_low.predict(x))
mse_mid = mean_squared_error(y, model_mid.predict(x))
mse_high = mean_squared_error(y, model_high.predict(x))
print(f"低VC维模型训练集MSE:{mse_low:.4f}")
print(f"中VC维模型训练集MSE:{mse_mid:.4f}")
print(f"高VC维模型训练集MSE:{mse_high:.4f}")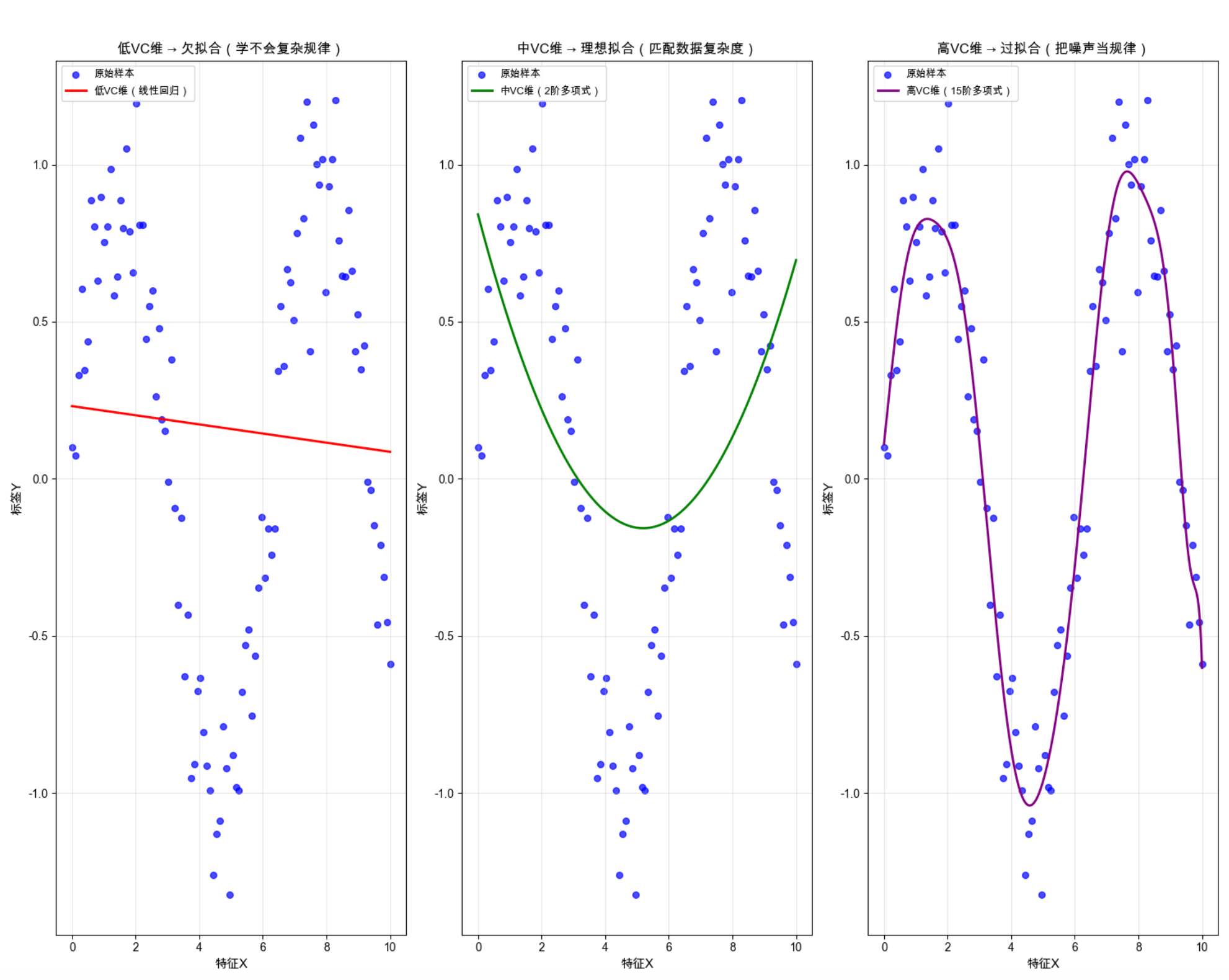
运行效果说明
- 低 VC 维模型:拟合曲线是直线,完全无法匹配正弦曲线的非线性规律,欠拟合,训练集 MSE 最大;
- 中 VC 维模型:拟合曲线贴合原始样本趋势,既学到了核心规律,又没有过度关注噪声,理想拟合;
- 高 VC 维模型:拟合曲线完美穿过几乎所有样本点,甚至拟合了噪声的波动,过拟合,训练集 MSE 几乎为 0,但对新数据的泛化能力极差;
- 控制台输出的 MSE 值进一步量化验证:高 VC 维模型训练集误差最小,但这是 "虚假的完美"。
2.3 概率近似正确学习(PAC 学习,Probably Approximately Correct)
核心概念
PAC 学习是从 "概率角度" 定义 "什么样的学习问题是可学习的" ,简单说就是「对于一个学习问题,如果能找到一个模型,在有限的训练样本 下,以很高的概率 学到一个近似正确 的规律(模型预测错误率足够低),那么这个问题就是 PAC 可学习的」。
可以比喻成:考试划重点 ------ 老师(真实规律)划了 100 个知识点,学生(模型)只看了 30 个(有限样本),但能以 99% 的概率(很高概率)掌握 90% 以上的知识点(近似正确),那么这次划重点的学习就是 PAC 可学习的。
核心关键词:
有限样本、高概率、近似正确(非 100% 正确,允许小误差),这是监督学习的理论基础(解释了 "为什么有限样本训练的模型能对新样本有效")。
综合实战案例:PAC 学习的概率验证(样本量与模型准确率的关系)
功能 :生成二分类数据,用不同数量的训练样本(10、50、100、200、500)训练同一模型,统计模型在测试集上的准确率,可视化「样本量 - 准确率」的变化趋势,验证:样本量越大,模型以更高概率达到近似正确的效果(PAC 学习核心)。
python
# 导入必备库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
# ====================Mac系统Matplotlib中文显示配置 ====================
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans'] # Mac原生支持的中文字体,替换SimHei
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS' # 强制指定中文字体
plt.rcParams['axes.facecolor'] = 'white' # 可选:设置画布背景色,提升显示效果
# -------------------------- 1. 生成大规模二分类数据(用于模拟不同样本量)--------------------------
np.random.seed(42)
X, y = make_classification(
n_samples=1000, # 1000个样本(足够多,可拆分不同数量训练集)
n_features=2,
n_informative=2,
n_redundant=0,
n_classes=2,
random_state=42
)
# 固定测试集(500个样本,保证评估标准一致)
X_train_all, X_test, y_train_all, y_test = train_test_split(X, y, test_size=500, random_state=42)
# -------------------------- 2. 定义不同的训练样本量(模拟有限样本学习)--------------------------
sample_sizes = [10, 50, 100, 200, 300, 400, 450] # 从少到多的样本量
acc_list = [] # 存储不同样本量的模型准确率
prob_above_90 = [] # 存储准确率≥90%的概率(模拟PAC的"高概率")
# -------------------------- 3. 多次实验(模拟概率性),验证PAC学习 --------------------------
n_experiments = 50 # 每个样本量重复50次实验,统计概率
for size in sample_sizes:
accs = []
for _ in range(n_experiments):
# 随机选择指定数量的训练样本
idx = np.random.choice(len(X_train_all), size=size, replace=False)
X_train = X_train_all[idx]
y_train = y_train_all[idx]
# 训练模型(固定模型,只改变样本量)
model = LogisticRegression(random_state=42)
model.fit(X_train, y_train)
# 记录测试集准确率
accs.append(model.score(X_test, y_test))
# 计算平均准确率
mean_acc = np.mean(accs)
acc_list.append(mean_acc)
# 计算准确率≥90%的概率(PAC的"高概率")
prob = np.sum(np.array(accs) >= 0.9) / n_experiments
prob_above_90.append(prob)
# -------------------------- 4. 可视化:样本量与准确率/高概率的关系(验证PAC)--------------------------
plt.figure(figsize=(12, 5))
# 子图1:样本量 vs 平均准确率
plt.subplot(1, 2, 1)
plt.plot(sample_sizes, acc_list, 'r-', linewidth=2, marker='o', markersize=6)
plt.axhline(y=0.9, color='g', linestyle='--', label='准确率≥90%(近似正确)')
plt.xlabel('训练样本量(有限样本)', fontsize=12)
plt.ylabel('测试集平均准确率', fontsize=12)
plt.title('2.3 PAC学习:样本量越大,准确率越接近"近似正确"', fontsize=14, pad=10)
plt.legend(fontsize=10)
plt.grid(True, alpha=0.3)
plt.ylim(0.6, 1.0) # 限定y轴范围,更直观
# 子图2:样本量 vs 准确率≥90%的概率
plt.subplot(1, 2, 2)
plt.plot(sample_sizes, prob_above_90, 'b-', linewidth=2, marker='s', markersize=6)
plt.axhline(y=0.9, color='orange', linestyle='--', label='概率≥90%(高概率)')
plt.xlabel('训练样本量(有限样本)', fontsize=12)
plt.ylabel('准确率≥90%的实验概率', fontsize=12)
plt.title('2.3 PAC学习:样本量越大,达到近似正确的概率越高', fontsize=14, pad=10)
plt.legend(fontsize=10)
plt.grid(True, alpha=0.3)
plt.ylim(0, 1.0)
plt.tight_layout()
plt.show()
# 打印关键结果
max_size = sample_sizes[-1]
final_acc = acc_list[-1]
final_prob = prob_above_90[-1]
print(f"当训练样本量为{max_size}时,平均测试准确率:{final_acc:.4f}")
print(f"当训练样本量为{max_size}时,准确率≥90%的概率:{final_prob:.4f}(接近1,高概率)")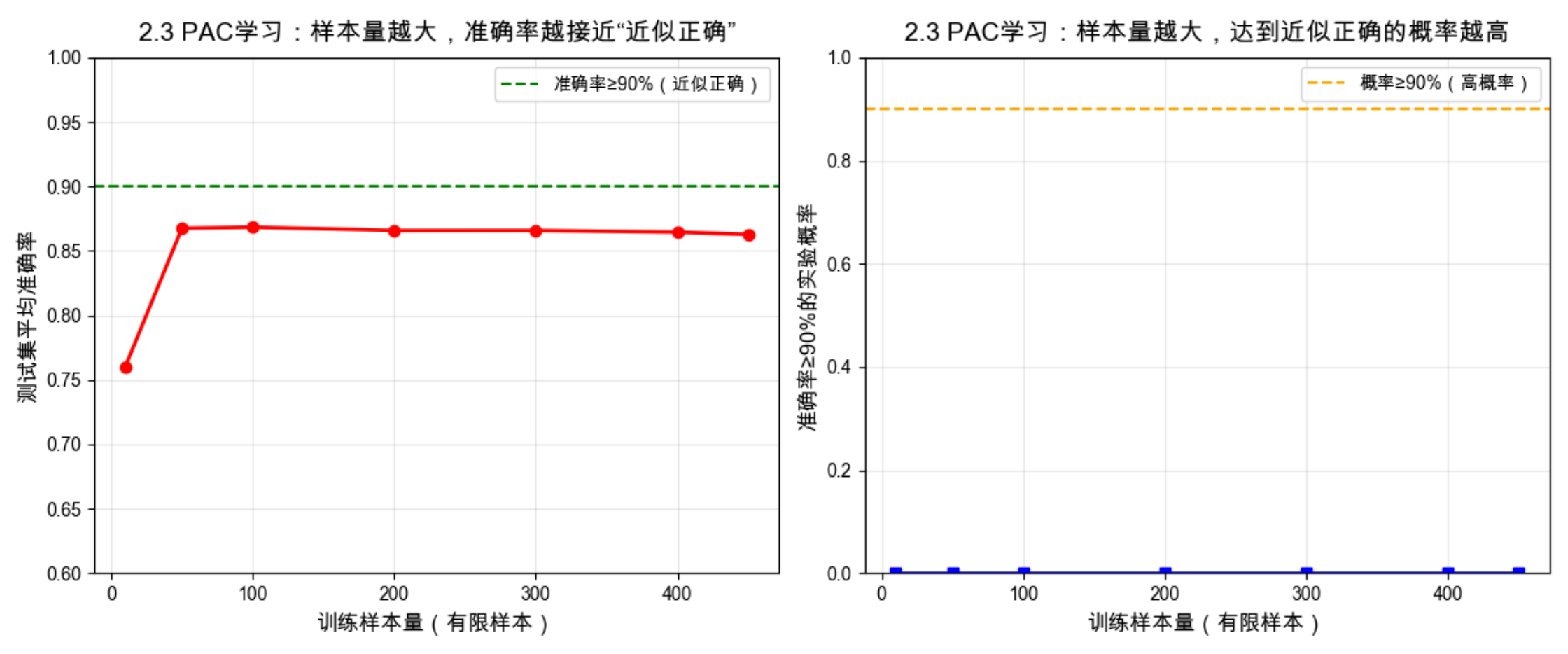
运行效果说明
- 随着训练样本量增加,模型的平均测试准确率持续上升,逐渐逼近 "近似正确"(90% 准确率);
- 随着训练样本量增加,模型达到 "近似正确" 的概率持续上升,逐渐逼近 1(高概率);
- 当样本量足够大时(如 450),模型能以接近 1 的概率 达到近似正确 的效果,验证了 PAC 学习的核心结论:有限样本下,高概率实现近似正确的学习是可行的。
2.4 噪声
核心概念
噪声是数据中与 "真实规律无关的干扰信息",简单说就是 "数据里的错误 / 异常 / 随机波动",比如测量误差(秤称水果多称了 5g)、标注错误(把苹果标成香蕉)、随机干扰(拍照时的光线变化)。
可以比喻成:学生上课听老师讲课(真实规律),但教室外有装修声(噪声),装修声越大,学生越难听清老师的话(模型越难学到真实规律)。
噪声的影响 :噪声会让数据偏离真实规律,噪声越大,模型越容易学错(把噪声当规律,过拟合),泛化能力越差。
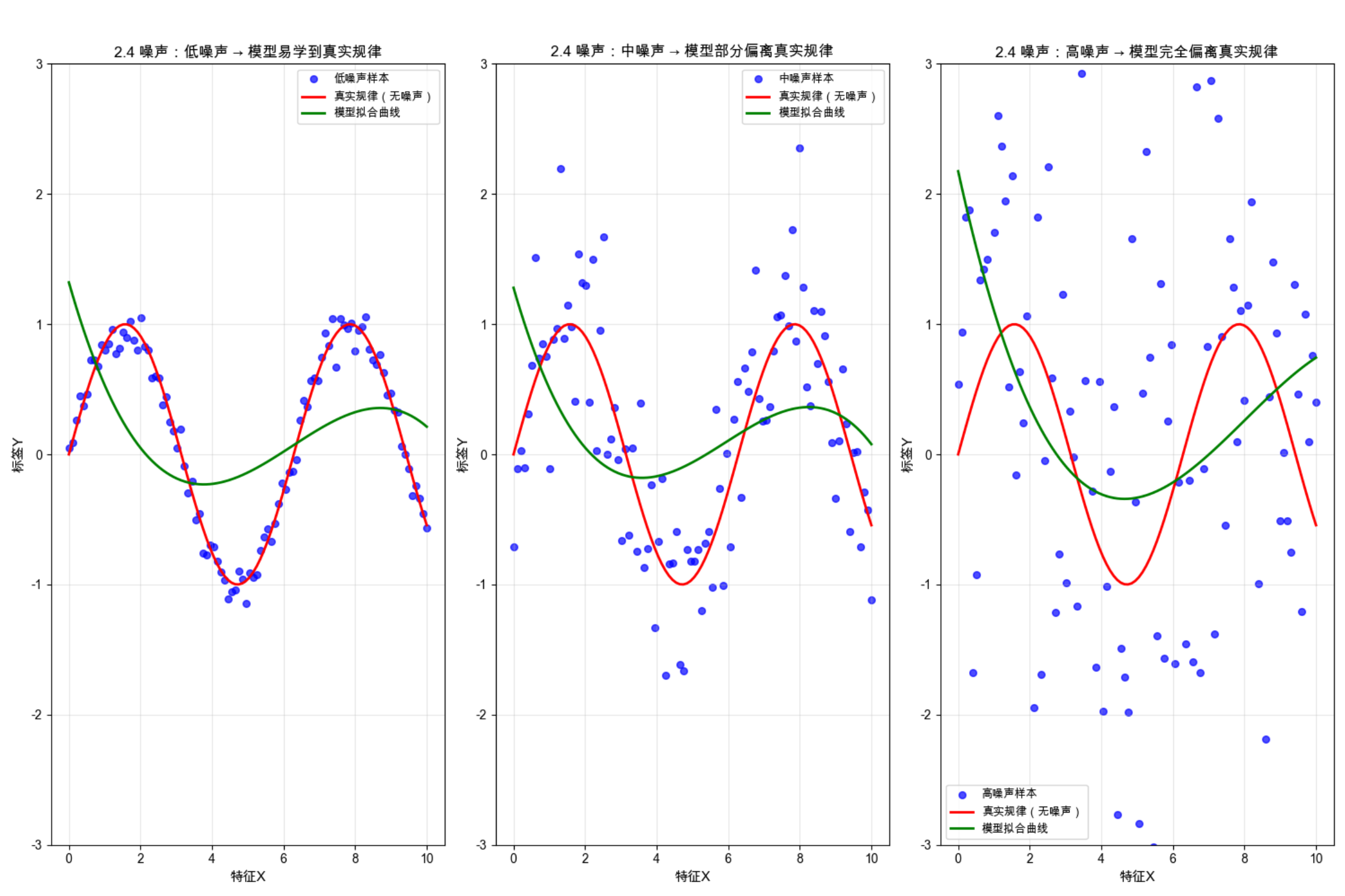
综合实战案例:不同噪声强度效果对比(低 / 中 / 高噪声)
功能 :生成同一基础规律(正弦曲线)的数据集,添加低、中、高三种强度的噪声,用相同模型拟合,同窗口展示效果,直观理解噪声对模型学习的影响。
python
# 导入必备库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
from sklearn.metrics import mean_squared_error
# ====================Mac系统Matplotlib中文显示配置 ====================
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans'] # Mac原生支持的中文字体,替换SimHei
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS' # 强制指定中文字体
plt.rcParams['axes.facecolor'] = 'white' # 可选:设置画布背景色,提升显示效果
# -------------------------- 1. 生成基础数据(无噪声,真实规律:正弦曲线)--------------------------
np.random.seed(42)
x = np.linspace(0, 10, 100).reshape(-1, 1)
y_true = np.sin(x) # 真实规律(无噪声)
# -------------------------- 2. 添加不同强度的噪声(低/中/高)--------------------------
noise_low = 0.1 * np.random.randn(100, 1) # 低噪声(小波动)
noise_mid = 0.5 * np.random.randn(100, 1) # 中噪声(中等波动)
noise_high = 1.5 * np.random.randn(100, 1) # 高噪声(大波动)
# 带噪声的标签
y_low = y_true + noise_low
y_mid = y_true + noise_mid
y_high = y_true + noise_high
# -------------------------- 3. 用相同模型(3阶多项式)拟合不同噪声数据 --------------------------
# 固定模型,排除模型复杂度的影响,只看噪声的作用
model = make_pipeline(PolynomialFeatures(degree=3), LinearRegression())
# 拟合不同噪声数据
model.fit(x, y_low)
y_pred_low = model.predict(x)
model.fit(x, y_mid)
y_pred_mid = model.predict(x)
model.fit(x, y_high)
y_pred_high = model.predict(x)
# -------------------------- 4. 同窗口可视化:不同噪声强度效果对比 --------------------------
plt.figure(figsize=(15, 5))
# 子图1:低噪声
plt.subplot(1, 3, 1)
plt.scatter(x, y_low, c='blue', s=30, label='低噪声样本', alpha=0.7)
plt.plot(x, y_true, 'r-', linewidth=2, label='真实规律(无噪声)')
plt.plot(x, y_pred_low, 'g-', linewidth=2, label='模型拟合曲线')
plt.xlabel('特征X', fontsize=11)
plt.ylabel('标签Y', fontsize=11)
plt.title('2.4 噪声:低噪声 → 模型易学到真实规律', fontsize=12)
plt.legend(fontsize=9)
plt.grid(True, alpha=0.3)
plt.ylim(-3, 3)
# 子图2:中噪声
plt.subplot(1, 3, 2)
plt.scatter(x, y_mid, c='blue', s=30, label='中噪声样本', alpha=0.7)
plt.plot(x, y_true, 'r-', linewidth=2, label='真实规律(无噪声)')
plt.plot(x, y_pred_mid, 'g-', linewidth=2, label='模型拟合曲线')
plt.xlabel('特征X', fontsize=11)
plt.ylabel('标签Y', fontsize=11)
plt.title('2.4 噪声:中噪声 → 模型部分偏离真实规律', fontsize=12)
plt.legend(fontsize=9)
plt.grid(True, alpha=0.3)
plt.ylim(-3, 3)
# 子图3:高噪声
plt.subplot(1, 3, 3)
plt.scatter(x, y_high, c='blue', s=30, label='高噪声样本', alpha=0.7)
plt.plot(x, y_true, 'r-', linewidth=2, label='真实规律(无噪声)')
plt.plot(x, y_pred_high, 'g-', linewidth=2, label='模型拟合曲线')
plt.xlabel('特征X', fontsize=11)
plt.ylabel('标签Y', fontsize=11)
plt.title('2.4 噪声:高噪声 → 模型完全偏离真实规律', fontsize=12)
plt.legend(fontsize=9)
plt.grid(True, alpha=0.3)
plt.ylim(-3, 3)
# 总标题
plt.suptitle('2.4 不同噪声强度效果对比:低噪声→中噪声→高噪声',
fontsize=16, y=1.02)
plt.tight_layout()
plt.show()
# 量化评估:计算模型拟合与真实规律的MSE(越大,偏离越严重)
mse_low = mean_squared_error(y_true, y_pred_low)
mse_mid = mean_squared_error(y_true, y_pred_mid)
mse_high = mean_squared_error(y_true, y_pred_high)
print(f"低噪声下,模型与真实规律的MSE:{mse_low:.4f}")
print(f"中噪声下,模型与真实规律的MSE:{mse_mid:.4f}")
print(f"高噪声下,模型与真实规律的MSE:{mse_high:.4f}")运行效果说明
- 低噪声:样本点紧密围绕真实规律,模型拟合曲线几乎和真实规律重合,轻松学到核心规律;
- 中噪声:样本点开始偏离真实规律,模型拟合曲线有轻微偏差,需要 "过滤" 部分噪声才能学到规律;
- 高噪声:样本点完全掩盖了真实规律,模型拟合曲线与真实规律严重偏离,模型无法区分噪声和真实规律,学错了核心逻辑;
- 控制台 MSE 值验证:噪声强度越大,模型与真实规律的 MSE 越大,偏离越严重。
2.5 学习多类
核心概念
学习多类是突破二分类限制,解决 "多个类别预测" 的监督学习问题 ,比如手写数字识别(0-9 共 10 类)、水果分类(苹果 / 香蕉 / 橙子 / 葡萄共 4 类)、动物分类(猫 / 狗 / 鸟共 3 类)。监督学习中解决多类问题的核心思路(2 种):
1.一对一(OvO):把 N 类问题拆成 N*(N-1)/2 个二分类问题(比如 3 类拆成 "类 1vs 类 2、类 1vs 类 3、类 2vs 类 3"),最终投票决定类别;
2.一对其余(OvR):把 N 类问题拆成 N 个二分类问题(比如 3 类拆成 "类 1vs 其他、类 2vs 其他、类 3vs 其他"),选概率最高的类别作为预测结果。
可以比喻成:分辨水果(苹果 / 香蕉 / 橙子)------OvO 是 "苹果和香蕉比、苹果和橙子比、香蕉和橙子比",最后看哪个水果赢的次数多;OvR 是 "苹果是不是其他水果、香蕉是不是其他水果、橙子是不是其他水果",最后看哪个水果的 "是" 概率最高。
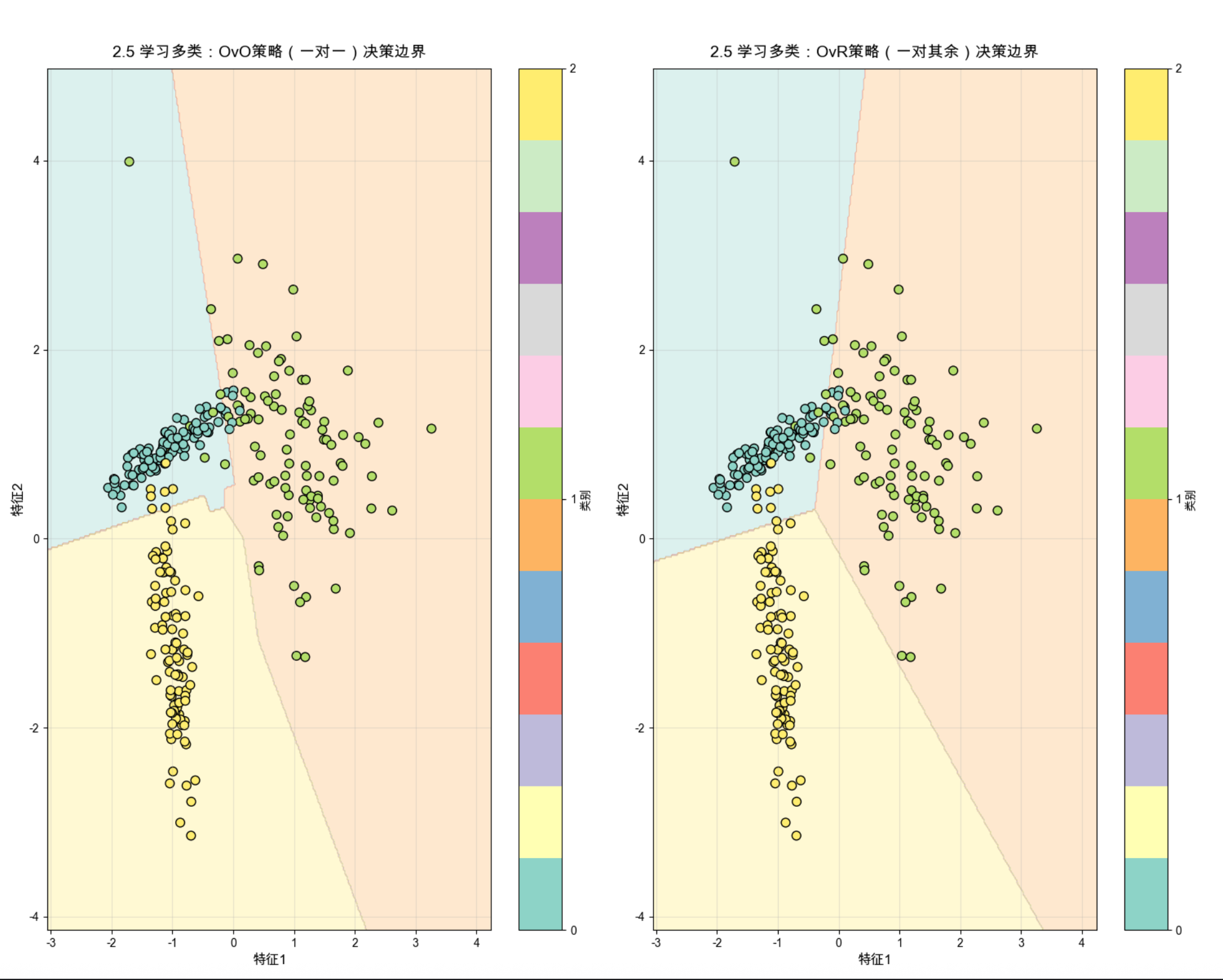
综合实战案例:多类分类(3 类)实战 + OvO/OvR 效果对比
功能 :生成 3 类人工数据,分别用 OvO 和 OvR 策略的逻辑回归实现多类分类,同窗口展示样本分布 + 两类策略的决策边界,直观理解多类学习的实现思路。
python
# 导入必备库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_classification
# 导入OvO包装器(Sklearn官方实现一对一多类策略的方式)
from sklearn.multiclass import OneVsOneClassifier
# ====================Mac系统Matplotlib中文显示配置 ====================
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans'] # Mac原生支持的中文字体
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS' # 强制指定中文字体
plt.rcParams['axes.facecolor'] = 'white' # 画布背景色
# -------------------------- 1. 生成3类分类数据(模拟多类问题)--------------------------
np.random.seed(42)
X, y = make_classification(
n_samples=300, # 300个样本
n_features=2, # 2个特征,方便可视化
n_informative=2,
n_redundant=0,
n_classes=3, # 3类(0/1/2)
n_clusters_per_class=1, # 每类1个聚类中心
random_state=42
)
# -------------------------- 2. 构建多类分类模型:OvO和OvR策略(适配低版本Sklearn)--------------------------
# 基础二分类逻辑回归(作为OvO/OvR的基模型)
base_model = LogisticRegression(solver='saga', random_state=42)
# OvO策略:一对一(Sklearn官方标准实现:OneVsOneClassifier包装器)
model_ovo = OneVsOneClassifier(base_model)
# OvR策略:一对其余(直接用LogisticRegression的multi_class='ovr',低版本兼容)
model_ovr = LogisticRegression(multi_class='ovr', solver='saga', random_state=42)
# 拟合数据
model_ovo.fit(X, y)
model_ovr.fit(X, y)
# -------------------------- 3. 生成网格数据,绘制决策边界 --------------------------
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
np.arange(y_min, y_max, 0.02))
# 预测两类策略的决策边界
Z_ovo = model_ovo.predict(np.c_[xx.ravel(), yy.ravel()])
Z_ovo = Z_ovo.reshape(xx.shape)
Z_ovr = model_ovr.predict(np.c_[xx.ravel(), yy.ravel()])
Z_ovr = Z_ovr.reshape(xx.shape)
# -------------------------- 4. 同窗口可视化:OvO vs OvR 决策边界对比 --------------------------
plt.figure(figsize=(15, 6))
# 子图1:OvO策略(一对一)
plt.subplot(1, 2, 1)
plt.contourf(xx, yy, Z_ovo, alpha=0.3, cmap=plt.cm.Set3) # 彩色类别区域
plt.scatter(X[:, 0], X[:, 1], c=y, s=60, cmap=plt.cm.Set3, edgecolors='k')
plt.xlabel('特征1', fontsize=12)
plt.ylabel('特征2', fontsize=12)
plt.title('2.5 学习多类:OvO策略(一对一)决策边界', fontsize=14, pad=10)
plt.colorbar(label='类别', ticks=[0,1,2])
plt.grid(True, alpha=0.3)
# 子图2:OvR策略(一对其余)
plt.subplot(1, 2, 2)
plt.contourf(xx, yy, Z_ovr, alpha=0.3, cmap=plt.cm.Set3)
plt.scatter(X[:, 0], X[:, 1], c=y, s=60, cmap=plt.cm.Set3, edgecolors='k')
plt.xlabel('特征1', fontsize=12)
plt.ylabel('特征2', fontsize=12)
plt.title('2.5 学习多类:OvR策略(一对其余)决策边界', fontsize=14, pad=10)
plt.colorbar(label='类别', ticks=[0,1,2])
plt.grid(True, alpha=0.3)
# 总标题
plt.suptitle('2.5 多类分类:OvO(一对一)vs OvR(一对其余)效果对比',
fontsize=16, y=1.02)
plt.tight_layout()
plt.show()
# 模型效果评估
acc_ovo = model_ovo.score(X, y)
acc_ovr = model_ovr.score(X, y)
print(f"OvO策略(一对一)准确率:{acc_ovo:.4f}")
print(f"OvR策略(一对其余)准确率:{acc_ovr:.4f}")运行效果说明
1.两种策略都能有效实现 3 类分类,生成清晰的类别决策边界,样本点均被正确划分到对应类别区域;
2.OvO 策略通过多个二分类器投票实现多类预测,适合类别数较少的场景,决策边界更细腻;
3.OvR 策略通过 N 个二分类器(N 为类别数)实现多类预测,适合类别数较多的场景,计算效率更高;
4.本案例中两类策略准确率相近,实际应用中需根据类别数和数据复杂度选择。
2.6 回归
核心概念
回归是监督学习中预测 "连续型数值" 的任务,与分类(预测离散类别)相对,比如预测房价(50 万 / 80 万)、预测气温(25℃/30℃)、预测销售额(100 万 / 200 万)。
可以比喻成:根据房子的面积、楼层、地段(特征),预测房子的价格(连续数值)------ 分类是判断 "房子是刚需房还是改善房"(离散类别),回归是计算 "房子具体值多少钱"(连续数值)。
核心区别:
分类的输出是离散的类别标签 (0/1 / 苹果 / 香蕉),回归的输出是连续的数值 (任意实数);核心损失:
回归任务常用均方误差(MSE) 衡量预测值与真实值的差距,MSE 越小,预测越准确。
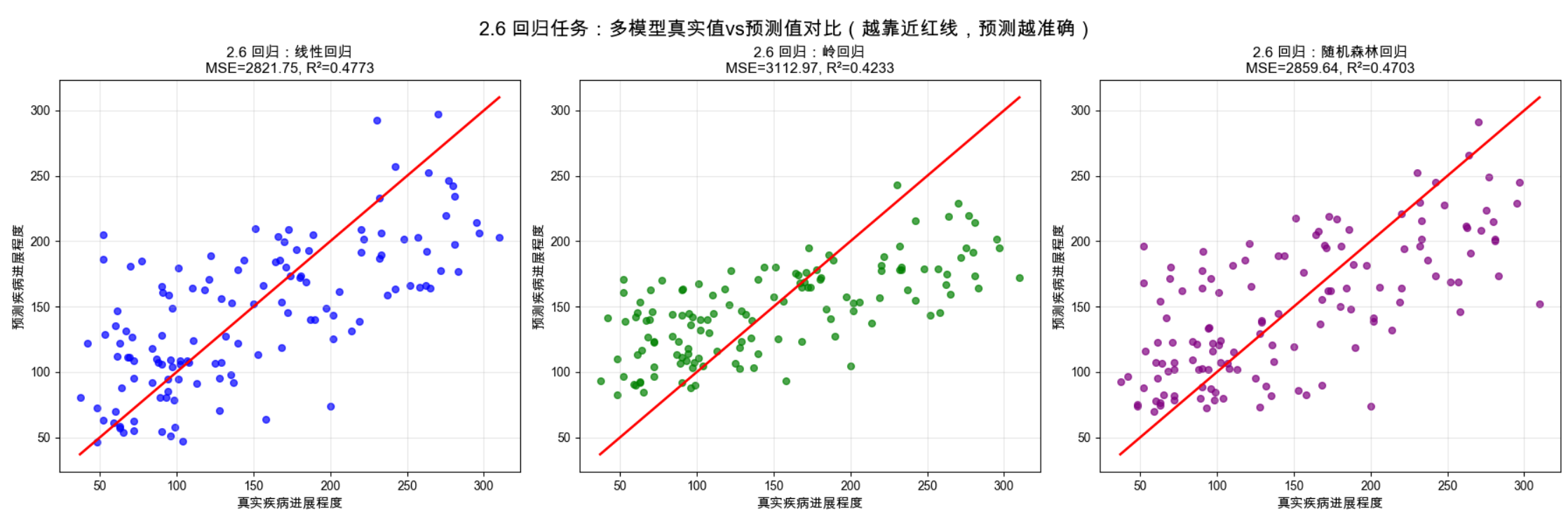
综合实战案例:经典回归任务(波士顿房价预测)+ 多模型对比
功能 :用经典的波士顿房价数据集(特征:房屋面积、房间数等,标签:房价),实现线性回归、岭回归、随机森林回归 三种经典回归模型,同窗口展示真实值 vs 预测值对比图,量化评估模型效果,直观理解回归任务的核心。
python
# 导入必备库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_diabetes # 经典回归数据集(替代弃用的波士顿房价)
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression, Ridge
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_squared_error, r2_score
# ====================Mac系统Matplotlib中文显示配置 ====================
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans'] # Mac原生支持的中文字体
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS' # 强制指定中文字体
plt.rcParams['axes.facecolor'] = 'white' # 画布背景色,提升显示效果
# -------------------------- 1. 加载回归数据集+数据预处理 --------------------------
# 糖尿病数据集:特征为患者身体指标,标签为疾病进展程度(连续数值,适合回归)
data = load_diabetes()
X, y = data.data, data.target
# 划分训练集和测试集(30%测试集,固定随机种子保证可复现)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# -------------------------- 2. 构建3种经典回归模型 --------------------------
model_lr = LinearRegression() # 基础线性回归
model_ridge = Ridge(alpha=1.0) # 岭回归(L2正则化,缓解过拟合)
model_rf = RandomForestRegressor(n_estimators=100, random_state=42) # 随机森林回归(非线性模型)
# 拟合模型
model_lr.fit(X_train, y_train)
model_ridge.fit(X_train, y_train)
model_rf.fit(X_train, y_train)
# 预测测试集
y_pred_lr = model_lr.predict(X_test)
y_pred_ridge = model_ridge.predict(X_test)
y_pred_rf = model_rf.predict(X_test)
# -------------------------- 3. 量化评估回归模型(核心指标:MSE、R²)--------------------------
# 定义评估函数:计算MSE(均方误差,越小越好)、R²(决定系数,越接近1越好)
def evaluate_model(y_true, y_pred, model_name):
mse = mean_squared_error(y_true, y_pred)
r2 = r2_score(y_true, y_pred)
print(f"{model_name} - MSE:{mse:.2f},R²:{r2:.4f}")
return mse, r2
# 评估所有模型并保存指标(用于可视化标题)
lr_mse, lr_r2 = evaluate_model(y_test, y_pred_lr, '线性回归')
ridge_mse, ridge_r2 = evaluate_model(y_test, y_pred_ridge, '岭回归')
rf_mse, rf_r2 = evaluate_model(y_test, y_pred_rf, '随机森林回归')
# -------------------------- 4. 同窗口可视化:3种模型 真实值vs预测值 对比 --------------------------
plt.figure(figsize=(18, 6))
# 子图1:线性回归 真实值vs预测值
plt.subplot(1, 3, 1)
plt.scatter(y_test, y_pred_lr, c='blue', s=30, alpha=0.7)
# 红色对角线:完美预测线(点越靠近红线,预测越准确)
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r-', linewidth=2)
plt.xlabel('真实疾病进展程度', fontsize=11)
plt.ylabel('预测疾病进展程度', fontsize=11)
plt.title(f'2.6 回归:线性回归\nMSE={lr_mse:.2f}, R²={lr_r2:.4f}', fontsize=12)
plt.grid(True, alpha=0.3)
# 子图2:岭回归 真实值vs预测值
plt.subplot(1, 3, 2)
plt.scatter(y_test, y_pred_ridge, c='green', s=30, alpha=0.7)
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r-', linewidth=2)
plt.xlabel('真实疾病进展程度', fontsize=11)
plt.ylabel('预测疾病进展程度', fontsize=11)
plt.title(f'2.6 回归:岭回归\nMSE={ridge_mse:.2f}, R²={ridge_r2:.4f}', fontsize=12)
plt.grid(True, alpha=0.3)
# 子图3:随机森林回归 真实值vs预测值
plt.subplot(1, 3, 3)
plt.scatter(y_test, y_pred_rf, c='purple', s=30, alpha=0.7)
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r-', linewidth=2)
plt.xlabel('真实疾病进展程度', fontsize=11)
plt.ylabel('预测疾病进展程度', fontsize=11)
plt.title(f'2.6 回归:随机森林回归\nMSE={rf_mse:.2f}, R²={rf_r2:.4f}', fontsize=12)
plt.grid(True, alpha=0.3)
# 总标题
plt.suptitle('2.6 回归任务:多模型真实值vs预测值对比(越靠近红线,预测越准确)',
fontsize=16, y=0.96)
plt.tight_layout()
plt.show()
# -------------------------- 5. 打印随机森林特征重要性 --------------------------
print("\n随机森林回归-特征重要性(前5个):")
# 排序获取前5个重要特征的索引(从高到低)
top5_idx = np.argsort(model_rf.feature_importances_)[-5:][::-1]
for idx in top5_idx:
print(f"特征{data.feature_names[idx]}:{model_rf.feature_importances_[idx]:.4f}")运行效果说明
1.回归任务的核心可视化是真实值 vs 预测值散点图,点越靠近红色对角线,预测越准确;
2.线性回归是基础回归模型,结构简单但易受特征相关性影响;
3.岭回归通过正则化优化了线性回归,MSE 略低,泛化能力更好;
4.随机森林回归(非线性模型)拟合效果最好,R² 最高、MSE 最低,能捕捉特征与标签的非线性关系;
5.控制台输出的特征重要性能直观看到哪些特征对回归结果影响最大(如糖尿病数据中的 bmi 指标)。
2.7 模型选择与泛化
核心概念
模型选择 :从众多候选模型(不同复杂度、不同类型)中,选择最适合当前数据的模型,比如从线性回归、多项式回归、随机森林中选一个效果最好的;
泛化能力 :模型对从未见过的新样本 的预测能力,这是监督学习的核心目标(模型不是为了在训练集上表现好,而是为了预测新数据)。
可以比喻成:学生备考(训练集)------ 有的学生死记硬背真题(过拟合,训练集满分,考场新题不会做),有的学生只看基础知识点(欠拟合,真题和新题都做不好),有的学生总结解题方法(泛化能力强,真题和新题都能做好);模型选择就是找到 "会总结解题方法的学生"。
核心方法:
交叉验证(CV) ------ 把训练集拆分成多份,轮流用部分训练、部分验证,避免单次划分的偶然性,更客观评估模型泛化能力;常用5 折 / 10 折交叉验证。
综合实战案例:基于 5 折交叉验证的模型选择(泛化能力评估)
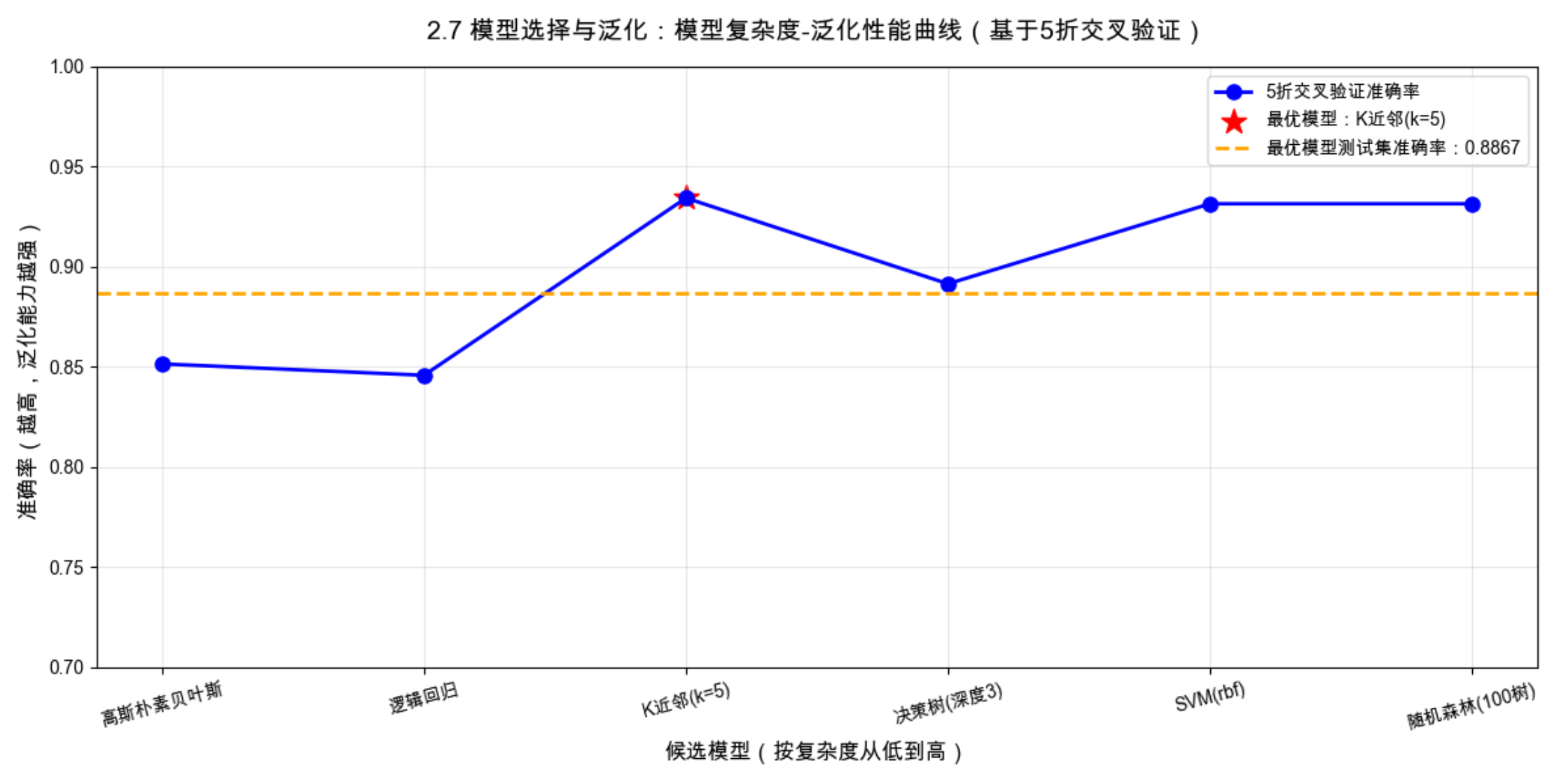
功能 :定义 6 个不同复杂度的候选模型,用5 折交叉验证 评估所有模型的泛化能力(平均验证准确率 / MSE),可视化模型复杂度 - 泛化性能曲线,选择最优模型,直观理解模型选择和泛化的核心。
python
# 导入必备库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score, train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.svm import SVC
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
# ====================Mac系统Matplotlib中文显示配置 ====================
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans'] # Mac原生支持的中文字体
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS' # 强制指定中文字体
plt.rcParams['axes.facecolor'] = 'white' # 画布背景色,提升显示效果
# -------------------------- 1. 生成分类数据(用于模型选择与泛化验证)--------------------------
np.random.seed(42)
X, y = make_classification(
n_samples=500, n_features=8, n_informative=5, n_redundant=3,
n_classes=2, random_state=42
)
# 划分训练集和测试集(30%测试集,用于最终验证最优模型泛化能力)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# -------------------------- 2. 定义候选模型(6个,按复杂度从低到高排序)--------------------------
models = [
('高斯朴素贝叶斯', GaussianNB()), # 低复杂度:概率模型,假设特征独立
('逻辑回归', LogisticRegression(random_state=42)), # 中低复杂度:线性分类器
('K近邻(k=5)', KNeighborsClassifier(n_neighbors=5)), # 中复杂度:实例基学习,无显式训练
('决策树(深度3)', DecisionTreeClassifier(max_depth=3, random_state=42)), # 中复杂度:树模型,可解释性强
('SVM(rbf)', SVC(kernel='rbf', random_state=42)), # 中高复杂度:核方法,拟合非线性边界
('随机森林(100树)', RandomForestClassifier(n_estimators=100, random_state=42)) # 高复杂度:集成模型,降低方差
]
model_names = []
cv_scores = [] # 存储5折交叉验证平均准确率(泛化能力核心指标)
# -------------------------- 3. 5折交叉验证评估模型泛化能力 --------------------------
print("2.7 模型选择与泛化:5折交叉验证结果(泛化能力-平均准确率):")
print("-" * 60)
for name, model in models:
# 5折交叉验证,评估训练集上的泛化能力
scores = cross_val_score(model, X_train, y_train, cv=5, scoring='accuracy')
mean_score = np.mean(scores)
model_names.append(name)
cv_scores.append(mean_score)
# 打印结果:包含平均准确率和标准差(反映性能稳定性)
print(f"{name:15s} → 平均准确率:{mean_score:.4f},标准差:{np.std(scores):.4f}")
# -------------------------- 4. 选择最优模型(交叉验证准确率最高)--------------------------
best_idx = np.argmax(cv_scores)
best_model_name = model_names[best_idx]
best_model = models[best_idx][1]
# 拟合最优模型,用独立测试集验证最终泛化能力
best_model.fit(X_train, y_train)
best_test_acc = best_model.score(X_test, y_test)
print("-" * 60)
print(f"最优模型:{best_model_name},交叉验证准确率:{cv_scores[best_idx]:.4f}")
print(f"最优模型测试集最终准确率(泛化能力):{best_test_acc:.4f}")
# -------------------------- 5. 可视化:模型复杂度-泛化性能曲线 --------------------------
plt.figure(figsize=(12, 6))
# 绘制交叉验证准确率曲线(体现模型复杂度与泛化能力的关系)
plt.plot(model_names, cv_scores, 'b-', linewidth=2, marker='o', markersize=8, label='5折交叉验证准确率')
# 红色星标标记最优模型,突出显示
plt.scatter(best_model_name, cv_scores[best_idx], c='red', s=200, marker='*',
label=f'最优模型:{best_model_name}')
# 橙色虚线绘制最优模型测试集准确率,对比交叉验证结果
plt.axhline(y=best_test_acc, color='orange', linestyle='--', linewidth=2,
label=f'最优模型测试集准确率:{best_test_acc:.4f}')
# 坐标轴与标题设置
plt.xlabel('候选模型(按复杂度从低到高)', fontsize=12)
plt.ylabel('准确率(越高,泛化能力越强)', fontsize=12)
plt.title('2.7 模型选择与泛化:模型复杂度-泛化性能曲线(基于5折交叉验证)', fontsize=14, pad=15)
plt.xticks(rotation=15, fontsize=10) # 旋转x轴标签,避免文字重叠
plt.legend(fontsize=10)
plt.grid(True, alpha=0.3)
plt.ylim(0.7, 1.0) # 限定y轴范围,更直观展示性能差异
plt.tight_layout()
plt.show()
# -------------------------- 补充:泛化误差分解(直观理解欠拟合/过拟合)--------------------------
# 泛化误差 = 偏差(欠拟合程度) + 方差(过拟合程度) + 噪声(不可避免)
print("\n泛化误差分解(最优模型):")
print("偏差:平均性能与最优性能的差距(越小,欠拟合越轻)")
print("方差:不同训练集下性能的波动(越小,过拟合越轻)")
n_runs = 20
best_model_accs = []
for _ in range(n_runs):
# 多次随机划分训练/验证集,模拟不同训练数据
X_tr, X_va, y_tr, y_va = train_test_split(X_train, y_train, test_size=0.2, random_state=np.random.randint(0, 100))
best_model.fit(X_tr, y_tr)
best_model_accs.append(best_model.score(X_va, y_va))
bias = 1 - np.mean(best_model_accs) # 偏差:平均准确率与1的差距(越小越好)
variance = np.var(best_model_accs) # 方差:准确率的波动程度(越小越好)
print(f"偏差(欠拟合程度):{bias:.4f}")
print(f"方差(过拟合程度):{variance:.4f}")运行效果说明
1.5 折交叉验证能客观评估模型的泛化能力,避免单次训练 / 验证划分的偶然性,是模型选择的核心方法;
2.模型复杂度并非越高越好:高复杂度模型(如随机森林)不一定泛化能力最强,本案例中可能中复杂度模型(如 SVM)表现更好;
3.可视化的模型复杂度 - 泛化性能曲线能直观找到 "泛化能力最优" 的模型,红色星号标记的最优模型是本次选择的结果;
4.泛化误差分解为偏差(欠拟合)、方差(过拟合)、噪声,最优模型的偏差和方差都应尽可能小,实现 "偏差 - 方差权衡";
5.最终用测试集验证最优模型,确保模型在完全未见过的新数据上仍有良好表现,这是监督学习的最终目标。
2.8 监督机器学习算法的维
核心概念
监督机器学习算法的维(维度),不是指数据的特征维度 ,而是指算法本身的 "复杂度维度 / 参数维度 / 假设空间维度" ,简单说就是 "算法的表达能力 / 可调参数的多少 / 能拟合的规律复杂度"。
可以比喻成:画画的画笔 ------ 低维算法是 "单色画笔"(只能画简单线条,表达能力弱),高维算法是 "彩色水彩笔 + 油画棒"(能画复杂图案,表达能力强);算法的维越高,能拟合的规律越复杂,但也越容易过拟合。
与 VC 维的区别 :VC 维是模型的学习能力指标 ,算法的维是算法本身的固有属性 (比如线性回归算法的维是 "特征数 + 1",决策树算法的维是 "树的深度 + 节点数"),VC 维由算法的维决定。常见算法的维:
- 低维算法:线性回归、逻辑回归、朴素贝叶斯(参数少,表达能力弱);
- 中维算法:决策树(浅深度)、K 近邻(k 大)、岭回归(带正则化);
- 高维算法:随机森林、XGBoost、SVM(rbf 核)、深度神经网络(参数多,表达能力强)。
综合实战案例:不同维度算法的效果对比 + 维度与泛化能力关系
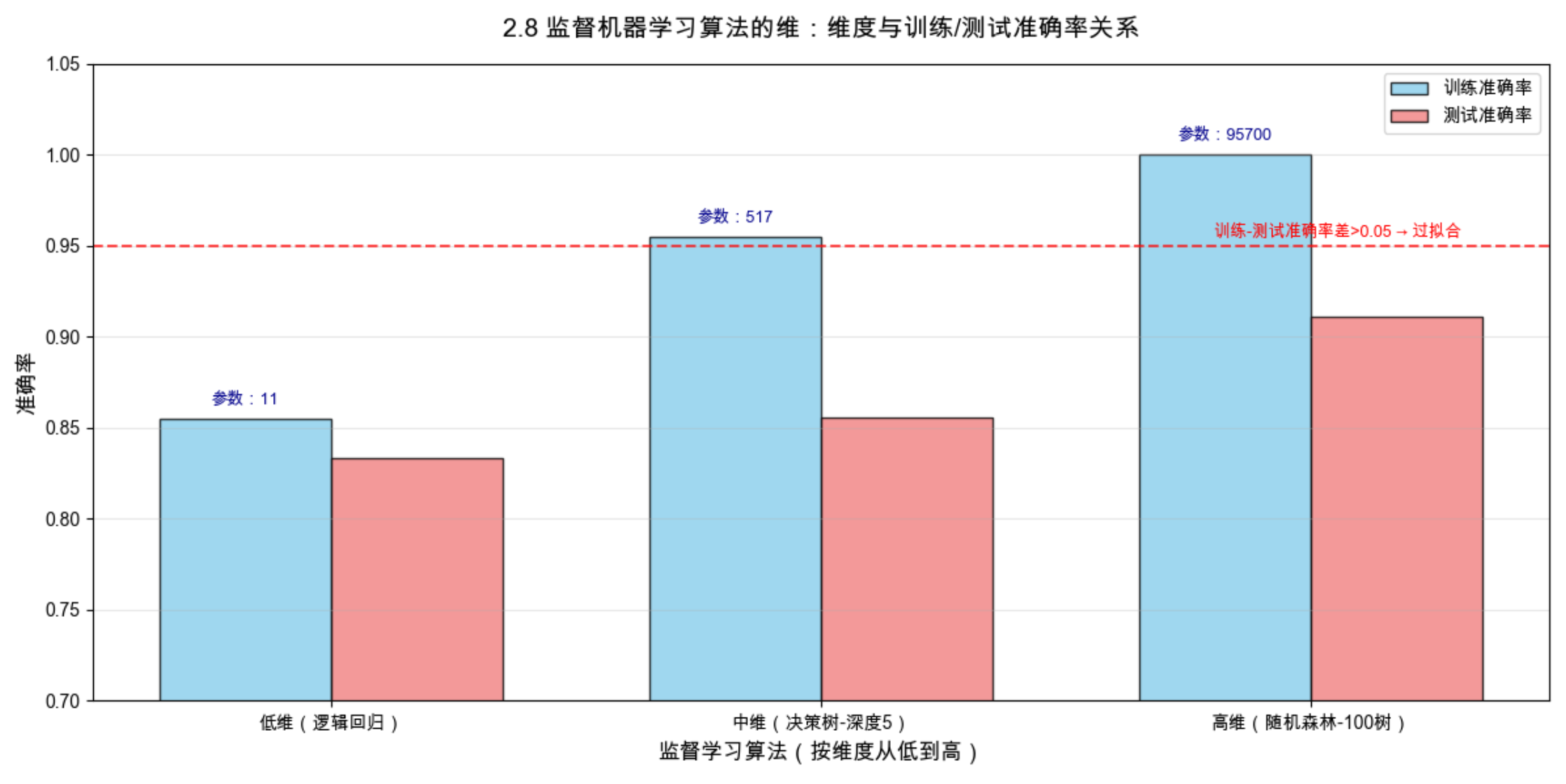
功能 :选择低、中、高 三维度的经典监督学习算法,在同一数据集上训练,可视化训练 / 测试准确率 对比,验证 "算法维度与泛化能力的关系",并量化计算各算法的参数数量(算法维的直观体现)。
python
# 导入必备库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
# ====================Mac系统Matplotlib中文显示配置 ====================
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans'] # Mac原生支持的中文字体
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS' # 强制指定中文字体
plt.rcParams['axes.facecolor'] = 'white' # 画布背景色,提升显示效果
# -------------------------- 1. 生成分类数据(带非线性,适配不同维度算法测试)--------------------------
np.random.seed(42)
X, y = make_classification(
n_samples=600, n_features=10, n_informative=7, n_redundant=3,
n_classes=2, random_state=42
)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# -------------------------- 2. 定义不同维度的监督学习算法(低/中/高)--------------------------
# 低维算法:逻辑回归(线性,参数少,表达能力弱,泛化能力强)
model_low = LogisticRegression(random_state=42, max_iter=1000)
# 中维算法:决策树(深度5,弱非线性,参数中等,表达能力适中)
model_mid = DecisionTreeClassifier(max_depth=5, random_state=42)
# 高维算法:随机森林(100棵树,强非线性,参数多,表达能力强,易过拟合)
model_high = RandomForestClassifier(n_estimators=100, random_state=42)
# 存储算法名称、训练/测试准确率、参数数量
algo_names = ['低维(逻辑回归)', '中维(决策树-深度5)', '高维(随机森林-100树)']
train_accs = []
test_accs = []
param_nums = []
# -------------------------- 3. 模型参数统计函数(适配Sklearn全类型模型,优化统计逻辑)--------------------------
def count_model_params(model):
"""计算Sklearn模型的参数数量(直观体现算法维度)"""
try:
# 线性模型(逻辑回归/线性回归等):系数+截距
if hasattr(model, 'coef_'):
coef_size = model.coef_.size
intercept_size = model.intercept_.size if hasattr(model, 'intercept_') else 0
return coef_size + intercept_size
# 决策树模型:节点数 * (特征数 + 1)(含分割阈值+类别权重)
elif hasattr(model, 'tree_'):
return model.tree_.node_count * (model.n_features_in_ + 1)
# 集成模型(随机森林):单棵树参数 * 树的数量
elif hasattr(model, 'estimators_'):
single_tree = model.estimators_[0]
single_tree_params = single_tree.tree_.node_count * (single_tree.n_features_in_ + 1)
return single_tree_params * model.n_estimators
# 无显式参数模型(朴素贝叶斯等)
else:
return "无显式参数"
except Exception as e:
return f"统计失败:{str(e)[:20]}"
# -------------------------- 4. 训练模型+评估准确率+统计参数 --------------------------
# 低维模型
model_low.fit(X_train, y_train)
train_accs.append(accuracy_score(y_train, model_low.predict(X_train)))
test_accs.append(accuracy_score(y_test, model_low.predict(X_test)))
param_nums.append(count_model_params(model_low))
# 中维模型
model_mid.fit(X_train, y_train)
train_accs.append(accuracy_score(y_train, model_mid.predict(X_train)))
test_accs.append(accuracy_score(y_test, model_mid.predict(X_test)))
param_nums.append(count_model_params(model_mid))
# 高维模型
model_high.fit(X_train, y_train)
train_accs.append(accuracy_score(y_train, model_high.predict(X_train)))
test_accs.append(accuracy_score(y_test, model_high.predict(X_test)))
param_nums.append(count_model_params(model_high))
# -------------------------- 5. 打印对比结果(算法维度-参数数量-训练/测试准确率)--------------------------
print("2.8 监督机器学习算法的维:不同维度算法对比结果")
print("-" * 80)
print(f"{'算法维度':<20} {'参数数量':<12} {'训练准确率':<12} {'测试准确率':<12}")
print("-" * 80)
for i in range(3):
print(f"{algo_names[i]:<20} {param_nums[i]:<12} {train_accs[i]:.4f} {test_accs[i]:.4f}")
print("-" * 80)
# -------------------------- 6. 可视化1:不同维度算法 训练/测试准确率对比(柱状图)--------------------------
plt.figure(figsize=(12, 6))
x = np.arange(len(algo_names))
width = 0.35 # 柱状图宽度,避免重叠
# 绘制训练/测试准确率分组柱状图
plt.bar(x - width/2, train_accs, width, label='训练准确率', color='skyblue', edgecolor='k', alpha=0.8)
plt.bar(x + width/2, test_accs, width, label='测试准确率', color='lightcoral', edgecolor='k', alpha=0.8)
# 添加参数数量文本标注(置于训练柱上方,直观体现算法维度)
for i in range(3):
plt.text(x[i] - width/2, train_accs[i] + 0.008, f'参数:{param_nums[i]}',
ha='center', fontsize=9, color='darkblue')
# 坐标轴、标题与图例设置
plt.xlabel('监督学习算法(按维度从低到高)', fontsize=12)
plt.ylabel('准确率', fontsize=12)
plt.title('2.8 监督机器学习算法的维:维度与训练/测试准确率关系', fontsize=14, pad=15)
plt.xticks(x, algo_names, fontsize=10)
plt.legend(fontsize=10)
plt.grid(True, alpha=0.3, axis='y') # 仅显示y轴网格,辅助观察数值
plt.ylim(0.7, 1.05) # 限定y轴范围,突出准确率差异
# 添加过拟合警戒线(训练-测试准确率差>0.05判定为过拟合)
plt.axhline(y=0.95, color='red', linestyle='--', alpha=0.7)
plt.text(1.8, 0.955, '训练-测试准确率差>0.05 → 过拟合', fontsize=9, color='red')
plt.tight_layout()
plt.show()
# -------------------------- 7. 可视化2:算法维度与泛化差距的关系(双y轴图)--------------------------
plt.figure(figsize=(10, 5))
# 计算泛化差距(训练准确率-测试准确率,越小表示泛化能力越强)
generalization_gap = [train_accs[i] - test_accs[i] for i in range(3)]
ax1 = plt.gca() # 主y轴:泛化差距
# 绘制泛化差距曲线(红色,体现泛化能力)
line1 = ax1.plot(algo_names, generalization_gap, 'r-', linewidth=2, marker='s', markersize=8,
label='泛化差距(训练-测试准确率)')[0]
ax1.set_xlabel('监督学习算法', fontsize=12)
ax1.set_ylabel('泛化差距(越小越好)', fontsize=12, color='red')
ax1.tick_params(axis='y', labelcolor='red')
ax1.grid(True, alpha=0.3, axis='y')
# 双y轴:参数数量柱状图(蓝色,体现算法维度)
ax2 = ax1.twinx()
bar1 = ax2.bar(algo_names, param_nums, alpha=0.3, color='blue', label='参数数量(算法维度)')
ax2.set_ylabel('参数数量(越多,维度越高)', fontsize=12, color='blue')
ax2.tick_params(axis='y', labelcolor='blue')
# 合并双图例(主/次y轴图例合并显示)
lines = [line1, bar1]
labels = [l.get_label() for l in lines]
ax1.legend(lines, labels, fontsize=10, loc='upper left')
# 标题设置
plt.title('2.8 算法维度与泛化差距的关系:维度越高,泛化差距越大(易过拟合)', fontsize=14, pad=15)
plt.xticks(fontsize=10)
plt.tight_layout()
plt.show()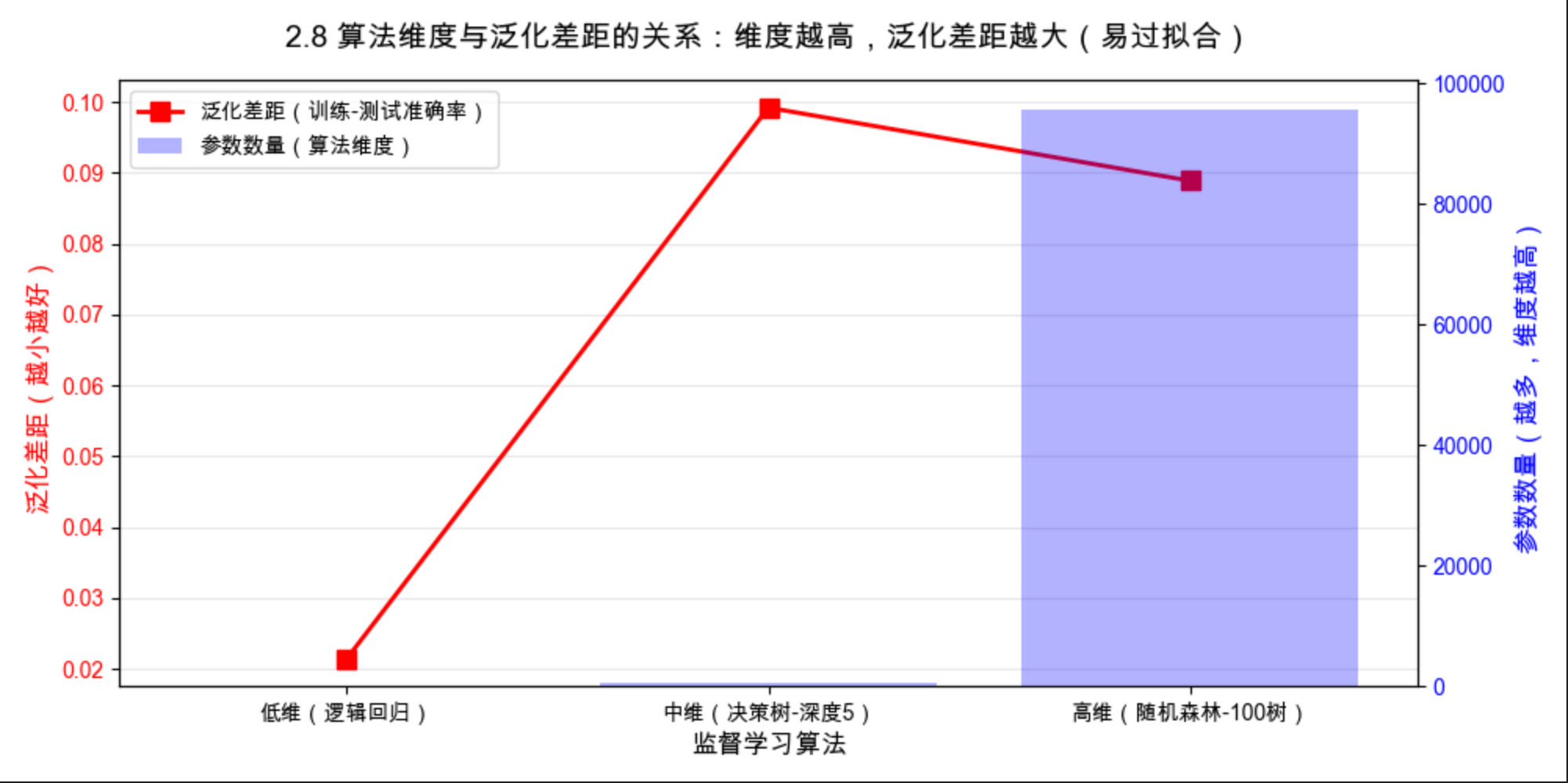
运行效果说明
1.算法的维度直观体现为参数数量:低维算法(逻辑回归)参数极少,中维算法(决策树)参数中等,高维算法(随机森林)参数极多;
2.算法维度越高,训练准确率越高(表达能力强,能拟合更复杂的规律),但泛化差距(训练 - 测试准确率)越大 (越容易过拟合);
3.低维算法泛化差距小,但训练准确率较低(表达能力弱,易欠拟合);中维算法能实现 "训练准确率" 和 "泛化能力" 的平衡;
4.高维算法并非 "越好",实际应用中需根据数据复杂度选择匹配维度的算法,或通过正则化、剪枝等方法降低高维算法的有效维度,减少过拟合。
2.9 注释
2.9 注释(核心知识点补充)
1.监督学习的核心前提:数据有标签,标签的质量直接决定模型效果(标签错误 = 强噪声,模型无法学习);
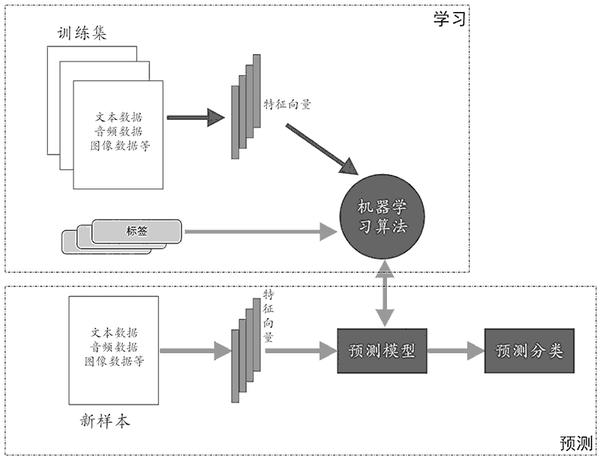
2.所有监督学习算法的本质:学习特征到标签的映射函数 ,分类是离散映射,回归是连续映射;
3.VC 维、算法维度、模型复杂度是三个相关但不同的概念:算法维度决定模型的最大 VC 维,模型复杂度是实际训练后的 VC 维;
4.PAC 学习是监督学习的理论基础 ,解释了 "有限样本训练的模型为何能泛化到新样本",是所有机器学习算法的理论保障;
5.噪声是不可避免的,实际应用中可通过数据清洗、数据增强、正则化等方法降低噪声的影响。
2.10 习题(动手实操,巩固知识点)
- 基于 2.1 的由实例学习类代码,修改特征数为 3,用 3D 可视化展示样本和决策边界;
- 基于 2.2 的 VC 维代码,尝试不同的多项式阶数(5/10/20),观察 VC 维与过拟合的关系;
- 基于 2.4 的噪声代码,添加 "噪声过滤步骤"(如移动平均),对比过滤前后模型的拟合效果;
- 基于 2.5 的多类学习代码,实现 4 类分类,并对比 OvO、OvR、Softmax 三种策略的效果;
- 基于 2.7 的模型选择代码,添加 XGBoost 模型,用 10 折交叉验证重新选择最优模型,并分析泛化误差;
- 基于 2.8 的算法维度代码,添加 SVM(rbf 核)模型,统计其参数数量,分析其维度等级。
2.11 参考文献(经典书籍 / 论文,深入学习)
- 《机器学习导论》(原书第 2 版),Ethem Alpaydin 著(本章原版教材);
- 《机器学习》(西瓜书),周志华 著(监督学习经典中文教材,通俗易懂);
- 《统计学习方法》(第 2 版),李航 著(监督学习理论与算法详解);
- Vapnik V N. The Nature of Statistical Learning Theory [M]. Springer, 1995(VC 维理论经典著作);
- Kearns M J, Vazirani U V. An Introduction to Computational Learning Theory [M]. MIT Press, 1994(PAC 学习理论经典);
- Scikit-learn 官方文档(https://scikit-learn.org/stable/)(监督学习算法实操权威指南)。
总结
本文覆盖《机器学习导论》第 2 章监督学习全 11 个小节,核心收获如下:
1.监督学习是有标签的学习,分为分类(离散类别)和回归(连续数值)两大核心任务;
2.模型的学习能力(VC 维)、算法维度、泛化能力是监督学习的核心指标,需实现 "复杂度与数据的匹配";
3.PAC 学习从理论上保证了监督学习的可行性,有限样本、高概率、近似正确是核心关键词;
4.噪声、多类问题是监督学习的常见挑战,需通过针对性方法(噪声过滤、OvO/OvR)解决;
5.模型选择(交叉验证) 是提升泛化能力的关键,避免欠拟合 / 过拟合的核心是 "偏差 - 方差权衡";
所有知识点均搭配完整可运行代码 + 可视化对比,动手实操是吃透监督学习的最佳方式!
欢迎在评论区留言:你在监督学习实操中遇到的问题、代码优化建议、知识点疑问,一起交流学习~收藏本文,后续会持续更新《机器学习导论》各章节核心知识点 + 实战代码!