一、ID3算法
衡量标准:
熵值:表示随机变量不确定性的度量,或者说是物体内部的混乱程度。熵值越小,该节点越"纯"。
熵值计算公式:
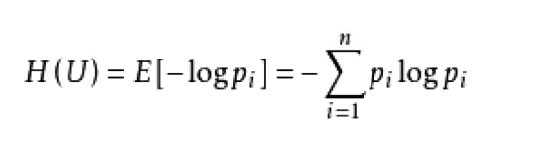
举个例子:
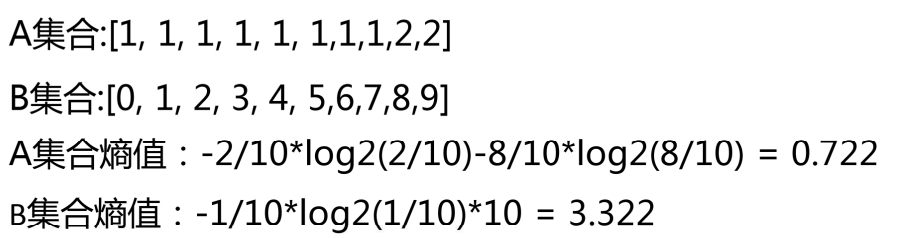
显然B的熵值更大,即更加混乱。
信息增益:它描述的是一个特征能够为整个系统带来多少信息量(熵),用于度量信息不确定性减少的程度。
如果一个特征能够为系统带来最大的信息量,则该特征最重要,将会被选作划分数据集的特征。
信息增益 = 标签的熵 - 特征的熵
示例:
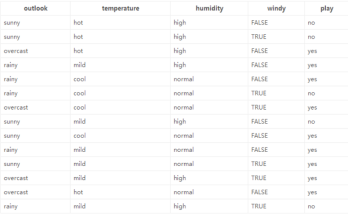
第一遍遍历:
1.标签(结果是否外出打球)的熵(类别熵):
14天中,9天打球,5天不打球,熵为:
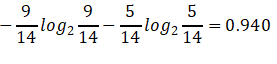
2.基于天气的划分
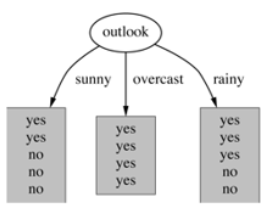
属性熵:
晴天【5天】的熵:
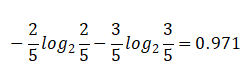
Overcast(阴天)【4天】的熵:
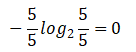
雨天【5天】的熵:
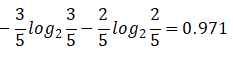
那么,天气对应标签结果的熵为:
5/14*0.971+4/14*0+5/14*0.971=0.693
则 信息增益为: 0.940-0.693 =0.247
以此类推:
3.基于温度 的划分
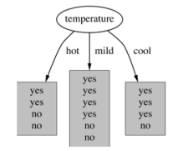
熵值计算:4/14*1+6/14*0.918+4/14*0.811=0.911
信息增益为:0.940 -- 0.911 = 0.029
4.基于湿度的划分
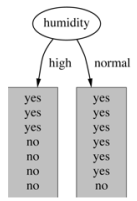
熵值计算:7/14*0.985+7/14*0.592=0.789
信息增益:0.940 -- 0.789 =0.151
5.基于有风的划分
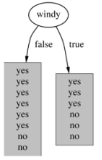
熵值计算:8/14*0.811 + 6/14*1 = 0.892
信息增益:0.940 - 0.892 = 0.048
综上:信息增益的大小:
天气:0.247
温度:0.029
湿度:0.151
有风:0.048
显然,信息增益最大的是: 天气 > 湿度 > 有风 > 温度
二、C4.5算法**(解决稀疏向量的问题,例如编号)**
衡量标准:
信息增益率。
信息增益率:

C4.5算法是一种决策树生成算法,它使用信息增益比(gain ratio)来选择最优分裂属性,具体步骤如下:
1、计算所有样本的类别熵(H)。
2、对于每一个属性,计算该属性的熵【也为自身熵】(Hi)。
3、对于每一个属性,计算该属性对于分类所能够带来的信息增益(Gi = H - Hi)。
4、计算每个属性的信息增益比(gain ratio = Gi / Hi),即信息增益与类别自身熵的比值。
选择具有最大信息增益比的属性作为分裂属性。
示例:
第一遍 计算: 【找 首要节点 】:
1、天气的信息增益为:0.247,
天气的自身熵值:
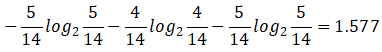
信息增益为: 0.940-0.693 =0.247
信息增益率:0.247/1.577 = 0.1566
2.温度的自身熵值:
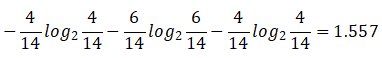
信息增益为:0.940 -- 0.911 = 0.029
信息增益率:0.029/1.557 = 0.0186
3.湿度的自身熵值:
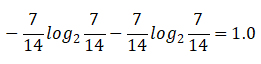
信息增益:0.940 -- 0.789 =0.151
信息增益率:0.151/1.0 = 0.151
4.有风的自身熵值:
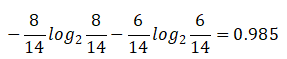
信息增益:0.940 - 0.892 = 0.048
信息增益率:0.048/0.985 = 0.049
信息增益率排序:天气(0.1566)湿度(0.151)有风(0.049) 温度(0.0186)
天气 >湿度>有风>温度
三、CART决策树
衡量标准:基尼系数
用Gini指数最小化准则来进行特征选择。
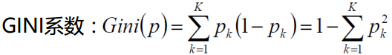

示例:
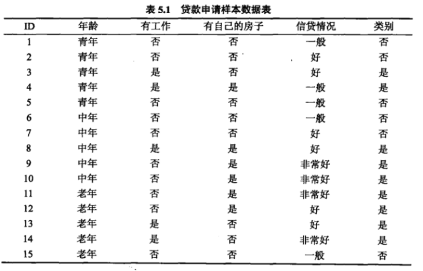

特征A1(年龄)的基尼系数:
青年(5人,2人贷款)的基尼系数:
1-(2/5)²-(3/5)²=0.48
非青年(10人,7人贷款)的基尼系数:
1-(7/10)²-(3/10)²=0.42
在A1=1(青年)条件下,D的基尼指数:
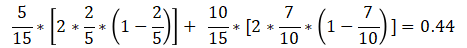
在A1=2(中年)条件下,D的基尼指数:
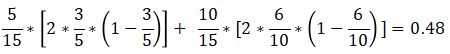
在A1=3(老年)条件下,D的基尼指数: