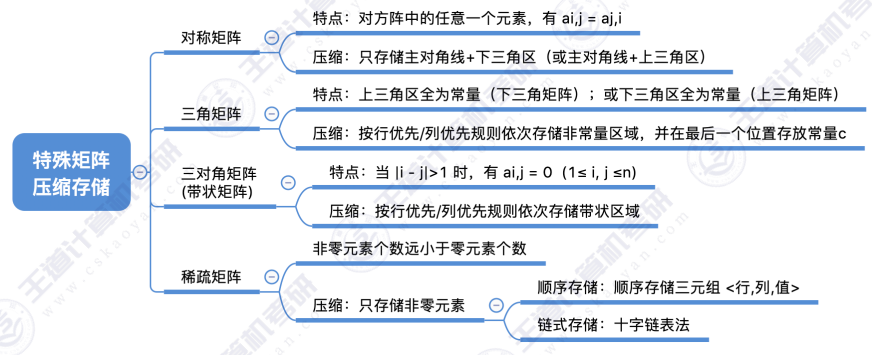
一、知识总览
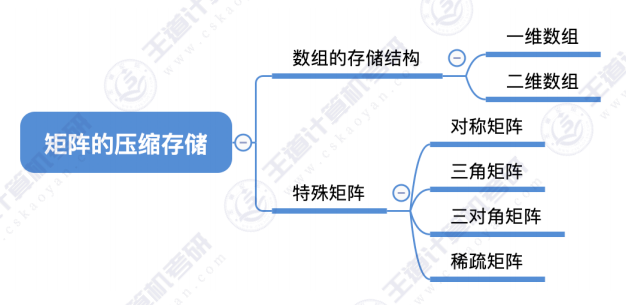
二、数组的存储结构
2.1 一维数组

2.2 二维数组

- 行优先存储

- 列优先存储

三、特殊矩阵
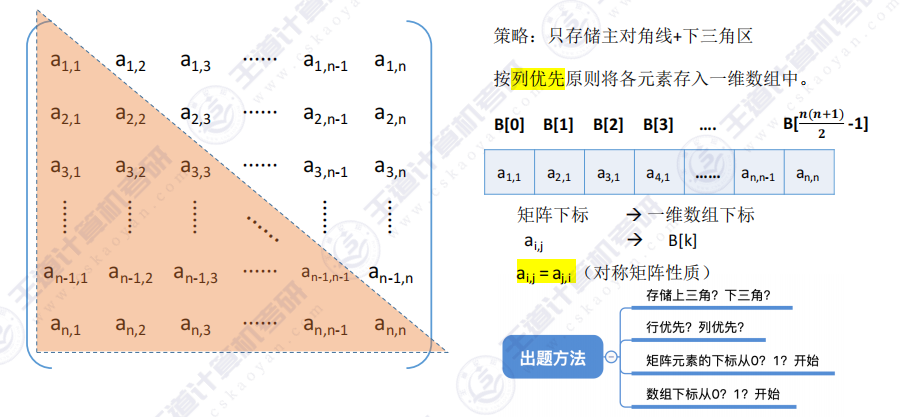
3.1 对称矩阵的压缩存储
-
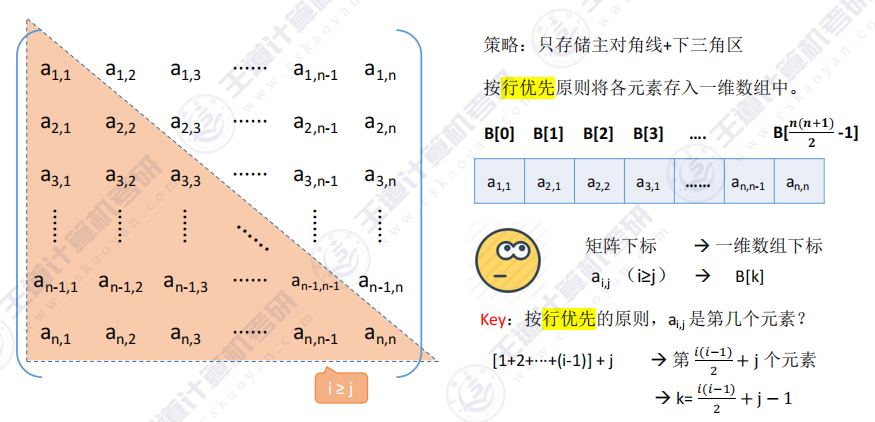
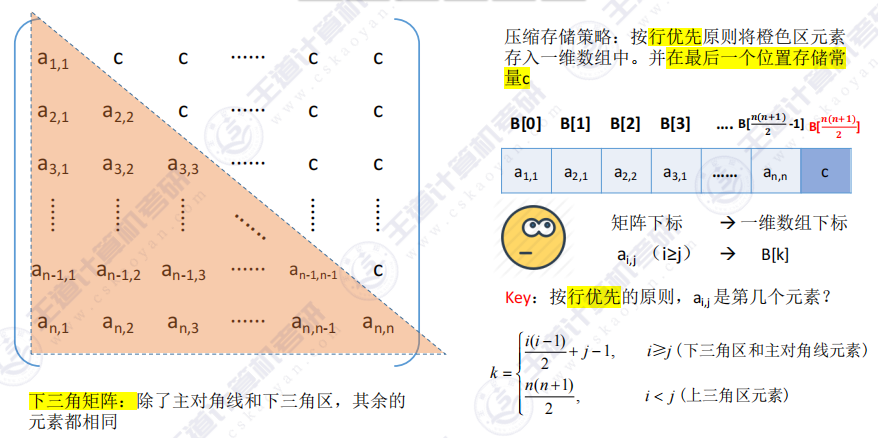
下三角情况
等差数列求和公式 :Sn=n(a1+an)2S_{n} =\frac{n(a_{1}+a_{n} )}{2}Sn=2n(a1+an)
构建k=f(n)k=f(n)k=f(n)的函数 :第一行1个元素,第二行2个元素,第n行有n个元素,根据等差数列公式 ,可以得到数据下标k=n(n+1)2k=\frac{n(n+1)}{2}k=2n(n+1),又因为数据下标一般是从0开始的,所以最终k=n(n+1)2−1k=\frac{n(n+1)}{2}-1k=2n(n+1)−1
构建k=f(i,j)k=f(i,j)k=f(i,j)的函数 :第一行1个元素,第二行2个元素,第(i-1)行(可以理解为倒数第二行 )有(i-1)个元素,最后一行有j个元素,所以由等差数列可以得到k=i(i−1)2+jk=\frac{i(i-1)}{2}+jk=2i(i−1)+j,又因为数据下标一般是从0开始的,所以最终k=i(i−1)2+j−1k=\frac{i(i-1)}{2}+j-1k=2i(i−1)+j−1
-
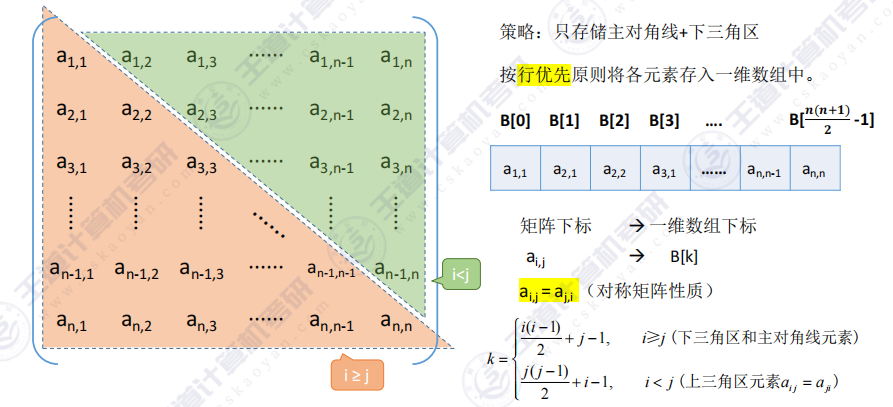
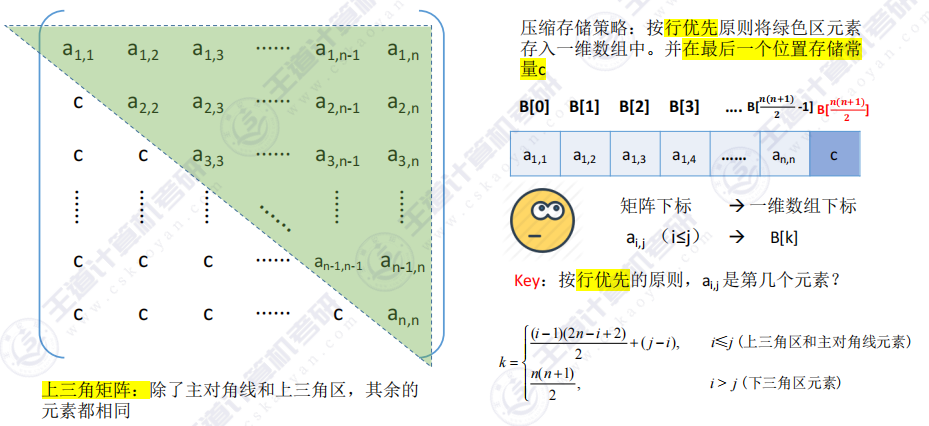
上三角情况
根据对称矩阵原理 :相关公式将i,ji,ji,j相互替换即成立
- 出题方法
3.2 三角矩阵的压缩存储
- 三角矩阵特点
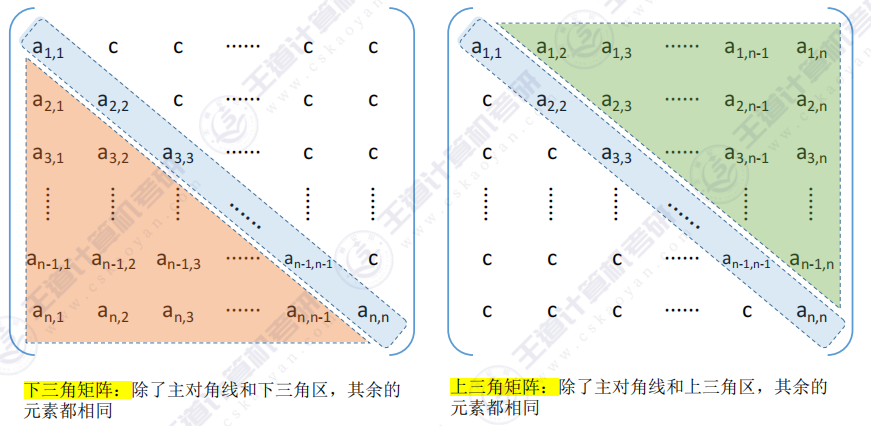
- 下三角矩阵
- 上三角矩阵
3.3 三角对称阵的压缩存储
-
由矩阵的行列编号i,ji,ji,j推导出数组的下标k
前 i−1 行的元素总数 :第 1 行有 2 个非零元素(a1,1,a1,2),第 2 到第 i−1 行,每行有 3 个非零元素(主对角线 + 上下邻对角线),所以前 i−1 行的总元素数为:2+3×(i−2)=3(i−1)−1
第 i 行中 ai,j 的位置 :第 i 行的非零元素是 ai,i−1,ai,i,ai,i+1,所以 ai,j 是第 i 行的第 (j−i+2) 个元素(比如 j=i−1 时是第 1 个,j=i 时是第 2 个,j=i+1 时是第 3 个,使用a21、a22、a23带入公式即可推导)
k=2i+j-2推导 :前 i−1 行的元素总数为3(i−1)−1 ,第 i 行中 ai,j 的位置为第**(j−i+2)**个元素,k=[3(i−1)−1] + (j−i+2) = 2i+j-2,又因为数组下标为0,所以k=2i+j−3k=2i+j-3k=2i+j−3
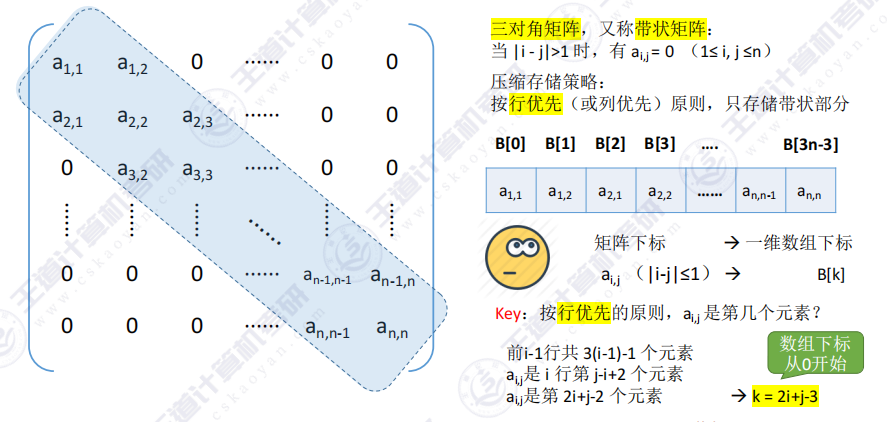
- 由数组的下标k推导出矩阵的行列编号i,ji,ji,j
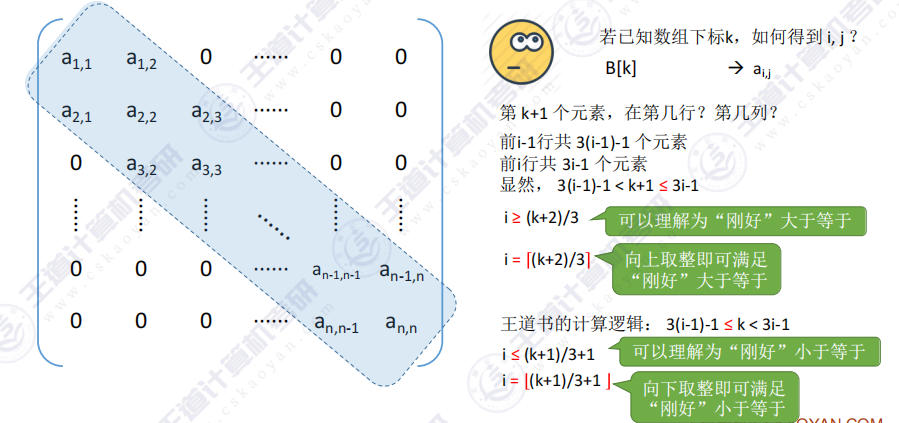
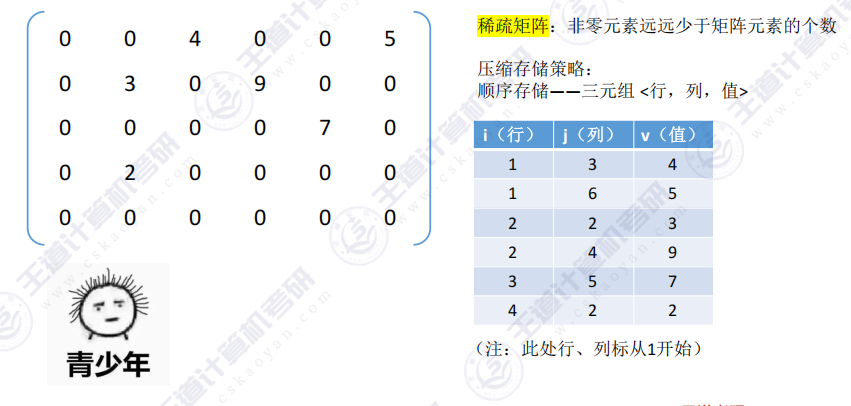
3.4 稀疏矩阵的压缩存储
- 顺序存储
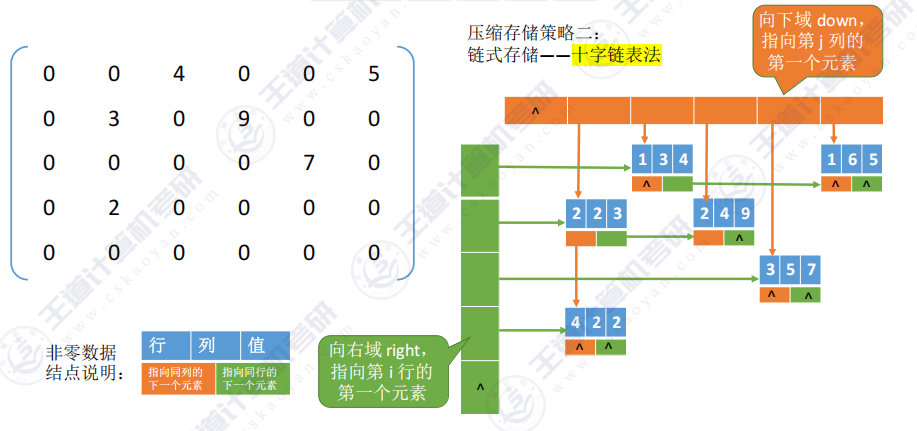
- 链式存储
3.5 总结