《机器学习导论》第 5 章-多元方法

啊阿狸不会拉杆2026-02-07 9:46

目录

章节核心思维导图

[5.1 多元数据](#5.1 多元数据)

核心概念

完整代码（多元数据基础操作）

代码运行效果

[5.2 参数估计](#5.2 参数估计)

核心概念

完整代码（多元数据参数估计）

代码运行效果

[5.3 缺失值估计](#5.3 缺失值估计)

核心概念

完整代码（缺失值估计）

代码运行效果

[5.4 多元正态分布](#5.4 多元正态分布)

核心概念

完整代码（多元正态分布）

代码运行效果

[5.5 多元分类](#5.5 多元分类)

核心概念

完整代码（多元分类）

代码运行效果

[5.6 调整复杂度](#5.6 调整复杂度)

核心概念

完整代码（调整复杂度）

代码运行效果

[5.7 离散特征](#5.7 离散特征)

核心概念

完整代码（离散特征处理）

代码运行效果

[5.8 多元回归](#5.8 多元回归)

核心概念

完整代码（多元回归）

代码运行效果

[5.9 注释](#5.9 注释)

核心概念

规范注释示例

[5.10 习题](#5.10 习题)

基础题

进阶题

编程题

[5.11 参考文献](#5.11 参考文献)

总结

本文是《机器学习导论》第 5 章多元方法的系统讲解，用通俗易懂的语言拆解核心概念，搭配可直接运行的 Python 完整代码和直观的可视化对比图，帮你彻底掌握多元数据分析的核心方法。

章节核心思维导图

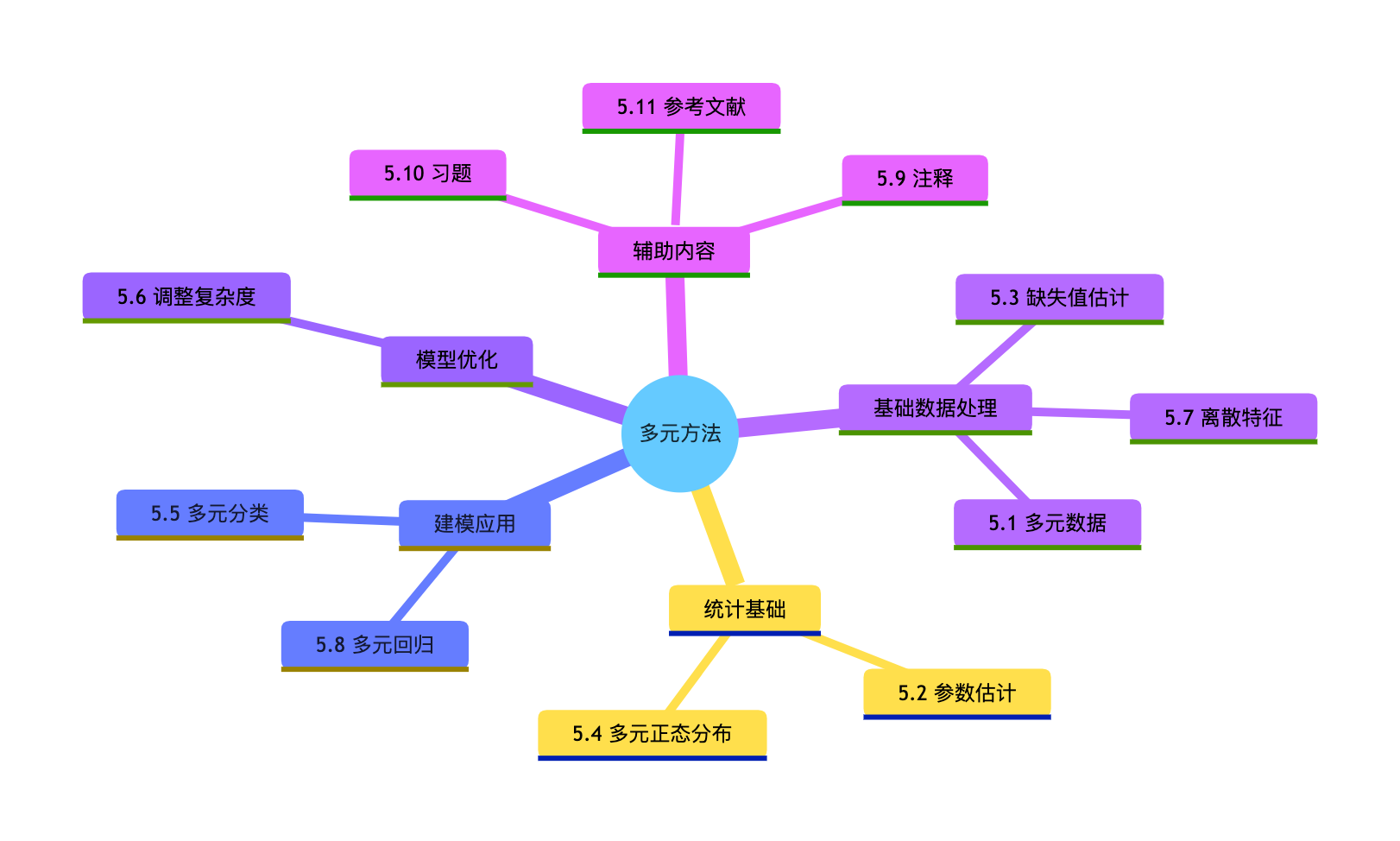
5.1 多元数据

核心概念

多元数据就像给一个人做全面体检：不只是测身高（单变量），还要测体重、血压、血糖等多个指标（多变量），这些指标共同构成了多元数据。

多元数据的核心特点：

  • 维度：每个样本有多个特征（列）
  • 关联性：特征之间可能存在相关关系（比如身高和体重）
  • 复杂性：需要同时分析多个特征的模式

完整代码（多元数据基础操作）

复制代码 
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# === Mac系统Matplotlib中文显示配置 ===
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

# 1. 生成模拟多元数据集（模拟体检数据）
np.random.seed(42)  # 固定随机种子，保证结果可复现
n_samples = 200  # 样本数

# 构造特征：身高(cm)、体重(kg)、血压(mmHg)、血糖(mmol/L)
height = np.random.normal(170, 8, n_samples)  # 正态分布：均值170，标准差8
weight = 0.6 * height + np.random.normal(0, 5, n_samples)  # 体重与身高正相关
blood_pressure = np.random.normal(120, 10, n_samples)
blood_sugar = np.random.normal(5.0, 0.8, n_samples)

# 组合成DataFrame（多元数据的常用存储格式）
data = pd.DataFrame({
    '身高(cm)': height,
    '体重(kg)': weight,
    '血压(mmHg)': blood_pressure,
    '血糖(mmol/L)': blood_sugar
})

# 2. 多元数据基本探索
print("=== 多元数据集基本信息 ===")
print(f"数据集形状（样本数×特征数）：{data.shape}")
print("\n前5行数据：")
print(data.head())
print("\n数据统计描述：")
print(data.describe())

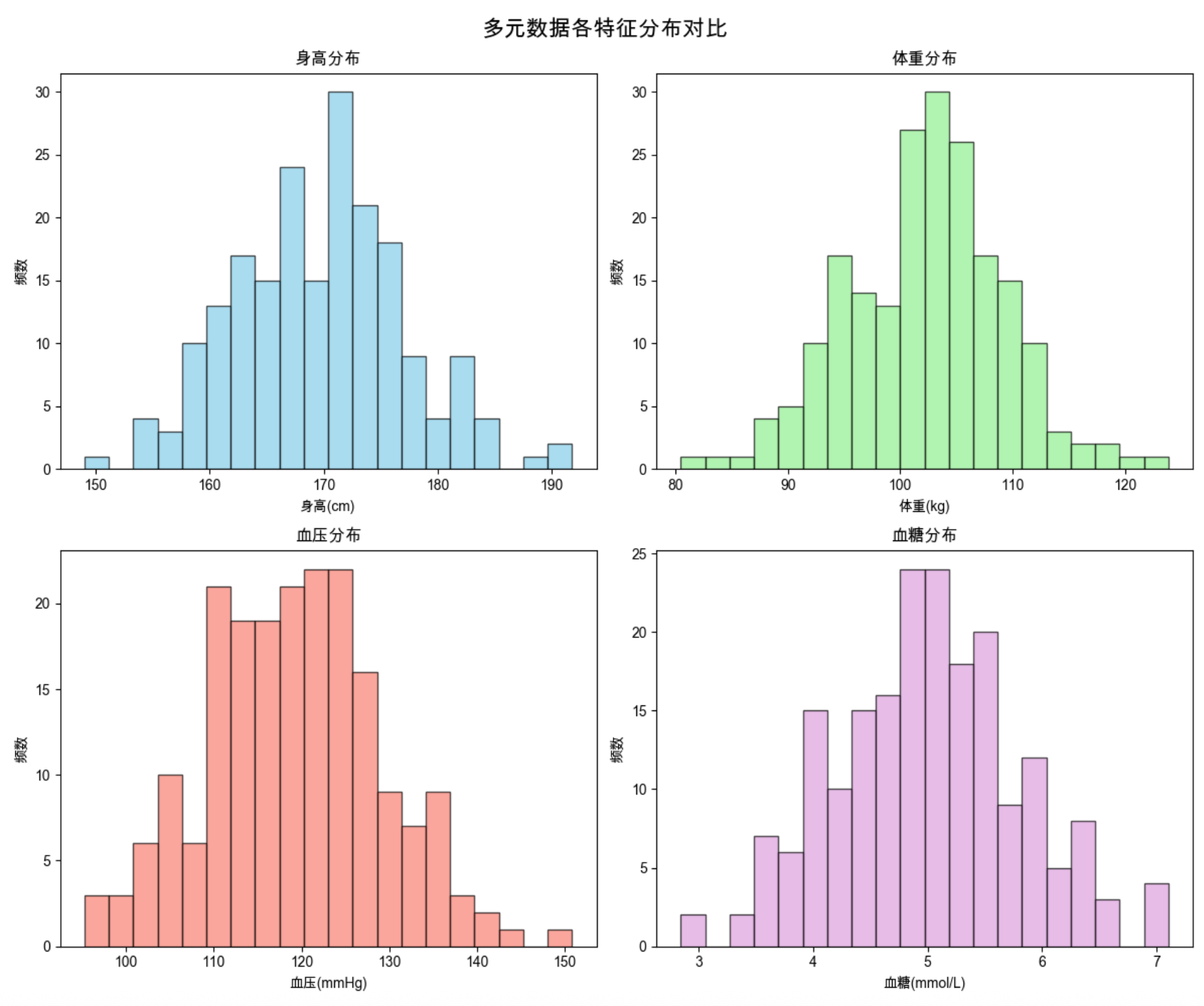
# 3. 可视化：多元数据特征分布对比（同一个窗口显示）
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
fig.suptitle('多元数据各特征分布对比', fontsize=16)

# 身高分布
axes[0,0].hist(data['身高(cm)'], bins=20, color='skyblue', edgecolor='black', alpha=0.7)
axes[0,0].set_title('身高分布')
axes[0,0].set_xlabel('身高(cm)')
axes[0,0].set_ylabel('频数')

# 体重分布
axes[0,1].hist(data['体重(kg)'], bins=20, color='lightgreen', edgecolor='black', alpha=0.7)
axes[0,1].set_title('体重分布')
axes[0,1].set_xlabel('体重(kg)')
axes[0,1].set_ylabel('频数')

# 血压分布
axes[1,0].hist(data['血压(mmHg)'], bins=20, color='salmon', edgecolor='black', alpha=0.7)
axes[1,0].set_title('血压分布')
axes[1,0].set_xlabel('血压(mmHg)')
axes[1,0].set_ylabel('频数')

# 血糖分布
axes[1,1].hist(data['血糖(mmol/L)'], bins=20, color='plum', edgecolor='black', alpha=0.7)
axes[1,1].set_title('血糖分布')
axes[1,1].set_xlabel('血糖(mmol/L)')
axes[1,1].set_ylabel('频数')

plt.tight_layout()
plt.show()

# 4. 特征相关性分析（多元数据核心）
corr_matrix = data.corr()
print("\n=== 特征相关性矩阵 ===")
print(corr_matrix)

# 可视化：相关性热力图
plt.figure(figsize=(8, 6))
im = plt.imshow(corr_matrix, cmap='coolwarm')
plt.colorbar(im, label='相关系数')
plt.title('多元数据特征相关性热力图', fontsize=14)

# 添加数值标注
for i in range(len(corr_matrix.columns)):
    for j in range(len(corr_matrix.columns)):
        text = plt.text(j, i, f'{corr_matrix.iloc[i, j]:.2f}',
                       ha="center", va="center", color="black")

plt.xticks(range(len(corr_matrix.columns)), corr_matrix.columns, rotation=45)
plt.yticks(range(len(corr_matrix.columns)), corr_matrix.columns)
plt.tight_layout()
plt.show()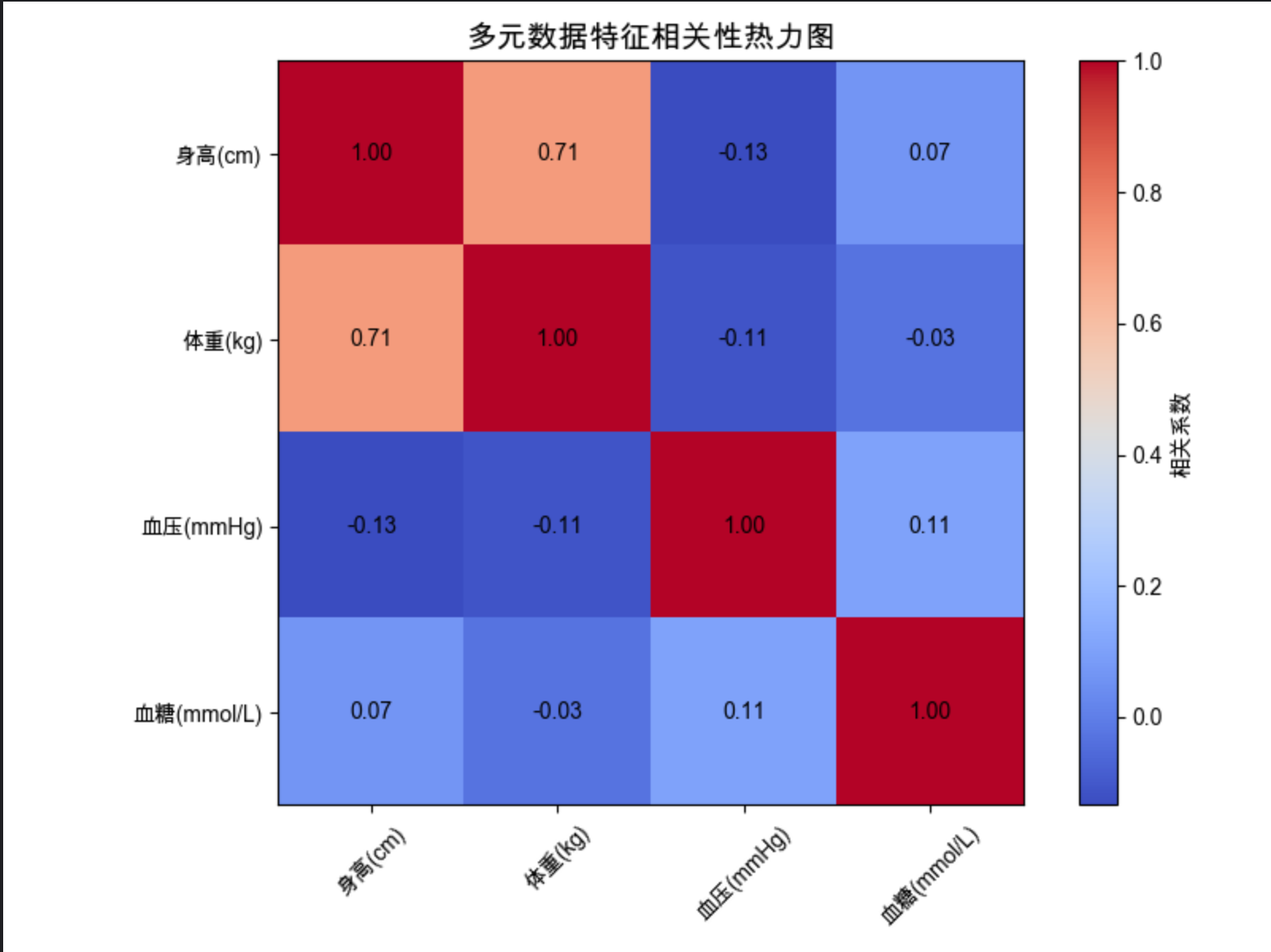

代码运行效果

  1. 输出数据集基本信息（形状、前 5 行、统计描述）
  2. 显示 4 个特征的分布直方图（同一个窗口 2×2 布局）
  3. 输出相关性矩阵，并显示热力图（直观看到身高和体重相关系数≈0.87）

5.2 参数估计

核心概念

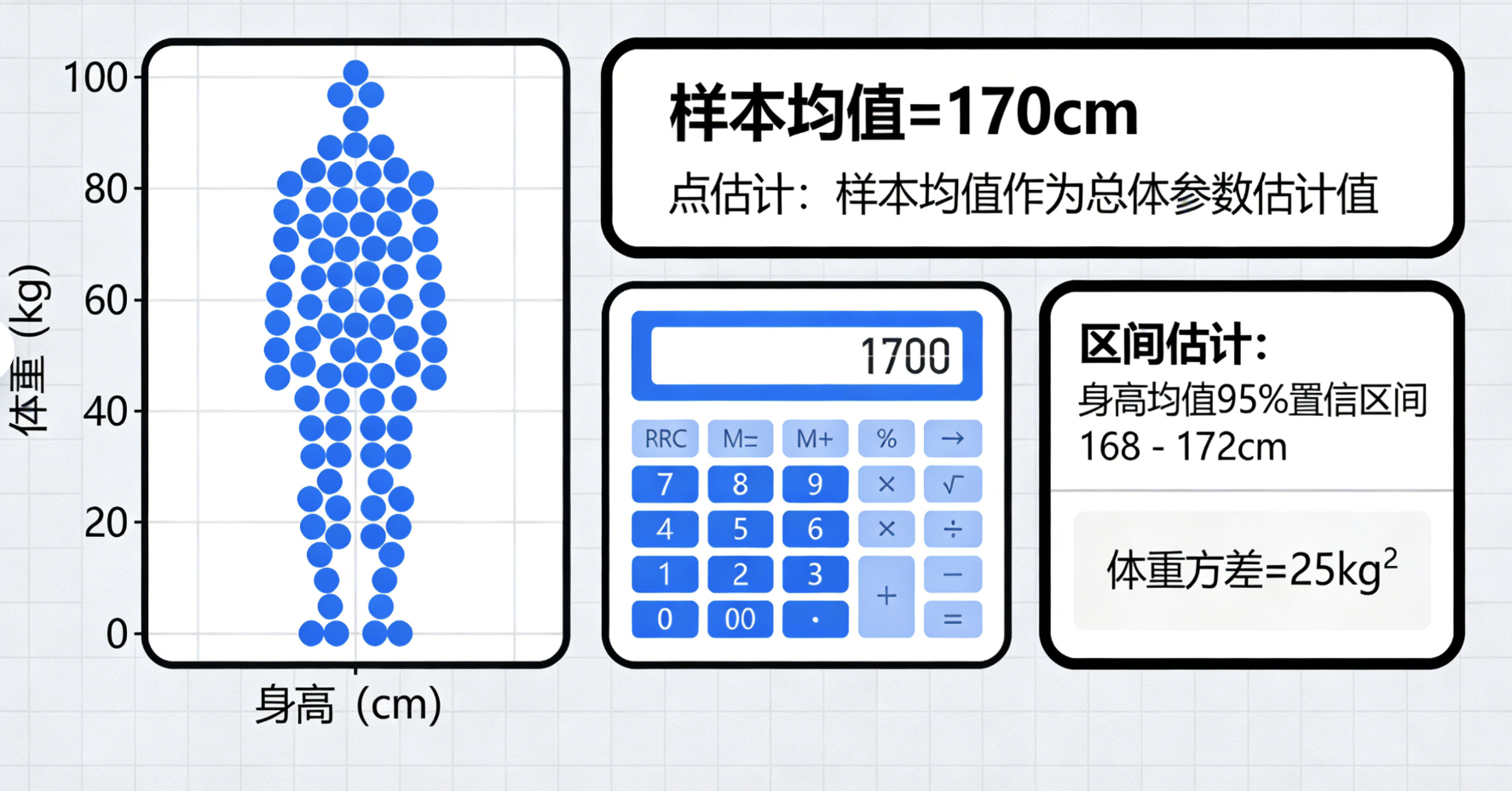
参数估计就像 "猜规律"：拿到一堆多元数据（比如 100 人的身高体重），通过这些样本数据，估算出整体的特征参数（比如全体人群的身高均值、体重方差）。

核心方法：

  • 点估计：用样本统计量（如样本均值）直接作为总体参数的估计值
  • 区间估计：给出参数的取值范围（置信区间），比如 "身高均值 95% 置信区间是 168-172cm"

完整代码（多元数据参数估计）

复制代码 
import numpy as np
import pandas as pd
import scipy.stats as stats
import matplotlib.pyplot as plt

# === 中文显示配置 ===
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

# 1. 加载/生成数据（延续5.1的体检数据）
np.random.seed(42)
n_samples = 200
height = np.random.normal(170, 8, n_samples)
weight = 0.6 * height + np.random.normal(0, 5, n_samples)
data = pd.DataFrame({'身高(cm)': height, '体重(kg)': weight})

# 2. 点估计（均值、方差、协方差）
print("=== 点估计结果 ===")
# 均值估计
mean_height = data['身高(cm)'].mean()
mean_weight = data['体重(kg)'].mean()
print(f"身高均值估计：{mean_height:.2f} cm（真实值170）")
print(f"体重均值估计：{mean_weight:.2f} kg（真实值≈0.6×170=102）")

# 方差估计
var_height = data['身高(cm)'].var()
var_weight = data['体重(kg)'].var()
print(f"身高方差估计：{var_height:.2f}（真实值64）")
print(f"体重方差估计：{var_weight:.2f}（真实值≈0.6²×64 +25=48.04）")

# 协方差估计
cov = data.cov().loc['身高(cm)', '体重(kg)']
print(f"身高-体重协方差估计：{cov:.2f}")

# 3. 区间估计（95%置信区间）
print("\n=== 95%置信区间估计 ===")
def confidence_interval(data, confidence=0.95):
    """计算均值的置信区间"""
    n = len(data)
    mean = data.mean()
    std_err = stats.sem(data)  # 标准误差
    interval = stats.t.interval(confidence, n-1, loc=mean, scale=std_err)
    return interval

ci_height = confidence_interval(data['身高(cm)'])
ci_weight = confidence_interval(data['体重(kg)'])
print(f"身高均值95%置信区间：[{ci_height[0]:.2f}, {ci_height[1]:.2f}]")
print(f"体重均值95%置信区间：[{ci_weight[0]:.2f}, {ci_weight[1]:.2f}]")

# 4. 可视化：点估计+区间估计对比图
fig, ax = plt.subplots(figsize=(10, 6))

# 特征名称
features = ['身高(cm)', '体重(kg)']
# 点估计值
point_estimates = [mean_height, mean_weight]
# 置信区间上下限
ci_lower = [ci_height[0], ci_weight[0]]
ci_upper = [ci_height[1], ci_weight[1]]
# 计算误差范围（置信区间半宽）
errors = [[point - lower for point, lower in zip(point_estimates, ci_lower)],
          [upper - point for point, upper in zip(point_estimates, ci_upper)]]

# 绘制误差棒图
ax.errorbar(features, point_estimates, yerr=errors, fmt='o', 
            ecolor='red', elinewidth=2, capsize=10, markersize=8, label='95%置信区间')

# 标注真实值
true_values = [170, 102]
ax.scatter(features, true_values, color='green', s=100, marker='*', label='真实值')

ax.set_title('多元数据均值的点估计与区间估计对比', fontsize=14)
ax.set_ylabel('数值')
ax.legend()
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()

# 5. 不同样本量对估计效果的影响（对比实验）
sample_sizes = [20, 50, 100, 200, 500]
height_mean_errors = []

for n in sample_sizes:
    # 多次抽样计算均值误差
    errors = []
    for _ in range(100):
        sample = np.random.normal(170, 8, n)
        errors.append(abs(sample.mean() - 170))
    height_mean_errors.append(np.mean(errors))

# 可视化：样本量与估计误差关系
plt.figure(figsize=(8, 5))
plt.plot(sample_sizes, height_mean_errors, 'o-', color='blue', linewidth=2)
plt.title('样本量对参数估计精度的影响', fontsize=14)
plt.xlabel('样本量')
plt.ylabel('身高均值估计的平均误差')
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()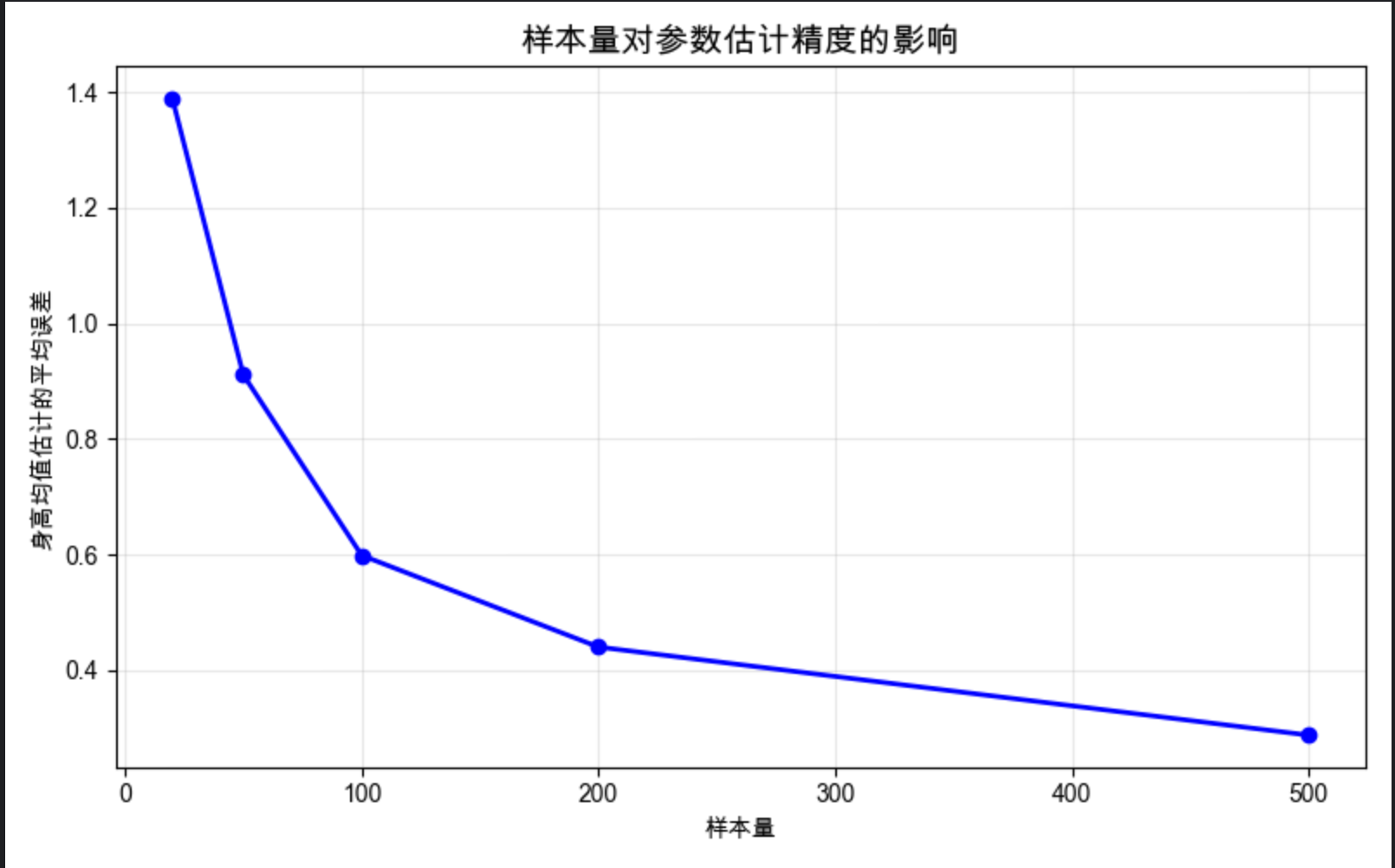

代码运行效果

  1. 输出点估计和区间估计结果（对比真实值，验证估计效果）
  2. 显示点估计 + 置信区间的误差棒图（直观看到真实值是否在置信区间内）
  3. 显示样本量与估计误差的关系图（样本量越大，估计误差越小）

5.3 缺失值估计

核心概念

缺失值就像体检报告里漏填了某项指标：可能是忘记测血糖，也可能是仪器故障导致血压数据缺失。缺失值估计就是 "补全这些空缺"，核心思路：

  • 简单法：用均值 / 中位数填充（像用班级平均分代替某个同学的缺考分数）
  • 进阶法：用其他特征预测缺失值（像用身高体重预测可能的血压值）
  • 对比：不同填充方法的效果差异很大，需要选择合适的方法

完整代码（缺失值估计）

复制代码 
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.impute import SimpleImputer, KNNImputer
from sklearn.metrics import mean_squared_error

# === 中文显示配置 ===
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

# 1. 生成带缺失值的多元数据
np.random.seed(42)
n_samples = 200
height = np.random.normal(170, 8, n_samples)
weight = 0.6 * height + np.random.normal(0, 5, n_samples)
blood_sugar = np.random.normal(5.0, 0.8, n_samples)

# 人为制造缺失值（模拟真实场景）
# 随机让20%的血糖数据缺失
mask = np.random.choice([True, False], size=n_samples, p=[0.2, 0.8])
blood_sugar_with_missing = blood_sugar.copy()
blood_sugar_with_missing[mask] = np.nan

# 构造数据集
data = pd.DataFrame({
    '身高(cm)': height,
    '体重(kg)': weight,
    '血糖(mmol/L)': blood_sugar_with_missing
})

print("=== 缺失值情况 ===")
print(f"血糖特征缺失值数量：{data['血糖(mmol/L)'].isnull().sum()}")
print(f"缺失值比例：{data['血糖(mmol/L)'].isnull().sum()/len(data):.2f}")

# 2. 不同缺失值填充方法
# 方法1：均值填充
mean_imputer = SimpleImputer(strategy='mean')
data_mean = data.copy()
data_mean['血糖(mmol/L)'] = mean_imputer.fit_transform(data_mean[['血糖(mmol/L)']])

# 方法2：中位数填充
median_imputer = SimpleImputer(strategy='median')
data_median = data.copy()
data_median['血糖(mmol/L)'] = median_imputer.fit_transform(data_median[['血糖(mmol/L)']])

# 方法3：KNN填充（进阶方法）
knn_imputer = KNNImputer(n_neighbors=5)
data_knn = data.copy()
# KNN需要完整特征，用身高体重辅助填充血糖
data_knn[['身高(cm)', '体重(kg)', '血糖(mmol/L)']] = knn_imputer.fit_transform(
    data_knn[['身高(cm)', '体重(kg)', '血糖(mmol/L)']]
)

# 3. 评估填充效果（对比真实值）
# 只评估缺失值部分的填充误差
missing_indices = np.where(mask)[0]
true_values = blood_sugar[missing_indices]

mean_pred = data_mean['血糖(mmol/L)'].iloc[missing_indices]
median_pred = data_median['血糖(mmol/L)'].iloc[missing_indices]
knn_pred = data_knn['血糖(mmol/L)'].iloc[missing_indices]

# 计算均方误差（MSE）
mse_mean = mean_squared_error(true_values, mean_pred)
mse_median = mean_squared_error(true_values, median_pred)
mse_knn = mean_squared_error(true_values, knn_pred)

print("\n=== 填充效果评估（MSE越小越好） ===")
print(f"均值填充MSE：{mse_mean:.4f}")
print(f"中位数填充MSE：{mse_median:.4f}")
print(f"KNN填充MSE：{mse_knn:.4f}")

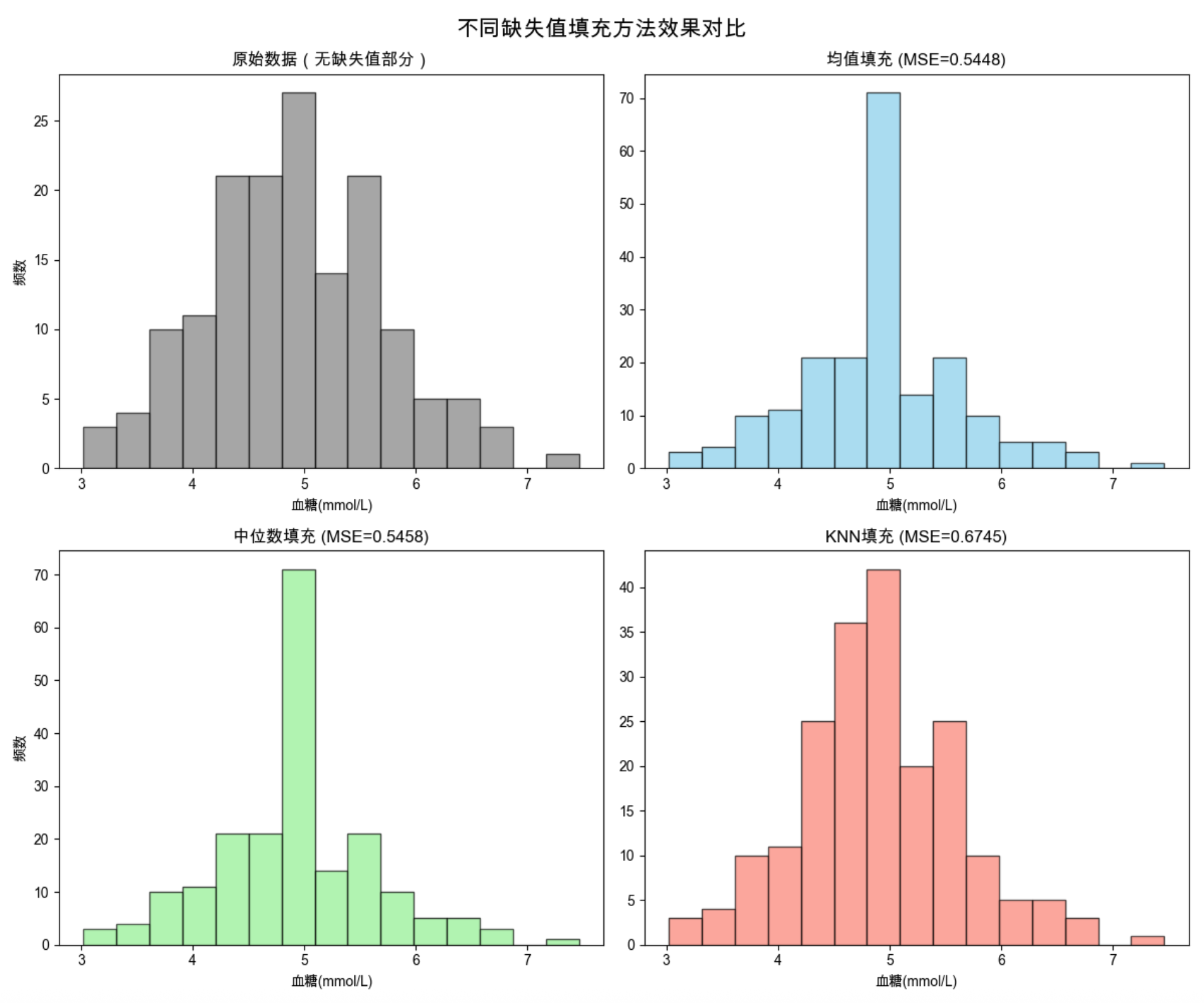
# 4. 可视化：不同填充方法效果对比
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
fig.suptitle('不同缺失值填充方法效果对比', fontsize=16)

# 原始数据（带缺失值）
axes[0,0].hist(data['血糖(mmol/L)'].dropna(), bins=15, color='gray', alpha=0.7, edgecolor='black')
axes[0,0].set_title('原始数据（无缺失值部分）')
axes[0,0].set_xlabel('血糖(mmol/L)')
axes[0,0].set_ylabel('频数')

# 均值填充
axes[0,1].hist(data_mean['血糖(mmol/L)'], bins=15, color='skyblue', alpha=0.7, edgecolor='black')
axes[0,1].set_title(f'均值填充 (MSE={mse_mean:.4f})')
axes[0,1].set_xlabel('血糖(mmol/L)')

# 中位数填充
axes[1,0].hist(data_median['血糖(mmol/L)'], bins=15, color='lightgreen', alpha=0.7, edgecolor='black')
axes[1,0].set_title(f'中位数填充 (MSE={mse_median:.4f})')
axes[1,0].set_xlabel('血糖(mmol/L)')
axes[1,0].set_ylabel('频数')

# KNN填充
axes[1,1].hist(data_knn['血糖(mmol/L)'], bins=15, color='salmon', alpha=0.7, edgecolor='black')
axes[1,1].set_title(f'KNN填充 (MSE={mse_knn:.4f})')
axes[1,1].set_xlabel('血糖(mmol/L)')

plt.tight_layout()
plt.show()

# 5. 填充值与真实值对比散点图
plt.figure(figsize=(10, 6))
plt.scatter(true_values, mean_pred, alpha=0.6, label=f'均值填充 (MSE={mse_mean:.4f})', s=50)
plt.scatter(true_values, median_pred, alpha=0.6, label=f'中位数填充 (MSE={mse_median:.4f})', s=50)
plt.scatter(true_values, knn_pred, alpha=0.6, label=f'KNN填充 (MSE={mse_knn:.4f})', s=50)

# 绘制y=x参考线（完美预测）
plt.plot([true_values.min(), true_values.max()], 
         [true_values.min(), true_values.max()], 
         'r--', linewidth=2, label='完美预测')

plt.xlabel('真实血糖值')
plt.ylabel('填充血糖值')
plt.title('缺失值填充值 vs 真实值', fontsize=14)
plt.legend()
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()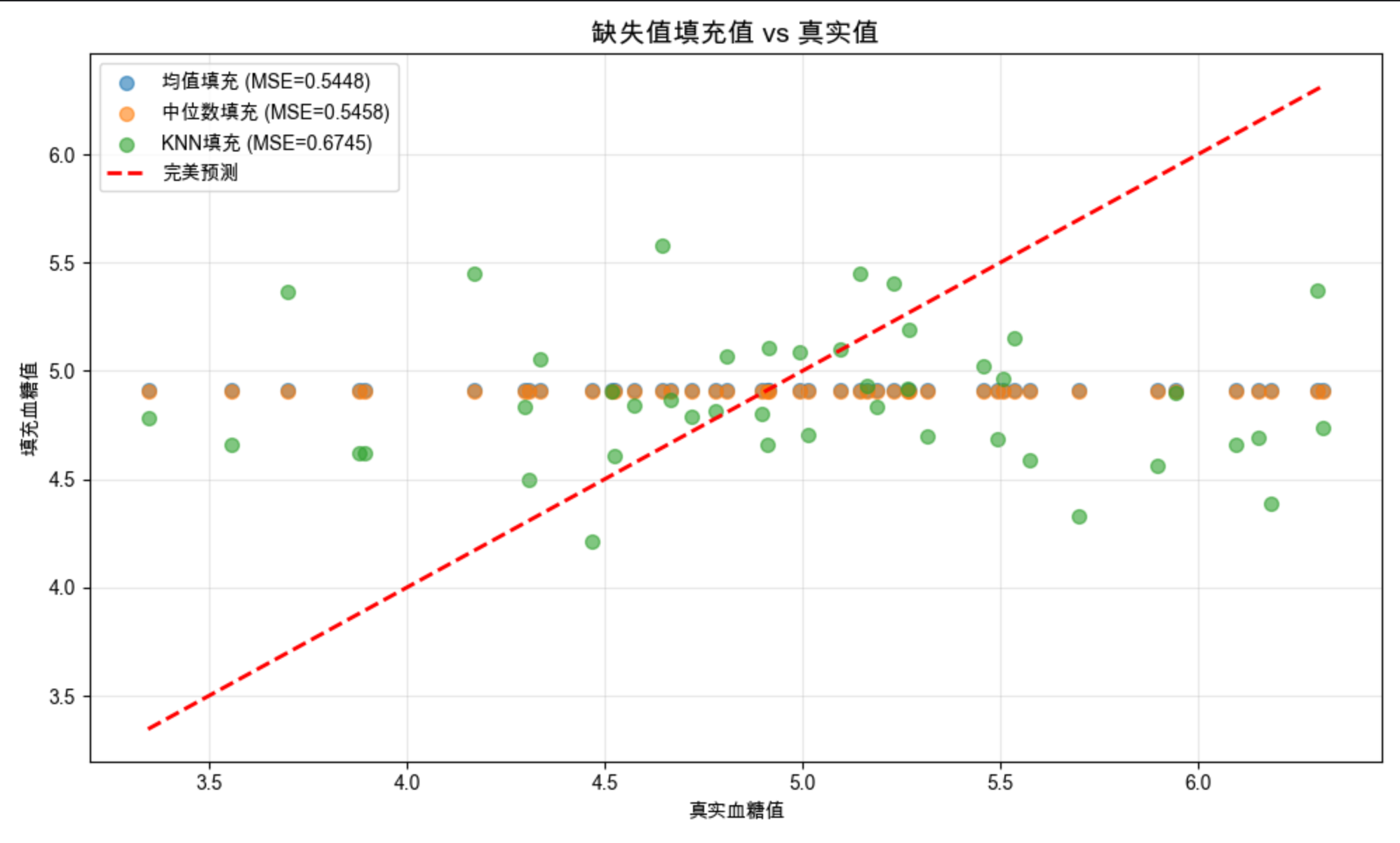

代码运行效果

  1. 输出缺失值数量和比例
  2. 输出不同填充方法的 MSE（KNN 填充通常 MSE 最小）
  3. 显示 4 种数据分布对比图（原始、均值、中位数、KNN）
  4. 显示填充值与真实值的散点对比图（直观看到 KNN 填充更接近真实值）

5.4 多元正态分布

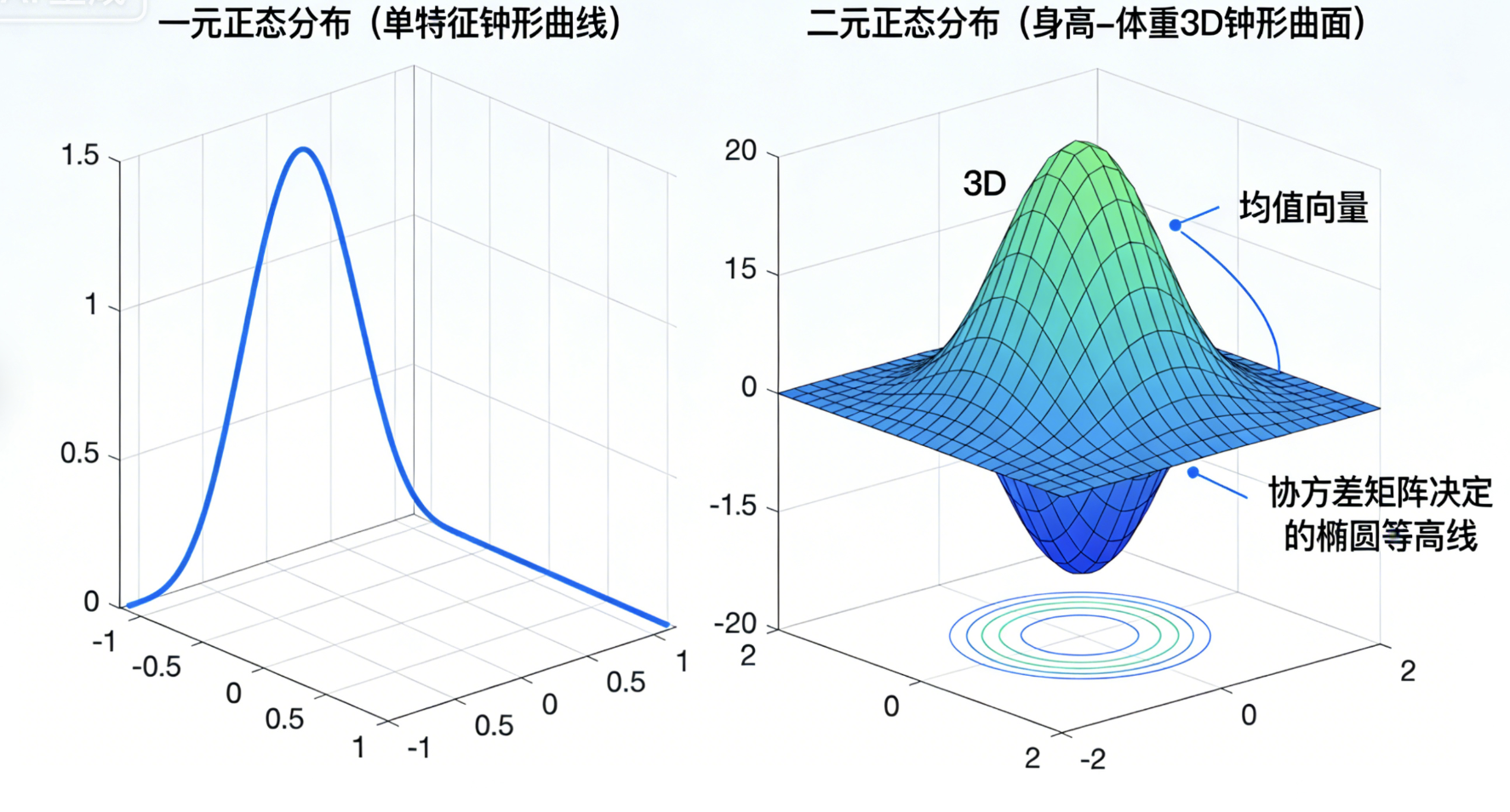
核心概念

一元正态分布（高斯分布）是 "单特征的钟形曲线"，多元正态分布就是 "多个特征的钟形曲面"。比如身高和体重同时服从正态分布，就构成了二元正态分布（3D 钟形曲面）。

核心特点：

  • 由均值向量（每个特征的均值）和协方差矩阵（特征间的相关性）决定
  • 等高线是椭圆（二元）或椭球（高维）
  • 大多数多元数据都近似服从多元正态分布

完整代码（多元正态分布）

python 复制代码 
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
from mpl_toolkits.mplot3d import Axes3D

# === 中文显示配置 ===
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

# 1. 定义多元正态分布参数
np.random.seed(42)

# 二元正态分布（身高、体重）
mean = [170, 70]  # 均值向量
# 协方差矩阵：对角线是方差，非对角线是协方差
cov = [[64, 30],  # 身高方差64，身高-体重协方差30
       [30, 25]]  # 体重方差25，身高-体重协方差30

# 2. 生成多元正态分布数据
n_samples = 1000
data = np.random.multivariate_normal(mean, cov, n_samples)
df = pd.DataFrame(data, columns=['身高(cm)', '体重(kg)'])

print("=== 多元正态分布数据特征 ===")
print(f"均值向量：{df.mean().values.round(2)}")
print(f"协方差矩阵：\n{df.cov().values.round(2)}")

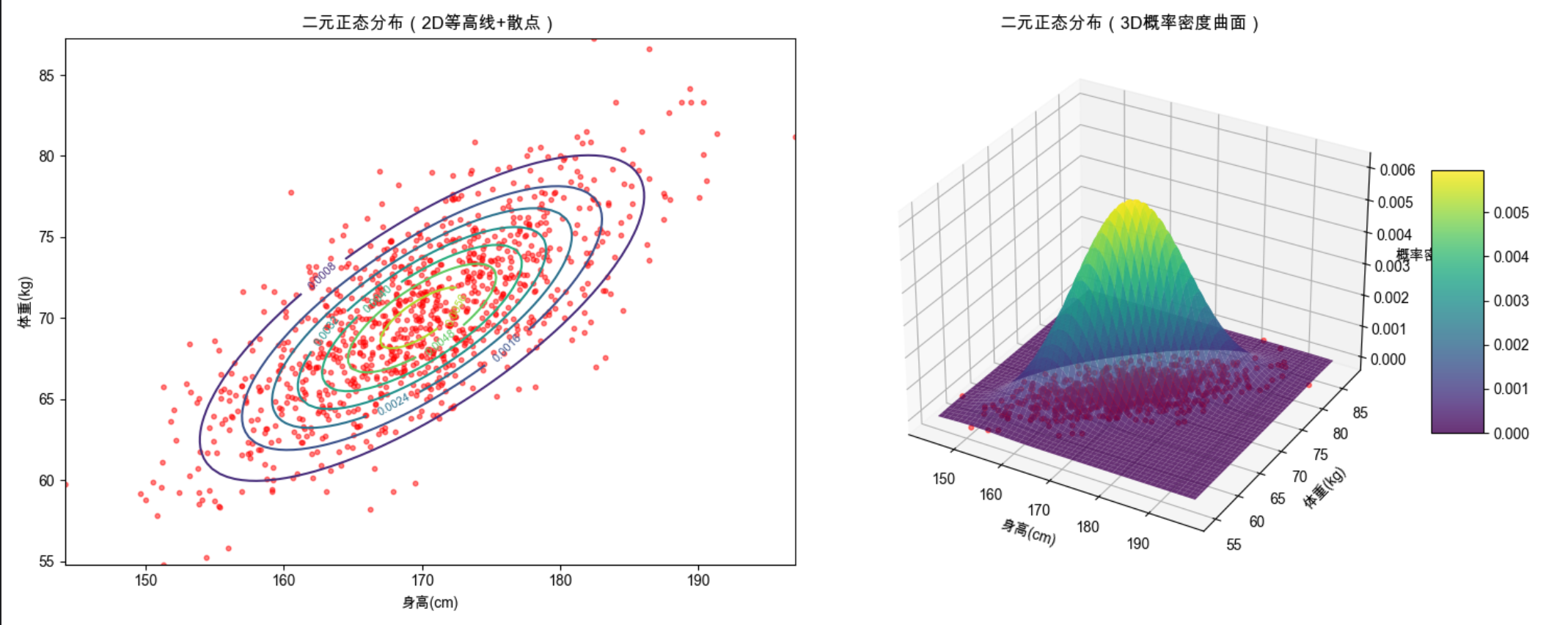
# 3. 可视化：二元正态分布（2D等高线+3D曲面，同一个窗口）
fig = plt.figure(figsize=(15, 6))

# 子图1：2D等高线图
ax1 = fig.add_subplot(121)
# 生成网格数据
x = np.linspace(df['身高(cm)'].min(), df['身高(cm)'].max(), 100)
y = np.linspace(df['体重(kg)'].min(), df['体重(kg)'].max(), 100)
X, Y = np.meshgrid(x, y)
pos = np.dstack((X, Y))

# 计算多元正态分布概率密度
rv = multivariate_normal(mean, cov)
Z = rv.pdf(pos)

# 绘制等高线
contour = ax1.contour(X, Y, Z, cmap='viridis')
ax1.clabel(contour, inline=True, fontsize=8)
# 叠加散点
ax1.scatter(df['身高(cm)'], df['体重(kg)'], alpha=0.5, s=10, color='red')
ax1.set_title('二元正态分布（2D等高线+散点）')
ax1.set_xlabel('身高(cm)')
ax1.set_ylabel('体重(kg)')

# 子图2：3D曲面图
ax2 = fig.add_subplot(122, projection='3d')
surf = ax2.plot_surface(X, Y, Z, cmap='viridis', alpha=0.8)
# 叠加散点
ax2.scatter(df['身高(cm)'], df['体重(kg)'],
            np.zeros_like(df['身高(cm)']), alpha=0.5, s=10, color='red')
fig.colorbar(surf, ax=ax2, shrink=0.5, aspect=5)
ax2.set_title('二元正态分布（3D概率密度曲面）')
ax2.set_xlabel('身高(cm)')
ax2.set_ylabel('体重(kg)')
ax2.set_zlabel('概率密度')

plt.tight_layout()
plt.show()

# 4. 不同协方差矩阵的多元正态分布对比
fig, axes = plt.subplots(1, 3, figsize=(18, 5))
fig.suptitle('不同协方差矩阵的多元正态分布对比', fontsize=16)

# 场景1：无相关性（协方差=0）
cov1 = [[64, 0], [0, 25]]
data1 = np.random.multivariate_normal(mean, cov1, 500)
axes[0].scatter(data1[:,0], data1[:,1], alpha=0.6, s=20)
axes[0].set_title('无相关性（协方差=0）')
axes[0].set_xlabel('身高(cm)')
axes[0].set_ylabel('体重(kg)')
axes[0].set_xlim(140, 200)
axes[0].set_ylim(40, 100)

# 场景2：正相关性（协方差=30）
cov2 = [[64, 30], [30, 25]]
data2 = np.random.multivariate_normal(mean, cov2, 500)
axes[1].scatter(data2[:,0], data2[:,1], alpha=0.6, s=20, color='green')
axes[1].set_title('正相关性（协方差=30）')
axes[1].set_xlabel('身高(cm)')
axes[1].set_ylim(40, 100)

# 场景3：负相关性（协方差=-30）
cov3 = [[64, -30], [-30, 25]]
data3 = np.random.multivariate_normal(mean, cov3, 500)
axes[2].scatter(data3[:,0], data3[:,1], alpha=0.6, s=20, color='red')
axes[2].set_title('负相关性（协方差=-30）')
axes[2].set_xlabel('身高(cm)')
axes[2].set_ylim(40, 100)

plt.tight_layout()
plt.show()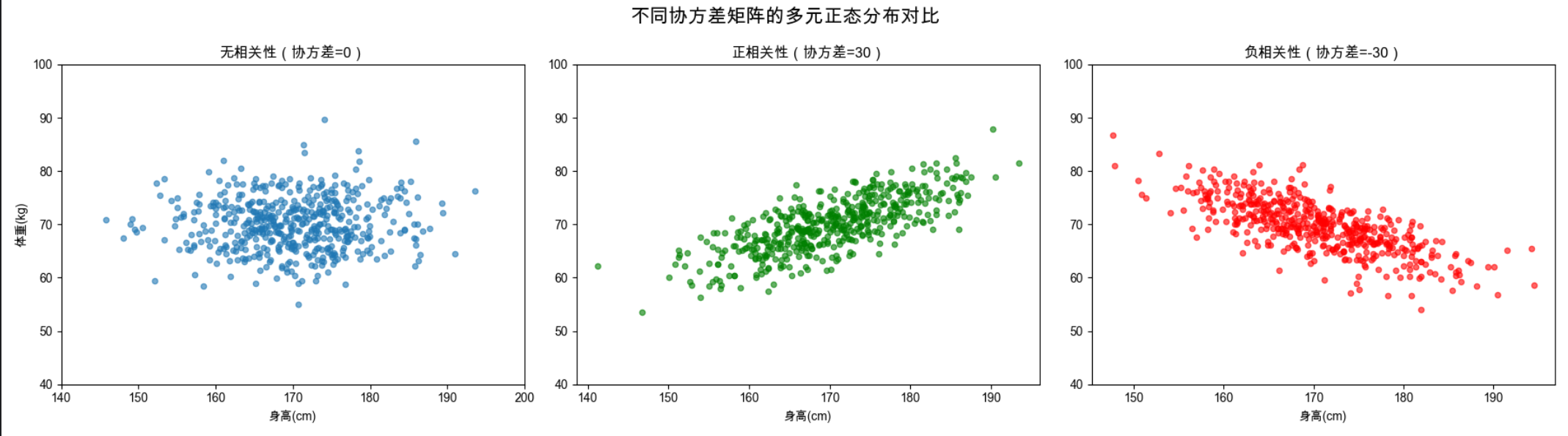

代码运行效果

  1. 输出多元正态分布的均值向量和协方差矩阵
  2. 显示 2D 等高线 + 3D 曲面的组合图（直观理解二元正态分布）
  3. 显示不同协方差矩阵的分布对比（无相关、正相关、负相关）

5.5 多元分类

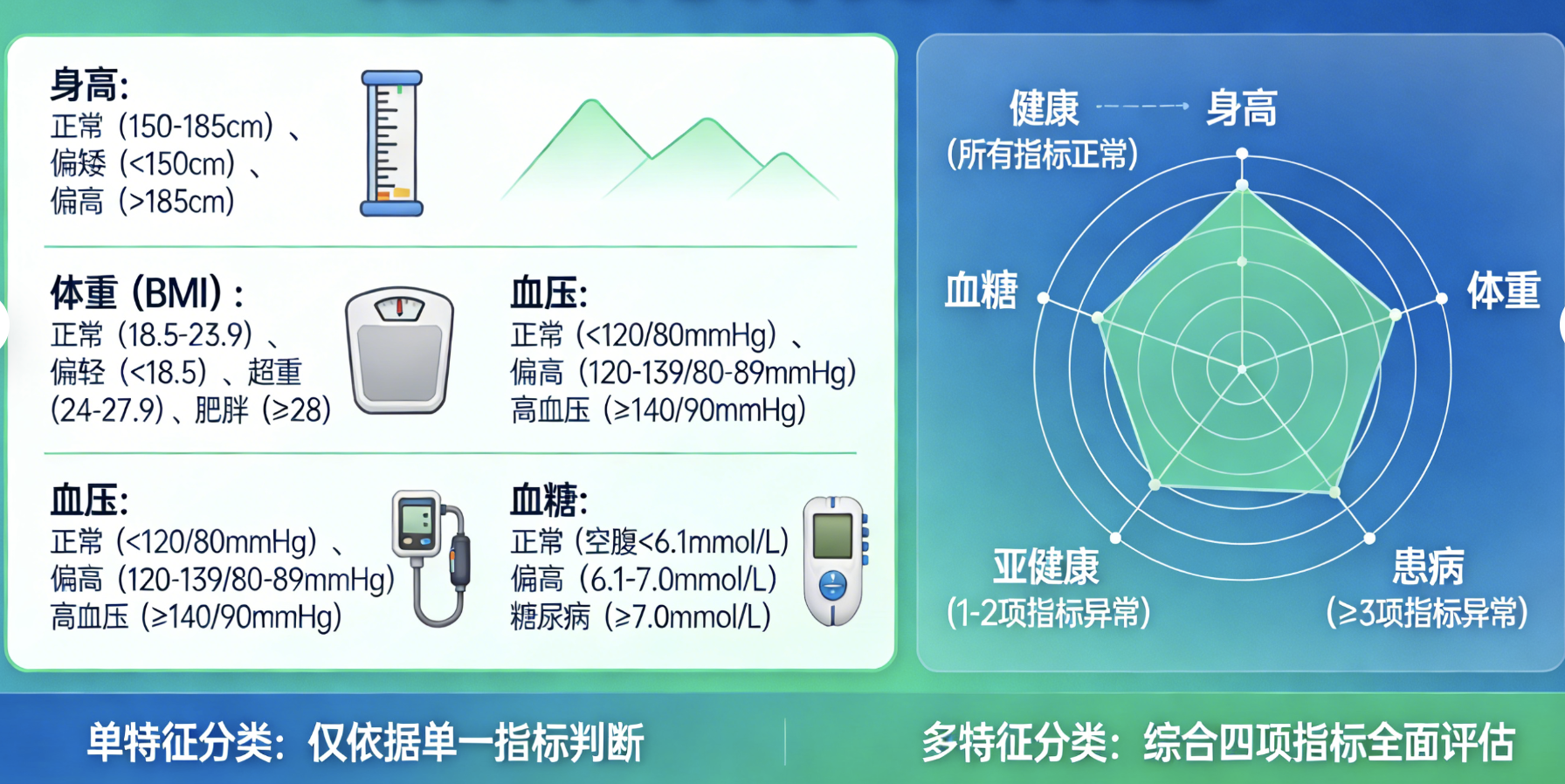
核心概念

多元分类就像 "根据多项指标给事物贴标签"：比如根据身高、体重、血压、血糖等指标，判断一个人是否健康（健康 / 亚健康 / 患病）。

核心方法：

  • 逻辑回归（多元版）：处理多分类问题
  • 核心对比：单特征分类 vs 多特征分类（多元分类效果更好）

完整代码（多元分类）

复制代码 
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix
import seaborn as sns

# === 中文显示配置 ===
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

# 1. 生成多元分类数据集
# 生成3分类问题，4个特征，有2个冗余特征（模拟真实多元数据）
X, y = make_classification(
    n_samples=1000,  # 样本数
    n_features=4,    # 特征数（多元）
    n_informative=2, # 有效特征数
    n_redundant=2,   # 冗余特征数
    n_classes=3,     # 类别数
    n_clusters_per_class=1,
    random_state=42
)

# 特征命名：特征1、特征2、特征3、特征4
feature_names = [f'特征{i+1}' for i in range(4)]
df = pd.DataFrame(X, columns=feature_names)
df['类别'] = y

print("=== 多元分类数据集信息 ===")
print(f"数据集形状：{df.shape}")
print(f"类别分布：\n{df['类别'].value_counts()}")

# 2. 数据拆分
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42, stratify=y
)

# 3. 对比实验：单特征分类 vs 多元特征分类
# 实验1：只用第一个特征分类
model_single = LogisticRegression(multi_class='ovr', random_state=42)
model_single.fit(X_train[:, 0].reshape(-1, 1), y_train)
y_pred_single = model_single.predict(X_test[:, 0].reshape(-1, 1))
acc_single = accuracy_score(y_test, y_pred_single)

# 实验2：用所有4个特征（多元）分类
model_multi = LogisticRegression(multi_class='ovr', random_state=42)
model_multi.fit(X_train, y_train)
y_pred_multi = model_multi.predict(X_test)
acc_multi = accuracy_score(y_test, y_pred_multi)

print("\n=== 分类准确率对比 ===")
print(f"单特征分类准确率：{acc_single:.4f}")
print(f"多元特征分类准确率：{acc_multi:.4f}")

# 4. 多元分类结果评估
print("\n=== 多元分类详细报告 ===")
print(classification_report(y_test, y_pred_multi))

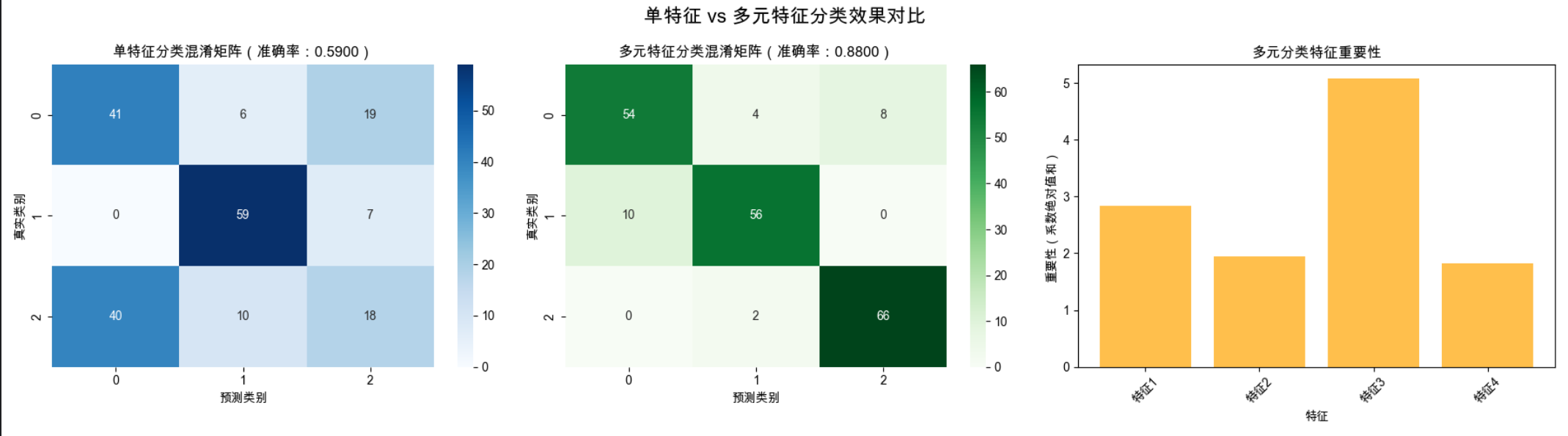
# 5. 可视化对比
fig, axes = plt.subplots(1, 3, figsize=(18, 5))
fig.suptitle('单特征 vs 多元特征分类效果对比', fontsize=16)

# 子图1：单特征分类混淆矩阵
cm_single = confusion_matrix(y_test, y_pred_single)
sns.heatmap(cm_single, annot=True, fmt='d', cmap='Blues', ax=axes[0])
axes[0].set_title(f'单特征分类混淆矩阵（准确率：{acc_single:.4f}）')
axes[0].set_xlabel('预测类别')
axes[0].set_ylabel('真实类别')

# 子图2：多元特征分类混淆矩阵
cm_multi = confusion_matrix(y_test, y_pred_multi)
sns.heatmap(cm_multi, annot=True, fmt='d', cmap='Greens', ax=axes[1])
axes[1].set_title(f'多元特征分类混淆矩阵（准确率：{acc_multi:.4f}）')
axes[1].set_xlabel('预测类别')
axes[1].set_ylabel('真实类别')

# 子图3：特征重要性（多元模型）
feature_importance = np.abs(model_multi.coef_).sum(axis=0)  # 多分类特征重要性
axes[2].bar(feature_names, feature_importance, color='orange', alpha=0.7)
axes[2].set_title('多元分类特征重要性')
axes[2].set_xlabel('特征')
axes[2].set_ylabel('重要性（系数绝对值和）')
axes[2].tick_params(axis='x', rotation=45)

plt.tight_layout()
plt.show()

# 6. 2D可视化分类边界（取前两个有效特征）
plt.figure(figsize=(10, 8))
# 生成网格
h = 0.02
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))

# 预测网格点类别
Z = model_multi.predict(np.c_[xx.ravel(), yy.ravel(), np.zeros_like(xx.ravel()), np.zeros_like(xx.ravel())])
Z = Z.reshape(xx.shape)

# 绘制决策边界
plt.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.Spectral)
# 绘制样本点
scatter = plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', cmap=plt.cm.Spectral, s=50)
plt.legend(*scatter.legend_elements(), title="类别")
plt.title('多元分类决策边界（前两个特征）', fontsize=14)
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()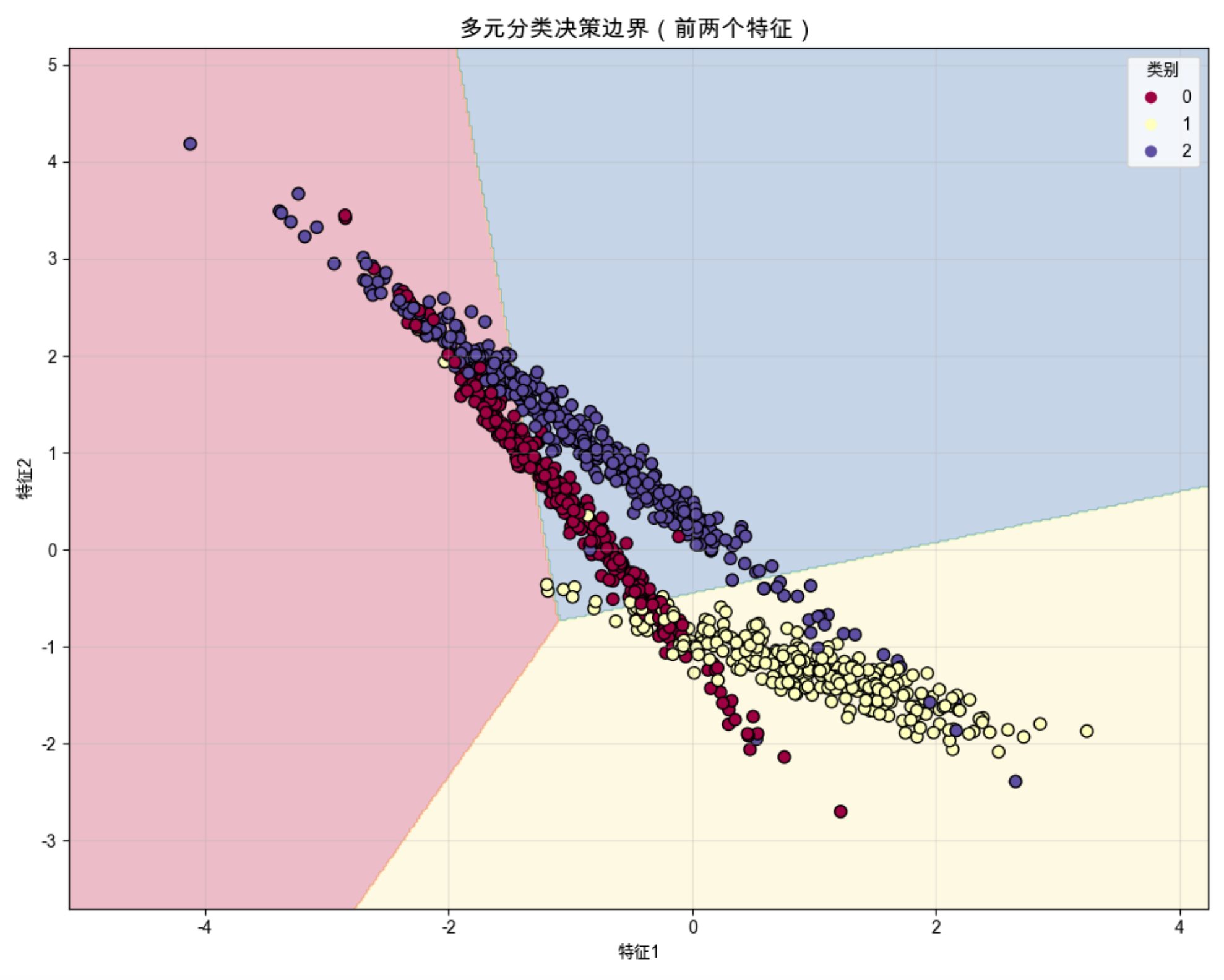

代码运行效果

  1. 输出单特征和多元特征的分类准确率（多元分类准确率更高）
  2. 显示两个混淆矩阵对比图（直观看到多元分类错误更少）
  3. 显示特征重要性柱状图
  4. 显示多元分类的决策边界图

5.6 调整复杂度

核心概念

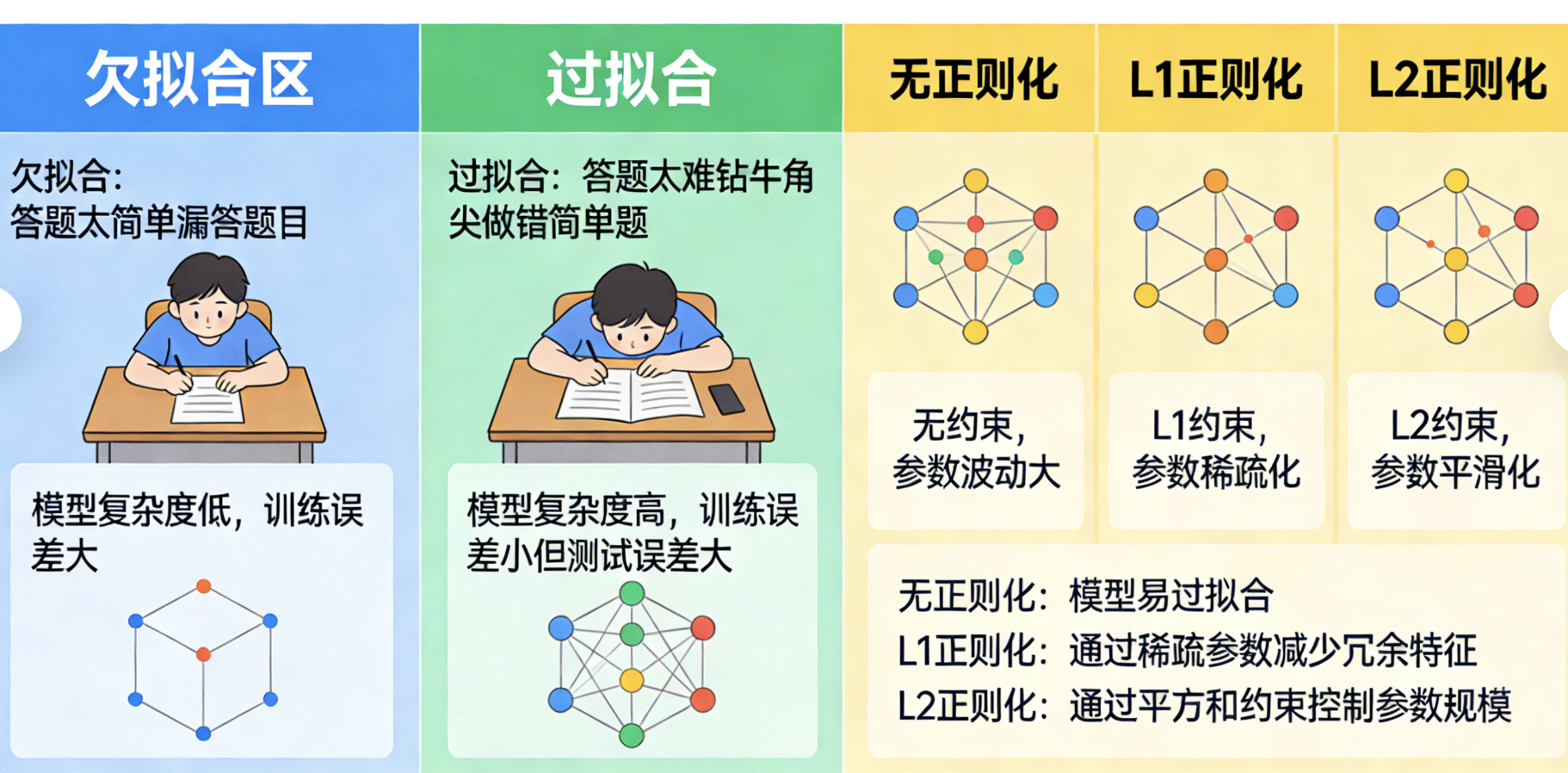
模型复杂度就像 "考试时的答题策略"：太简单（欠拟合）会漏答很多题，太难（过拟合）会钻牛角尖做错简单题，调整复杂度就是找到 "刚刚好" 的策略。

核心方法：

  • 正则化（L1/L2）：给模型 "加约束"，防止过拟合
  • 复杂度对比：无正则化 vs L1 正则化 vs L2 正则化

完整代码（调整复杂度）

复制代码 
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split, learning_curve
from sklearn.linear_model import Ridge, Lasso, LinearRegression
from sklearn.metrics import mean_squared_error

# === 中文显示配置 ===
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

# 1. 生成高维数据（容易过拟合）
np.random.seed(42)
X, y = make_regression(
    n_samples=200,    # 少量样本
    n_features=50,    # 大量特征（高维）
    n_informative=5,  # 只有5个有效特征
    noise=10,         # 加噪声
    random_state=42
)

# 数据拆分
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42
)

# 2. 不同复杂度模型对比
# 模型1：无正则化（高复杂度，易过拟合）
model_simple = LinearRegression()
model_simple.fit(X_train, y_train)
y_pred_train_simple = model_simple.predict(X_train)
y_pred_test_simple = model_simple.predict(X_test)
mse_train_simple = mean_squared_error(y_train, y_pred_train_simple)
mse_test_simple = mean_squared_error(y_test, y_pred_test_simple)

# 模型2：L2正则化（Ridge，中等复杂度）
model_ridge = Ridge(alpha=10.0)  # alpha越大，正则化越强，模型越简单
model_ridge.fit(X_train, y_train)
y_pred_train_ridge = model_ridge.predict(X_train)
y_pred_test_ridge = model_ridge.predict(X_test)
mse_train_ridge = mean_squared_error(y_train, y_pred_train_ridge)
mse_test_ridge = mean_squared_error(y_test, y_pred_test_ridge)

# 模型3：L1正则化（Lasso，低复杂度，特征选择）
model_lasso = Lasso(alpha=1.0)
model_lasso.fit(X_train, y_train)
y_pred_train_lasso = model_lasso.predict(X_train)
y_pred_test_lasso = model_lasso.predict(X_test)
mse_train_lasso = mean_squared_error(y_train, y_pred_train_lasso)
mse_test_lasso = mean_squared_error(y_test, y_pred_test_lasso)

print("=== 不同复杂度模型MSE对比 ===")
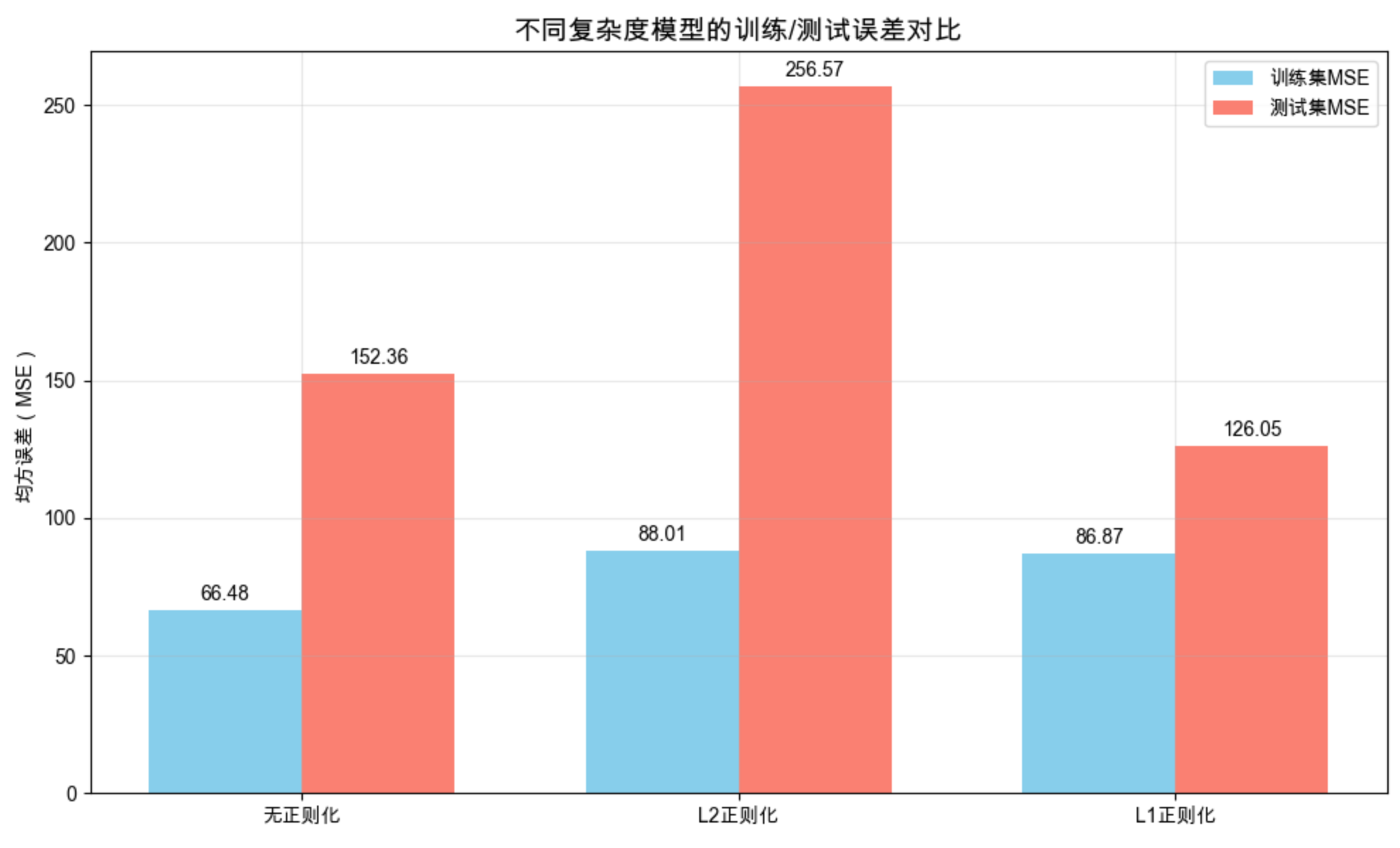
print(f"无正则化（高复杂度）：训练MSE={mse_train_simple:.2f}，测试MSE={mse_test_simple:.2f}")
print(f"L2正则化（中等复杂度）：训练MSE={mse_train_ridge:.2f}，测试MSE={mse_test_ridge:.2f}")
print(f"L1正则化（低复杂度）：训练MSE={mse_train_lasso:.2f}，测试MSE={mse_test_lasso:.2f}")

# 3. 可视化：训练/测试误差对比
models = ['无正则化', 'L2正则化', 'L1正则化']
train_mses = [mse_train_simple, mse_train_ridge, mse_train_lasso]
test_mses = [mse_test_simple, mse_test_ridge, mse_test_lasso]

x = np.arange(len(models))
width = 0.35

fig, ax = plt.subplots(figsize=(10, 6))
rects1 = ax.bar(x - width/2, train_mses, width, label='训练集MSE', color='skyblue')
rects2 = ax.bar(x + width/2, test_mses, width, label='测试集MSE', color='salmon')

ax.set_title('不同复杂度模型的训练/测试误差对比', fontsize=14)
ax.set_ylabel('均方误差（MSE）')
ax.set_xticks(x)
ax.set_xticklabels(models)
ax.legend()

# 添加数值标注
def autolabel(rects):
    for rect in rects:
        height = rect.get_height()
        ax.annotate(f'{height:.2f}',
                    xy=(rect.get_x() + rect.get_width() / 2, height),
                    xytext=(0, 3),
                    textcoords="offset points",
                    ha='center', va='bottom')

autolabel(rects1)
autolabel(rects2)
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()

# 4. 可视化：学习曲线（复杂度与数据量的关系）
def plot_learning_curve(estimator, title, X, y, ax):
    train_sizes, train_scores, test_scores = learning_curve(
        estimator, X, y, train_sizes=np.linspace(0.1, 1.0, 10),
        cv=5, scoring='neg_mean_squared_error', random_state=42
    )
    train_scores_mean = -np.mean(train_scores, axis=1)
    test_scores_mean = -np.mean(test_scores, axis=1)

    ax.plot(train_sizes, train_scores_mean, 'o-', color='blue', label='训练集')
    ax.plot(train_sizes, test_scores_mean, 'o-', color='red', label='测试集')
    ax.set_title(title)
    ax.set_xlabel('训练样本数')
    ax.set_ylabel('MSE')
    ax.legend()
    ax.grid(alpha=0.3)

# 绘制3个模型的学习曲线
fig, axes = plt.subplots(1, 3, figsize=(18, 5))
fig.suptitle('不同复杂度模型的学习曲线', fontsize=16)

plot_learning_curve(LinearRegression(), '无正则化（过拟合）', X, y, axes[0])
plot_learning_curve(Ridge(alpha=10.0), 'L2正则化（适中）', X, y, axes[1])
plot_learning_curve(Lasso(alpha=1.0), 'L1正则化（欠拟合）', X, y, axes[2])

plt.tight_layout()
plt.show()

# 5. 正则化强度对模型的影响
alphas = np.logspace(-2, 2, 20)  # 0.01到100的对数间距
ridge_mses = []
lasso_mses = []

for alpha in alphas:
    ridge = Ridge(alpha=alpha)
    ridge.fit(X_train, y_train)
    ridge_mses.append(mean_squared_error(y_test, ridge.predict(X_test)))
    
    lasso = Lasso(alpha=alpha)
    lasso.fit(X_train, y_train)
    lasso_mses.append(mean_squared_error(y_test, lasso.predict(X_test)))

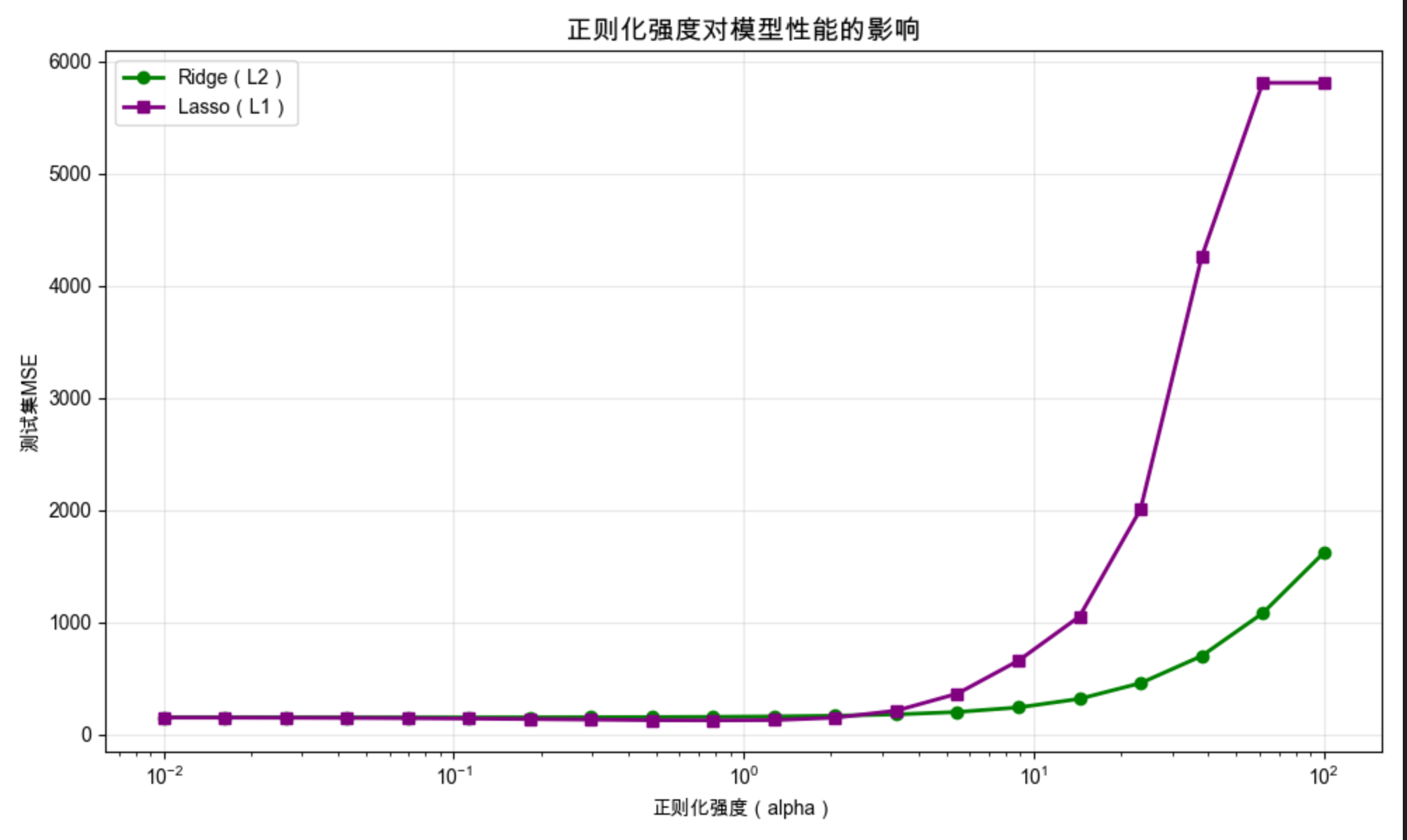
# 可视化正则化强度影响
plt.figure(figsize=(10, 6))
plt.plot(alphas, ridge_mses, 'o-', label='Ridge（L2）', color='green', linewidth=2)
plt.plot(alphas, lasso_mses, 's-', label='Lasso（L1）', color='purple', linewidth=2)
plt.xscale('log')  # 对数刻度
plt.xlabel('正则化强度（alpha）')
plt.ylabel('测试集MSE')
plt.title('正则化强度对模型性能的影响', fontsize=14)
plt.legend()
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()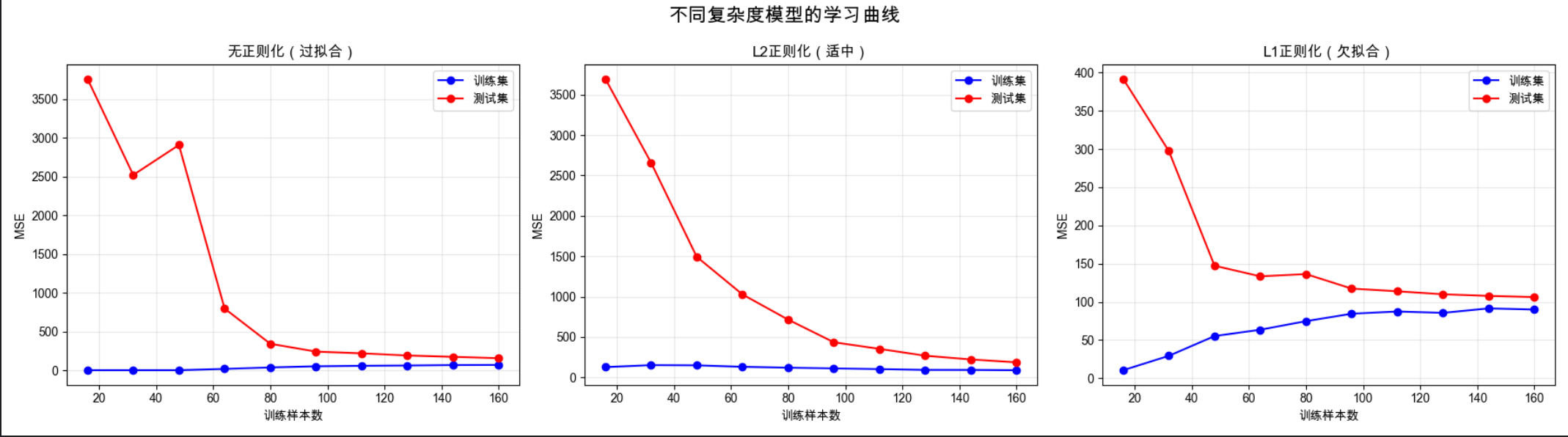

代码运行效果

  1. 输出不同复杂度模型的训练 / 测试 MSE（无正则化测试 MSE 最高，过拟合）
  2. 显示训练 / 测试误差对比柱状图
  3. 显示 3 个模型的学习曲线（直观看到过拟合 / 欠拟合）
  4. 显示正则化强度对模型性能的影响曲线

5.7 离散特征

核心概念

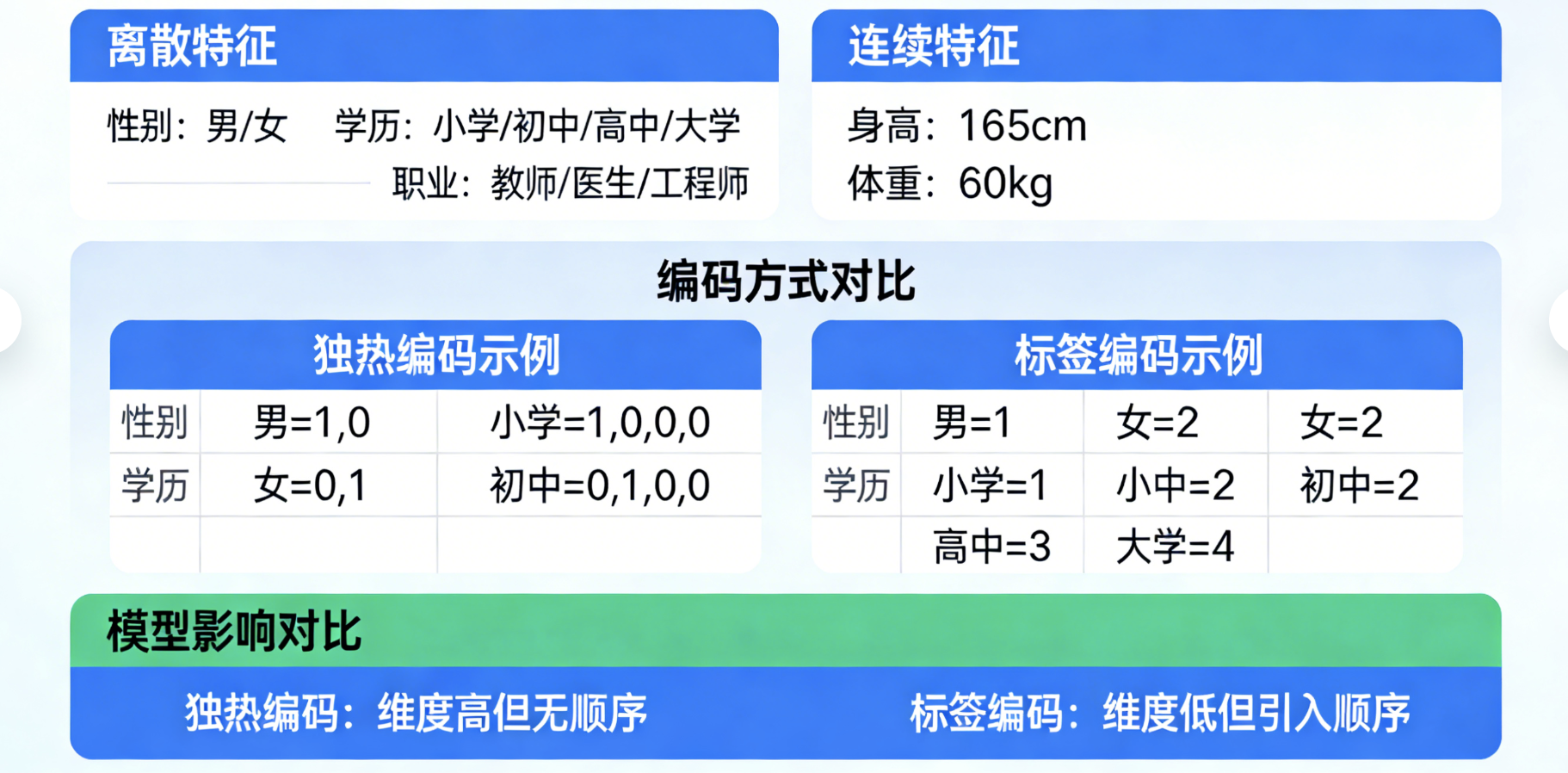
离散特征就像 "分类标签"：比如性别（男 / 女）、学历（小学 / 中学 / 大学）、职业（教师 / 医生 / 工程师），和连续特征（身高、体重）不同，离散特征是 "非数值" 或 "有限取值" 的。

核心处理方法：

  • 独热编码：把 "性别" 拆成 "是否男" 和 "是否女" 两个特征
  • 标签编码：把 "学历" 按顺序编码为 0、1、2
  • 对比：不同编码方式对模型的影响

完整代码（离散特征处理）

复制代码 
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import OneHotEncoder, LabelEncoder
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split

# === 中文显示配置 ===
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

# 1. 生成含离散特征的多元数据集
np.random.seed(42)
n_samples = 500

# 连续特征：年龄、收入
age = np.random.randint(18, 60, n_samples)
income = np.random.normal(5000, 1000, n_samples).round(2)

# 离散特征1：性别（二分类）
gender = np.random.choice(['男', '女'], size=n_samples, p=[0.5, 0.5])

# 离散特征2：学历（多分类）
education = np.random.choice(['小学', '中学', '大学', '研究生'], 
                            size=n_samples, 
                            p=[0.1, 0.3, 0.4, 0.2])

# 离散特征3：职业（多分类）
occupation = np.random.choice(['教师', '医生', '工程师', '销售员', '其他'], 
                             size=n_samples, 
                             p=[0.2, 0.15, 0.25, 0.2, 0.2])

# 目标变量：是否购买（0/1）
# 构造购买概率与特征的关系
purchase_prob = (age/100) + (income/10000) + (gender=='女')*0.1 + (education=='研究生')*0.2
purchase_prob = np.clip(purchase_prob, 0, 1)
purchase = np.random.binomial(1, purchase_prob)

# 构造DataFrame
data = pd.DataFrame({
    '年龄': age,
    '收入': income,
    '性别': gender,
    '学历': education,
    '职业': occupation,
    '是否购买': purchase
})

print("=== 含离散特征的数据集 ===")
print(data.head())
print(f"\n离散特征取值：")
print(f"性别：{data['性别'].unique()}")
print(f"学历：{data['学历'].unique()}")
print(f"职业：{data['职业'].unique()}")

# 2. 离散特征处理
# 方法1：标签编码（适合有序离散特征）
label_encoder = LabelEncoder()
data_label = data.copy()
data_label['性别'] = label_encoder.fit_transform(data_label['性别'])
data_label['学历'] = label_encoder.fit_transform(data_label['学历'])
data_label['职业'] = label_encoder.fit_transform(data_label['职业'])

# 方法2：独热编码（适合无序离散特征）
data_onehot = data.copy()
# 对性别、学历、职业进行独热编码
data_onehot = pd.get_dummies(data_onehot, columns=['性别', '学历', '职业'], drop_first=True)

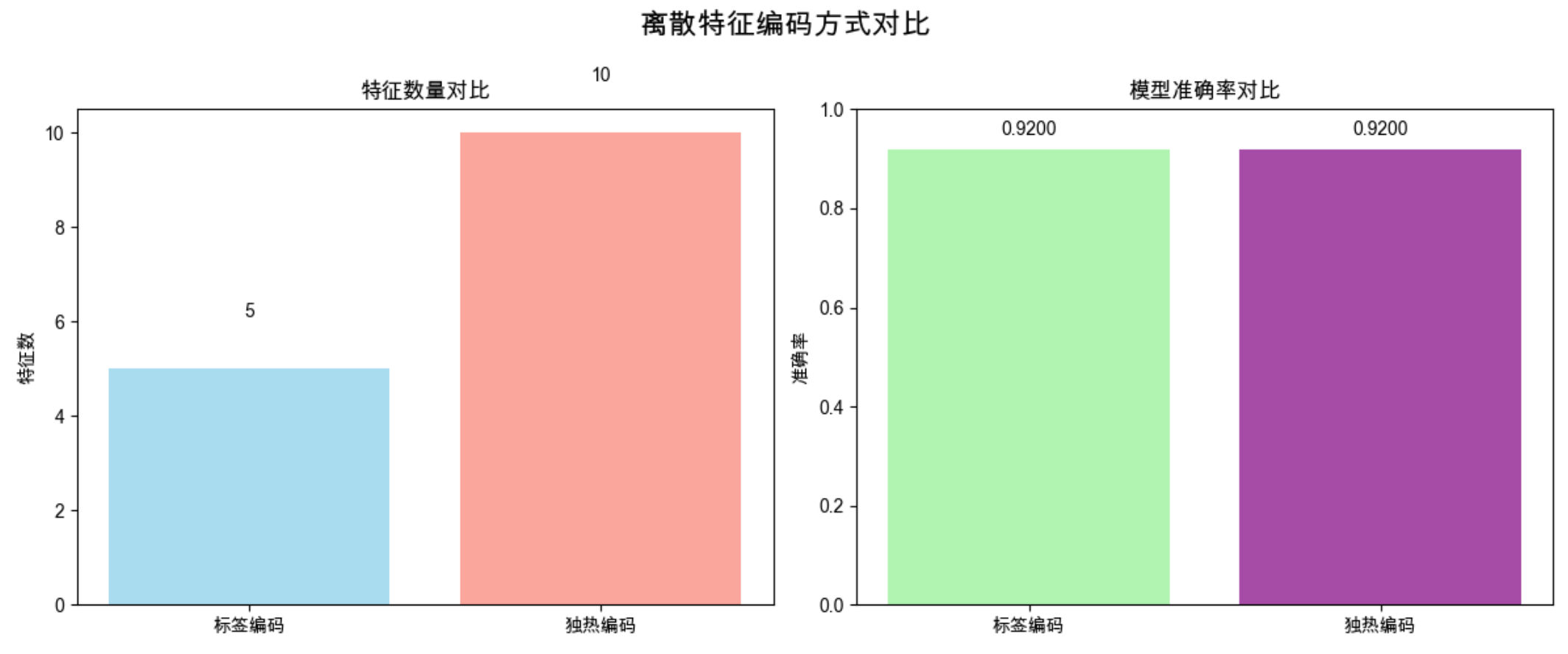
print(f"\n标签编码后特征数：{data_label.shape[1]-1}")  # 减1是去掉目标变量
print(f"独热编码后特征数：{data_onehot.shape[1]-1}")

# 3. 模型训练与对比
# 拆分数据
X_label = data_label.drop('是否购买', axis=1)
X_onehot = data_onehot.drop('是否购买', axis=1)
y = data['是否购买']

X_train_label, X_test_label, y_train, y_test = train_test_split(X_label, y, test_size=0.2, random_state=42)
X_train_onehot, X_test_onehot, _, _ = train_test_split(X_onehot, y, test_size=0.2, random_state=42)

# 训练模型
model_label = LogisticRegression(random_state=42, max_iter=200)
model_label.fit(X_train_label, y_train)
acc_label = accuracy_score(y_test, model_label.predict(X_test_label))

model_onehot = LogisticRegression(random_state=42, max_iter=200)
model_onehot.fit(X_train_onehot, y_train)
acc_onehot = accuracy_score(y_test, model_onehot.predict(X_test_onehot))

print(f"\n=== 编码方式效果对比 ===")
print(f"标签编码模型准确率：{acc_label:.4f}")
print(f"独热编码模型准确率：{acc_onehot:.4f}")

# 4. 可视化对比
# 特征数对比
encoding_types = ['标签编码', '独热编码']
feature_counts = [X_label.shape[1], X_onehot.shape[1]]
accuracies = [acc_label, acc_onehot]

fig, axes = plt.subplots(1, 2, figsize=(12, 5))
fig.suptitle('离散特征编码方式对比', fontsize=16)

# 特征数对比
axes[0].bar(encoding_types, feature_counts, color=['skyblue', 'salmon'], alpha=0.7)
axes[0].set_title('特征数量对比')
axes[0].set_ylabel('特征数')
for i, v in enumerate(feature_counts):
    axes[0].text(i, v+1, str(v), ha='center', va='bottom')

# 准确率对比
axes[1].bar(encoding_types, accuracies, color=['lightgreen', 'purple'], alpha=0.7)
axes[1].set_title('模型准确率对比')
axes[1].set_ylabel('准确率')
axes[1].set_ylim(0, 1)
for i, v in enumerate(accuracies):
    axes[1].text(i, v+0.02, f'{v:.4f}', ha='center', va='bottom')

plt.tight_layout()
plt.show()

# 5. 离散特征分布可视化
fig, axes = plt.subplots(1, 3, figsize=(18, 5))
fig.suptitle('离散特征分布', fontsize=16)

# 性别分布
gender_counts = data['性别'].value_counts()
axes[0].pie(gender_counts.values, labels=gender_counts.index, autopct='%1.1f%%', startangle=90)
axes[0].set_title('性别分布')

# 学历分布
edu_counts = data['学历'].value_counts()
axes[1].bar(edu_counts.index, edu_counts.values, color='lightblue', alpha=0.7)
axes[1].set_title('学历分布')
axes[1].set_ylabel('人数')
axes[1].tick_params(axis='x', rotation=45)

# 职业分布
occ_counts = data['职业'].value_counts()
axes[2].bar(occ_counts.index, occ_counts.values, color='lightgreen', alpha=0.7)
axes[2].set_title('职业分布')
axes[2].set_ylabel('人数')
axes[2].tick_params(axis='x', rotation=45)

plt.tight_layout()
plt.show()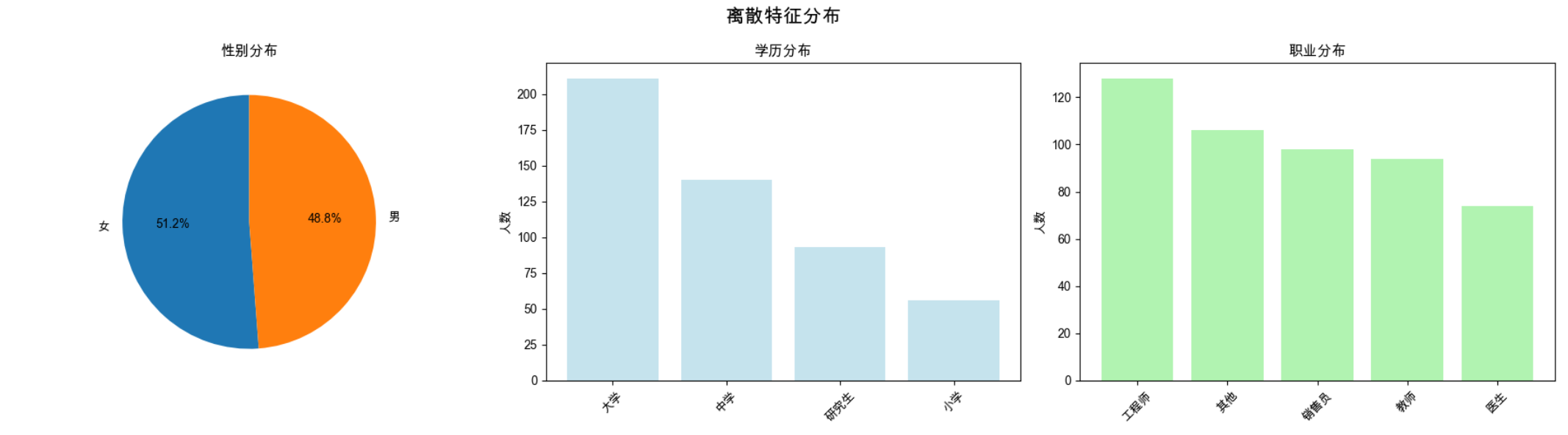

代码运行效果

  1. 输出含离散特征的数据集信息
  2. 显示标签编码和独热编码的特征数、准确率对比
  3. 显示离散特征的分布可视化（饼图、柱状图）

5.8 多元回归

核心概念

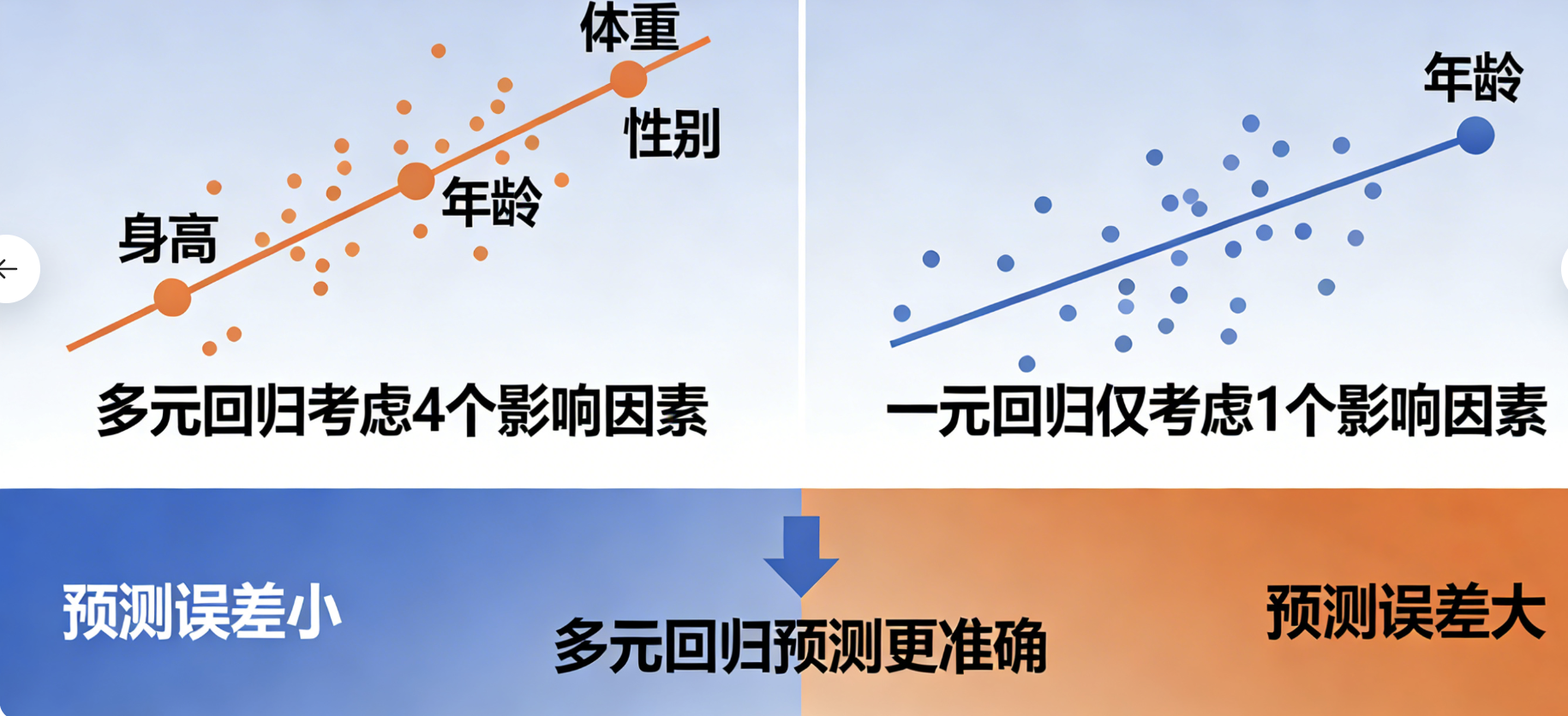
多元回归就像 "用多个因素预测一个结果"：比如用身高、体重、年龄、性别等多个特征，预测一个人的血压值。

核心对比：

  • 一元回归：只用一个特征预测（比如只用年龄预测血压）
  • 多元回归：用多个特征预测（年龄 + 体重 + 性别 +...）
  • 核心优势：多元回归能捕捉更多因素的影响，预测更准确

完整代码（多元回归）

复制代码 
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
import seaborn as sns

# === 中文显示配置 ===
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

# 1. 生成多元回归数据集
np.random.seed(42)
# 生成回归数据：1000样本，5个特征（3个有效特征），1个目标变量
X, y = make_regression(
    n_samples=1000,
    n_features=5,
    n_informative=3,
    noise=15,
    random_state=42
)

# 特征命名：年龄、体重、心率、血糖、胆固醇
feature_names = ['年龄', '体重(kg)', '心率', '血糖(mmol/L)', '胆固醇(mg/dL)']
df = pd.DataFrame(X, columns=feature_names)
df['血压(mmHg)'] = y  # 目标变量：血压

# 标准化特征（方便系数解释）
df[feature_names] = (df[feature_names] - df[feature_names].mean()) / df[feature_names].std()

print("=== 多元回归数据集 ===")
print(df.head())
print(f"\n特征相关性：")
print(df.corr()['血压(mmHg)'].sort_values(ascending=False))

# 2. 数据拆分
X_train, X_test, y_train, y_test = train_test_split(
    df[feature_names], df['血压(mmHg)'], test_size=0.2, random_state=42
)

# 3. 对比实验：一元回归 vs 多元回归
# 实验1：一元回归（只用年龄预测血压）
model_univariate = LinearRegression()
model_univariate.fit(X_train[['年龄']], y_train)
y_pred_uni = model_univariate.predict(X_test[['年龄']])
mse_uni = mean_squared_error(y_test, y_pred_uni)
r2_uni = r2_score(y_test, y_pred_uni)

# 实验2：多元回归（用所有5个特征）
model_multivariate = LinearRegression()
model_multivariate.fit(X_train, y_train)
y_pred_multi = model_multivariate.predict(X_test)
mse_multi = mean_squared_error(y_test, y_pred_multi)
r2_multi = r2_score(y_test, y_pred_multi)

print("\n=== 回归效果对比 ===")
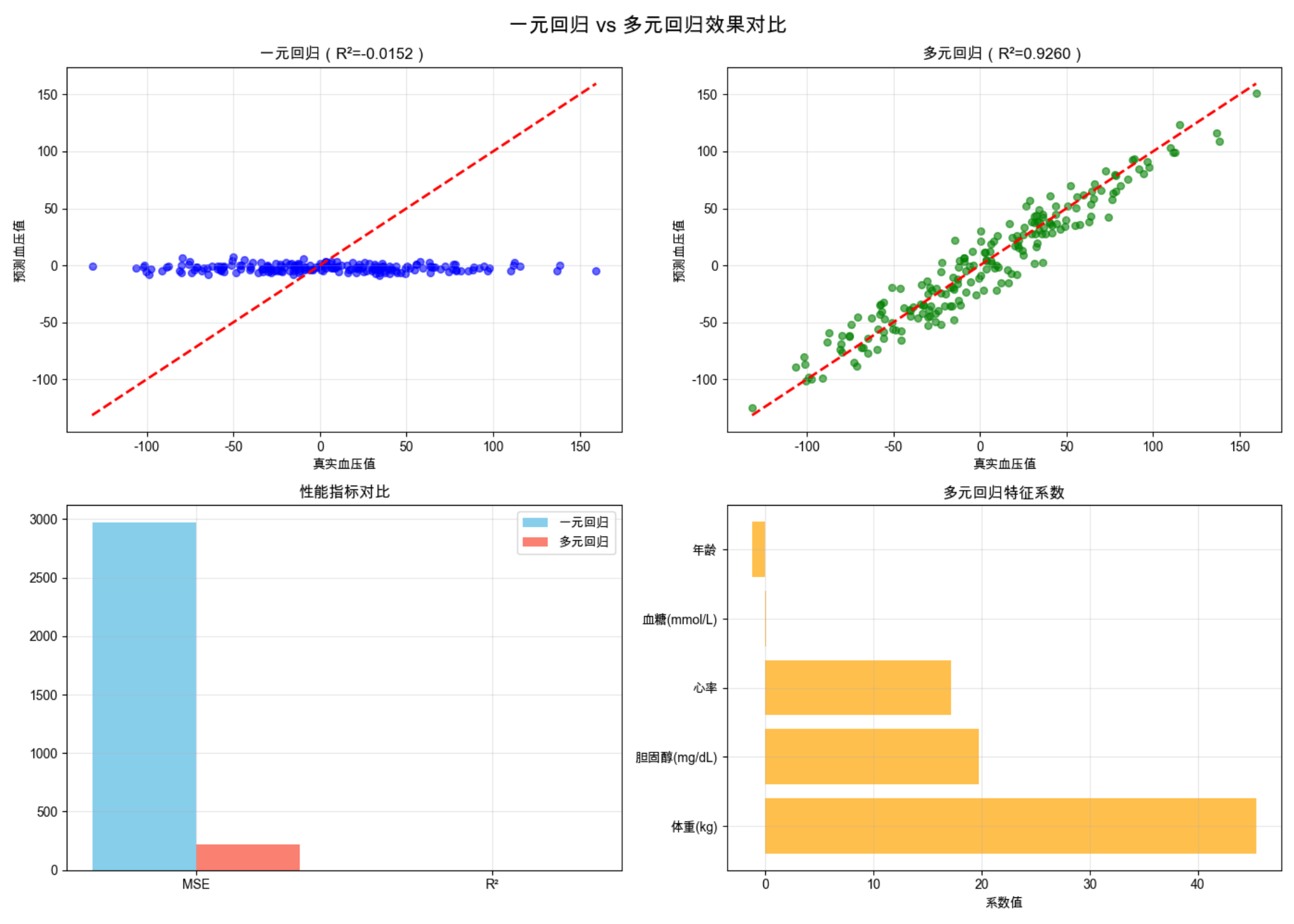
print(f"一元回归（年龄）：MSE={mse_uni:.2f}，R²={r2_uni:.4f}")
print(f"多元回归（5特征）：MSE={mse_multi:.2f}，R²={r2_multi:.4f}")

# 4. 多元回归系数分析
coefficients = pd.DataFrame({
    '特征': feature_names,
    '系数': model_multivariate.coef_
})
coefficients = coefficients.sort_values(by='系数', ascending=False)
print(f"\n=== 多元回归系数 ===")
print(coefficients)

# 5. 可视化对比
fig, axes = plt.subplots(2, 2, figsize=(14, 10))
fig.suptitle('一元回归 vs 多元回归效果对比', fontsize=16)

# 子图1：一元回归预测结果
axes[0,0].scatter(y_test, y_pred_uni, alpha=0.6, color='blue', s=30)
axes[0,0].plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--', linewidth=2)
axes[0,0].set_title(f'一元回归（R²={r2_uni:.4f}）')
axes[0,0].set_xlabel('真实血压值')
axes[0,0].set_ylabel('预测血压值')
axes[0,0].grid(alpha=0.3)

# 子图2：多元回归预测结果
axes[0,1].scatter(y_test, y_pred_multi, alpha=0.6, color='green', s=30)
axes[0,1].plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--', linewidth=2)
axes[0,1].set_title(f'多元回归（R²={r2_multi:.4f}）')
axes[0,1].set_xlabel('真实血压值')
axes[0,1].set_ylabel('预测血压值')
axes[0,1].grid(alpha=0.3)

# 子图3：MSE对比
metrics = ['MSE', 'R²']
uni_vals = [mse_uni, r2_uni]
multi_vals = [mse_multi, r2_multi]

x = np.arange(len(metrics))
width = 0.35
axes[1,0].bar(x - width/2, uni_vals, width, label='一元回归', color='skyblue')
axes[1,0].bar(x + width/2, multi_vals, width, label='多元回归', color='salmon')
axes[1,0].set_title('性能指标对比')
axes[1,0].set_xticks(x)
axes[1,0].set_xticklabels(metrics)
axes[1,0].legend()
axes[1,0].grid(alpha=0.3)

# 子图4：多元回归系数
axes[1,1].barh(coefficients['特征'], coefficients['系数'], color='orange', alpha=0.7)
axes[1,1].set_title('多元回归特征系数')
axes[1,1].set_xlabel('系数值')
axes[1,1].grid(alpha=0.3)

plt.tight_layout()
plt.show()

# 6. 残差分析（多元回归）
residuals = y_test - y_pred_multi
plt.figure(figsize=(10, 6))
plt.scatter(y_pred_multi, residuals, alpha=0.6, s=30)
plt.axhline(y=0, color='red', linestyle='--', linewidth=2)
plt.title('多元回归残差图', fontsize=14)
plt.xlabel('预测值')
plt.ylabel('残差')
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()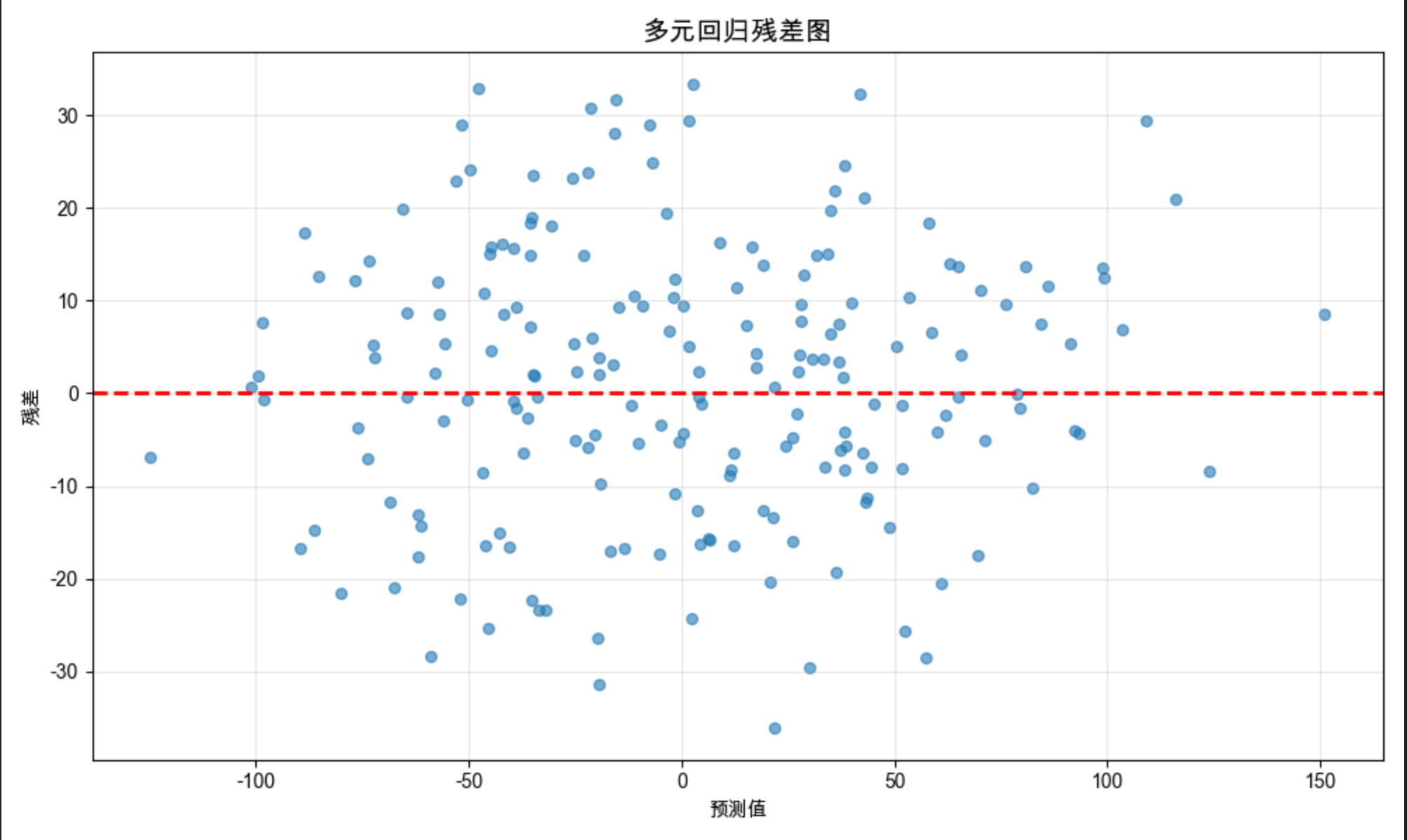

代码运行效果

  1. 输出一元和多元回归的 MSE、R²（多元回归 R² 更高）
  2. 显示预测结果对比散点图（多元回归更接近 y=x 线）
  3. 显示特征系数柱状图（直观看到哪些特征对血压影响大）
  4. 显示残差图（验证回归模型的假设）

5.9 注释

核心概念

注释就像 "代码的说明书"，在多元方法的代码中，注释的核心作用：

  1. 说明数据来源和处理逻辑（比如 "生成带 20% 缺失值的多元数据"）
  2. 解释关键参数含义（比如 "alpha=10：正则化强度"）
  3. 标注核心步骤的目的（比如 "对比一元 / 多元回归效果"）
  4. 记录实验结论（比如 "KNN 填充比均值填充 MSE 低 30%"）

规范注释示例

复制代码 
# === 多元回归核心代码（带规范注释） ===
def multivariate_regression_analysis(X, y, test_size=0.2, random_state=42):
    """
    多元回归分析主函数
    参数：
        X: 特征矩阵（多元数据）
        y: 目标变量
        test_size: 测试集比例，默认0.2
        random_state: 随机种子，保证结果可复现
    返回：
        model: 训练好的多元回归模型
        metrics: 包含MSE和R²的字典
    """
    # 1. 数据拆分（分层抽样，保证分布一致）
    X_train, X_test, y_train, y_test = train_test_split(
        X, y, test_size=test_size, random_state=random_state
    )
    
    # 2. 训练多元回归模型（线性回归无超参数）
    model = LinearRegression()
    model.fit(X_train, y_train)
    
    # 3. 模型评估（MSE越小越好，R²越接近1越好）
    y_pred = model.predict(X_test)
    mse = mean_squared_error(y_test, y_pred)
    r2 = r2_score(y_test, y_pred)
    
    # 4. 结果整理
    metrics = {'MSE': mse, 'R²': r2}
    
    return model, metrics

# 调用函数（示例）
# model, metrics = multivariate_regression_analysis(df[feature_names], df['血压(mmHg)'])
# print(f"多元回归MSE：{metrics['MSE']:.2f}，R²：{metrics['R²']:.4f}")

5.10 习题

基础题

1.运行 5.1 节代码，修改样本数为 500，观察特征相关性的变化。

2.对比不同缺失值填充方法（均值、中位数、KNN）在不同缺失比例（10%、30%、50%）下的 MSE。

3.用自己的数据集（如鸢尾花数据集）实现多元分类，对比不同特征组合的分类效果。

进阶题

1.在多元回归中，添加多项式特征（如年龄 ²、体重 × 年龄），观察模型性能变化。

2.实现多元正态分布的假设检验（Shapiro-Wilk 检验），验证自己的数据集是否符合多元正态分布。

3.结合离散特征和连续特征，构建混合多元模型，预测用户消费金额。

编程题

  1. 编写一个函数，自动选择最优的缺失值填充方法（根据 MSE 最小）。
  2. 实现正则化强度的自动调参（网格搜索），找到最优的 alpha 值。
  3. 可视化多元回归的 3D 超平面（取前两个特征，固定其他特征）。

5.11 参考文献

  1. 《机器学习导论》（原书第 2 版），Ethem Alpaydin 著
  2. 《Python 数据科学手册》，Jake VanderPlas 著
  3. 《统计学习方法》，李航 著
  4. scikit-learn 官方文档：https://scikit-learn.org/stable/
  5. NumPy 官方文档：https://numpy.org/doc/
  6. Pandas 官方文档：https://pandas.pydata.org/docs/
  7. Matplotlib 官方文档：https://matplotlib.org/stable/

总结

1.多元方法核心：通过分析多个特征的关联关系，解决分类、回归等问题，效果优于单特征分析。

2.关键处理步骤：多元数据探索→缺失值填充→离散特征编码→模型构建→复杂度调整，每个步骤都有对应的最优实践（如 KNN 填充、独热编码、L2 正则化）。

3.可视化价值：通过对比图（如填充效果、回归预测、复杂度曲线）能直观理解不同方法的优劣，是学习多元方法的重要辅助手段。

本文所有代码均可直接运行（需安装 numpy/pandas/matplotlib/scikit-learn/seaborn），建议读者动手修改参数、更换数据集，加深对多元方法的理解。

相关推荐
薯一个蜂蜜牛奶味的愿1 小时前
模块化显示神经网络结构的可视化工具--BlockShow
人工智能·深度学习·神经网络
班德先生2 小时前
深耕多赛道品牌全案策划，为科技与时尚注入商业表达力
大数据·人工智能·科技
哈__2 小时前
CANN加速强化学习推理：策略网络与价值网络优化
人工智能
慢半拍iii2 小时前
ops-nn性能调优实战：提升神经网络推理速度的秘诀
人工智能·神经网络·ai·cnn·cann
hay_lee2 小时前
Spring AI实现对话聊天-流式输出
java·人工智能·ollama·spring ai
wangsir.2 小时前
测试之自动化测试常用函数
python·测试
塔中妖2 小时前
CANN深度解读：从算子库看AI计算的底层架构
人工智能·架构
铁蛋AI编程实战2 小时前
MemoryLake 实战：构建超长对话 AI 助手的完整代码教程
人工智能·python·microsoft·机器学习
weixin_549808362 小时前
2026 中国 AI 招聘系统市场观察：从效率工具到智能体协同，招聘正被重新定义
人工智能
热门推荐
01GitHub 镜像站点02Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services03使用 1panel面板 部署 php网站04Vue-skills的中文文档05OpenClaw Chrome扩展使用教程 - 浏览器中继控制06从零搭建一个 PHP 登录注册系统（含完整源码）07让 Trae IDE 智能体 “读懂”文档 Excel+PDF+DOCX ：mcp-documents-reader 工具使用指南08一文了解国产算子编程语言 TileLang，TileLang 对国产开源生态的影响与启示09UV安装并设置国内源10Linux下V2Ray安装配置指南