数学建模-day4

一时间序列ARIMA

1 理解

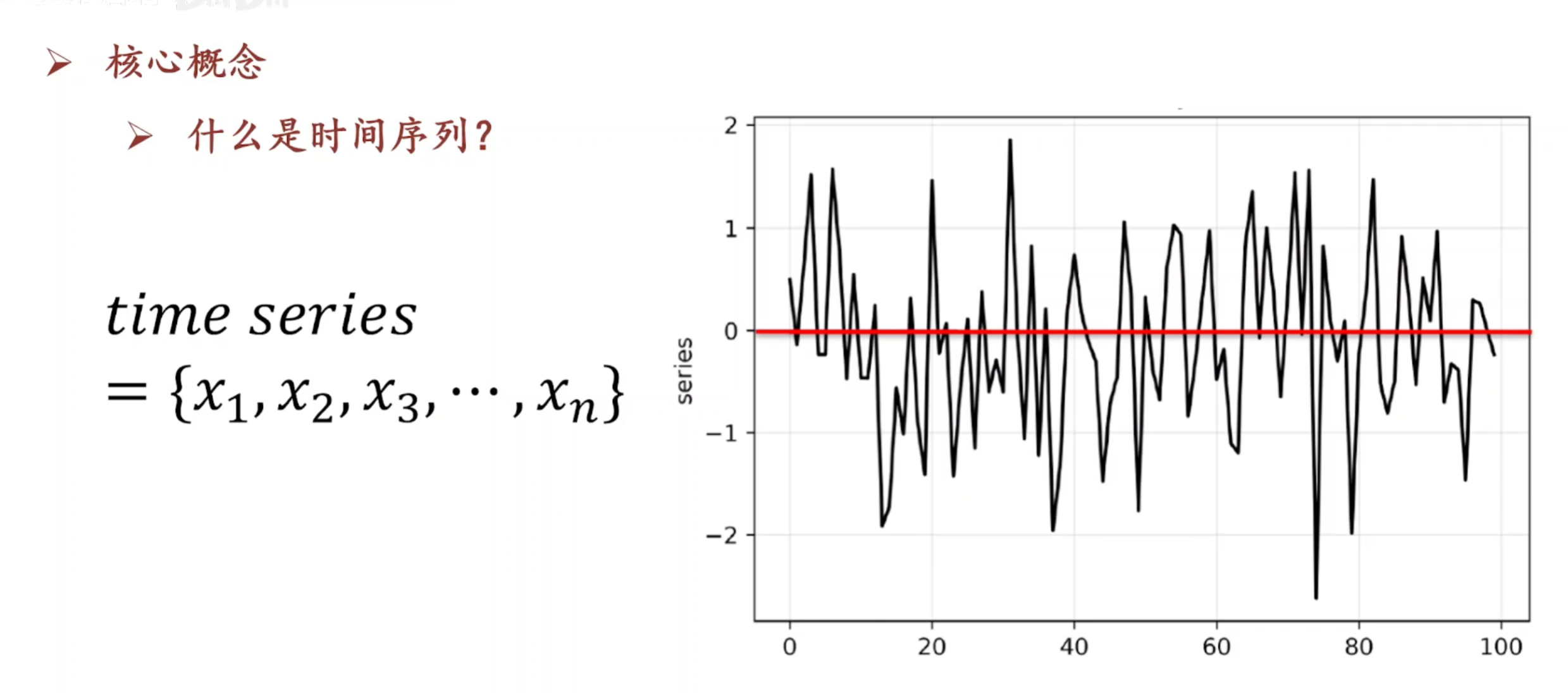
时间序列是：明天的天气是根据今天的天气进行的预测很难确定时间和其他变量（人数等）的关系明天的结果会受今天的影响

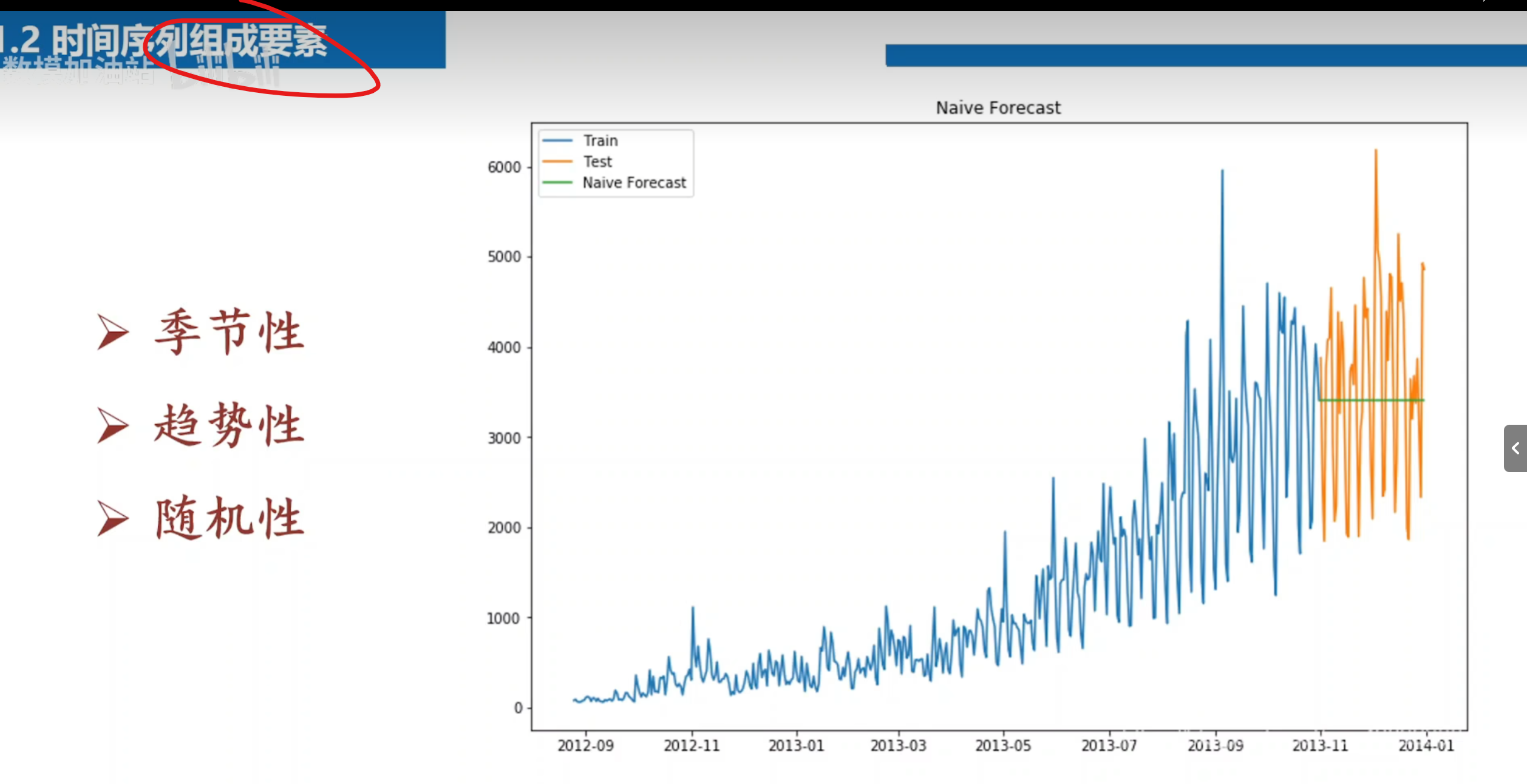
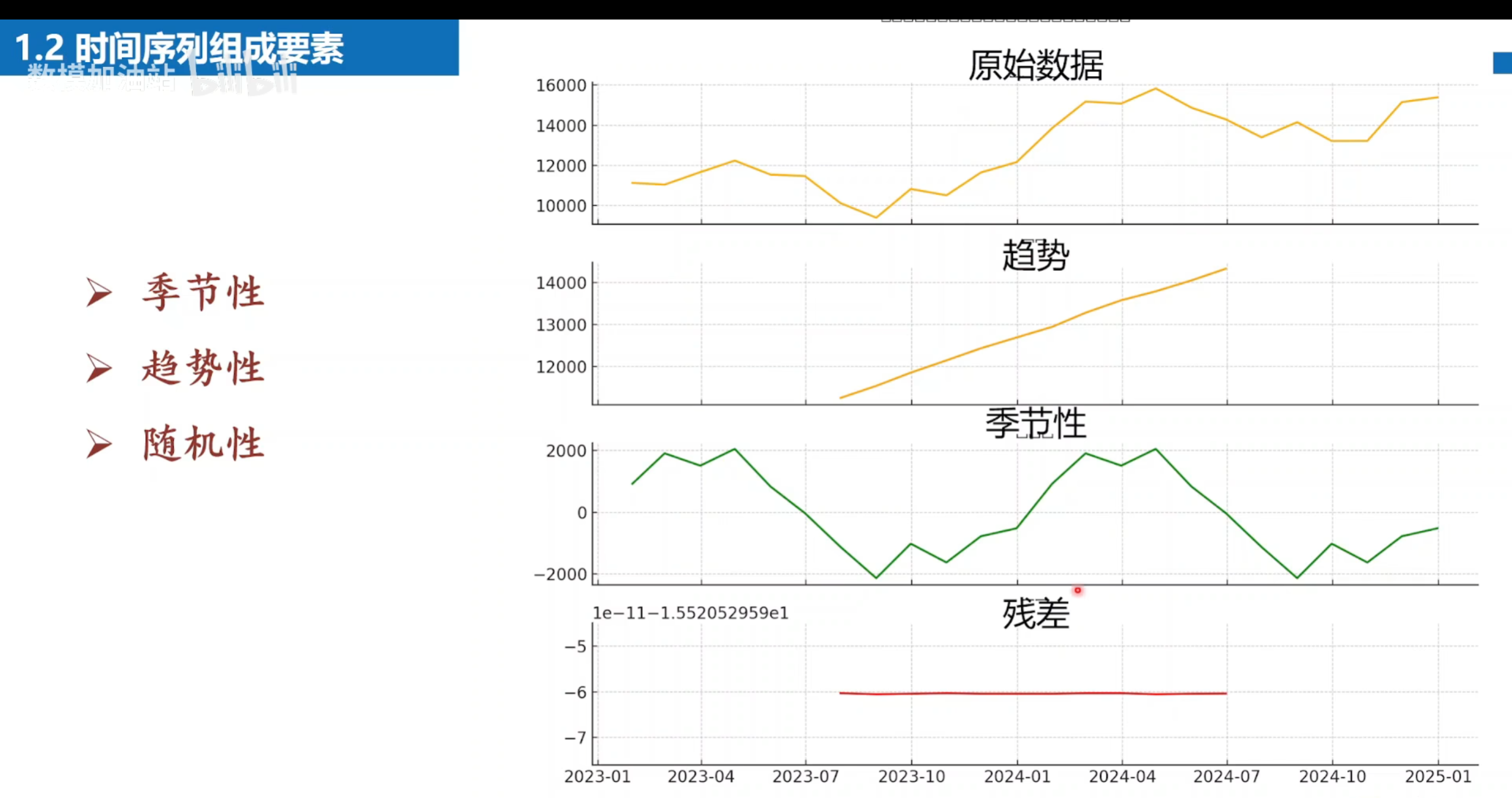
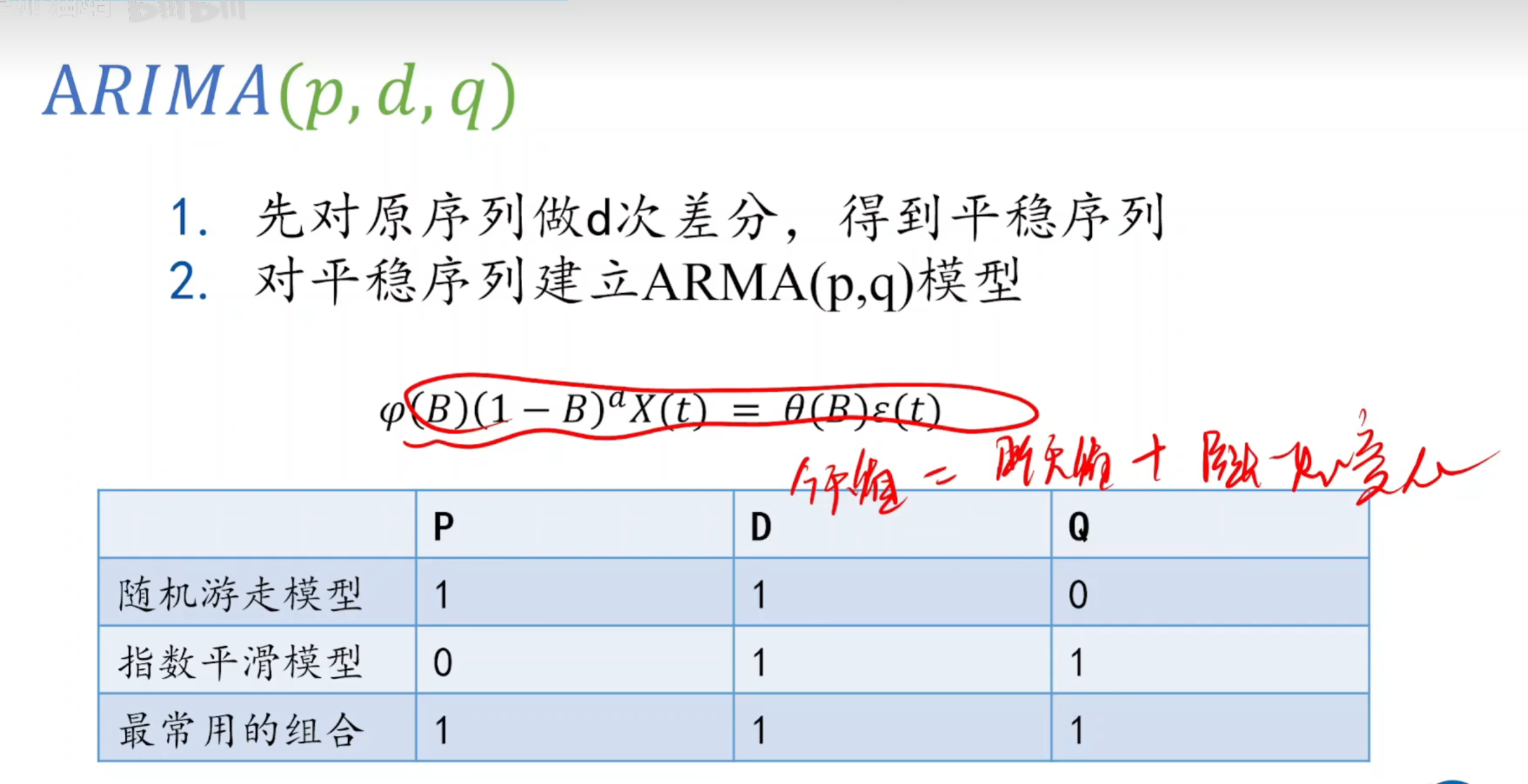
步骤

2 python代码

（1）数据的生成

python 复制代码

dates = pd.date_range(start=start_date, periods=periods, freq='D')
生成一个从 start_date开始、长度为 periods、频率为日（'D'）
的 DatetimeIndex，作为数据的时间轴。

returns = np.random.normal(0.001, 0.02, periods)
生成服从正态分布的日收益率序列：
均值 0.001：表示每日平均上涨 0.1%。
标准差 0.02：表示每日波动幅度约为 2%。

trend = np.linspace(0, 0.5, periods) / periods
returns = returns + trend
trend是一个从 0 到 0.5 的线性递增序列，然后除以 periods使其值非常小。
作用：为收益率添加一个微弱的上升趋势，模拟长期看涨的市场环境。

volatility = 1 + 0.3 * np.sin(np.linspace(0, 4 * np.pi, periods))
returns = returns * volatility
volatility是一个基于正弦函数的周期性序列（周期数：2，因为 4 * π表示两个完整周期）。
作用：模拟波动率的周期性变化（如市场情绪周期），使收益率在某些时段放大或缩小。

python 复制代码

prices = [initial_price]
for r in returns[1:]:
    prices.append(prices[-1] * (1 + r))

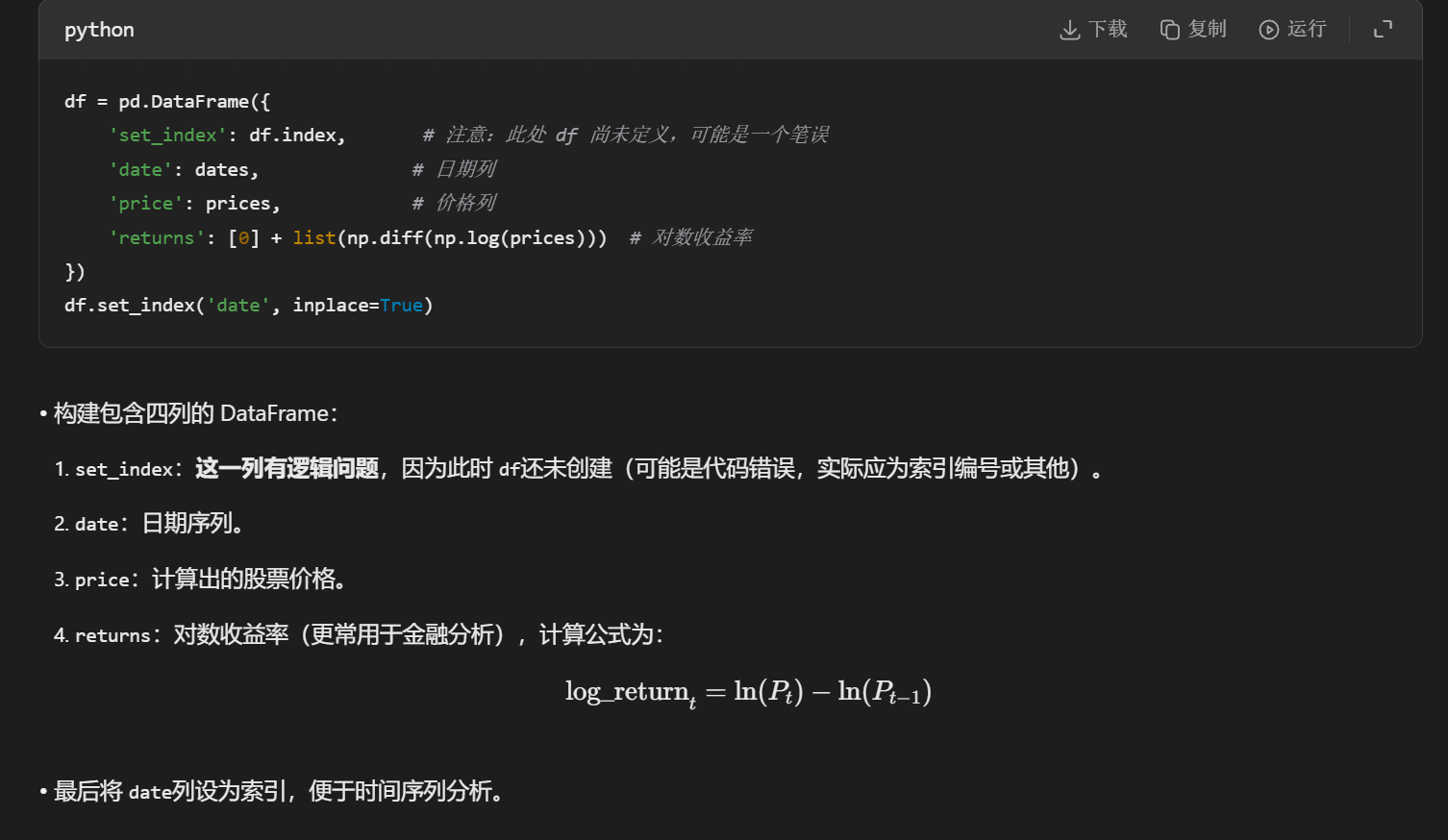
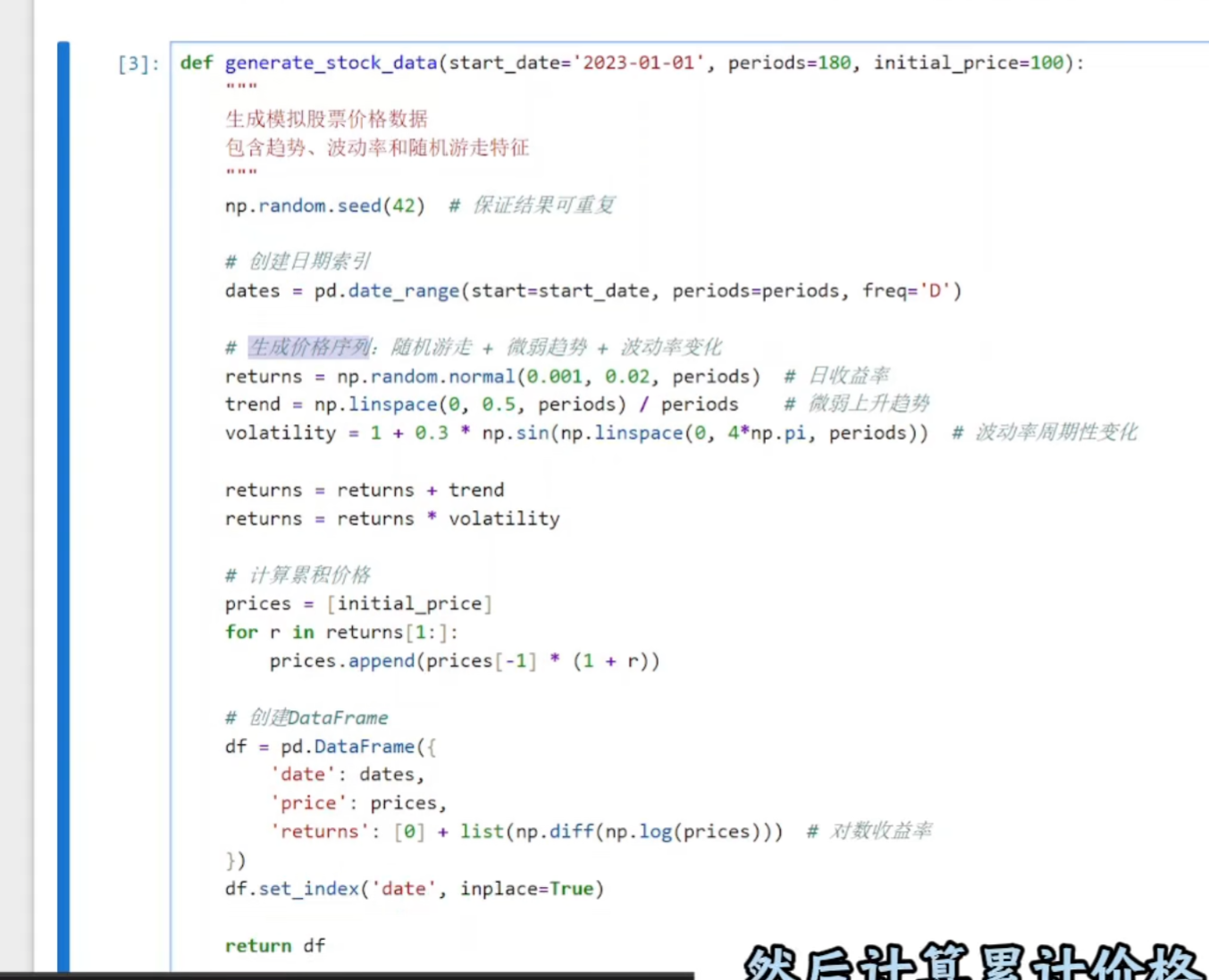
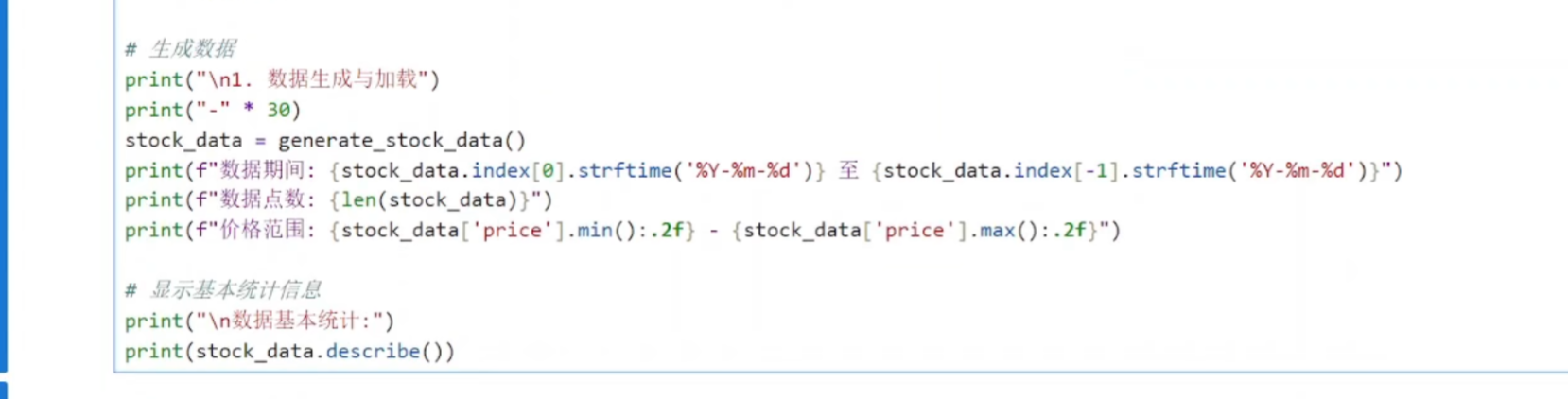
（2）数据探索和可视化

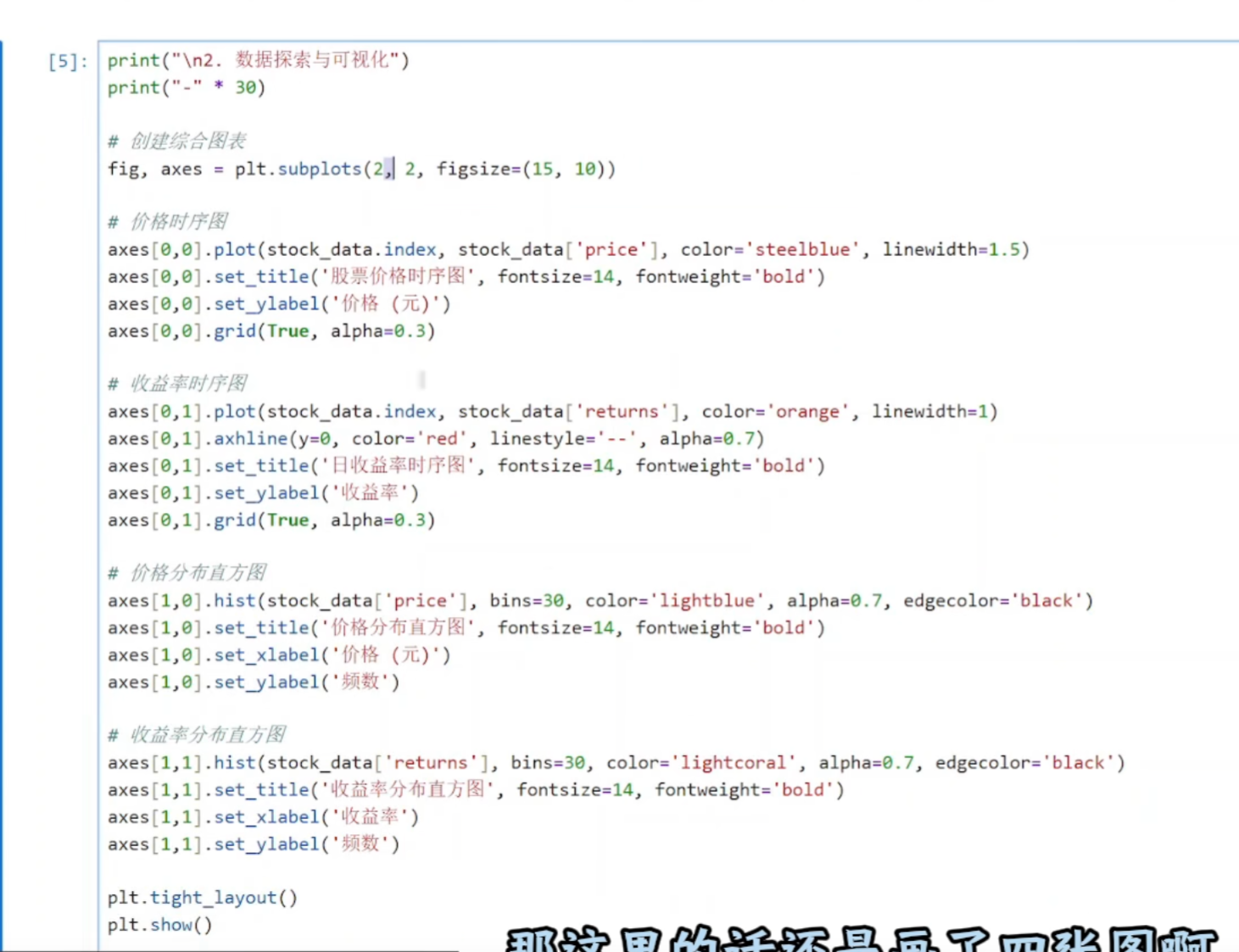
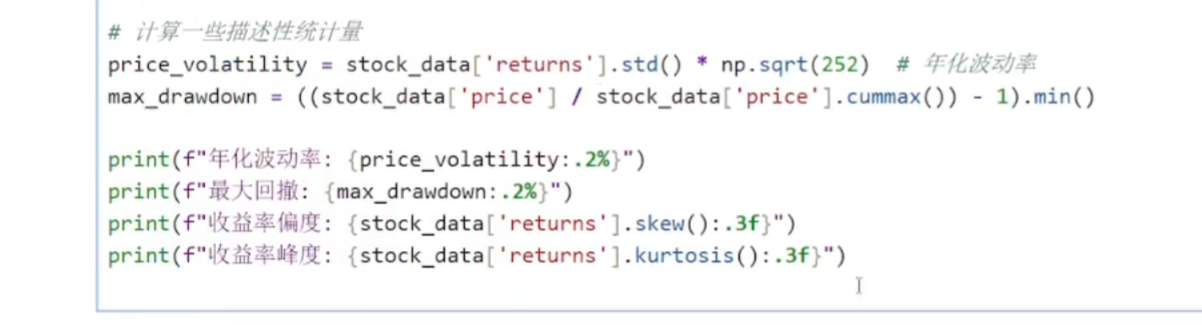
（3）进行平稳性检验

python 复制代码

def detailed_adf_test(timeseries, title="时间序列"):
功能：执行增强的迪基-富勒检验，判断时间序列是否平稳
参数：
timeseries：要检验的时间序列数据（如股价、收益率等）
title：序列名称（用于结果展示，默认"时间序列"）

result = adfuller(timeseries.dropna())
adfuller()：来自statsmodels库的ADF检验函数
dropna()：删除缺失值，确保检验数据完整
返回包含ADF统计量、p值、临界值等信息的元组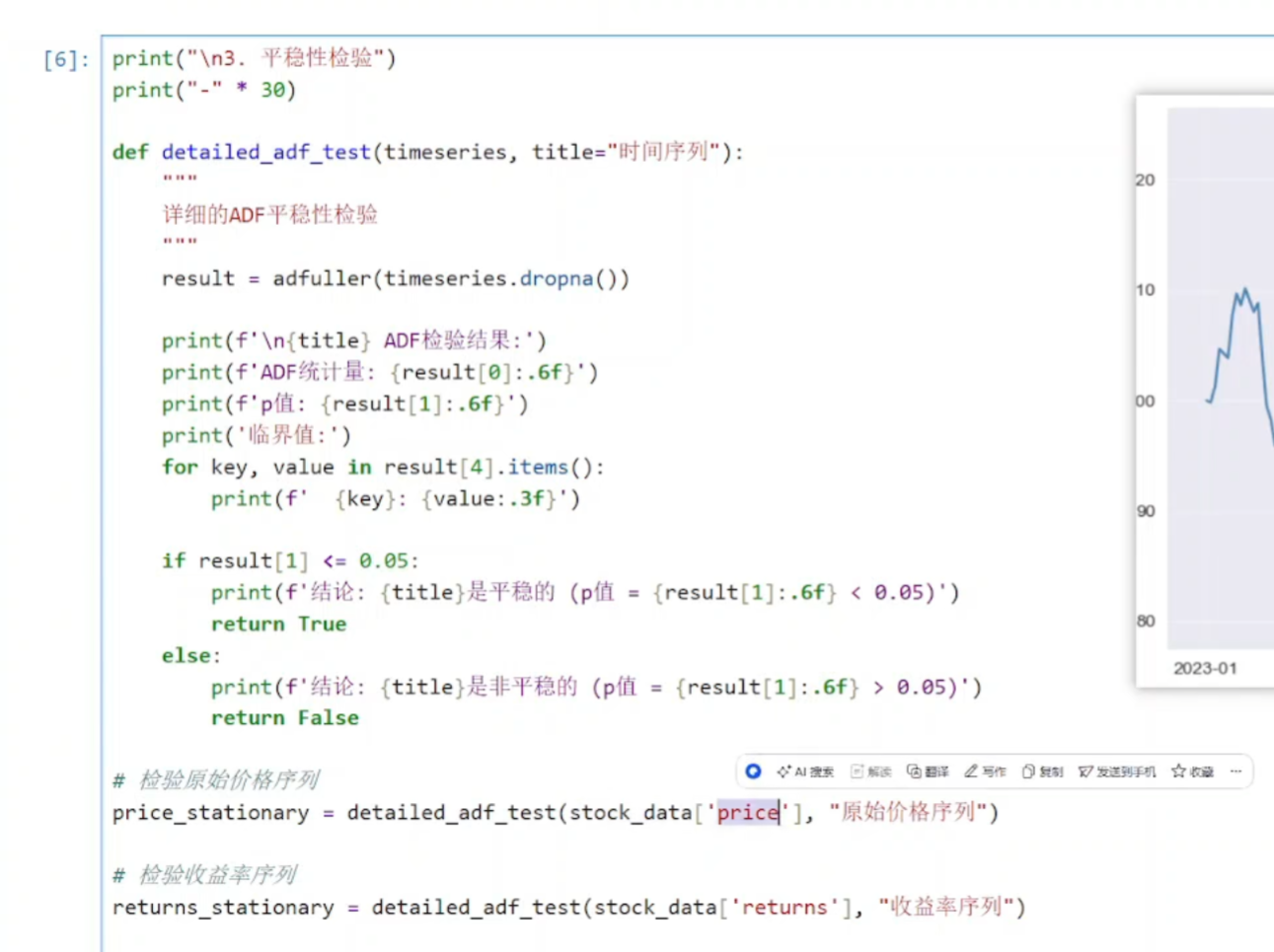

.diff()表示差分 .diff.diff表示二阶差分

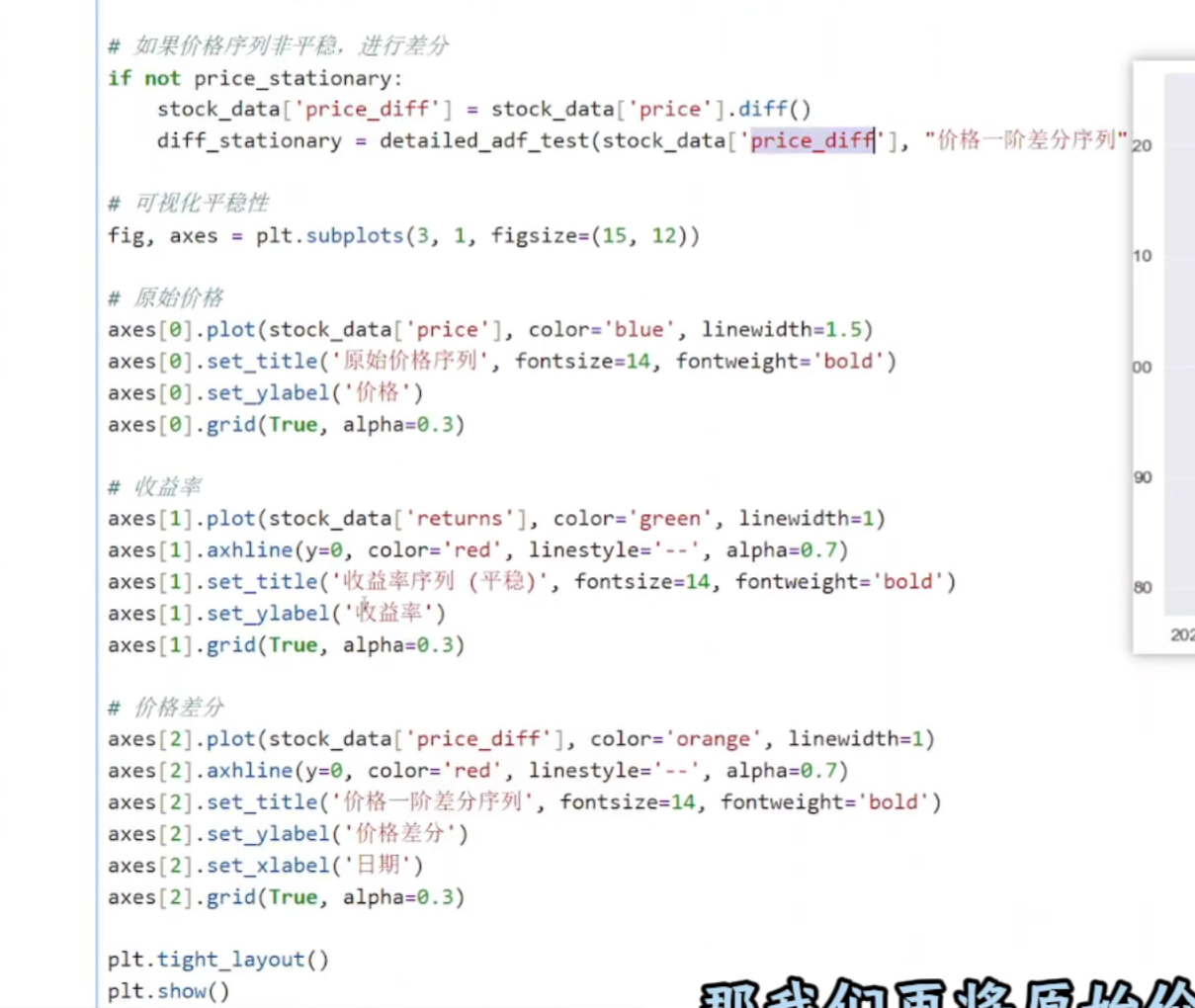
（4）ACF和PACF分析

python 复制代码

lot_acf(analysis_data, ax=axes[0], lags=20, title='自相关函数 (ACF)')
axes[0].set_xlabel('滞后期')
axes[0].grid(True, alpha=0.3)
参数详解：
plot_acf()：来自statsmodels.graphics.tsaplots的ACF绘图函数
analysis_data：要分析的平稳时间序列
ax=axes[0]：指定绘制到第一个子图
lags=20：显示前20期的自相关系数
title='自相关函数 (ACF)'：子图标题

绘制图像

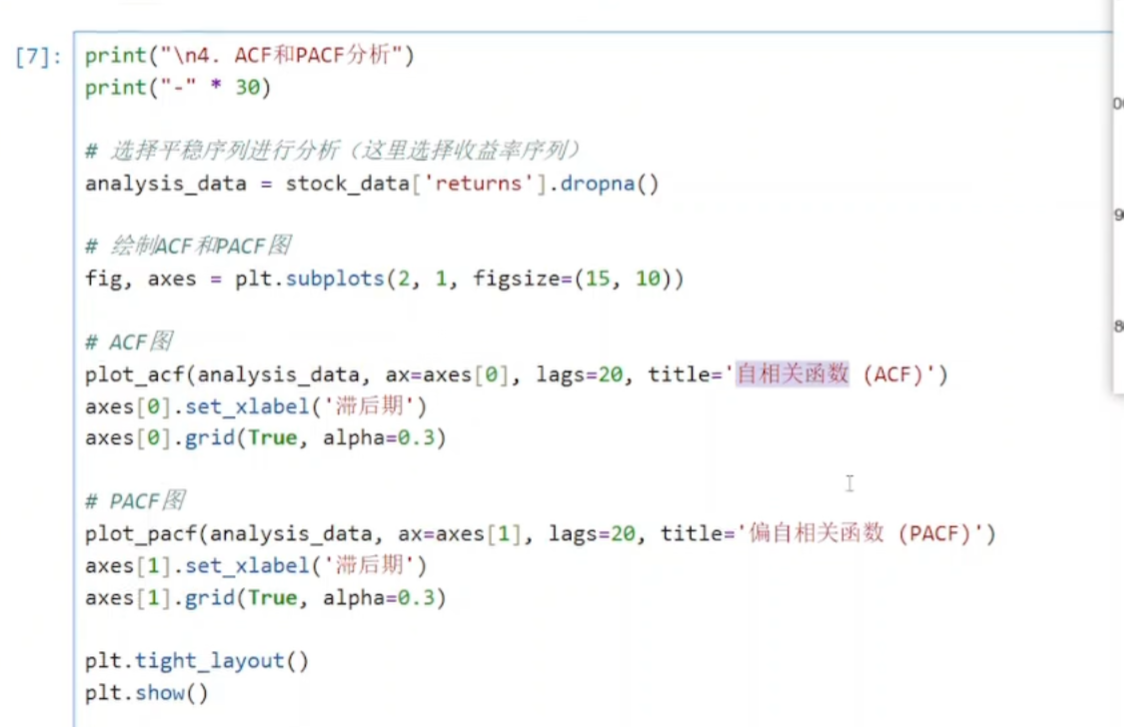
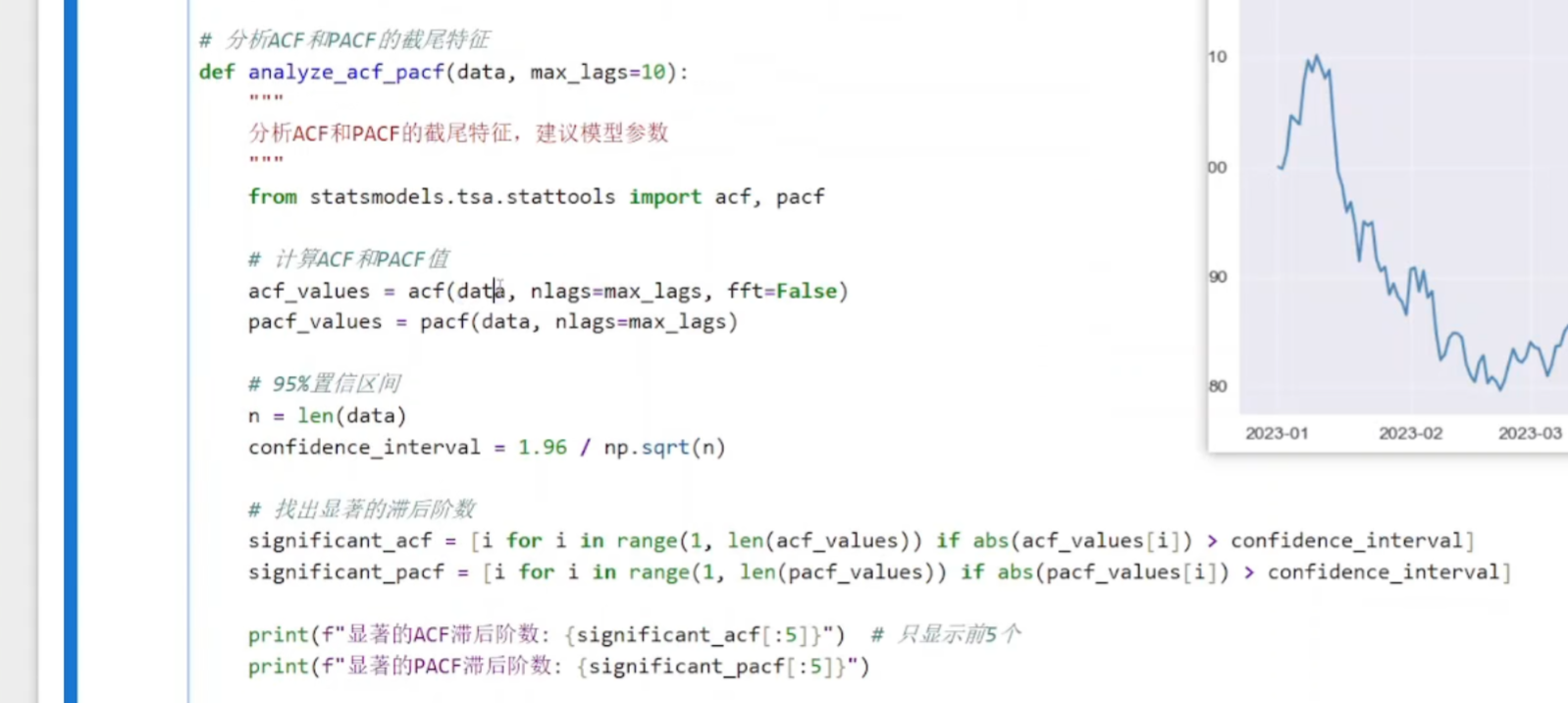
python 复制代码

from statsmodels.tsa.stattools import acf, pacf
从statsmodels库中导入acf和pacf函数，用于计算自相关和偏自相关系数

进行计算

python 复制代码

acf_values = acf(data, nlags=max_lags, fft=False)
pacf_values = pacf(data, nlags=max_lags)
acf()：计算自相关函数值
fft=False：不使用快速傅里叶变换，直接计算
pacf()：计算偏自相关函数值
输出：两个数组，包含从滞后0到max_lags的相关系数

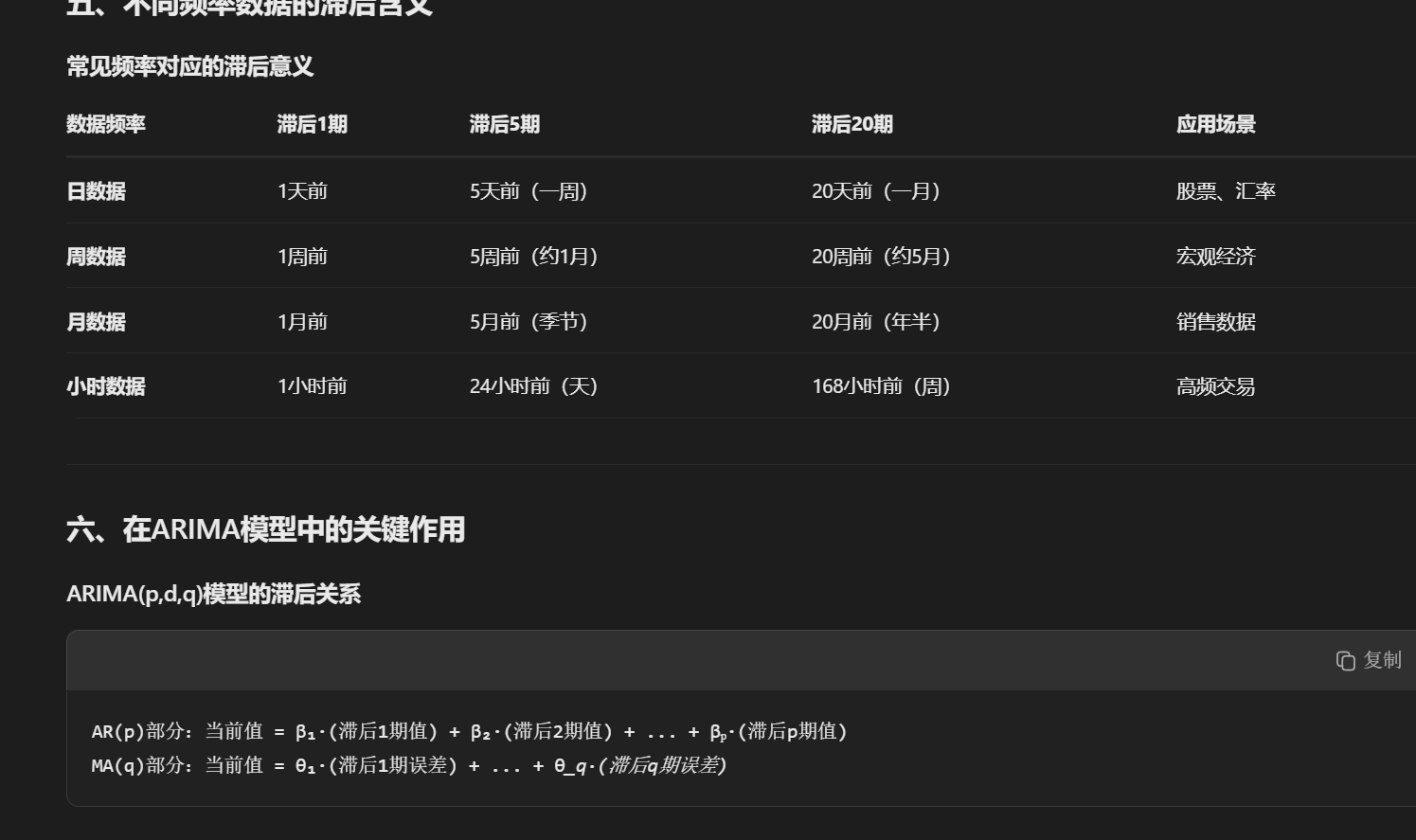
python 复制代码

f len(significant_pacf) > 0:
    suggested_p = min(3, max(significant_pacf[:3]))  # 限制在3以内
else:
    suggested_p = 0
逻辑：
如果有显著PACF滞后：
取前3个显著滞后的最大值
用min(3, ...)限制最大阶数为3（防止过拟合）
如果没有显著滞后 → p=0（无自回归部分）
理论基础：PACF的截尾点通常对应AR模型的阶数p

（5）ARIMA模型识别与选择

python 复制代码

itertools.product()：笛卡尔积生成器，产生所有可能的组合

float('inf')：Python中表示正无穷大的特殊浮点数

AIC适合复杂模型
BIC适合简单模型

python 复制代码

model = ARIMA(data, order=(p, d, q))
fitted_model = model.fit()
ARIMA()：创建ARIMA模型对象
order=(p,d,q)：指定模型阶数
.fit()：使用最大似然估计等方法拟合模型参数

aic = fitted_model.aic
bic = fitted_model.bic
AIC（赤池信息准则）：
公式：AIC = 2k - 2ln(L)
平衡模型拟合优度与复杂度
值越小越好
BIC（贝叶斯信息准则）：
公式：BIC = k·ln(n) - 2ln(L)
对模型复杂度惩罚更重（样本量n大时）
值越小越好

if aic < best_aic:
    best_aic = aic
    best_params = (p, d, q)
更新逻辑：当当前模型的AIC比历史最低AIC更小时
记录：
best_aic：最低AIC值
best_params：对应的(p,d,q)参数
注意：这里使用AIC作为选择标准，也可改用BIC

python 复制代码

top_models = search_results.nsmallest(10, 'AIC')
作用：从search_results数据框中找出AIC最小的10行数据
详细解释：
search_results：包含所有ARIMA模型结果的数据框
通常包含列：params（参数）、AIC、BIC等
nsmallest(10, 'AIC')：Pandas DataFrame方法
按'AIC'列的值从小到大排序
取前10个（即AIC最小的10个）
返回一个新的数据框

python 复制代码

for idx, row in top_models.iterrows():
    print(f"ARIMA{row['params']}) - AIC: {row['AIC']:.2f}, 
BIC: {row['BIC']:.2f}")
行遍历：
top_models.iterrows()：遍历数据框的每一行
idx：当前行的索引（0-9）
row：当前行的数据（Series对象），可以通过列名访问
格式化输出：
f"..."：f-string格式化字符串
ARIMA{row['params']})：
row['params']：获取参数元组，如(2,1,1)
输出示例：ARIMA(2,1,1)
AIC: {row['AIC']:.2f}：
row['AIC']：获取AIC值
:.2f：格式化为保留2位小数的浮点数
BIC: {row['BIC']:.2f}：同理

（6）模型拟合与参数估计

python 复制代码

fitted_model = optimal_model.fit()
.fit()：使用最大似然估计等方法估计模型参数
返回：一个包含所有估计结果、诊断信息的拟合模型对象
内部计算：
估计AR和MA系数
计算残差
计算统计量（AIC、BIC等）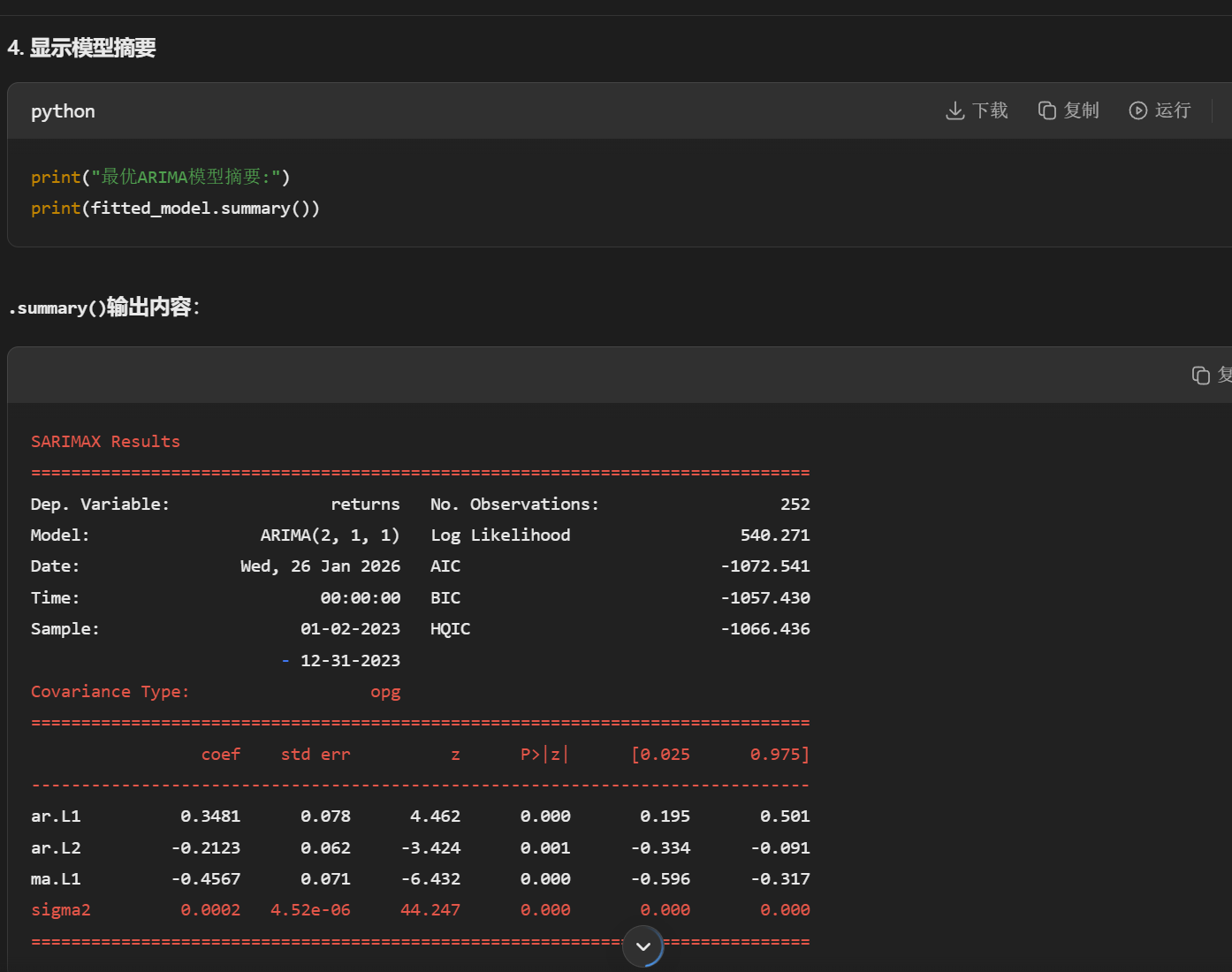

（7）模型诊断

（8）模型预测

python 复制代码

forecast = fitted_model.forecast(steps=forecast_steps)
forecast_ci = fitted_model.get_forecast(steps=forecast_steps).conf_int()
详细说明：
fitted_model：之前拟合好的ARIMA模型（如ARIMA(2,1,1)）
forecast(steps=30)：预测未来30期的收益率
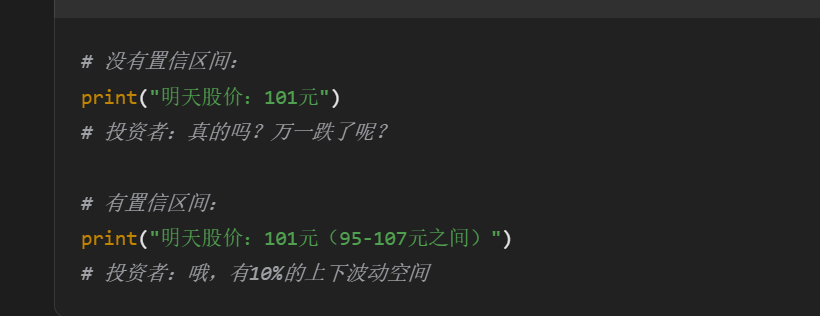
get_forecast().conf_int()：获取预测的置信区间

last_date = stock_data.index[-1]
forecast_dates = pd.date_range(start=last_date + timedelta(days=1),
                                periods=forecast_steps, freq='D')
步骤分解：
last_date = stock_data.index[-1]：获取历史数据最后一个日期
last_date + timedelta(days=1)：从第二天开始预测
pd.date_range()：生成30个连续的每日日期

python 复制代码

f = pd.DataFrame({
    '姓名': ['张三', '李四', '王五', '赵六', '钱七'],
    '成绩': [85, 92, 78, 95, 88]
})
例子1：.iloc[-1]（你代码中的用法）
last_student = df.iloc[-1]
print(last_student)
# 输出：姓名-钱七, 成绩-88

Python中[-1]表示列表最后一个元素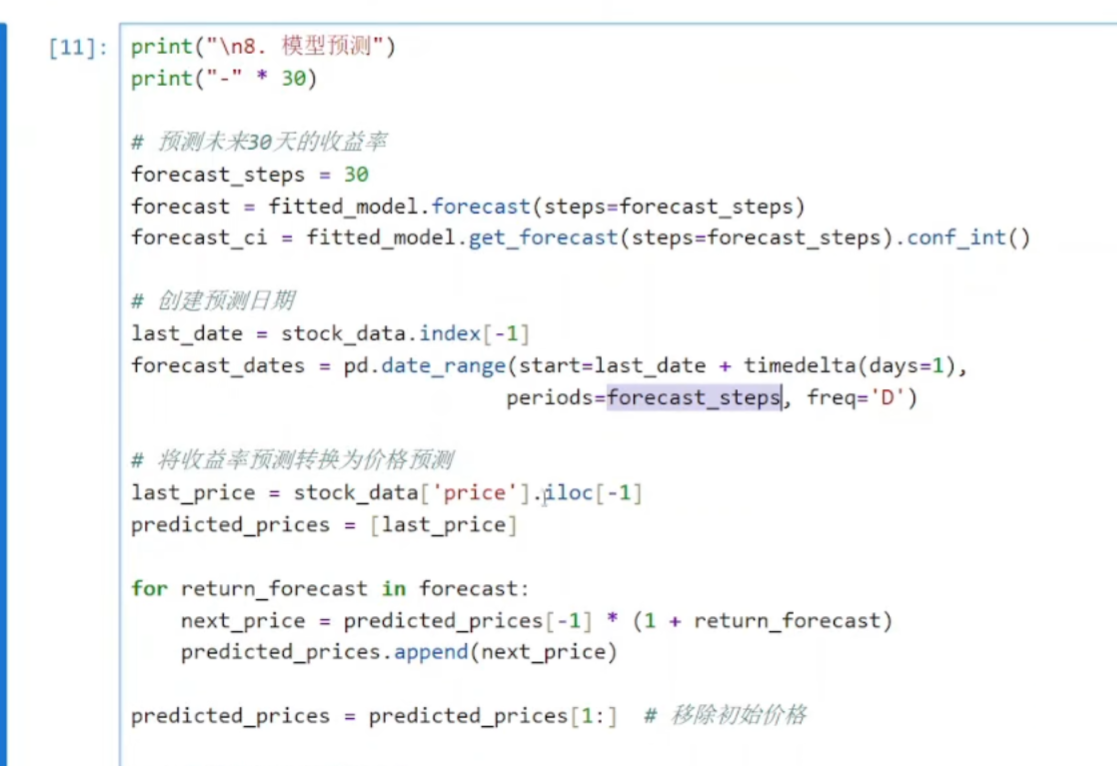

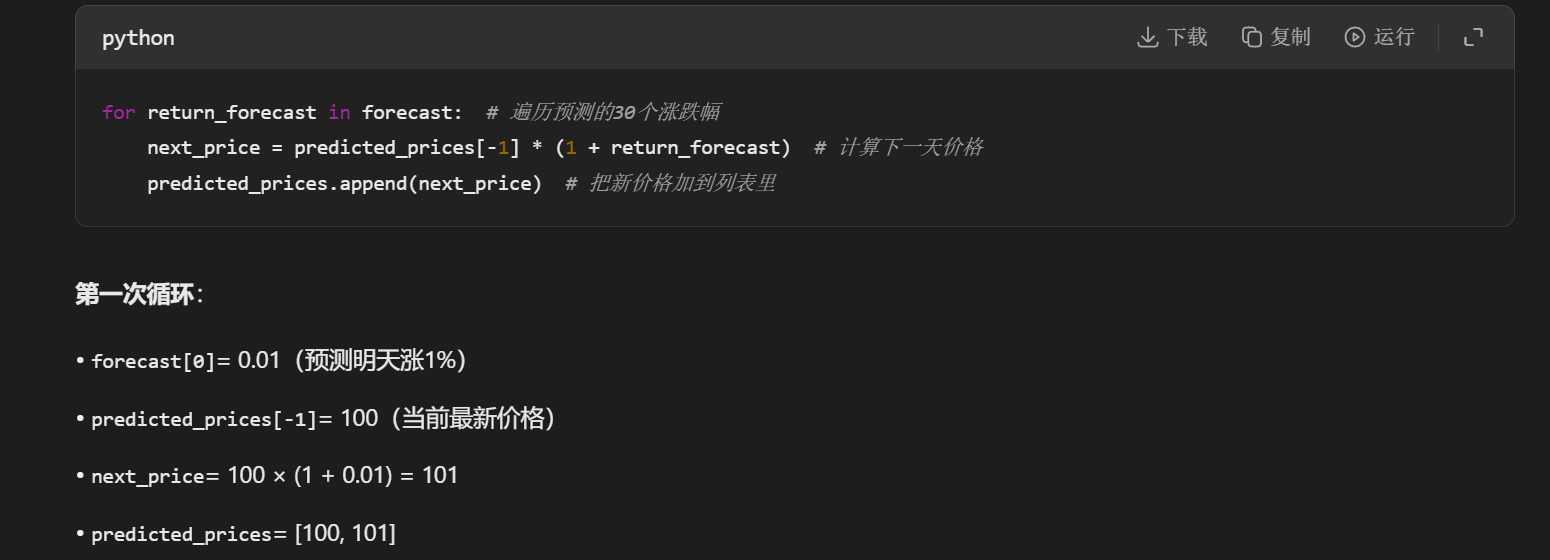
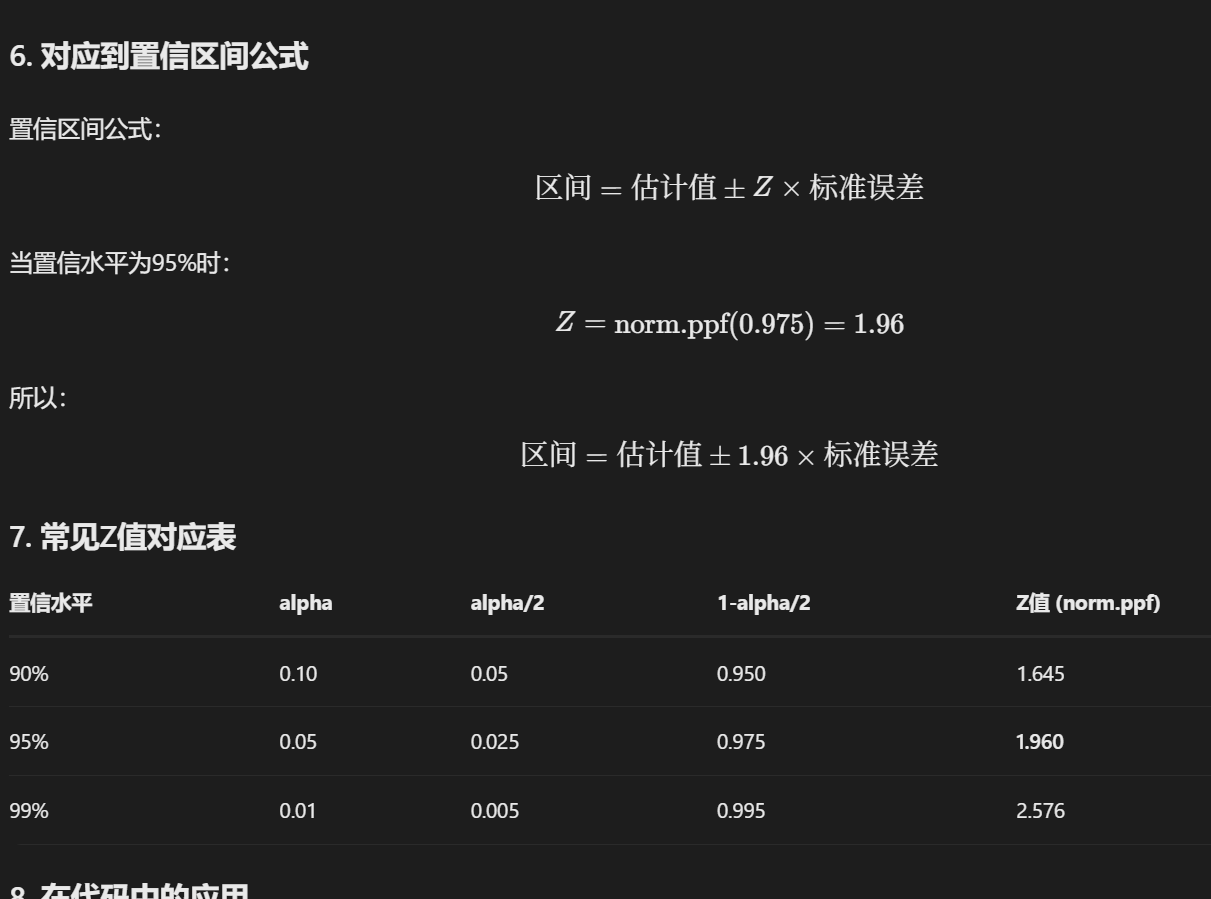
置信区间是价格的范围

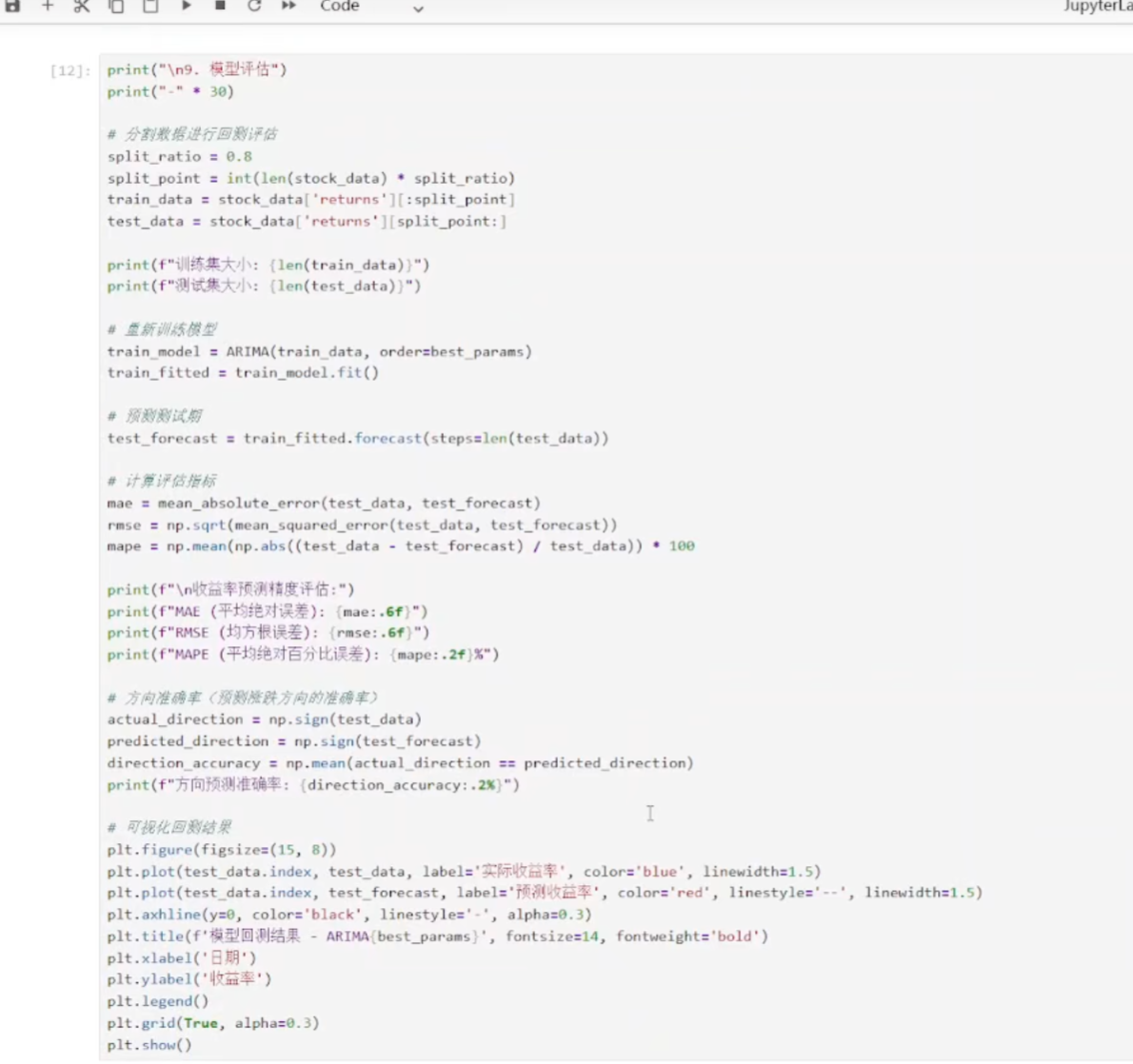
（9）模型评估

3 当是季节的时候

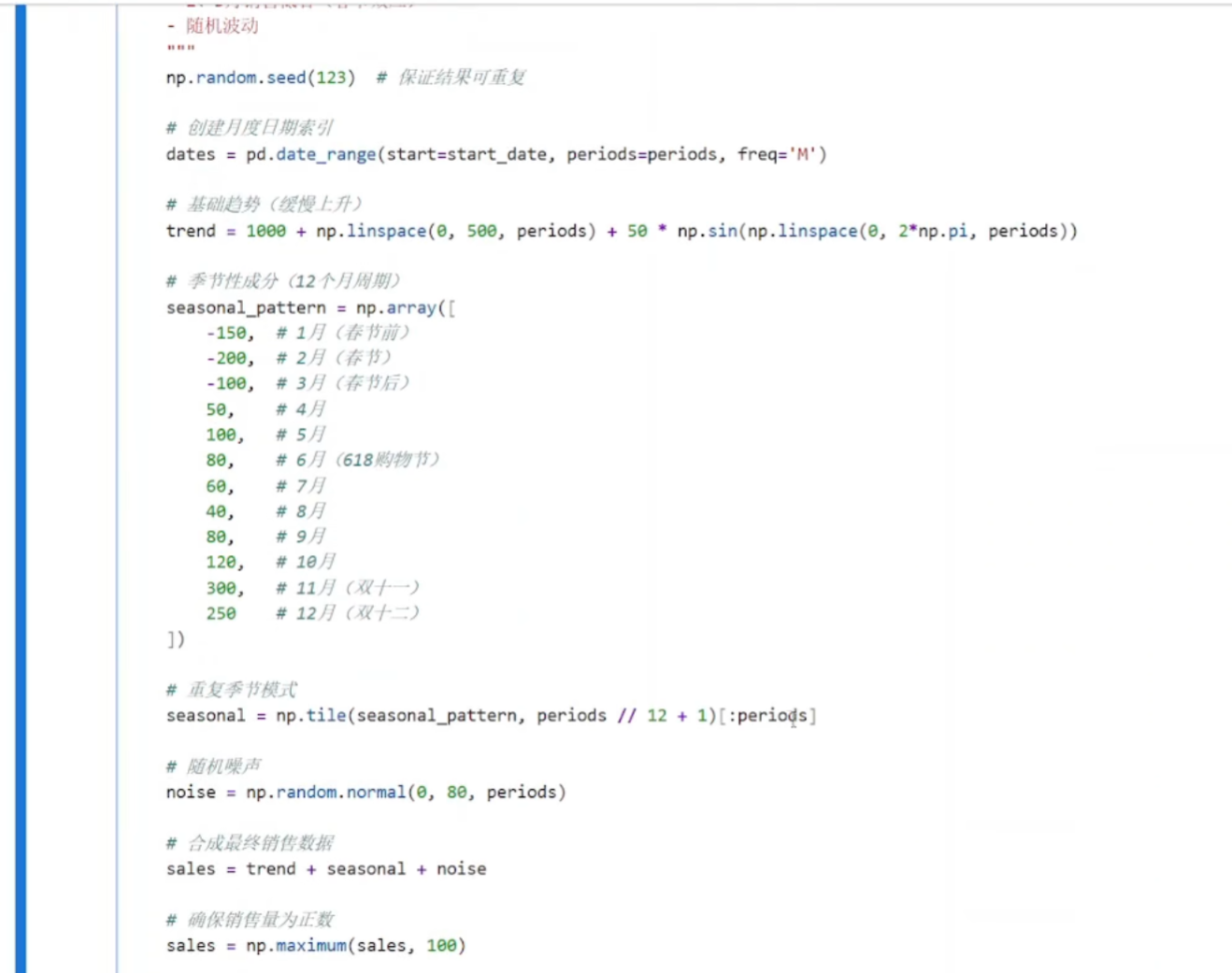
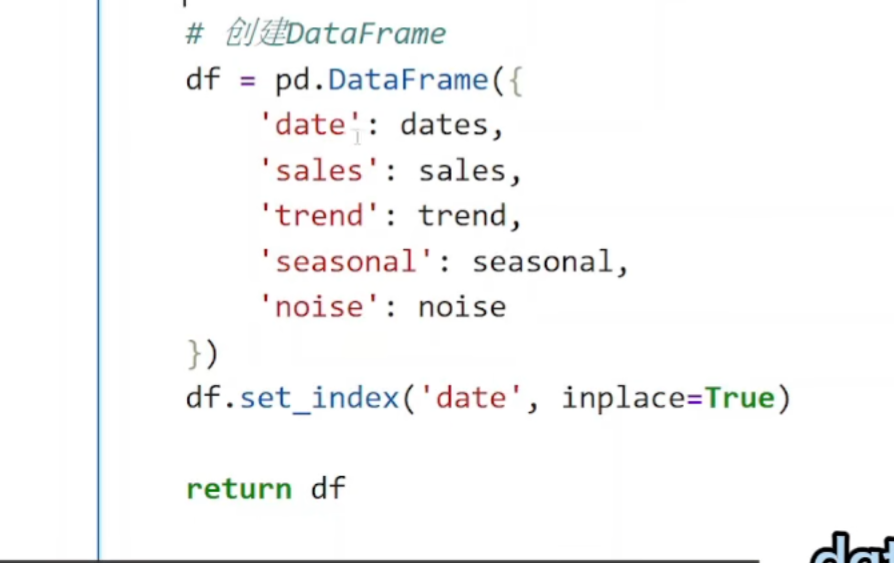
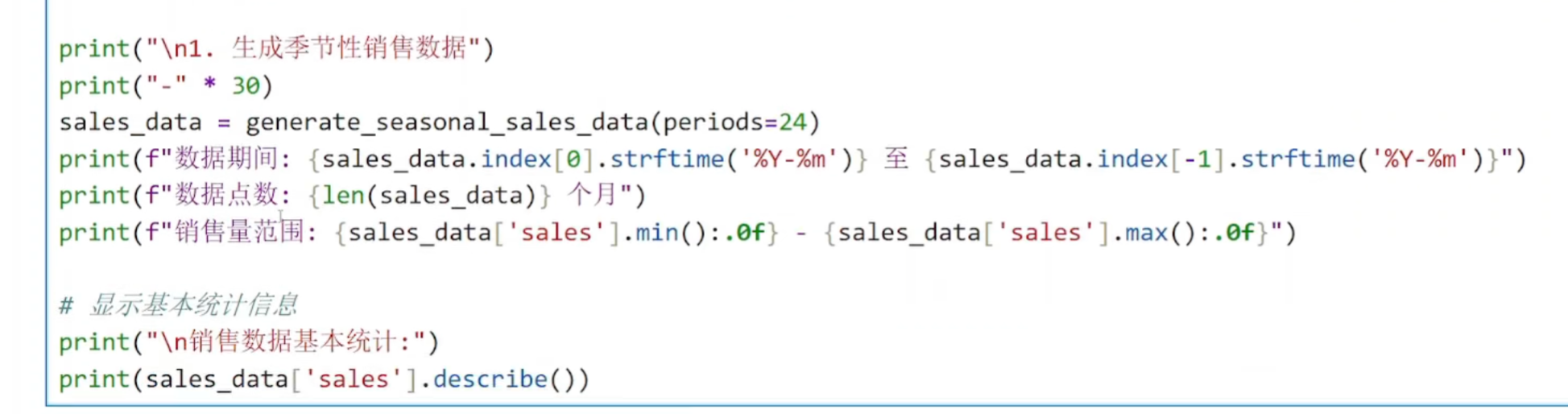
使用季节分解

python 复制代码

decomposition = seasonal_decompose(sales_data['sales'], model='additive', period=12)
参数说明：
sales_data['sales']：要分析的销售数据序列
model='additive'：使用加法模型
公式：观测值 = 趋势 + 季节性 + 残差
适用于季节波动幅度不随时间变化的序列
另一种是 'multiplicative'（乘法模型）：观测值 = 趋势 × 季节性 × 残差
period=12：设置周期为12个月
因为这是月度数据（12个月为一个完整周期）
如果是季度数据：period=4
如果是周度数据：period=7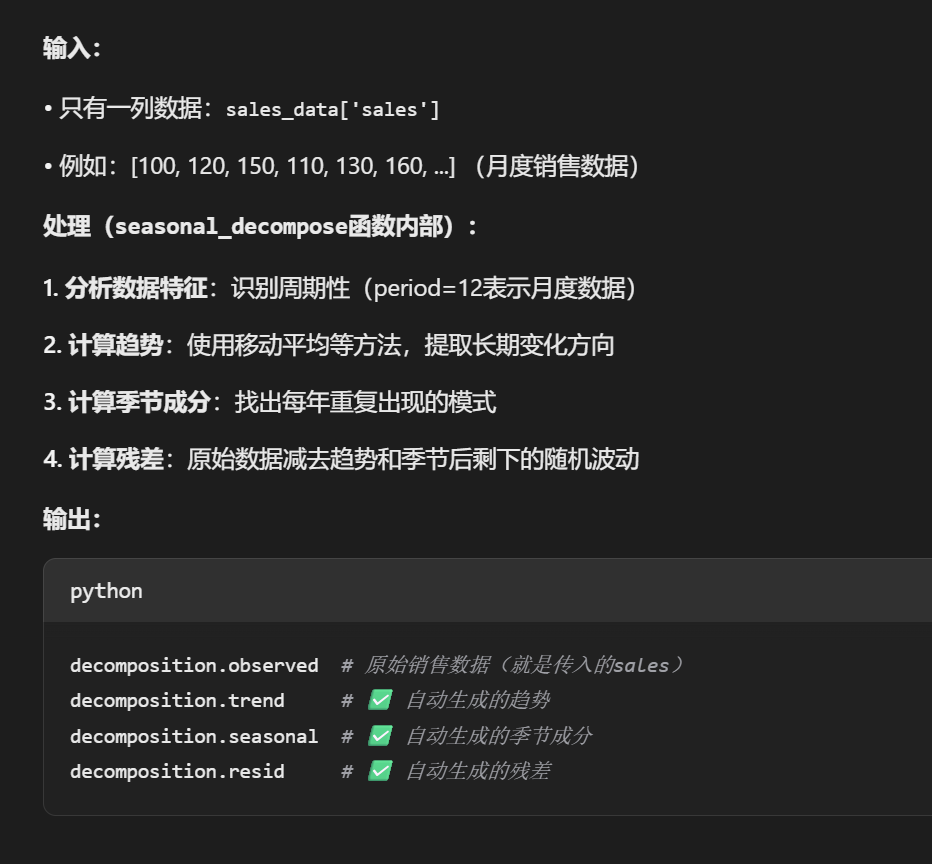

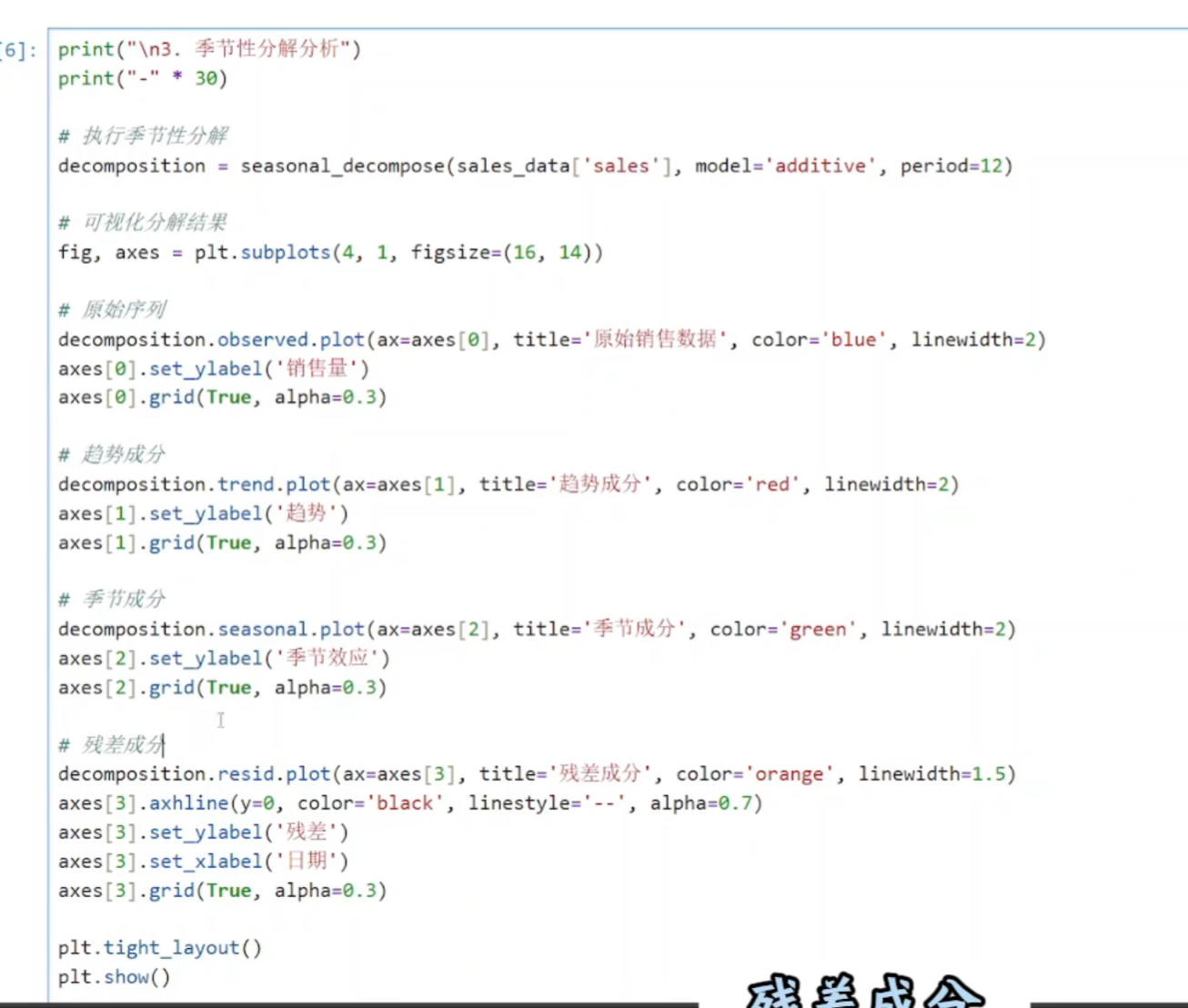
进行差分的时候

python 复制代码

.diff(12)：计算间隔12期的差值
公式：sales[t] - sales[t-12]
消除季节性（seasonality）
为什么是12？：因为是月度数据，一年12个月
作用：检验仅消除季节性是否能使数据平稳
适用场景：数据有强季节性（如每年重复模式），但无明显趋势

建议使用SARIMA进行模型的网格搜索

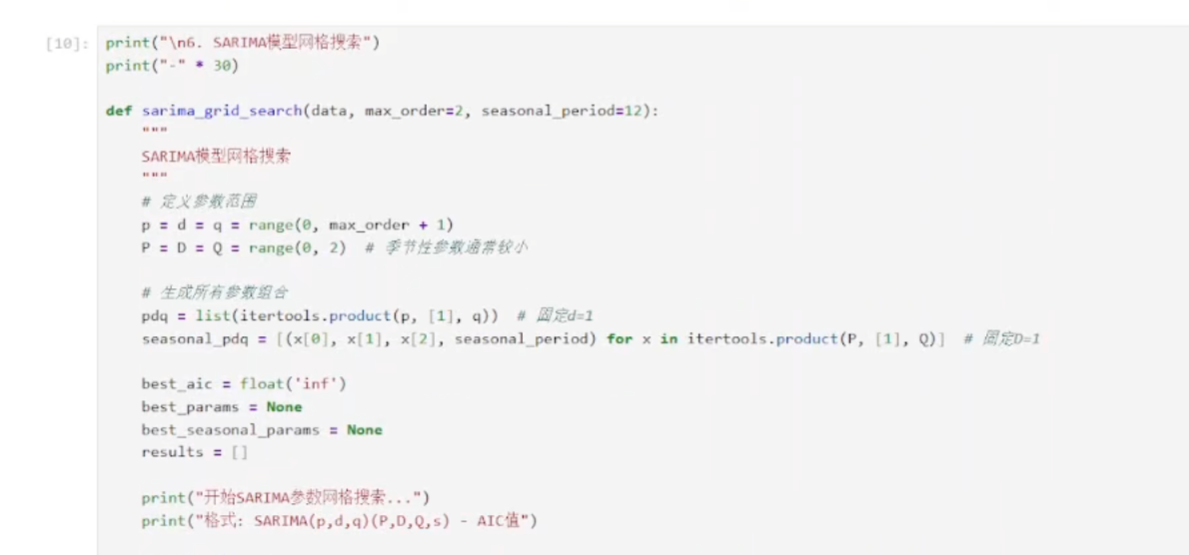
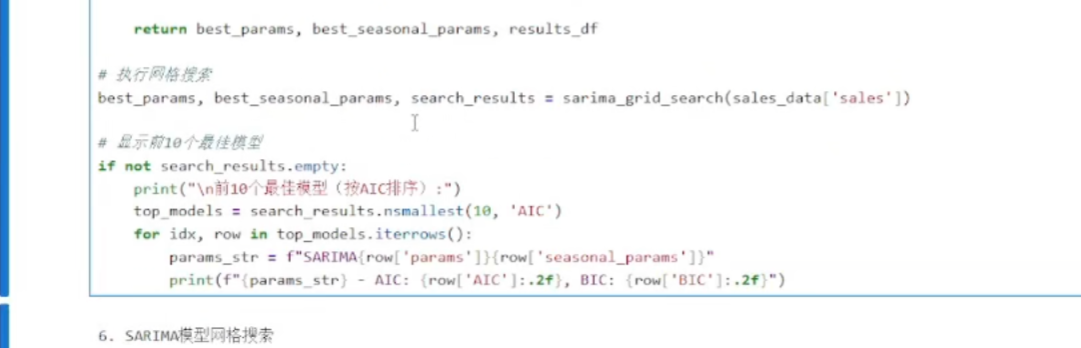
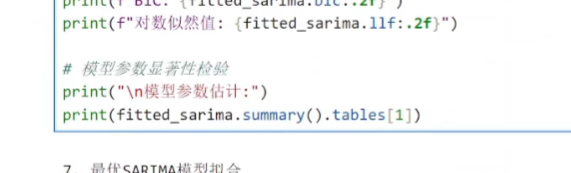
4

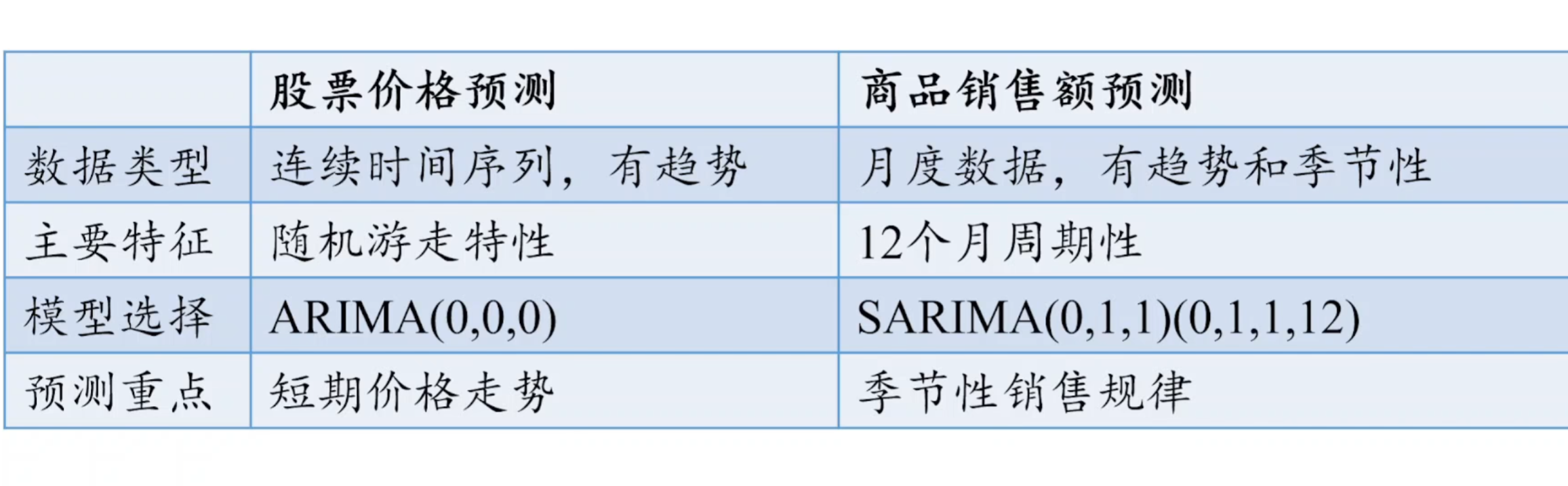
适合单变量问题

二蒙特卡洛算法-进行估计

1 理解:随机性解决明确性

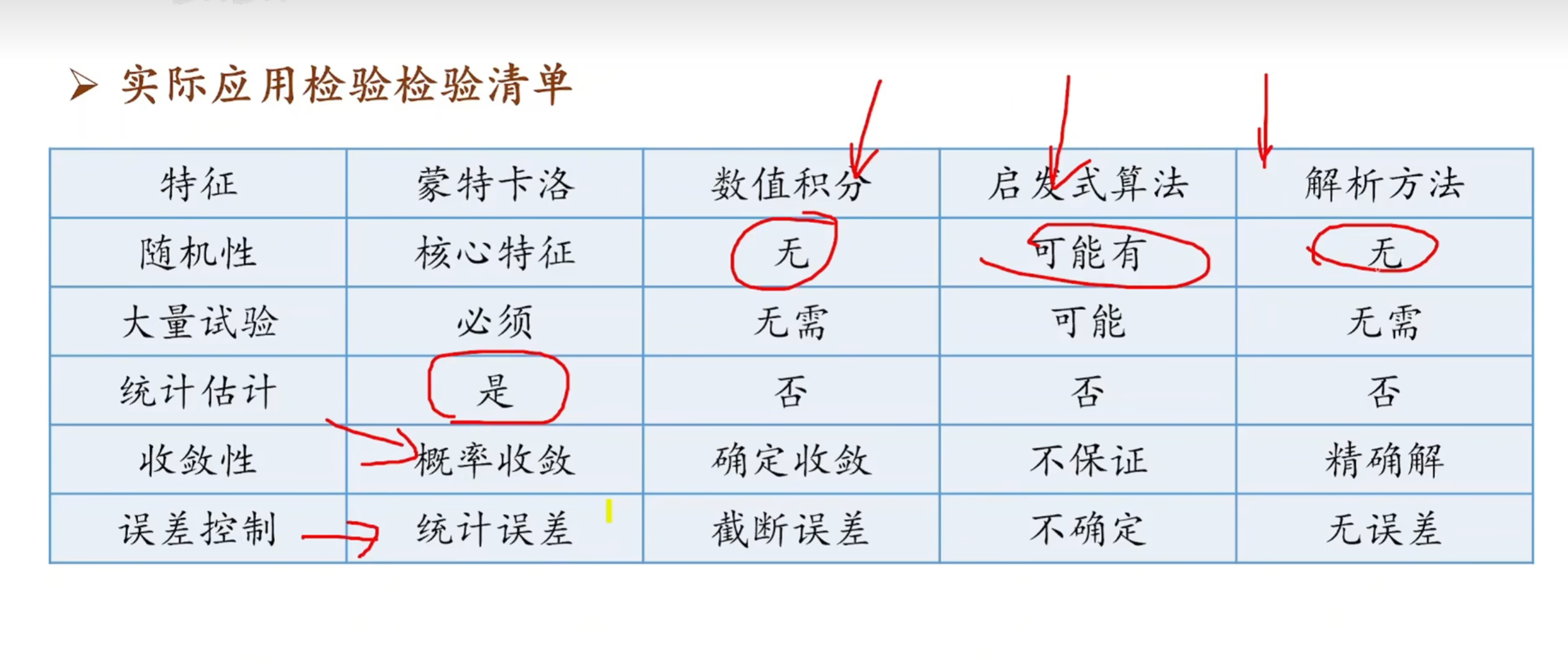
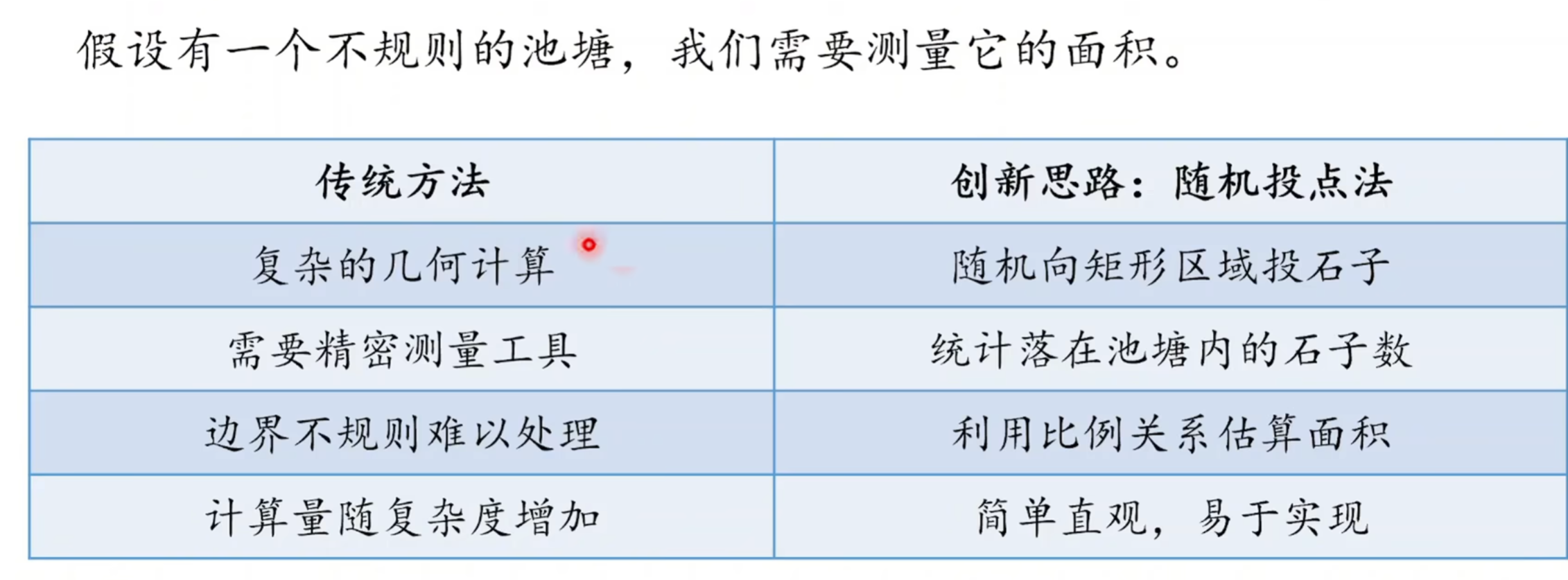
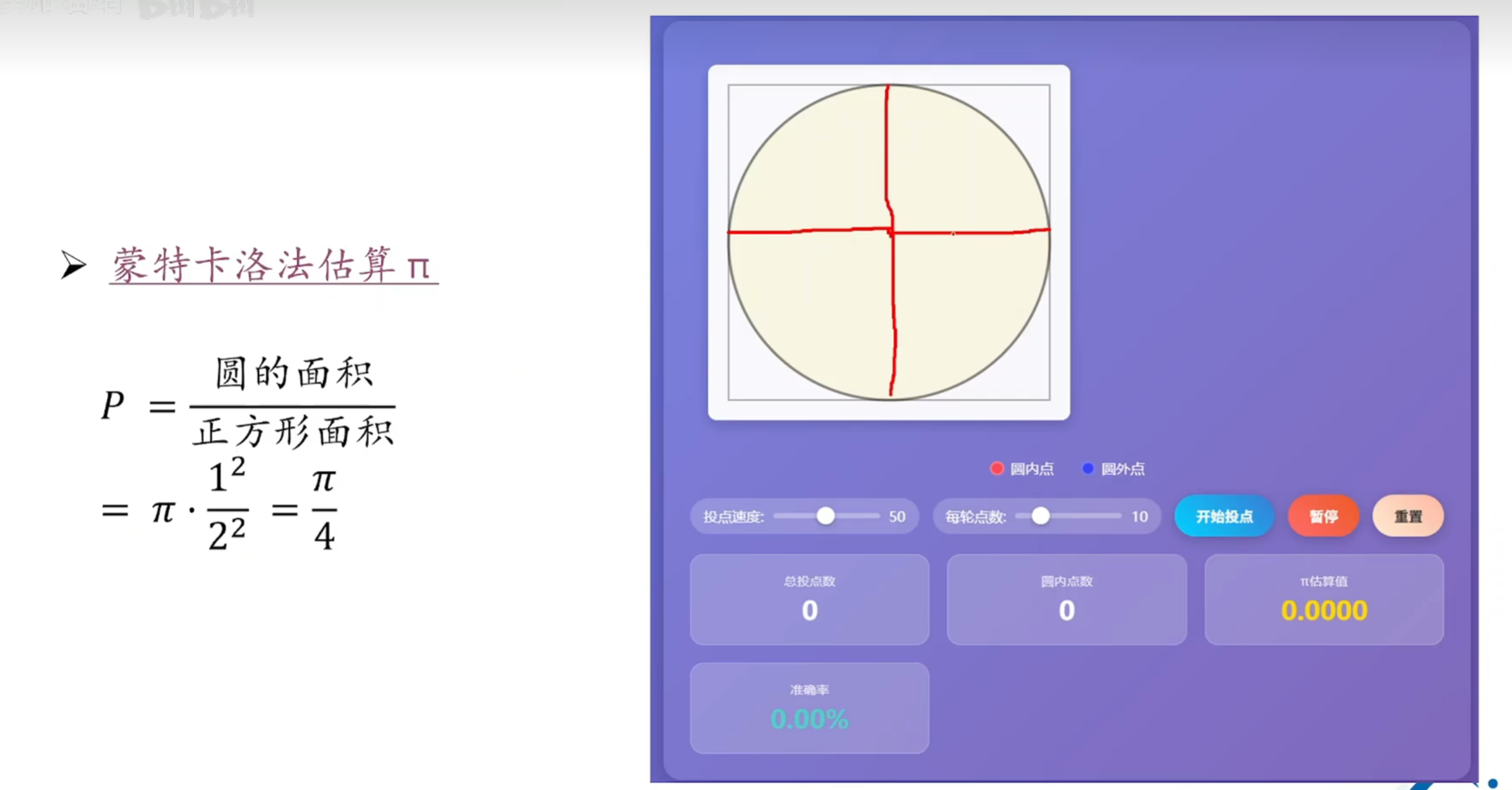
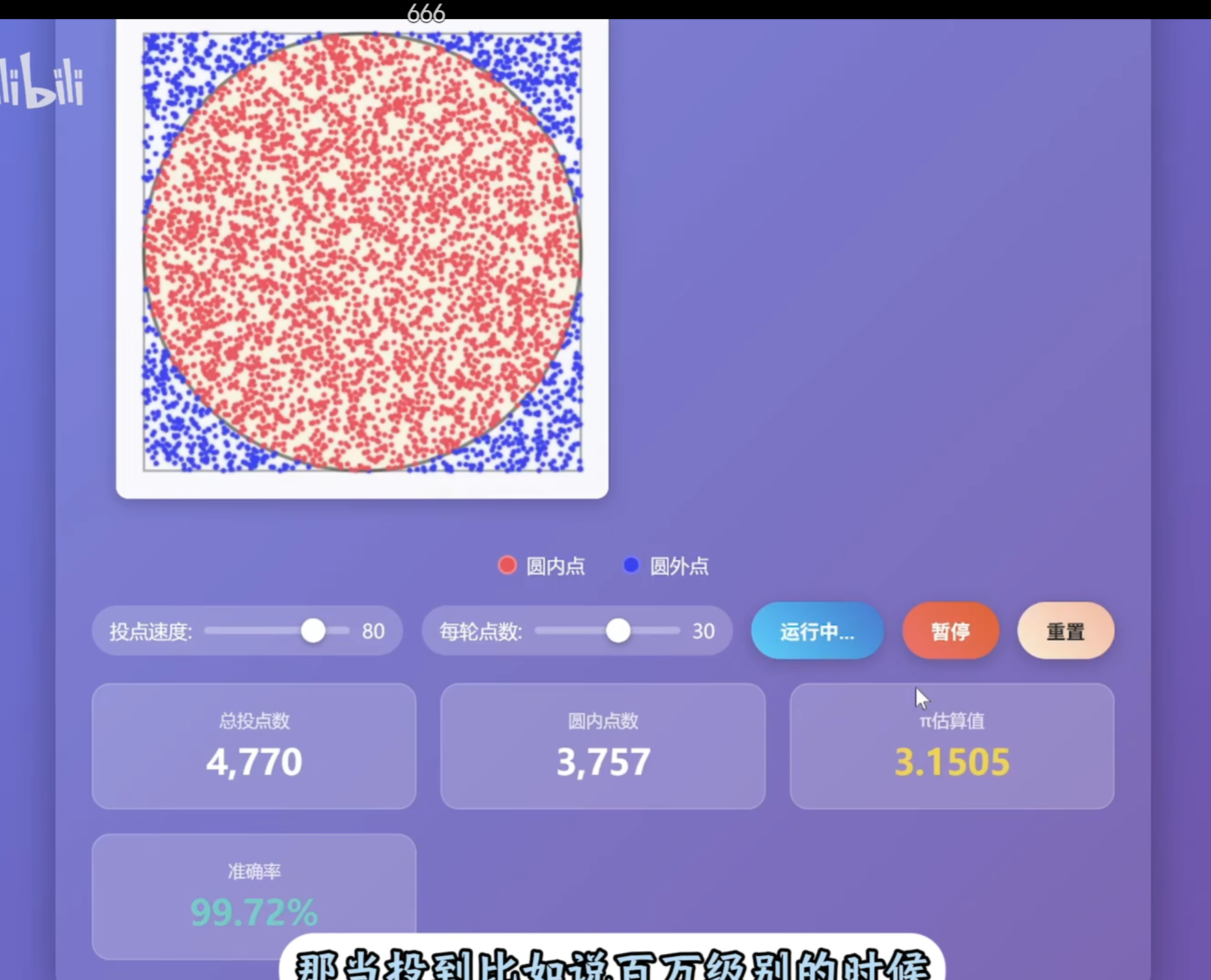
2 基本思想

3 python代码

（1）计算Π

python 复制代码

plt.rcParams['font.sans-serif'] = ['SimHei', 'Arial Unicode MS', 'DejaVu Sans']
设置 matplotlib 绘图时的中文字体，避免图表标签中的中文显示为方框。
指定字体优先级顺序：
SimHei（黑体，Windows 常见）
Arial Unicode MS（Mac 系统常用）
DejaVu Sans（跨平台开源字体）
系统会按顺序尝试使用这些字体渲染中文。
plt.rcParams['axes.unicode_minus'] = False
解决 matplotlib 中负号显示异常的问题。
设为 False后，负号将使用系统默认字体显示（而非特殊符号）。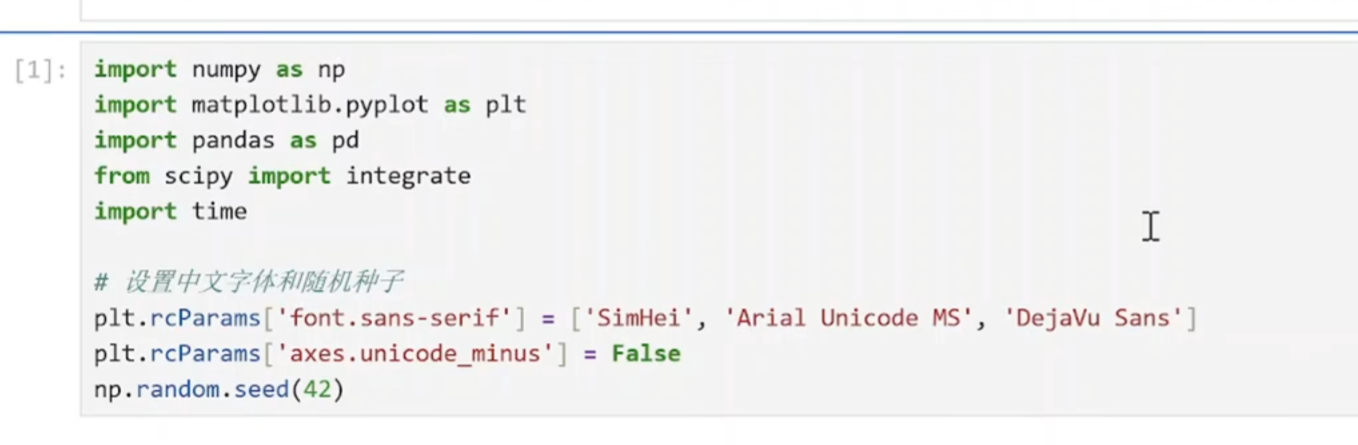

python 复制代码

x = np.random.uniform(-1, 1, n)
y = np.random.uniform(-1, 1, n)
在区间 [-1, 1] 内生成 n个均匀分布的随机坐标，覆盖整个正方形区域。

np.random.uniform()是 NumPy 库中生成均匀分布随机数的函数。
详细解释：
基本语法
np.random.uniform(low, high, size)
low：随机数范围的下界（包含）
high：随机数范围的上界（不包含）
size：输出数组的形状

python 复制代码

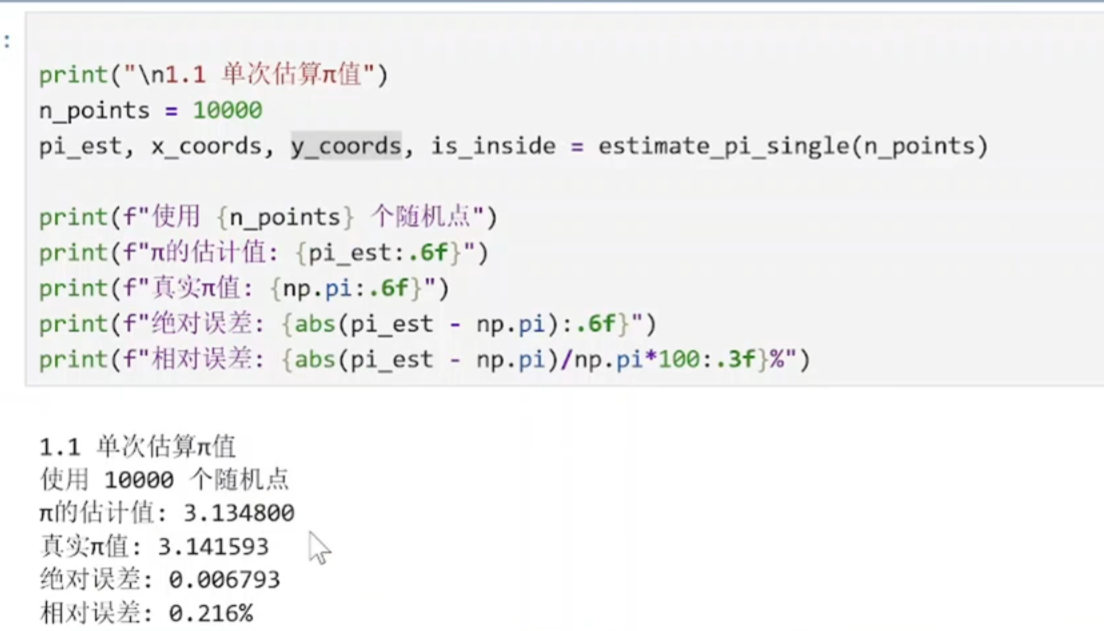
pi_estimate = 4 * np.sum(inside_circle) / n
np.sum(inside_circle)统计圆内点数（True计为 1）。
按公式计算 π 的近似值。

pi_estimate = 4 * np.sum(inside_circle) / n
这里 inside_circle是布尔数组（True/False）：
在 NumPy 中，True被当作 1计算
False被当作 0计算
所以 np.sum(inside_circle)就是统计 True的个数（落在圆内的点数）

python 复制代码

plt.scatter(x_coords[is_inside], y_coords[is_inside], 
            c='red', s=1, alpha=0.6, label='圆内点')
x_coords[is_inside]：筛选出圆内点的x坐标
y_coords[is_inside]：筛选出圆内点的y坐标
c='red'：点颜色设为红色
s=1：点的大小为1像素
alpha=0.6：透明度60%（便于重叠点观察）
label='圆内点'：图例标签

plt.scatter(x_coords[~is_inside], y_coords[~is_inside], 
            c='blue', s=1, alpha=0.6, label='圆外点')
~is_inside：~是逻辑非运算符，选取圆外点 ~对布尔值取反
其他参数类似，颜色设为蓝色

python 复制代码

theta = np.linspace(0, 2*np.pi, 100)
生成从0到2π（完整圆周）的100个等间距角度值
用于参数化绘制圆

plt.plot(np.cos(theta), np.sin(theta), 'k-', linewidth=2, label='单位圆')
np.cos(theta), np.sin(theta)：圆的参数方程 x=cosθ, y=sinθ
'k-'：黑色实线（'k'表示黑色，'-'表示实线）
linewidth=2：线宽2像素
label='单位圆'：图例标签

plt.xlim(-1.1, 1.1)
plt.ylim(-1.1, 1.1)
设置x轴和y轴显示范围为-1.1到1.1
比单位圆的范围（-1到1）稍大，留出边距美观

plt.axis('equal')
设置x轴和y轴的缩放比例相等
确保圆形显示为正圆而非椭圆

lt.grid(True, alpha=0.3)
显示网格线
alpha=0.3：设置网格透明度为30%，使网格不太明显，不干扰数据点
plt.legend()
显示图例，根据label参数自动生成

plt.xlabel('x')
plt.ylabel('y')
设置x轴和y轴标签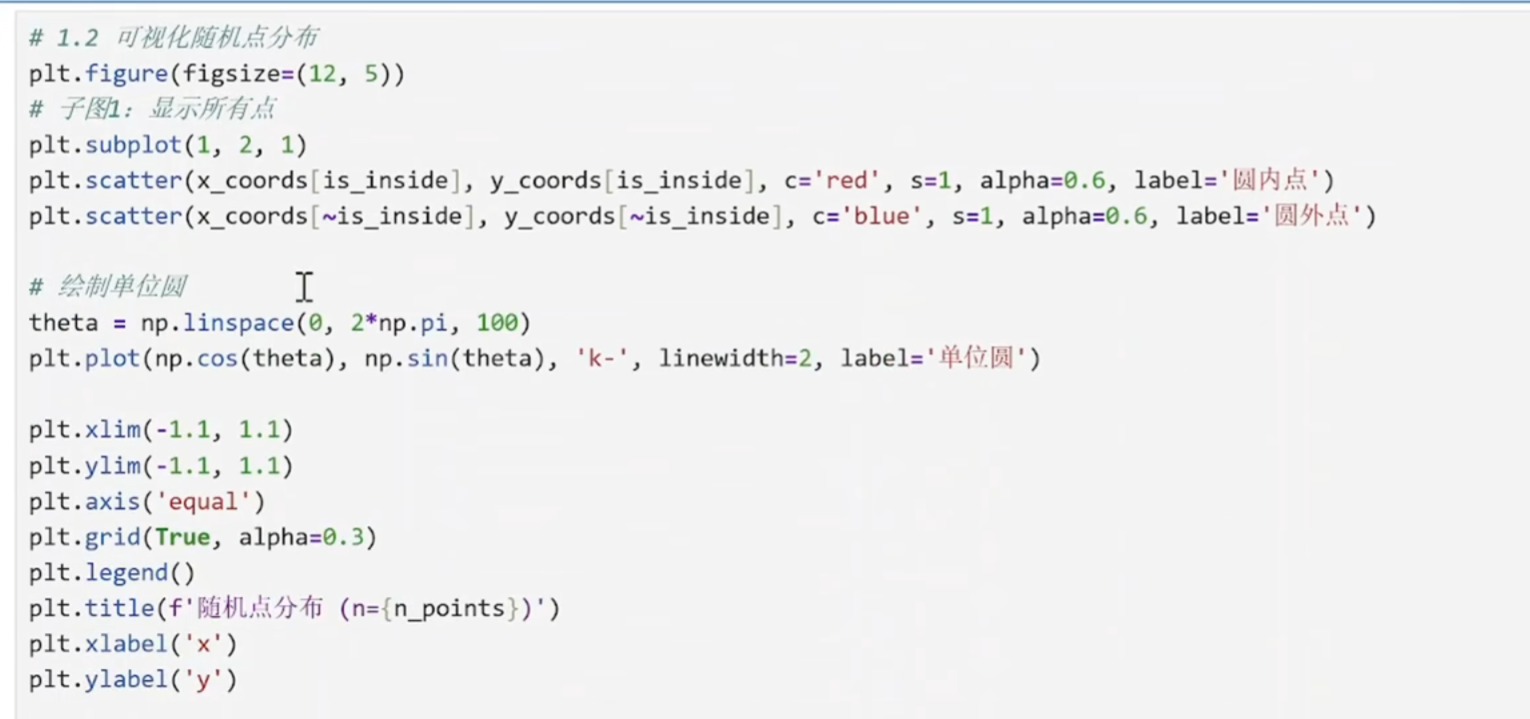

python 复制代码

plt.scatter(x_coords[:n_show][is_inside[:n_show]], 
           y_coords[:n_show][is_inside[:n_show]],
           c='red', s=10, alpha=0.7, label='圆内点')
x_coords[:n_show]：只取前1000个x坐标
is_inside[:n_show]：只取前1000个布尔值
s=10：点的大小设为10像素（比第一个子图的s=1大10倍）
alpha=0.7：透明度70%（比第一个子图更不透明）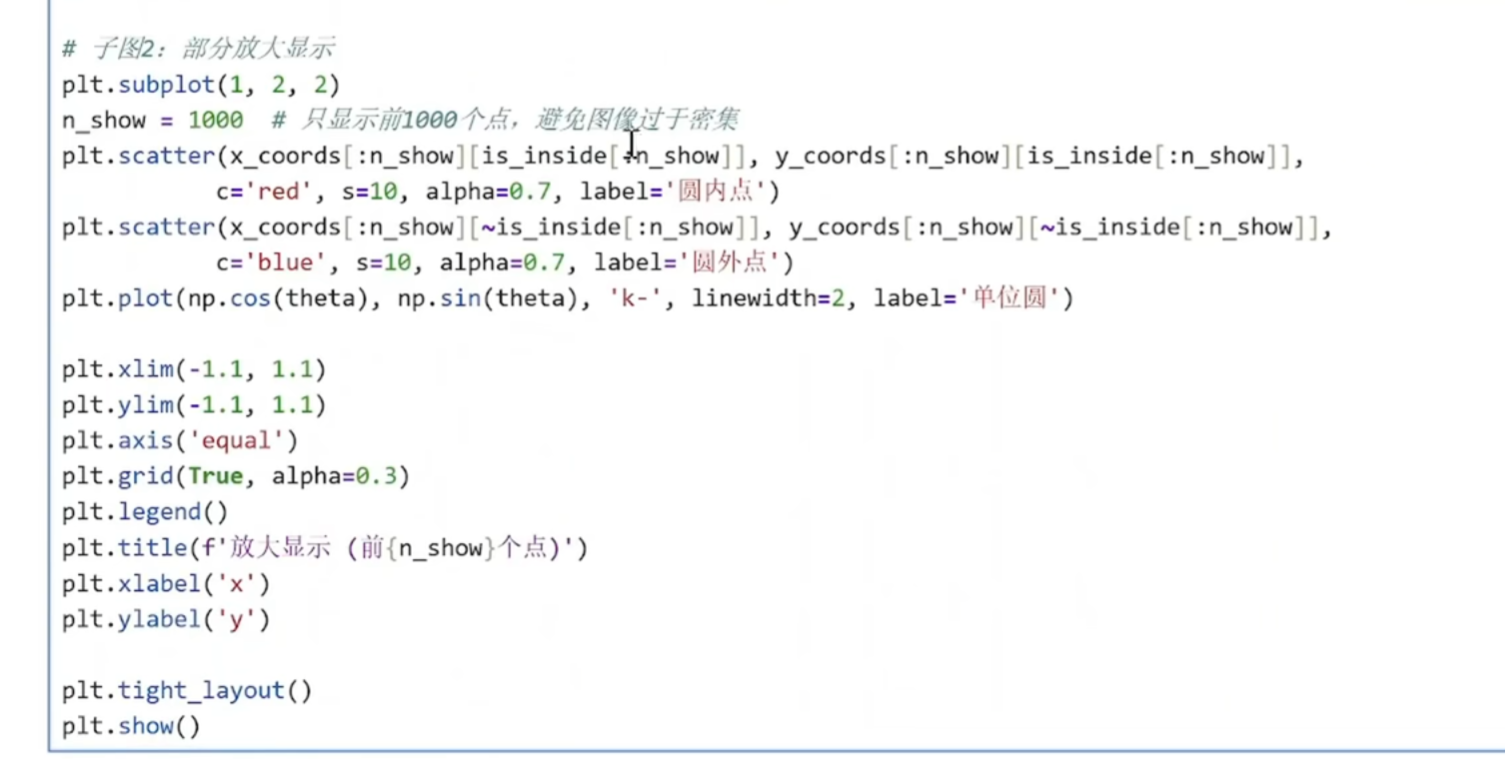

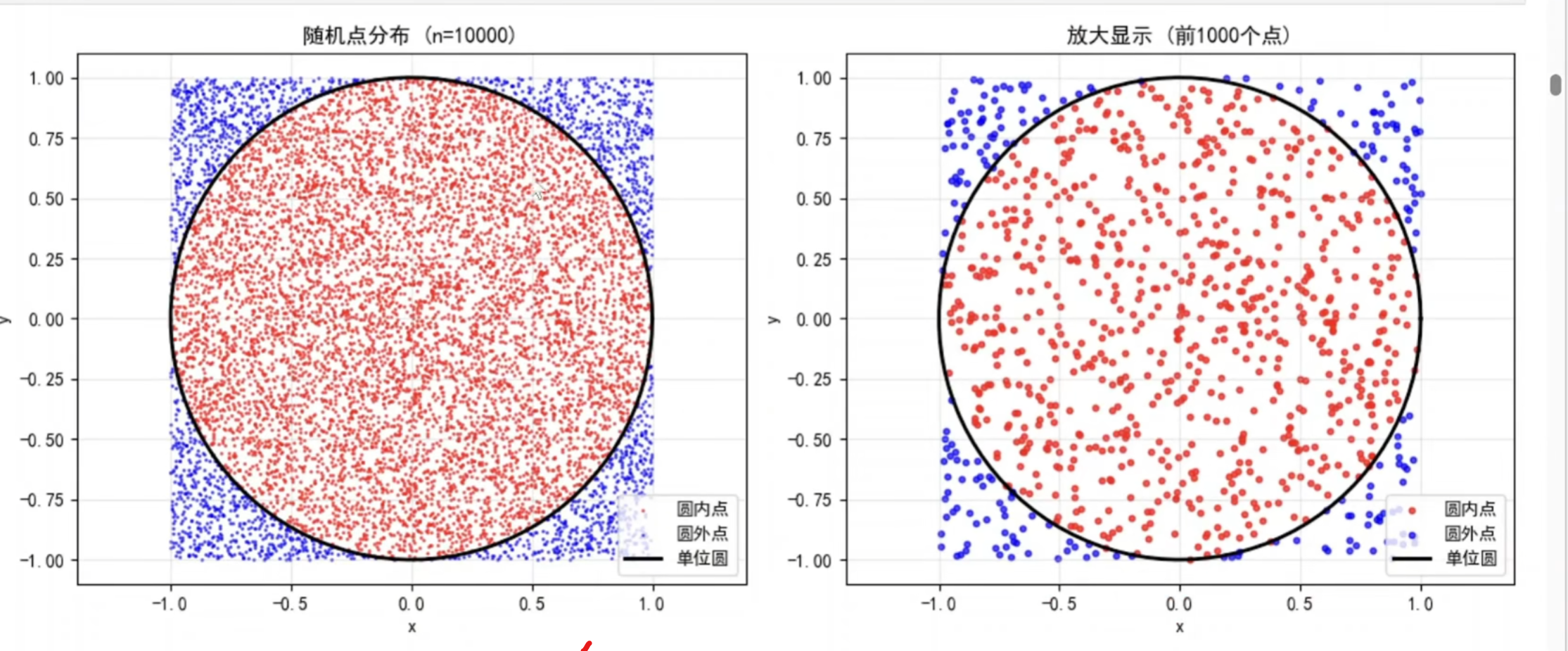
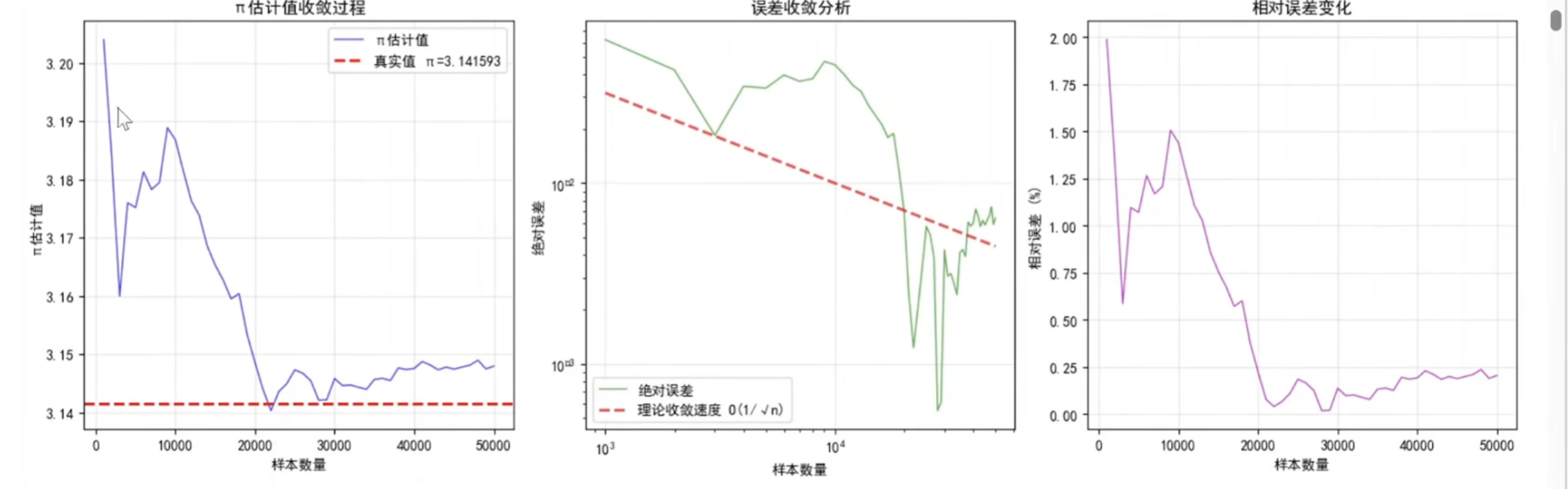
收敛分析

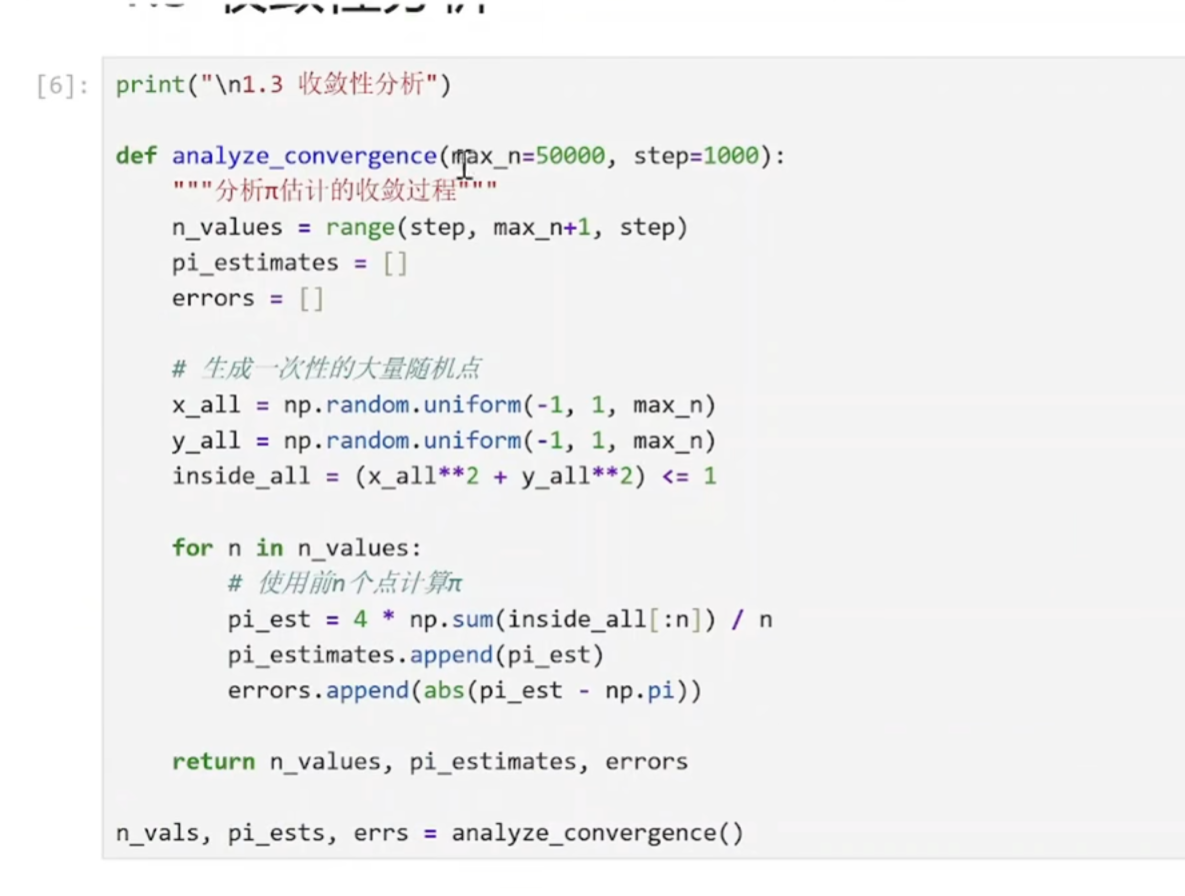
python 复制代码

红色虚线：理论收敛速度 1/√n

python 复制代码

相对误差(%) = (|π_est - π| / π) × 100%
例如：误差0.01对应相对误差约0.318%
误差0.001对应相对误差约0.0318%
实用意义
更直观的精度表示（百分比）
工程上常用指标
回答"估计值偏差了百分之几？"

'g'
代表 绿色（Green）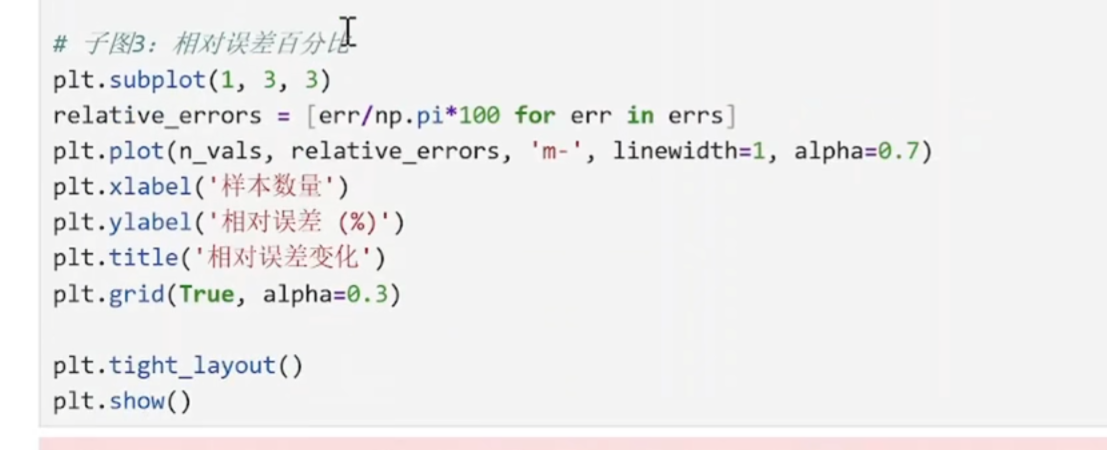

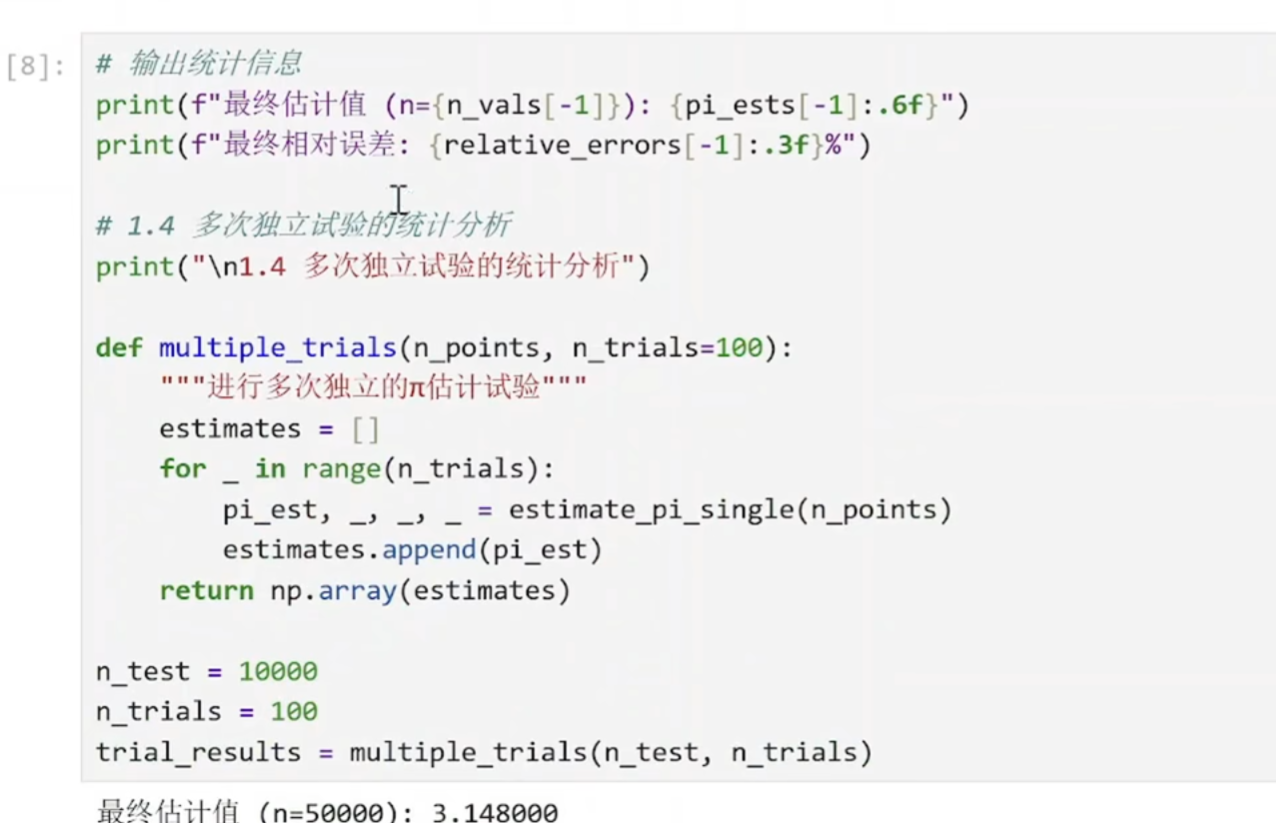
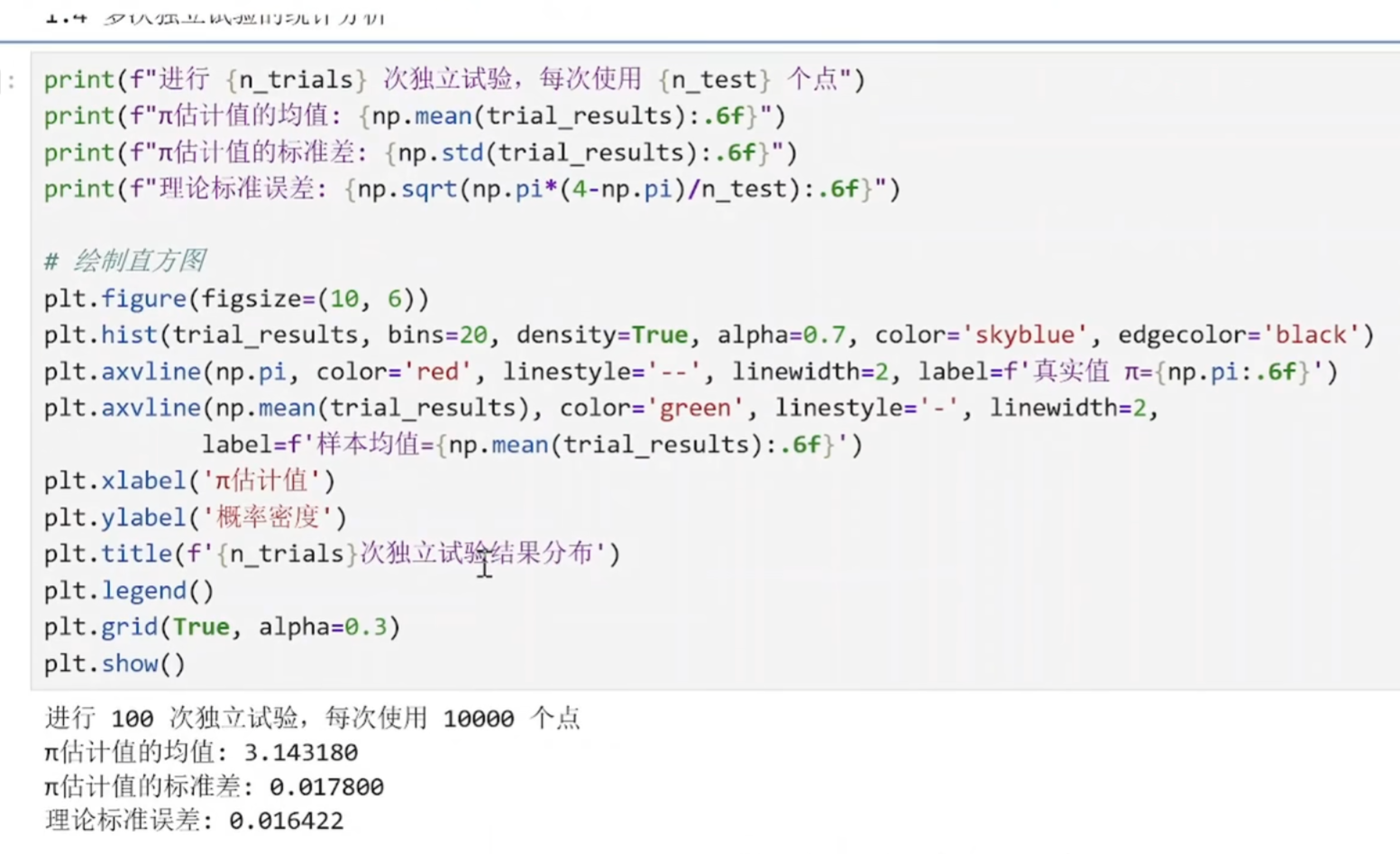
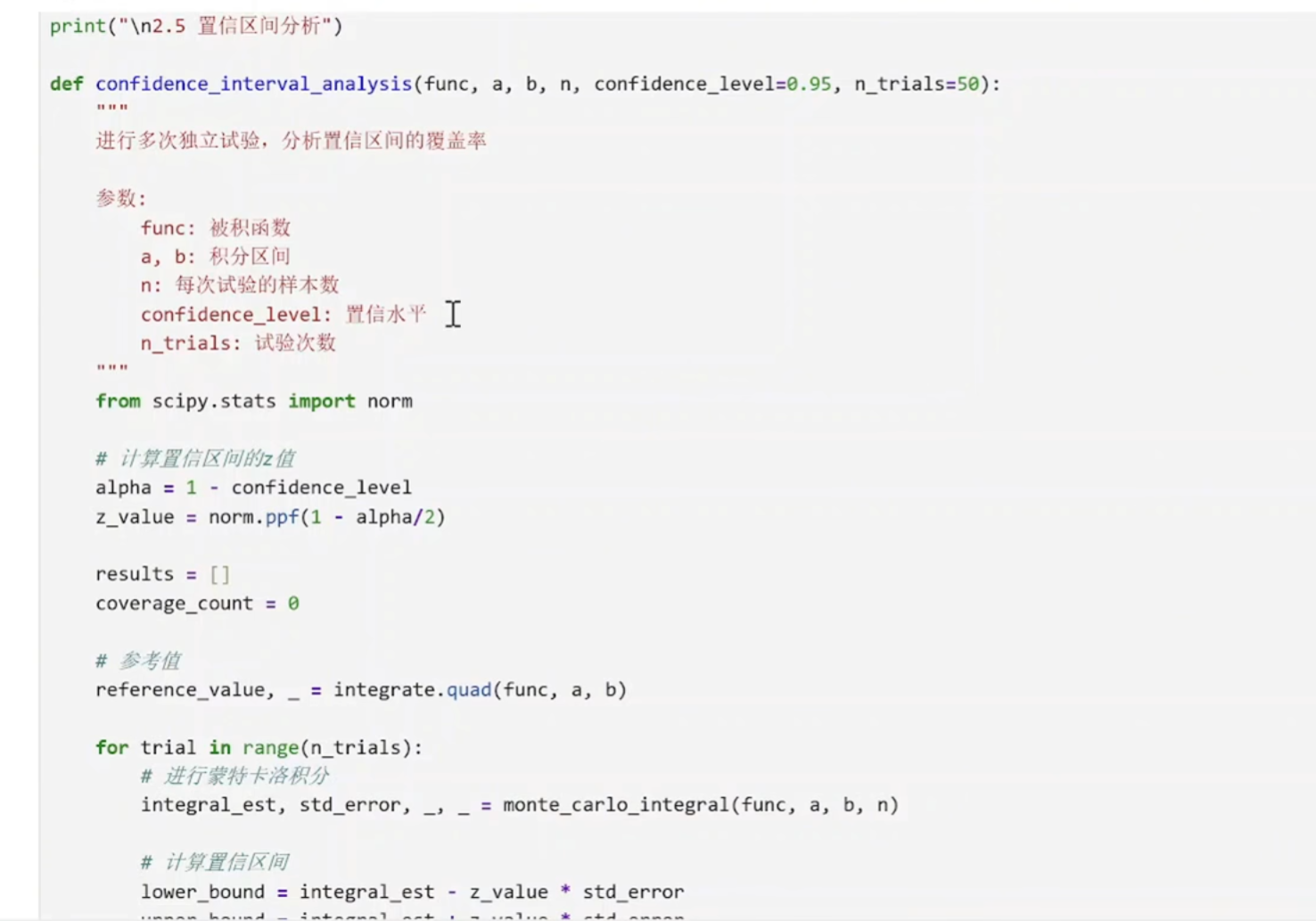
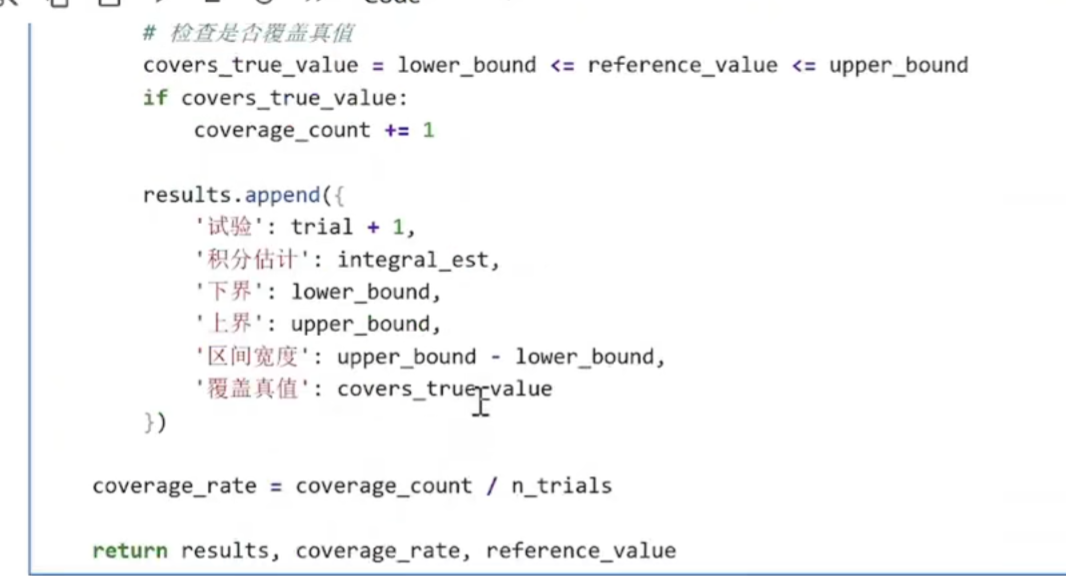
进行多次独立估计

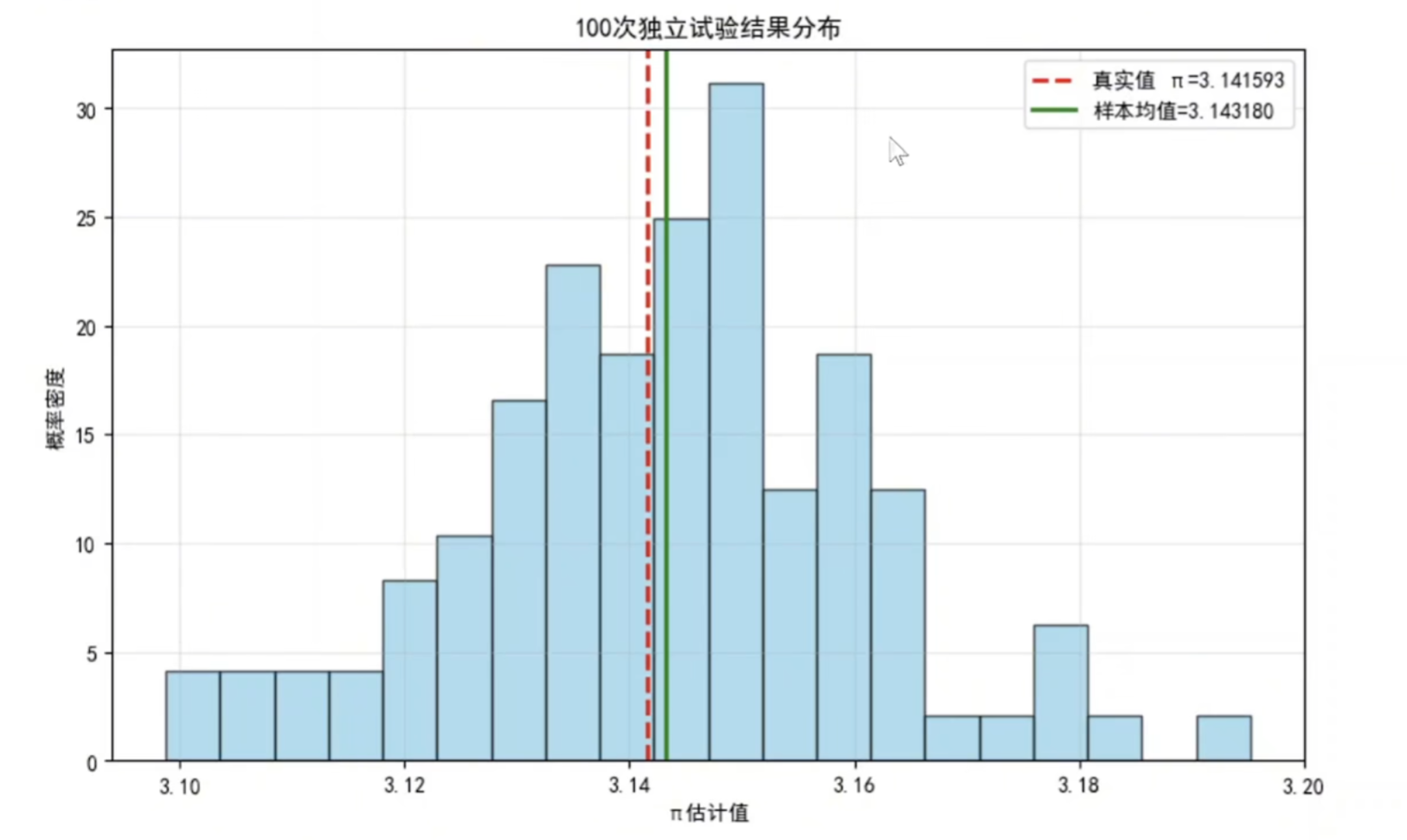
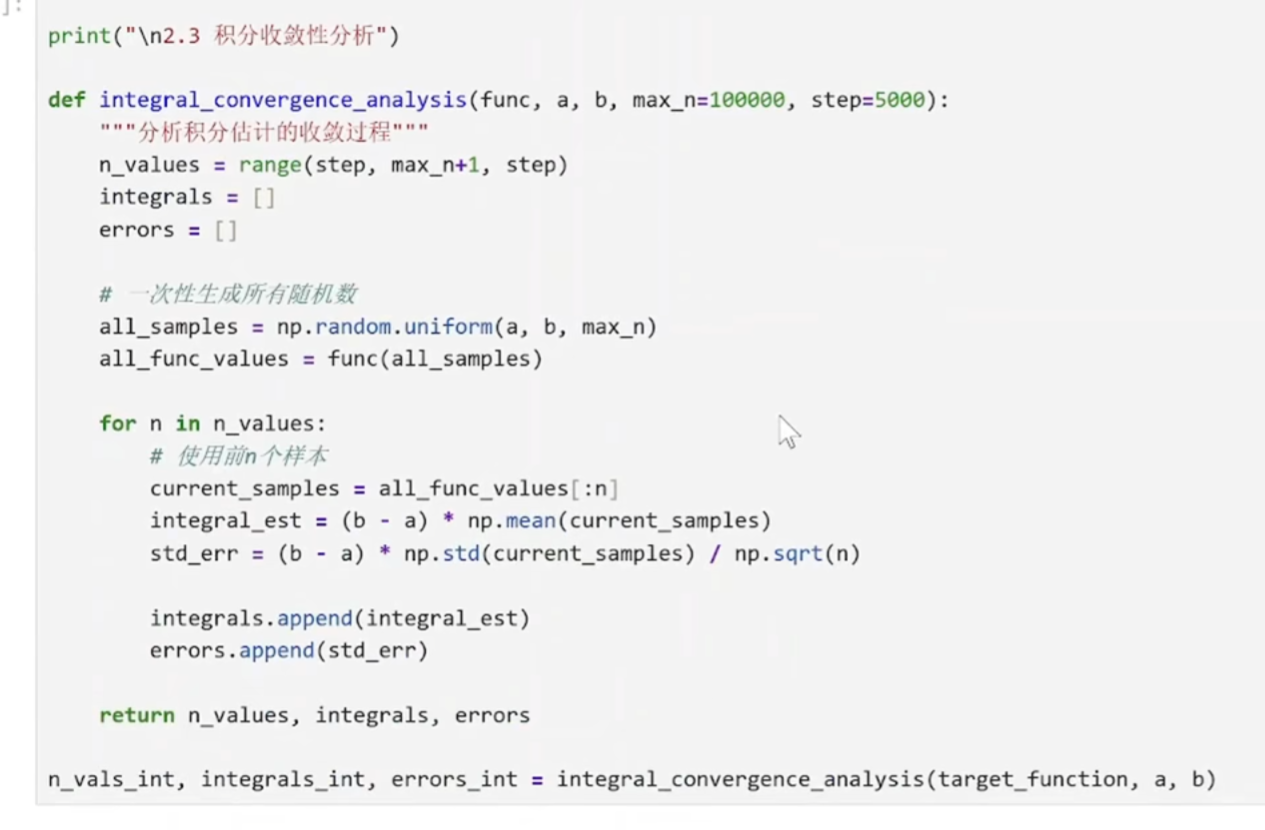
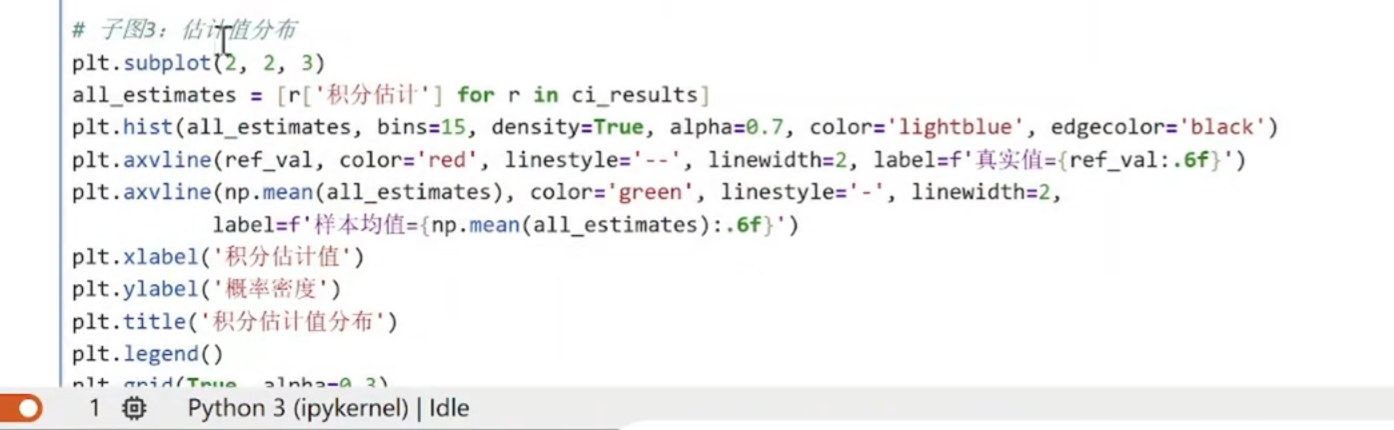
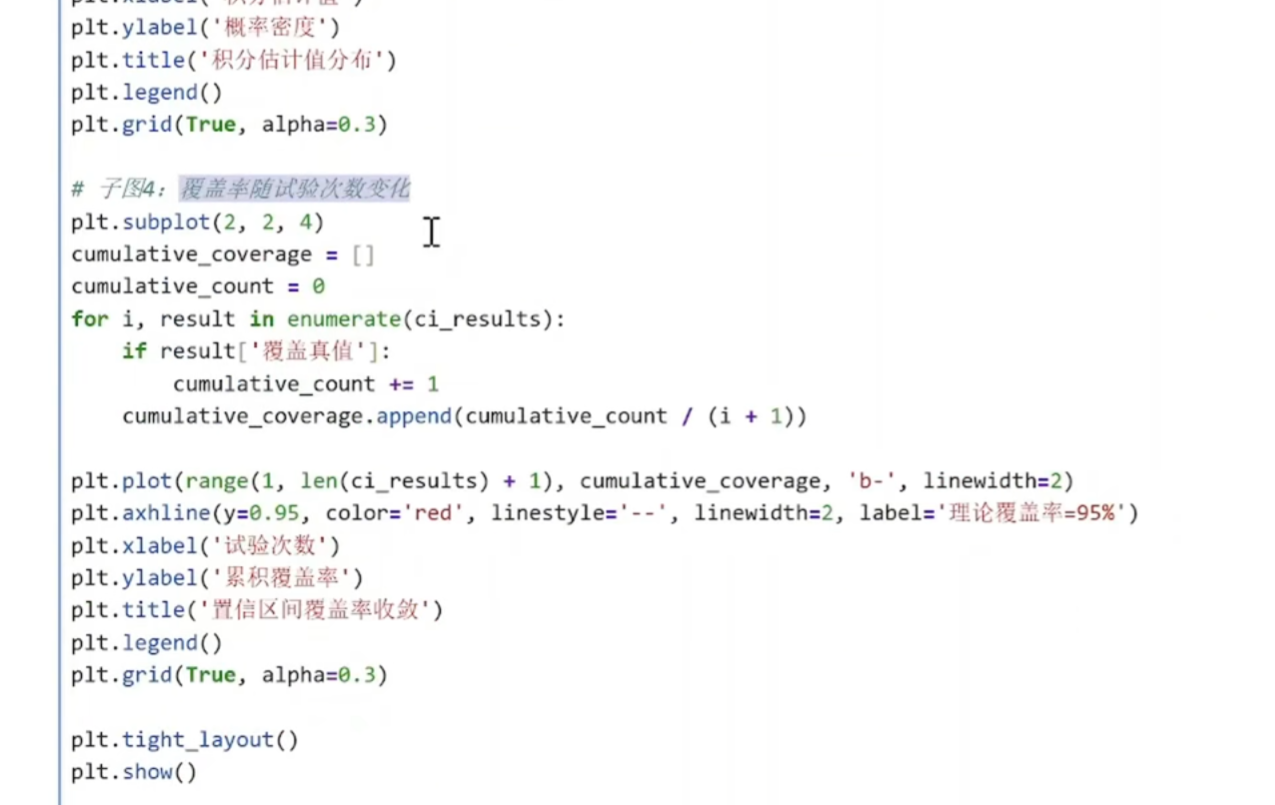
（2）复杂函数的定积分运算

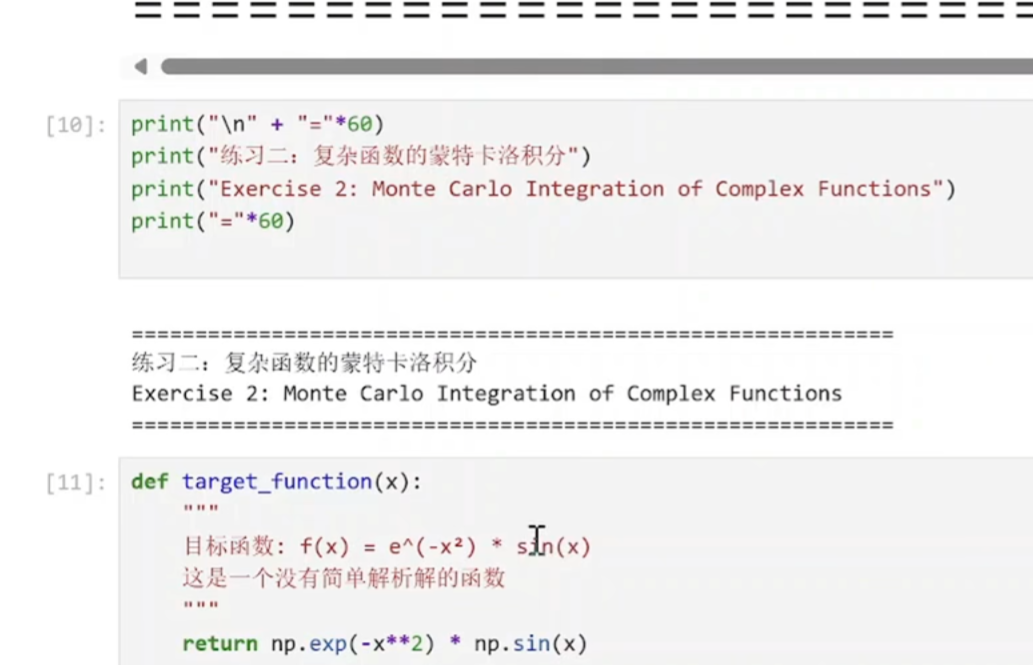
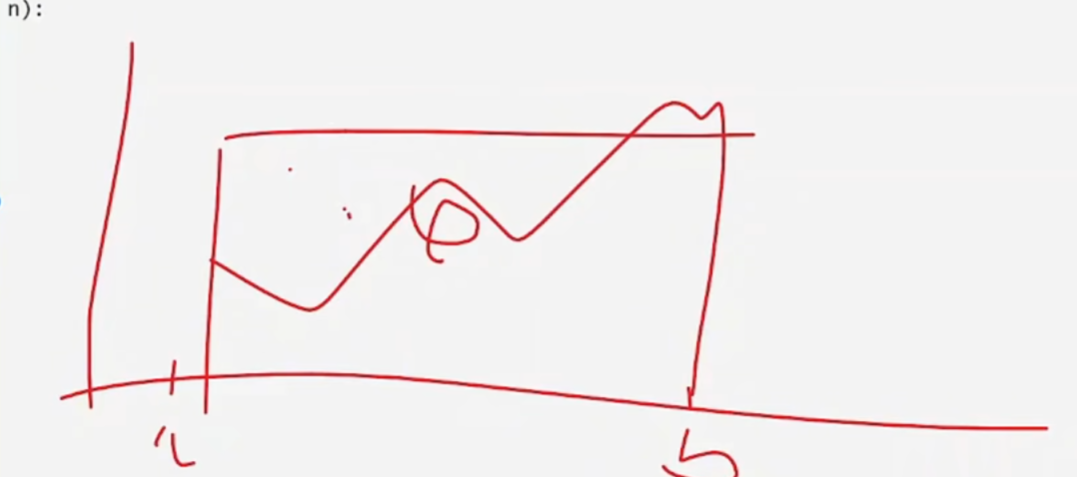
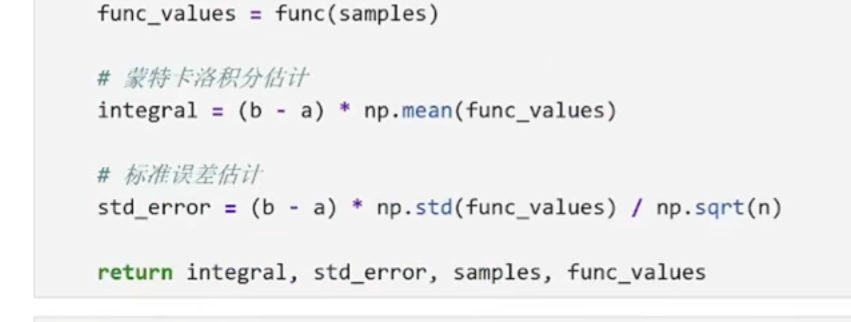
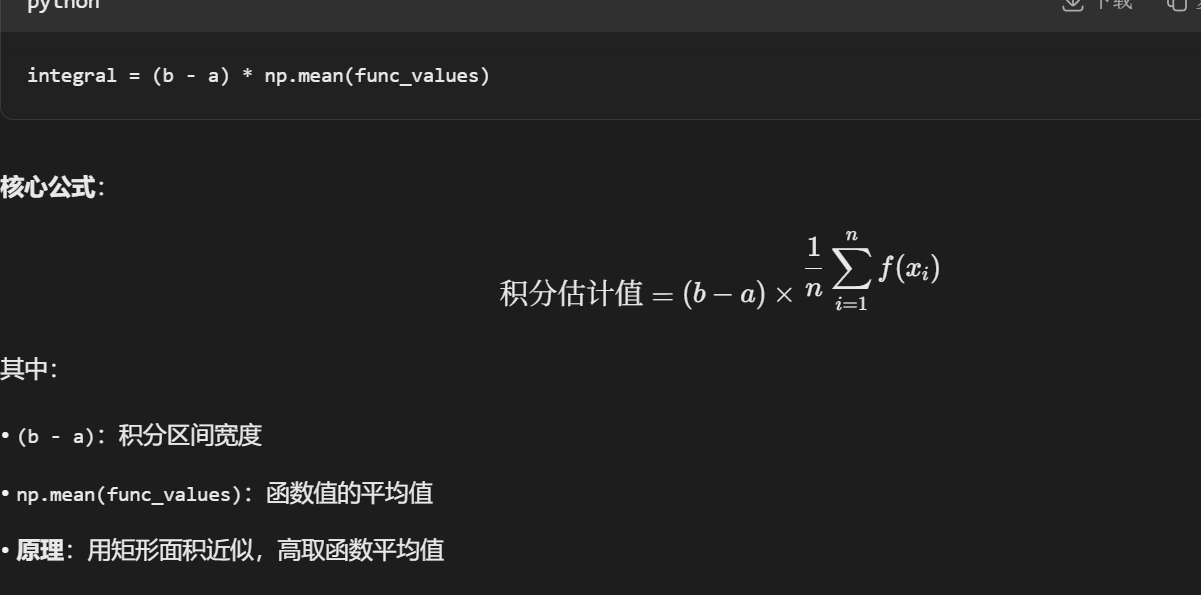
python 复制代码

采样点：np.linspace(0, 2, 1000)在区间[0,2]上均匀生成1000个点，确保绘图光滑
函数计算：target_function(x_plot)计算每个采样点的函数值

plt.fill_between(x_plot, 0, y_plot, alpha=0.3, color='lightblue')
关键填充操作：填充函数曲线与x轴之间的区域
参数说明：
x_plot：x坐标范围
0：填充的下边界（x轴）
y_plot：填充的上边界（函数值）
alpha=0.3：30%透明度，使填充区域半透明
color='lightblue'：浅蓝色填充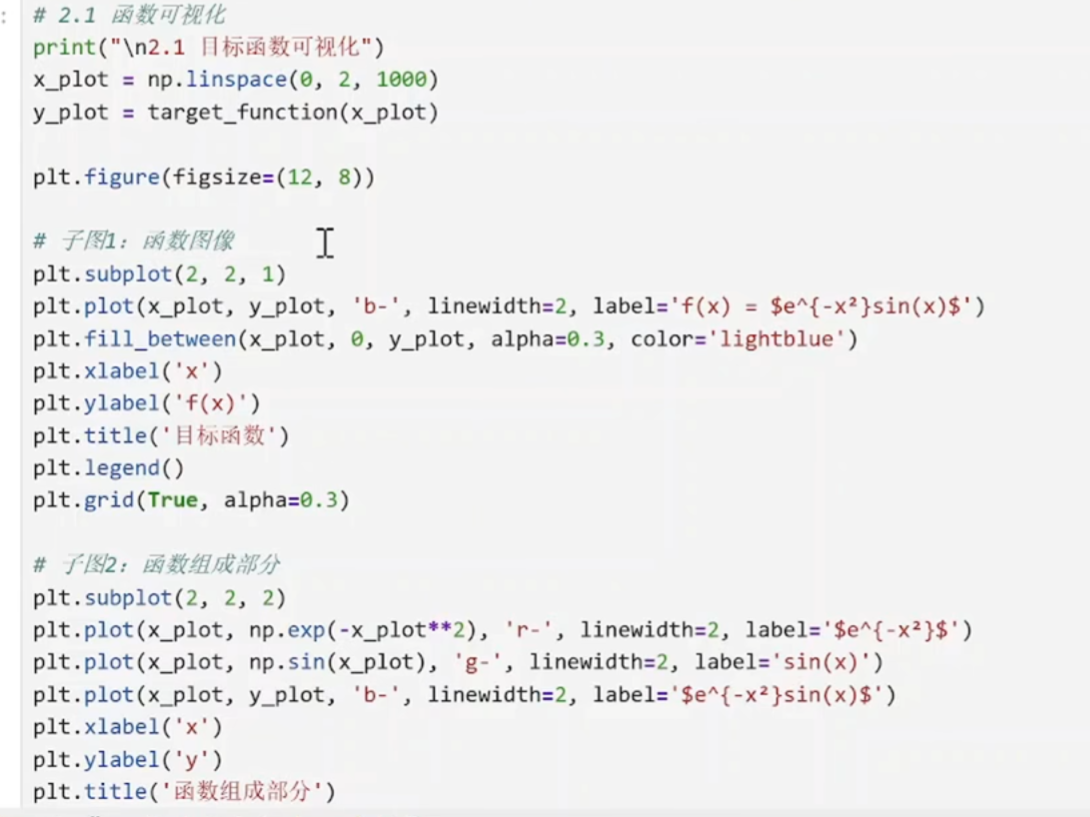

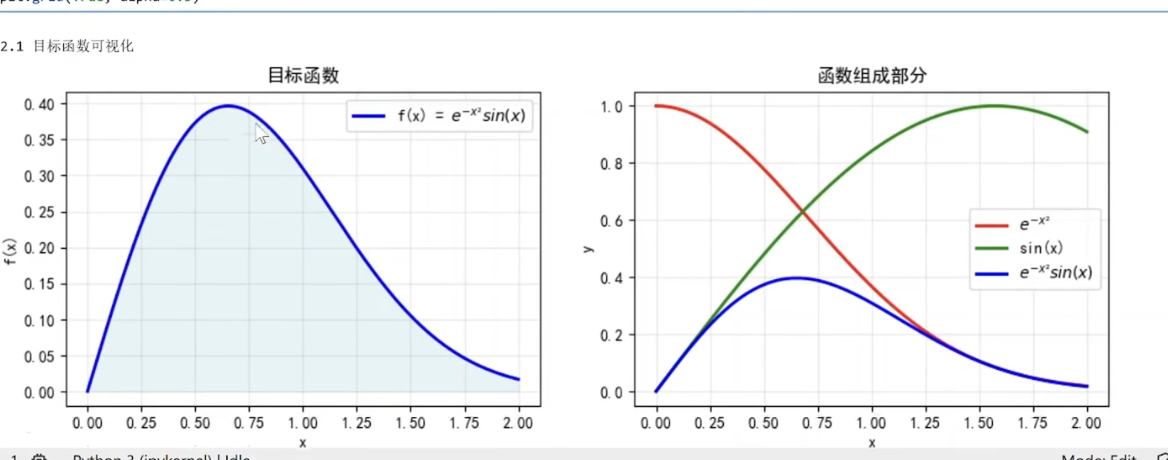
python 复制代码

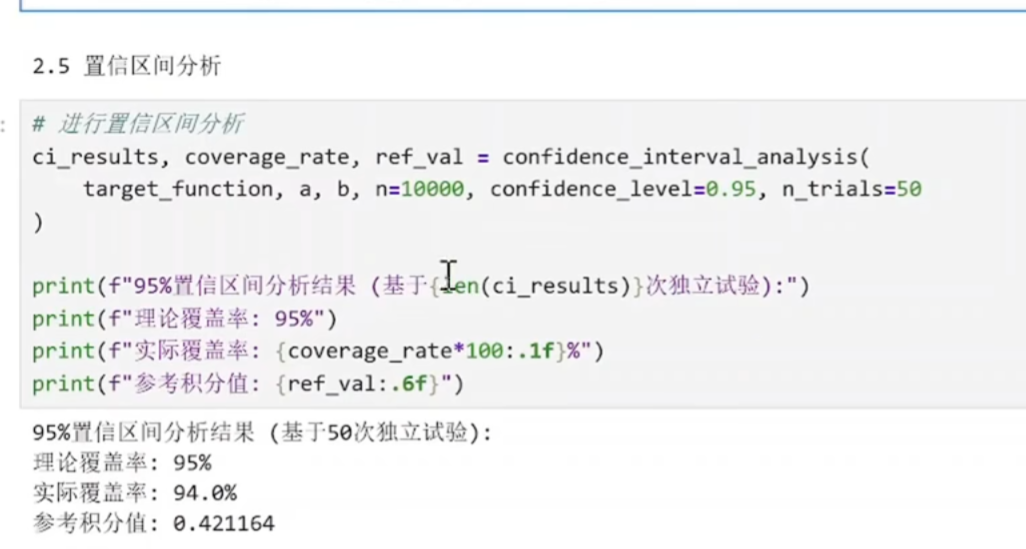
integral_scipy, _ = integrate.quad(target_function, a, b)
使用 SciPy 的 quad函数进行高精度数值积分：
quad使用自适应算法，精度非常高（默认相对误差约1e-8）
结果作为"真实值"参考，用于评估蒙特卡洛方法的精度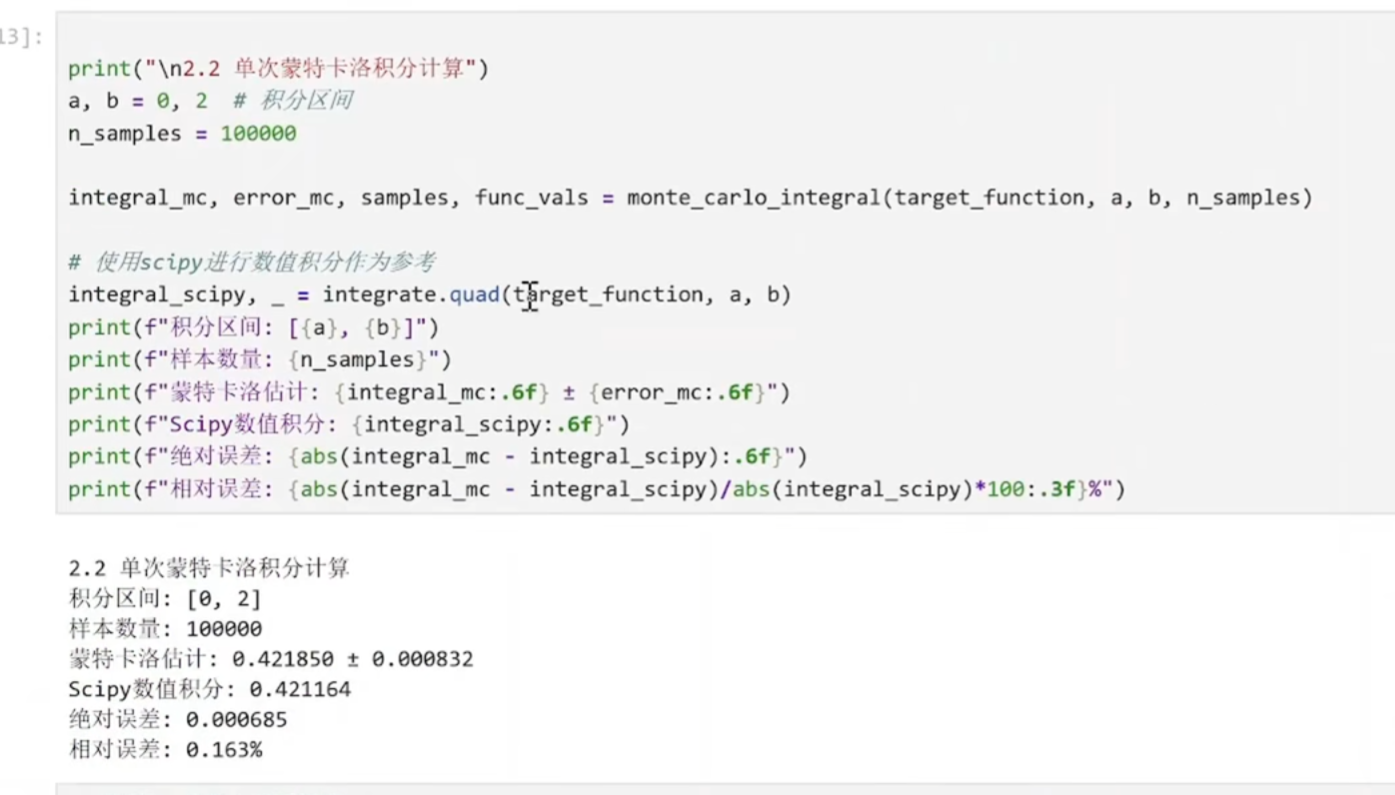

python 复制代码

func_vals = [0.12, 0.35, 0.08, 0.42, 0.21, ...]  # 共100,000个
这些是函数值，不是积分值！
直方图如何工作：
plt.hist(func_vals, bins=30)
找出 func_vals的最小值和最大值（比如 0.001 到 0.42）
将这个范围分成30个等宽区间（bins）
统计有多少个 func_vals的值落在每个区间里

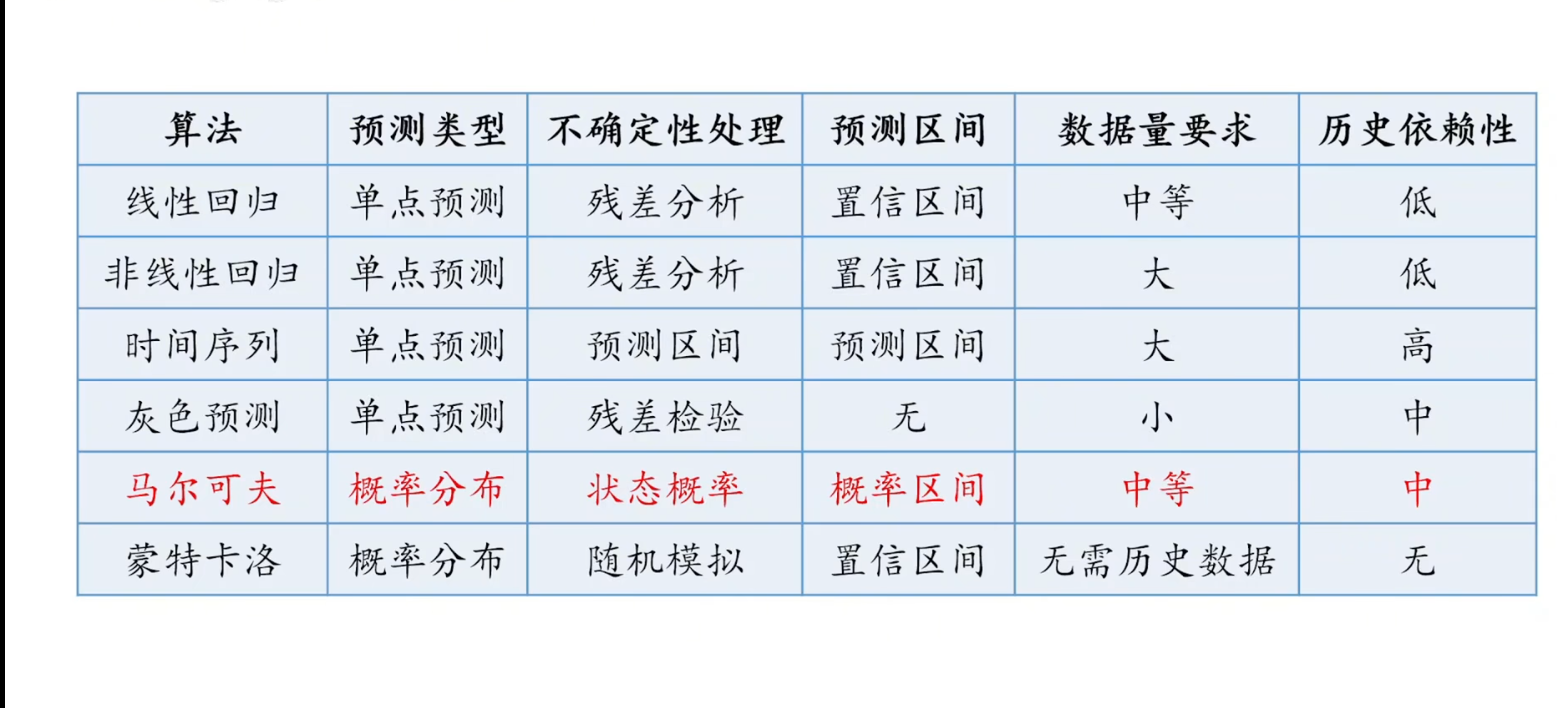
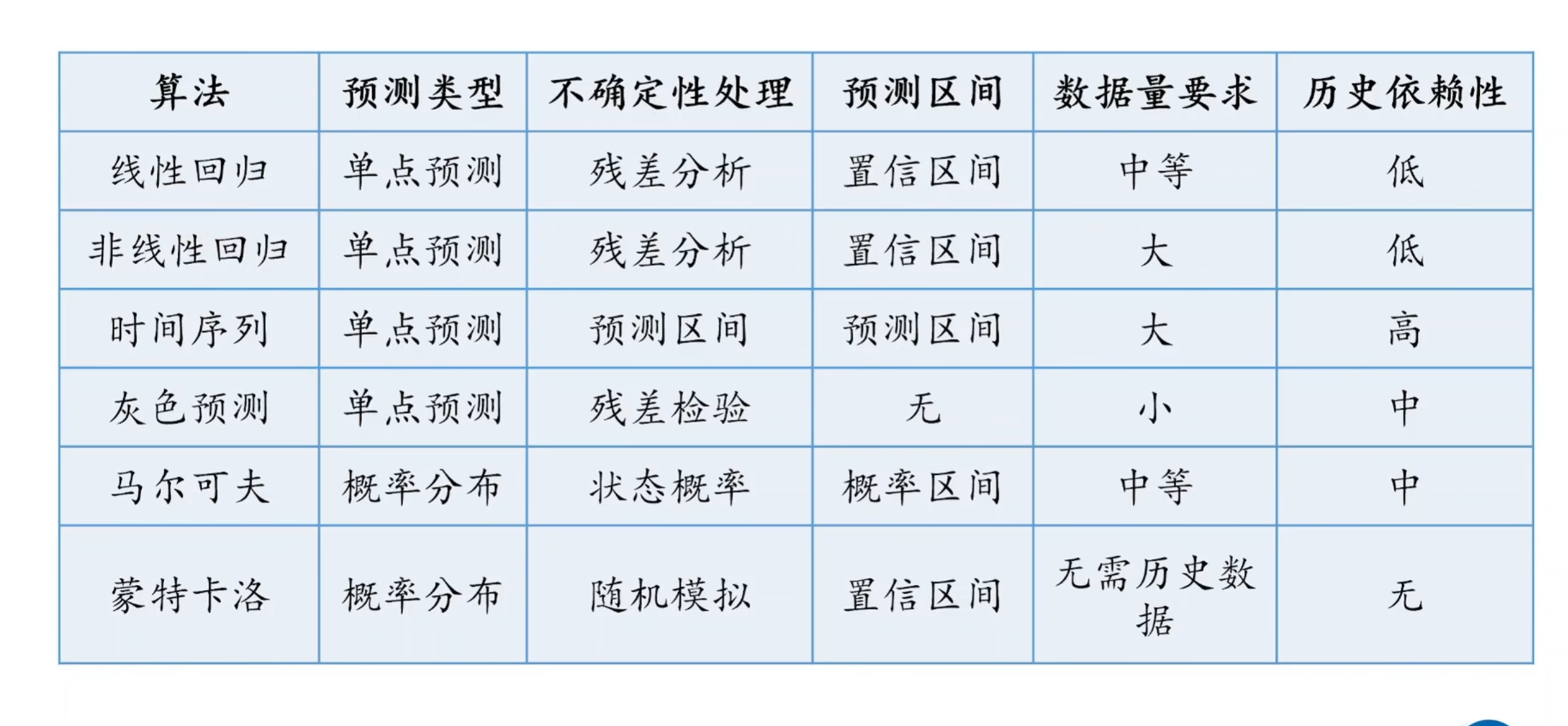
三总结

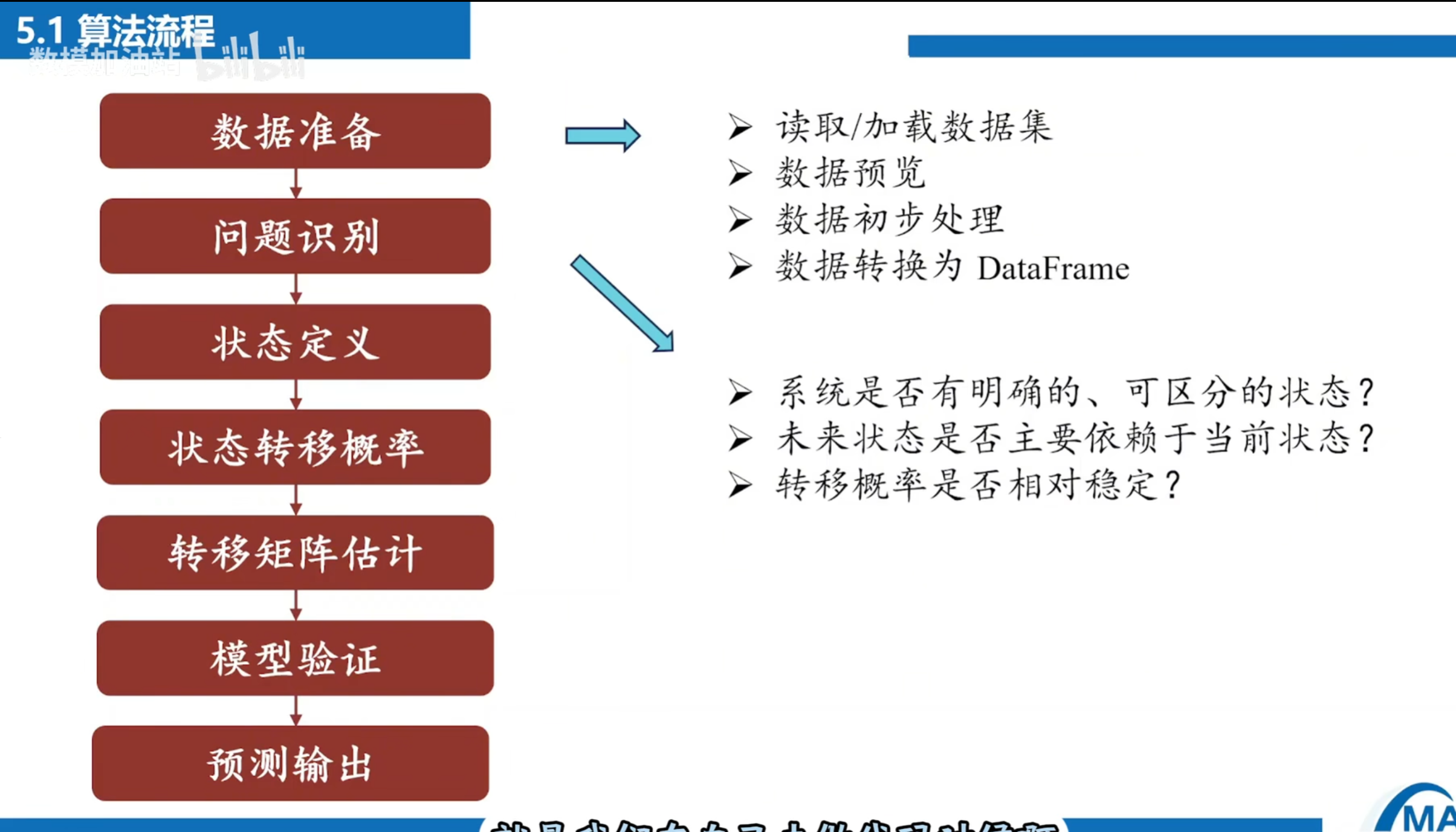
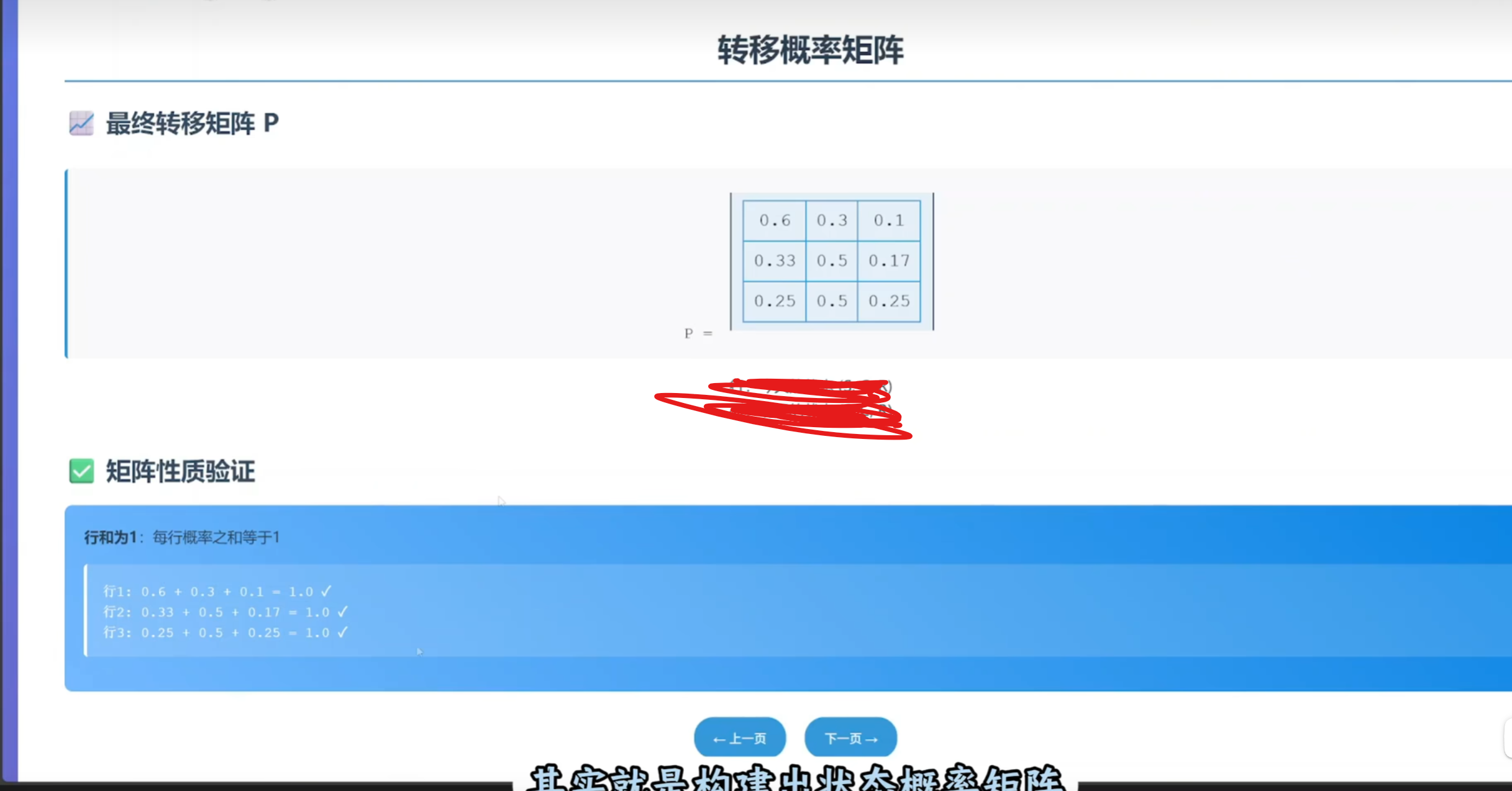
四马尔可夫预测

1 理解：对现在的情况预测未来的情况

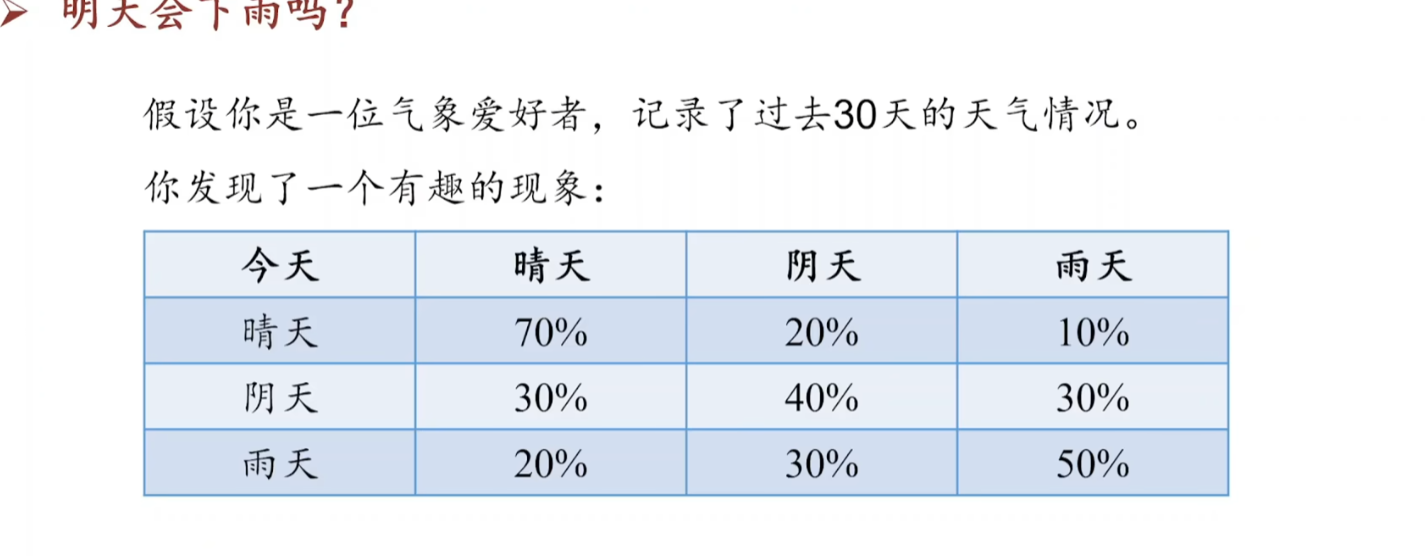
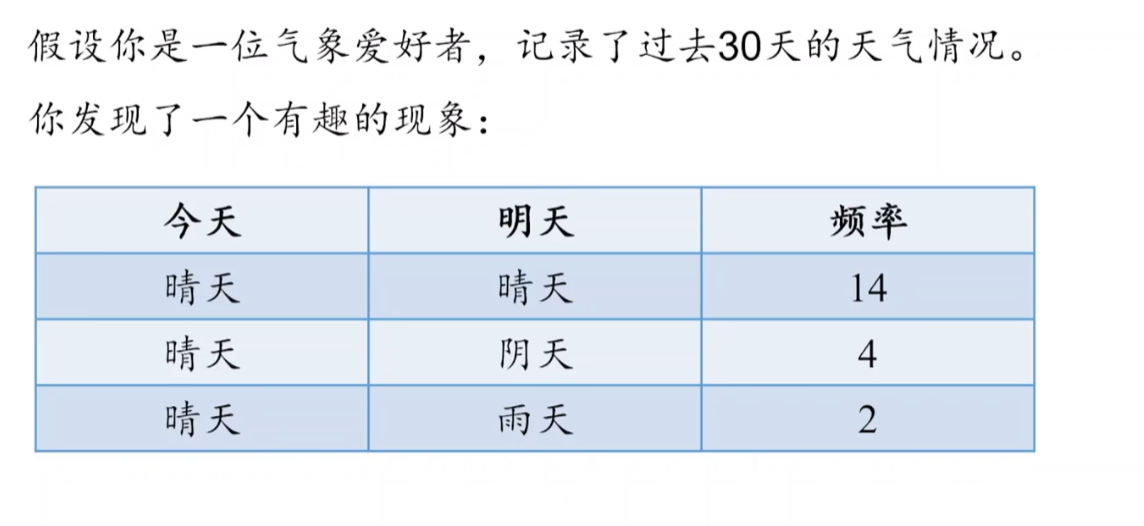
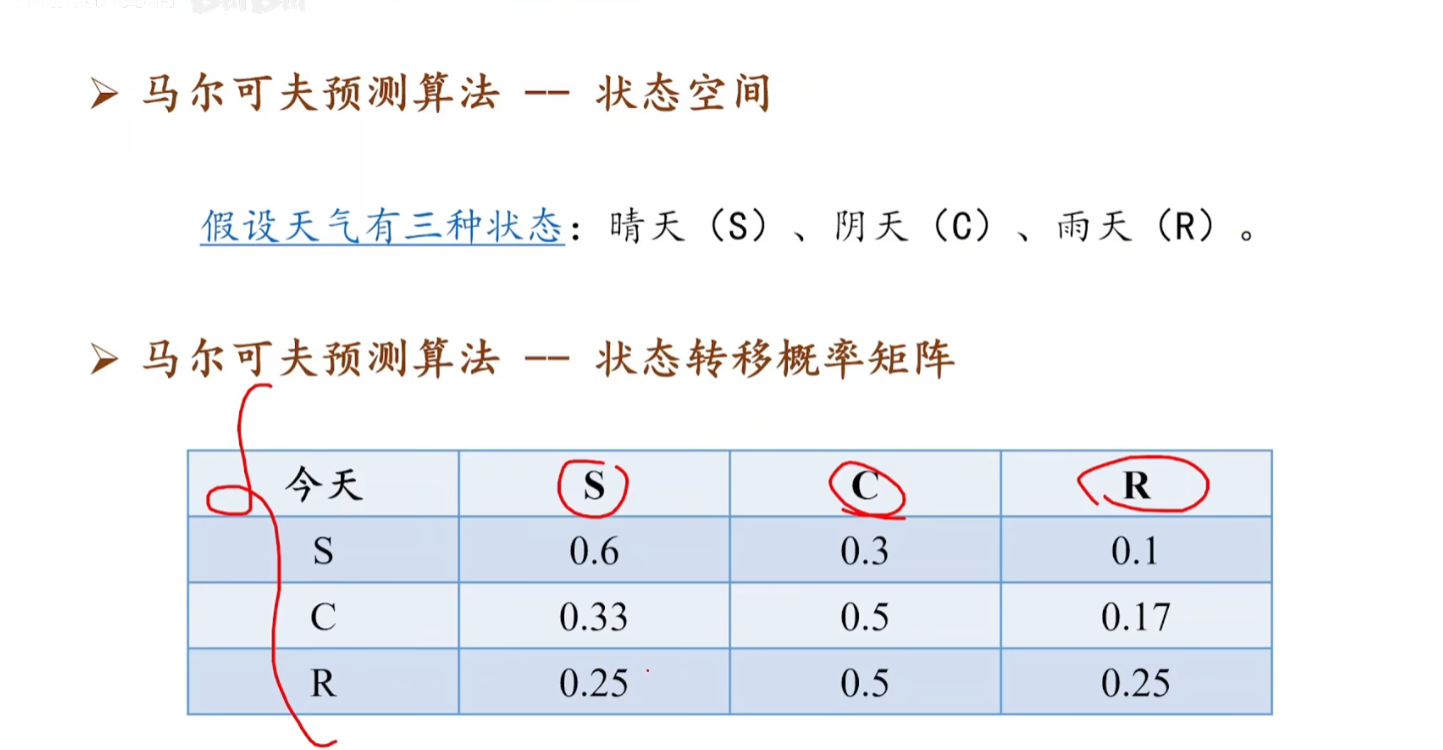
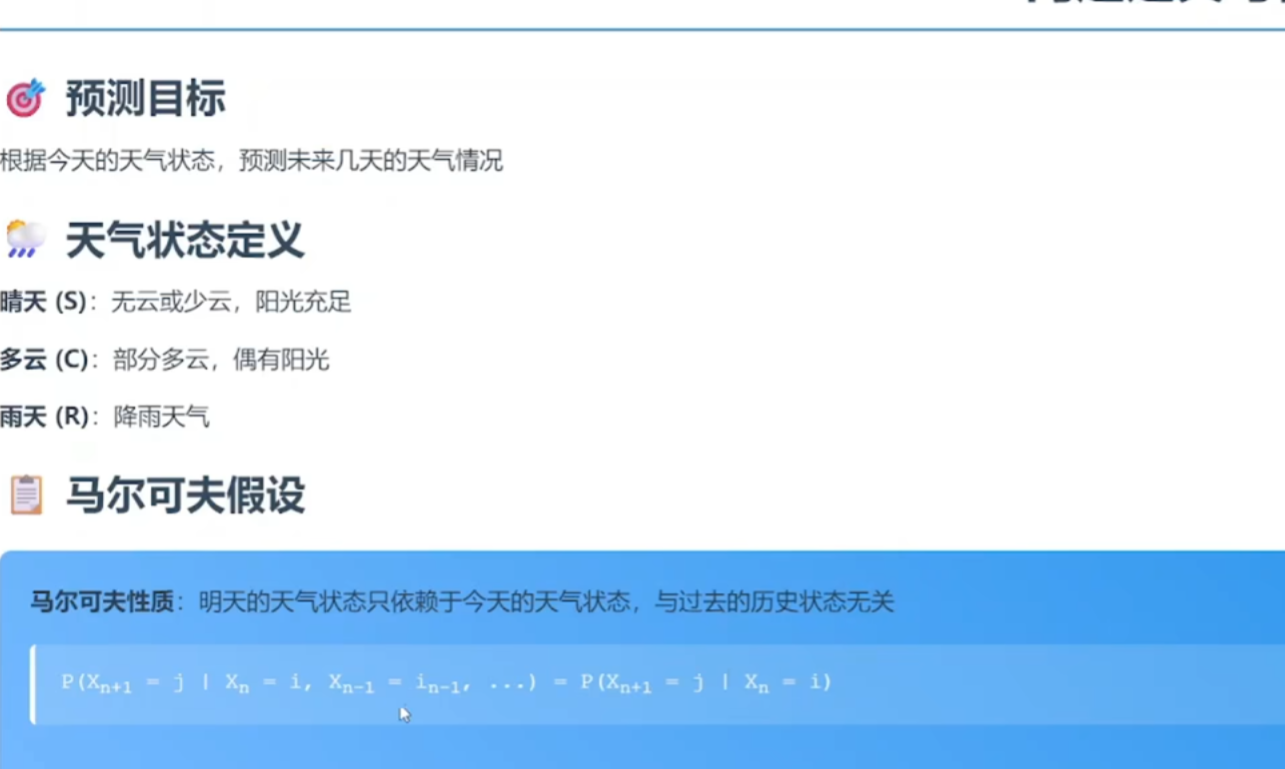
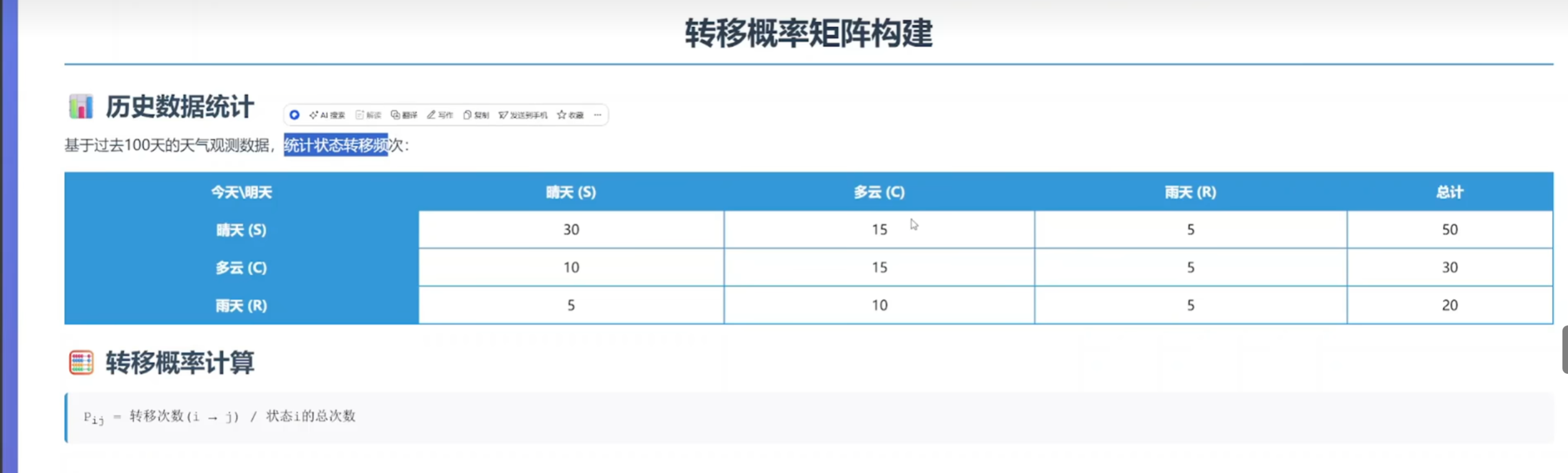
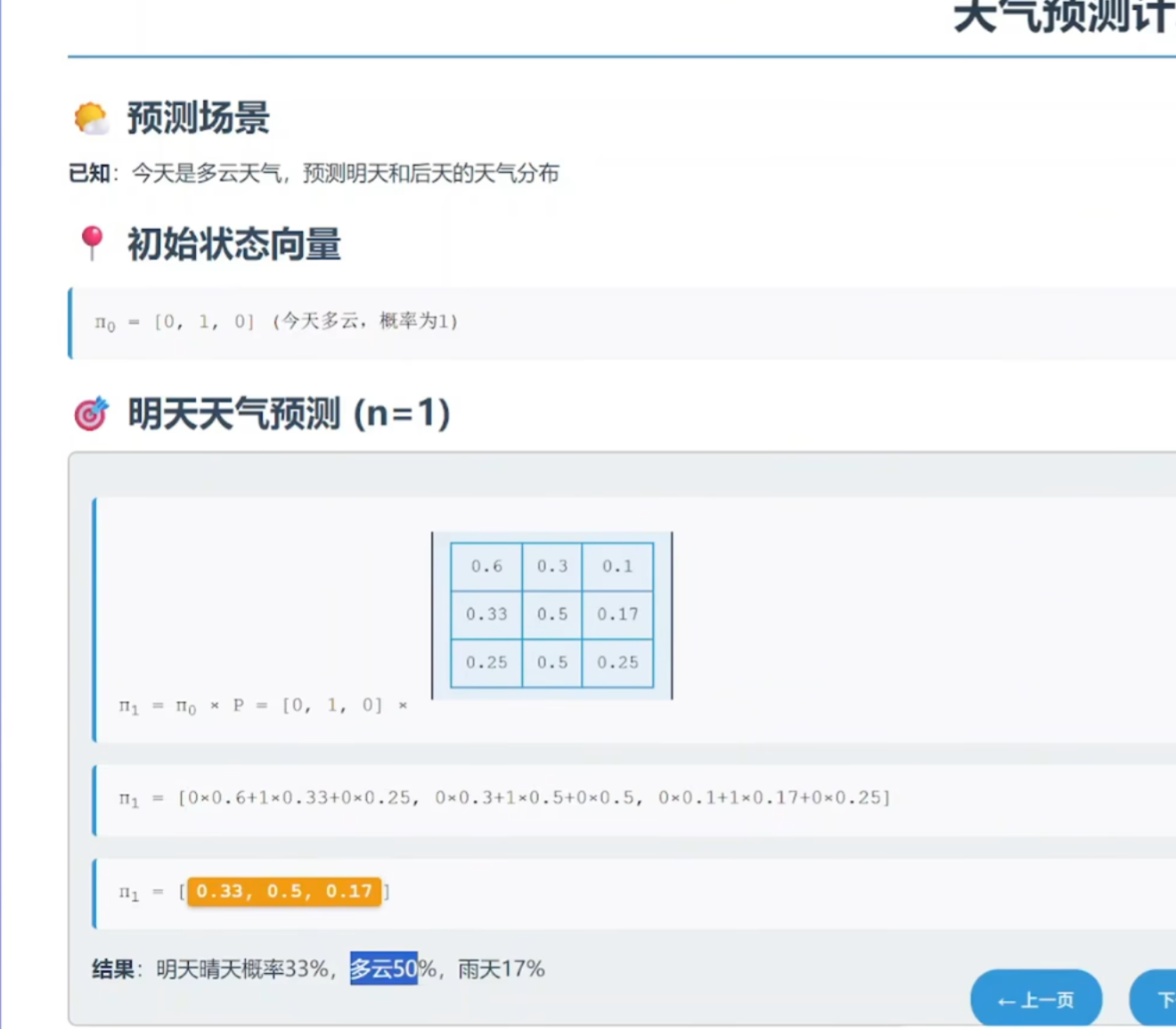
今晴明晴-30天，明云-15天

2 pyhton代码

（1）创建数据

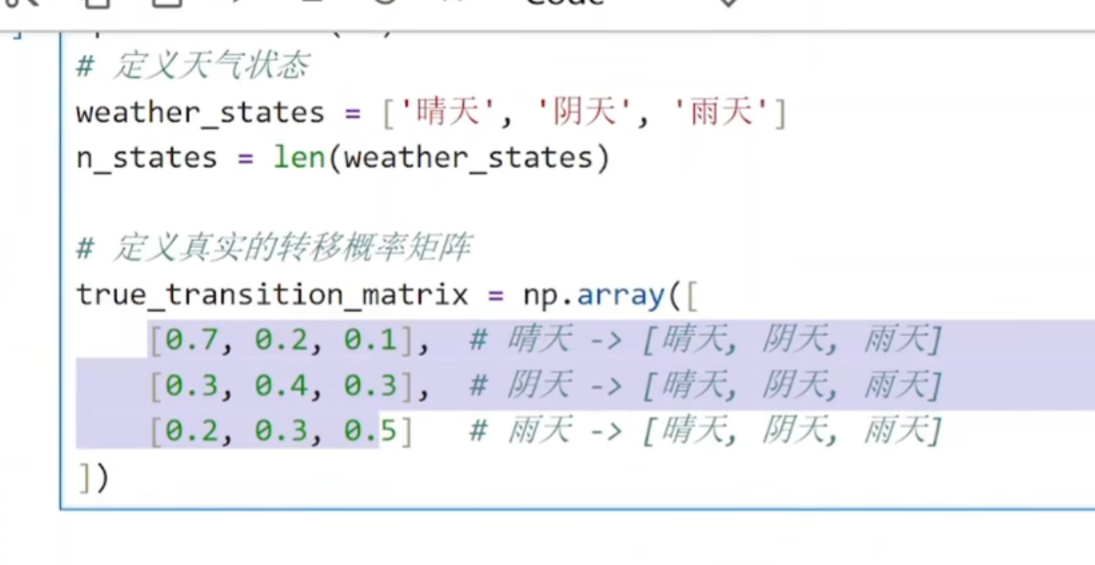
python 复制代码

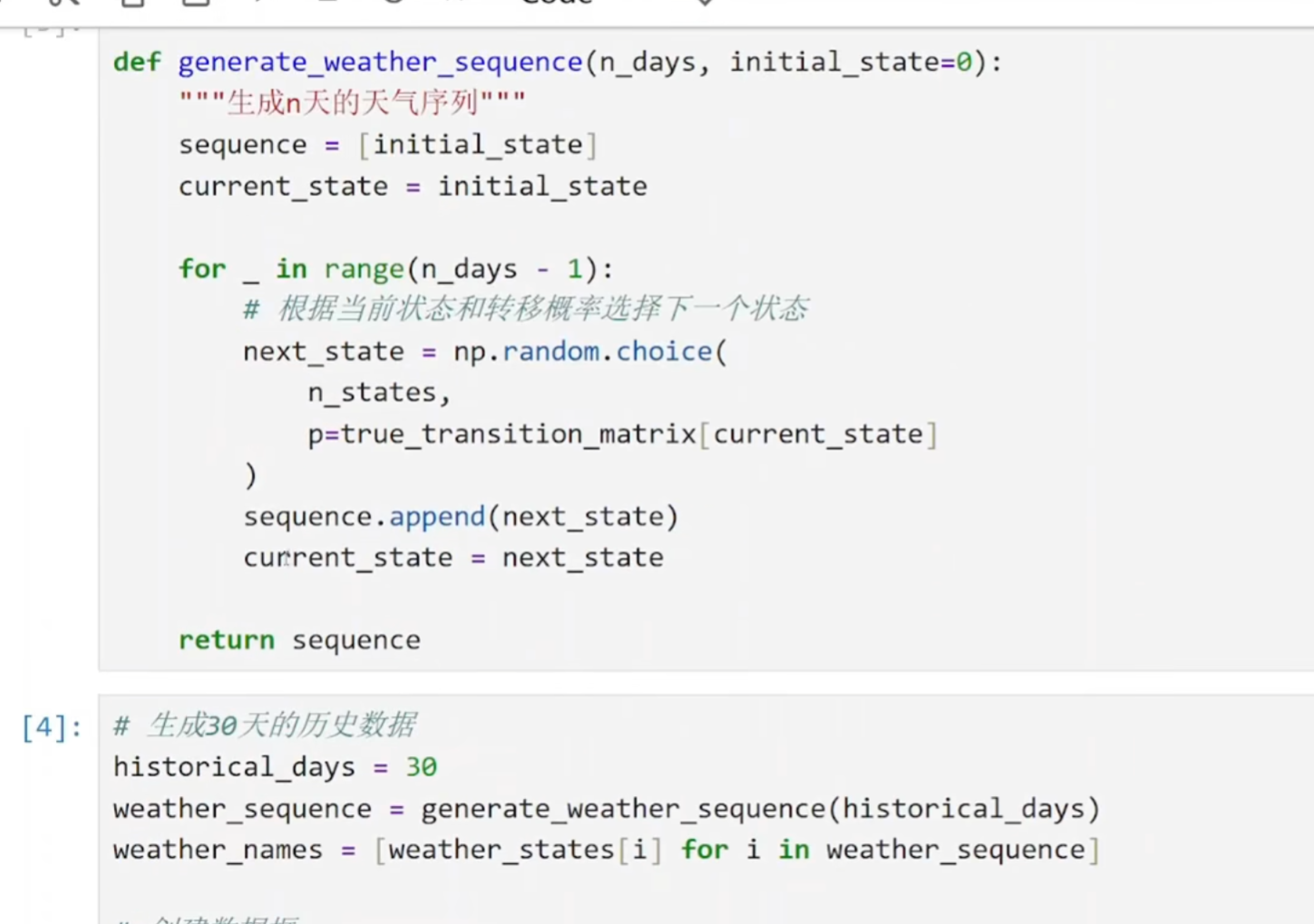
def generate_weather_sequence(n_days, initial_state=0):
这个函数接收两个参数：
n_days：要生成多少天的天气数据
initial_state：第一天的初始天气（默认为晴天 0）

next_state = np.random.choice(
    n_states,  # 选择范围：[0, 1, 2] 对应晴天、阴天、雨天
    p=true_transition_matrix[current_state]  # 当前天气对应的概率分布
)

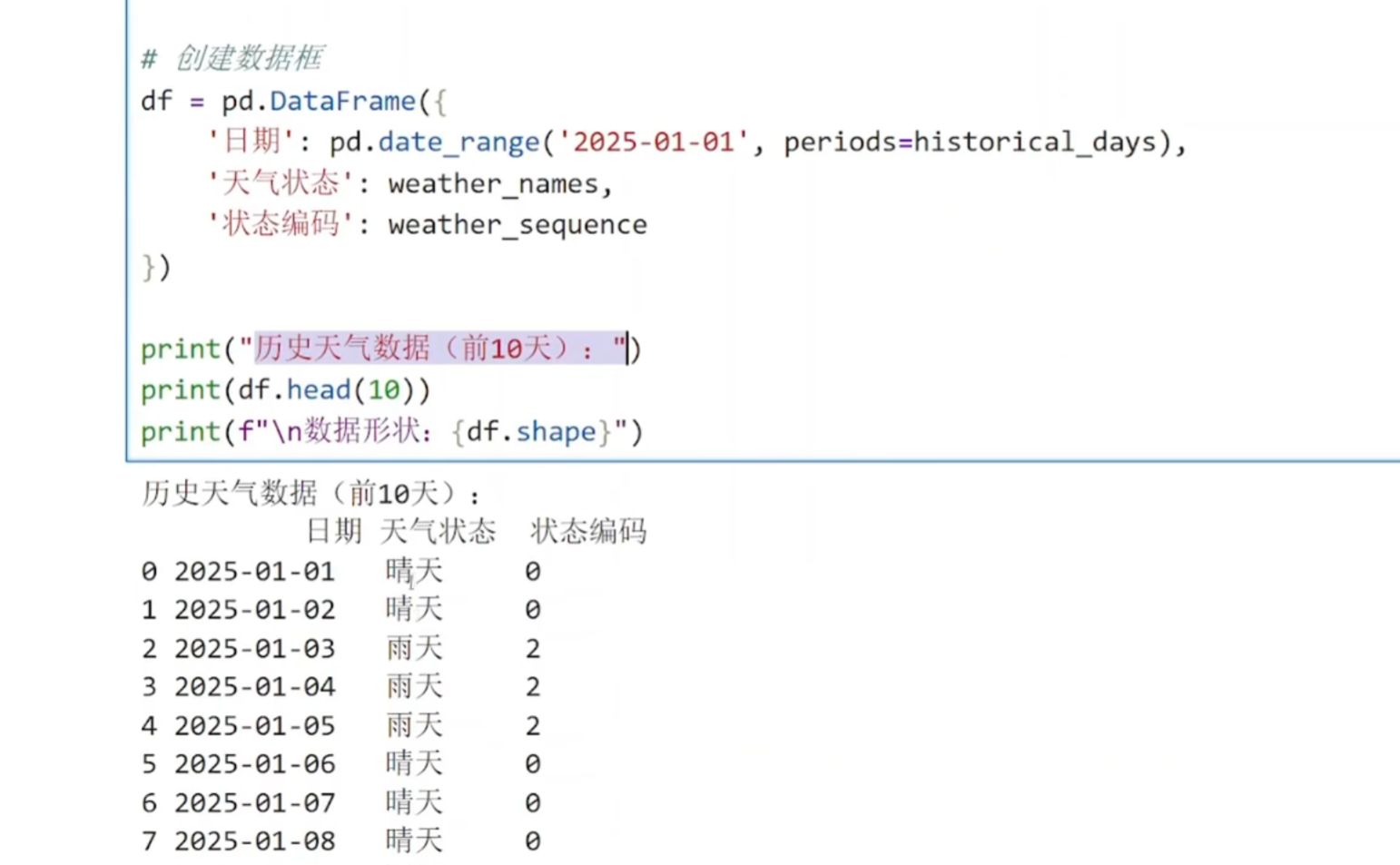
（2）创建观察矩阵

python 复制代码

n_states = len(set(sequence))
set(sequence)：去除重复，得到所有不同的状态
例如：序列 [0, 0, 1, 2, 0, 1]→ 集合 {0, 1, 2}→ 3种状态
这决定了转移矩阵的大小（3×3）

for i in range(n_states):
    row_sum = transition_counts[i].sum()  # 从状态i出发的总次数
    if row_sum > 0:
        transition_matrix[i] = transition_counts[i] / row_sum
    else:
        transition_matrix[i] = 1.0 / n_states  # 均匀分布
关键逻辑：
对每一行（每个当前状态）：
计算从该状态出发的总次数
如果确实有观察到转移（row_sum > 0）：
将每个转移次数除以总次数，得到概率
例如：[1, 2, 0]→ 总和3 → 概率 [0.33, 0.67, 0]
如果从未观察到该状态（row_sum = 0）：
给一个均匀分布（每个后续状态概率相等）
例如：3个状态 → 每个概率 [0.33, 0.33, 0.33]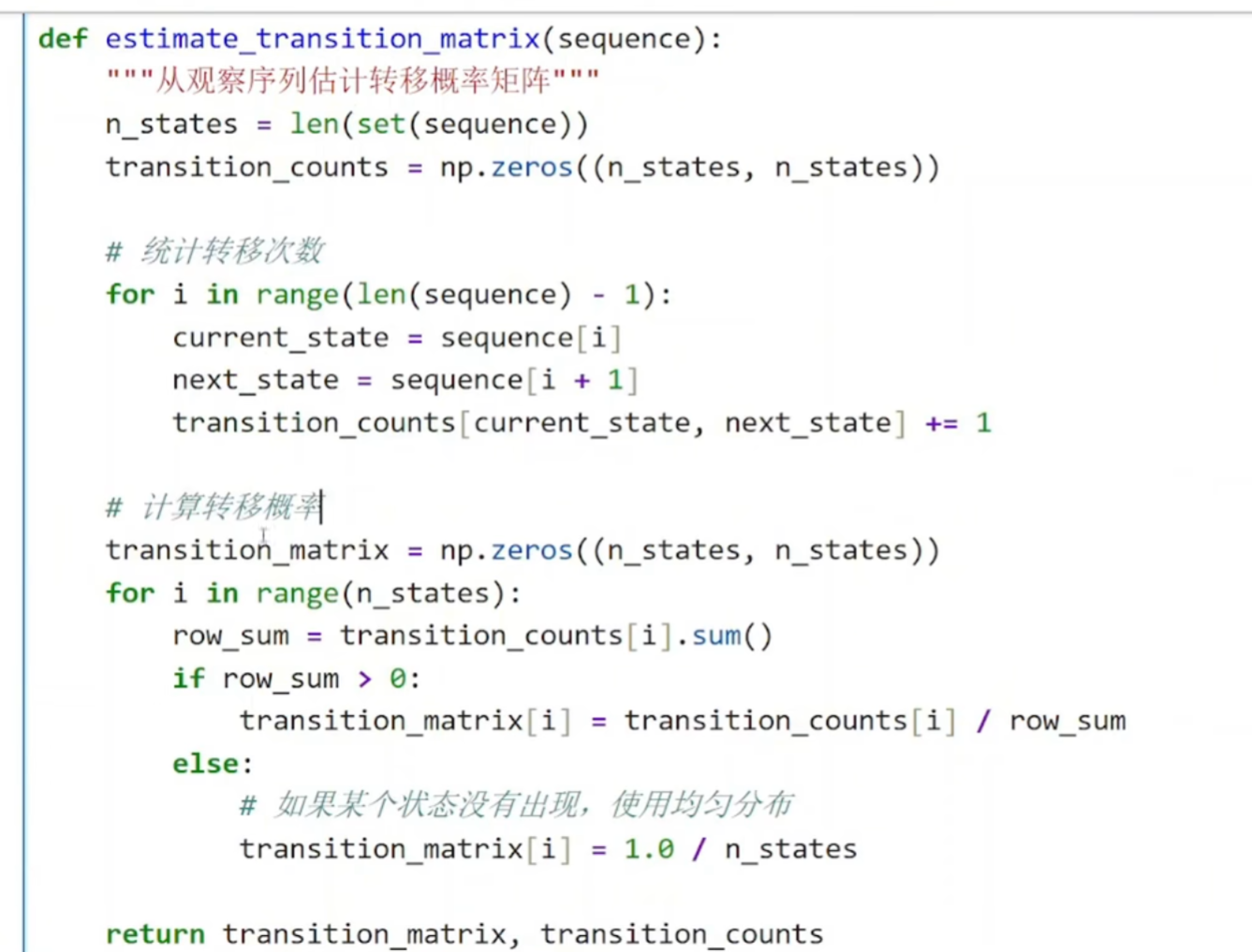

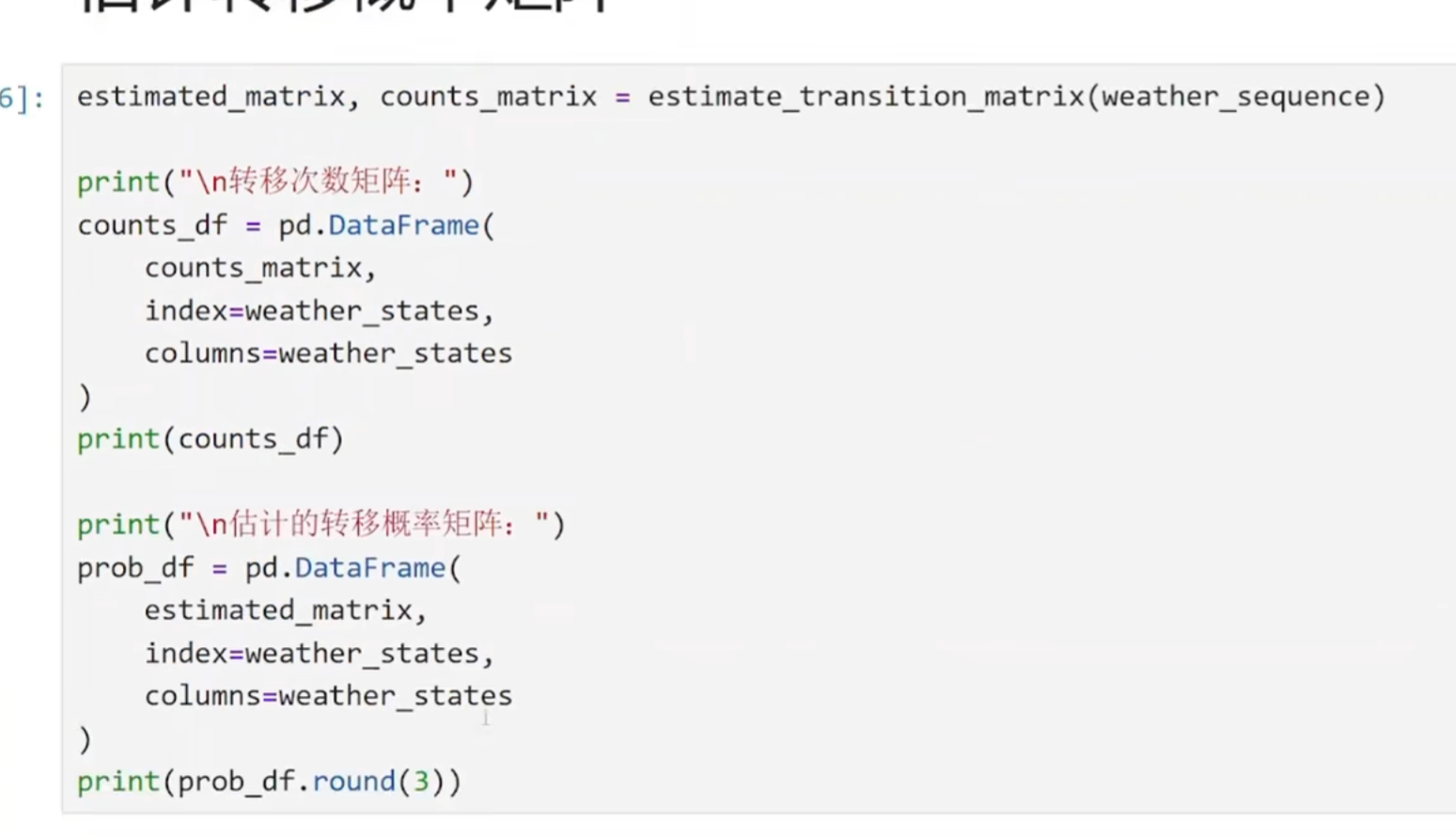
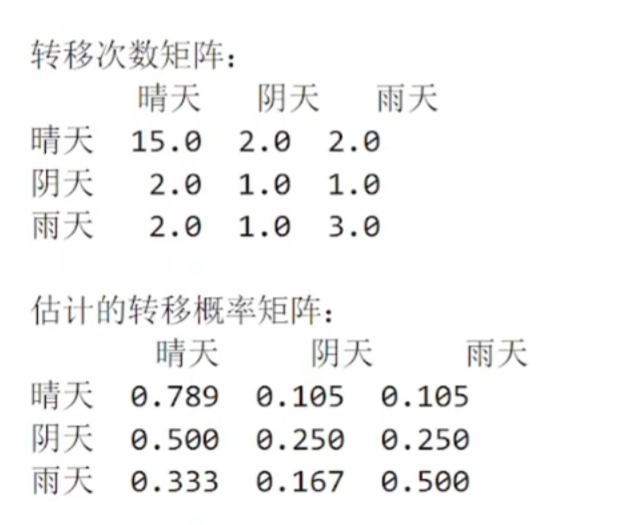
可视化图像

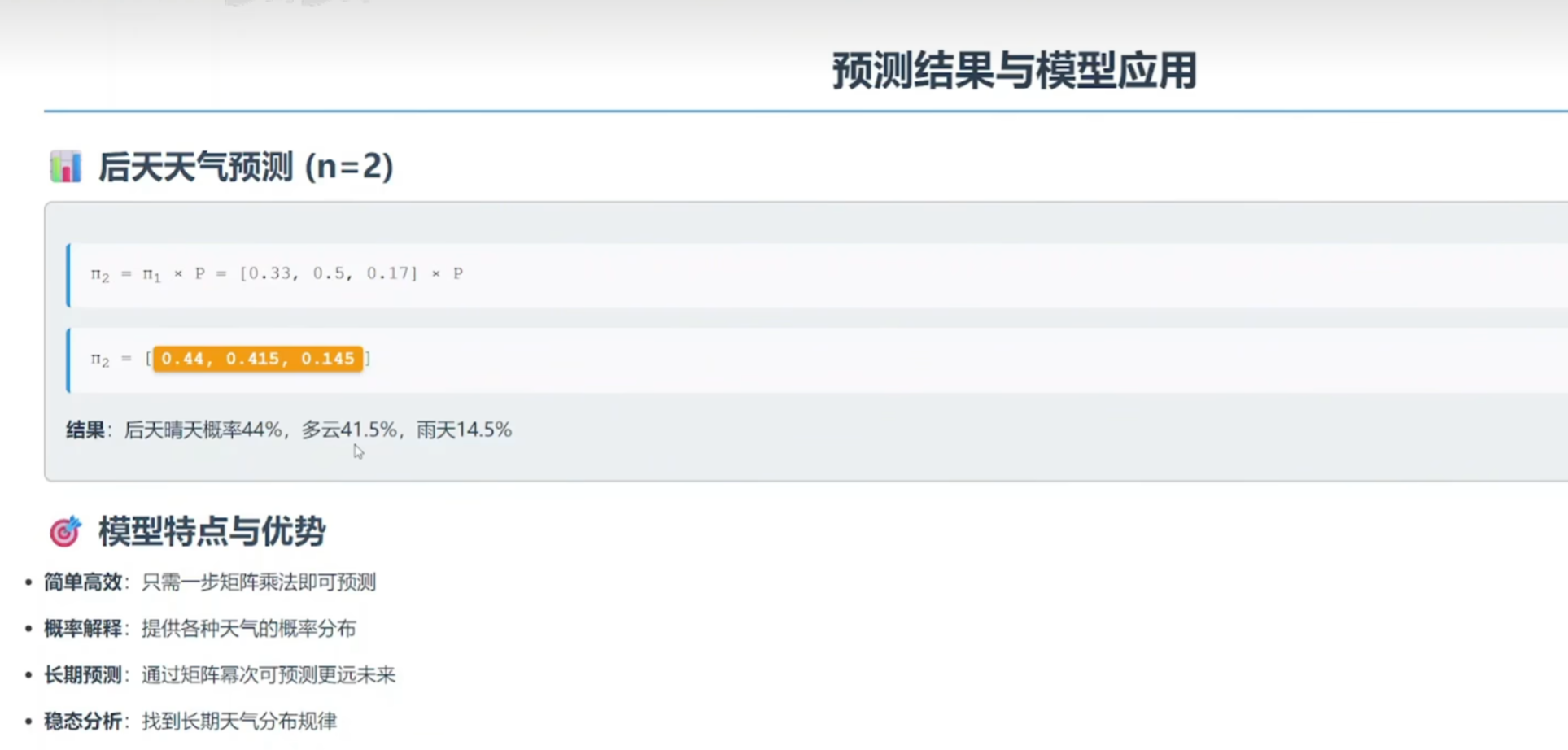
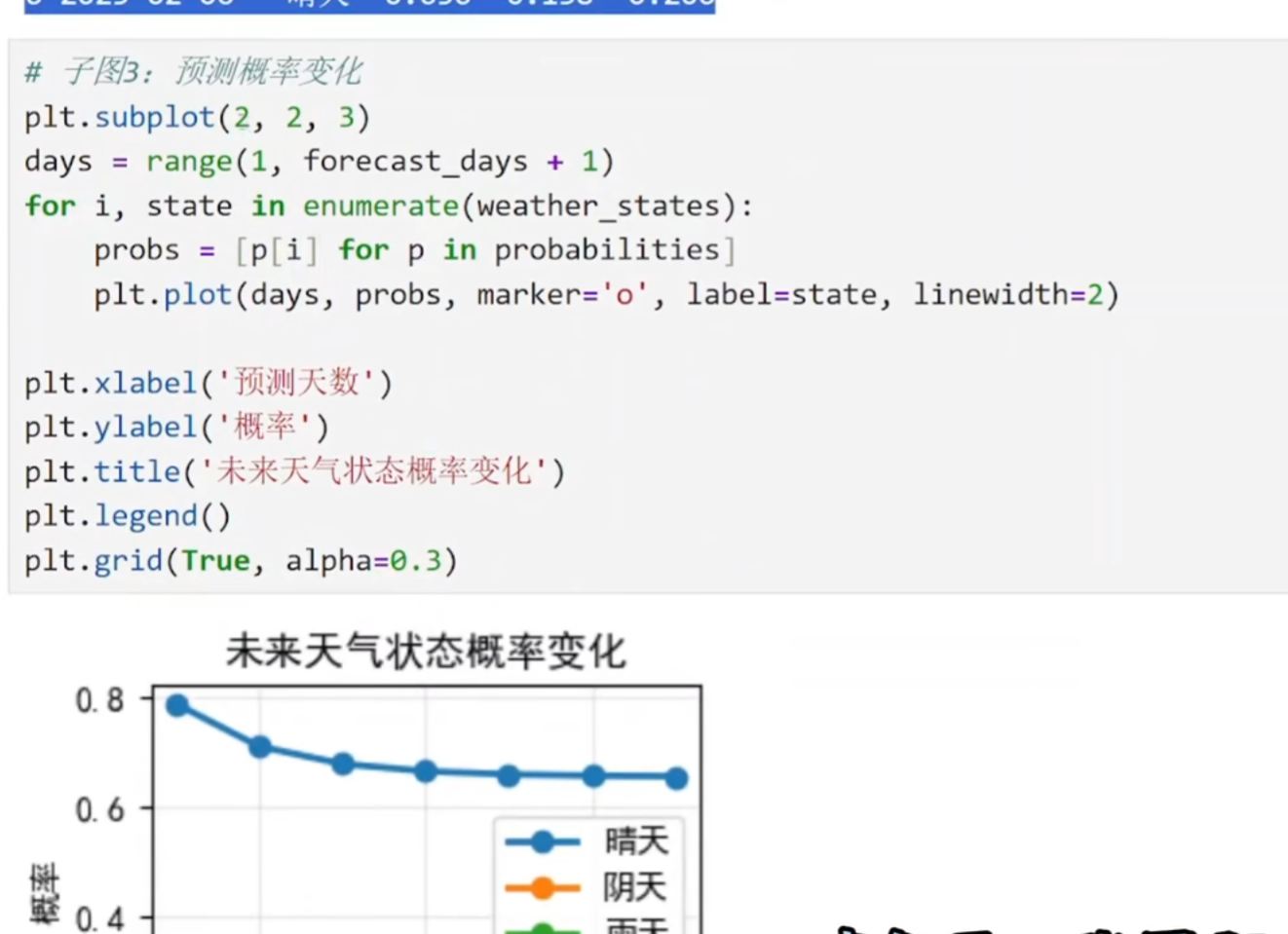
（3）天气预测

@是矩阵乘法

np.argmax 取最大值

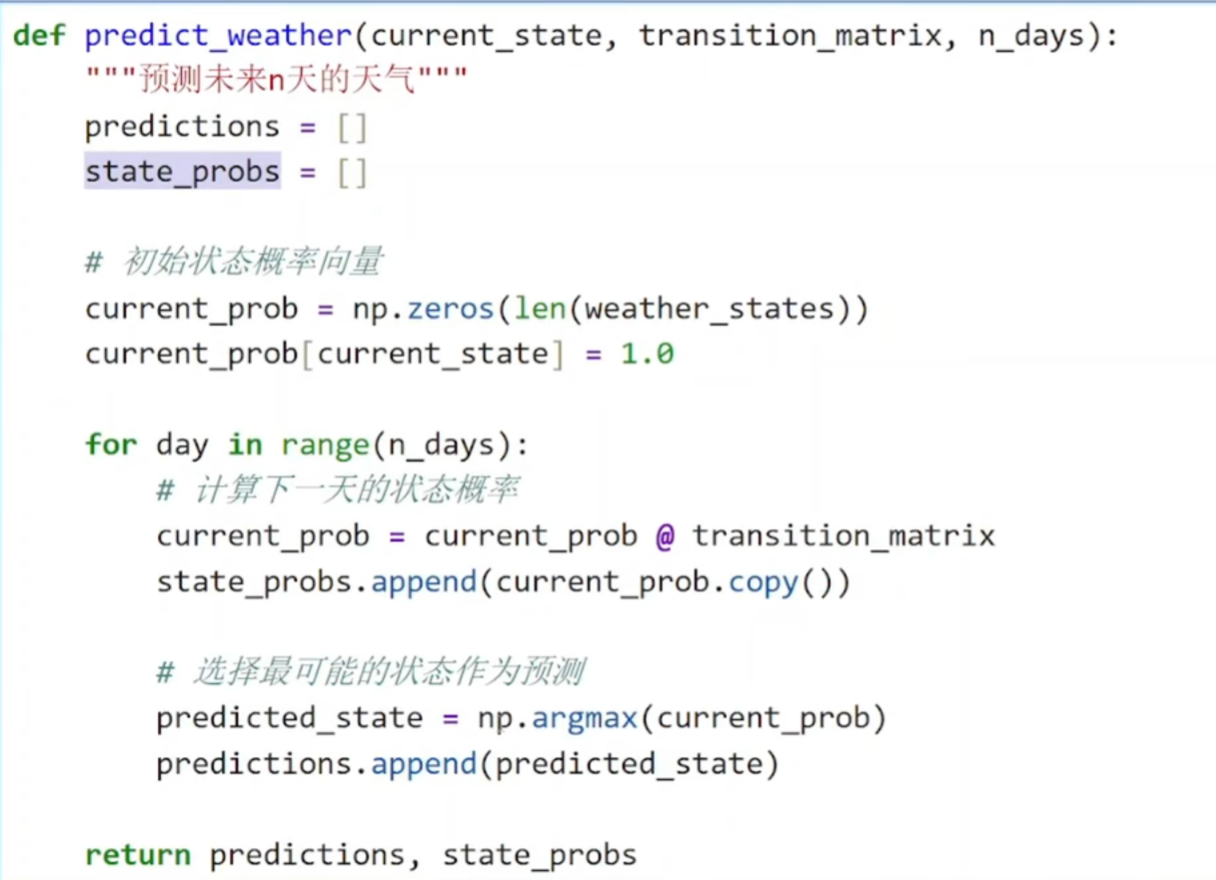
对某个日期或时间索引中的 最后一个元素（用 [-1]表示）
加上 1天的时间间隔（用 pd.Timedelta(days=1)表示）

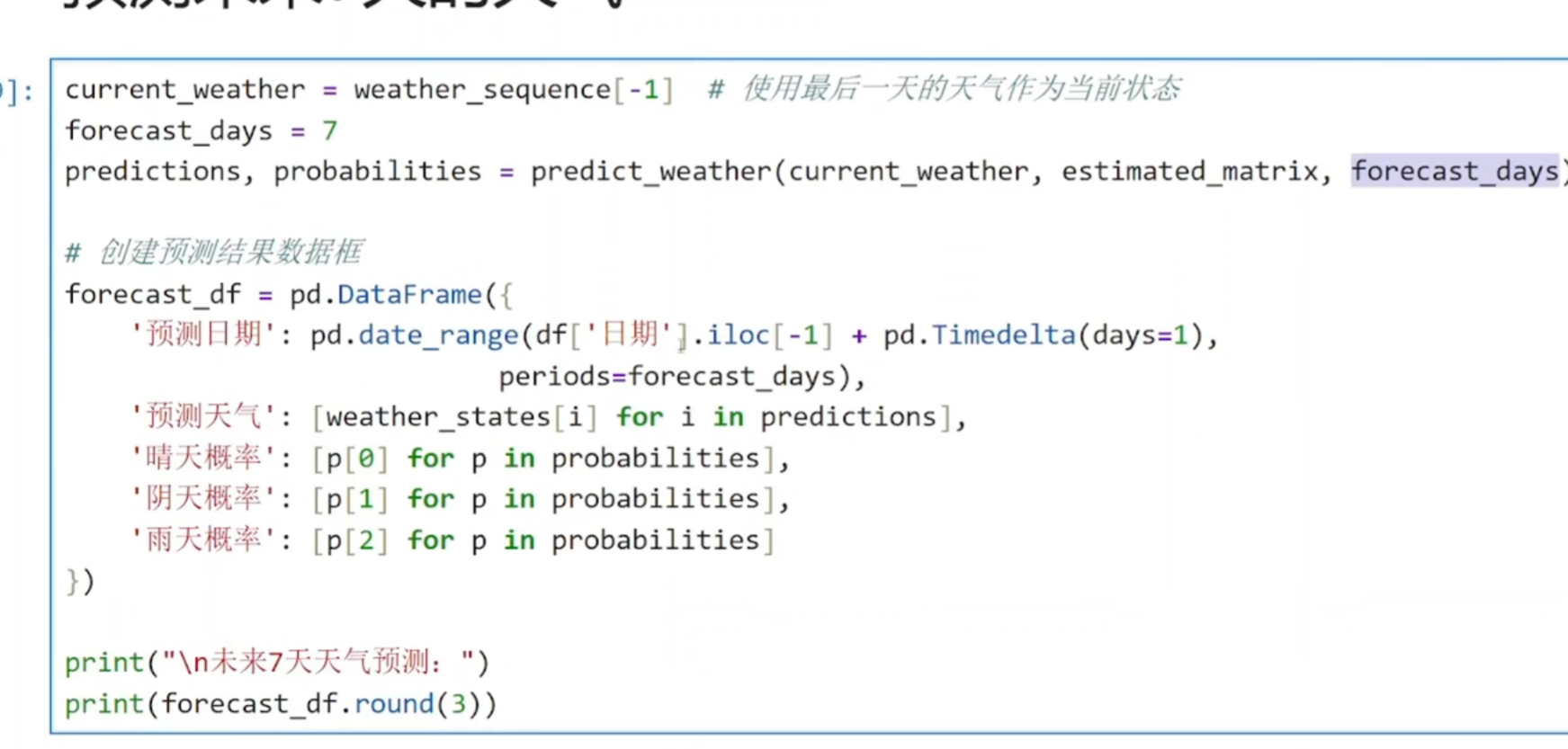
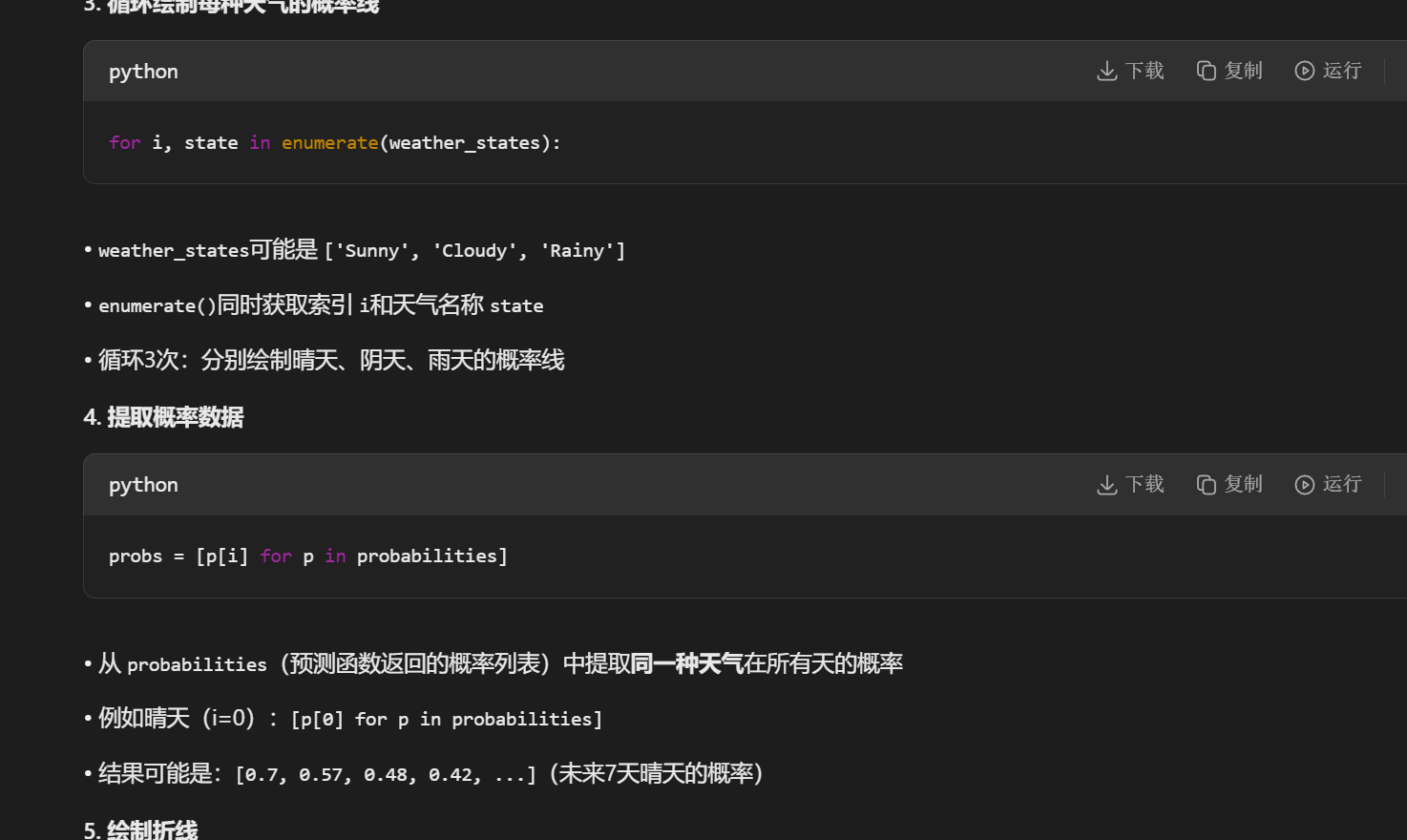
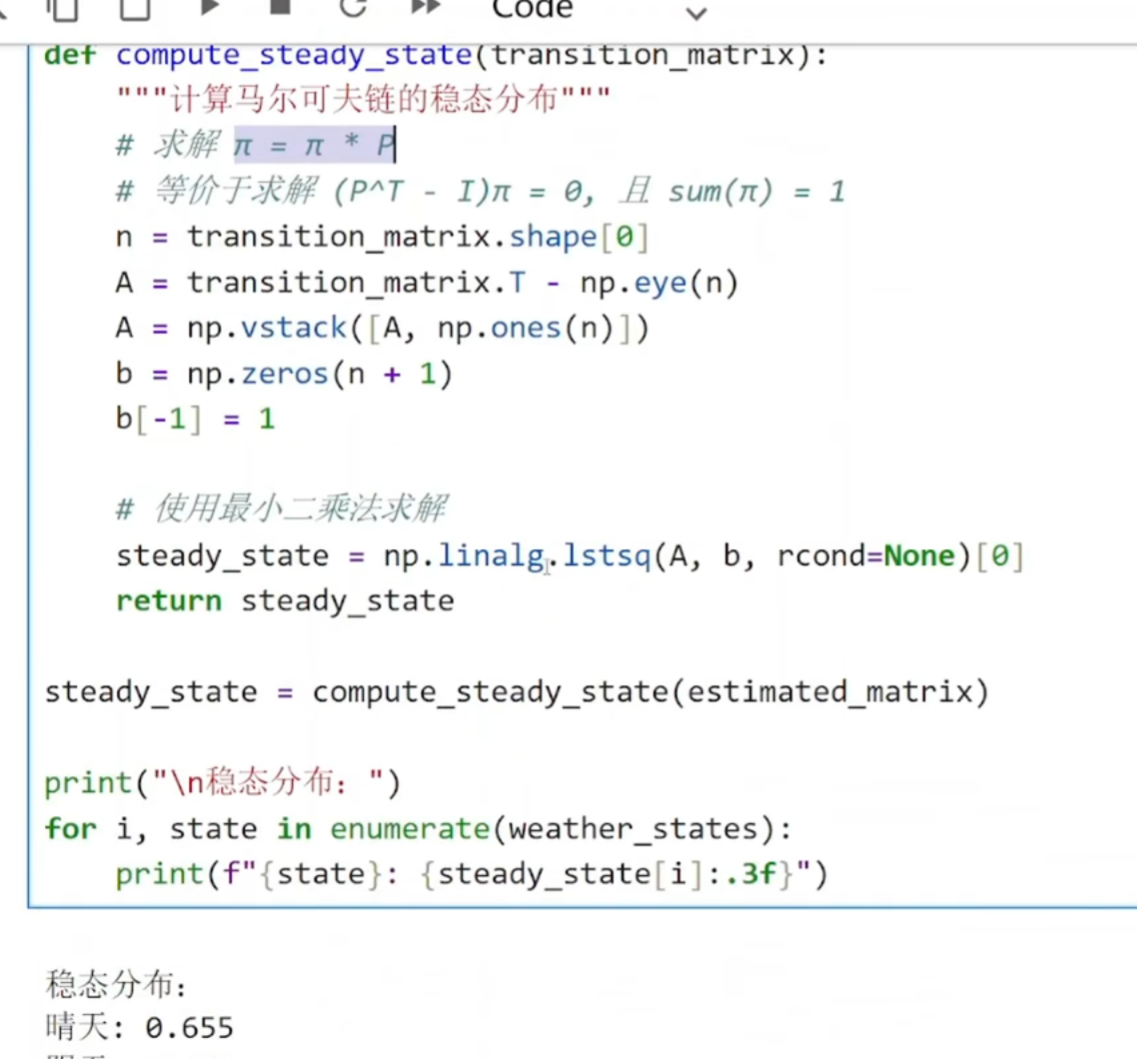
python 复制代码

n = transition_matrix.shape[0]  # 状态数量（3）
A = transition_matrix.T - np.eye(n)  # (P^T - I)
P.T：转移矩阵的转置
np.eye(n)：n×n的单位矩阵
这样构造是因为方程 πP = π可改写为 P^Tπ^T = π^T，再整理为 (P^T - I)π^T = 0

A = np.vstack([A, np.ones(n)])  # 在A底部添加一行全1
b = np.zeros(n + 1)             # 创建零向量
b[-1] = 1                       # 最后一个元素设为1

steady_state = np.linalg.lstsq(A, b, rcond=None)[0]
lstsq：最小二乘法求解线性方程组
为什么用最小二乘？因为 (P^T - I)π = 0的方程线性相关（不是所有方程独立），
需要加入归一化条件并用最小二乘求最优解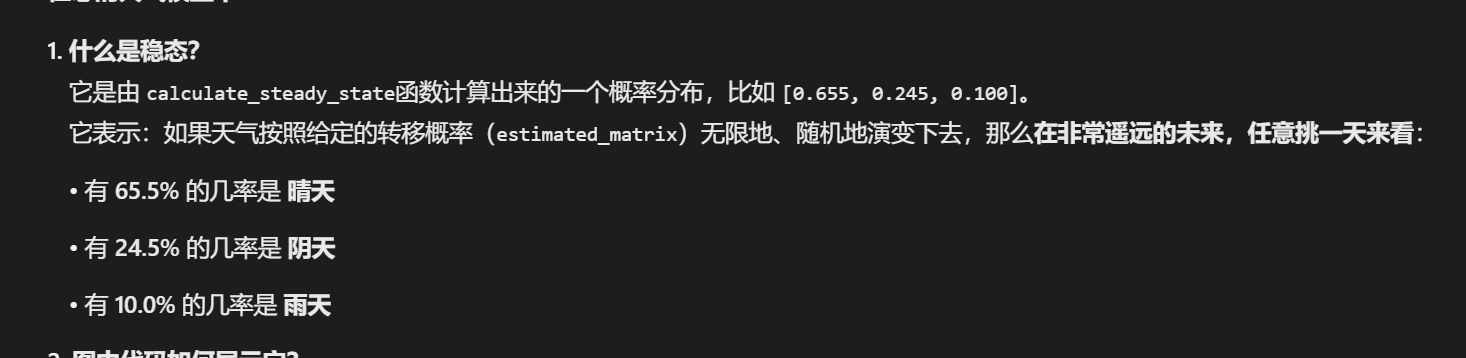

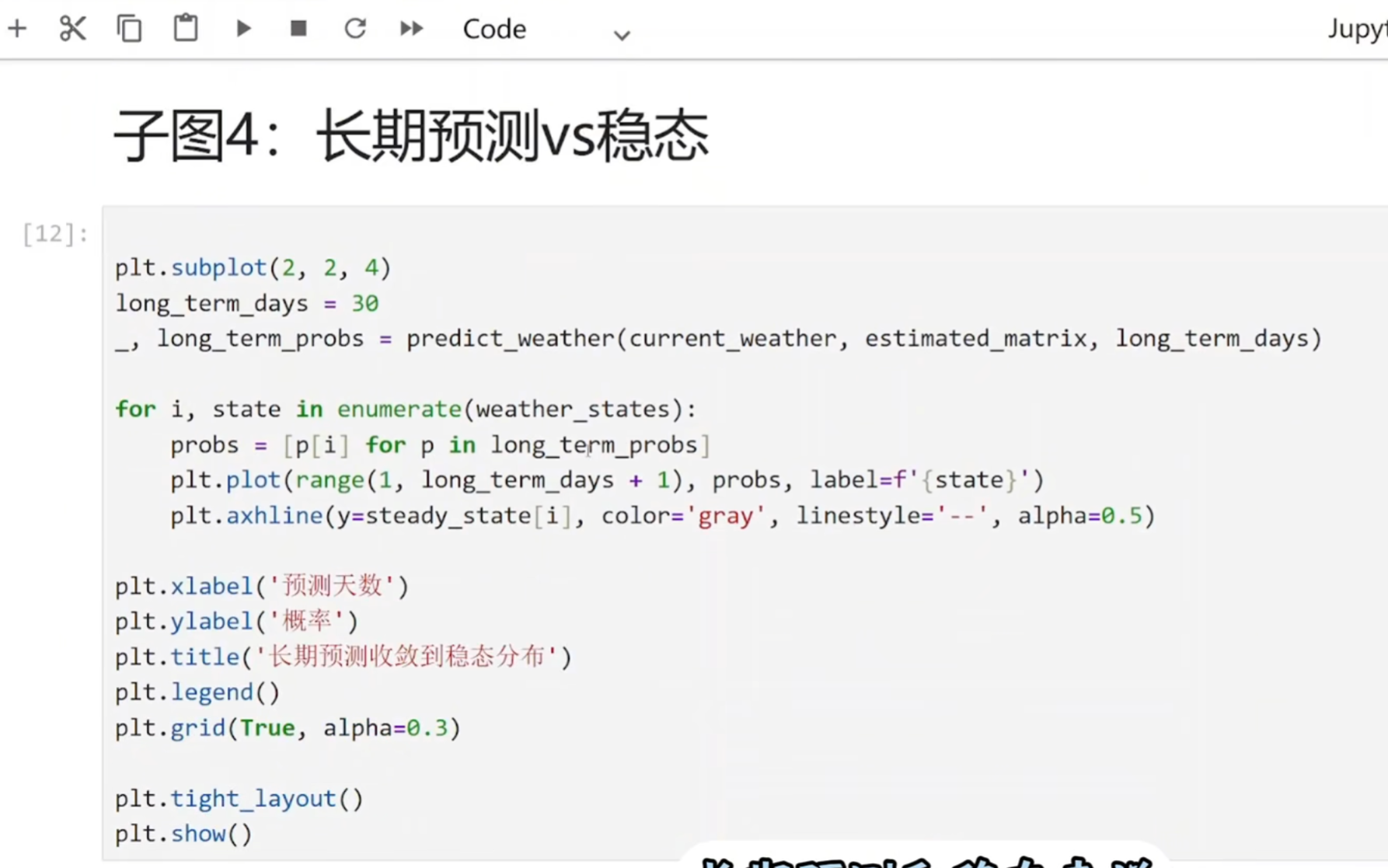
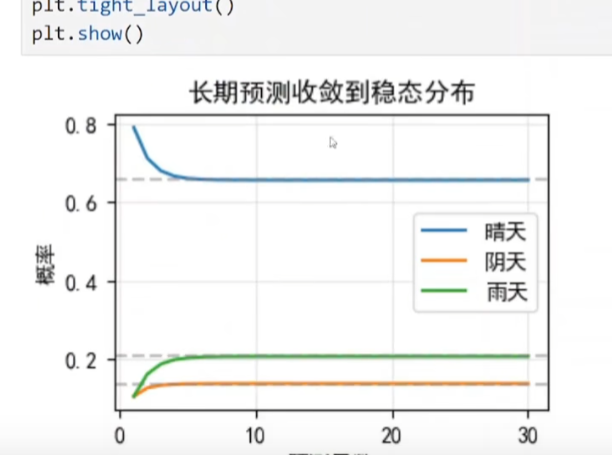
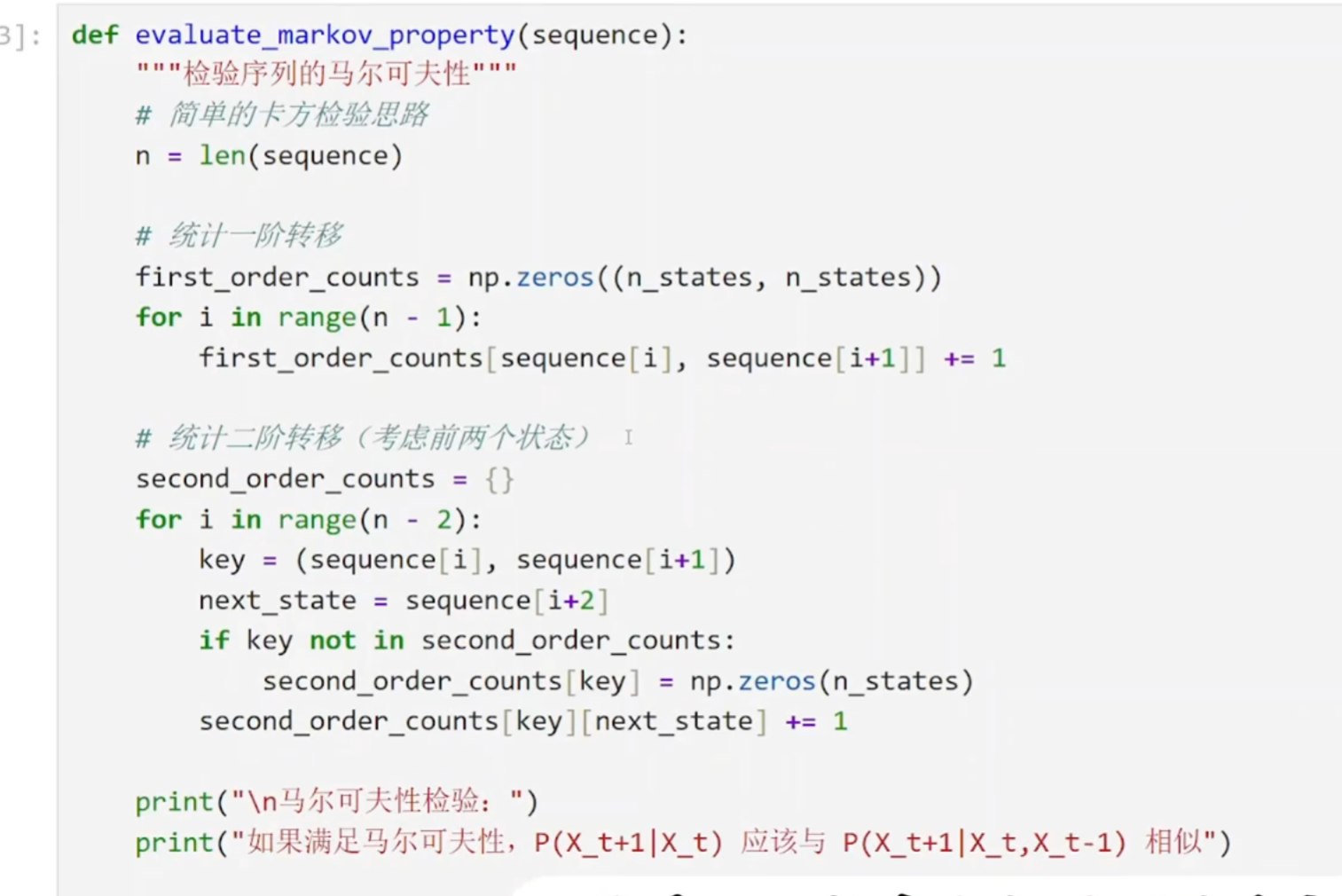
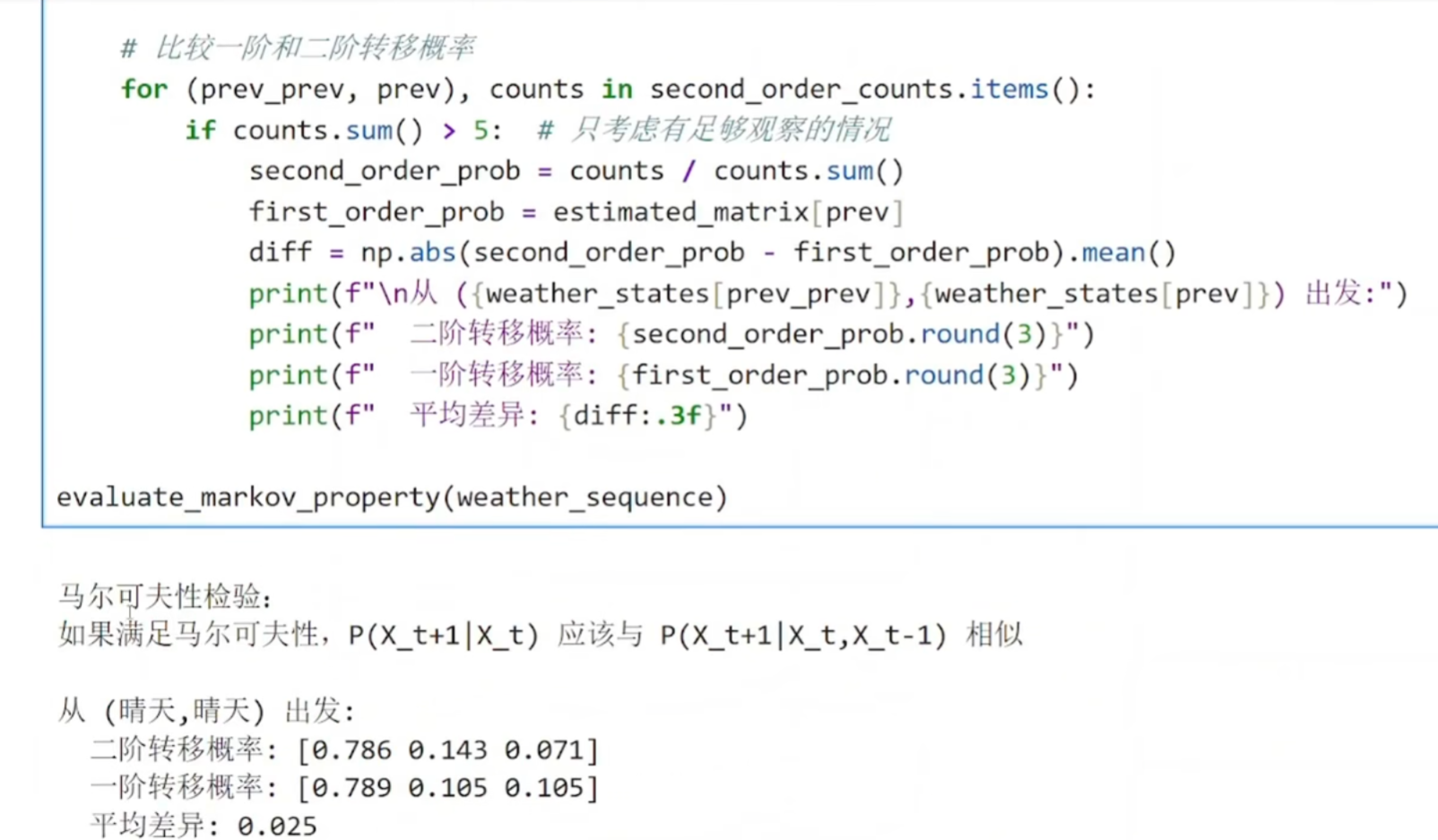
（4）验证

python 复制代码

一阶转移概率：P(明天天气 | 今天天气)
（只考虑今天的影响）
二阶转移概率：P(明天天气 | 昨天天气, 今天天气)
（考虑昨天和今天两天的影响）

first_order_counts = [[0,0,0], [0,0,0], [0,0,0]]

for i in range(n-1):
    今天 = sequence[i]
    明天 = sequence[i+1]
    first_order_counts[今天][明天] += 1
例如：统计"晴天→阴天"这种转换发生了多少次