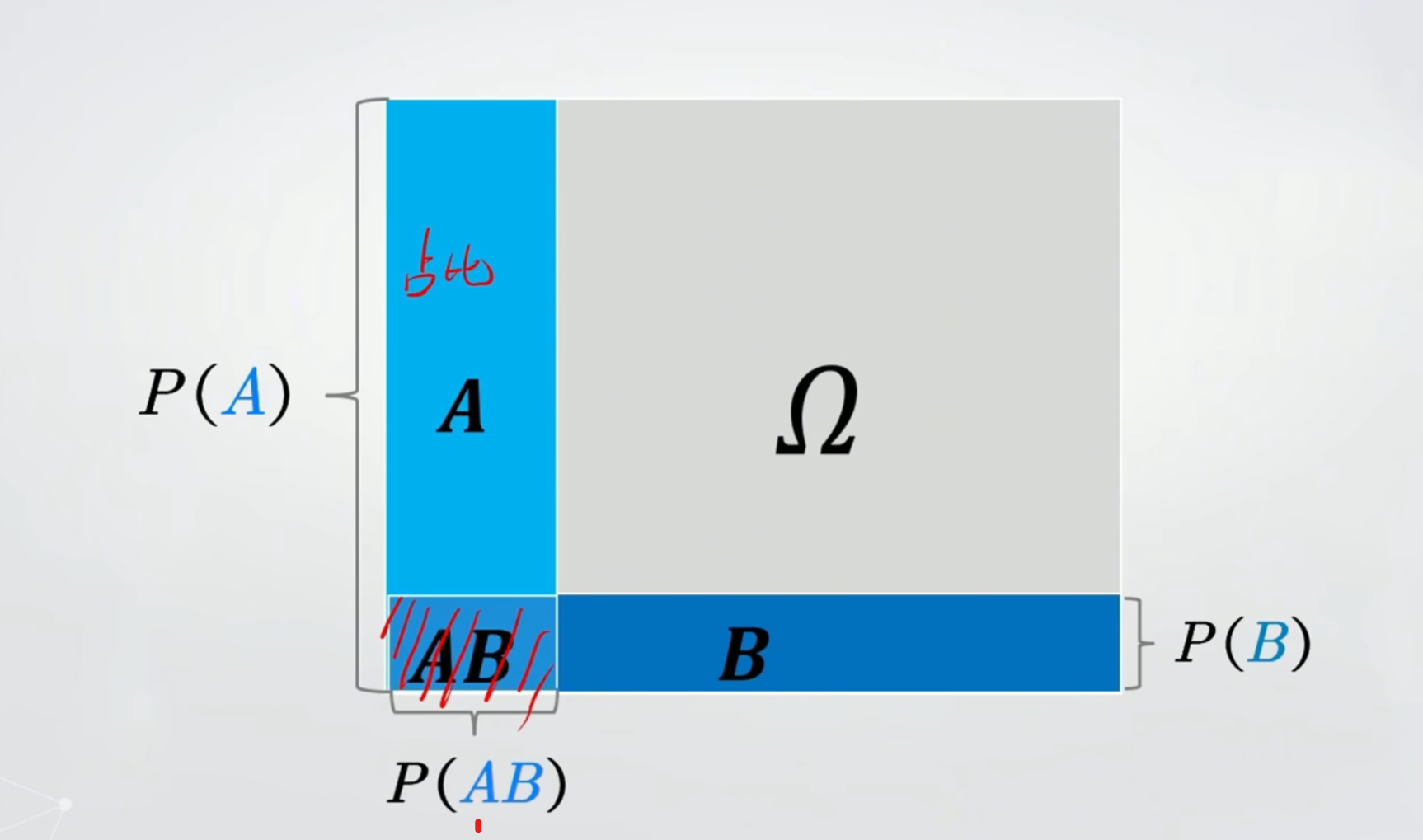
一 条件概率
1 理解
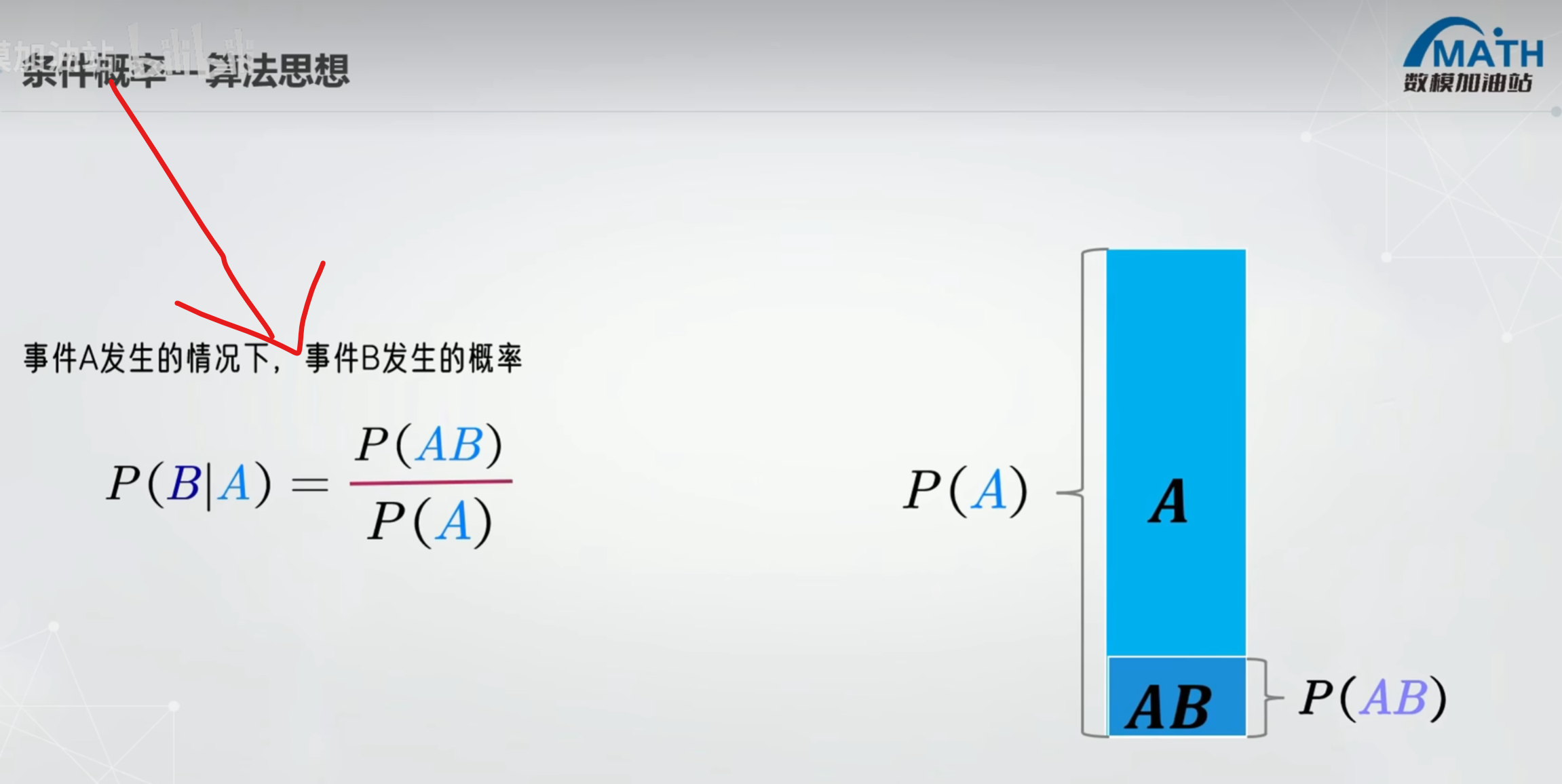
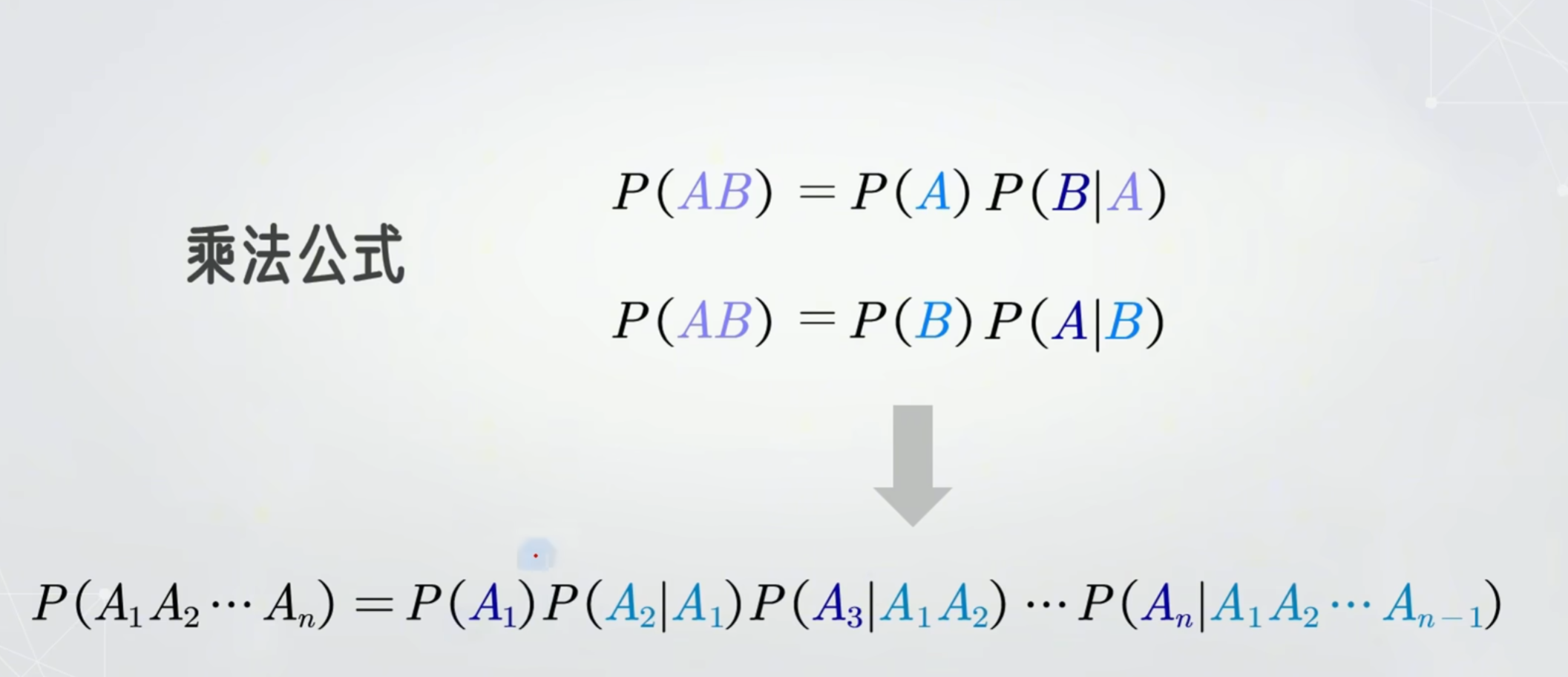

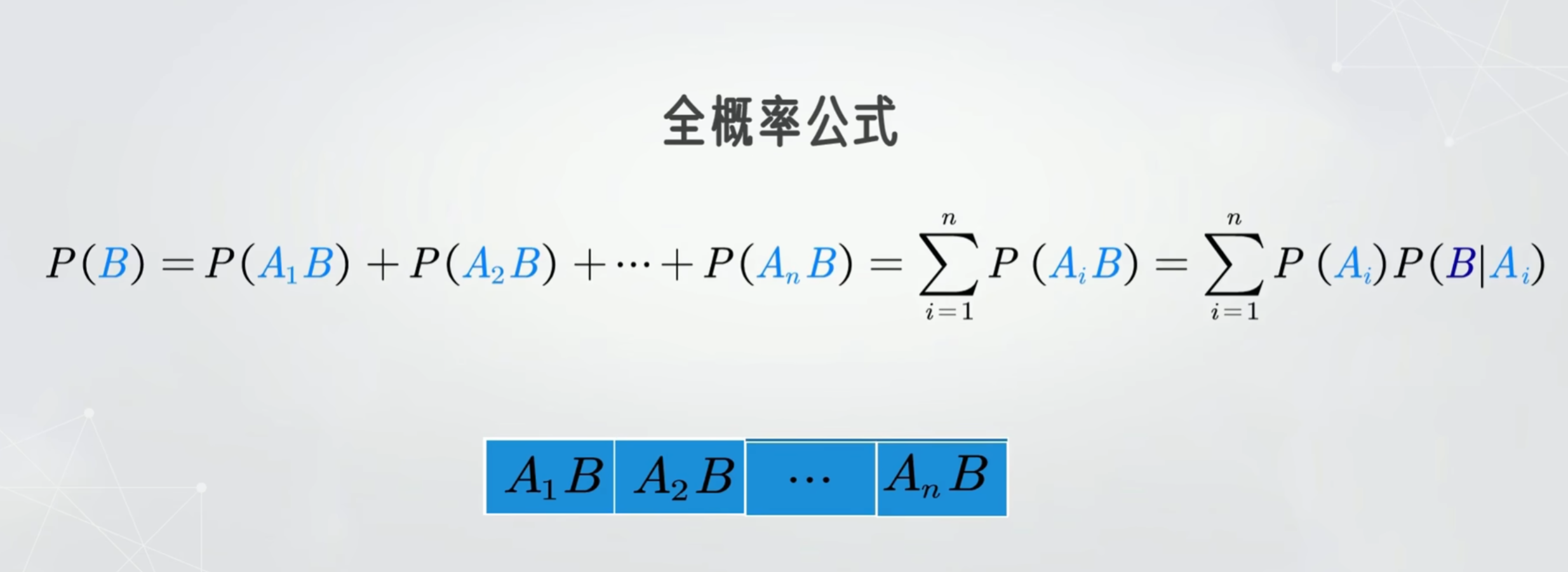





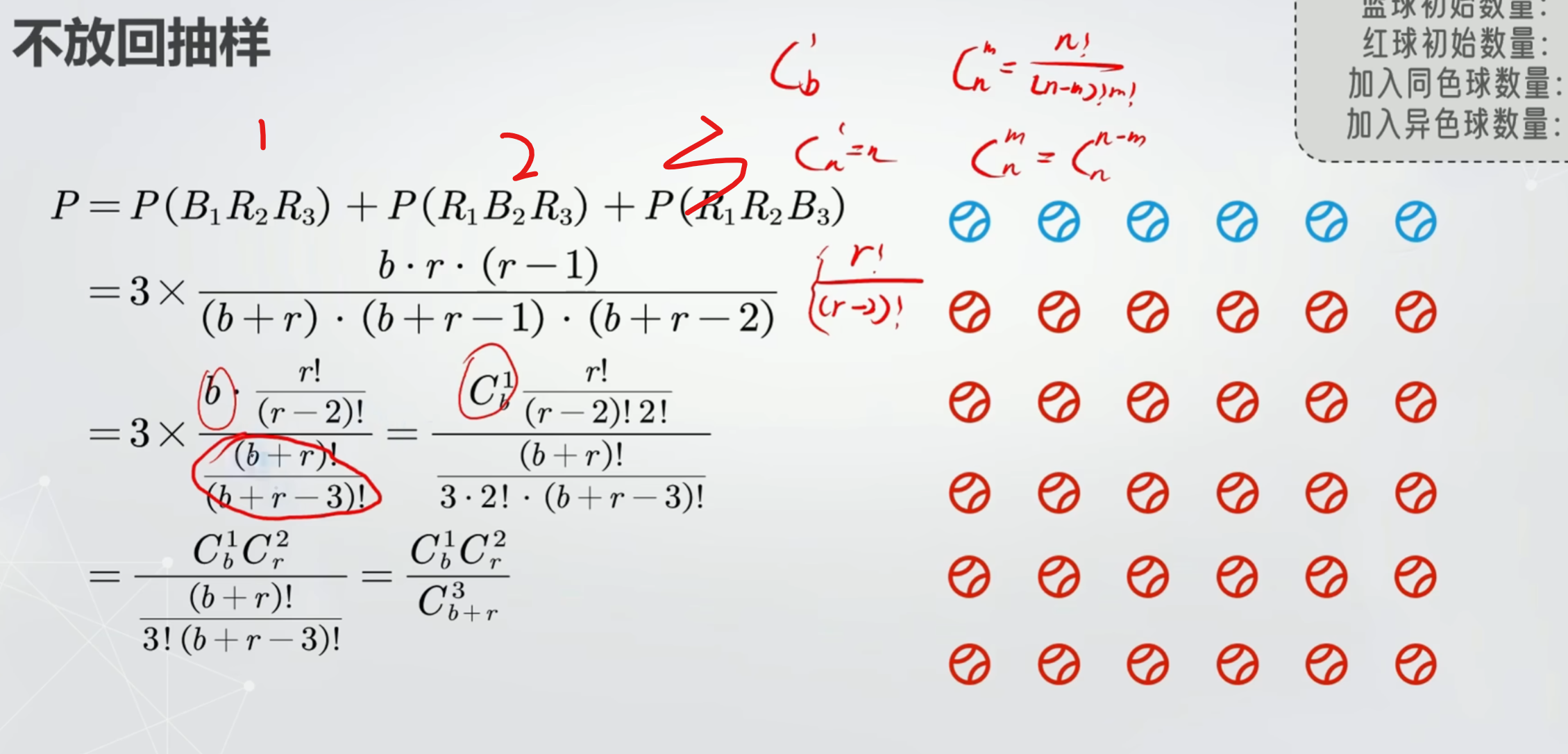




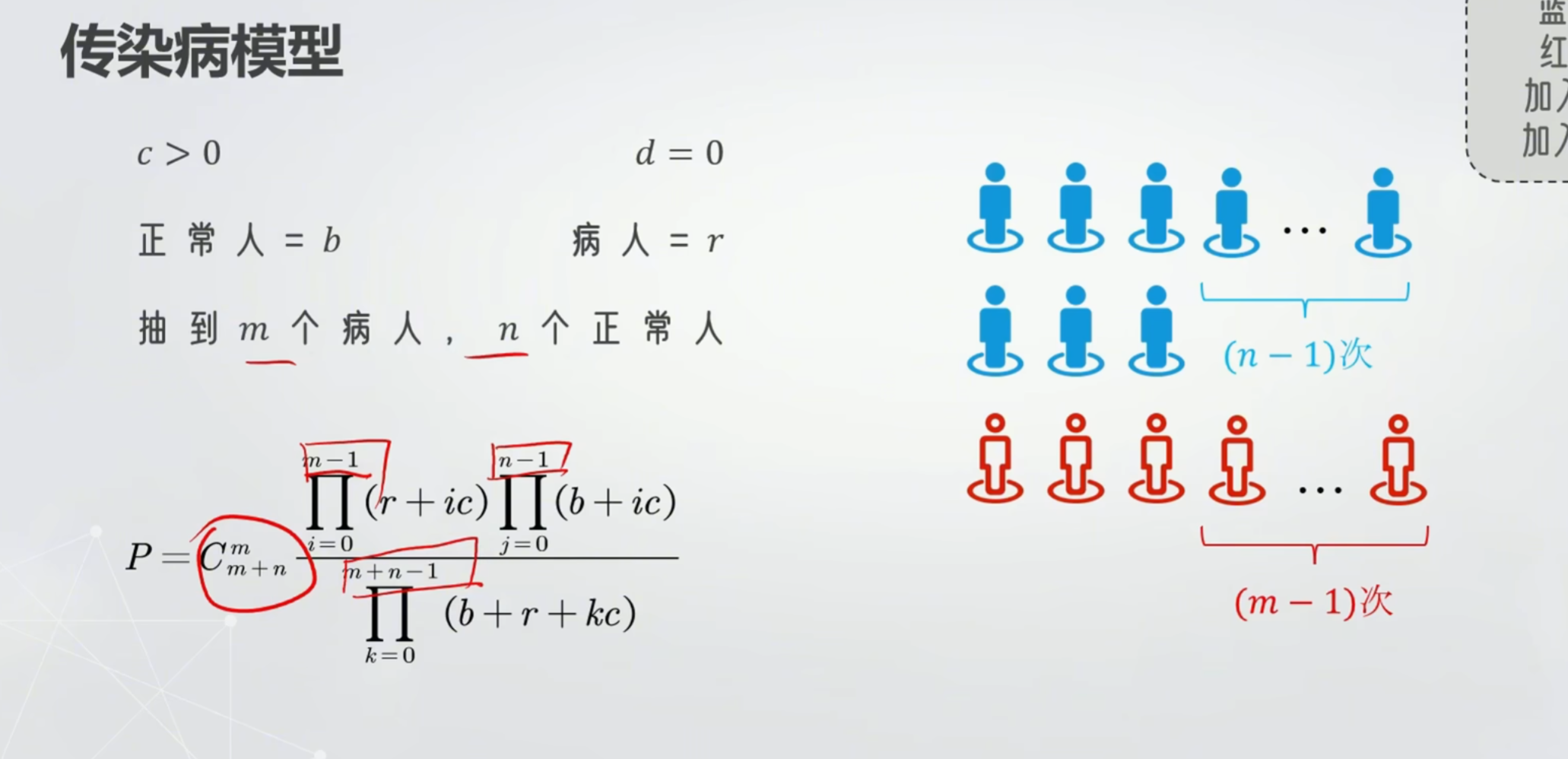

抽到安全加事故 抽到事故加安全

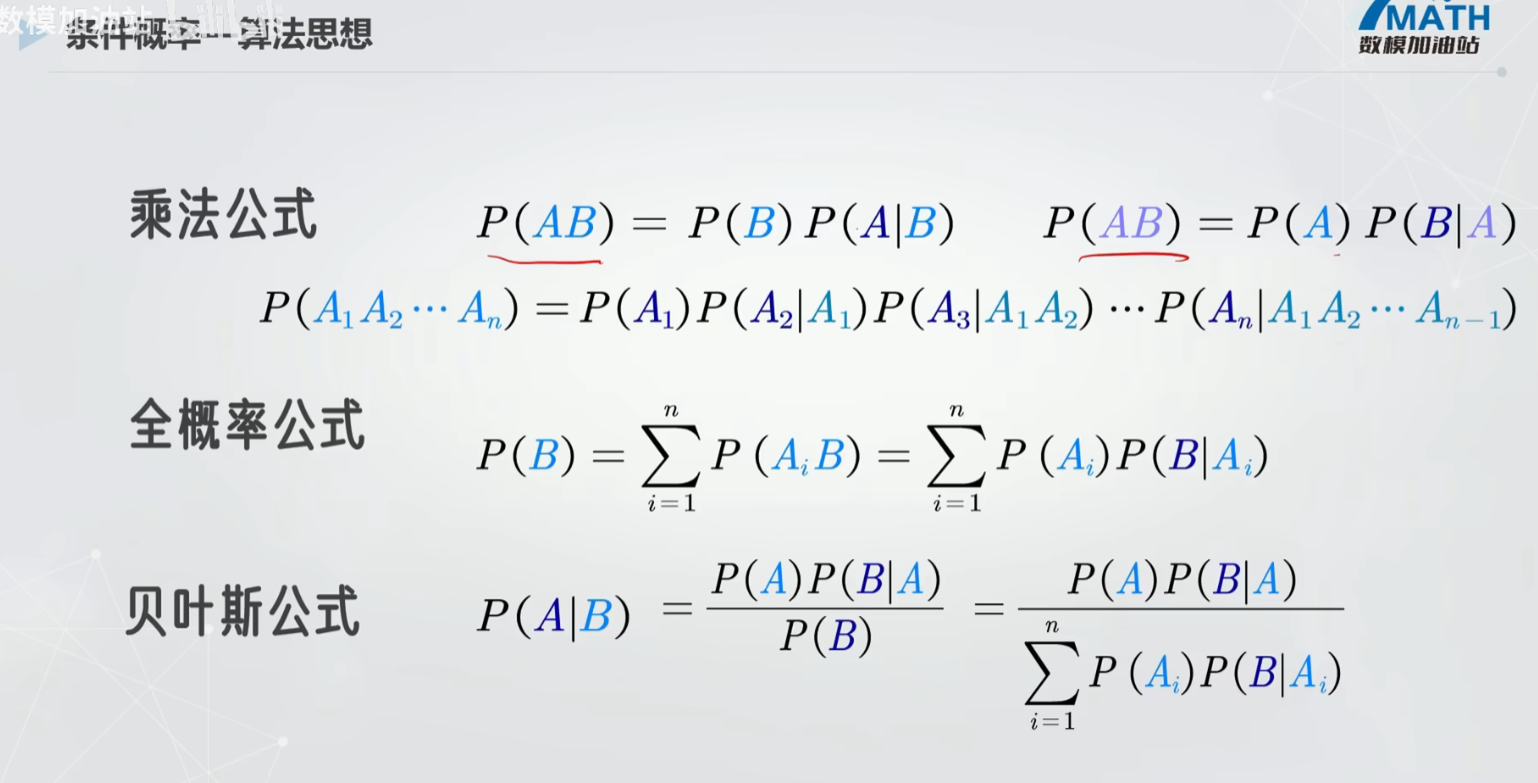
2 python算法
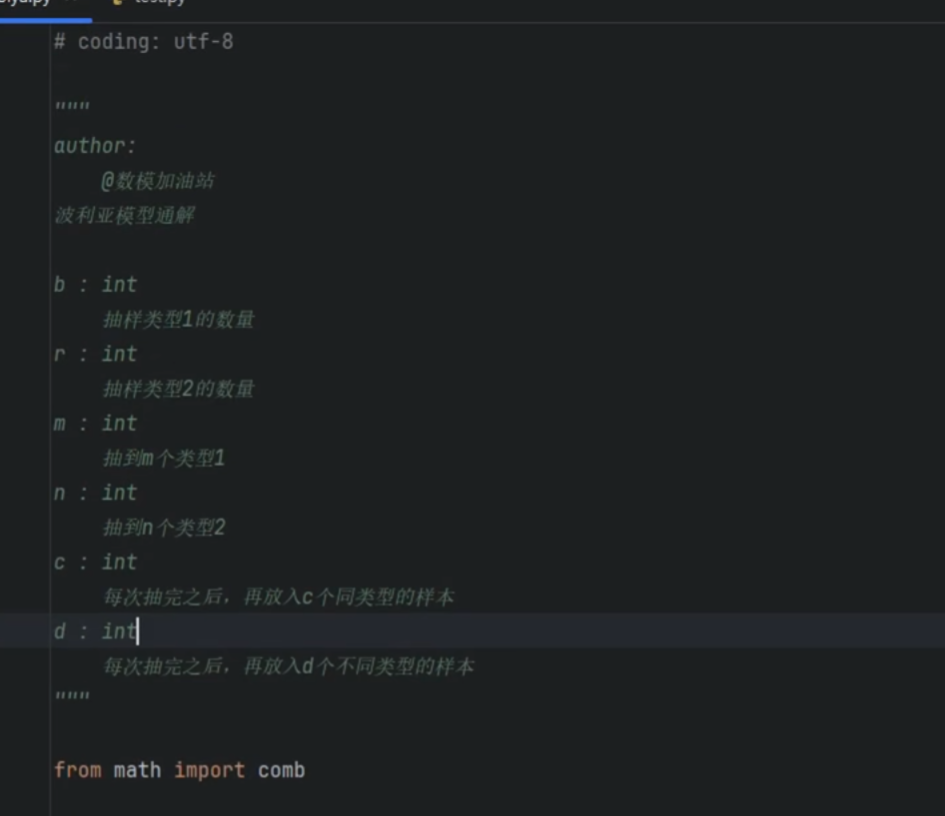
不放回抽样
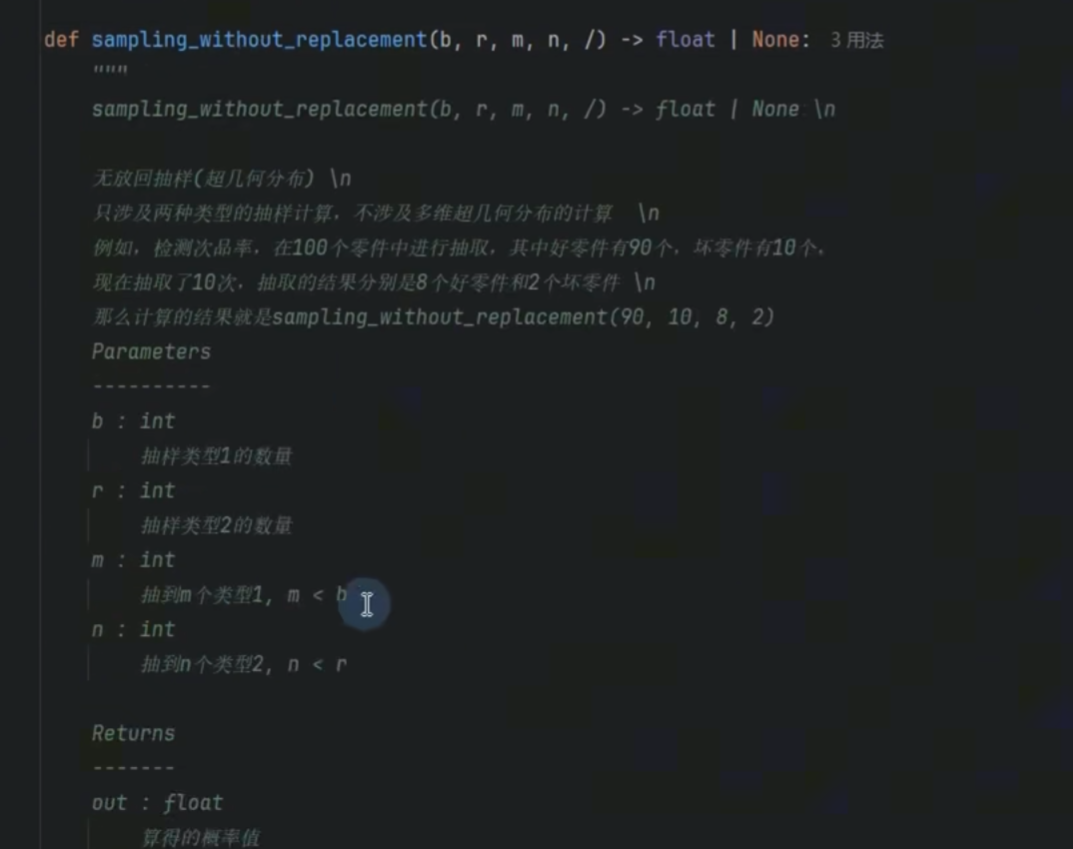
python
P = C(b, m) × C(r, n) / C(b+r, m+n)
其中:
C(n, k)是组合数,表示从n个不同元素中取k个的方式数
分子:从b个第一类中取m个的方式数 × 从r个第二类中取n个的方式数
分母:从总数(b+r)中取总数(m+n)的所有可能方式数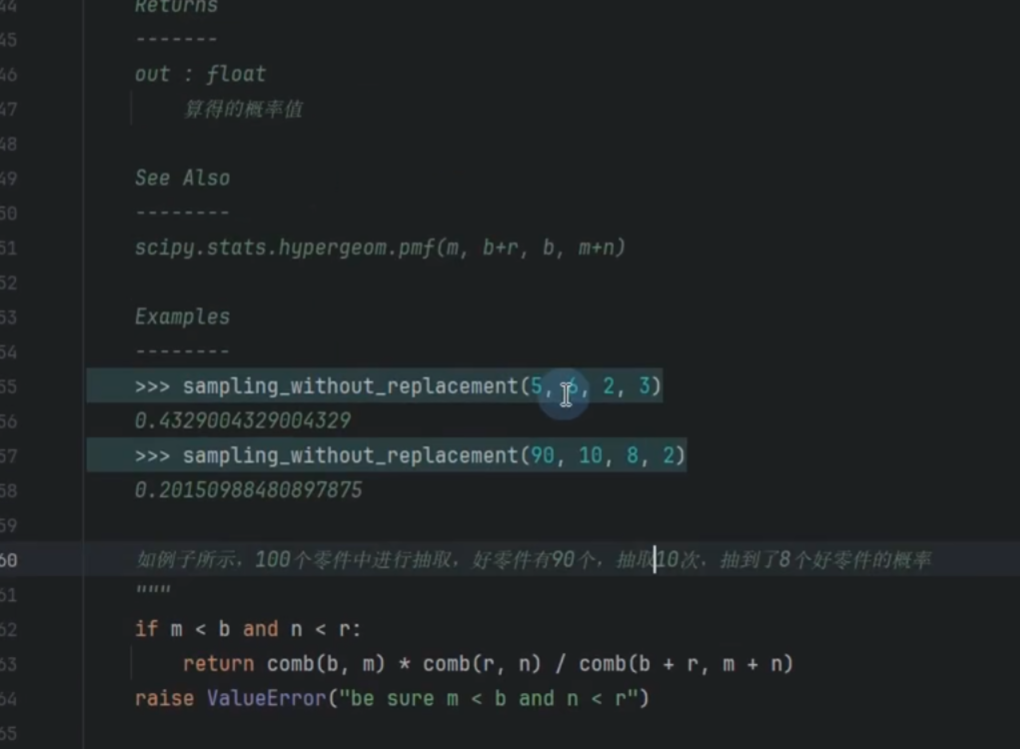
放回抽样
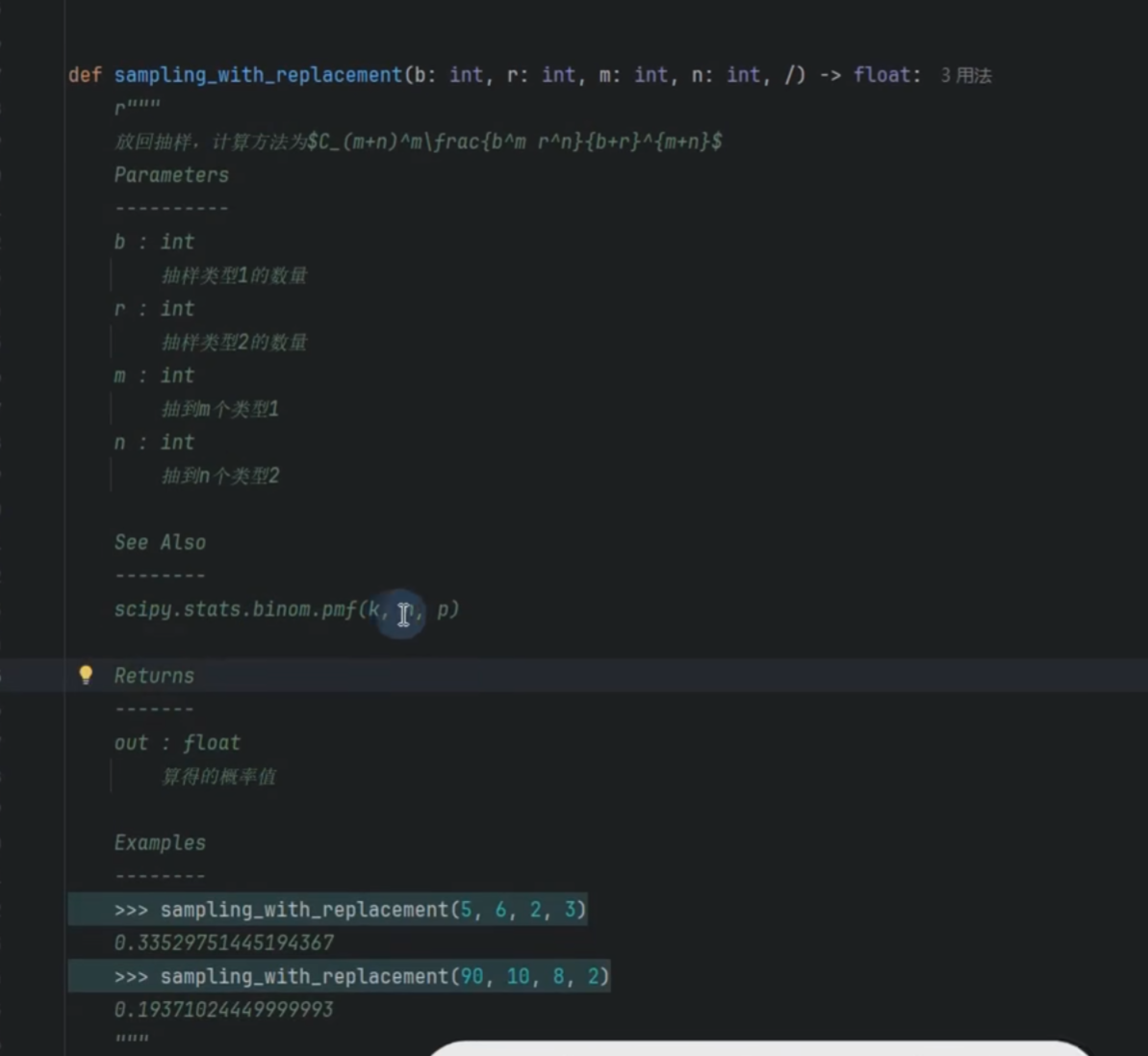
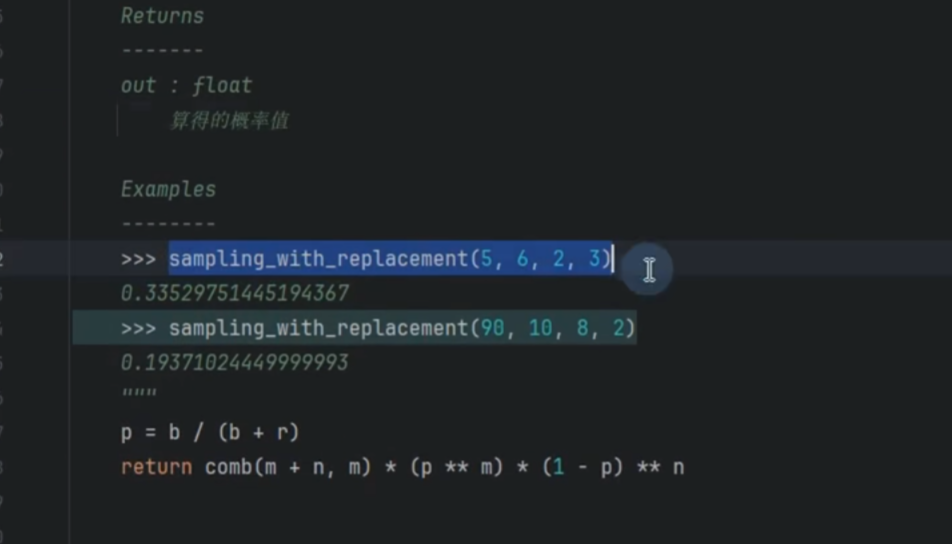
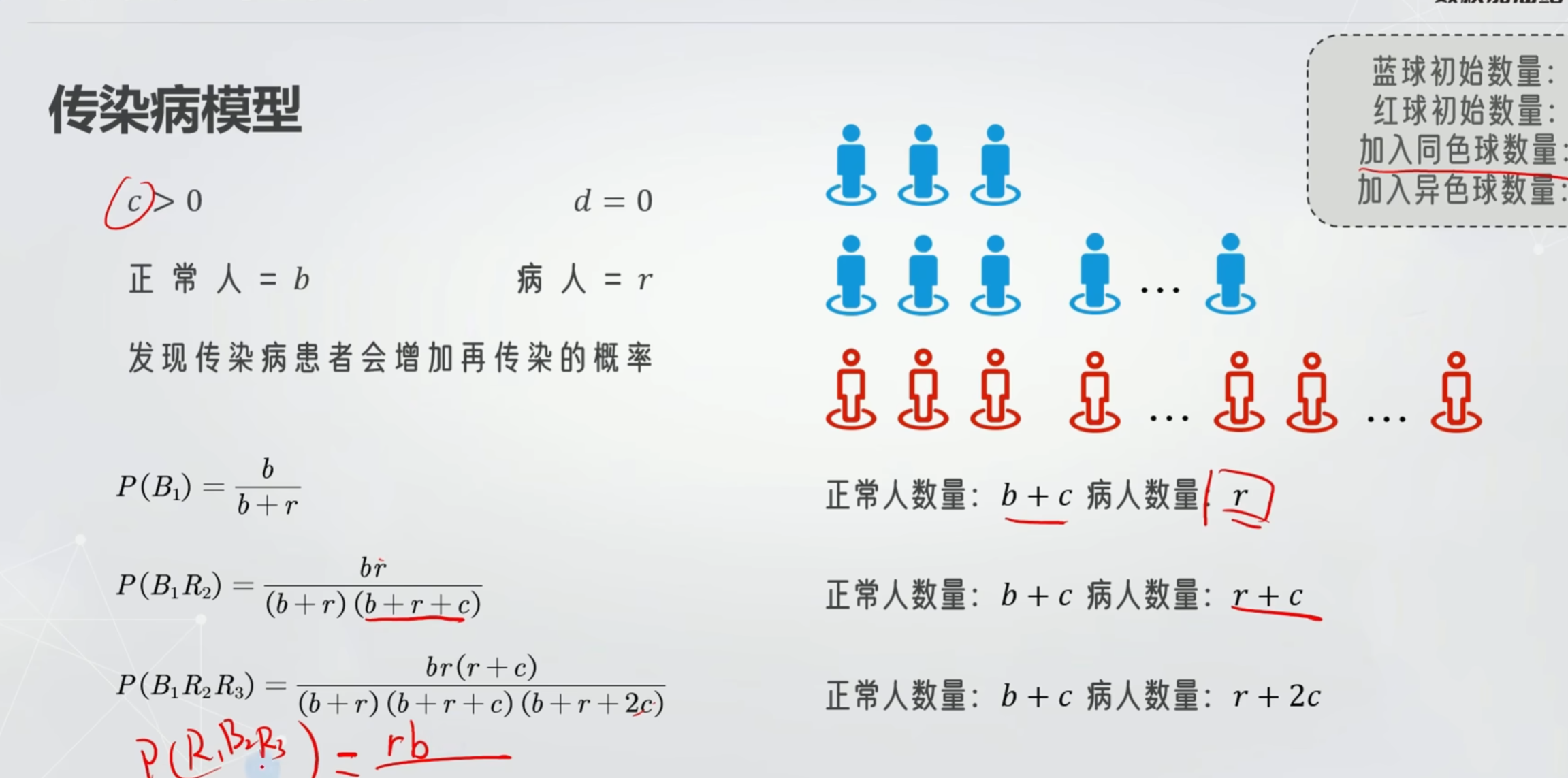
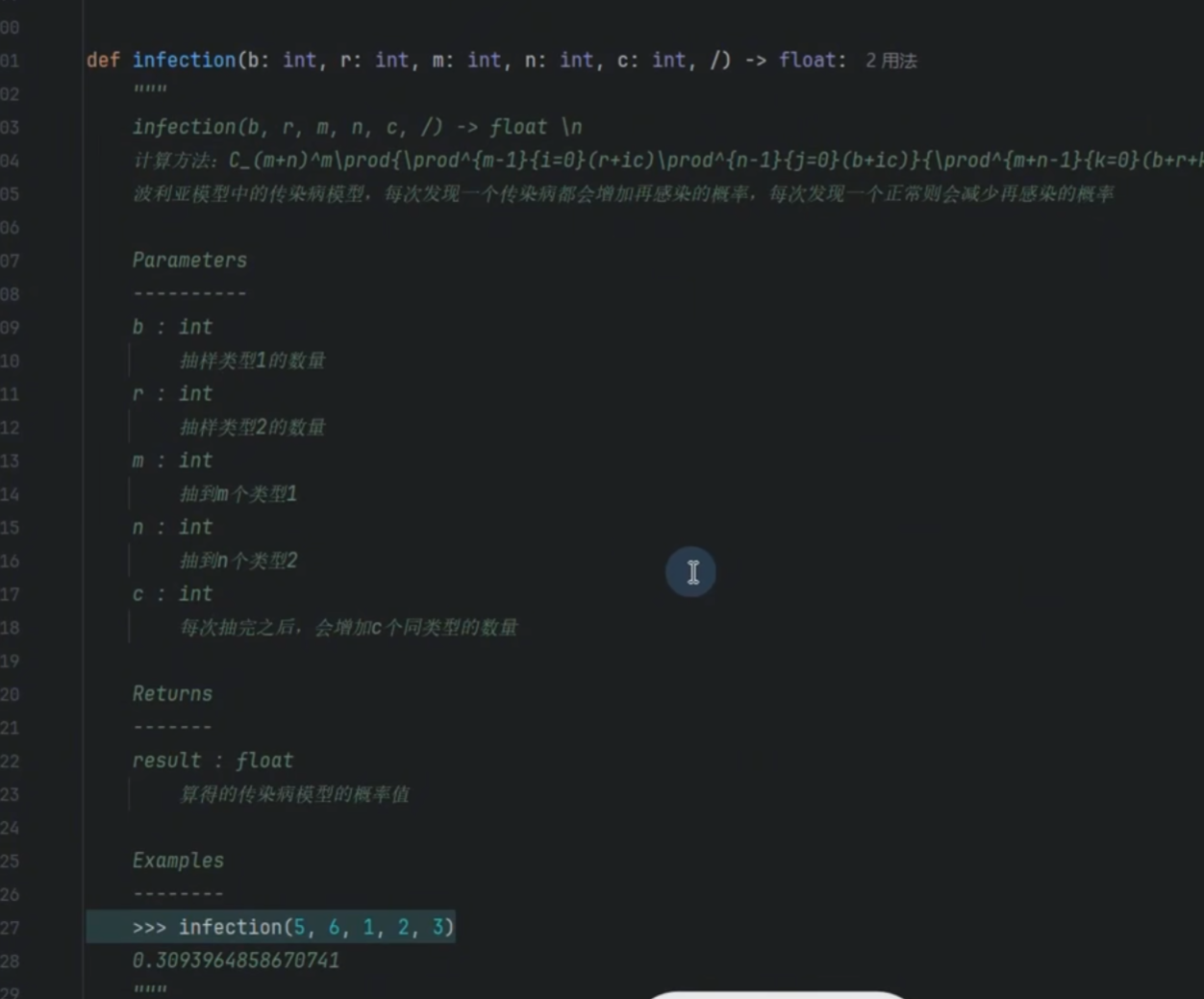
传染病模型
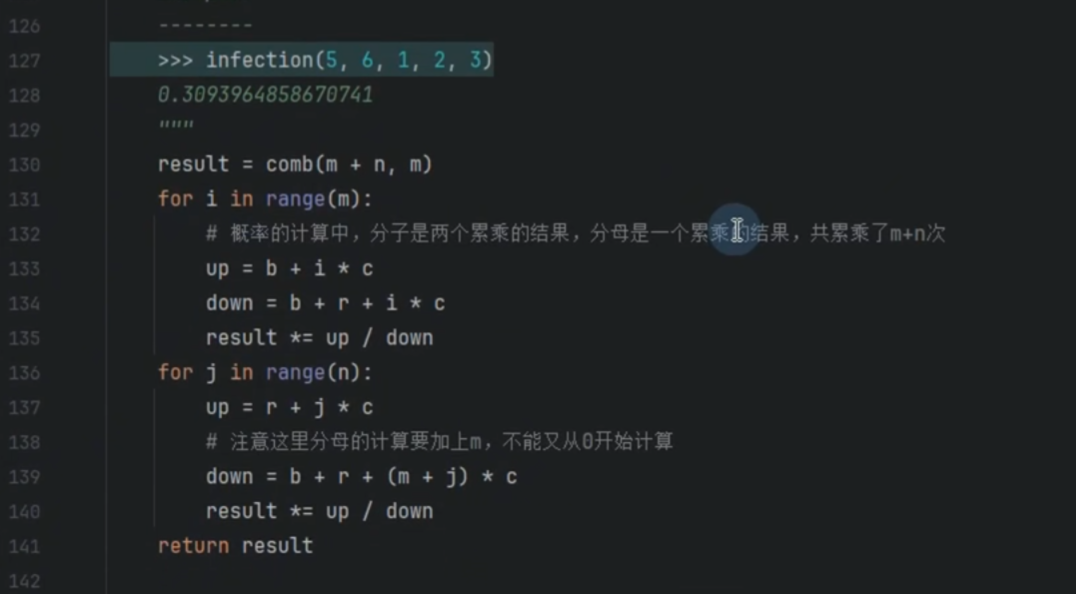
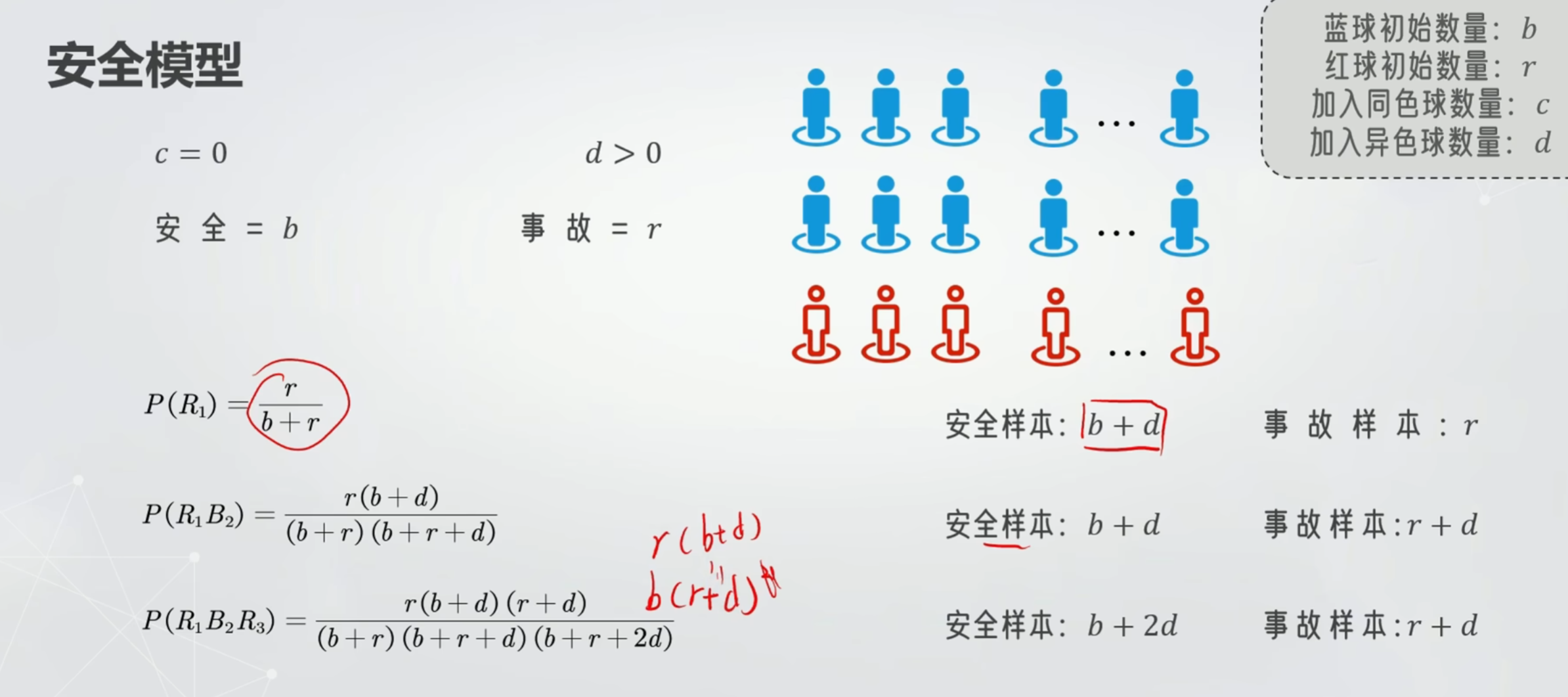
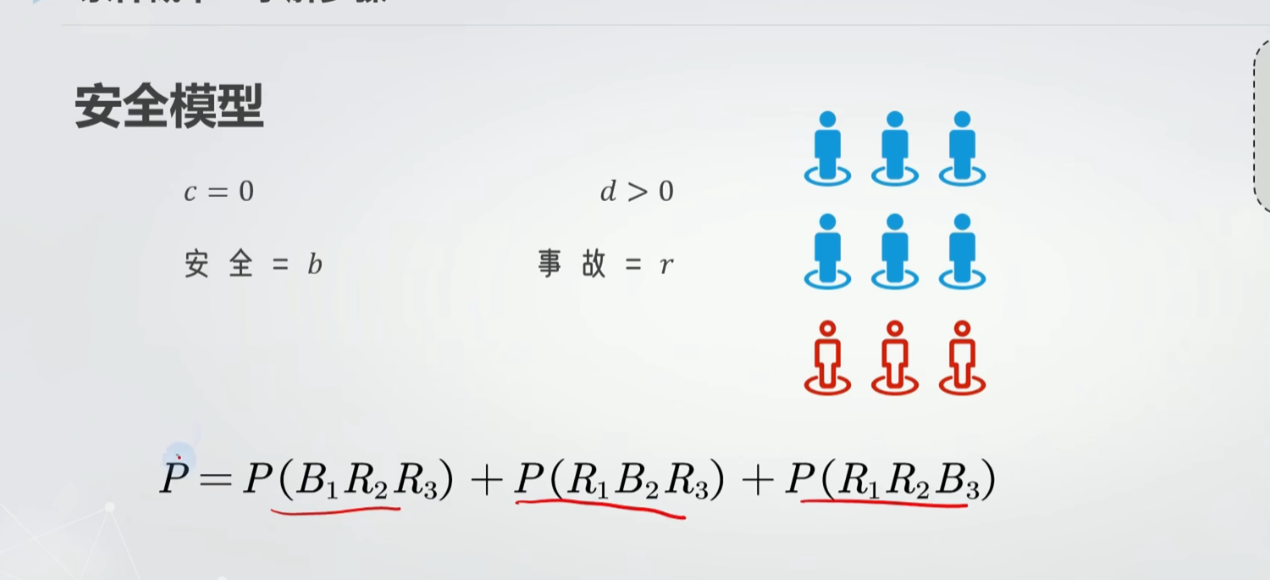
安全模型
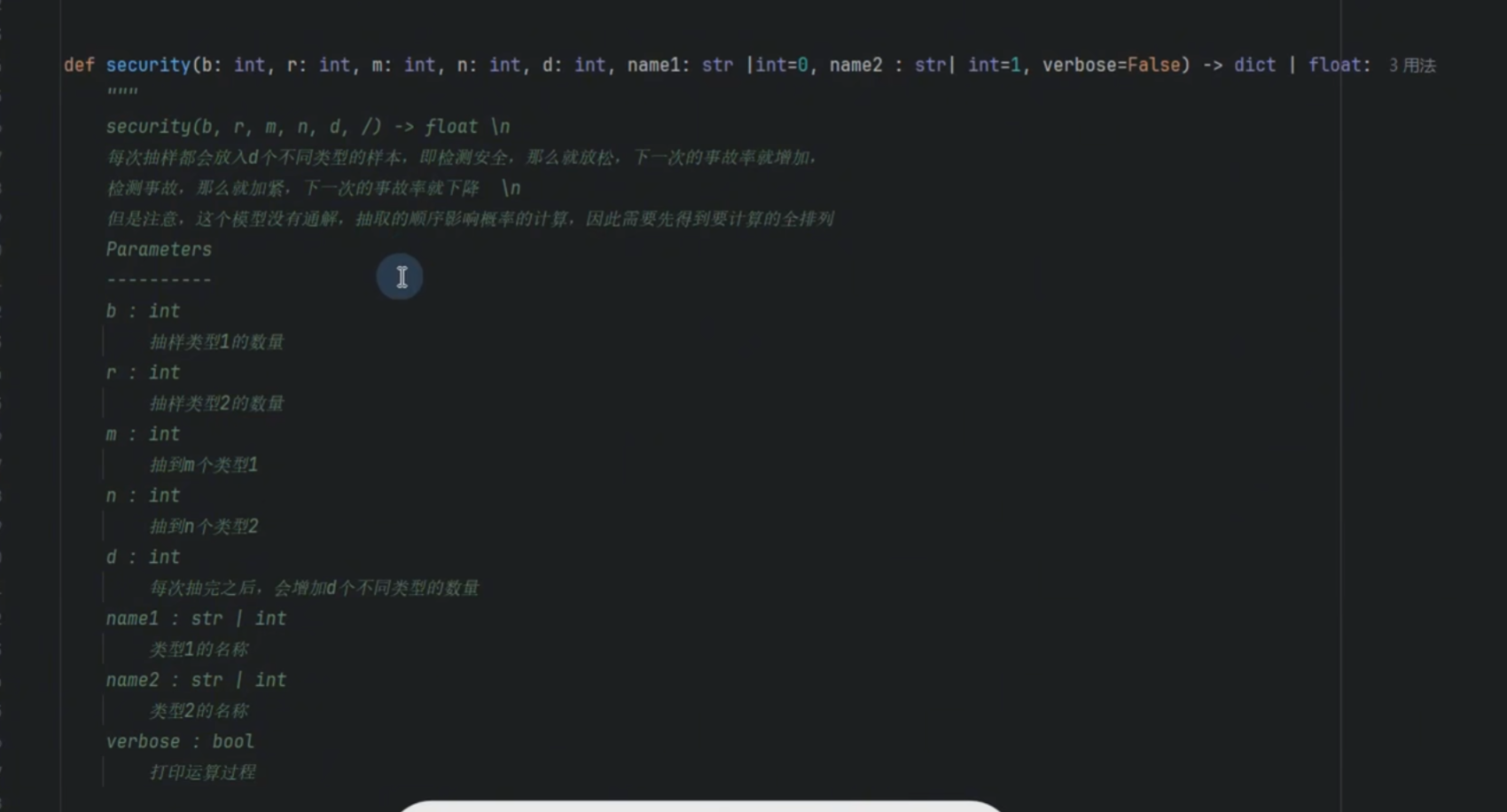
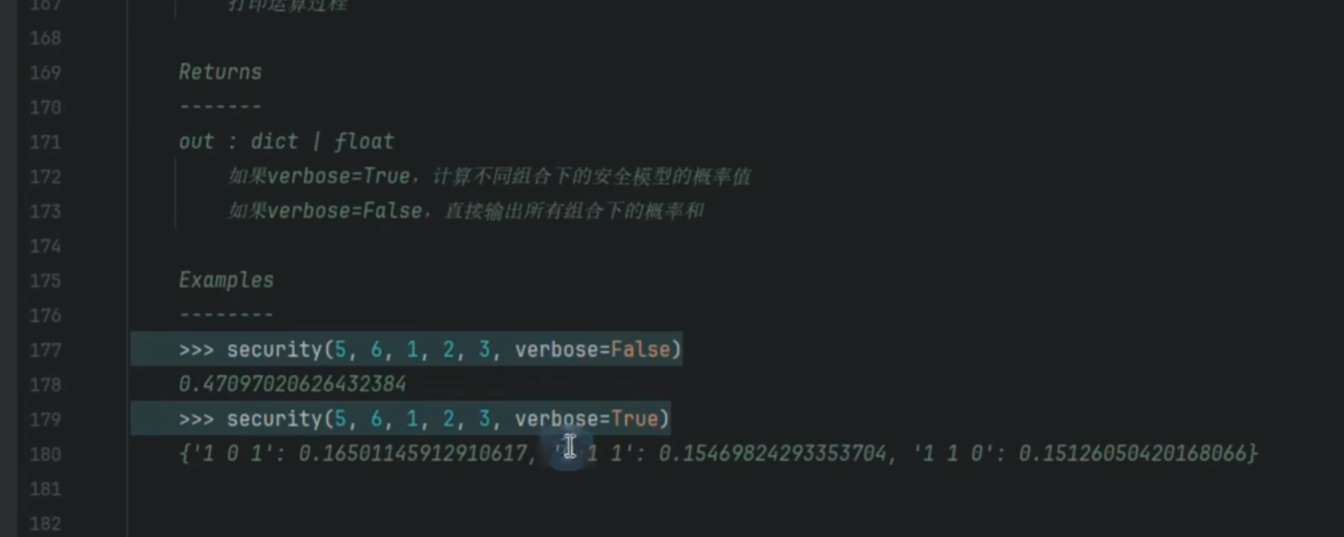
python
name1, name2 = str(name1), str(name2)
array = [name1] * m + [name2] * n
将两个类型名称转为字符串
创建包含 m个 name1和 n个 name2的列表
permutations = set(itertools.permutations(array))
生成所有可能的抽取顺序排列
使用 set()去除重复排列(因为有相同元素)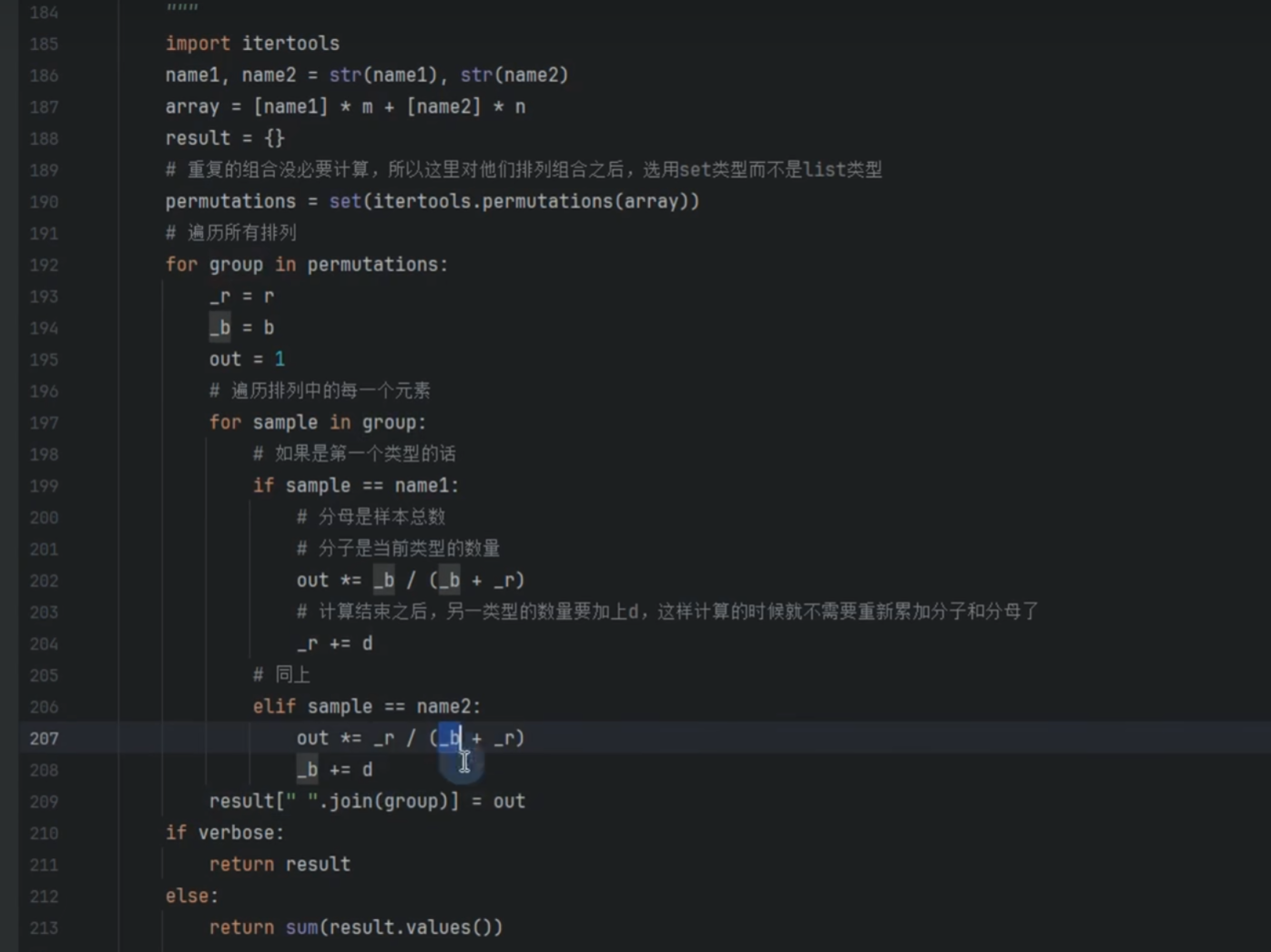
二 独立性
1 理解




2 案例

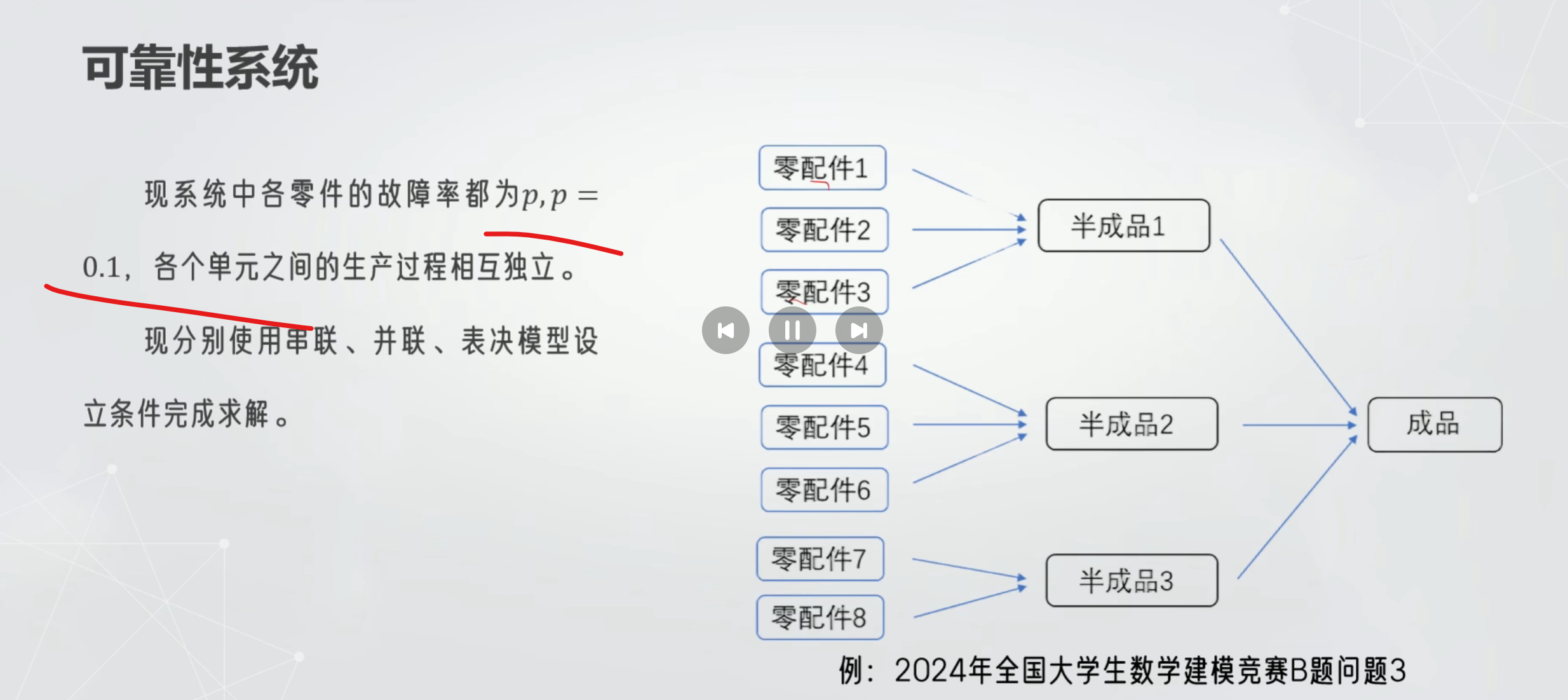
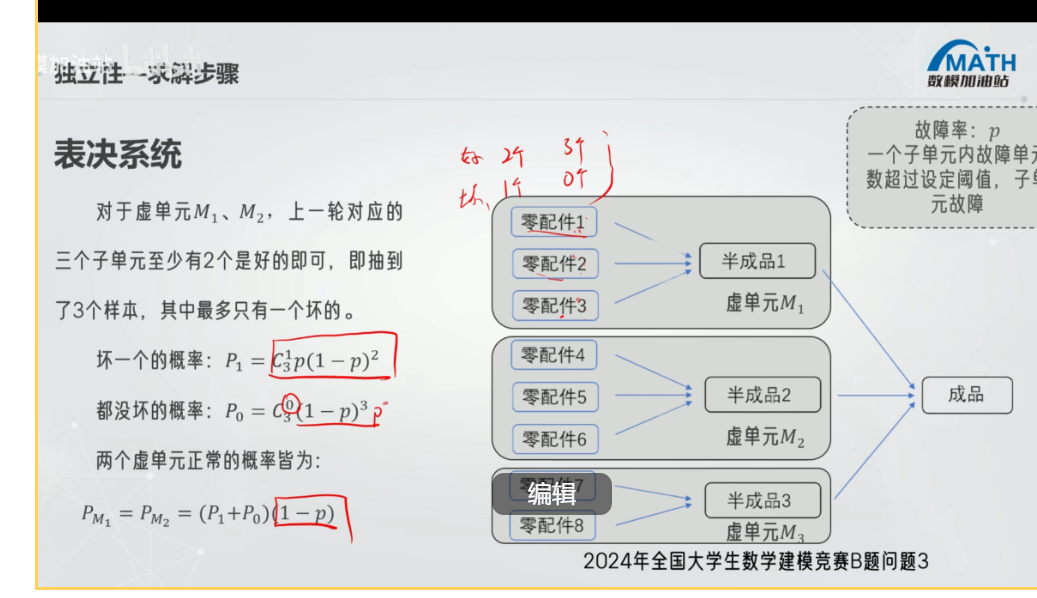
创建虚单元
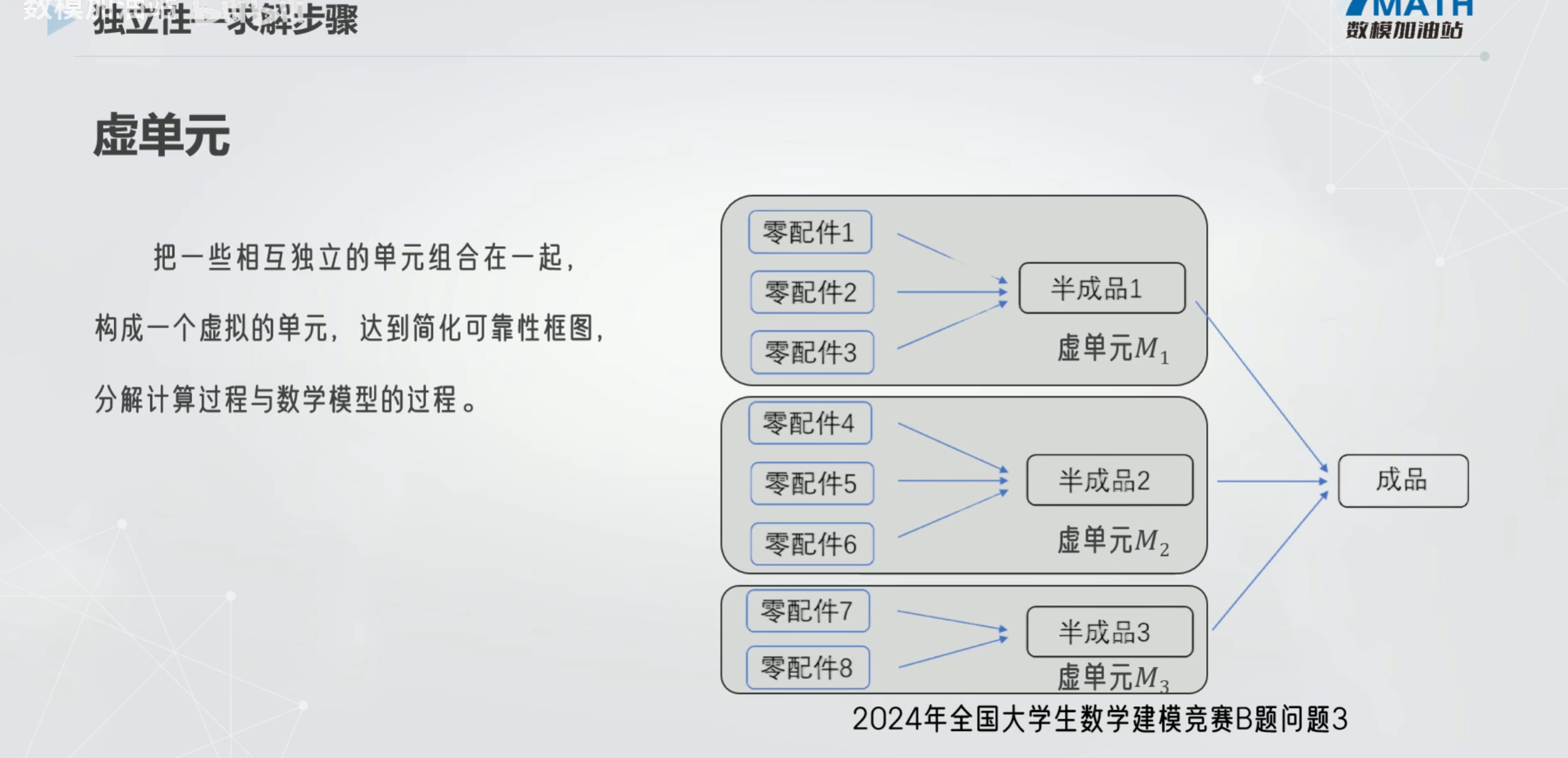
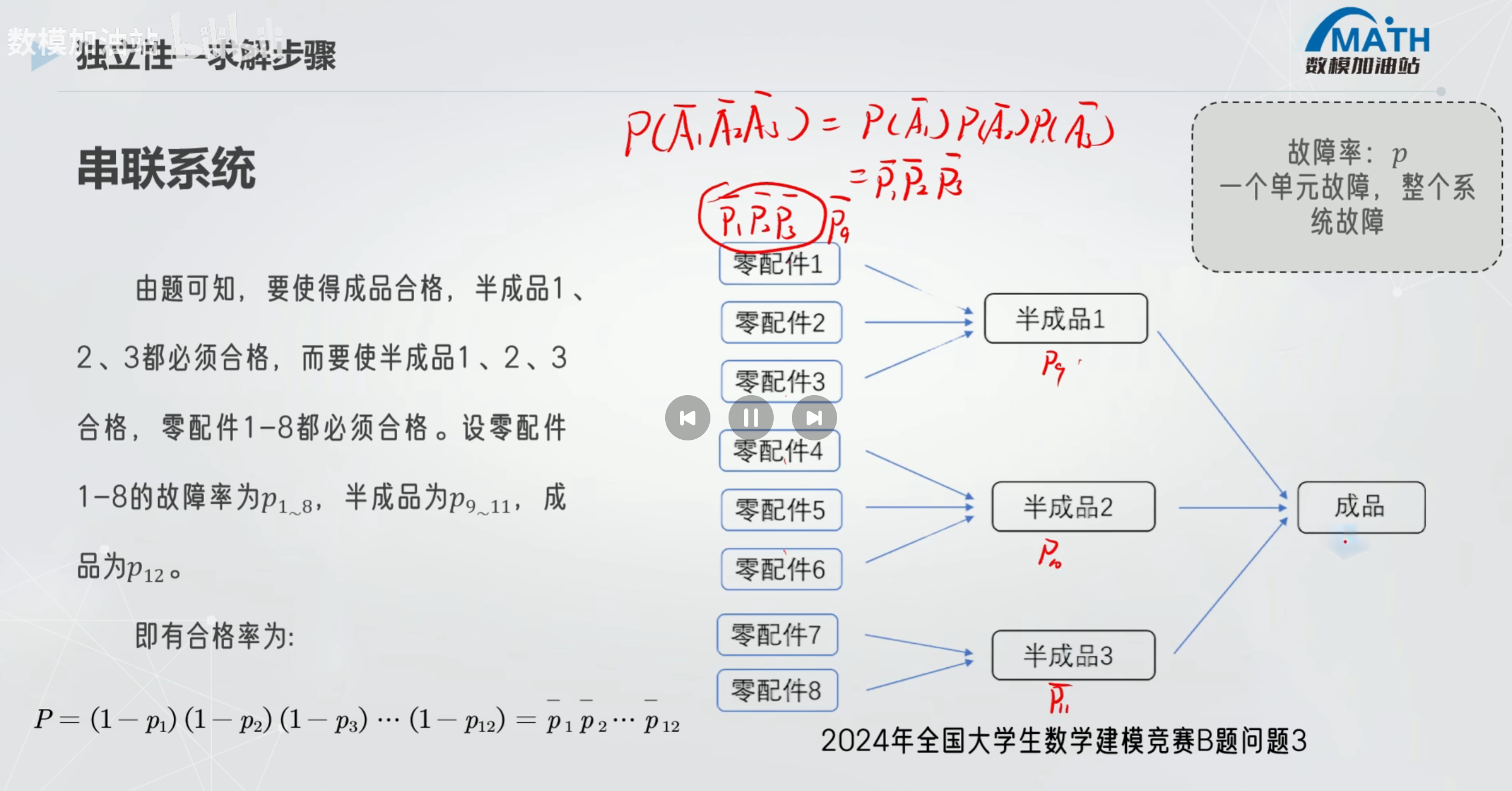

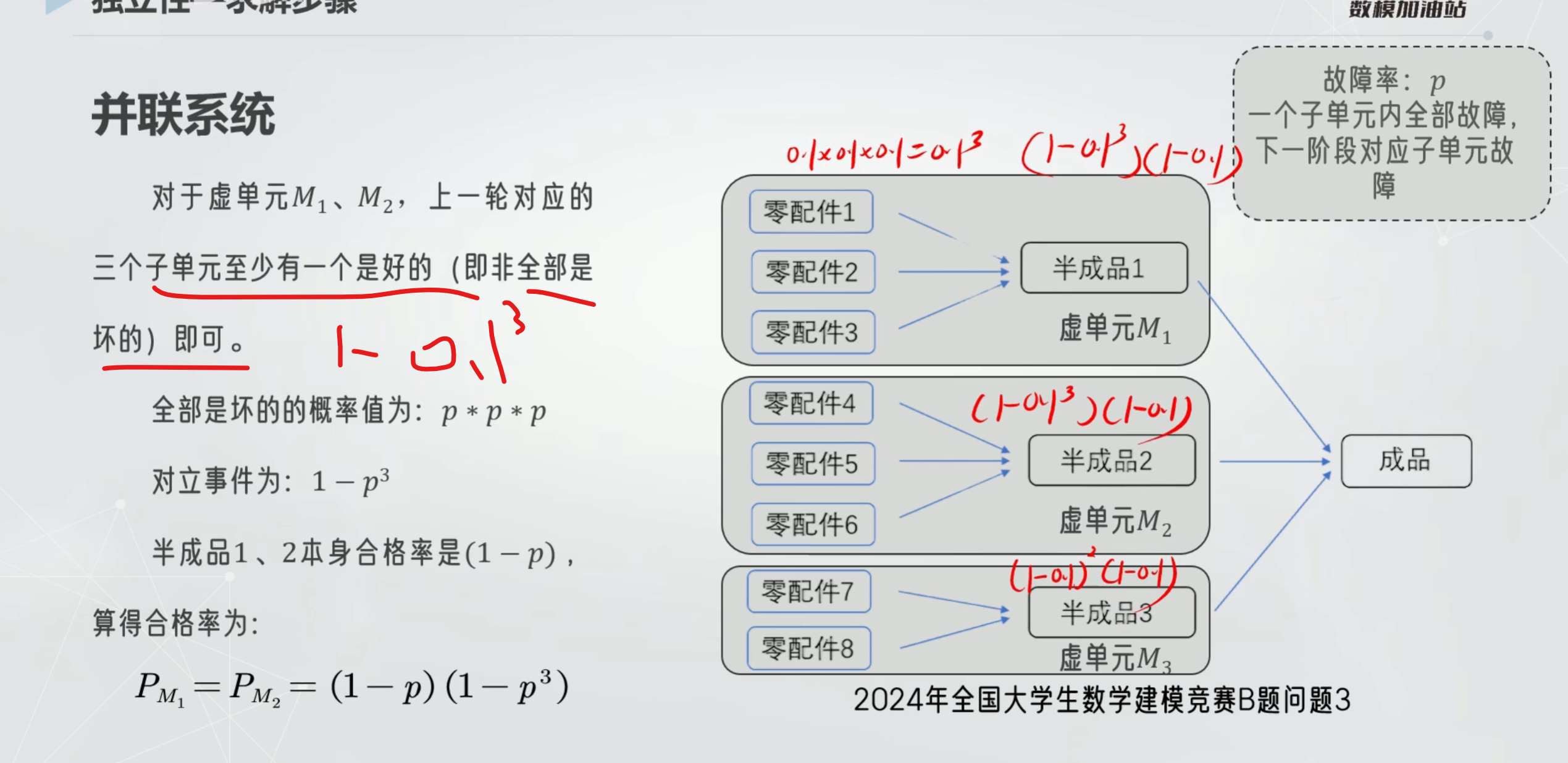

当成品失效 那么至少有一个成功的就是1-全部失效

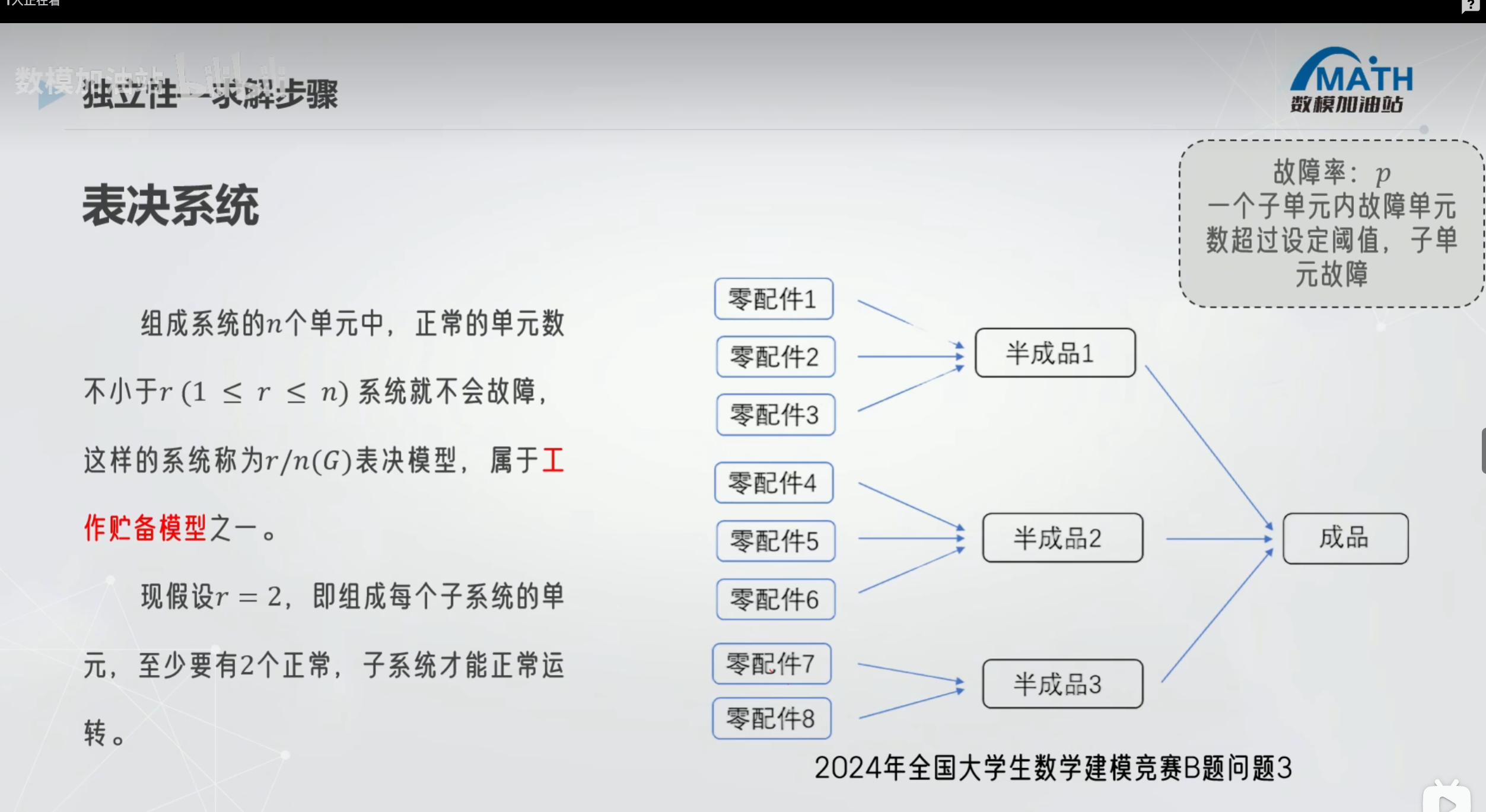
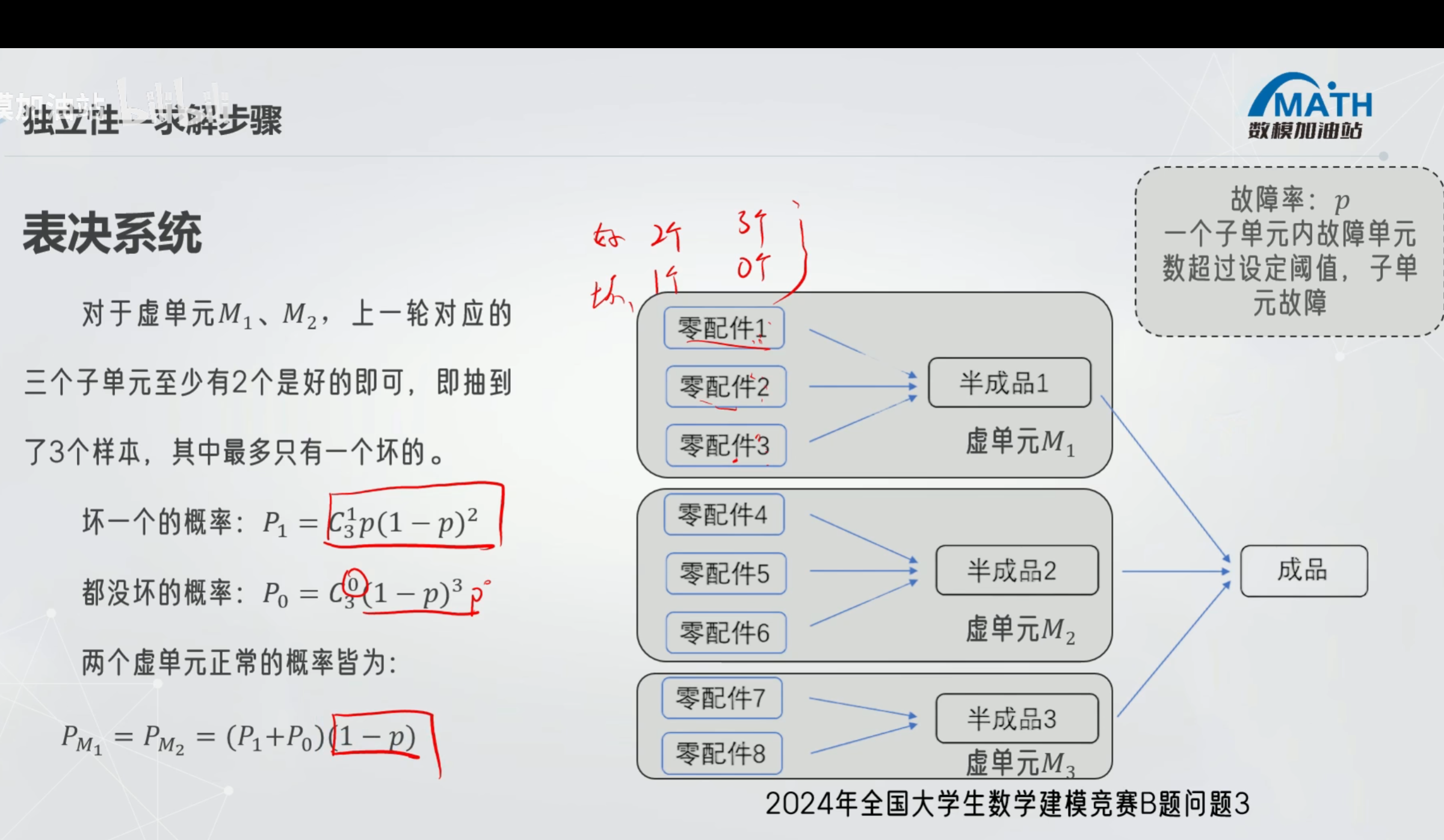
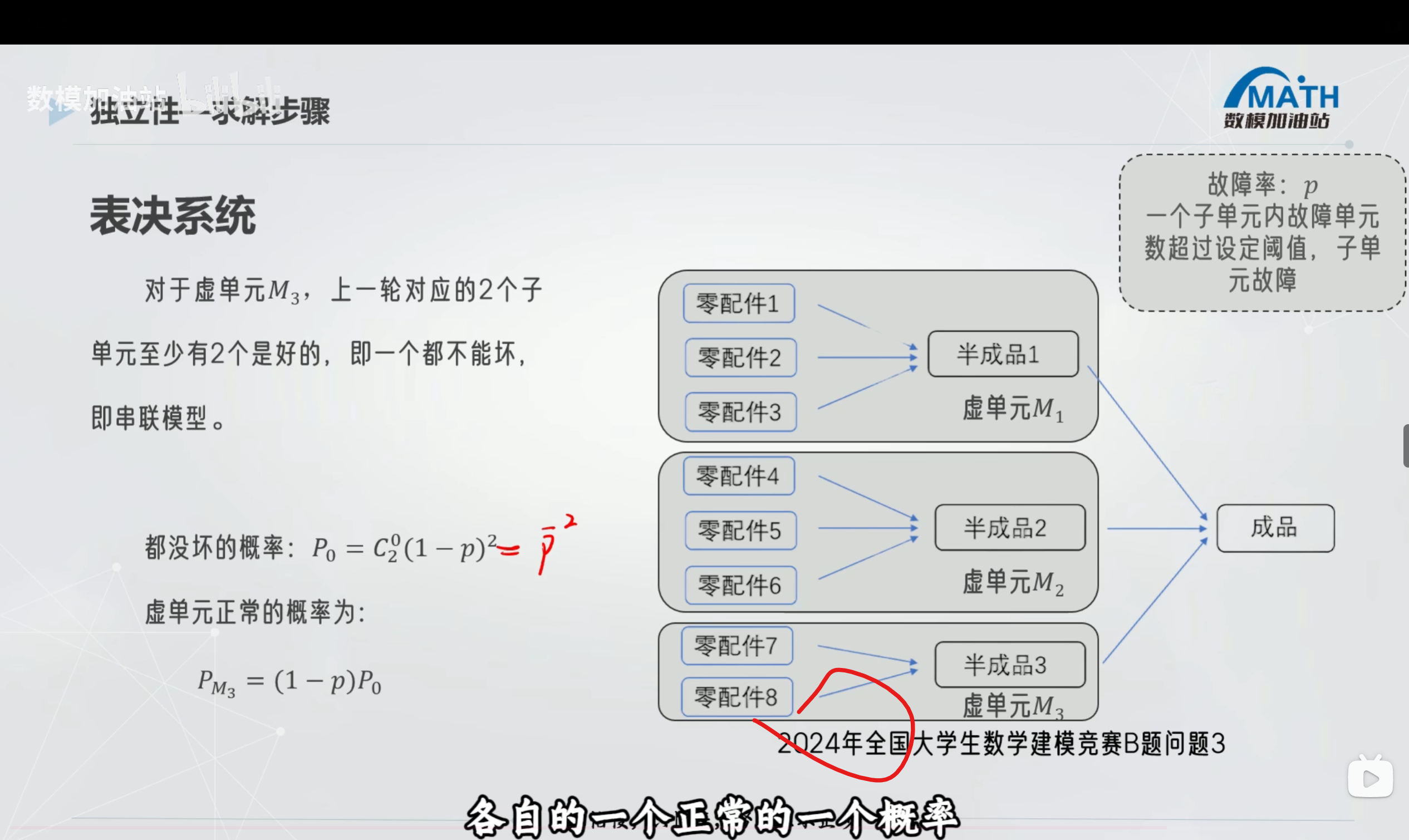

3 python代码
串联
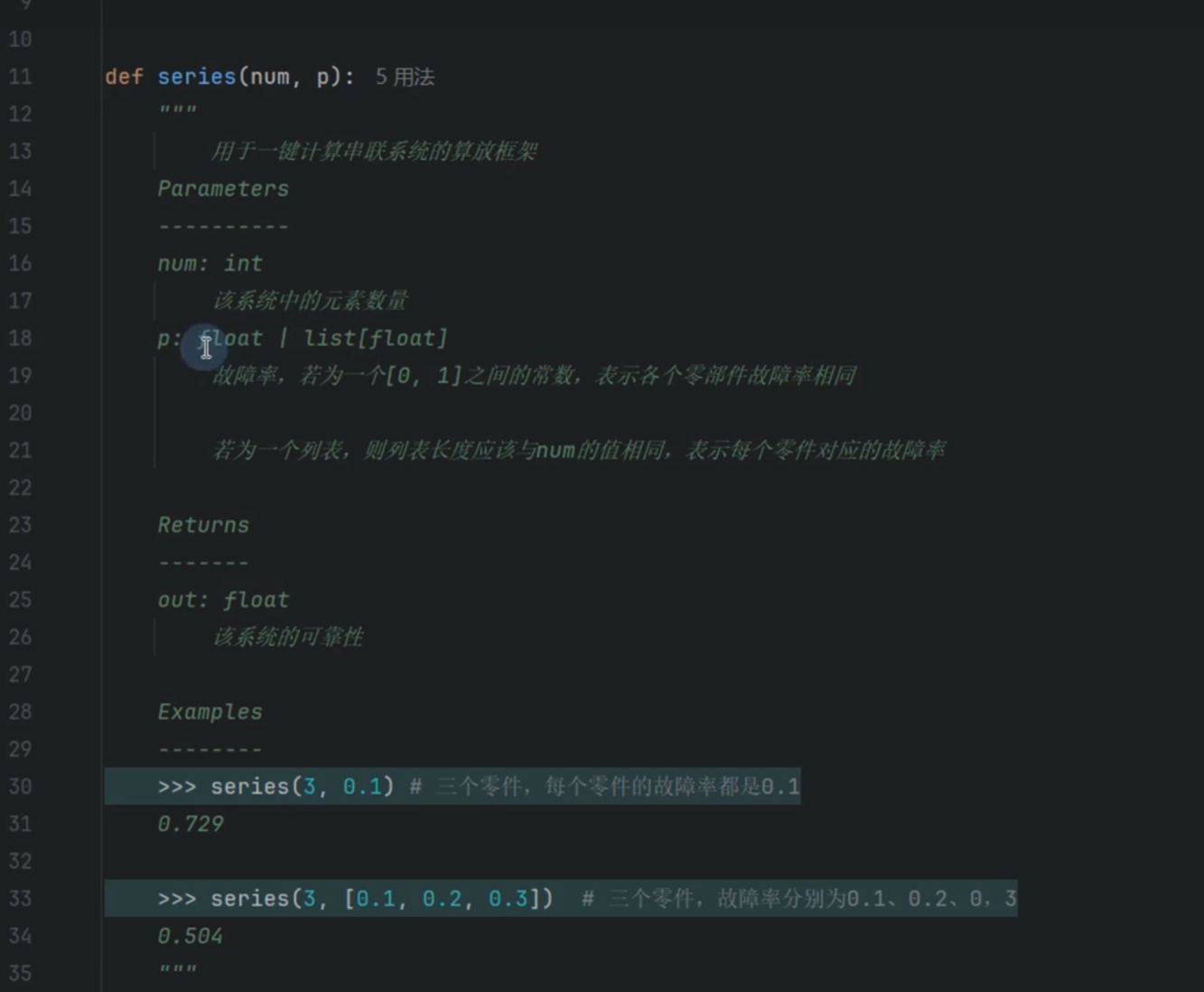
python
p = [p] * num将单个浮点数扩展为长度为 num的列表,每个元素都是这个浮点数
p = [1 - i for i in p]
此时 p已经是列表,每个元素是故障率。
列表推导式遍历每个故障率 i,计算 1 - i得到单个部件的可靠率。
原地重命名变量:这里变量名 p被重新赋值为可靠率列表。
python
return round(reduce(lambda x, y: x * y, p), 5)
reduce函数(来自 functools模块):
对列表 p执行累积乘法。lambda x, y: x * y等价于乘法运算,
例如列表p为[0.9, 0.8, 0.7]计算过程是:
((0.9 * 0.8) * 0.7) = 0.504
round(..., 5):
保留 5 位小数,避免浮点数精度问题输出过长小数,符合工程精度要求。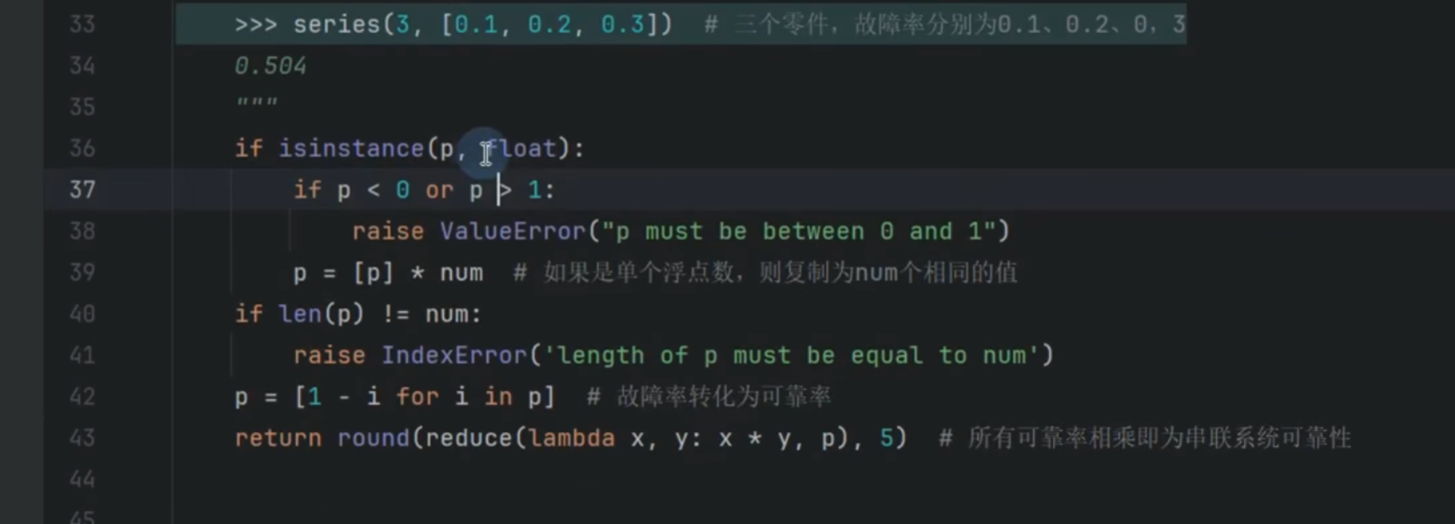
并联
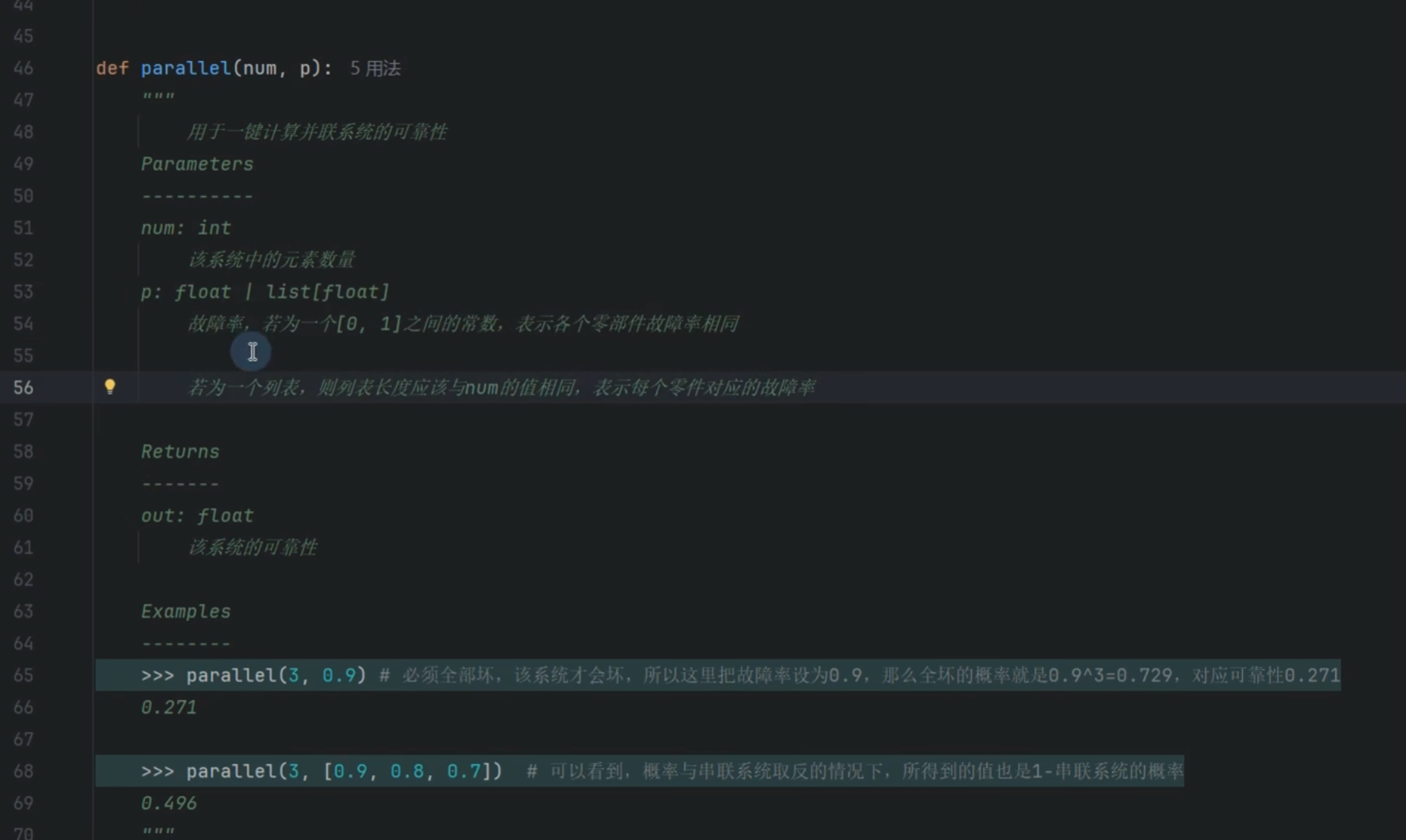
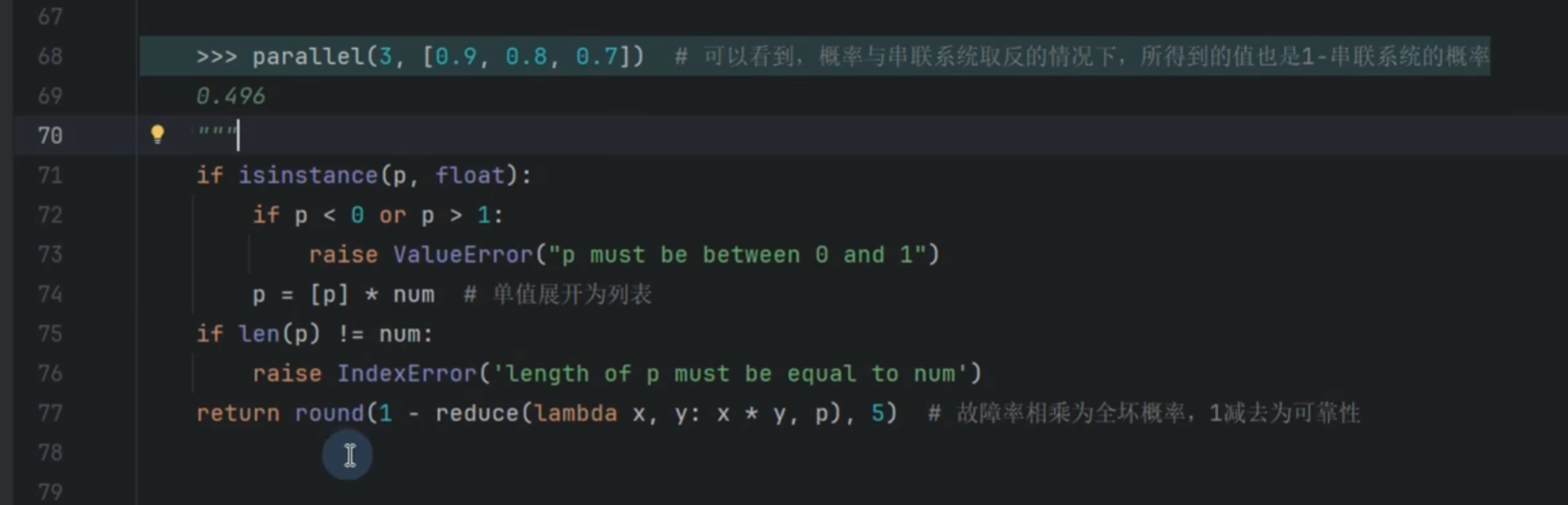
表决系统
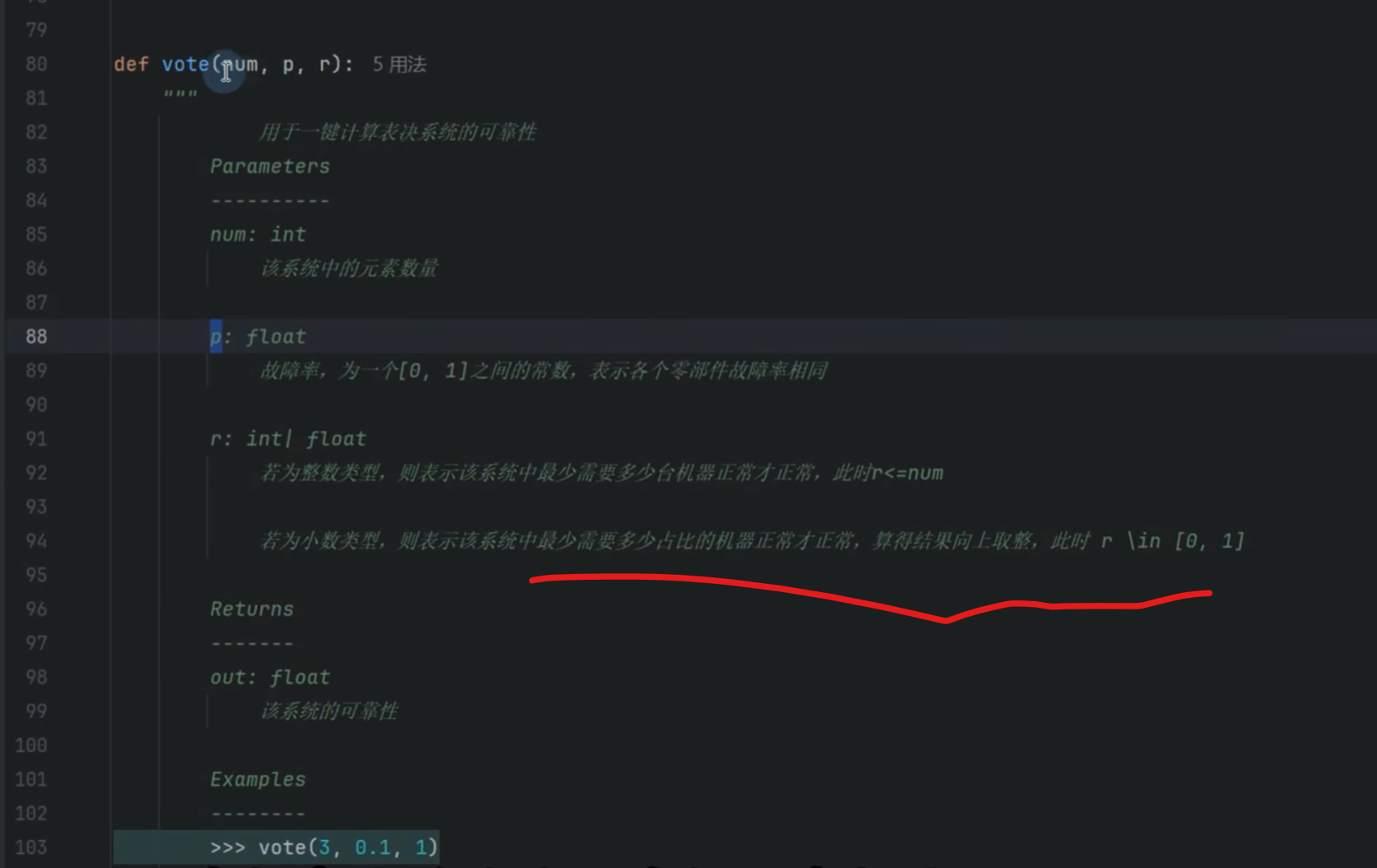
python
r = math.ceil(num * r)
这里输入的 r其实是"至少需要正常的比例"(比如 0.7 表示 70%),并不是整数。
math.ceil(num * r)将其转为至少需要多少台设备正常的最小整数 k
if isinstance(r, float) and 0 < r < 1:
r = math.ceil(num * r)
浮点数 r处理:如果 r是 0 到 1 之间的浮点数,则视为比例,
计算最小正常部件数,并向上取整。
例如:num = 10,r = 0.7→ r = math.ceil(7) = 7。
math.ceil作用:确保至少需要的整数部件数,向上取整是安全保守的工程做法。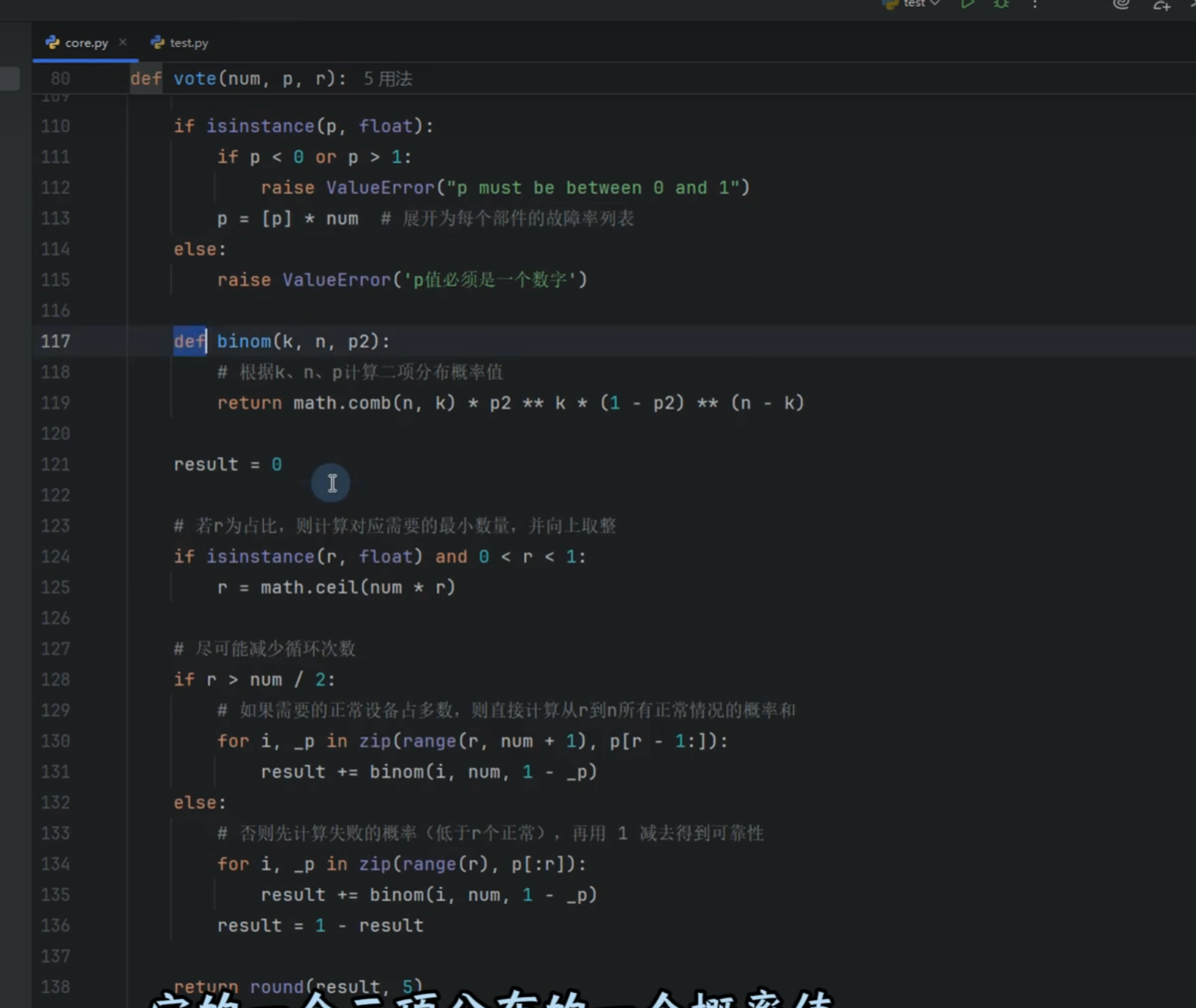
选择小的数

三 常用分布
1 理解





2 python代码
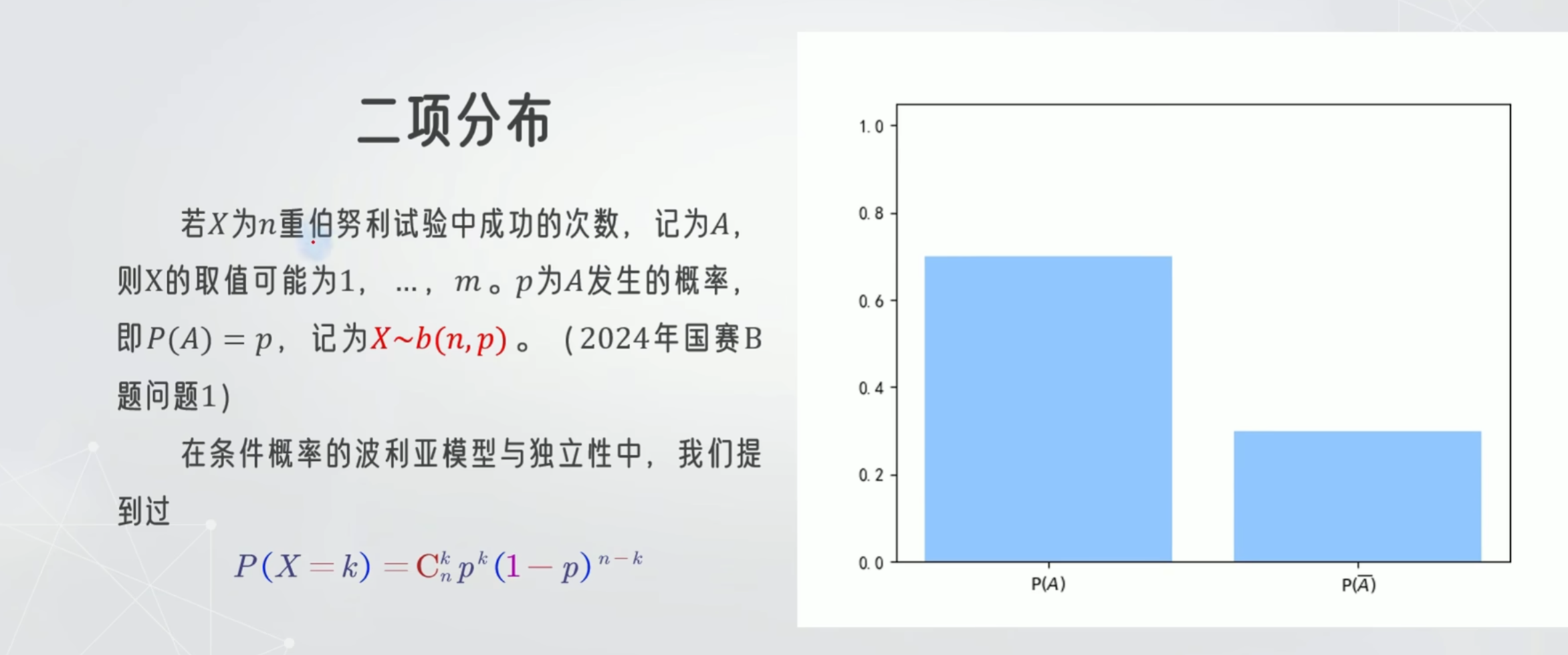
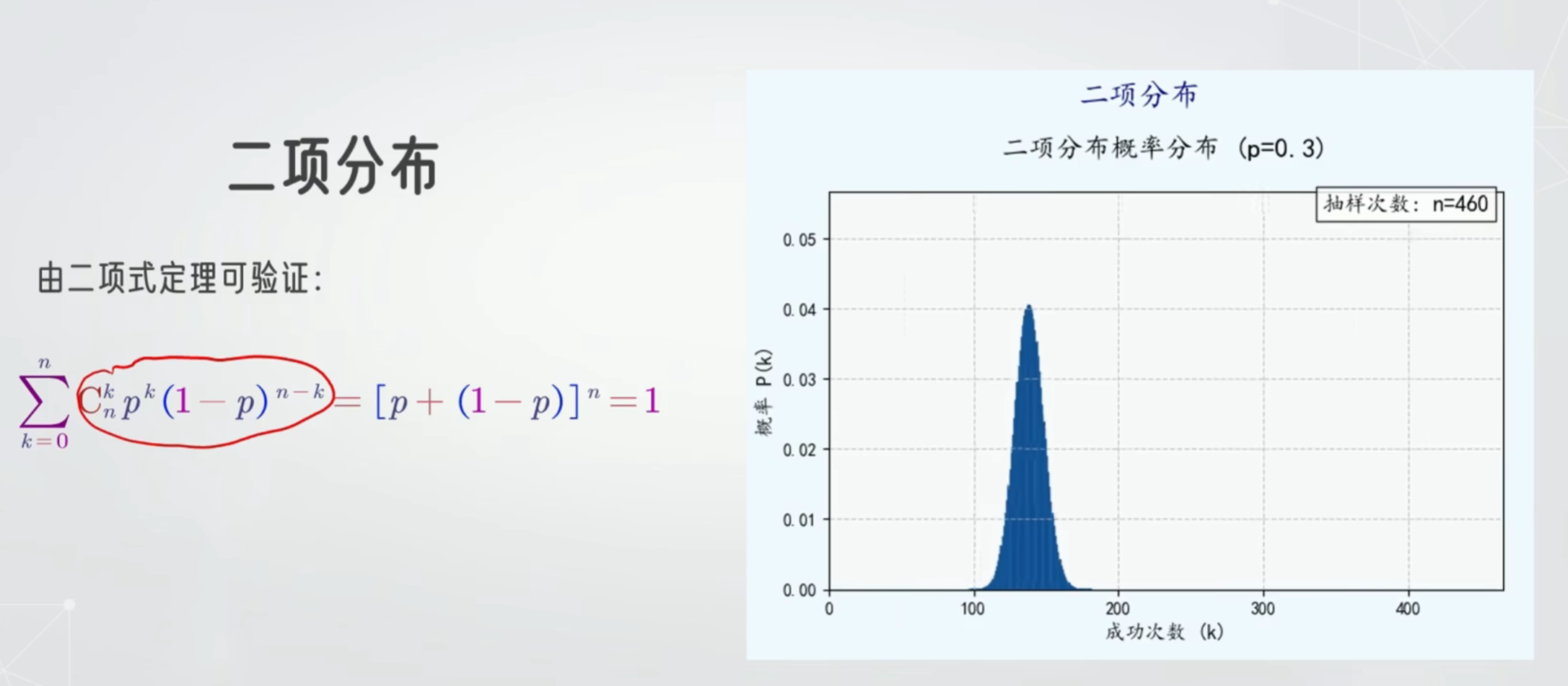
二项分布
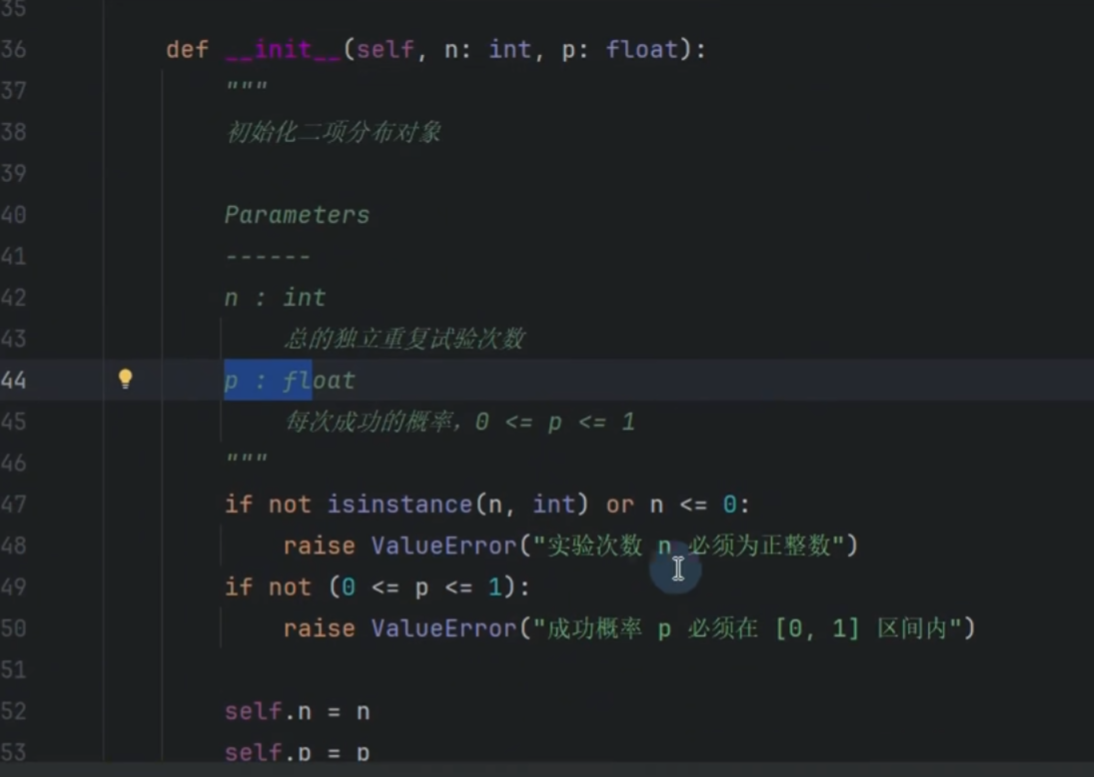
python
self.n = n
self.p = p
将外部传入的 n和 p参数存储为对象的属性。这是创建对象状态的基础。
python
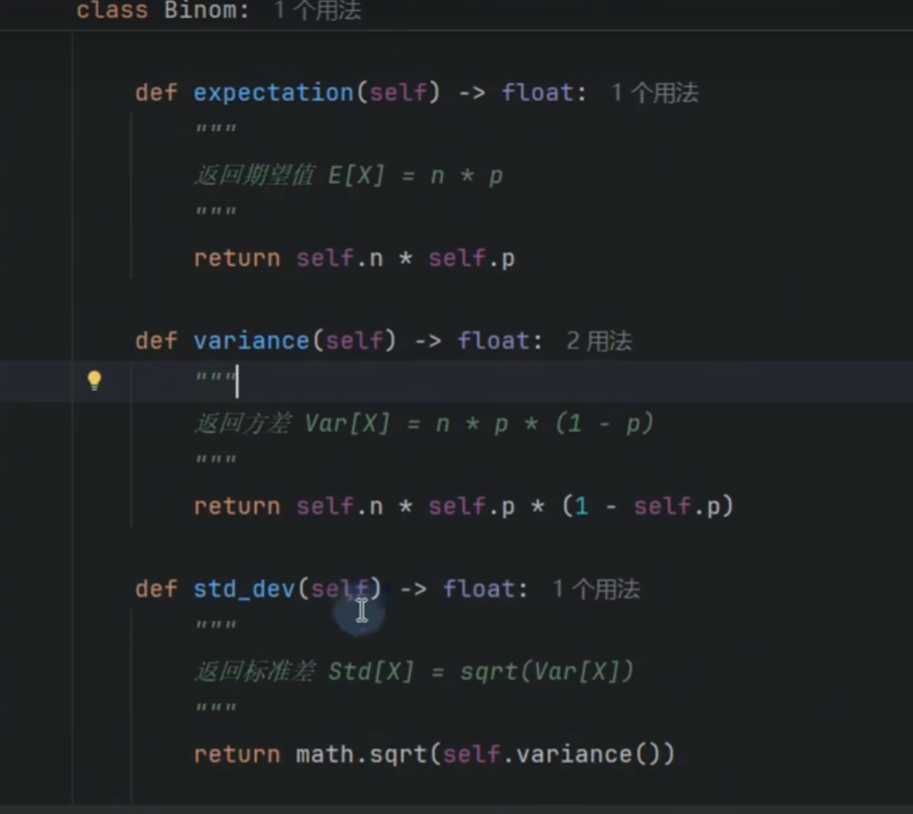
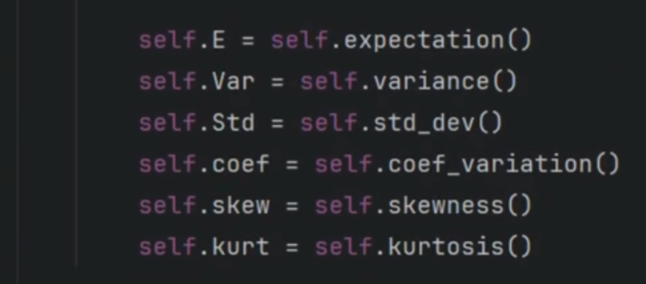
self.E = self.expectation()
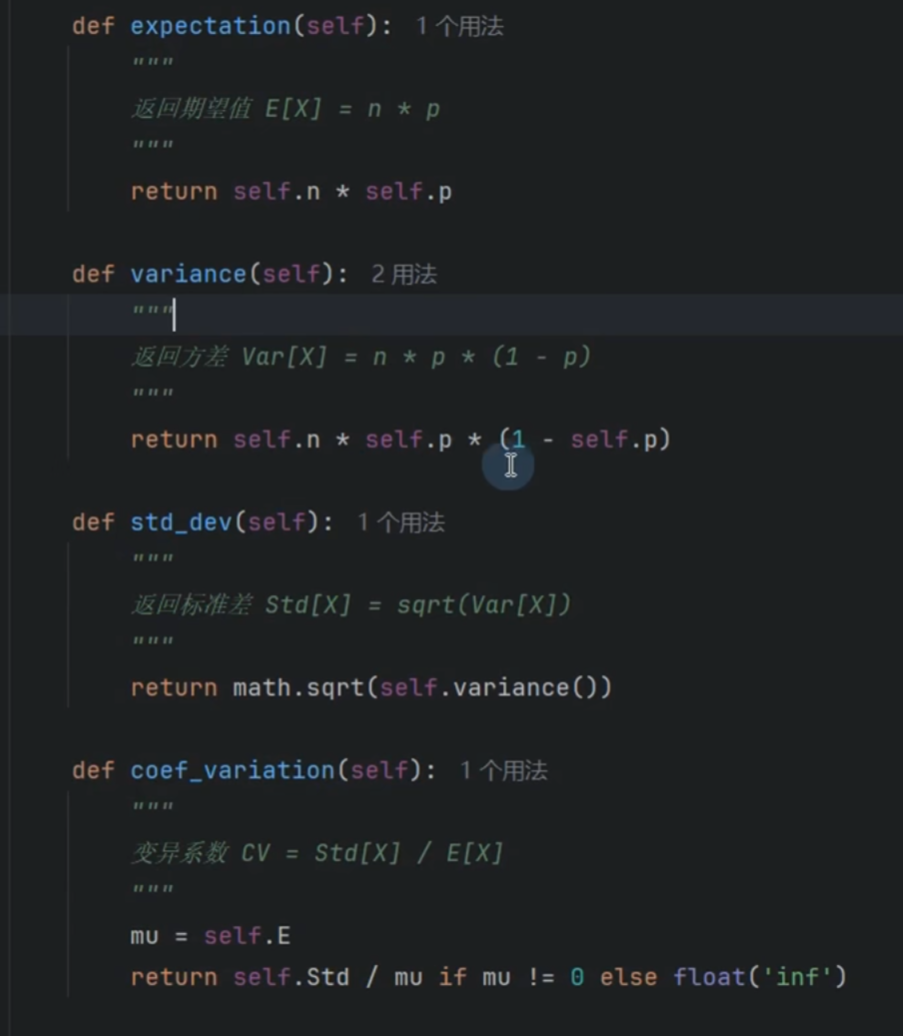
功能:计算并存储该分布的数学期望(Expectation)。
计算公式:对于二项分布,期望的公式是 E = n * p。
self.Var = self.variance()
功能:计算并存储该分布的方差(Variance)。
计算公式:对于二项分布,方差的公式是 Var = n * p * (1-p)。
self.Std = self.variance() ❌ 这里有错误
意图:本意是计算并存储该分布的标准差(Standard Deviation,Std)。
实际错误:错误地再次调用了 self.variance()方法,
导致 self.Std变量中存储的实际上是方差的值,而不是标准差。
正确做法:标准差是方差的算术平方根。应该改为:
# 方法一:直接计算
self.Std = self.Var ** 0.5
# 或方法二:如果类中有专门的方法
self.Std = self.standard_deviation()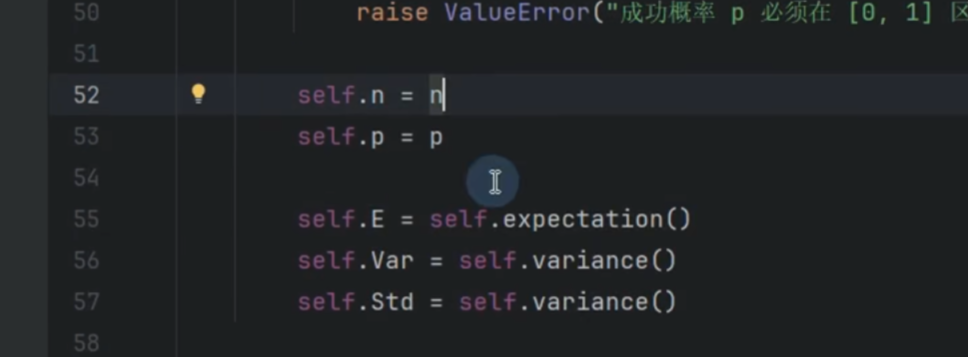
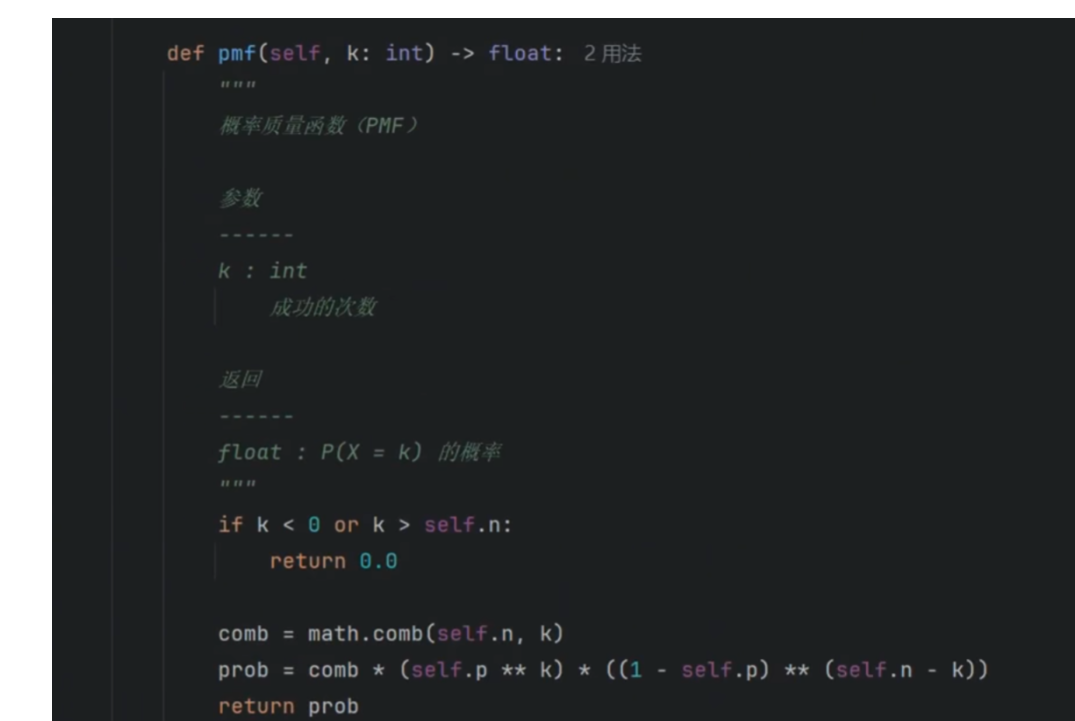
求二项分布的概率
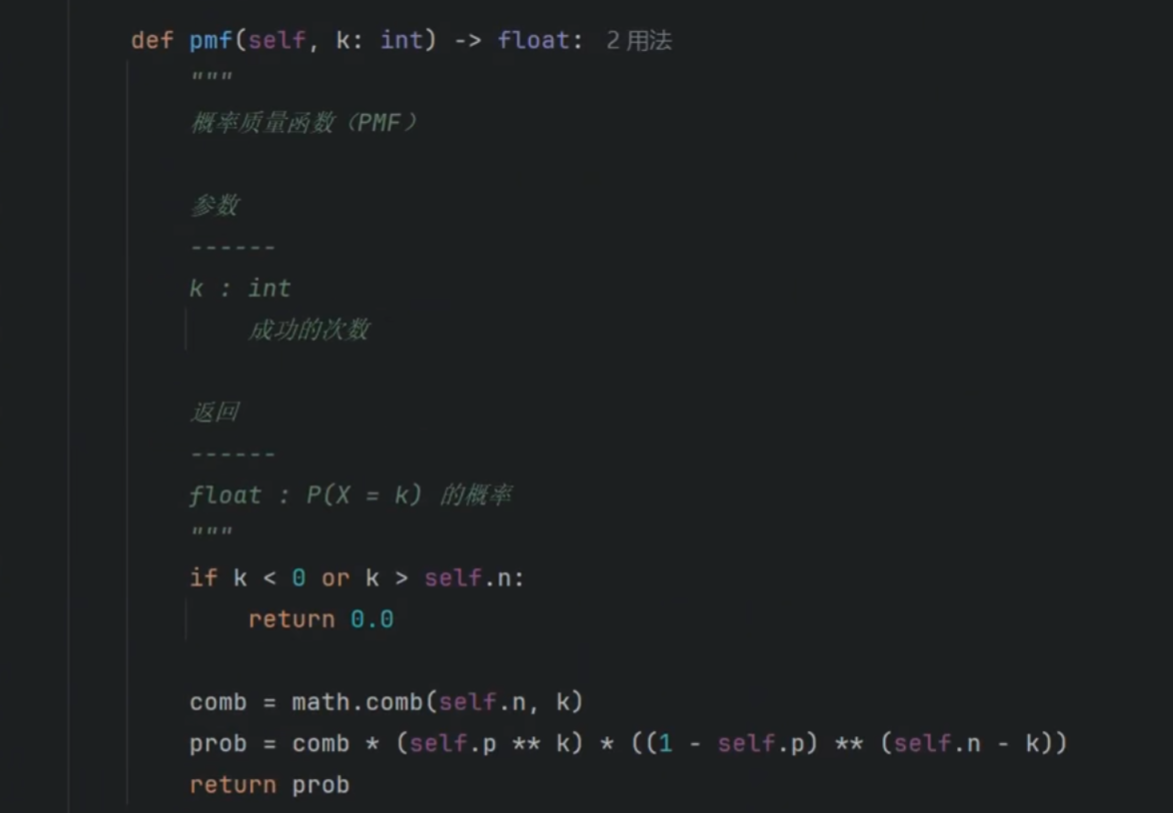
二项分布的累计函数
python
range(0, k + 1)函数创建了一个从 0 开始,到 k+1 结束(但 不包含 k+1本身)的整数序列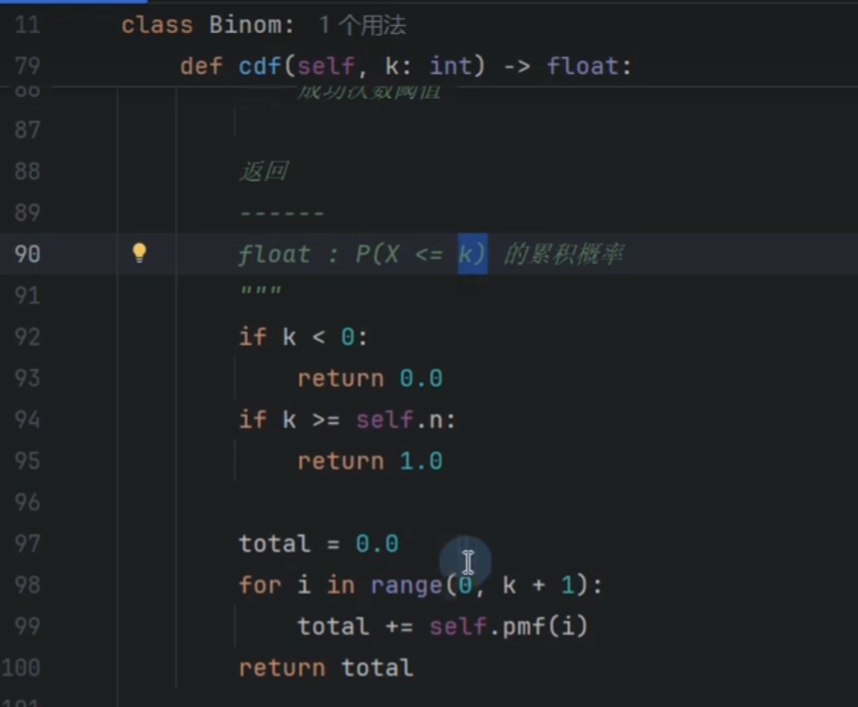
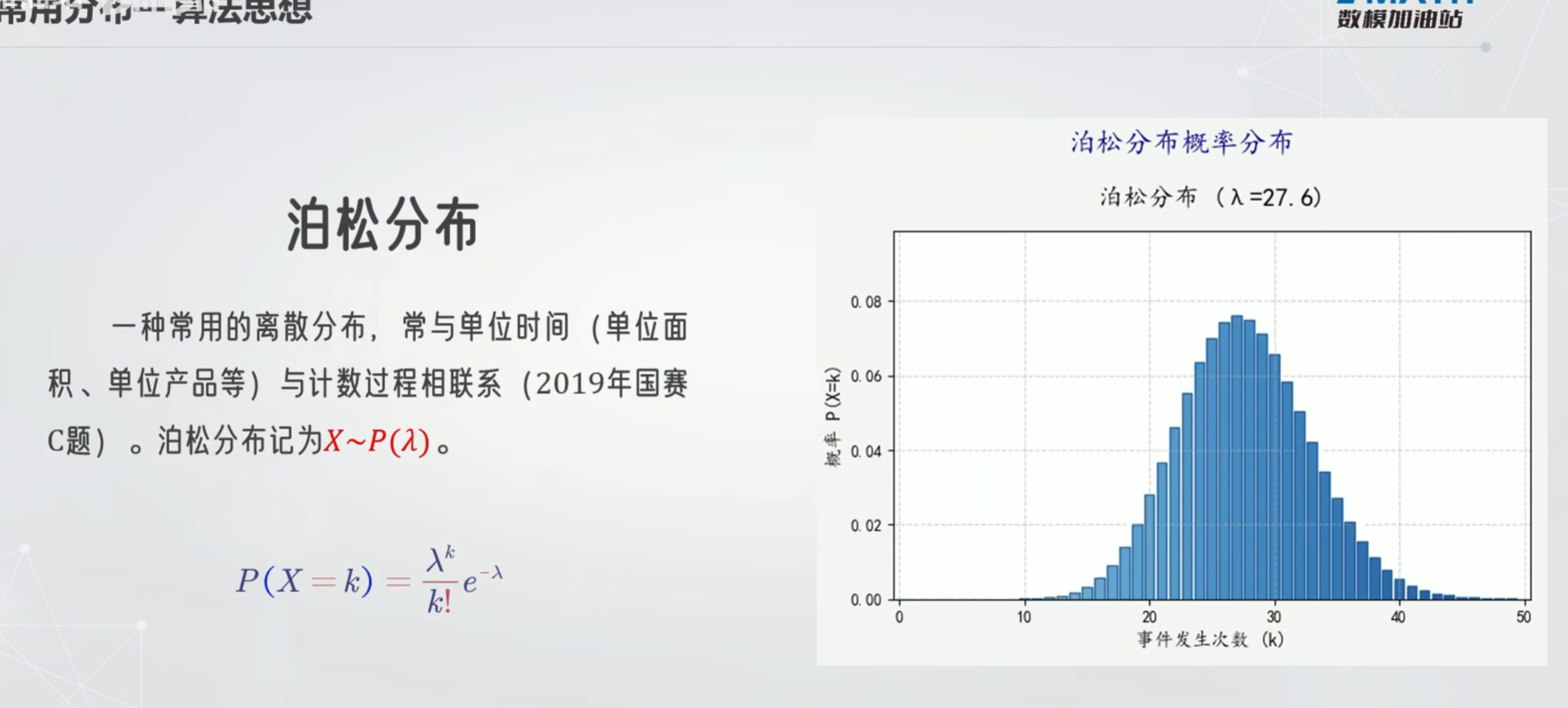
泊松分布

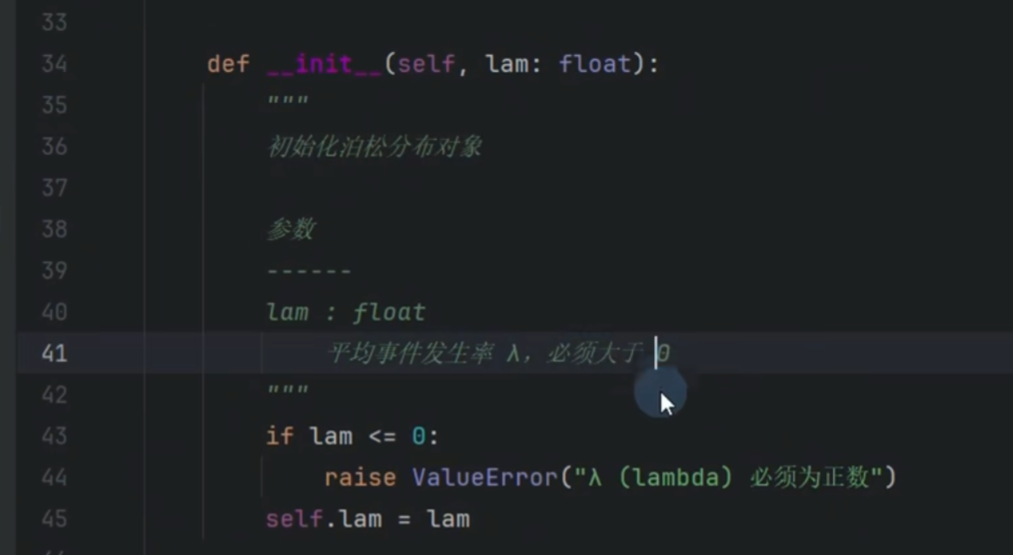
定义阶层函数
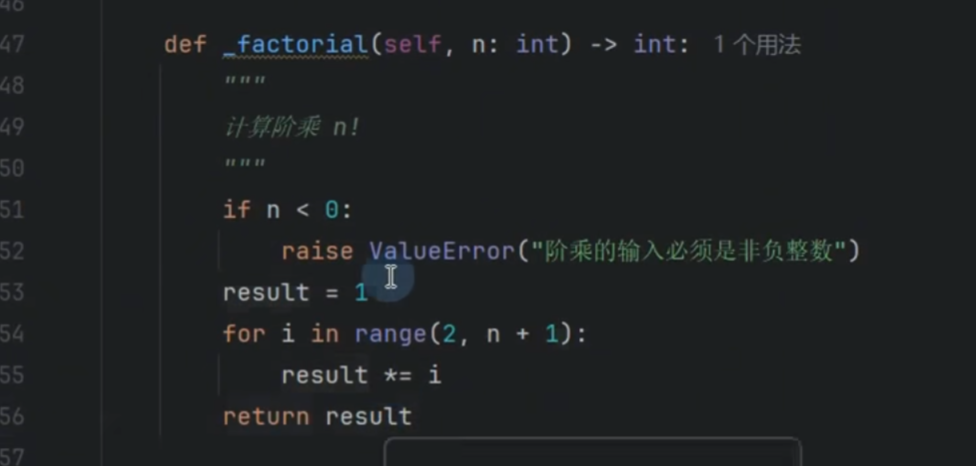
计算得数
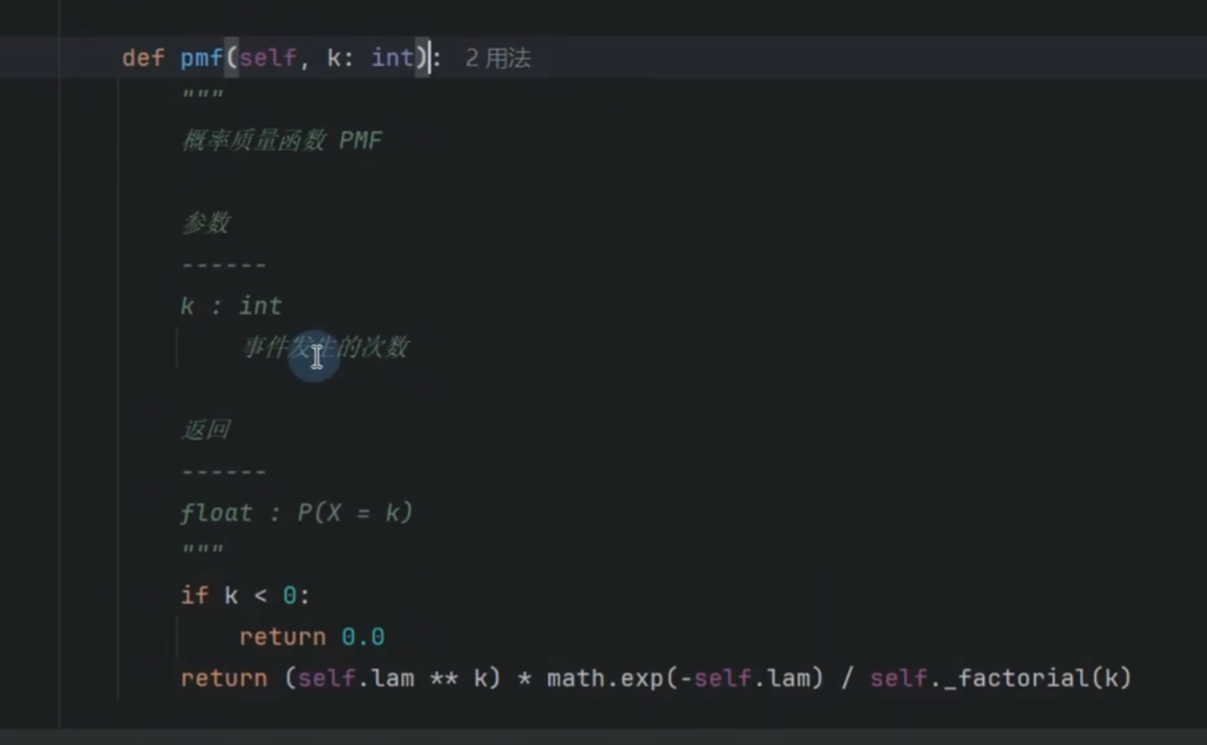
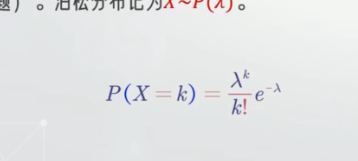
求累计泊松分布
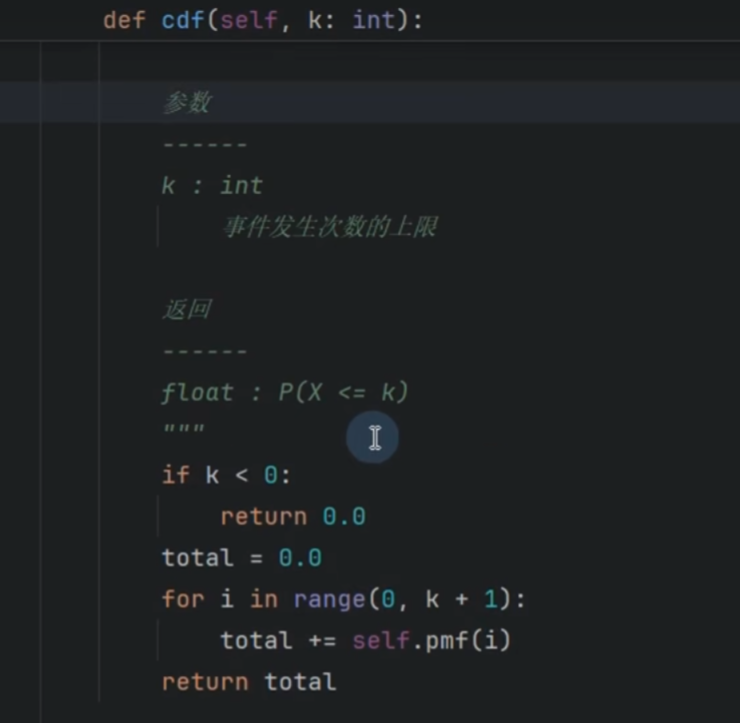
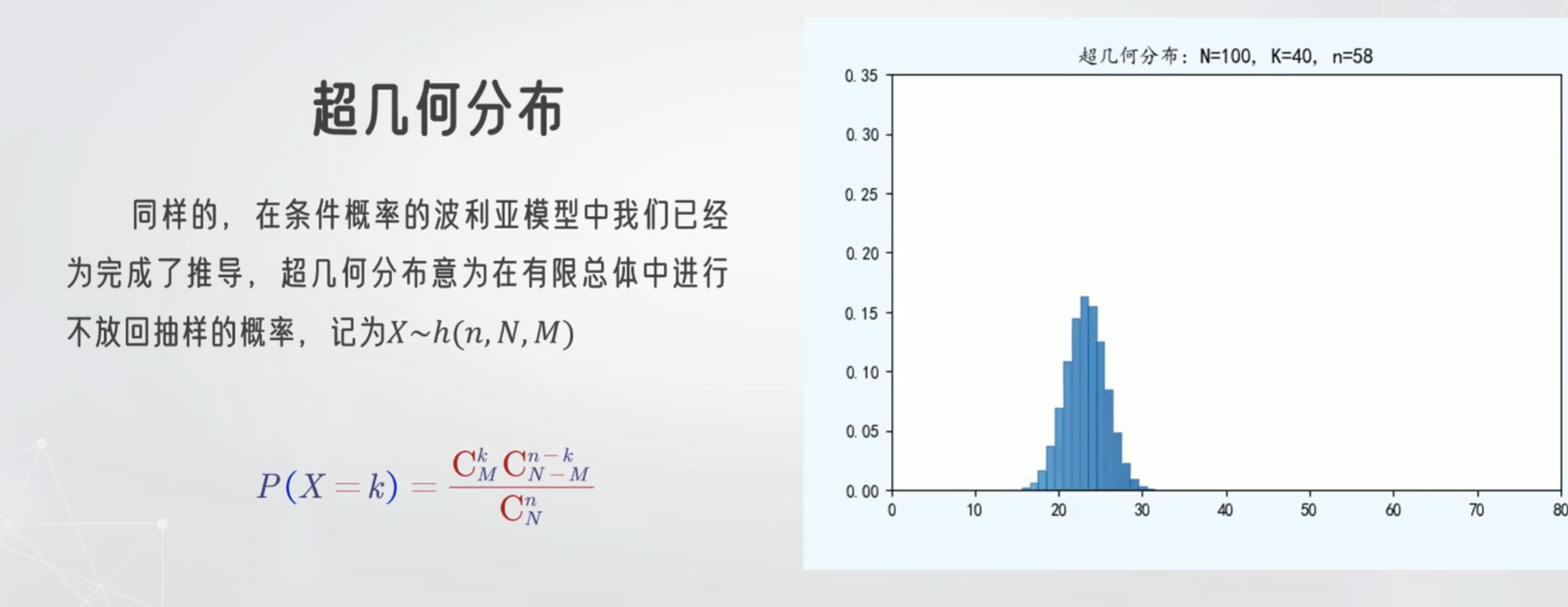
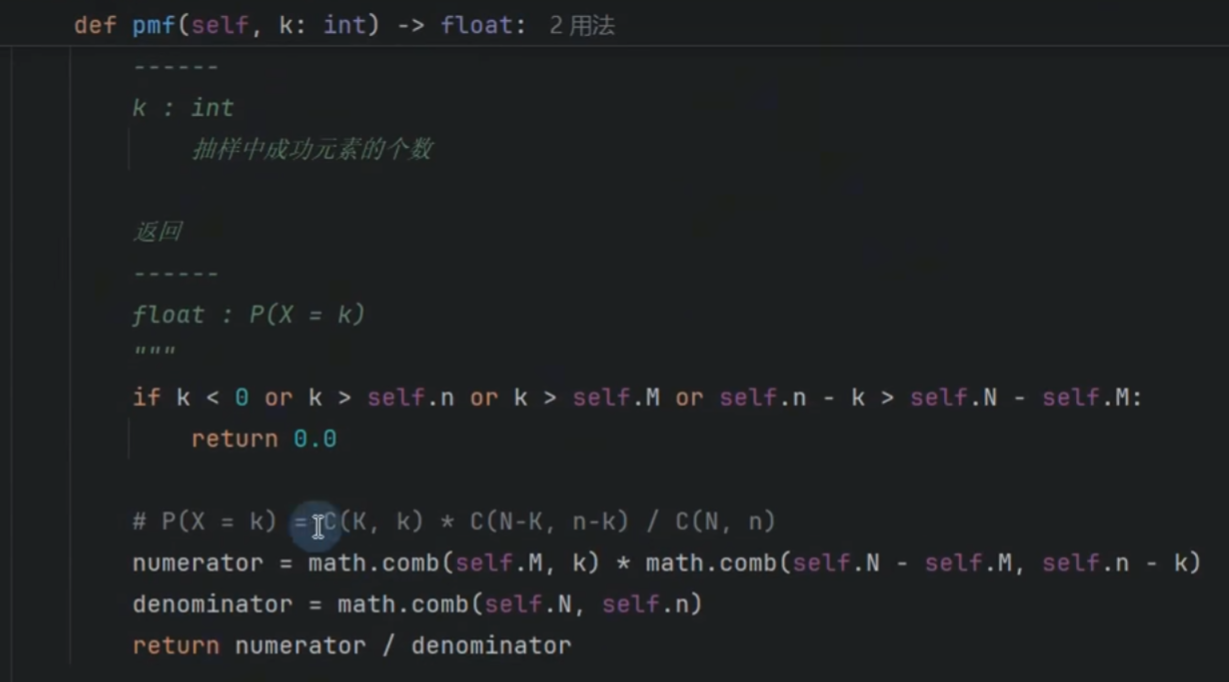
超几何分布-不放回
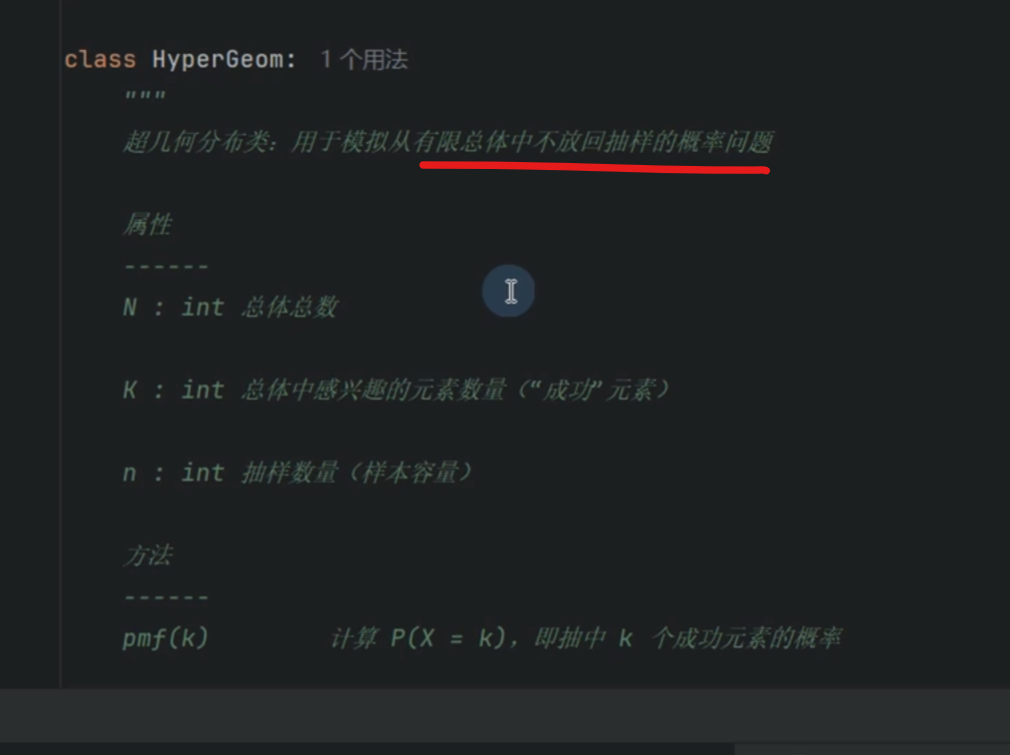

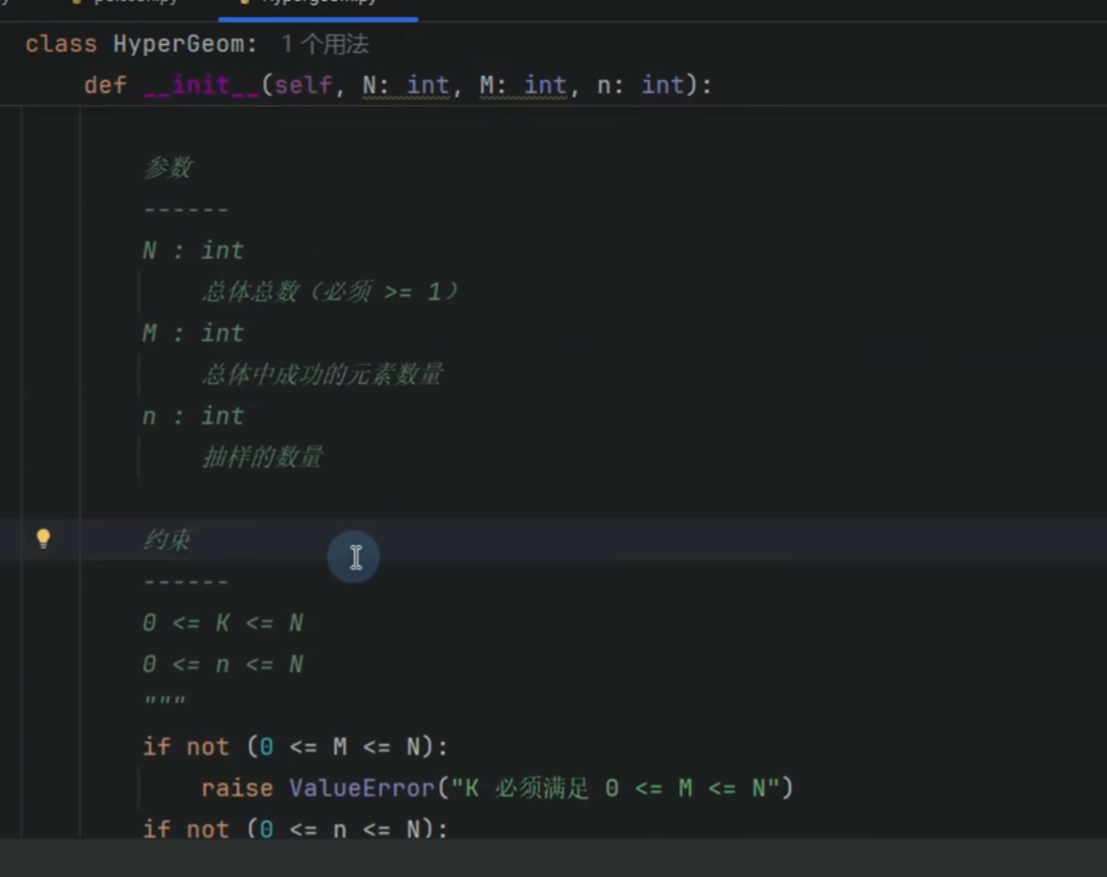
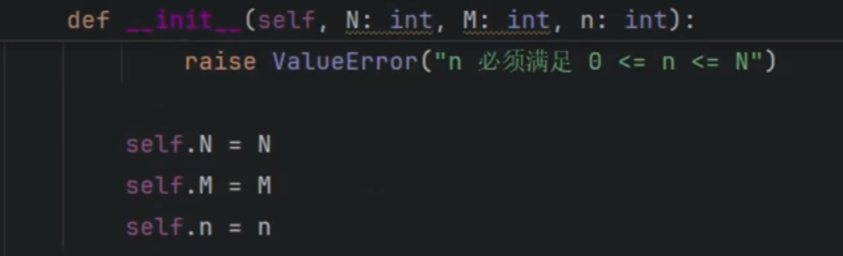

计算
求累计
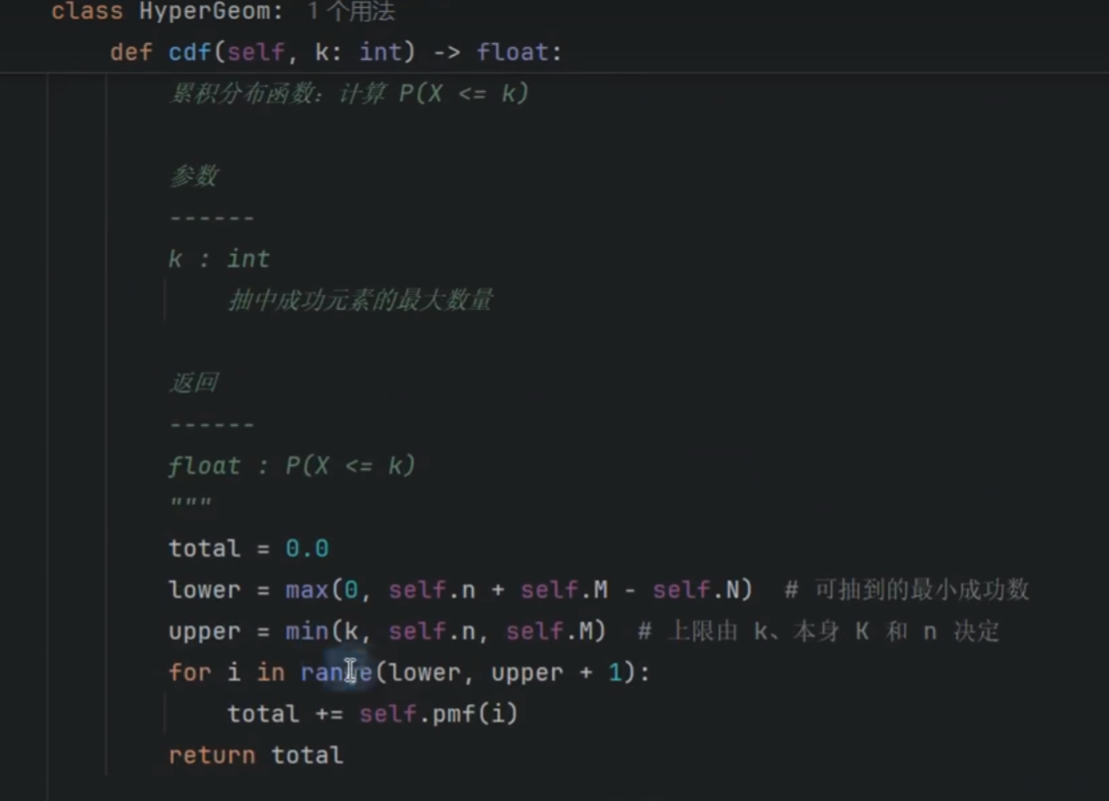
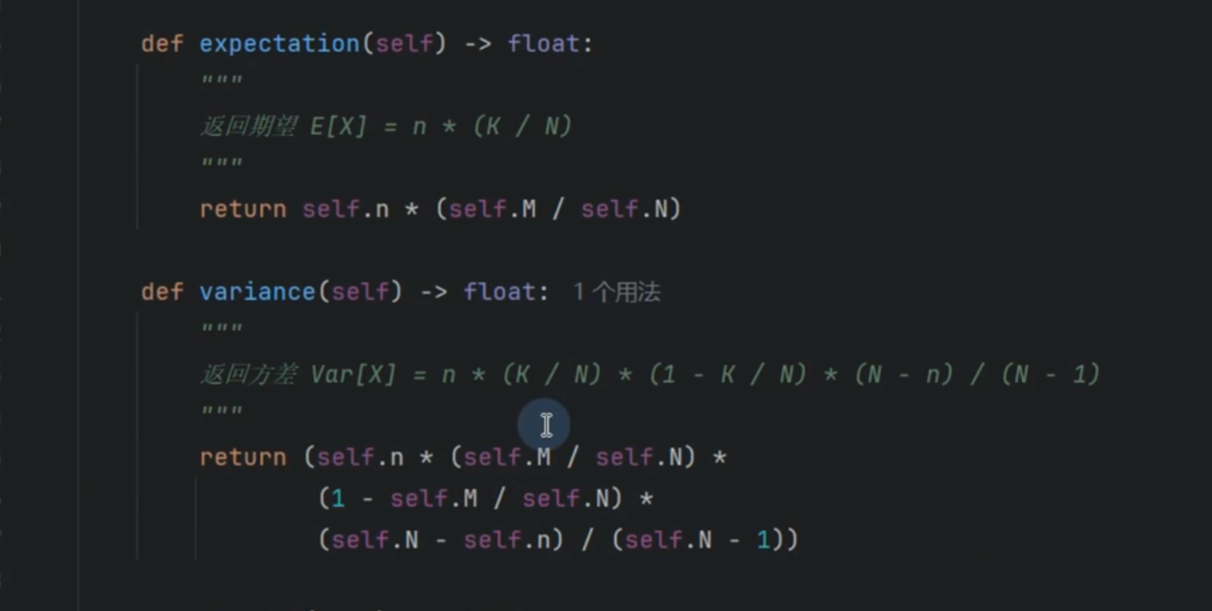
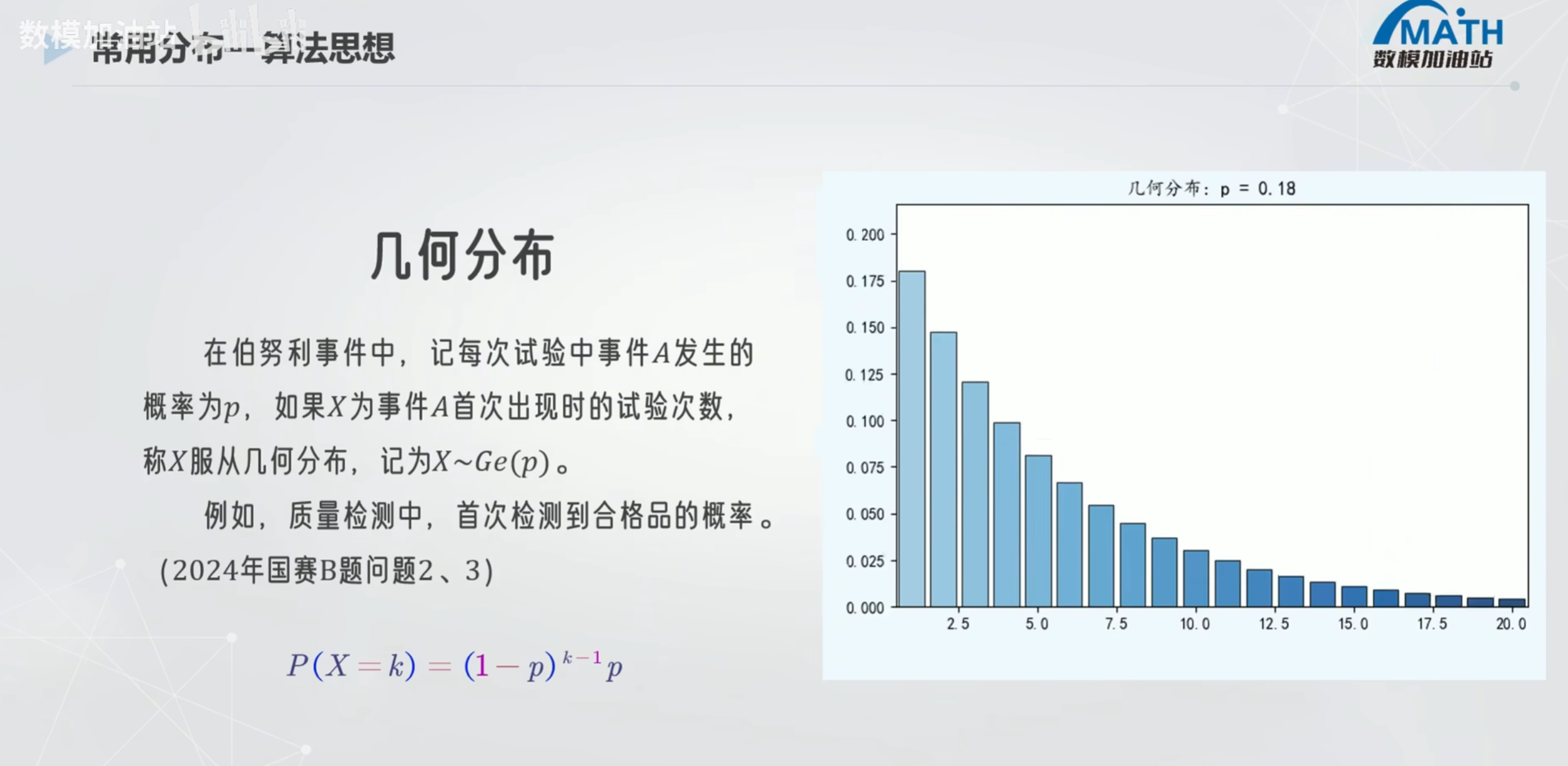
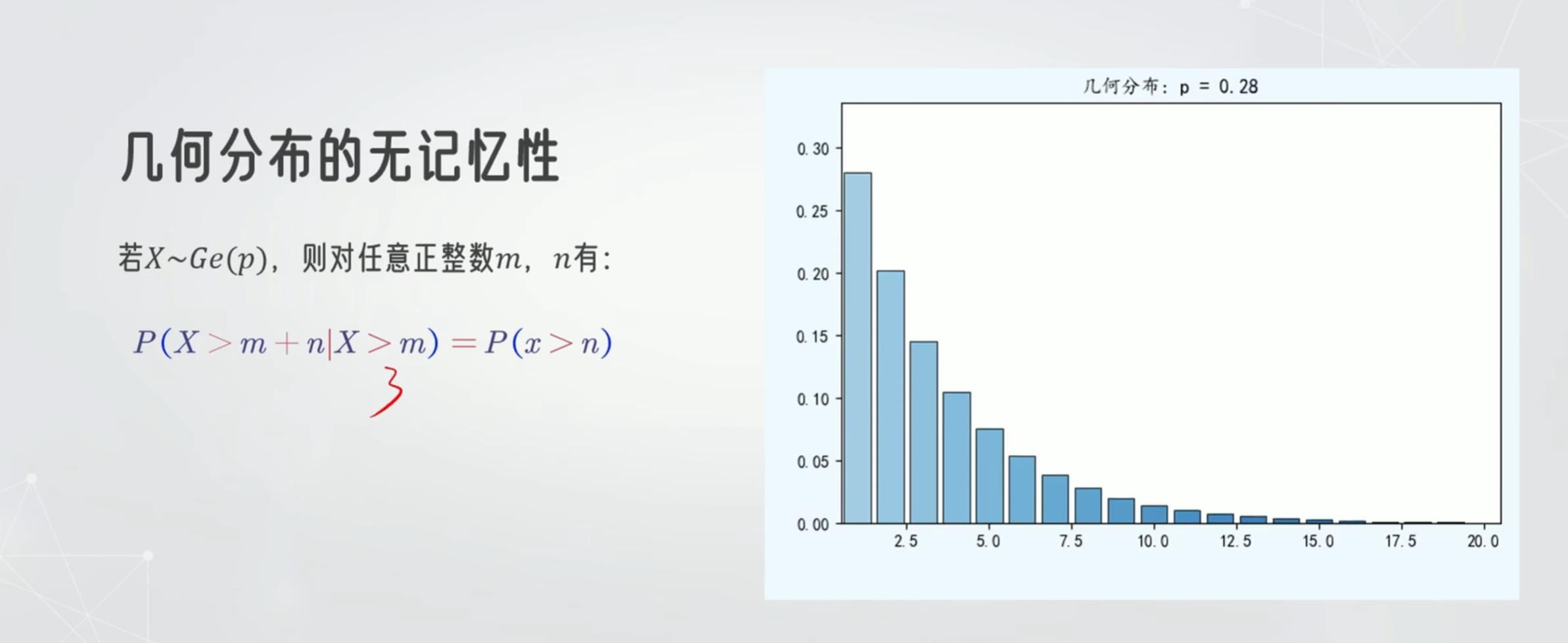
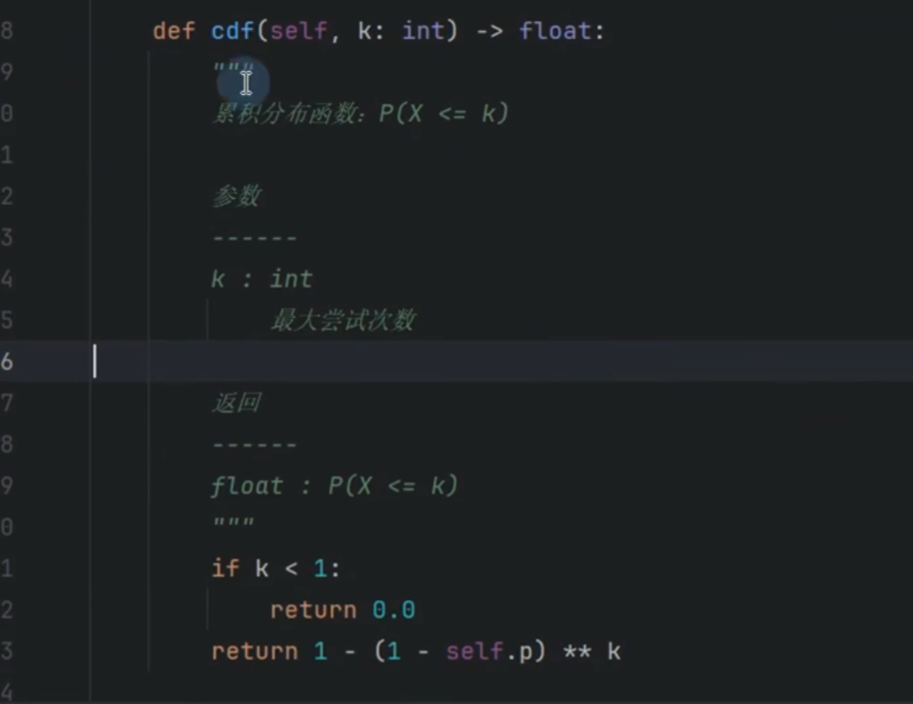
几何分布
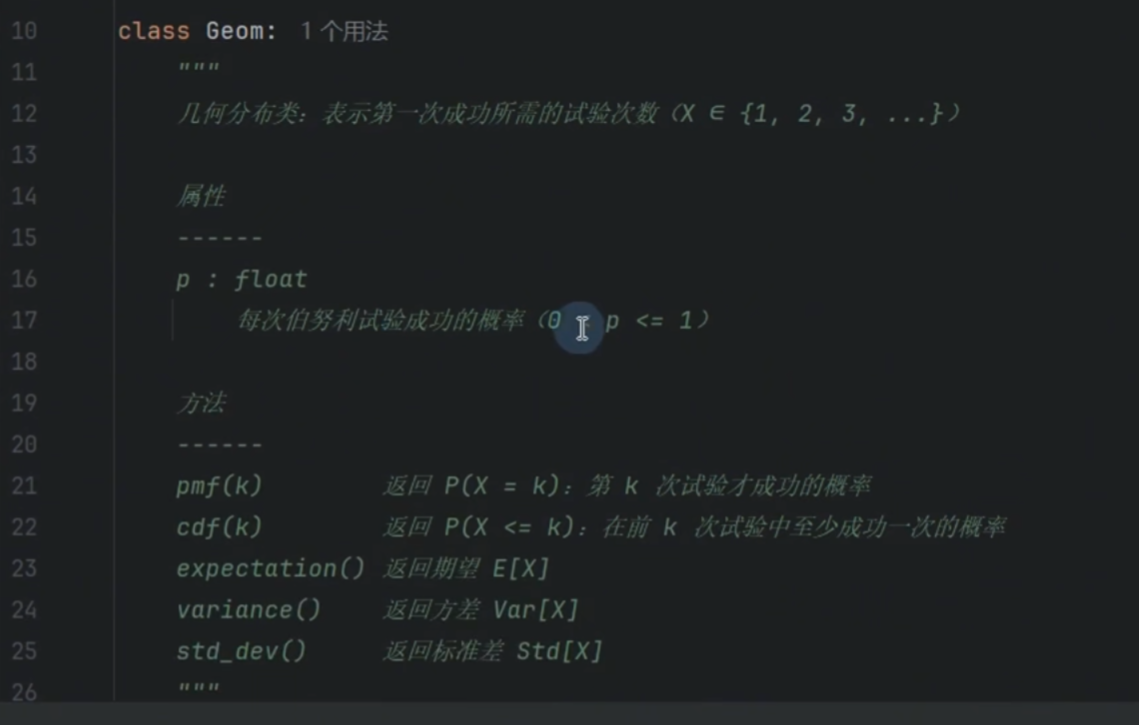
第几次成功的概率
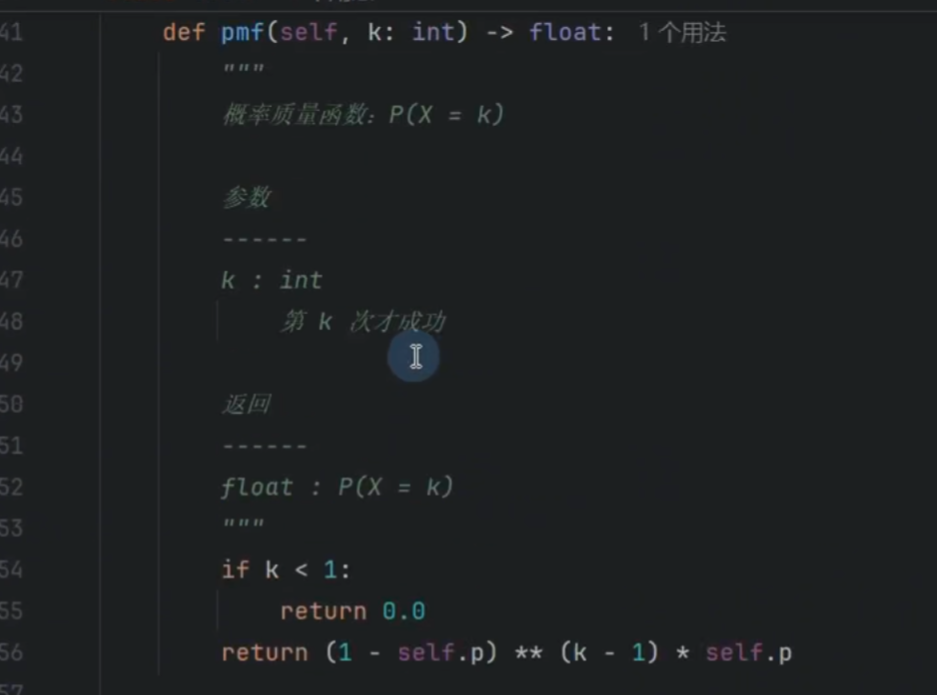
前k次成功的次数

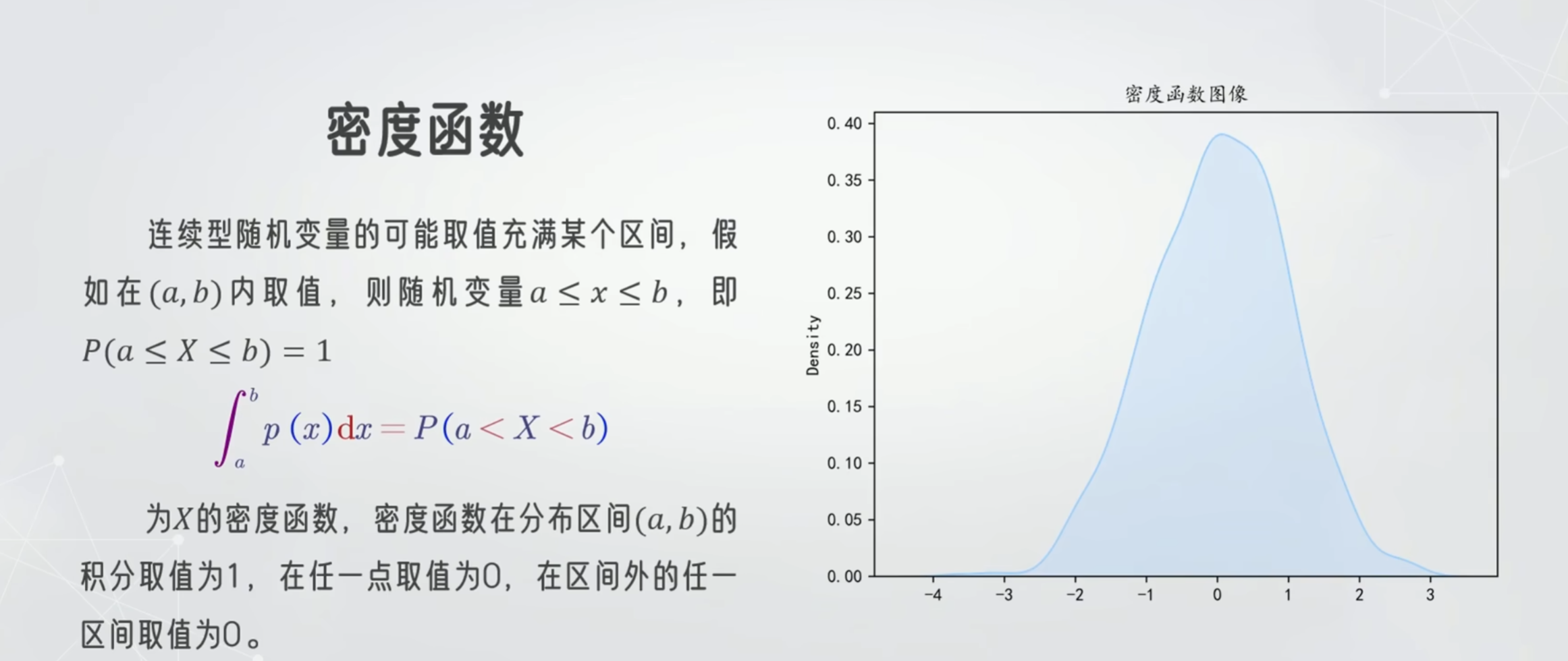
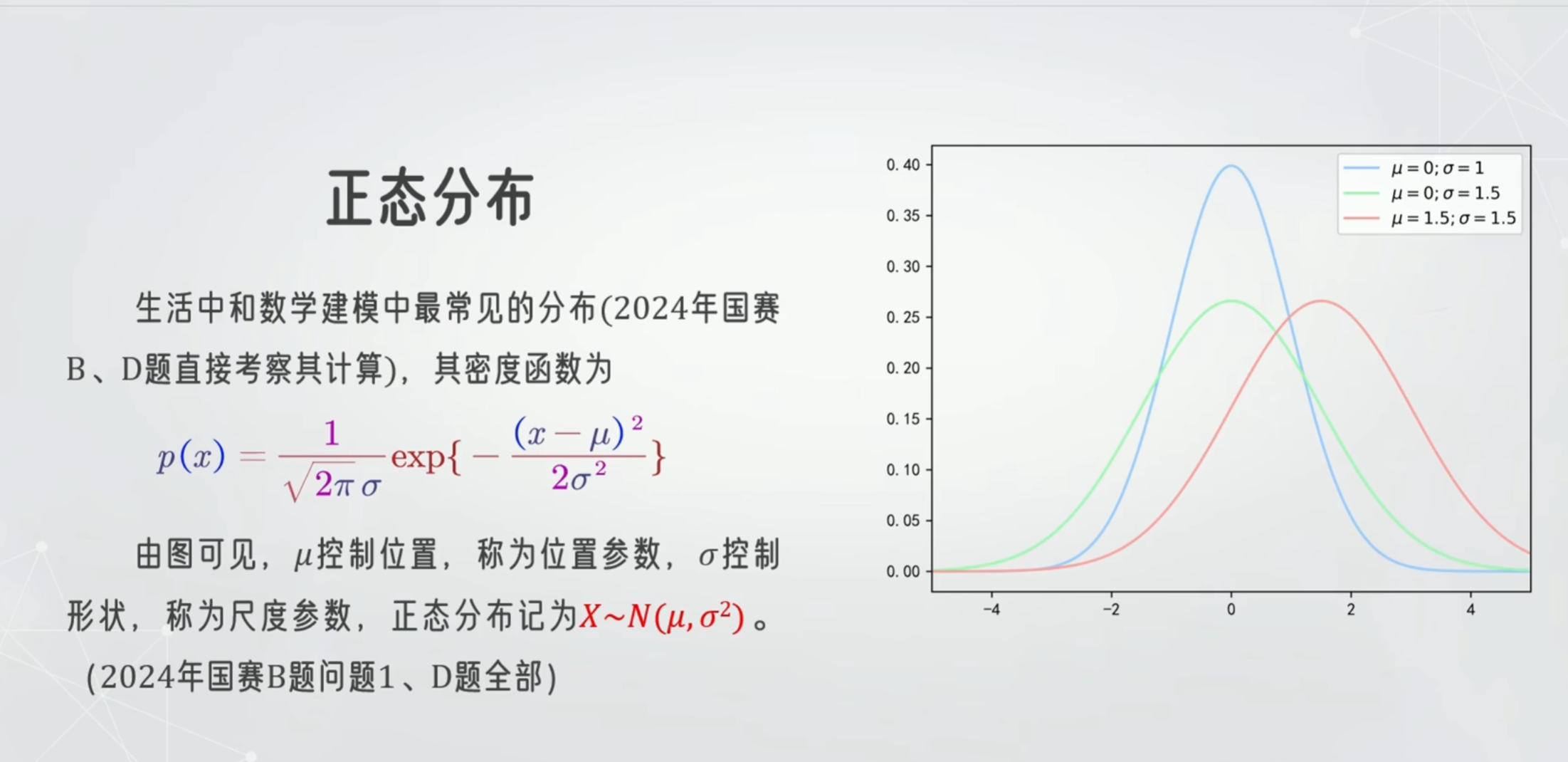
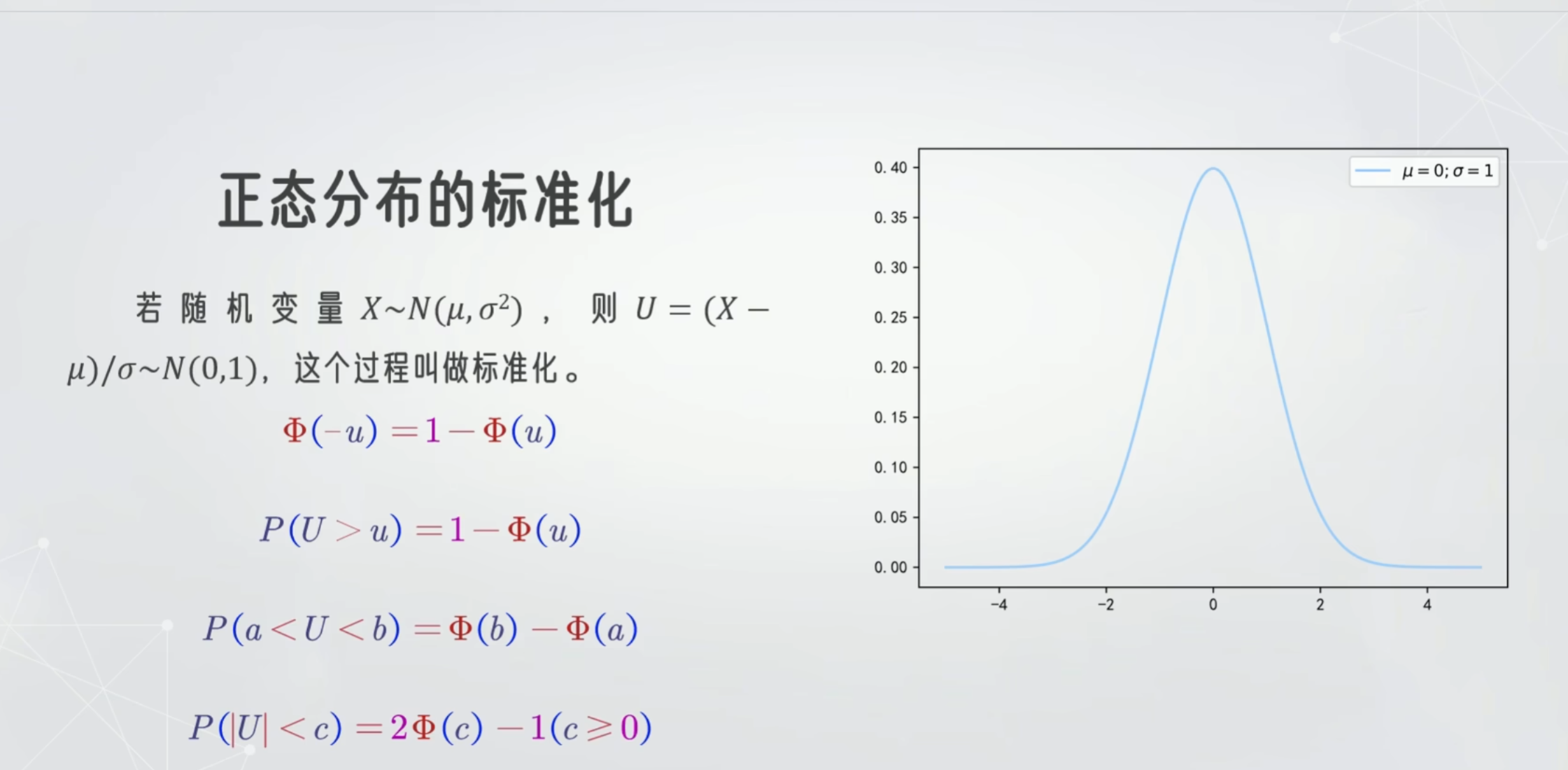
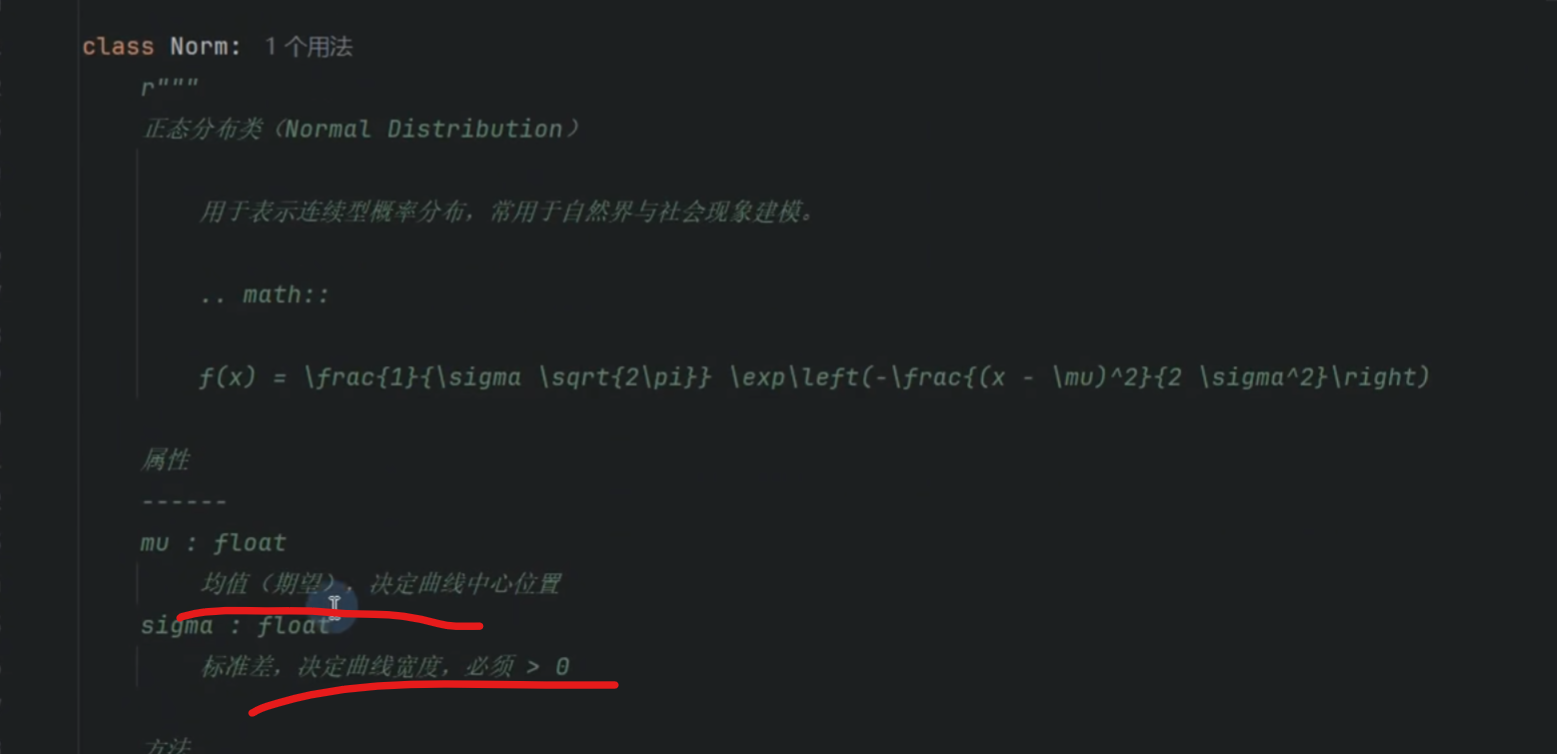
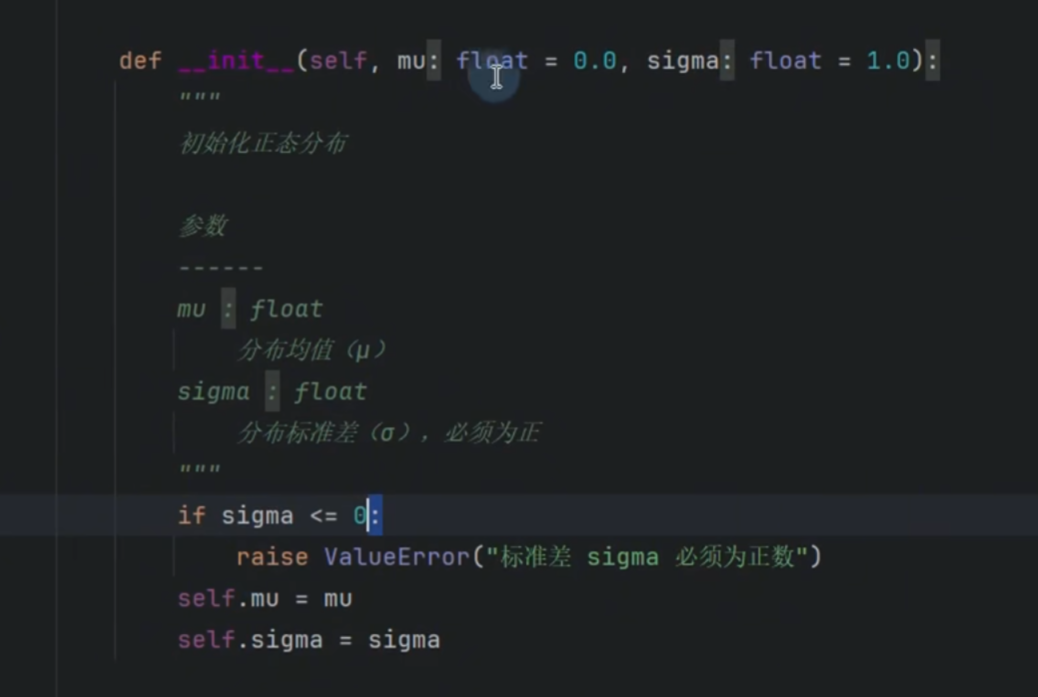
正态分布
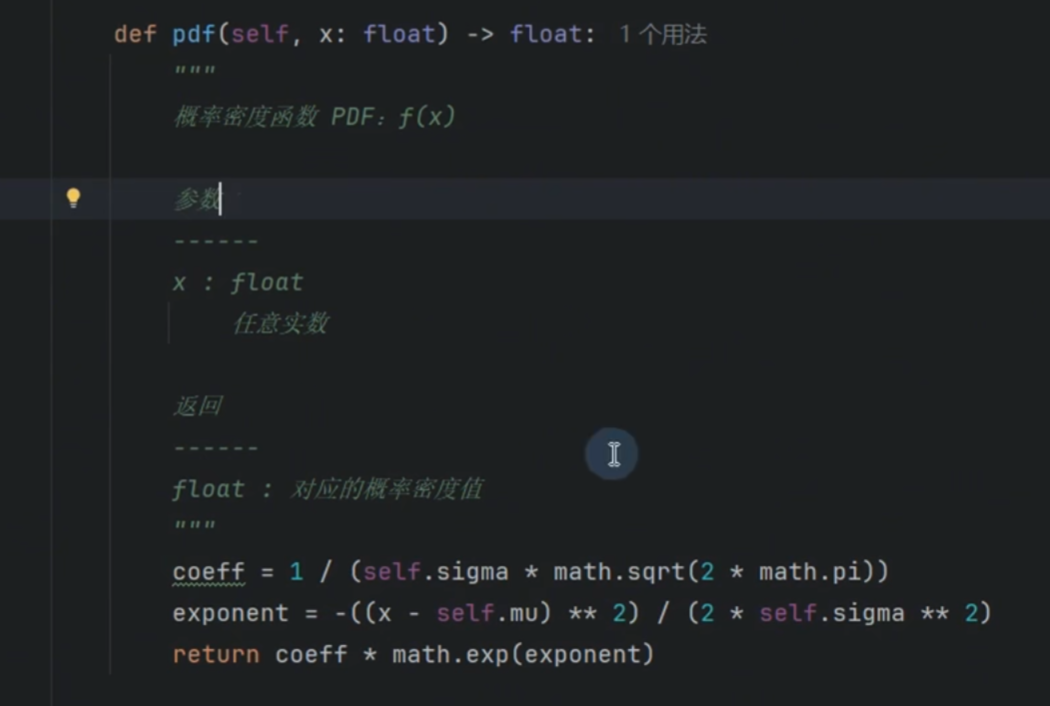
求值:因为是连续性的 所以在一个点的时候值为0
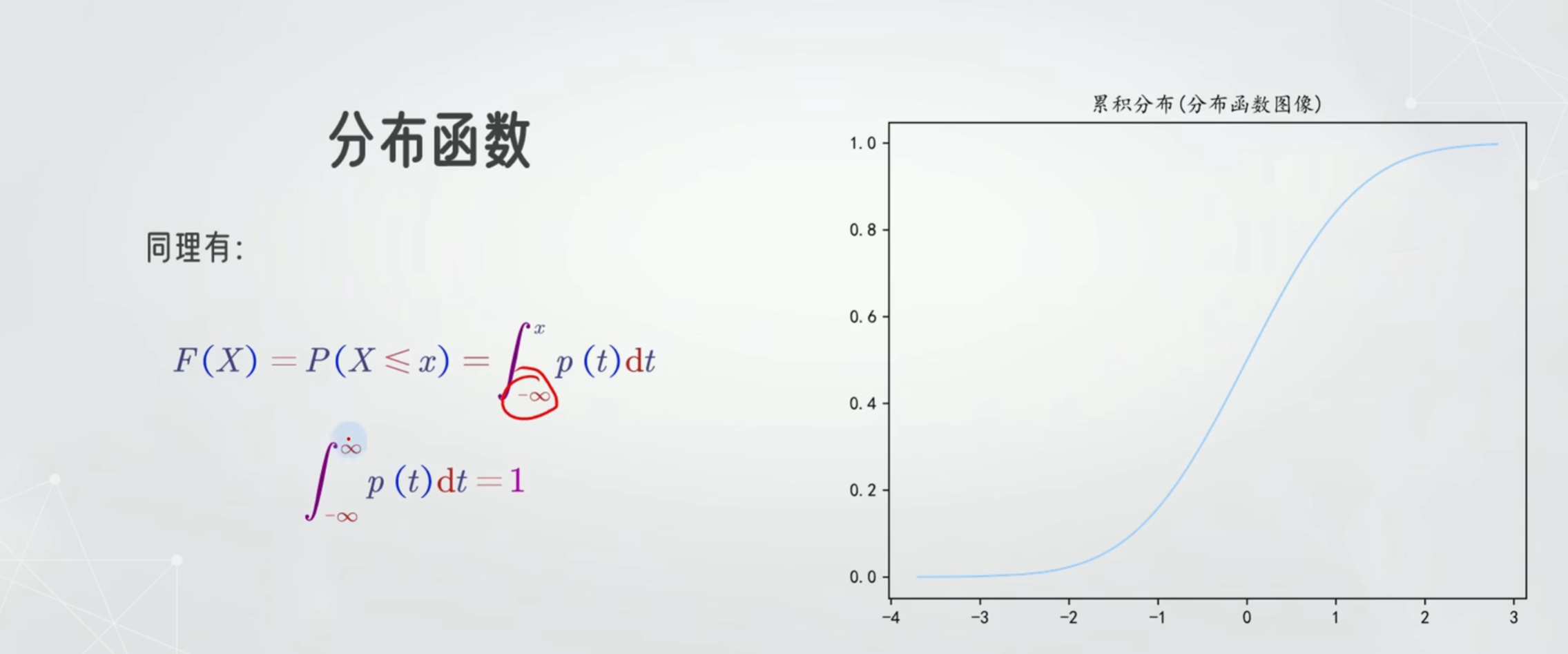
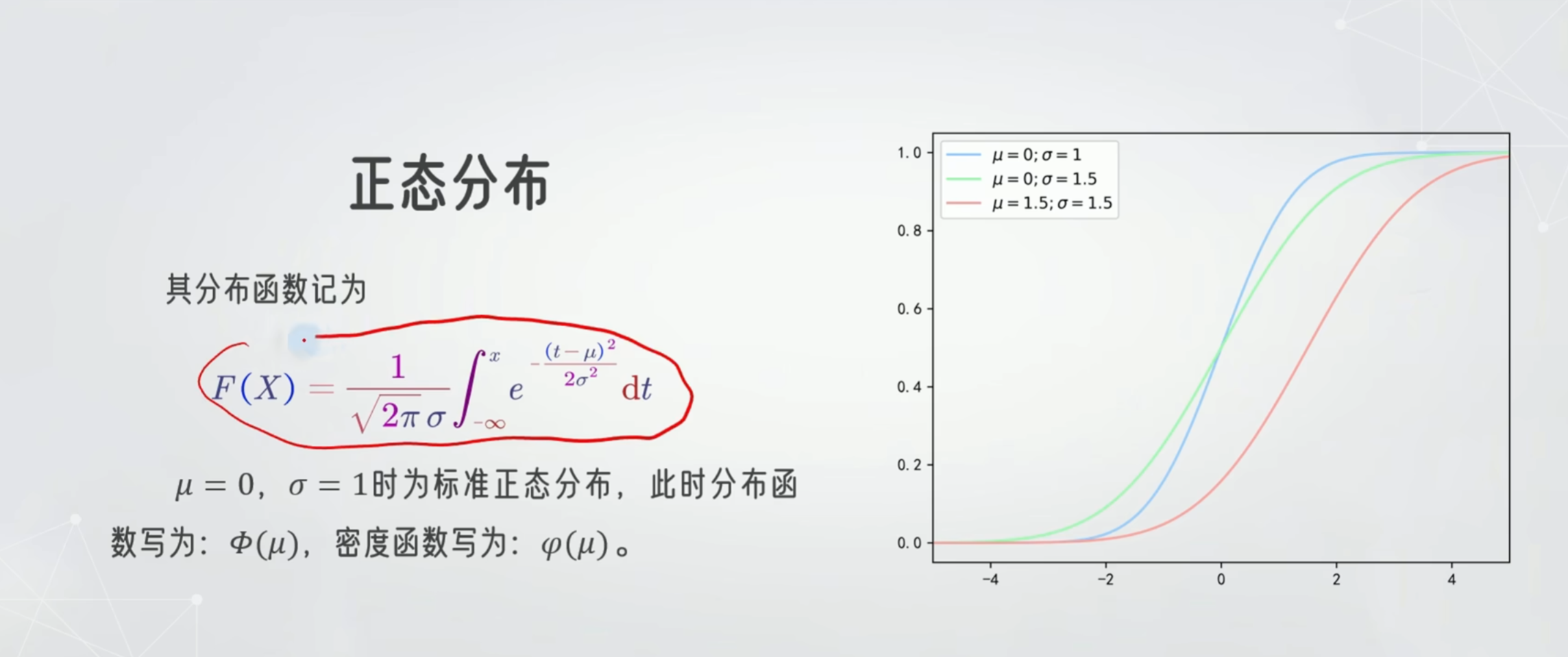
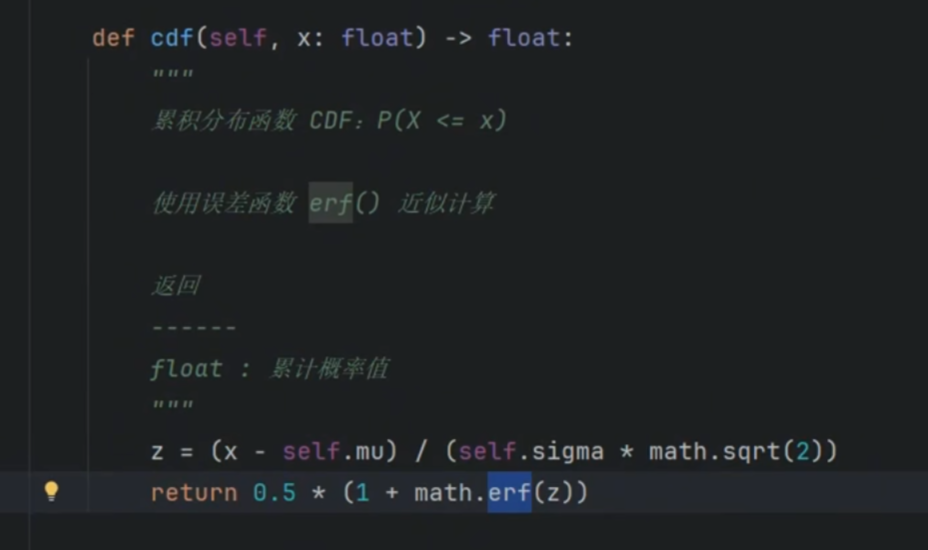
累计分布
python
math.erf(z)
erf()是数学中的误差函数
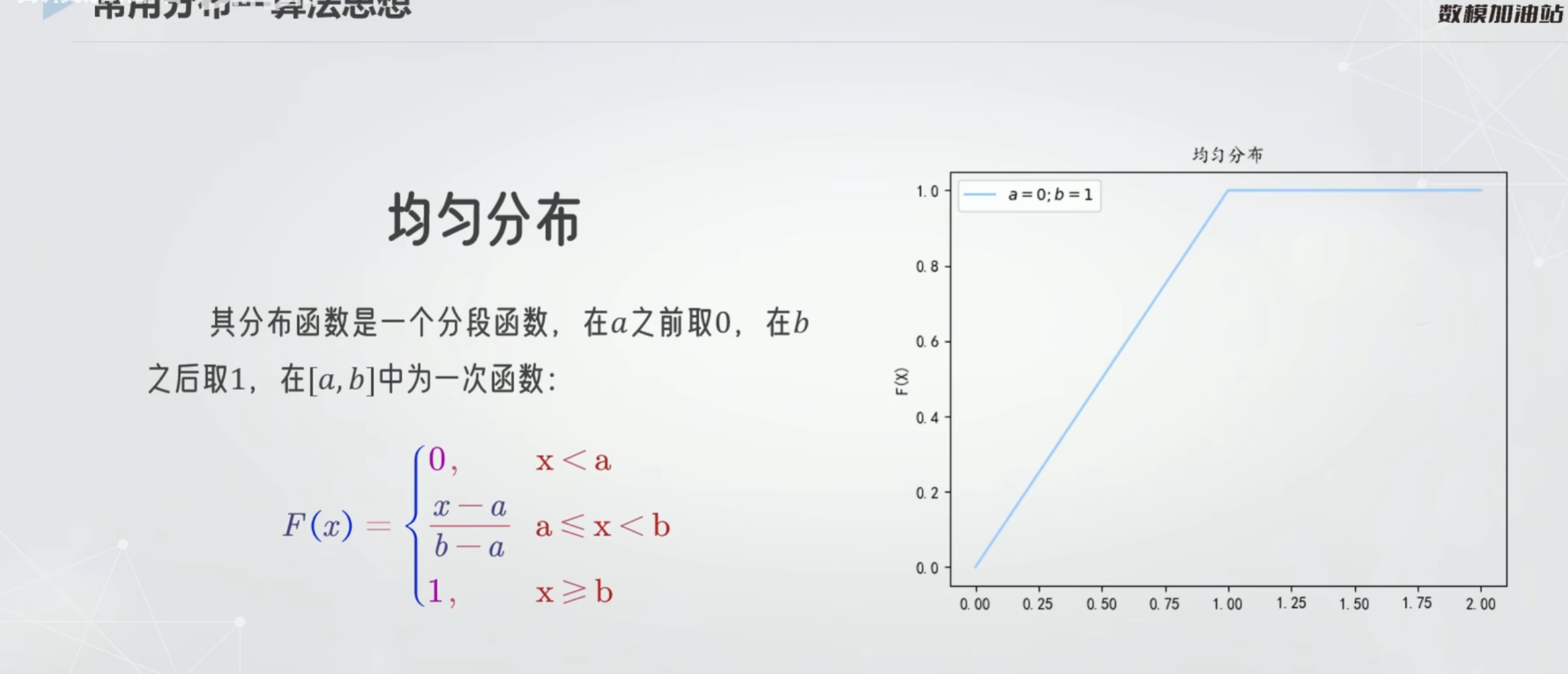
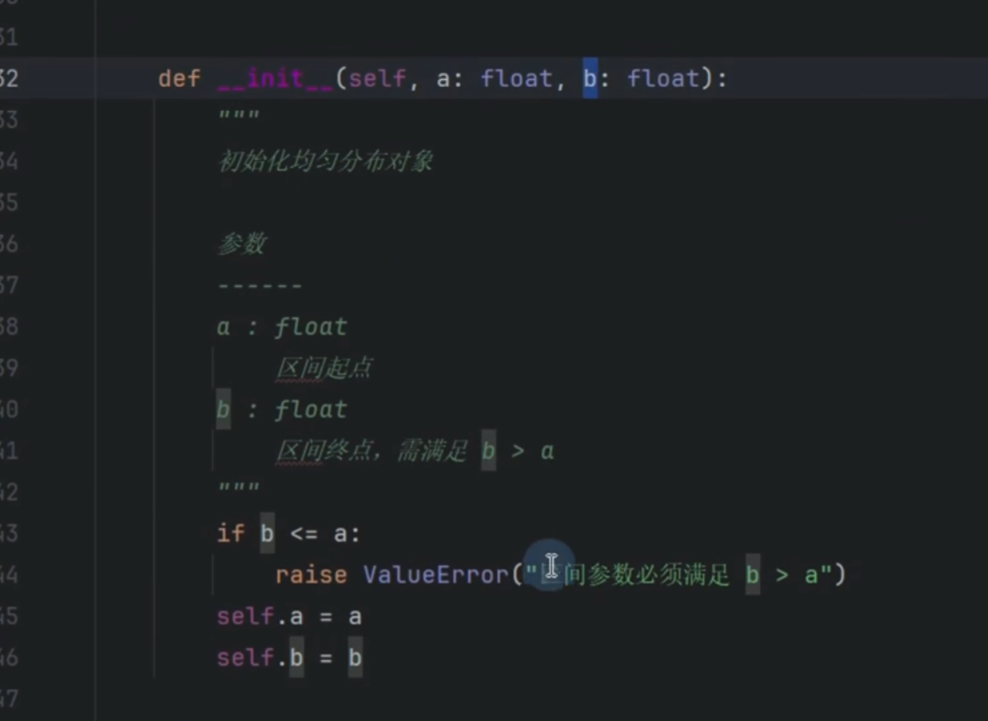
均匀分布
在起点和终点中间是一条直线 值为pdf的返回值 恒定的
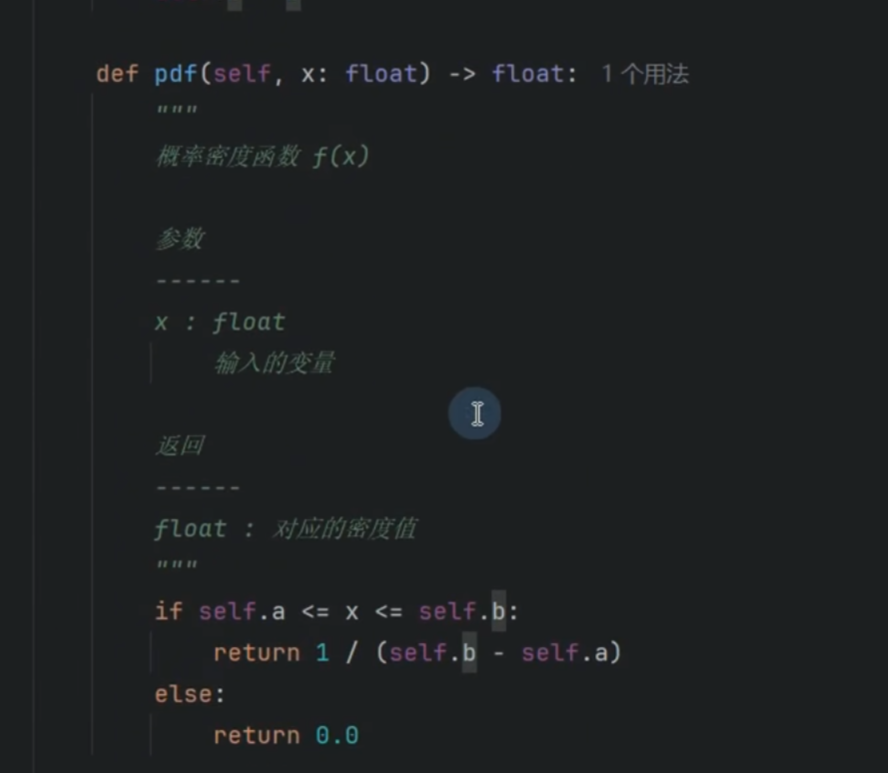
求值
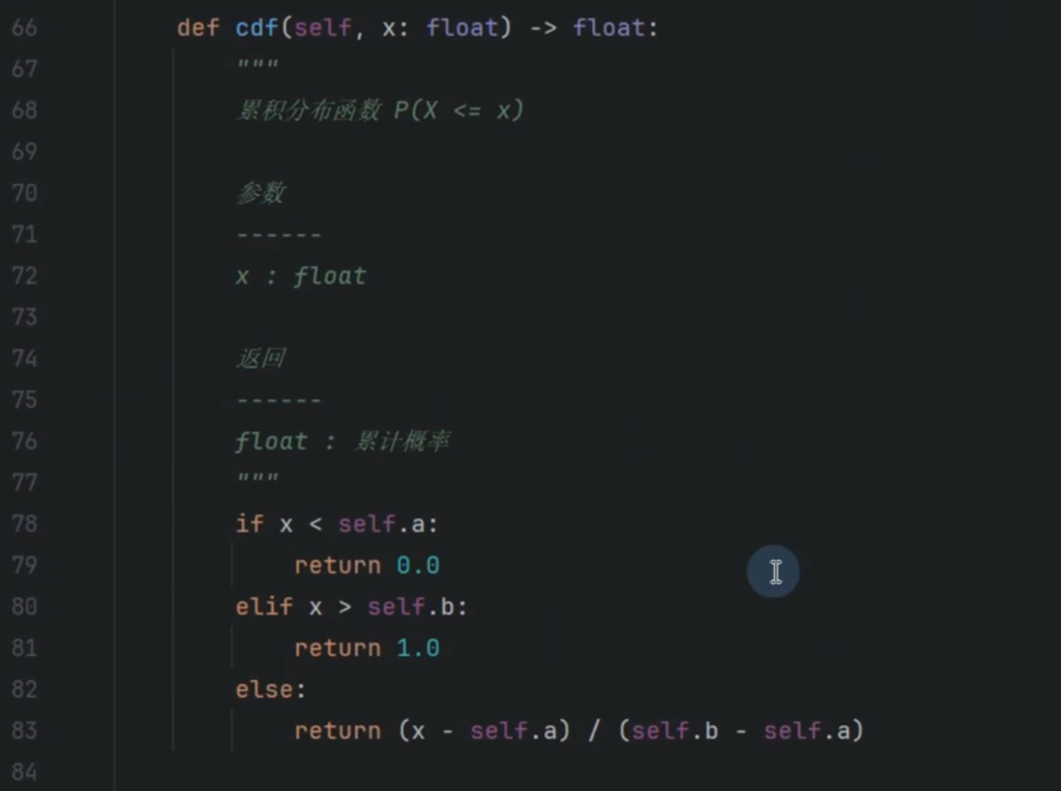
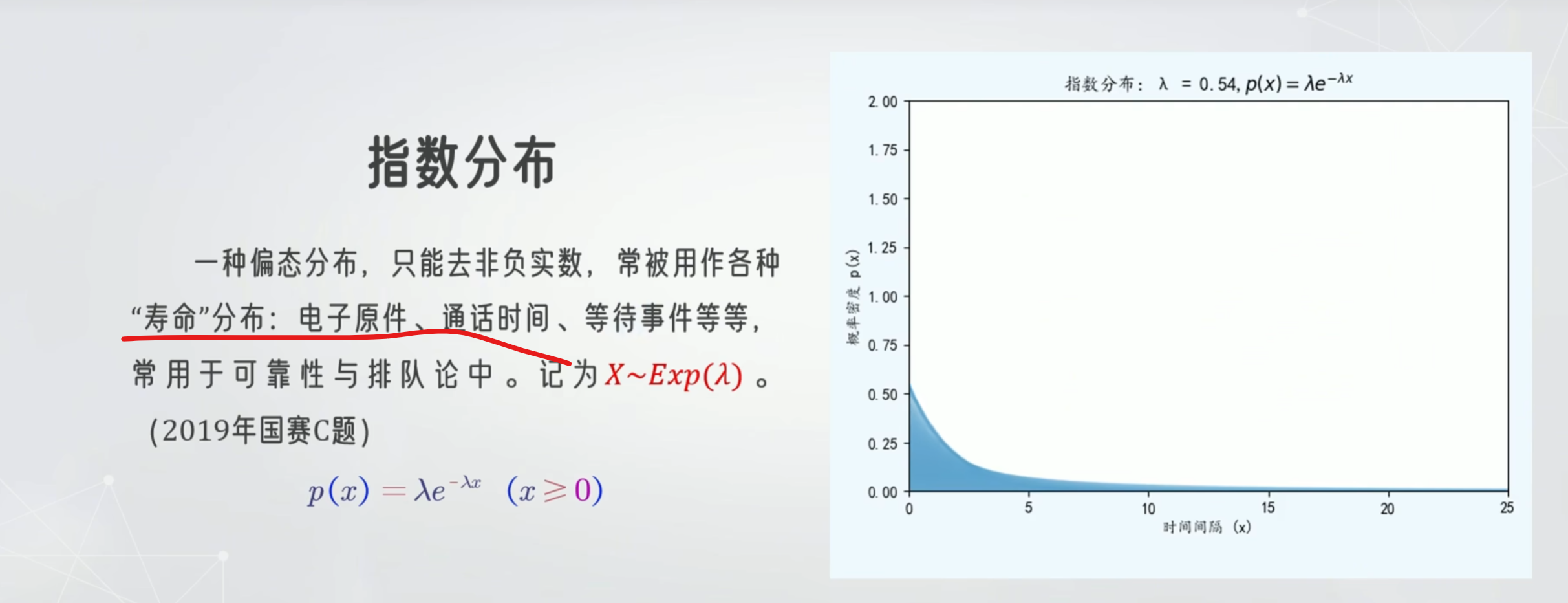
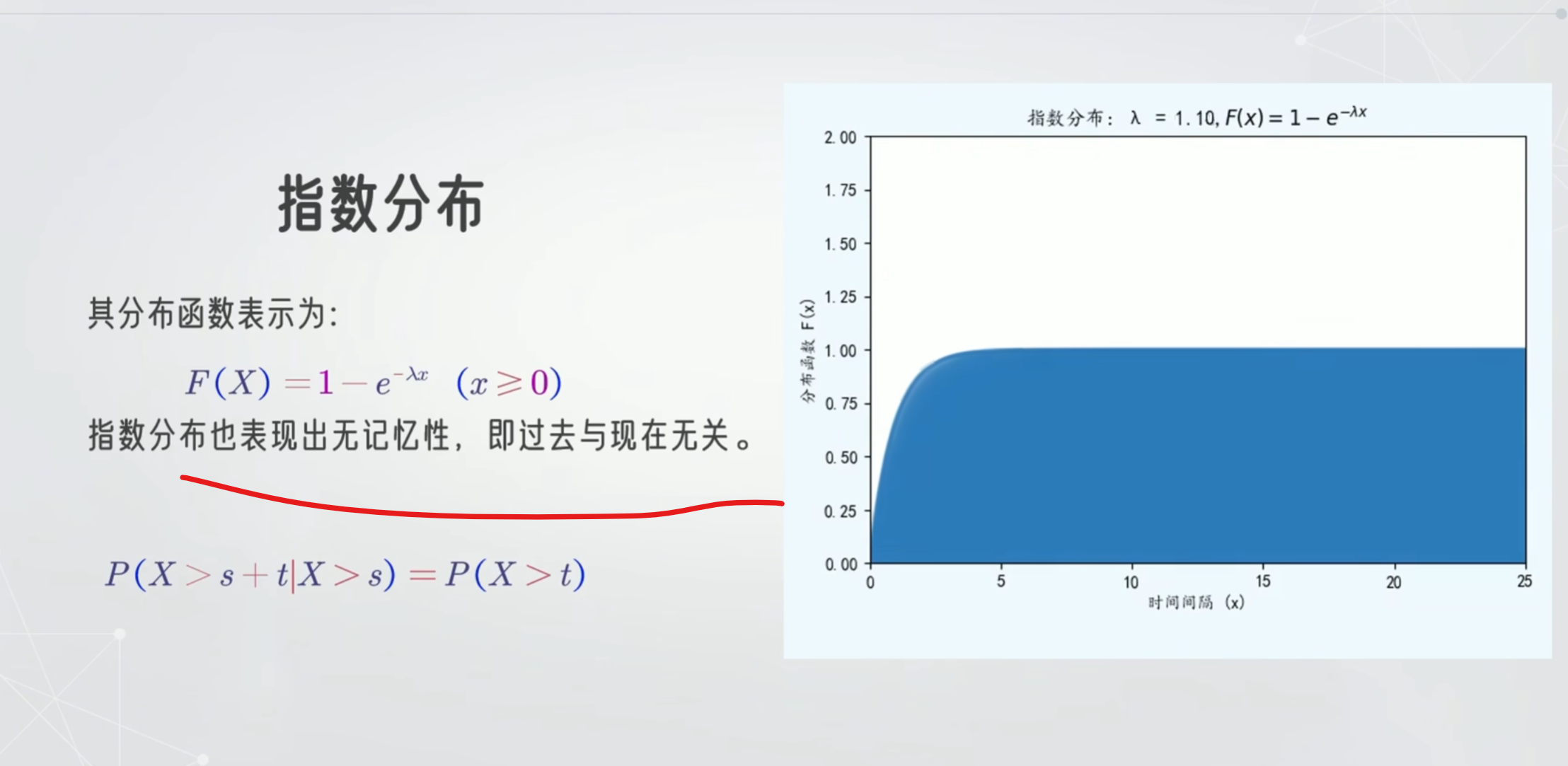
指数分布
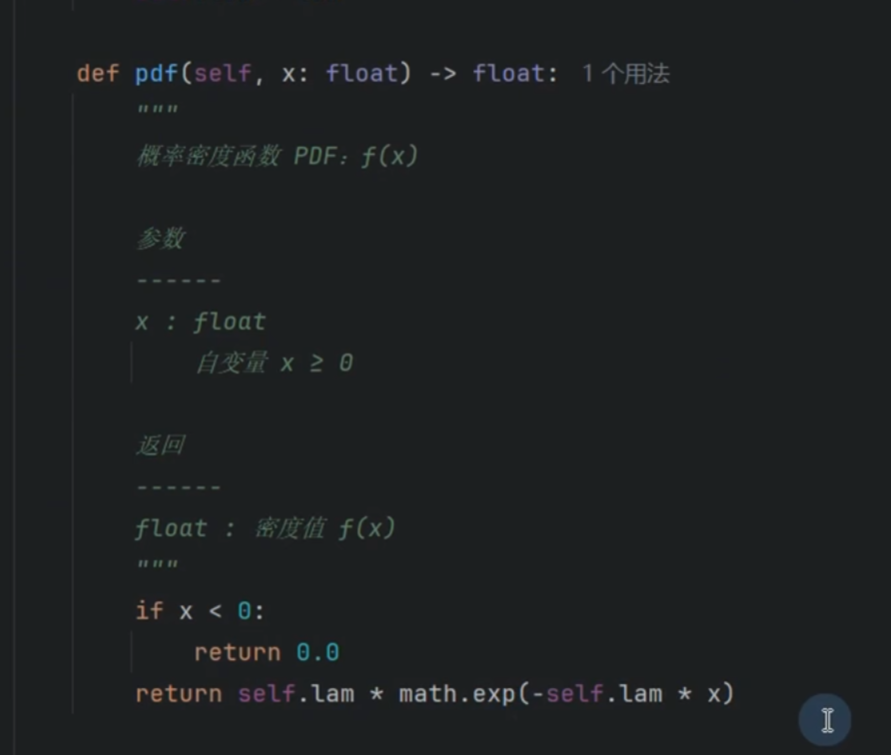
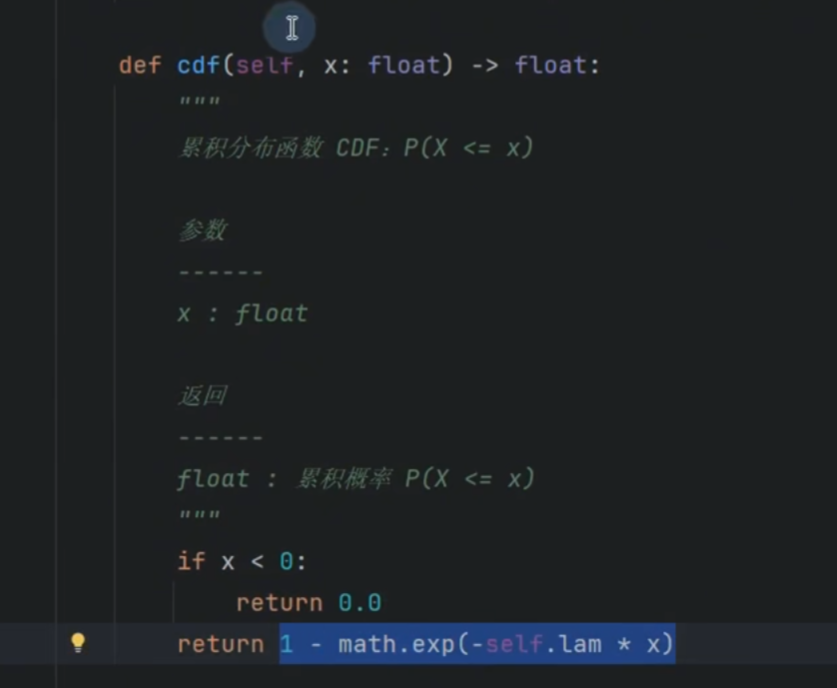
累计值
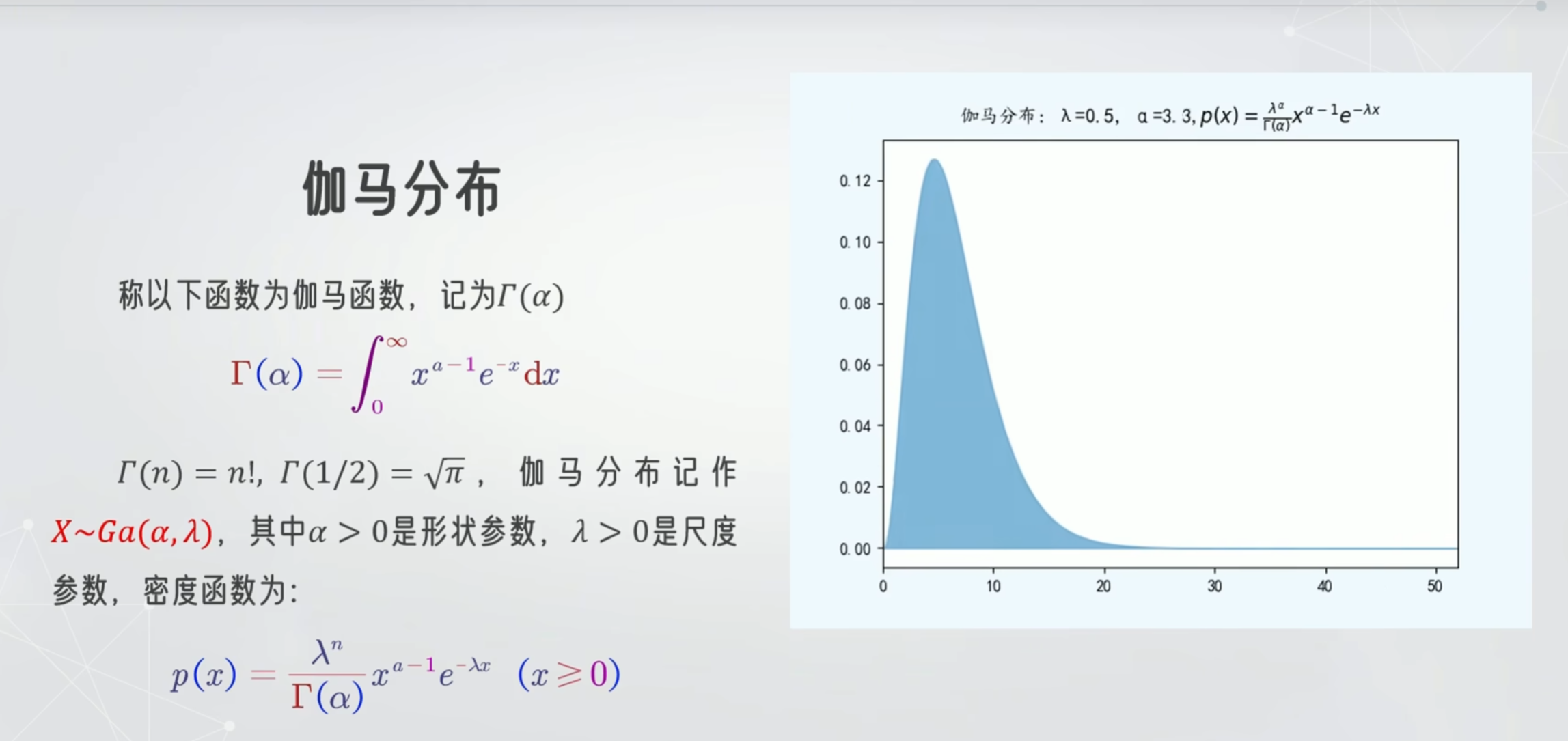
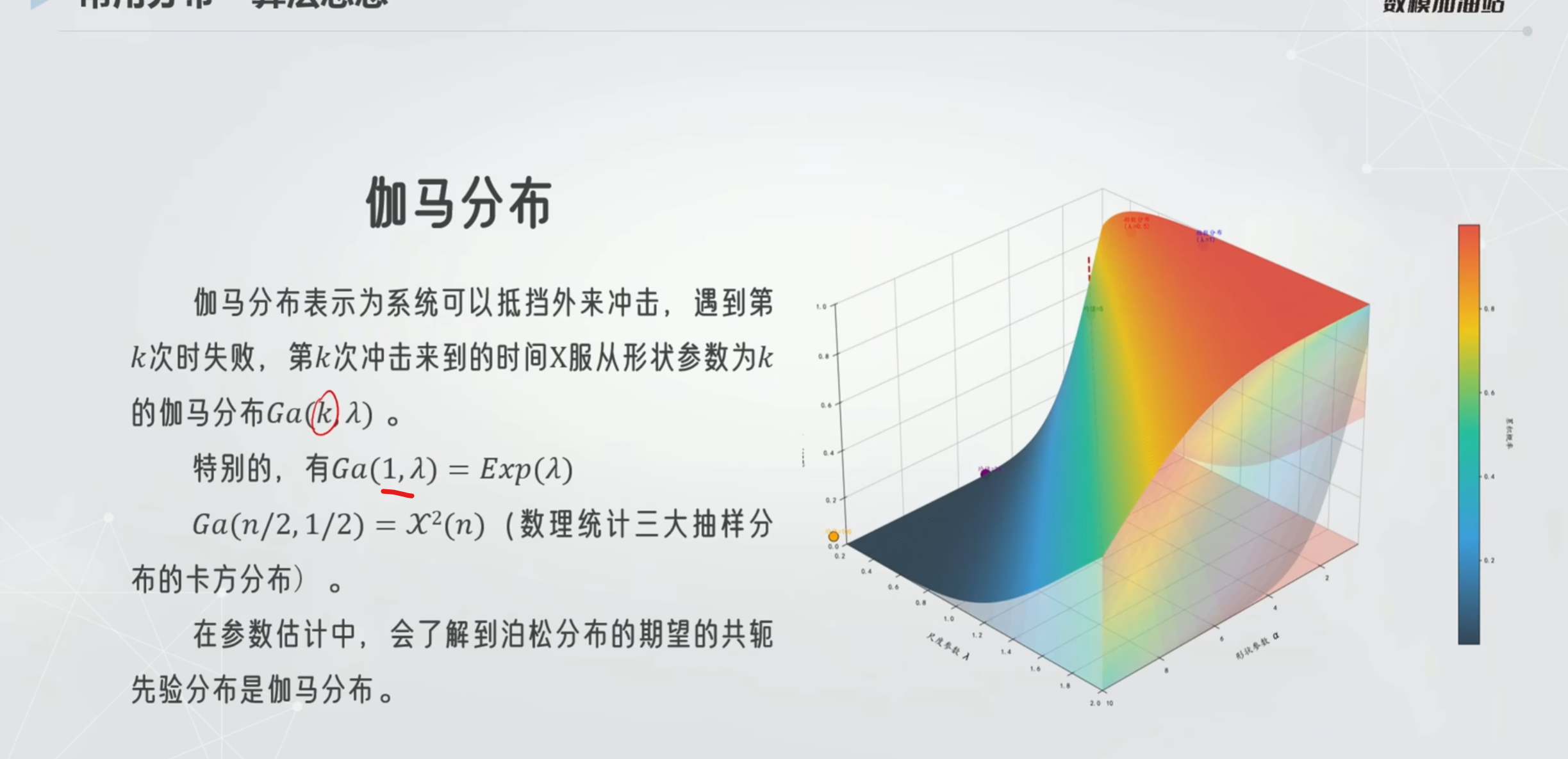
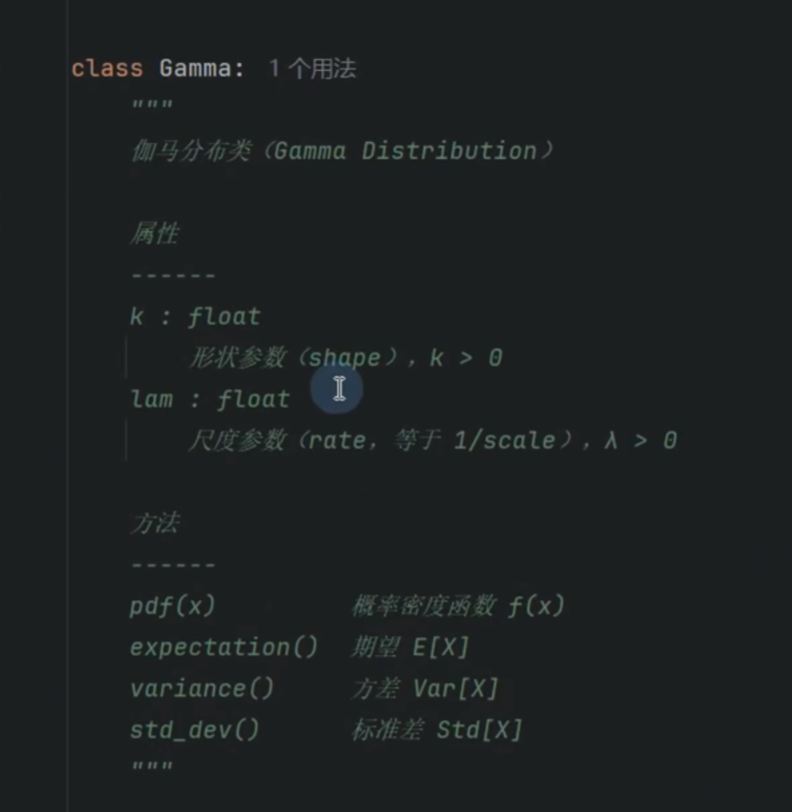
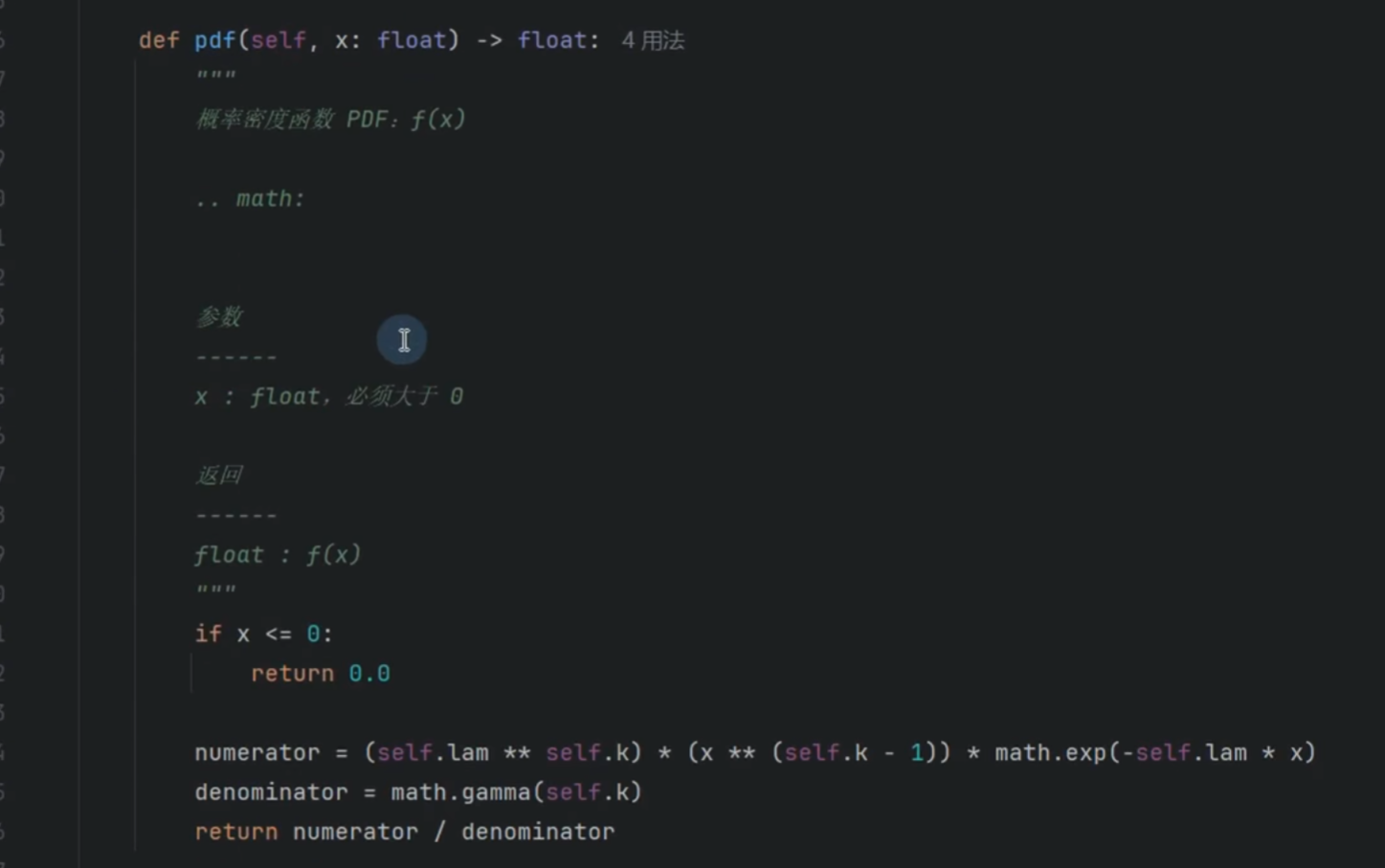
伽马分布
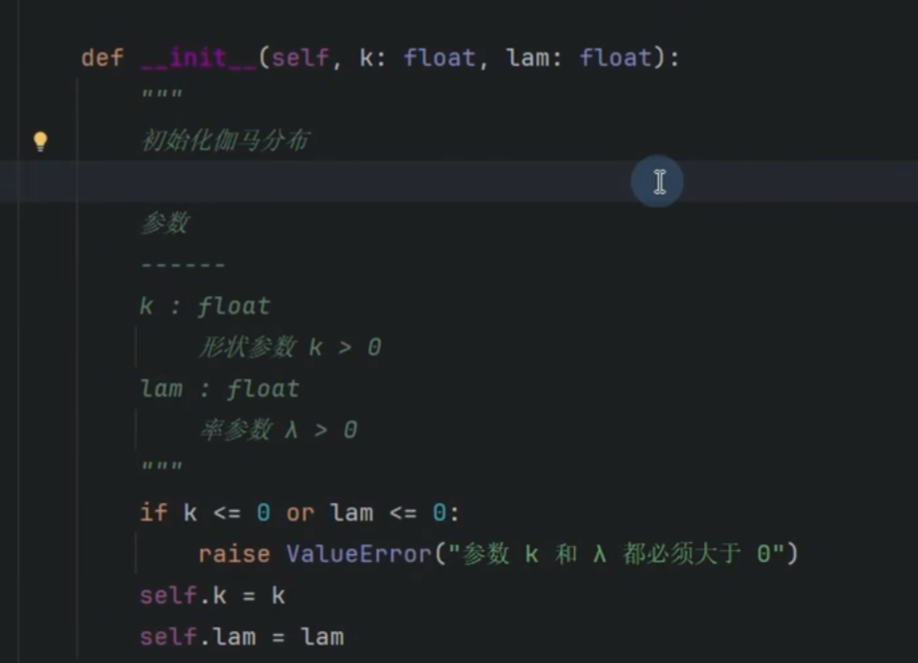
计算


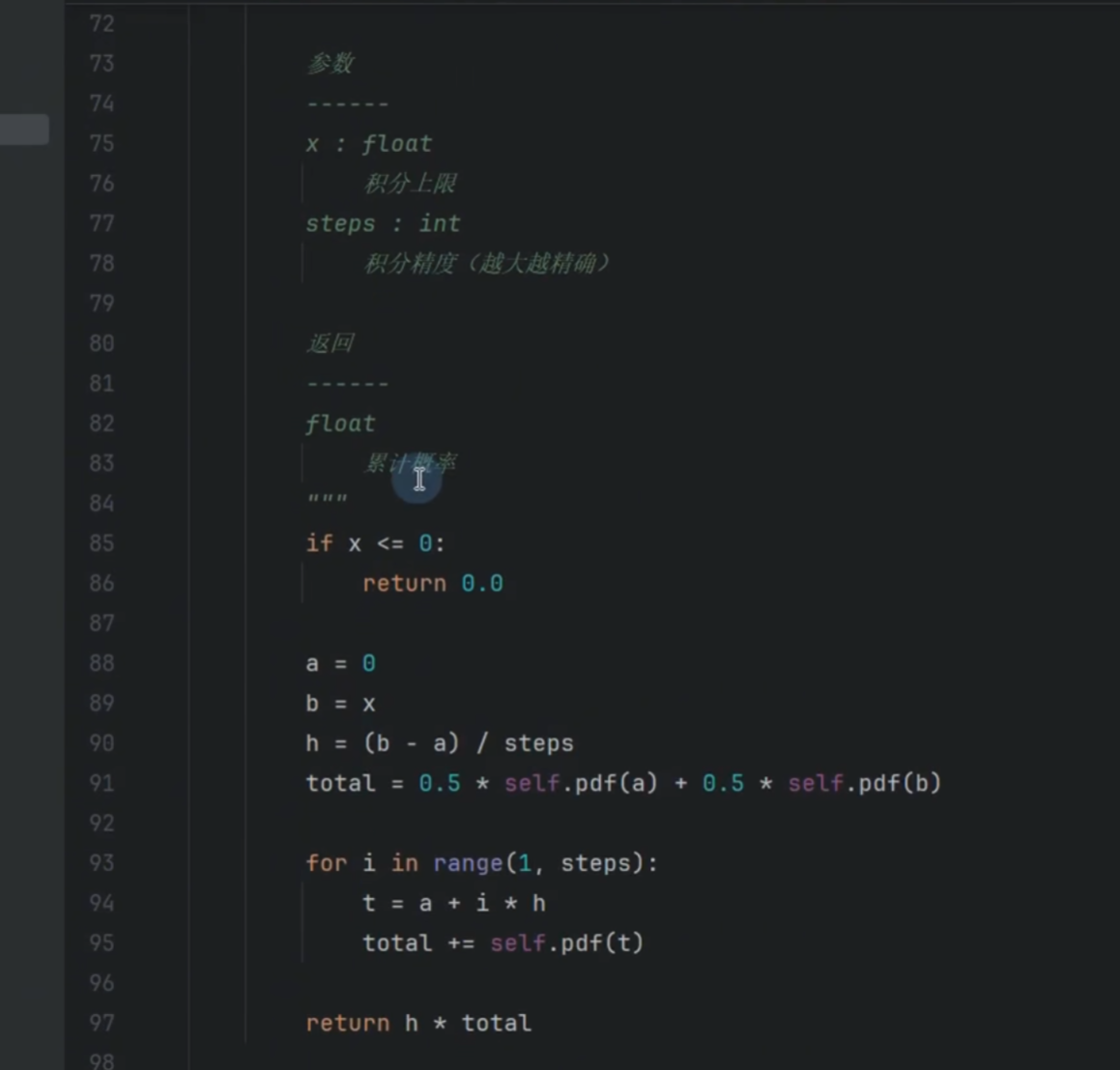
累计计算:利用梯形的进行逼近
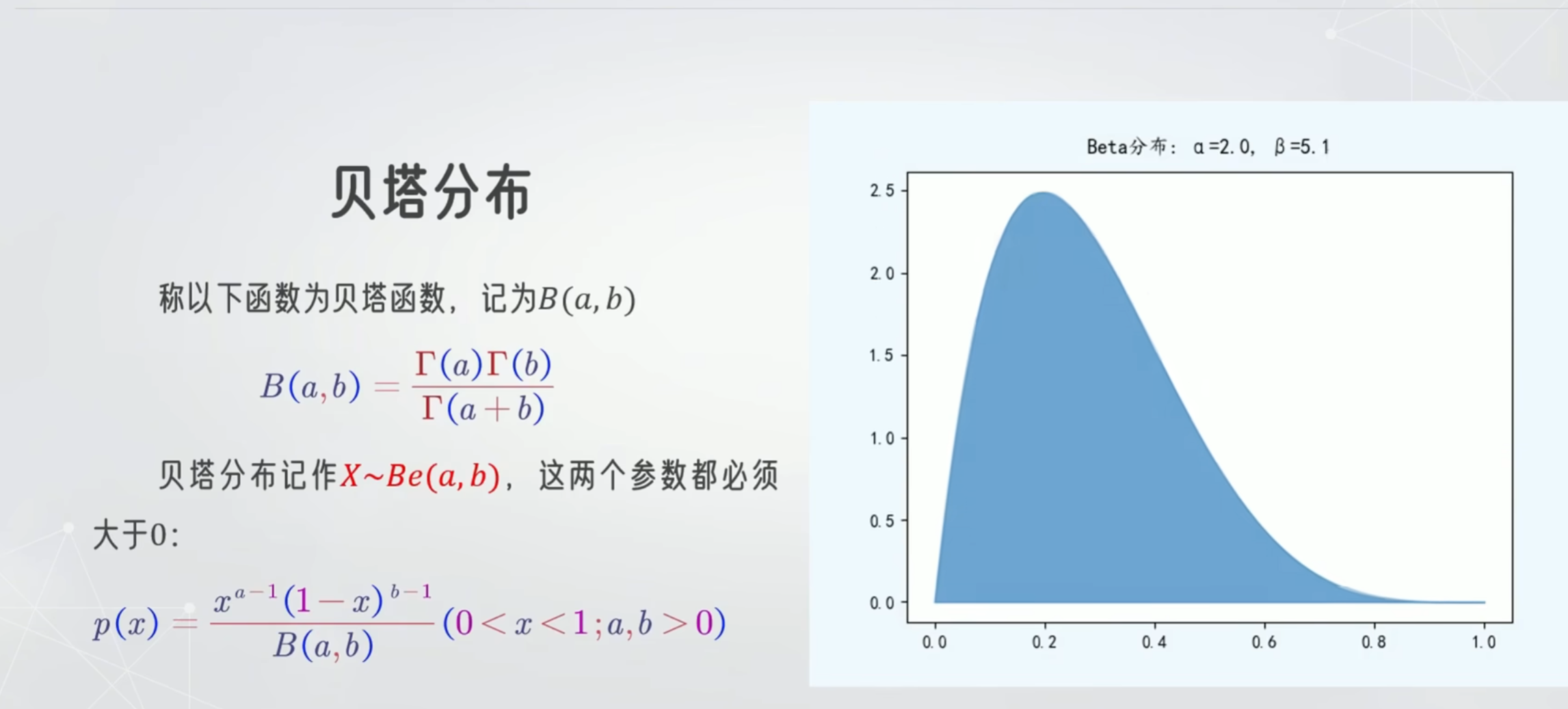
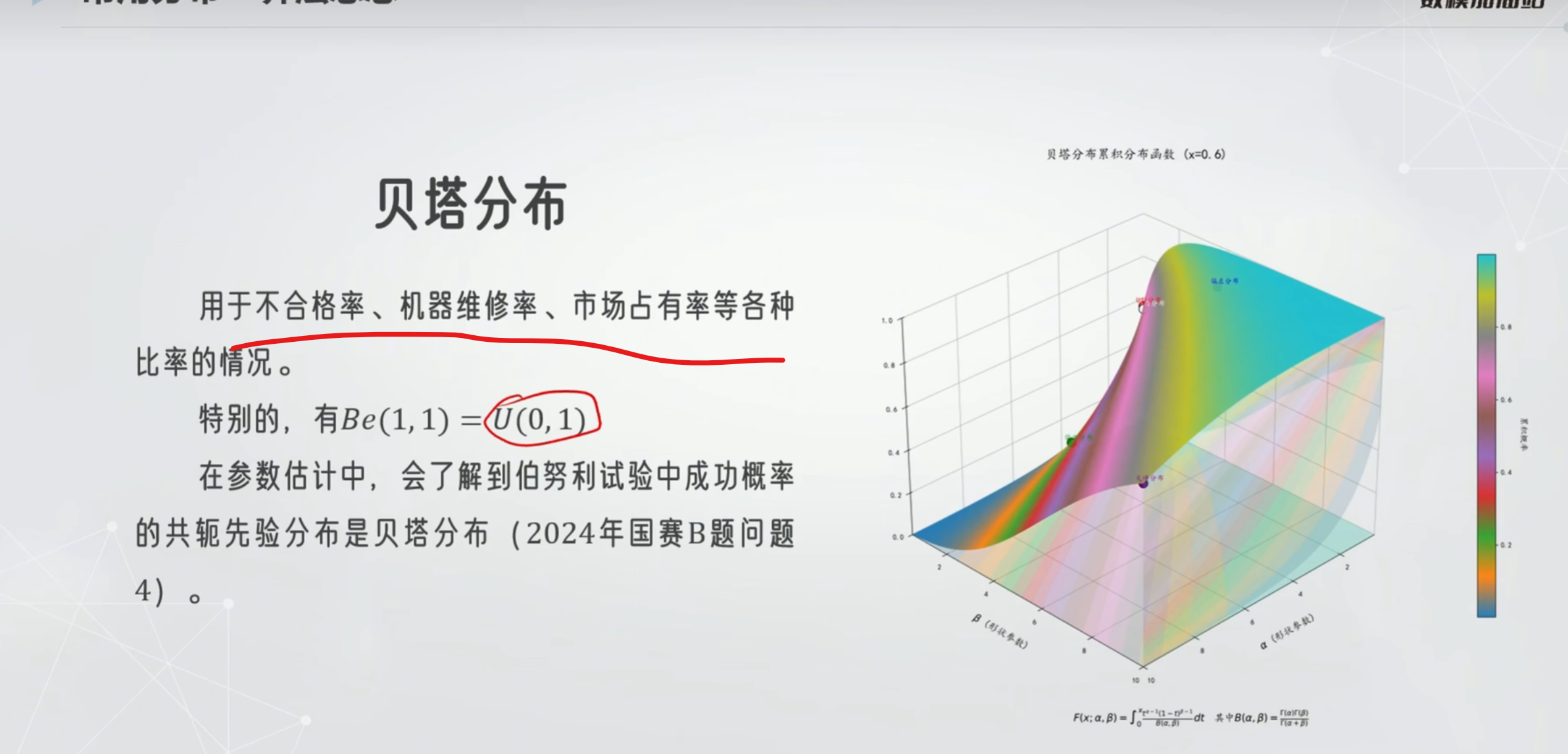
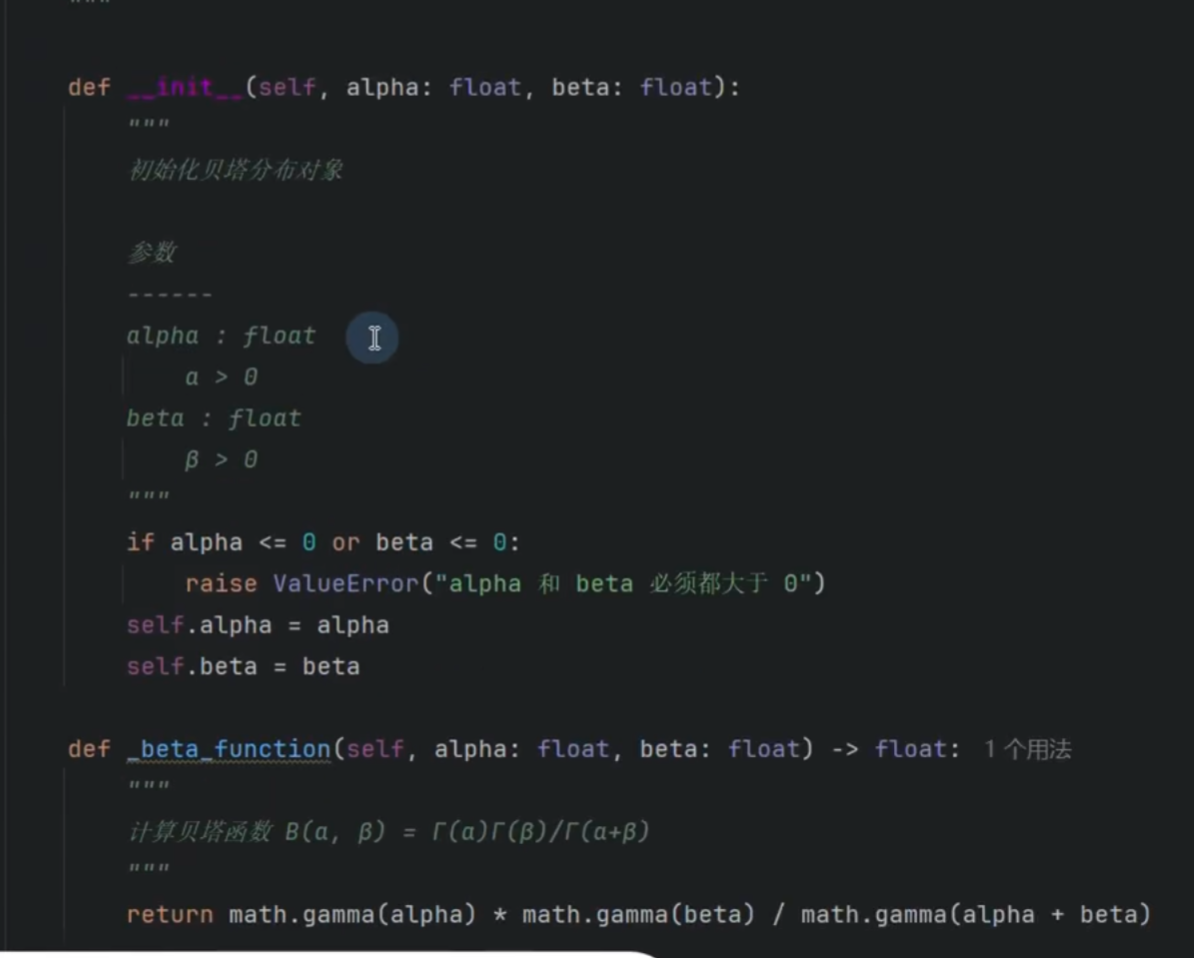
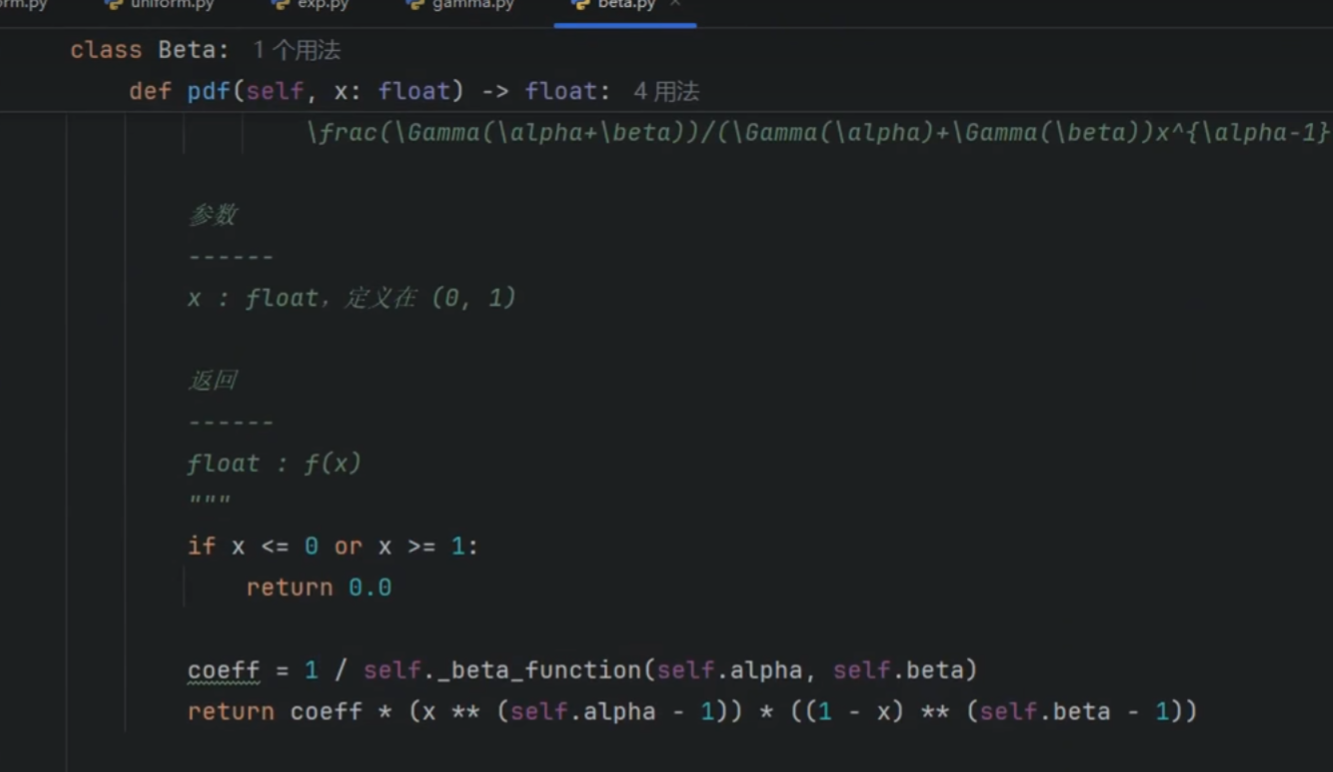
贝塔分布

计算
四 统计量计算
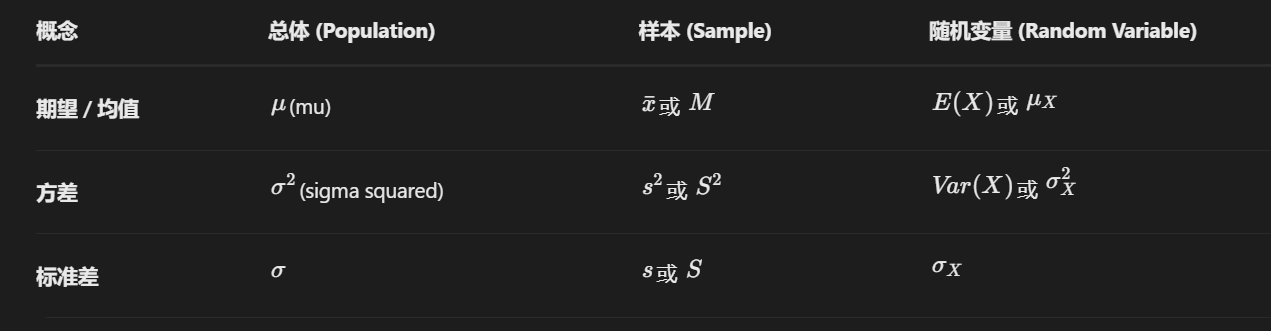
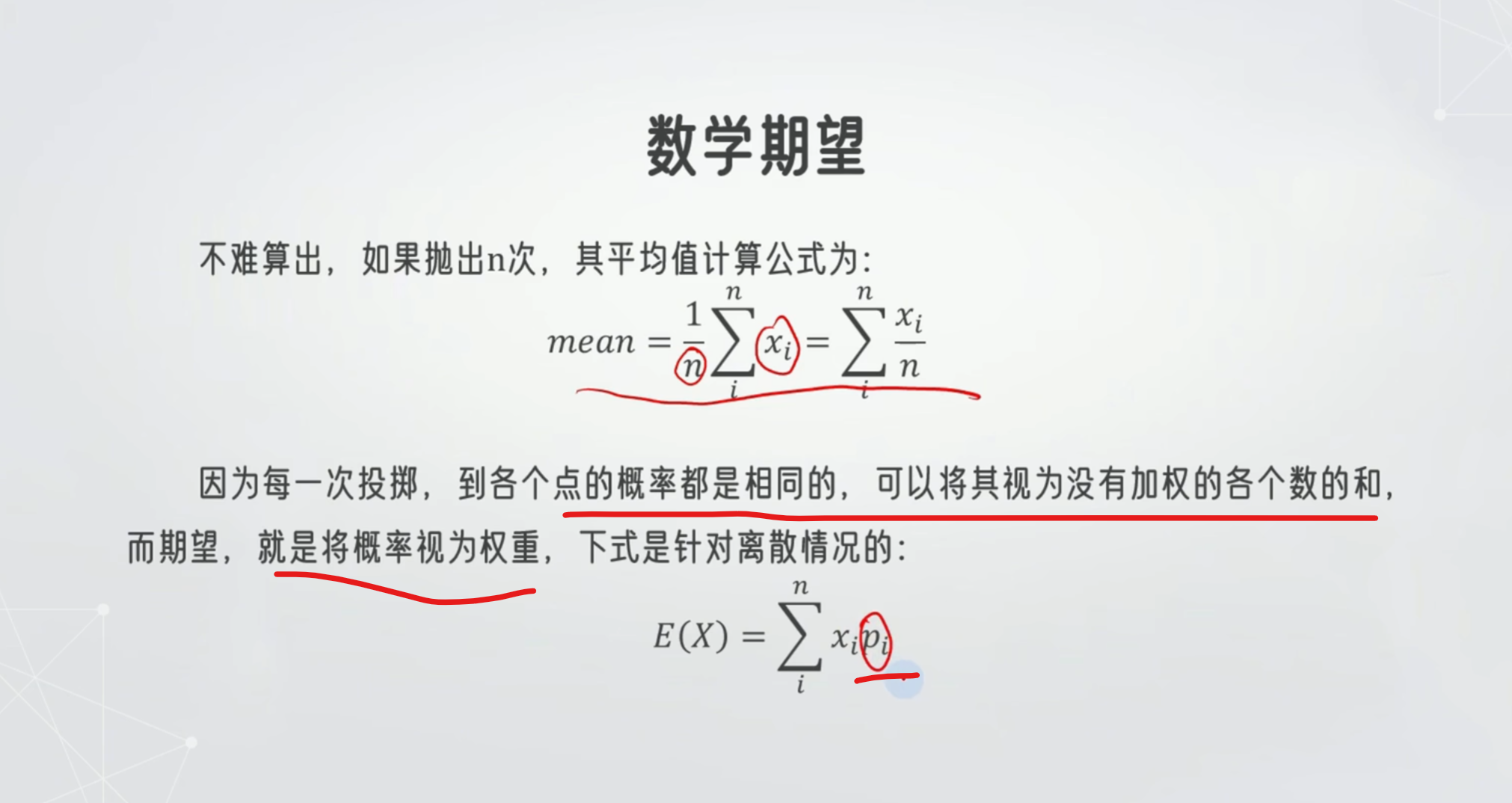
数学期望

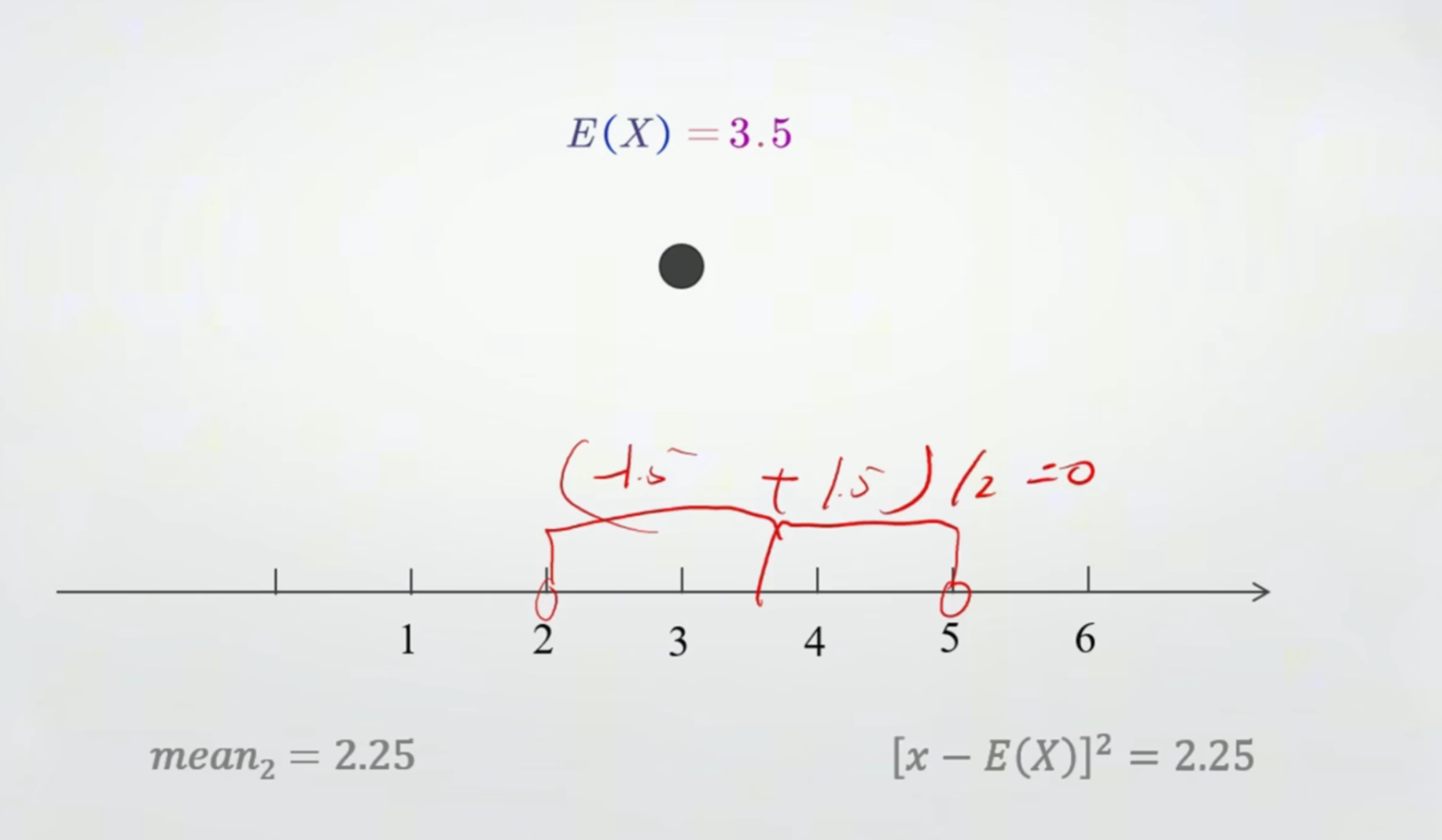
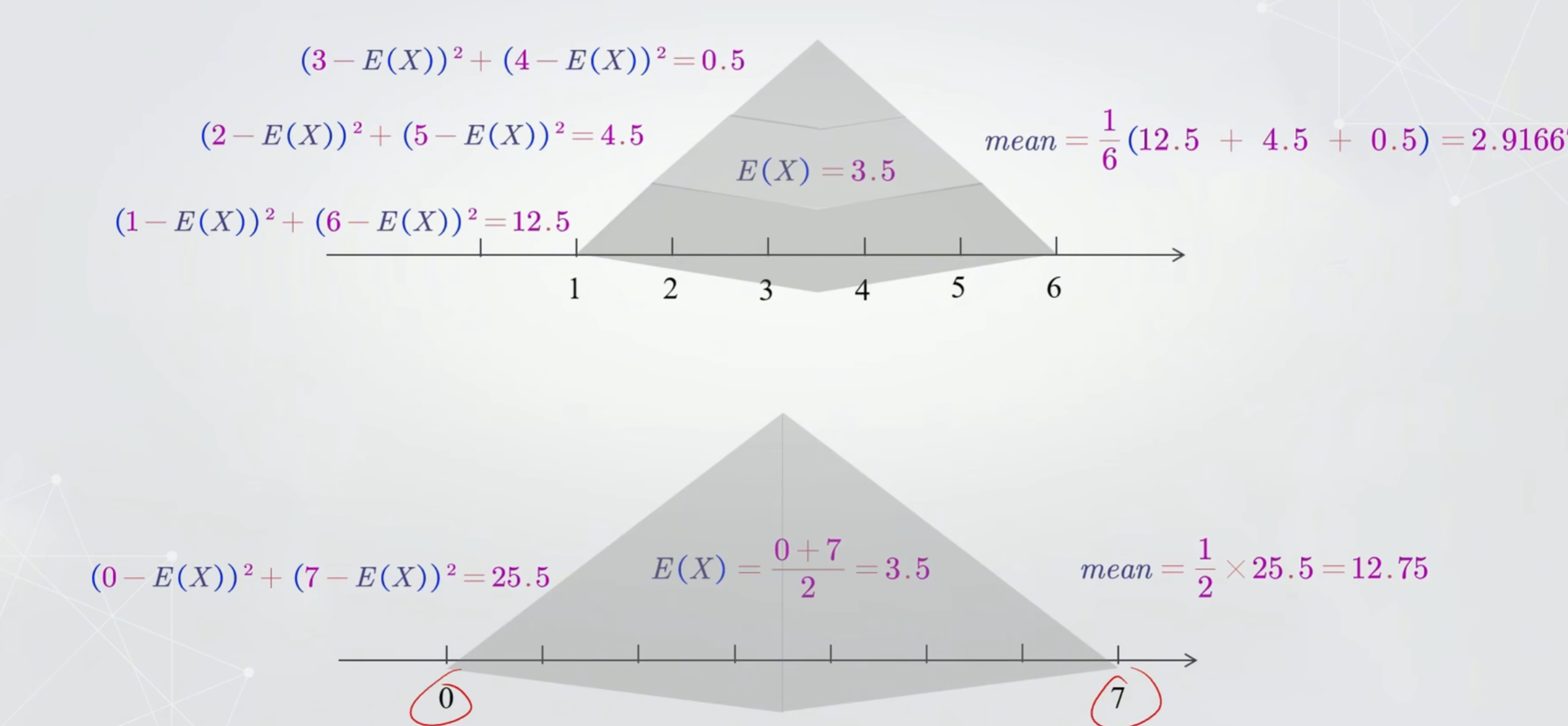
方差


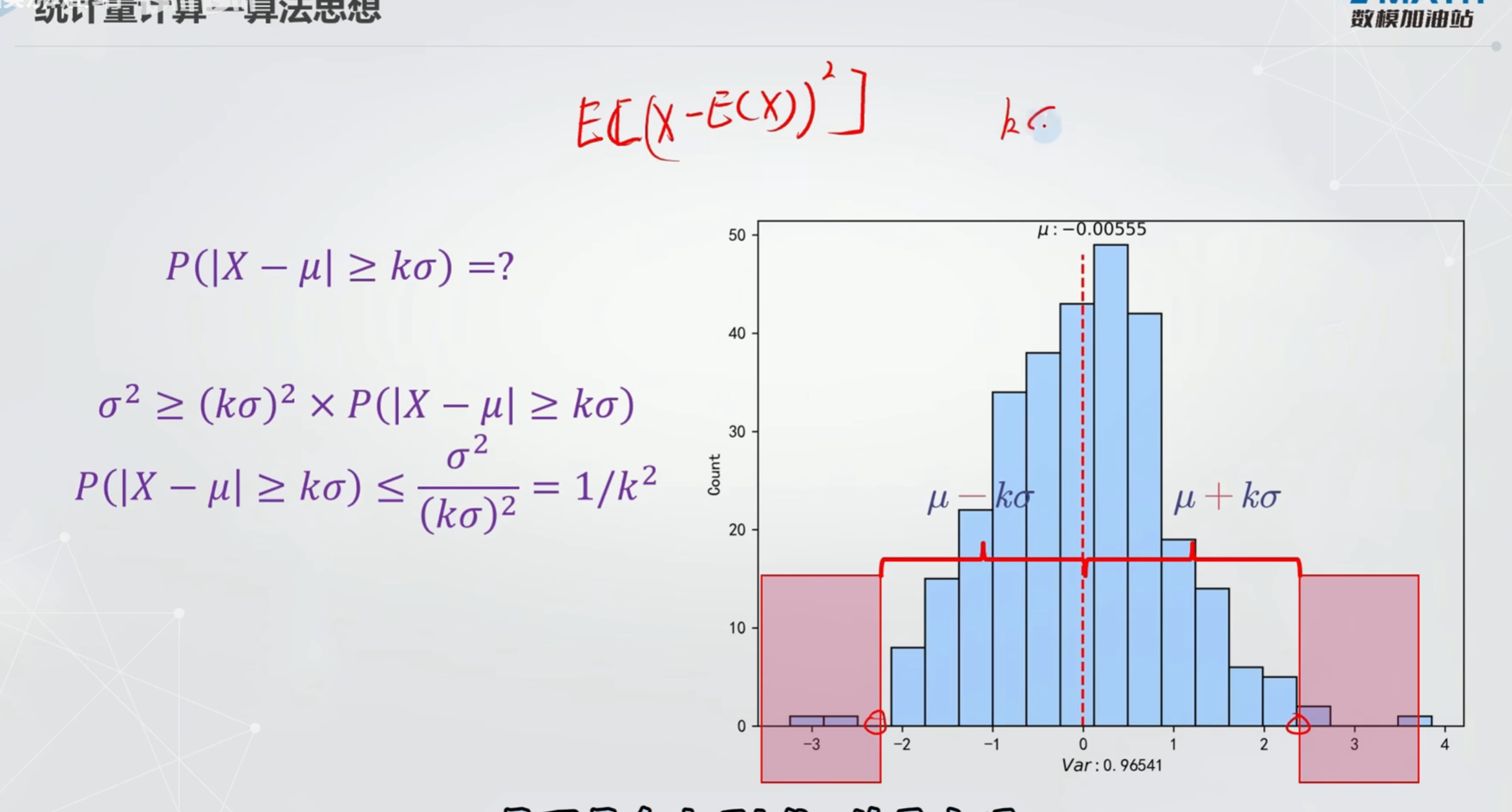
 常用的分布
常用的分布
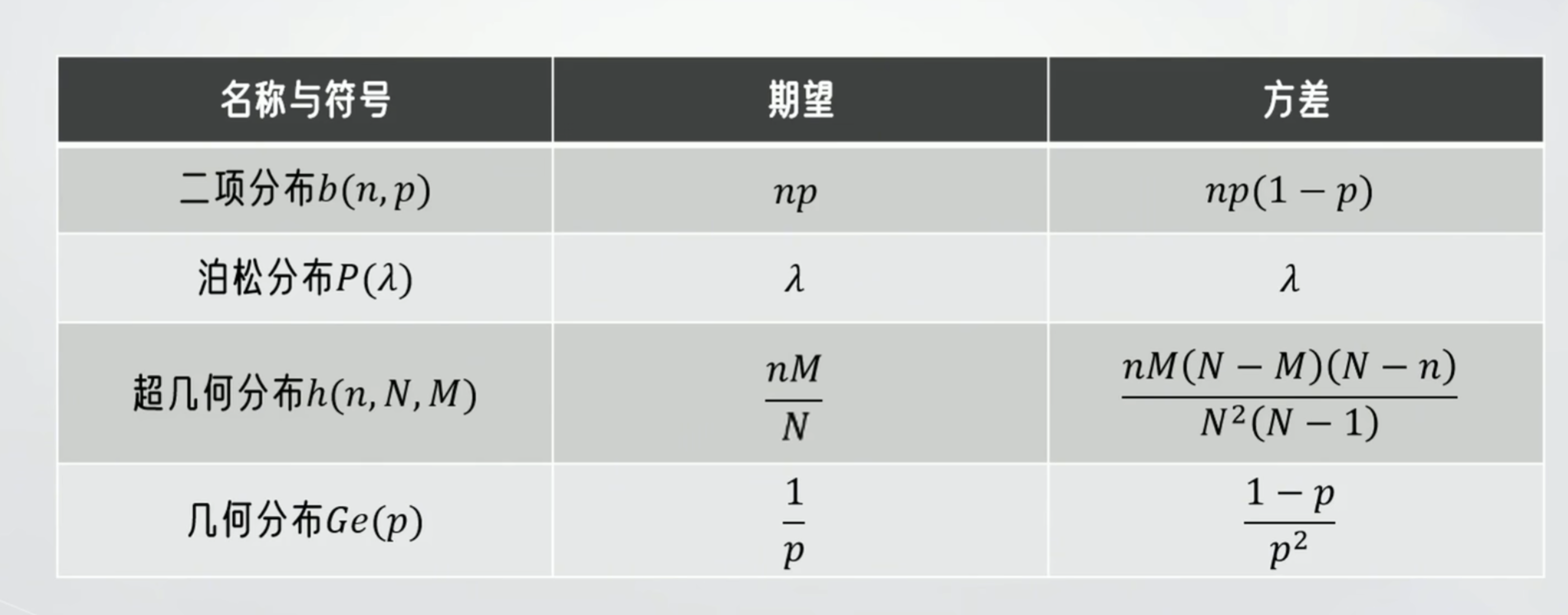
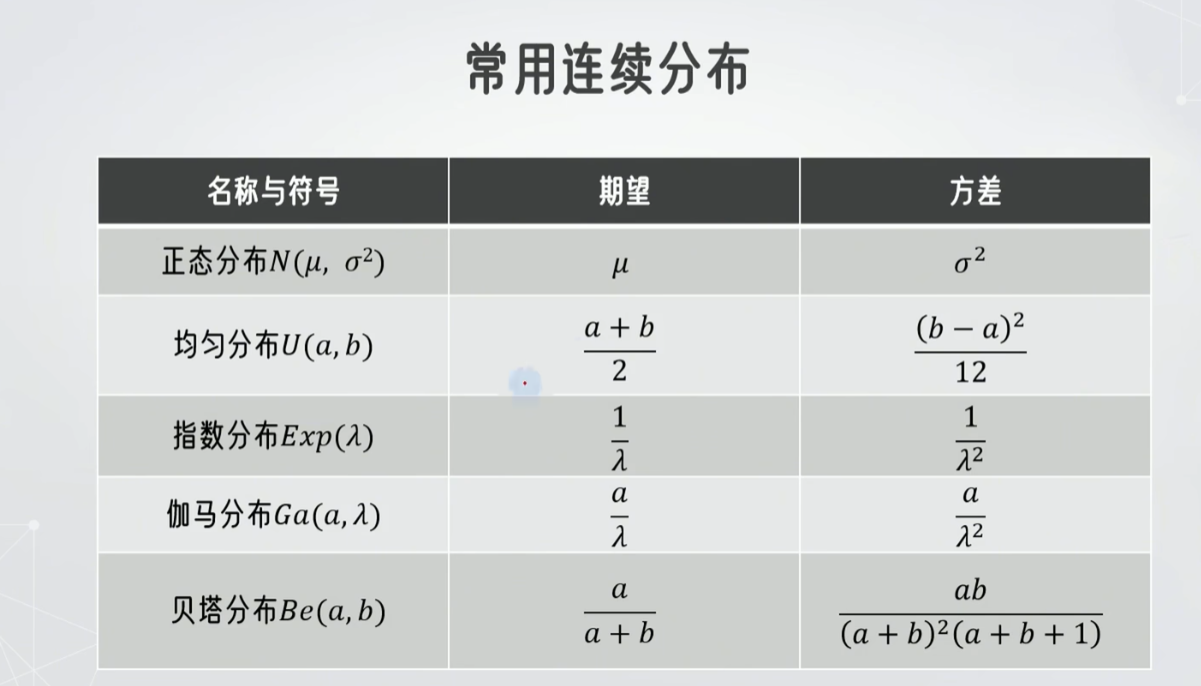
变异系数


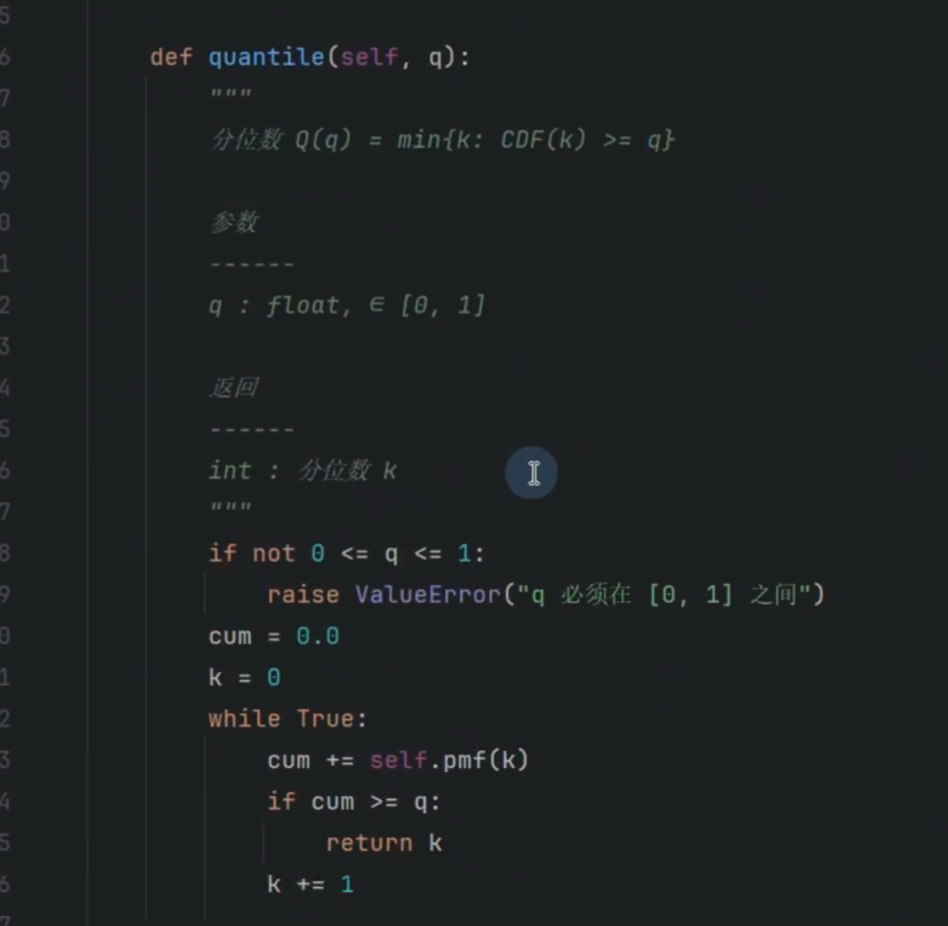
分位数

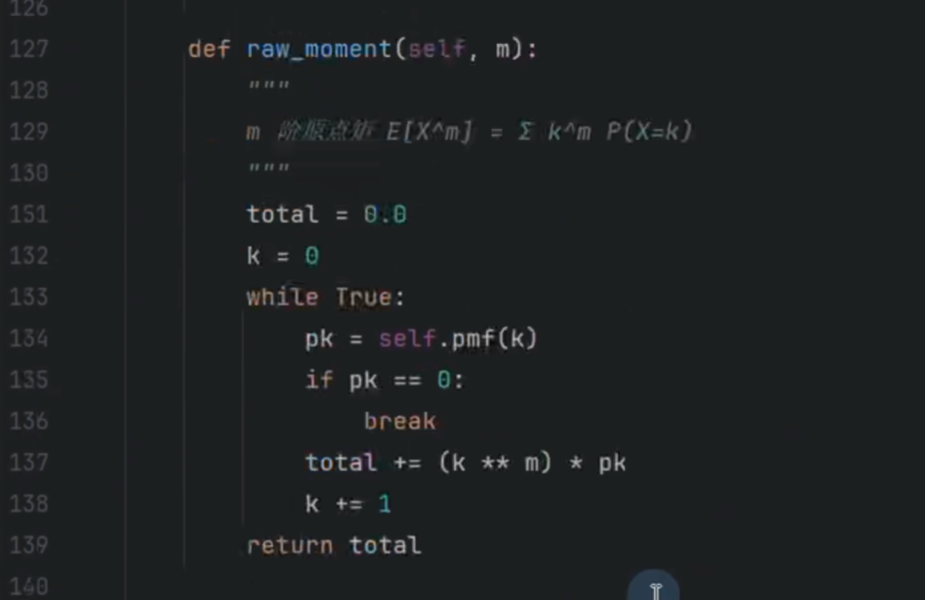
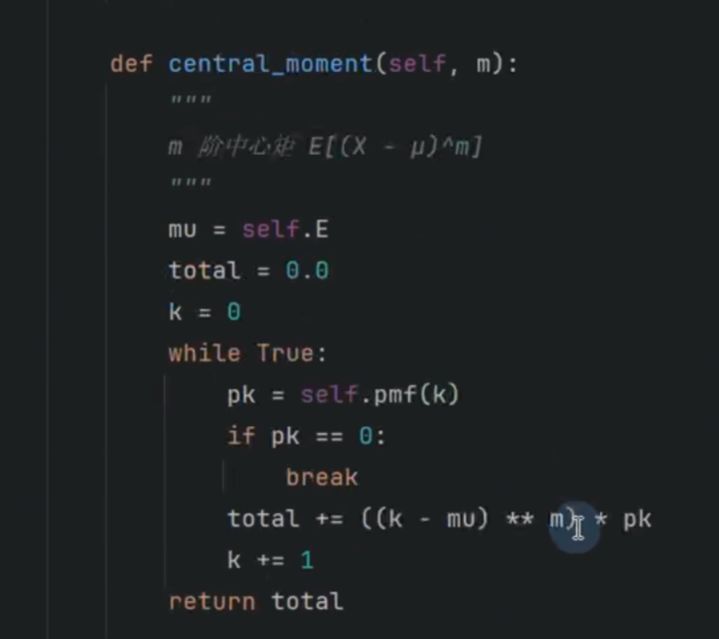
k阶矩

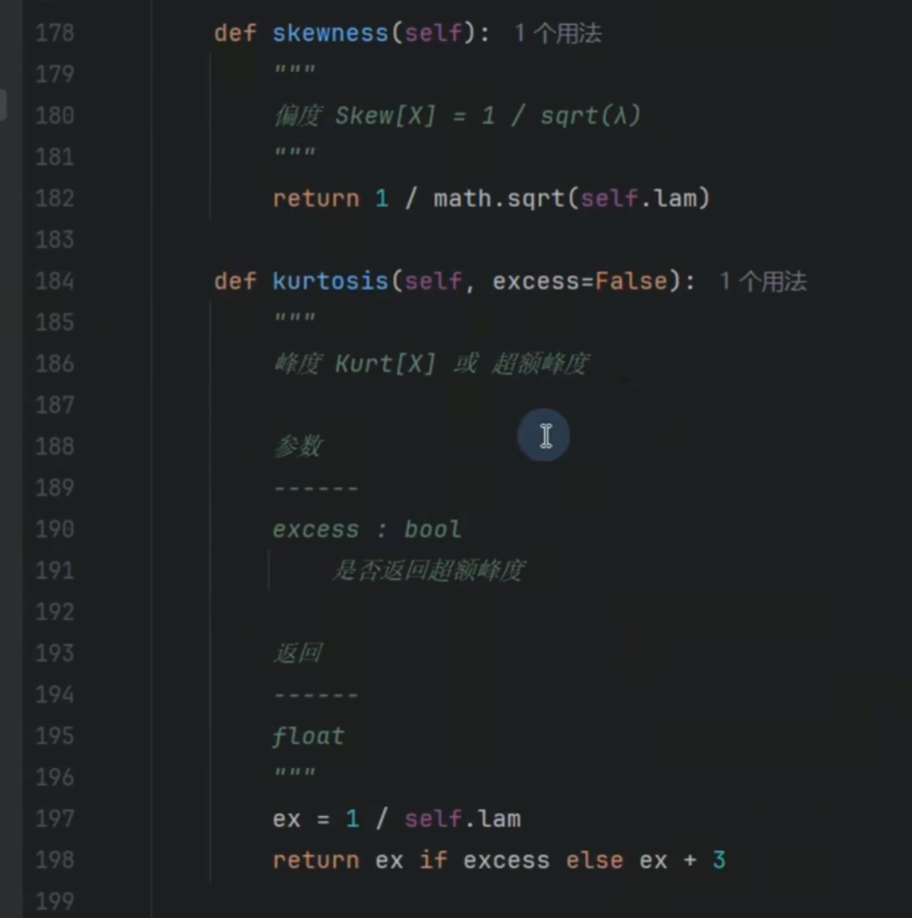
偏度和峰度

多维随机变量的统计量计算

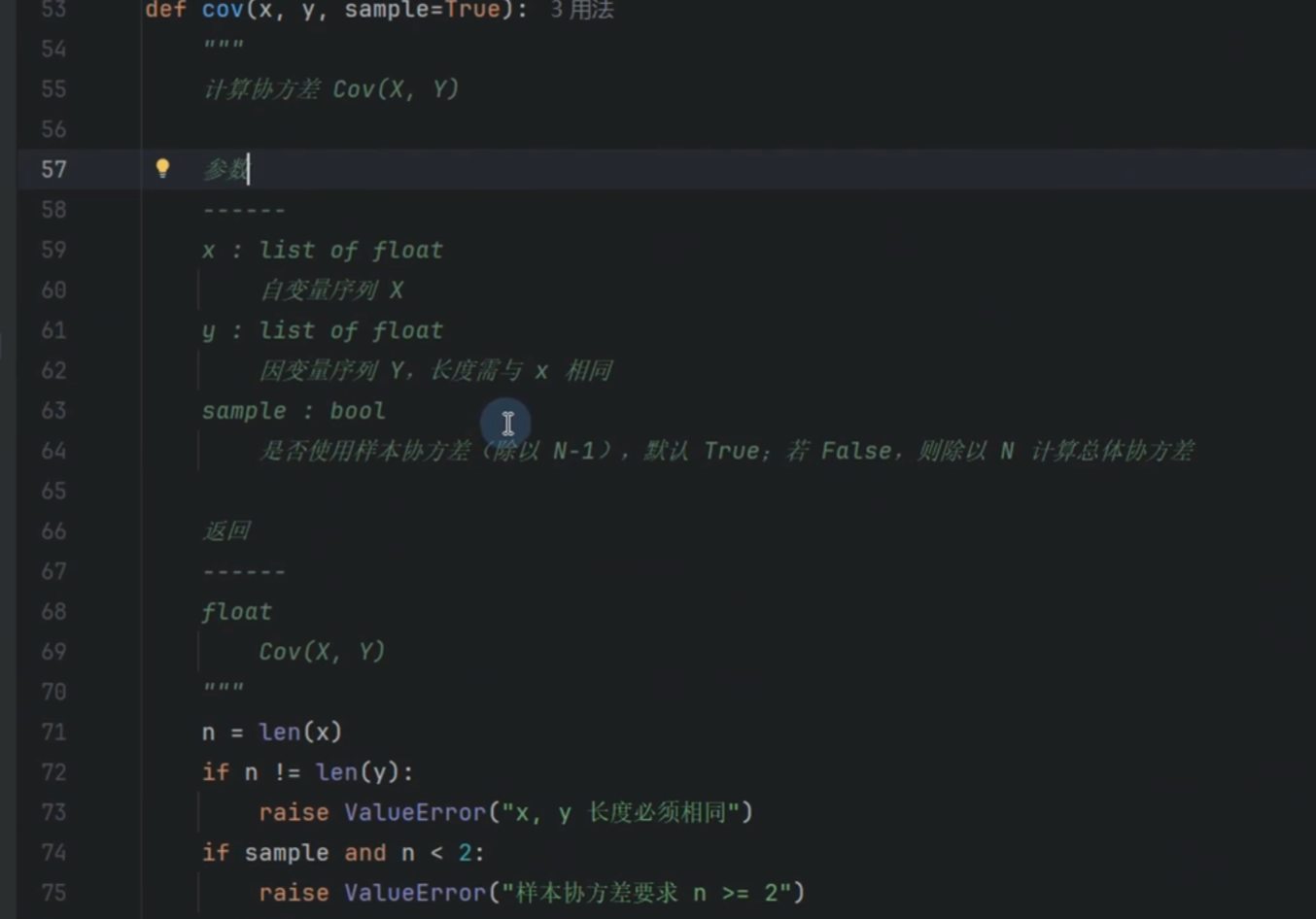
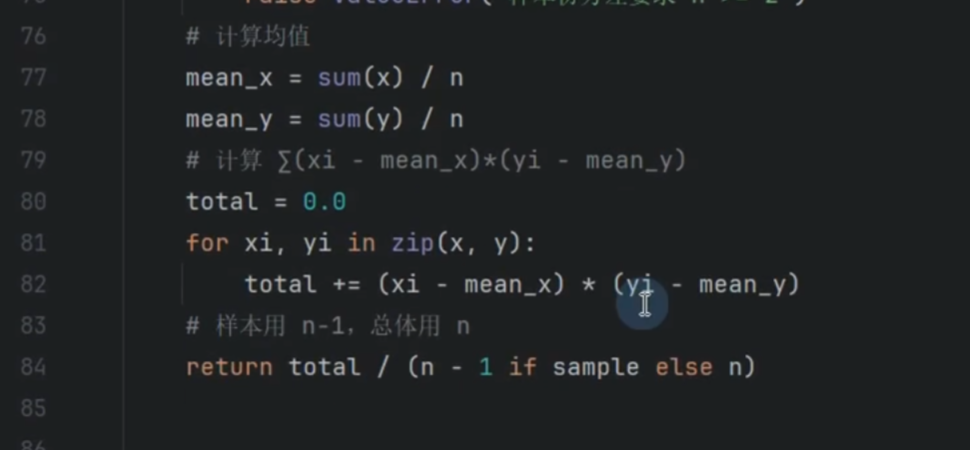
协方差

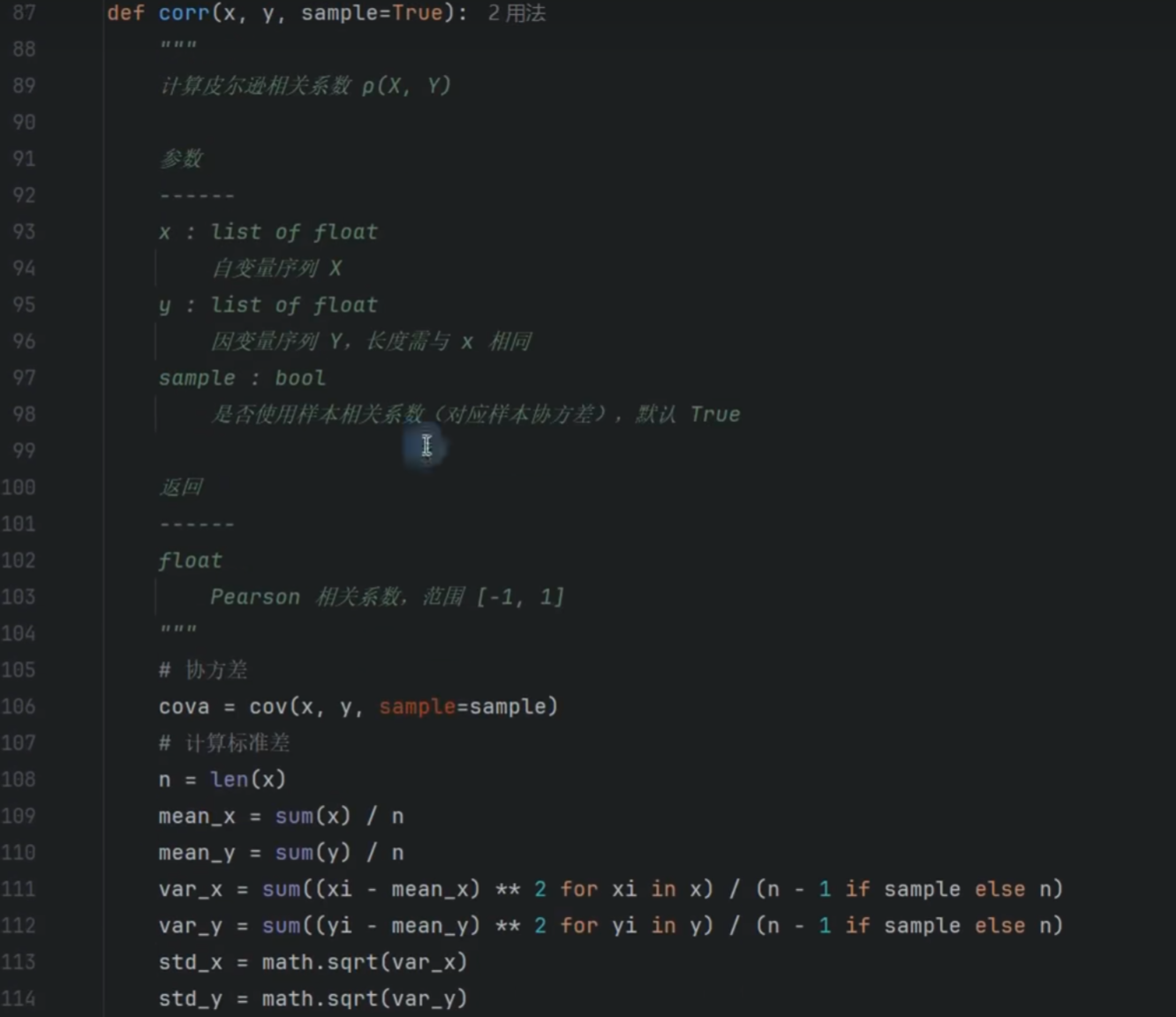
相关系数

2 pyhon代码
二项分布
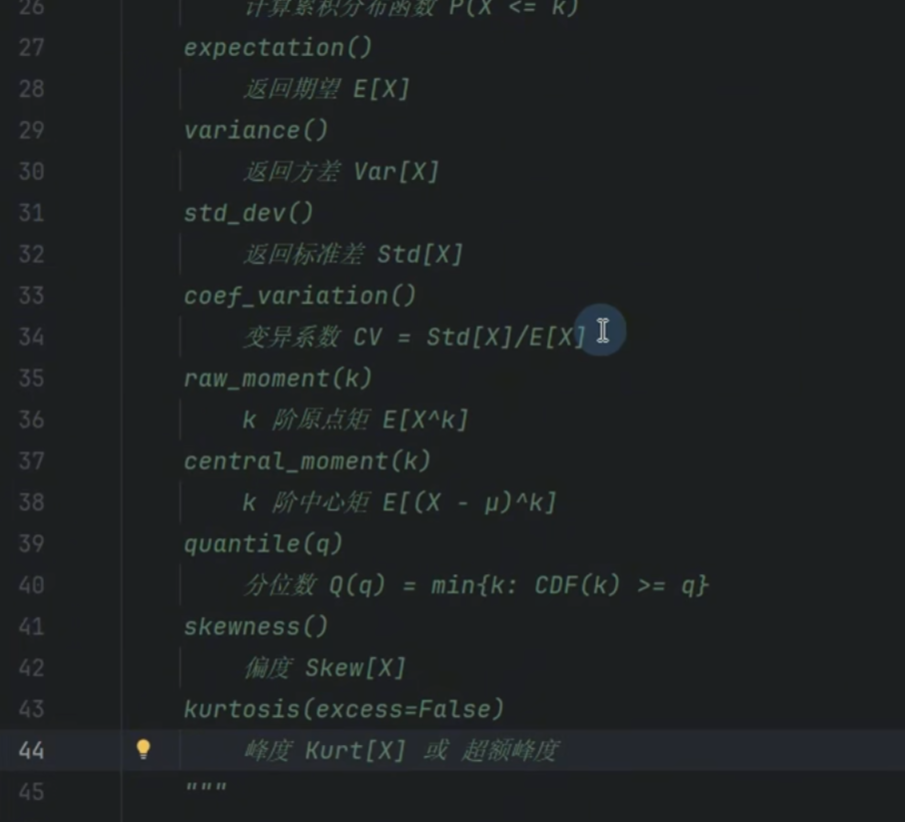
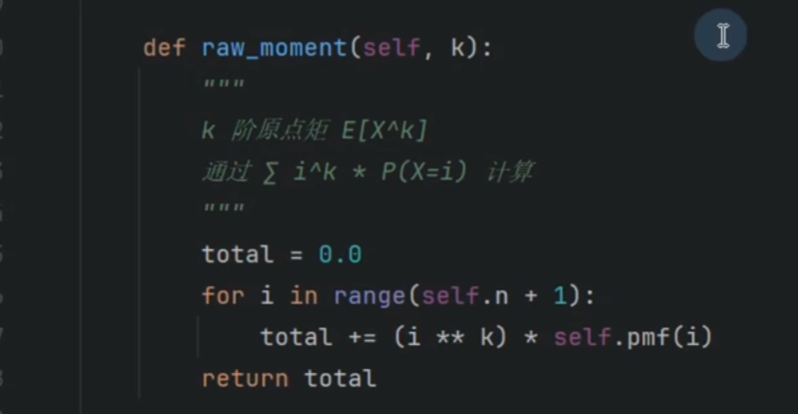
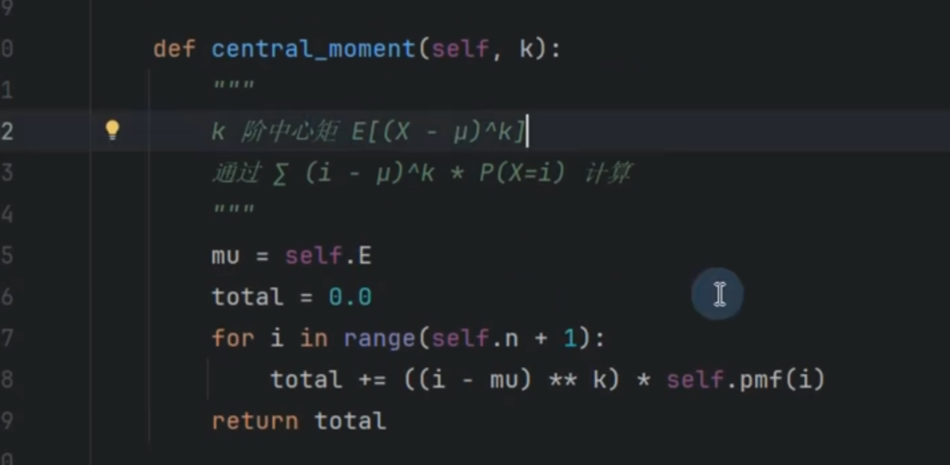
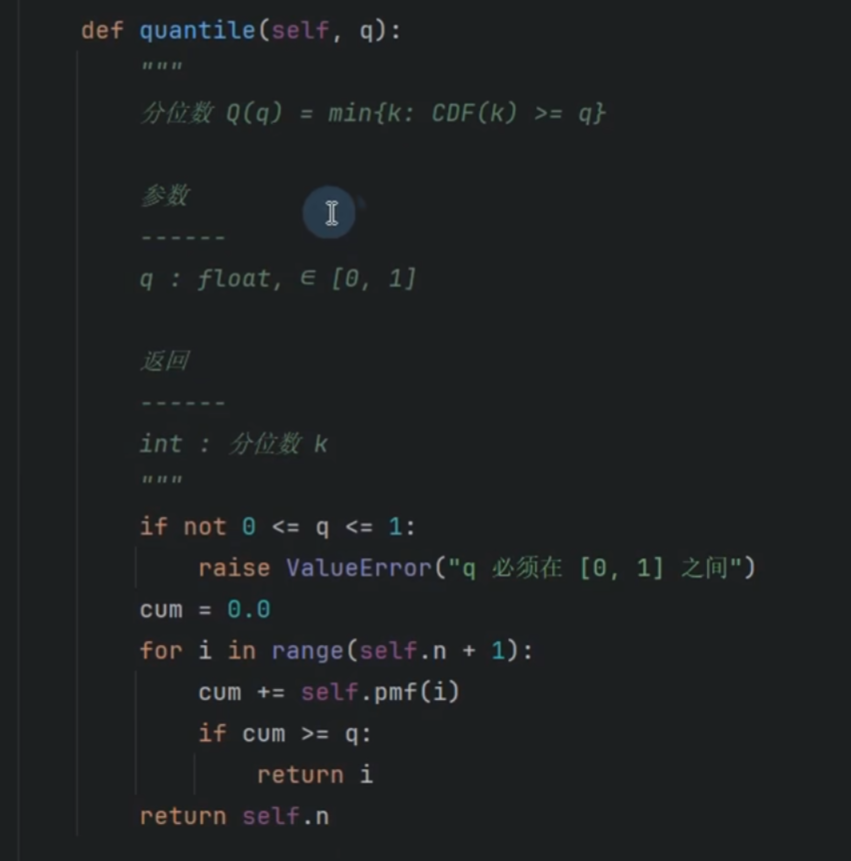
偏离中心的程度
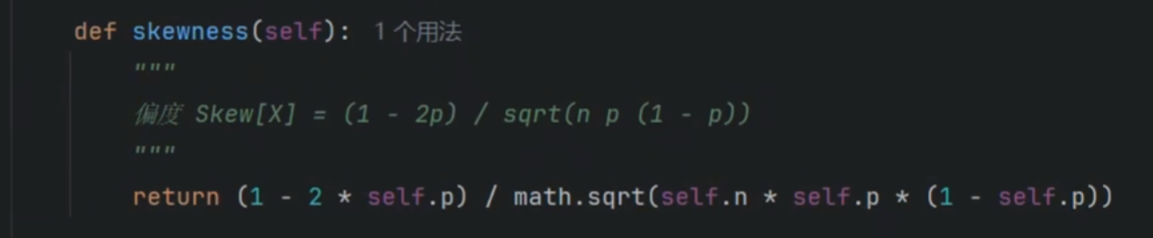
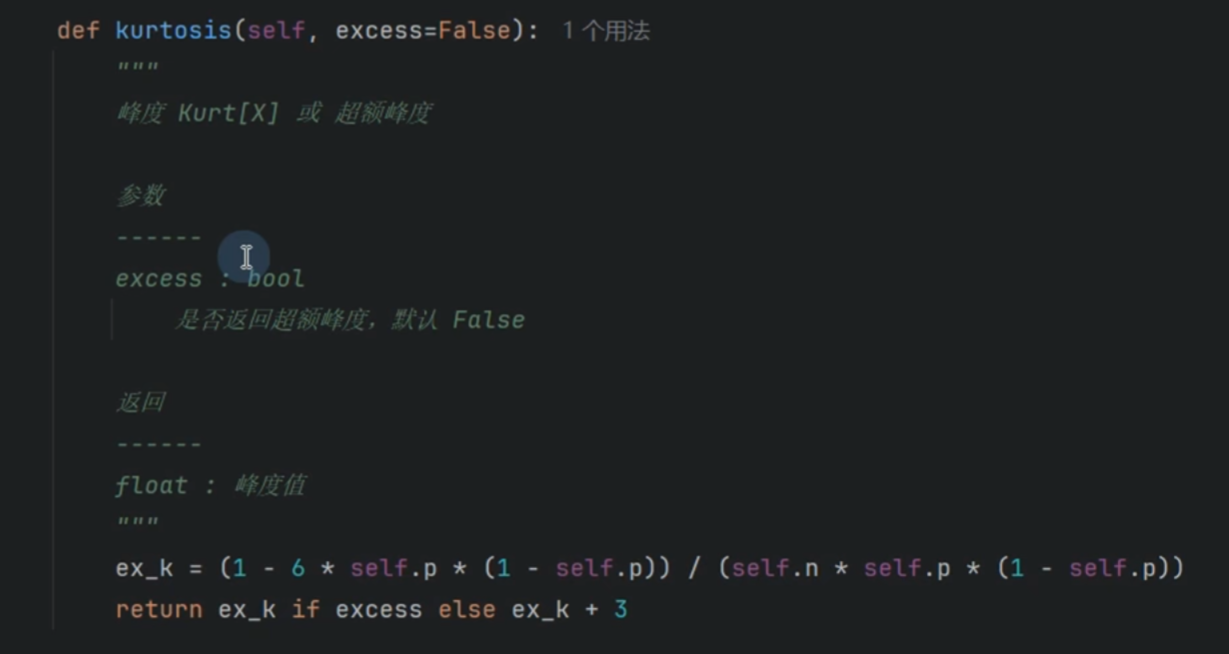
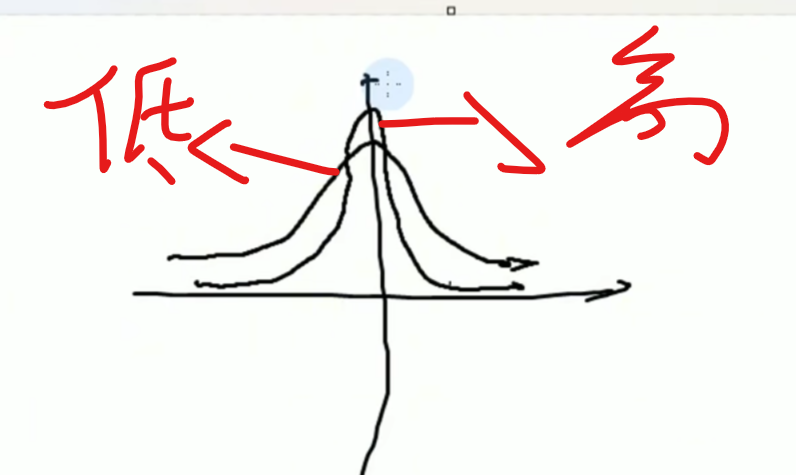
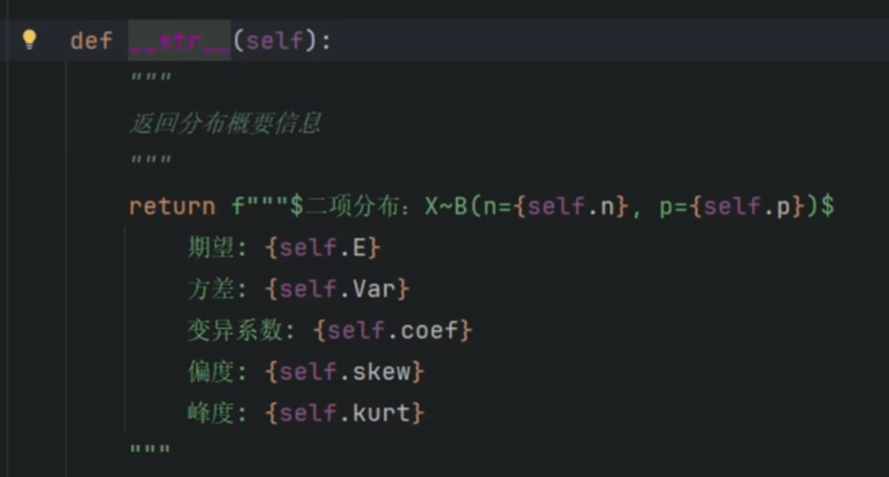
泊松分布
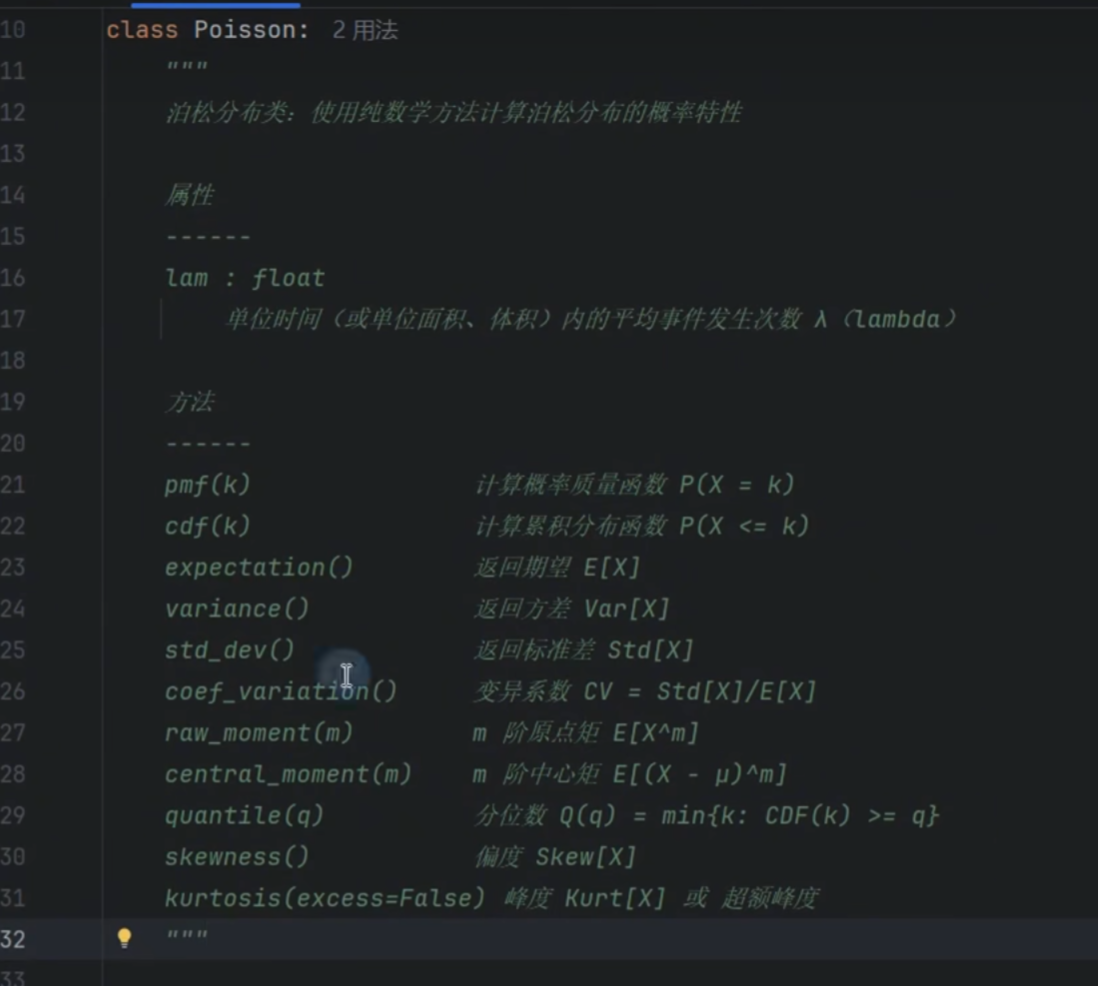
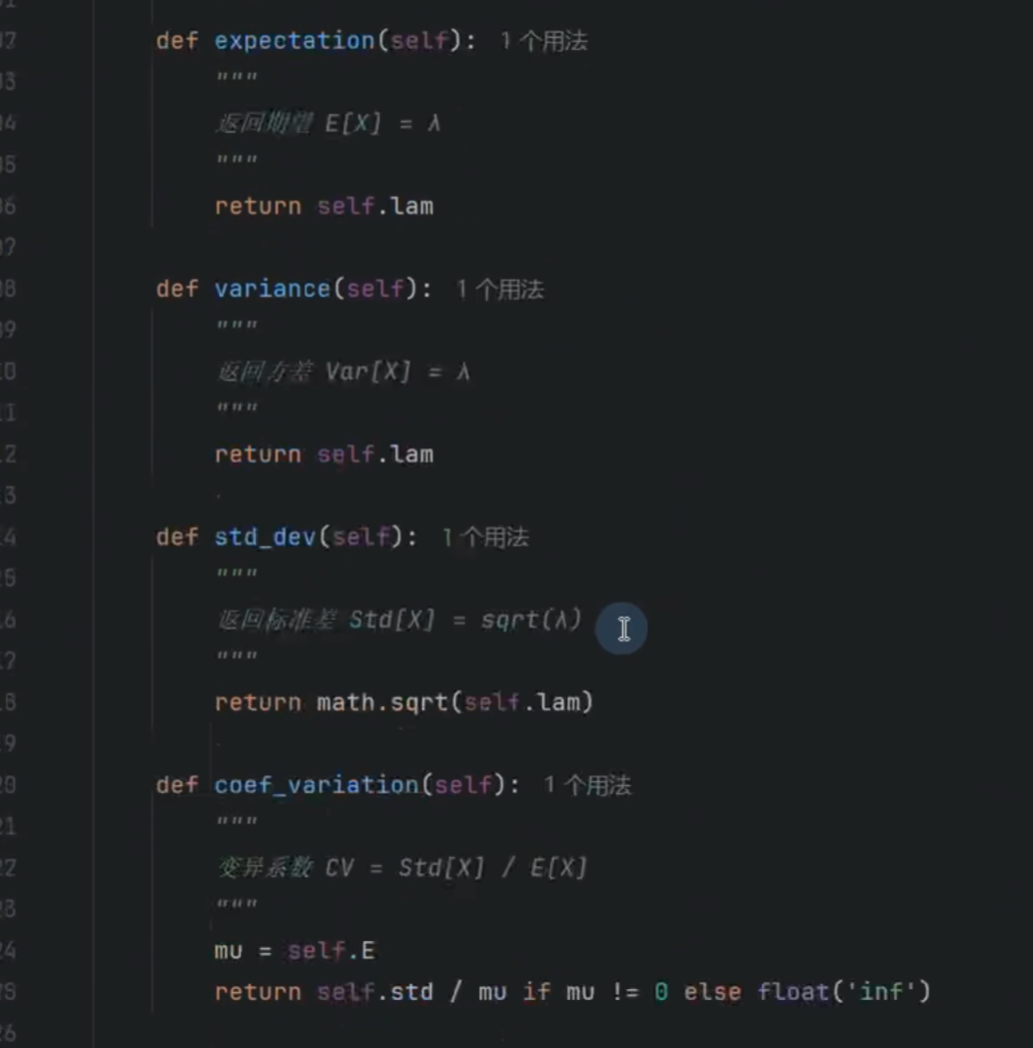
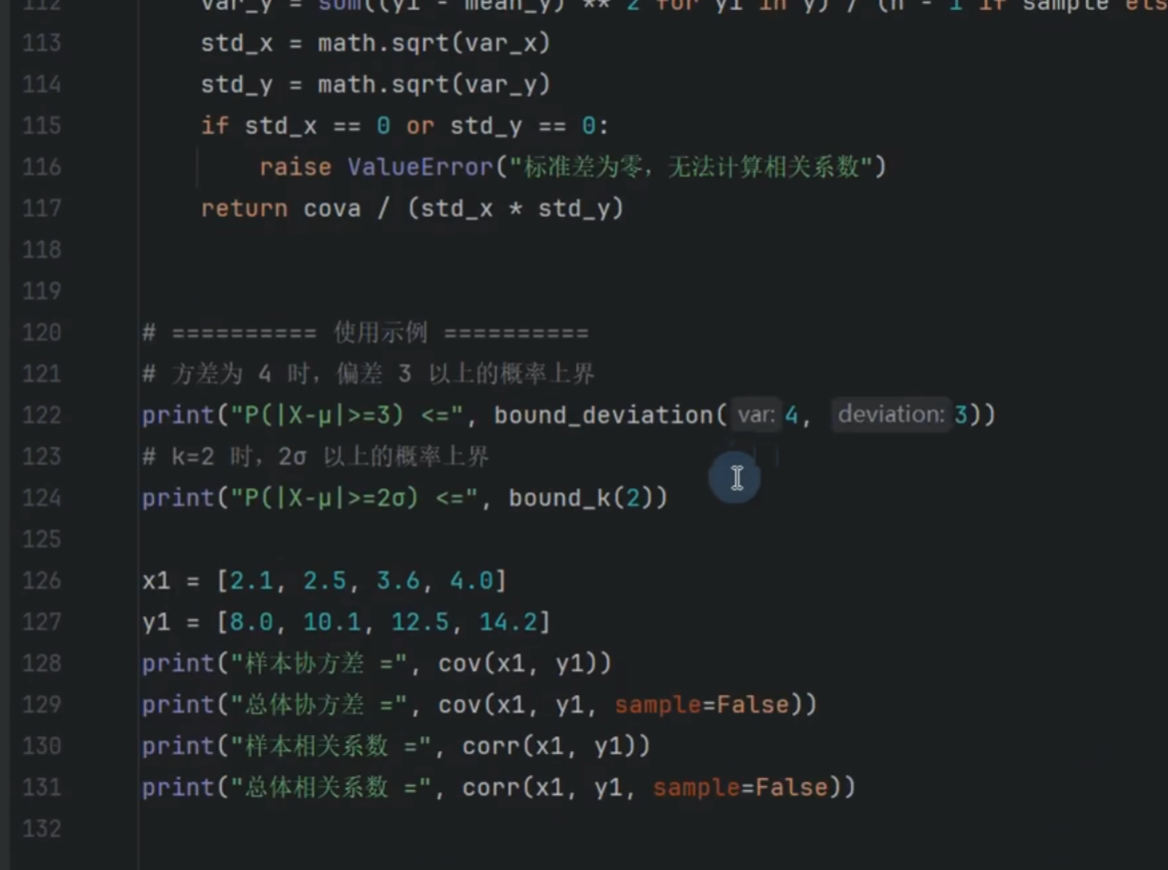
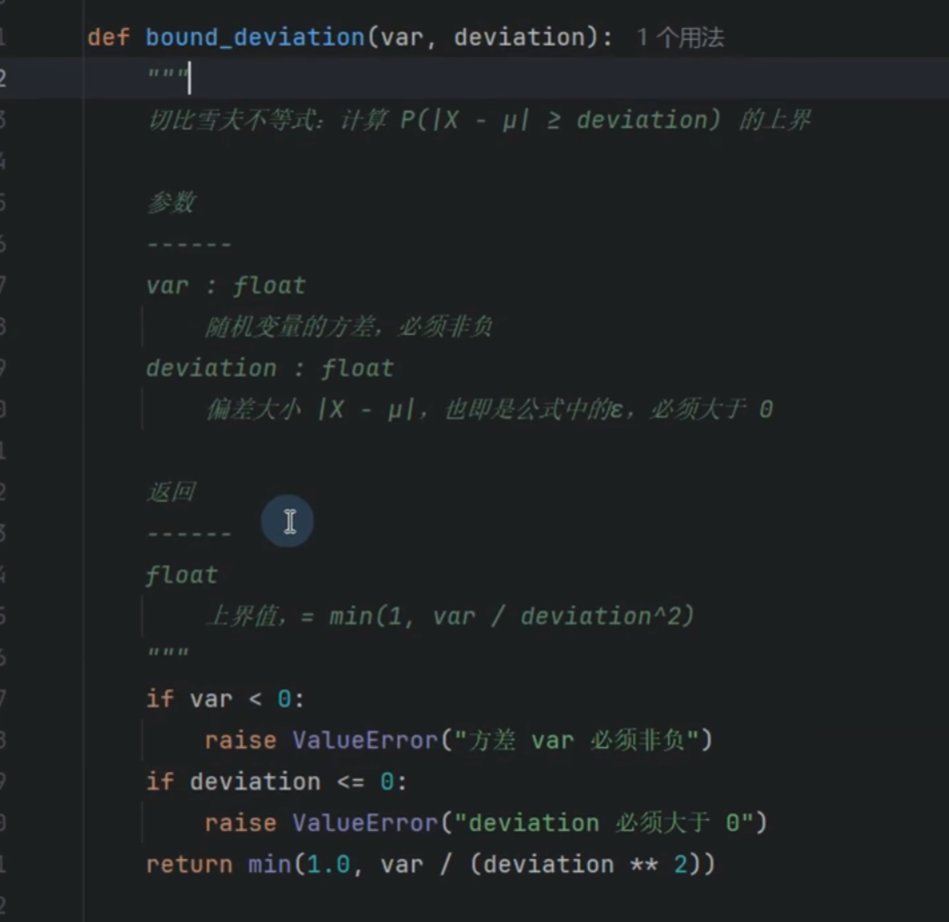
切比雪夫不等式

协方差
相关系数