目录
[1.1 最小生成树【模板】](#1.1 最小生成树【模板】)
[1.2 买礼物(非联通图)](#1.2 买礼物(非联通图))
[1.3 繁忙的都市(瓶颈生成树)](#1.3 繁忙的都市(瓶颈生成树))
[1.4 滑雪(有向图)](#1.4 滑雪(有向图))
[2. 拓扑排序](#2. 拓扑排序)
[2.1 【模板】拓扑排序/家谱树](#2.1 【模板】拓扑排序/家谱树)
[2.2 摄像头](#2.2 摄像头)
[2.3 最大食物链计数(拓扑排序+路径类dp)](#2.3 最大食物链计数(拓扑排序+路径类dp))
[2.4 杂务 (拓扑排序+递推)](#2.4 杂务 (拓扑排序+递推))
[3. 单源最短路](#3. 单源最短路)
[3.1 【模板】单源最短路径(弱化版)](#3.1 【模板】单源最短路径(弱化版))
[3.2 【模板】单源最短路径(标准版)](#3.2 【模板】单源最短路径(标准版))
[bellman-ford(BF) 算法(负权处理)](#bellman-ford(BF) 算法(负权处理))
[spfa(Shortest Path Faster Algorithm) 算法(BF优化)](#spfa(Shortest Path Faster Algorithm) 算法(BF优化))
[3.3 【模板】负环](#3.3 【模板】负环)
[bf 算法](#bf 算法)
[spfa 算法](#spfa 算法)
[3.4 单源最短路总结](#3.4 单源最短路总结)
[3.5 邮递员送信(Dijkstra+建反图)](#3.5 邮递员送信(Dijkstra+建反图))
[3.6 采购特价商品(无向图+坐标图)](#3.6 采购特价商品(无向图+坐标图))
[3.7 拉近距离(负环)](#3.7 拉近距离(负环))
[3.8 最短路计数(重边处理+dp)](#3.8 最短路计数(重边处理+dp))
[4. 多源最短路](#4. 多源最短路)
[4.1 【模板】Floyd](#4.1 【模板】Floyd)
[4.2 Clear And Present Danger S](#4.2 Clear And Present Danger S)
[4.3 灾后重建](#4.3 灾后重建)
[4.4 无向图的最小环问题](#4.4 无向图的最小环问题)
1.最小生成树
最小生成树一般基于无向图的场景,特殊情况下可以接入有向图
1.1 最小生成树【模板】

代码实现如下:
Prim算法
核心:不断加点

时间复杂度n^2
邻接矩阵存图
cpp
#include <bits/stdc++.h>
using namespace std;
const int N=5010,M=2e5+10,INF=0x3f3f3f3f;
int n,m;
int dist[N],edge[N][N];//邻接矩阵存图
bool st[N];
int prime()
{
memset(dist,INF,sizeof(dist));
dist[1]=0;
int ret=0;
for (int i=1;i<=n;++i)//循环加入n个点
{
//1.找最近点,必须满足:(1)未加入生成树(2)距离最小
int t=0;
for (int j=1;j<=n;++j)
if (!st[j]&&dist[j]<dist[t])
t=j;
//判断是否联通,不连通说明存在某个点不能与其他点相连
if (dist[t]==INF)return INF;
ret+=dist[t];
st[t]=true;//别忘了标记
//2.更新该点到能接触到的点的最小距离
for (int j=1;j<=n;++j)
dist[j]=min(dist[j],edge[t][j]);
}
return ret;
}
int main()
{
std::cin.tie(nullptr);
std::cout.tie(nullptr);
std::ios::sync_with_stdio(false);
cin>>n>>m;
memset(edge,INF,sizeof(edge));
while(m--)
{
int u,v,w;
cin>>u>>v>>w;
edge[u][v]=edge[v][u]=min(edge[u][v],w);
}
int ans=prime();
if (ans==INF)cout<<"orz"<<endl;
else cout<<ans<<endl;
return 0;
}vector数组存图
cpp
#include <bits/stdc++.h>
using namespace std;
const int N=5010,M=2e5+10,INF=0x3f3f3f3f;
typedef pair<int,int> PII;
int n,m;
vector<PII> edge[N];//vector数组存图
int dist[N];
bool st[N];
int prime()
{
memset(dist,INF,sizeof(dist));
dist[1]=0;
int ret=0;
for (int i=1;i<=n;++i)//循环加入n个点
{
//1.找最近点
int t=0;
for (int j=1;j<=n;++j)
if (!st[j]&&dist[j]<dist[t])
t=j;
//判断是否联通
if (dist[t]==INF)return INF;
ret+=dist[t];
st[t]=true;//别忘了标记
//2.更新该点到能接触到的点的最小距离
for (auto&[v,w]:edge[t])
{
dist[v]=min(dist[v],w);
}
}
return ret;
}
int main()
{
std::cin.tie(nullptr);
std::cout.tie(nullptr);
std::ios::sync_with_stdio(false);
cin>>n>>m;
while(m--)
{
int u,v,w;
cin>>u>>v>>w;
//不用考虑重边,因为在prim中我们取min
edge[u].push_back({v,w});
edge[v].push_back({u,w});
}
int ans=prime();
if (ans==INF)cout<<"orz"<<endl;
else cout<<ans<<endl;
return 0;
}Kruskal算法
核心:不断加边

由于只和边相关,所以我们不用考虑建图,时间复杂度mlogm
cpp
#include <bits/stdc++.h>
using namespace std;
const int N=5010,M=2e5+10,INF=0x3f3f3f3f;
struct node
{
int u,v,w;
}a[M];
int n,m,fa[N];//基于并查集
bool cmp(const node &a,const node &b)
{
return a.w<b.w;
}
int find(int x)
{
return x==fa[x]?x:fa[x]=find(fa[x]);
}
int kruskal()
{
sort(a+1,a+m+1,cmp);
int cnt=0;
int ret=0;
for (int i=1;i<=m;++i)
{
int u=a[i].u,v=a[i].v,w=a[i].w;
int fu=find(u),fv=find(v);
if (fu!=fv)
{
++cnt;
ret+=w;
fa[fu]=fv;
}
}
return cnt==n-1?ret:INF;
}
int main()
{
std::cin.tie(nullptr);
std::cout.tie(nullptr);
std::ios::sync_with_stdio(false);
cin>>n>>m;
for (int i=1;i<=m;++i)cin>>a[i].u>>a[i].v>>a[i].w;
//初始化并查集
for (int i=1;i<=n;++i)fa[i]=i;
int ans=kruskal();
if (ans==INF)cout<<"orz"<<endl;
else cout<<ans<<endl;
return 0;
}1.2 买礼物(非联通图)
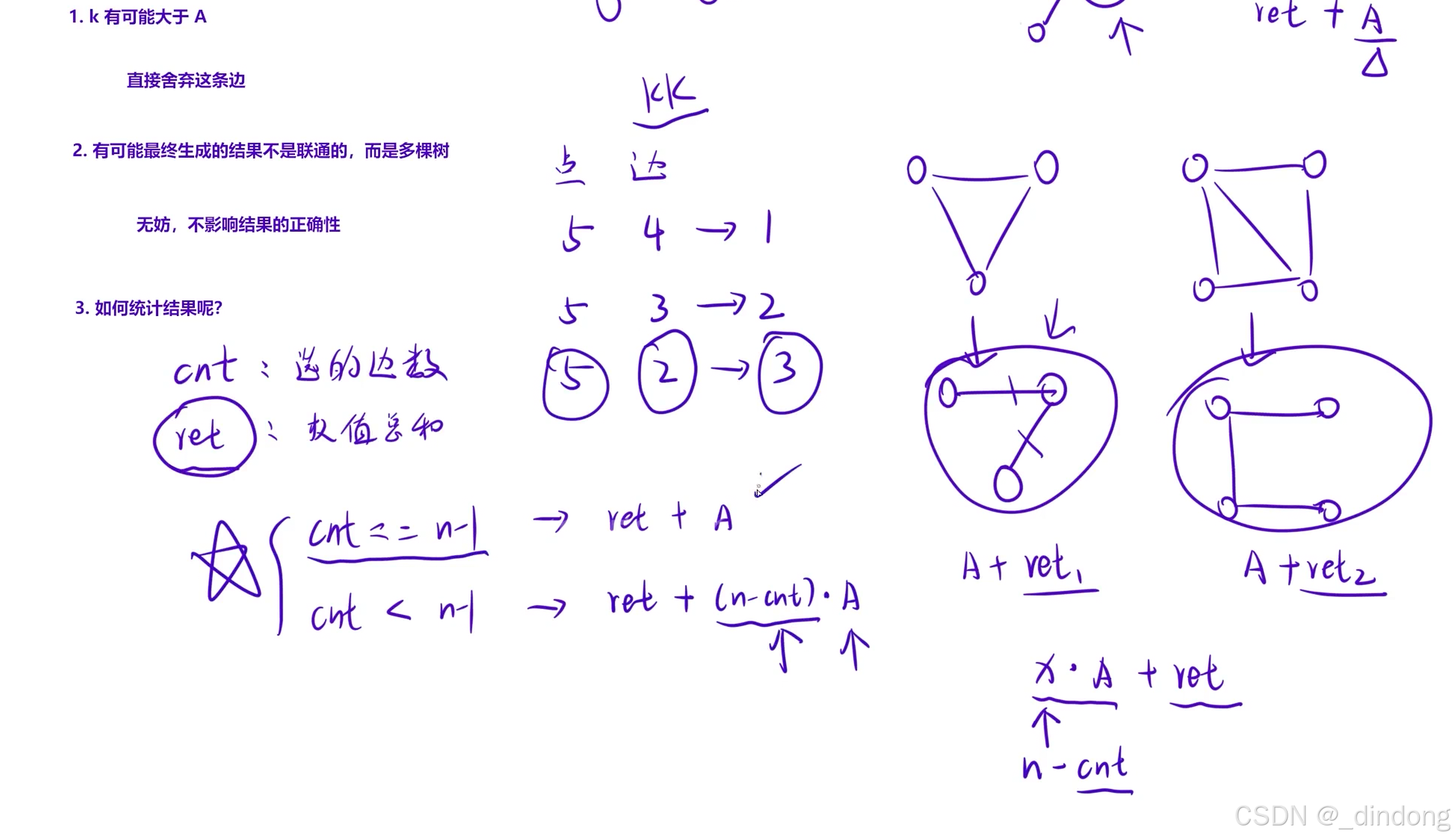
代码实现如下:
cpp
#include <bits/stdc++.h>
using namespace std;
const int N=500*500+10;
int a,n,fa[N];
struct node
{
int u,v,w;
}e[N];
int find(int x)
{
return x==fa[x]?x:fa[x]=find(fa[x]);
}
bool cmp(node a,node b)
{
return a.w<b.w;
}
int pos,cnt,ret;
void kruskal()
{
sort(e+1,e+pos+1,cmp);
for (int i=1;i<=pos;++i)
{
int u=e[i].u,v=e[i].v,w=e[i].w;
int fu=find(u),fv=find(v);
if (fu!=fv)
{
++cnt;//可能为非联通,标记树的个数
ret+=w;
fa[fu]=fv;
}
}
}
int main()
{
std::cin.tie(nullptr);
std::cout.tie(nullptr);
std::ios::sync_with_stdio(false);
cin>>a>>n;
for (int i=1;i<=n;++i)fa[i]=i;
for (int i=1;i<=n;++i)
{
for (int j=1;j<=n;++j)
{
int k;cin>>k;
//只存有效边
if (i>=j||k>a||k==0)continue;
++pos;
e[pos].u=i;e[pos].v=j,e[pos].w=k;
}
}
kruskal();
cout<<(n-cnt)*a+ret<<endl;
return 0;
}1.3 繁忙的都市(瓶颈生成树)

最小生成树即为题意要求的瓶颈生成树(最大边权最小的生成树),然后kruskal中维护边权最大值即可。
代码实现如下:
cpp
#include <bits/stdc++.h>
using namespace std;
const int N=5010,M=2e5+10,INF=0x3f3f3f3f;
struct node
{
int u,v,w;
}a[M];
int n,m,fa[N];//基于并查集
bool cmp(const node &a,const node &b)
{
return a.w<b.w;
}
int find(int x)
{
return x==fa[x]?x:fa[x]=find(fa[x]);
}
int ans;
void kruskal()
{
sort(a+1,a+m+1,cmp);
for (int i=1;i<=m;++i)
{
int u=a[i].u,v=a[i].v,w=a[i].w;
int fu=find(u),fv=find(v);
if (fu!=fv)
{
ans=max(ans,w);
fa[fu]=fv;
}
}
}
int main()
{
std::cin.tie(nullptr);
std::cout.tie(nullptr);
std::ios::sync_with_stdio(false);
cin>>n>>m;
cout<<n-1<<" ";
for (int i=1;i<=m;++i)cin>>a[i].u>>a[i].v>>a[i].w;
//初始化并查集
for (int i=1;i<=n;++i)fa[i]=i;
kruskal();
cout<<ans<<endl;
return 0;
}1.4 滑雪(有向图)

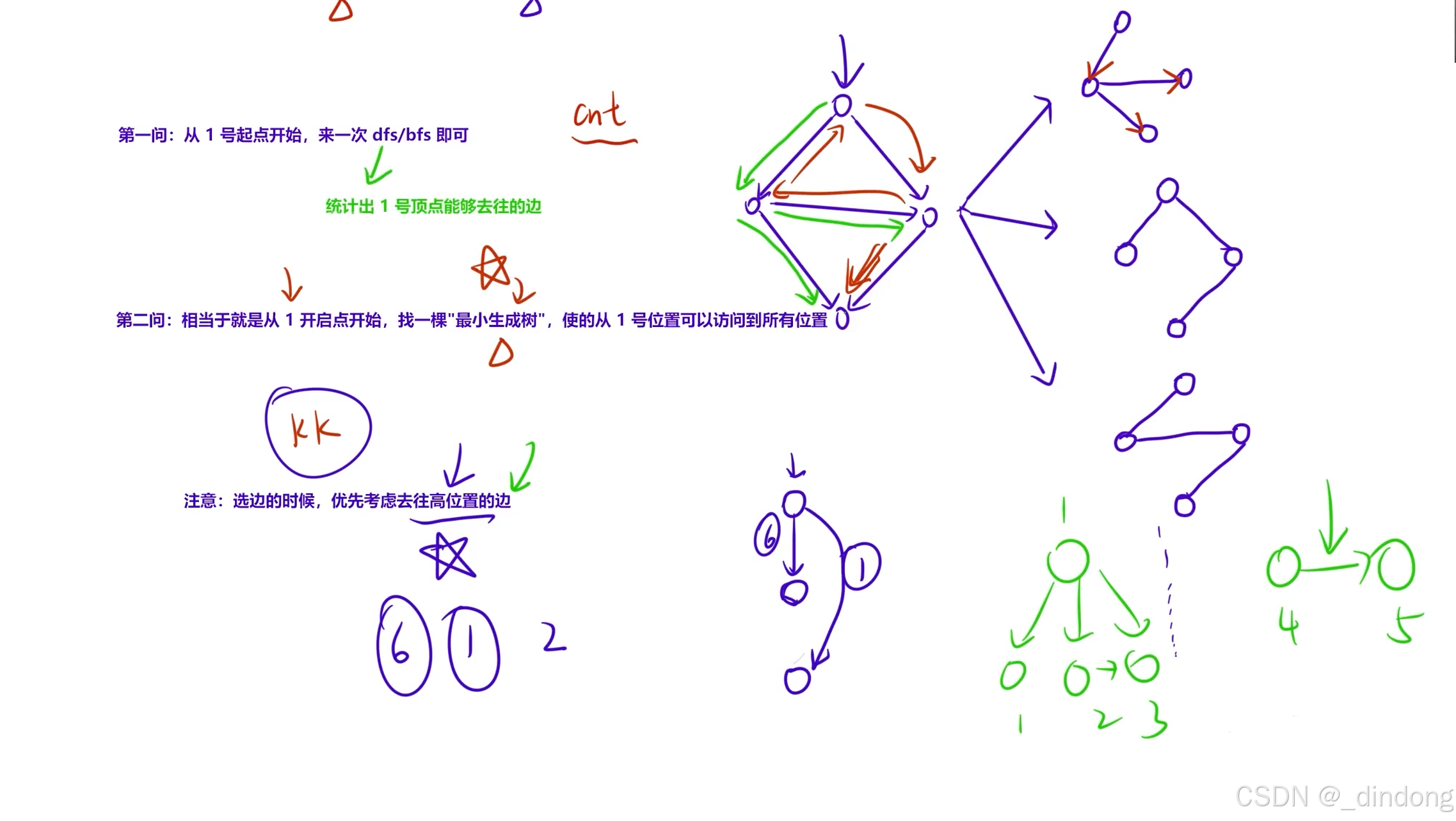
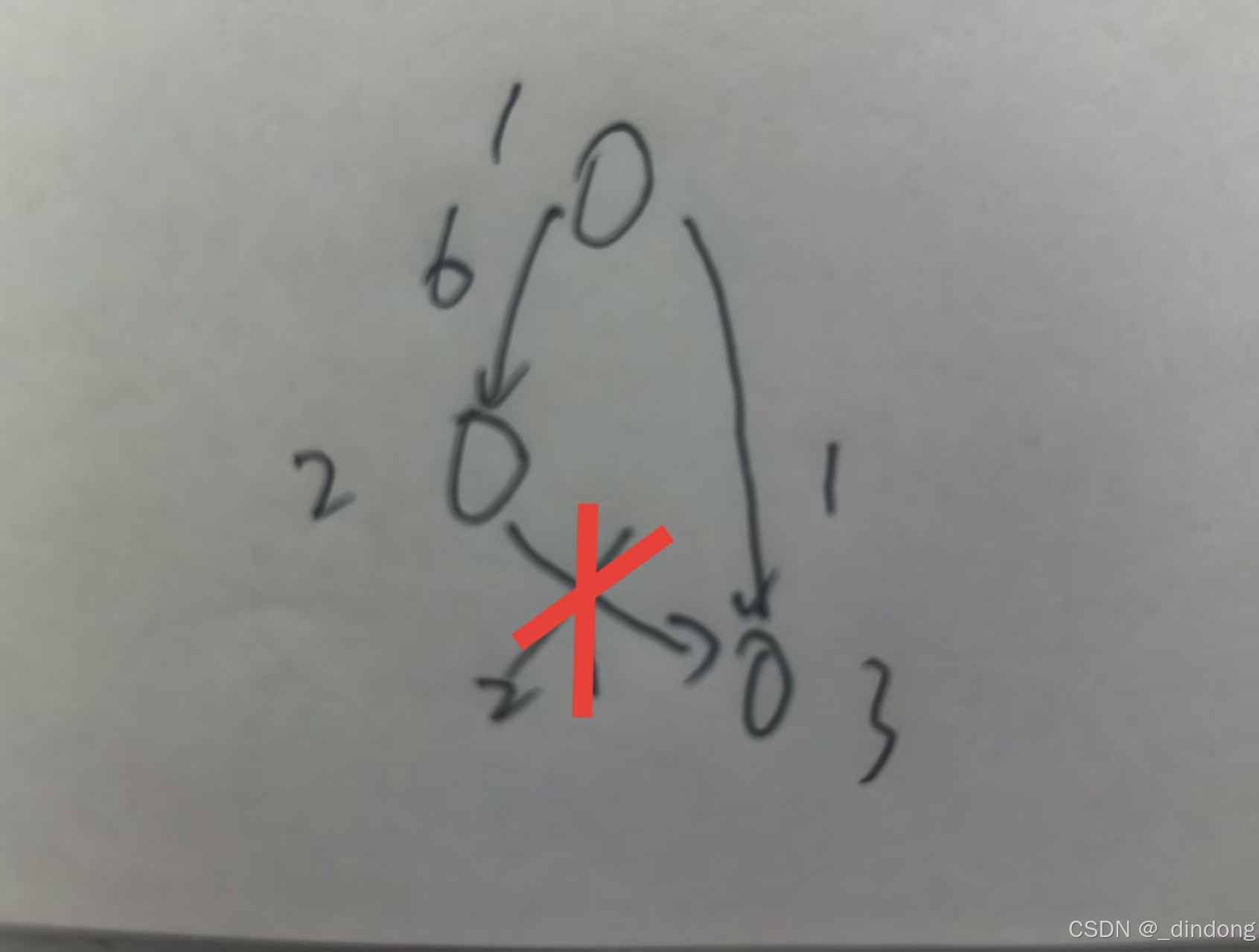
同样是最小生成树问题,本题选择kruskal算法解决。
不同以往,为符合题意回溯的特性(1为起点,也就是说要从1开始访问所有能到达的点),选边得先考虑去往高度更高的点 再考虑权重,这样从1开始代码往后运行,高到低的那条路径的高点,一定能和1相连(直接或间接),这样才能符合从1开始这个设定。(见如上例子,正确权重和为7,非2)
如此道路才是以1为根,由高到低,且以最低权重和访问所有点的。
代码实现如下:
cpp
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
#define endl '\n'
const int N=1e5+10,M=2e6+10;
int n,m,fa[N],h[N];
vector<PII> edges[N];//建图
struct node
{
int u,v,w;
}e[M];
int find(int x)
{
return x==fa[x]?x:fa[x]=find(fa[x]);
}
ll pos,cnt,ret;
bool vis[N];//防止重复计数
void dfs(int u)
{
++cnt;
vis[u]=true;
for (auto&[v,w]:edges[u])
{
//同时创建边集
++pos;
e[pos].u=u,e[pos].v=v,e[pos].w=w;
if (!vis[v])dfs(v);
}
}
bool cmp(node a,node b)
{
//先考虑高度,再考虑权重
int v1=a.v,v2=b.v;
if (h[v1]!=h[v2])return h[v1]>h[v2];//先去往更高的
return a.w<b.w;
}
void kruskal()
{
sort(e+1,e+pos+1,cmp);
for (int i=1;i<=pos;++i)
{
int u=e[i].u,v=e[i].v,w=e[i].w;
int fu=find(u),fv=find(v);
if (fu!=fv)
{
ret+=w;
fa[fu]=fv;
}
}
}
int main()
{
std::cin.tie(nullptr);
std::cout.tie(nullptr);
std::ios::sync_with_stdio(false);
cin>>n>>m;
for (int i=1;i<=n;++i)cin>>h[i];
for (int i=1;i<=n;++i)fa[i]=i;
for (int i=1;i<=m;++i)
{
int u,v,w;
cin>>u>>v>>w;
//建图,只能从高到低滑,相等时是双向边,所以两个if
if (h[u]>=h[v])edges[u].push_back({v,w});
if (h[v]>=h[u])edges[v].push_back({u,w});
}
dfs(1);//找出从1能访问到的全部节点,同时存边以用kruskal
cout<<cnt<<" ";
kruskal();
cout<<ret<<endl;
return 0;
}2. 拓扑排序
不同于最小生成树,拓扑排序是基于有向图的算法
实际上就是BFS+入度数组
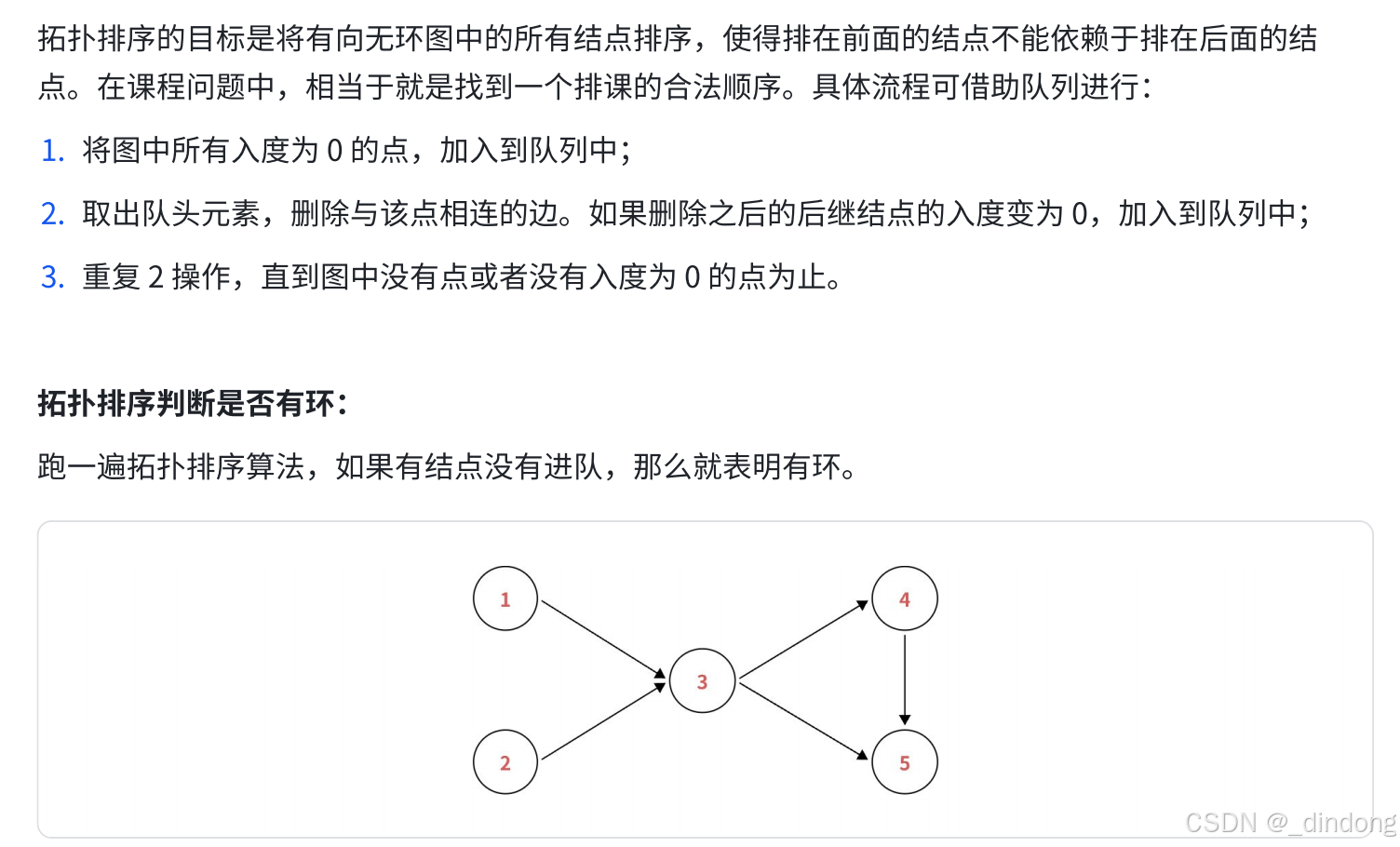
2.1 【模板】拓扑排序/家谱树
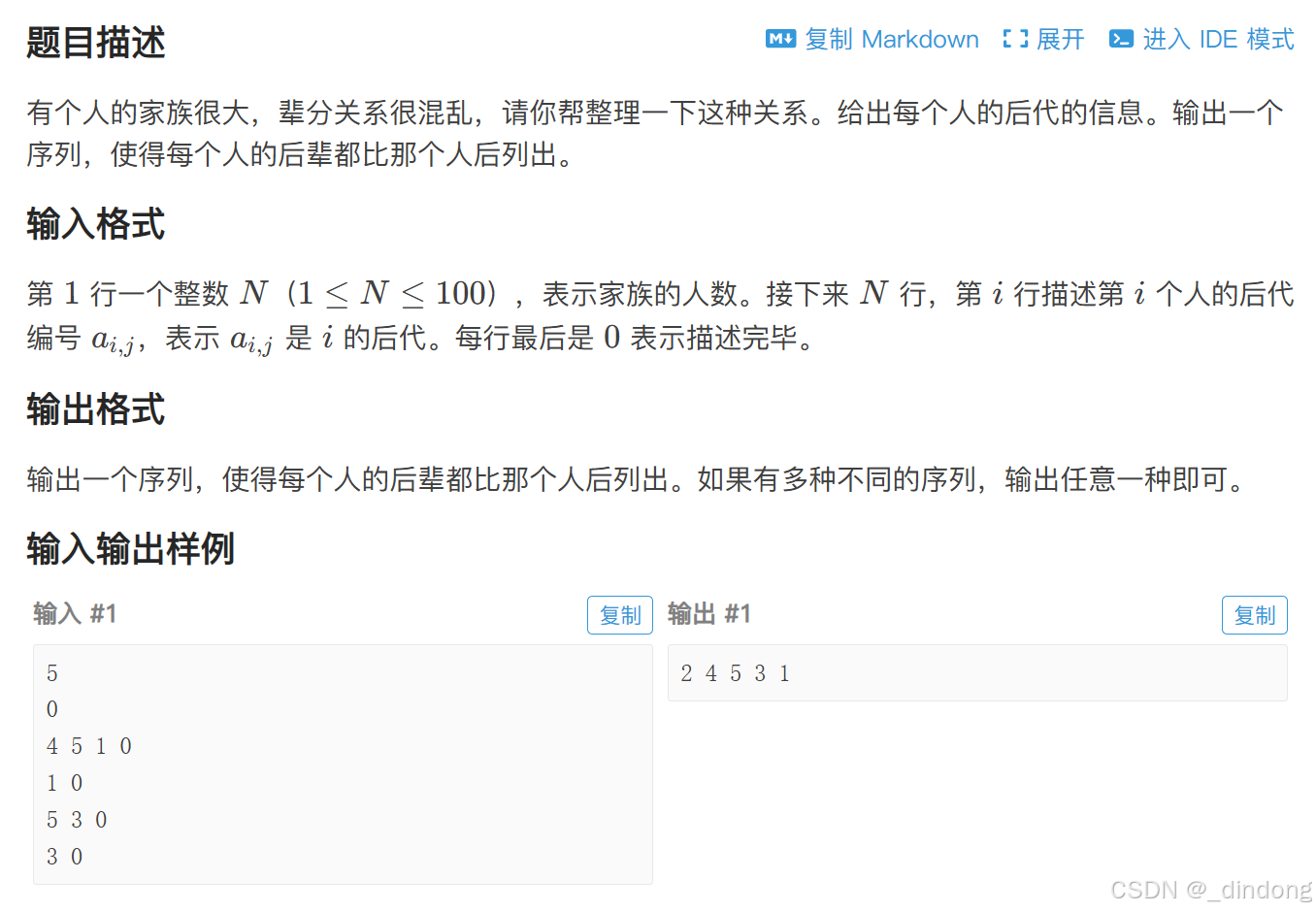
代码实现如下:
cpp
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const int N=1010;
int n;
void solve()
{
cin>>n;
vector<int> in(n+1);
unordered_map<int,vector<int>> comp;
int i=1;
while(i<=n)
{
int x;
while (cin>>x)
{
if (x==0)break;
++in[x];
comp[i].push_back(x);
}
++i;
}
queue<int> q;
for(int i=1;i<=n;i++)
{
if (in[i]==0)q.push(i);
}
vector<int> ans;
while(!q.empty())
{
int sz=q.size();
while(sz--)
{
int x=q.front();
q.pop();
ans.push_back(x);
for (int a:comp[x])
{
if (--in[a]==0)q.push(a);
}
}
}
for (int i=0;i<n;i++)cout<<ans[i]<<" ";
cout<<endl;
}
int main()
{
std::cin.tie(nullptr);
std::cout.tie(nullptr);
std::ios::sync_with_stdio(false);
solve();
return 0;
}2.2 摄像头

代码实现如下:
cpp
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const int N=510;
int n,in[N];
vector<int> edges[N];
bool vis[N];//标记摄像头
int main()
{
std::cin.tie(nullptr);
std::cout.tie(nullptr);
std::ios::sync_with_stdio(false);
//建图
cin>>n;
for(int i=0;i<n;i++)
{
int x,m,y;
cin>>x>>m;
vis[x]=true;
while (m--)
{
cin>>y;
++in[y];
edges[x].push_back(y);
}
}
queue<int> q;
for(int i=0;i<N;i++)
{
if (vis[i]&&in[i]==0)q.push(i);
}
while(!q.empty())
{
int sz=q.size();
while(sz--)
{
int x=q.front();
q.pop();
for (auto i:edges[x])
{
if (vis[i]&&--in[i]==0)q.push(i);
}
}
}
int ans=0;
for(int i=0;i<N;i++)
{
if (vis[i]&&in[i]!=0)++ans;
}
if(ans==0)cout<<"YES"<<endl;
else cout<<ans<<endl;
return 0;
}2.3 最大食物链计数(拓扑排序+路径类dp)

依照先前路径类dp问题的启发,这题也可以转换成求抵达最终点的路径条数

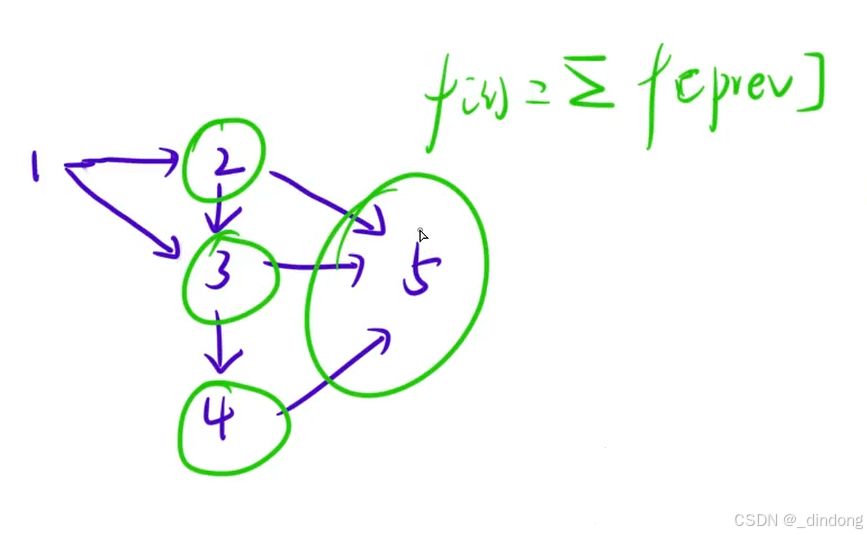
利用拓扑排序确定填表顺序
cpp
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const int N=5010,MOD=80112002;
int n,m,in[N],out[N],f[N];
vector<int> edges[N];
int main()
{
std::cin.tie(nullptr);
std::cout.tie(nullptr);
std::ios::sync_with_stdio(false);
//建图
cin>>n>>m;
while (m--)
{
int u,v;
cin>>u>>v;
edges[u].push_back(v);
++in[v],++out[u];
}
queue<int> q;
for(int i=1;i<=n;i++)
{
if (in[i]==0)
{
f[i]=1;//初始化
q.push(i);
}
}
while(!q.empty())
{
int sz=q.size();
while(sz--)
{
int u=q.front();
q.pop();
for (auto v:edges[u])
{
f[v]=(f[v]+f[u])%MOD;
if (--in[v]==0)q.push(v);
}
}
}
int ans=0;
for(int i=1;i<=n;i++)
{
//出度为0的点是食物链的终点
if (out[i]==0)ans=(ans+f[i])%MOD;
}
cout<<ans<<endl;
return 0;
}2.4 杂务 (拓扑排序+递推)

代码实现如下:
cpp
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const int N=1e4+10;
int n,m,in[N],len[N],f[N];//f[i]表示做完i需要的最大时长(最大保证在这之前能处理完全部准备事务)
vector<int> edges[N];
int main()
{
std::cin.tie(nullptr);
std::cout.tie(nullptr);
std::ios::sync_with_stdio(false);
//建图
cin>>n;
for(int i=1;i<=n;i++)
{
int v,u;
cin>>v>>len[v];
while (cin>>u&&u)
{
edges[u].push_back(v);
++in[v];
}
}
queue<int> q;
for(int i=1;i<=n;i++)
{
if (in[i]==0)
{
q.push(i);
}
}
int ans=0;
while(!q.empty())
{
int sz=q.size();
while(sz--)
{
int u=q.front();
q.pop();
f[u]+=len[u];
ans=max(ans,f[u]);
for (auto v:edges[u])
{
//初始化f[v],保证做v活动之前,为了做v,最耗时间的做完了
f[v]=max(f[v],f[u]);
if (--in[v]==0)q.push(v);
}
}
}
cout<<ans<<endl;
return 0;
}3. 单源最短路
3.1 【模板】单源最短路径(弱化版)
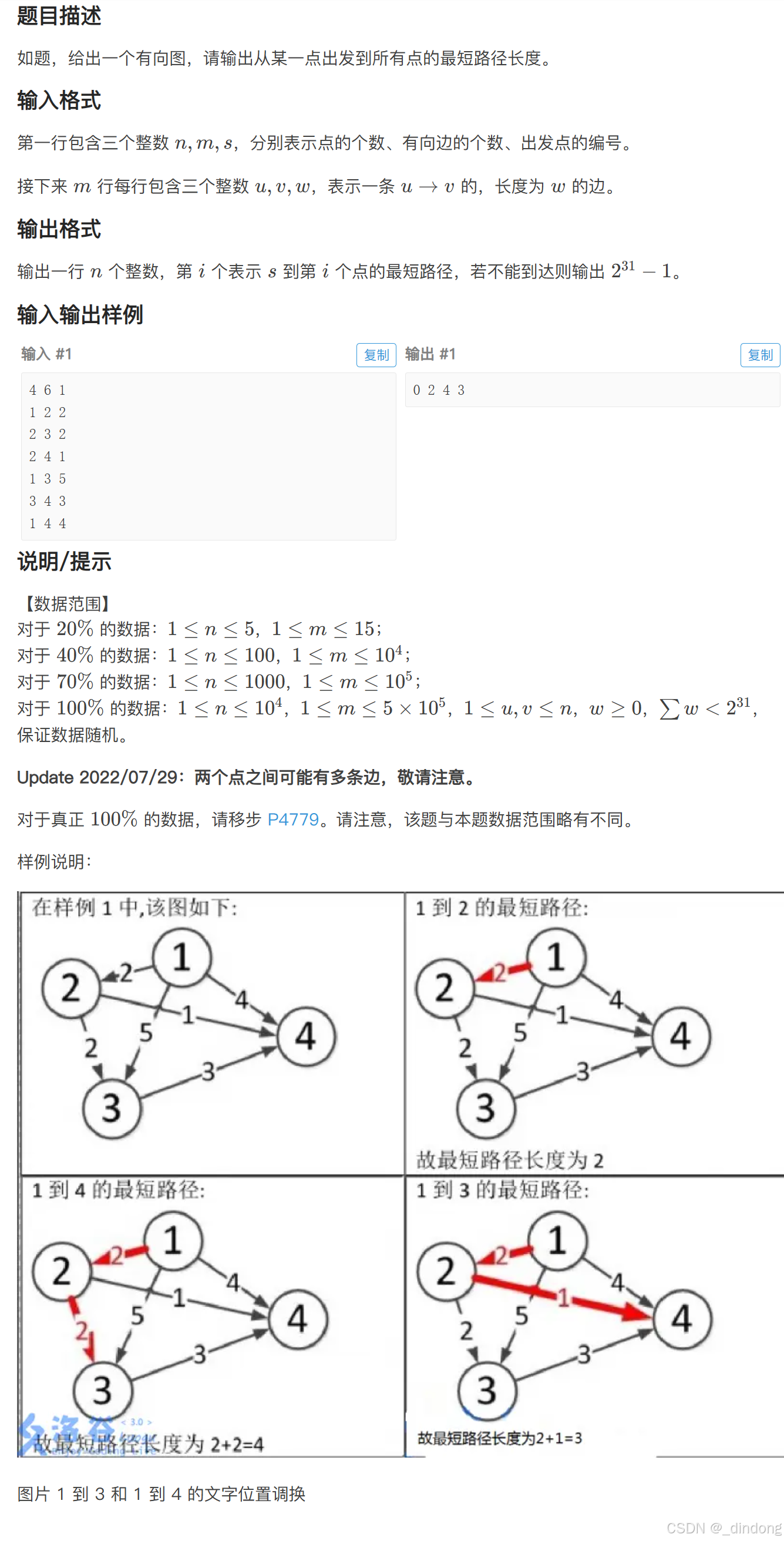

代码实现如下:
朴素Dijkstra
cpp
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
typedef pair<int, int> PII;
const int N=1e4+10,INF=2147483647;
int n,m,s;
vector<PII> edges[N];
int dist[N];
bool vis[N];
void dijsktra()
{
//初始化
for (int i=0;i<=n;++i)dist[i]=INF;
dist[s]=0;
//将剩余n-1个点加入路径
for (int i=1;i<n;++i)
{
//1.找出没有确定最短路的一系列点中,当前最短路最小的点
int t=0;
for (int j=1;j<=n;++j)
if (!vis[j]&&dist[j]<dist[t])
t=j;
//2.打上标记,然后依据该点松弛
vis[t]=true;
for (auto&[v,w]:edges[t])
{
if (dist[t]+w<dist[v])
{
dist[v]=dist[t]+w;
}
}
}
for (int i=1;i<=n;++i)cout<<dist[i]<<" ";
}
int main()
{
std::cin.tie(nullptr);
std::cout.tie(nullptr);
std::ios::sync_with_stdio(false);
cin>>n>>m>>s;
while (m--)
{
int u,v,w;
cin>>u>>v>>w;
edges[u].push_back({v,w});
}
//dijsktra算法找最短路
dijsktra();
return 0;
}3.2 【模板】单源最短路径(标准版)

优先级队列优化Dijkstra
使用优先级队列就不用遍历去找 当前最短路 距离最小的点了.
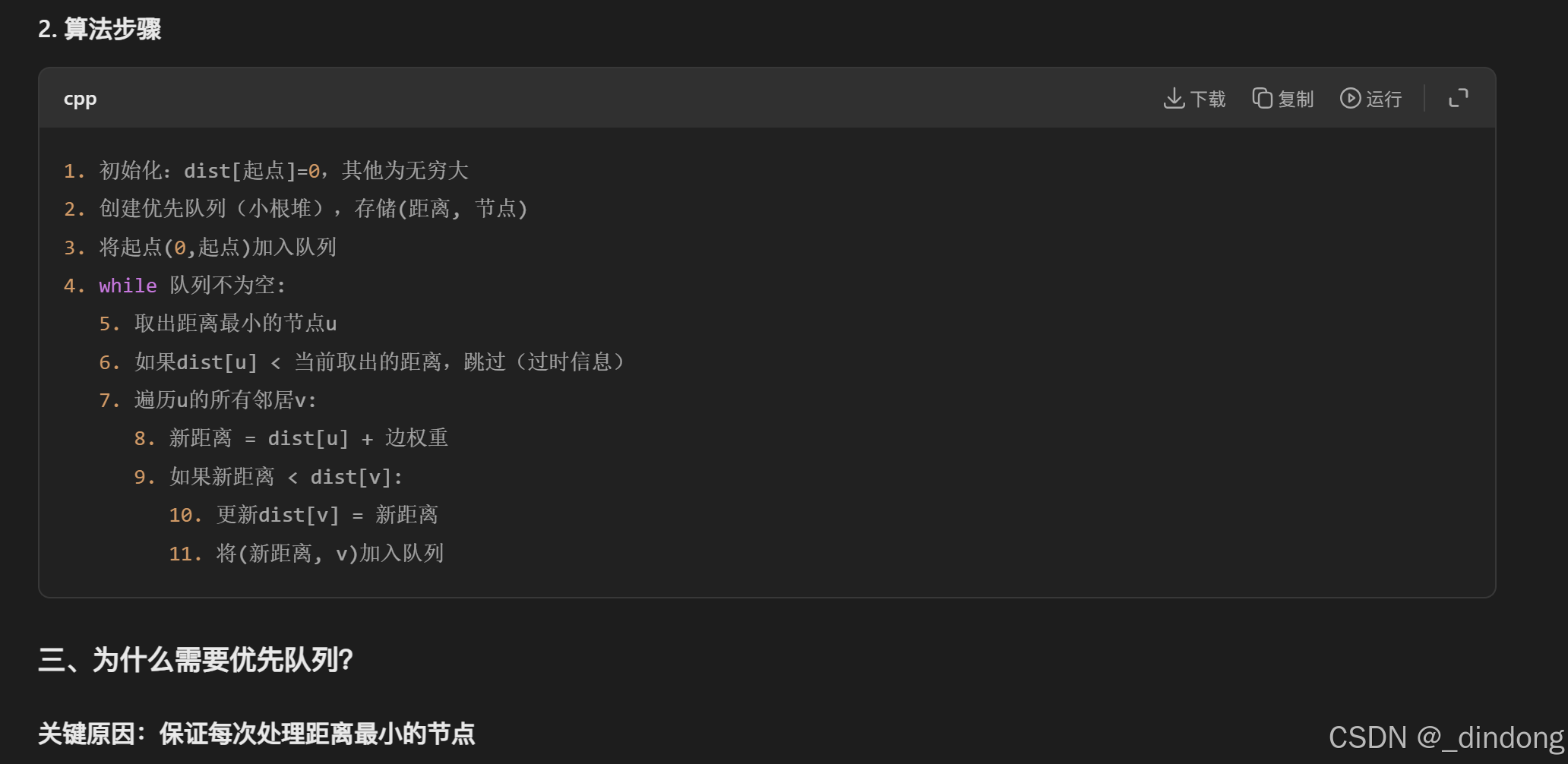
代码参考如下:
cpp
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
typedef pair<int, int> PII;
const int N=1e5+10;
int n,m,s;
vector<PII> edges[N];//{距离,节点}
int dist[N];
bool vis[N];//标记已经确定最短路的节点
//小根堆
priority_queue<PII, vector<PII>, greater<PII> > heap;
void dijkstra()
{
//初始化
memset(dist,0x3f,sizeof(dist));
dist[s]=0;
heap.push({0,s});
while(!heap.empty())
{
int u=heap.top().second;
heap.pop();
if (vis[u])continue;
vis[u]=true;
for (auto[v,w] : edges[u])
{
if(dist[v]>dist[u]+w)
{
dist[v]=dist[u]+w;
heap.push({dist[v],v});
}
}
}
for (int i=1;i<=n;++i)cout<<dist[i]<<" ";
}
int main()
{
std::cin.tie(nullptr);
std::cout.tie(nullptr);
std::ios::sync_with_stdio(false);
cin>>n>>m>>s;
for(int i=0;i<m;i++)
{
int u,v,w;cin>>u>>v>>w;
edges[u].push_back({v,w});
}
dijkstra();
return 0;
}bellman-ford(BF) 算法(负权处理)
Dijkstra在处理有负权的最短路问题时会出错,这时可以用bellman-ford 算法来解决.
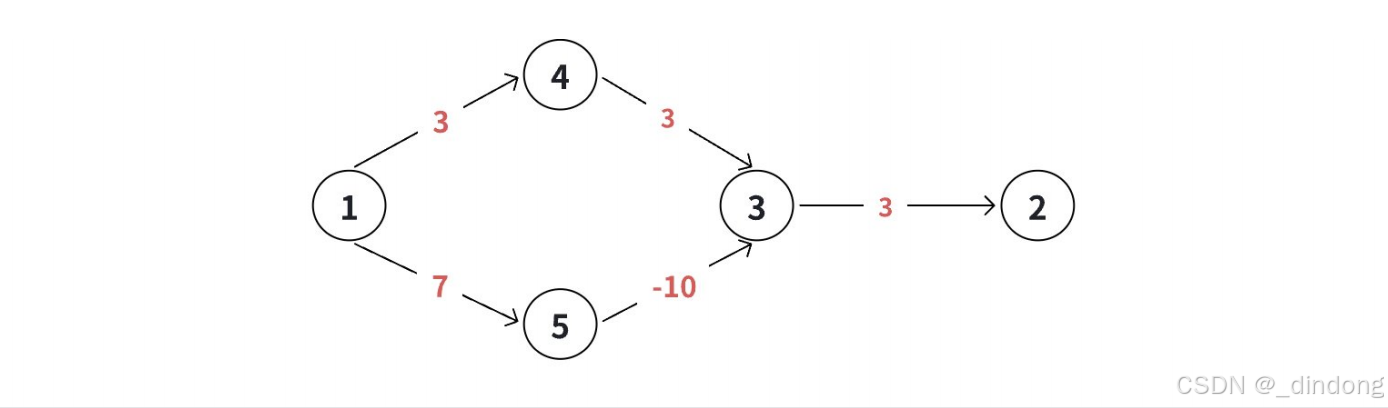
bellman-ford 算法是⼀种基于松弛操作的最短路算法,可以求出++有负权++的图的最短路,并可以对最短路不存在(负环)的情况进⾏判断。
算法核⼼思想:不断尝试对图上每⼀条边进⾏松弛,直到所有的点都⽆法松弛为⽌。
代码参考如下(会超时):
cpp
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
typedef pair<int, int> PII;
const int N=1e5+10;
// struct Node
// {
// int u,v,w;
// }e[N];
int n,m,s,dist[N];
vector<PII> edges[N];
void bf()
{
memset(dist,0x3f,sizeof(dist));
dist[s]=0;
for (int i=1;i<n;++i)
{
bool flag=true;
for (int u=1;u<=n;++u)
{
for (auto[v,w]:edges[u])
{
if (dist[v]>dist[u]+w)
{
dist[v]=dist[u]+w;
flag=false;
}
}
}
if (flag)break;
}
for (int i=1;i<=n;++i)cout<<dist[i]<<" ";
}
int main()
{
std::cin.tie(nullptr);
std::cout.tie(nullptr);
std::ios::sync_with_stdio(false);
cin>>n>>m>>s;
for(int i=0;i<m;i++)
{
int u,v,w;cin>>u>>v>>w;
edges[u].push_back({v,w});
}
bf();
return 0;
}spfa(Shortest Path Faster Algorithm) 算法(BF优化)
本质就是用队列对BF进行优化

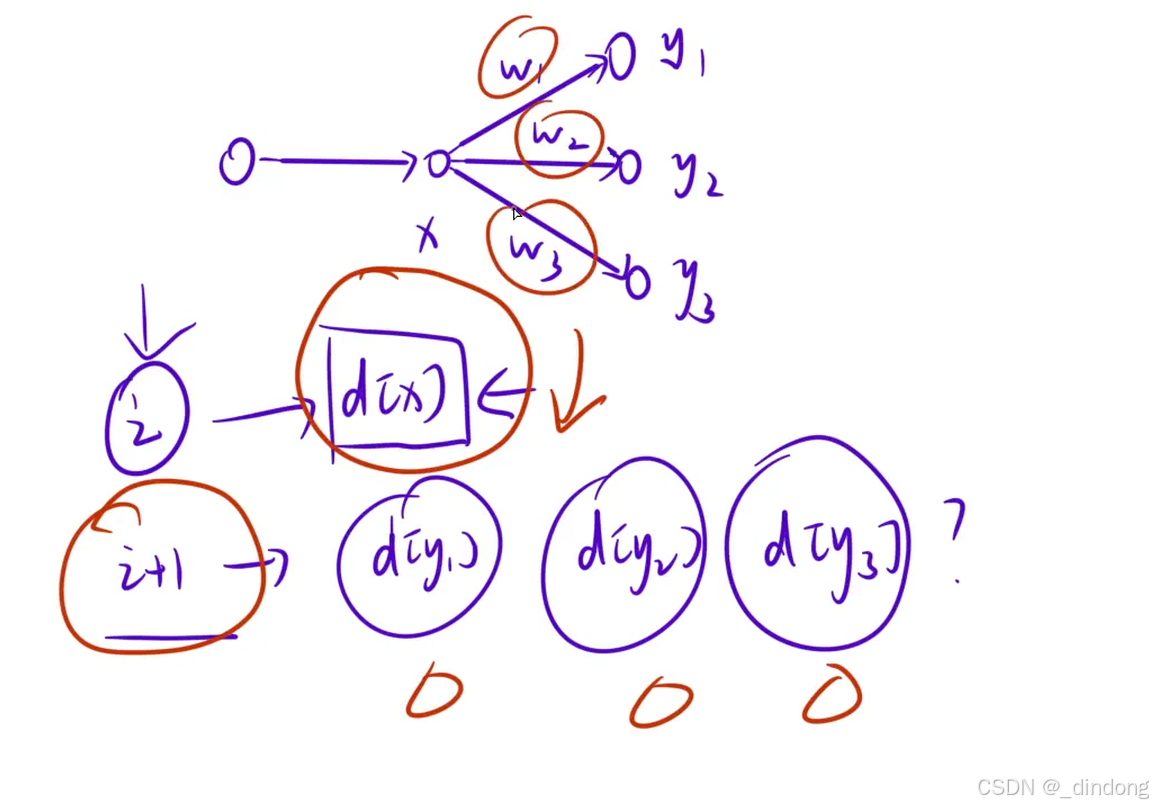

代码参考如下(同样会超时,所以没有负权优先Dijkstra算法):
cpp
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
typedef pair<int, int> PII;
const int N=1e5+10;
// struct Node
// {
// int u,v,w;
// }e[N];
int n,m,s,dist[N];
vector<PII> edges[N];
bool st[N];
void spfa()
{
memset(dist,0x3f,sizeof(dist));
dist[s]=0;
st[s]=true;
queue<int> q;
q.push(s);
while(!q.empty())
{
int u=q.front();
q.pop();
st[u]=false;
for (auto[v,w]:edges[u])
{
if (dist[v]>dist[u]+w)
{
dist[v]=dist[u]+w;
if (!st[v])
{
st[v]=true;
q.push(v);
}
}
}
}
for (int i=1;i<=n;++i)cout<<dist[i]<<" ";
}
int main()
{
std::cin.tie(nullptr);
std::cout.tie(nullptr);
std::ios::sync_with_stdio(false);
cin>>n>>m>>s;
for(int i=0;i<m;i++)
{
int u,v,w;cin>>u>>v>>w;
edges[u].push_back({v,w});
}
spfa();
return 0;
}3.3 【模板】负环

bf 算法
cpp
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const int N=2e3+10,M=3e3+10;
struct Node
{
int u,v,w;
}e[M*2];
int t,pos,n,m,dist[N];
bool bf()
{
memset(dist,0x3f,sizeof(dist));
dist[1]=0;
for (int i=1;i<=n;++i)//n-1轮是最大的松弛操作次数,再跑一遍第n轮,如果还能松弛就是有负环
{
bool flag=true;
for (int j=1;j<=pos;++j)
{
int u=e[j].u,v=e[j].v,w=e[j].w;
if (dist[u]==0x3f3f3f3f)continue;//还没更新这个点的时候不能考虑
if (dist[u]+w<dist[v])
{
flag=false;
dist[v]=dist[u]+w;
}
}
//没有进行松弛操作->存在最短路->不存在负环
if (flag)return false;
}
return true;
}
int main()
{
std::cin.tie(nullptr);
std::cout.tie(nullptr);
std::ios::sync_with_stdio(false);
cin>>t;
while(t--)
{
cin>>n>>m;
pos=0;//清空!!!
for(int i=0;i<m;i++)
{
int u,v,w;cin>>u>>v>>w;
++pos;
e[pos].u=u,e[pos].v=v,e[pos].w=w;
if (w>=0)
{
++pos;
e[pos].u=v,e[pos].v=u,e[pos].w=w;
}
}
if (bf())cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
return 0;
}spfa 算法
存在负环时,spfa算法会死循环
此时用cnt[i]标记从起点到达 i 位置经过多少条边即可,cnt[i]上限为n-1,超过n-1就是有负环。

代码实现如下:
cpp
#include<bits/stdc++.h>
using namespace std;
#define ll long long
typedef pair<int,int> PII;
const int N=2e3+10;
int t,pos,n,m,dist[N];
vector<PII> edges[N];
bool st[N];//标记哪些点在队列中
int cnt[N];//判断负环
bool spfa()
{
memset(dist,0x3f,sizeof(dist));
memset(st,false,sizeof(st));
memset(cnt,0,sizeof(cnt));
dist[1]=0;
st[1]=true;
queue<int> q;
q.push(1);
while(!q.empty())
{
int u=q.front();
q.pop();
st[u]=false;
if (dist[u]==0x3f3f3f3f)continue;
for (auto[v,w] : edges[u])
{
if (dist[v]>dist[u]+w)
{
dist[v]=dist[u]+w;
cnt[v]=cnt[u]+1;
if (cnt[v]>=n)return true;
if (!st[v])
{
st[v]=true;
q.push(v);
}
}
}
}
return false;
}
int main()
{
std::cin.tie(NULL);
std::cout.tie(NULL);
std::ios::sync_with_stdio(false);
cin>>t;
while(t--)
{
cin>>n>>m;
//多组数据别忘了清空
for (int i=1;i<=n;++i)edges[i].clear();
while(m--)
{
int u,v,w;cin>>u>>v>>w;
edges[u].push_back({v,w});
if (w>=0)edges[v].push_back({u,w});
}
if (spfa())cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
return 0;
}3.4 单源最短路总结
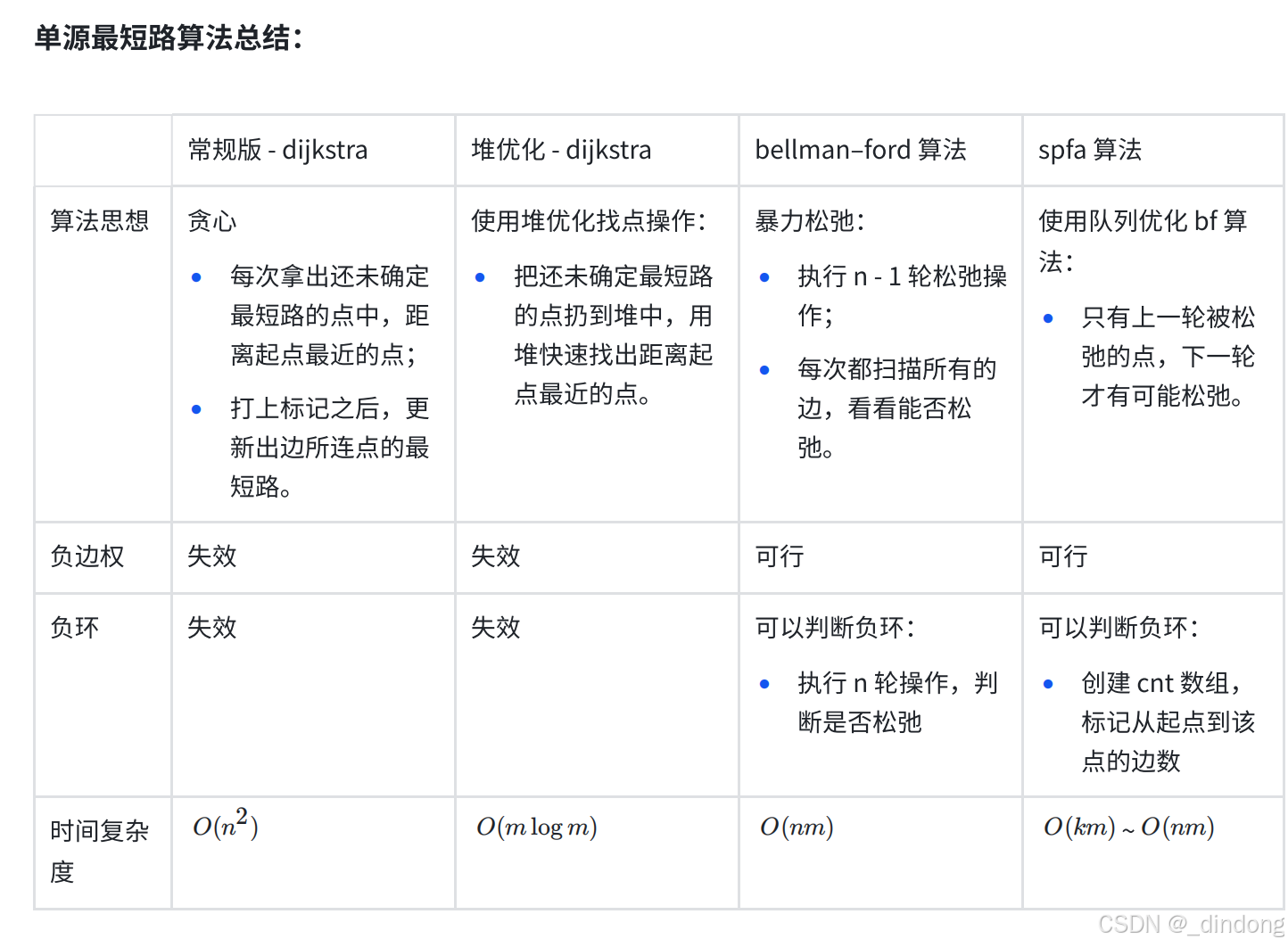

3.5 邮递员送信(Dijkstra+建反图)

起点都一样->正向图求1,到任何节点的最短距离,
终点都一样->建反向图再跑一遍dijkstra就是任何节点返回1的最短距离
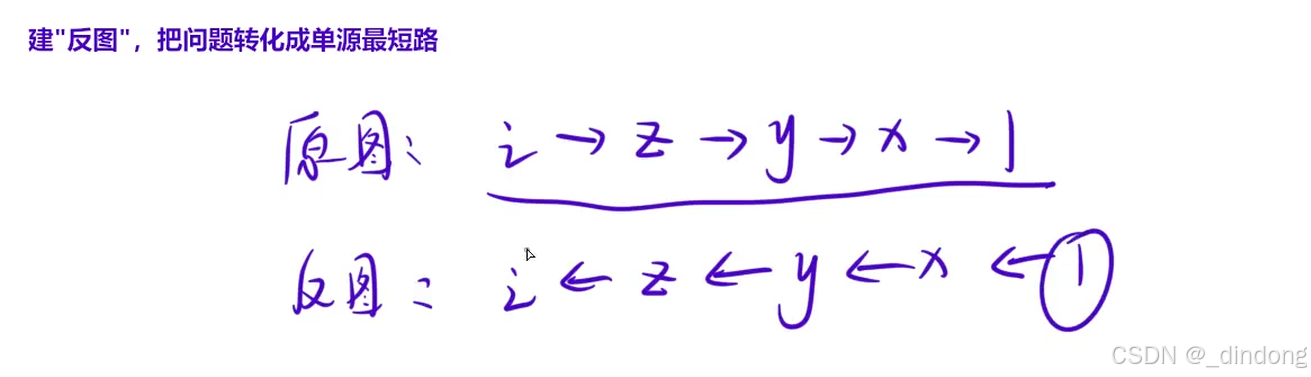
由于n的范围不是很大,我们用邻接矩阵存图
代码实现如下:
cpp
#include<bits/stdc++.h>
using namespace std;
#define ll long long
typedef pair<int,int> PII;
const int N=1e3+10;
int n,m;
int e[N][N];//邻接矩阵存图
int dist[N];
bool st[N];
void dijkstra()
{
memset(dist,0x3f,sizeof(dist));
memset(st,false,sizeof(st));
dist[1]=0;
priority_queue<PII,vector<PII>,greater<PII> > pq;
pq.push({0,1});
while (!pq.empty())
{
int u=pq.top().second;
pq.pop();
if (st[u])continue;
st[u]=true;
for (int v=1;v<=n;++v)
{
if (e[u][v]!=0x3f3f3f3f && dist[v]>dist[u]+e[u][v])
{
dist[v]=dist[u]+e[u][v];
pq.push({dist[v],v});
}
}
}
}
int main()
{
std::cin.tie(NULL);
std::cout.tie(NULL);
std::ios::sync_with_stdio(false);
cin>>n>>m;
memset(e,0x3f,sizeof(e));
while (m--)
{
int u,v,w;
cin>>u>>v>>w;
e[u][v] = min(w, e[u][v]);//处理重边
}
dijkstra();
int ans=0;
for (int i=1;i<=n;++i)ans+=dist[i];
//建反图
for (int i=1;i<=n;++i)
for (int j=i+1;j<=n;++j)
swap(e[i][j],e[j][i]);
dijkstra();
for (int i=1;i<=n;++i)ans+=dist[i];
cout<<ans<<endl;
return 0;
}3.6 采购特价商品(无向图+坐标图)
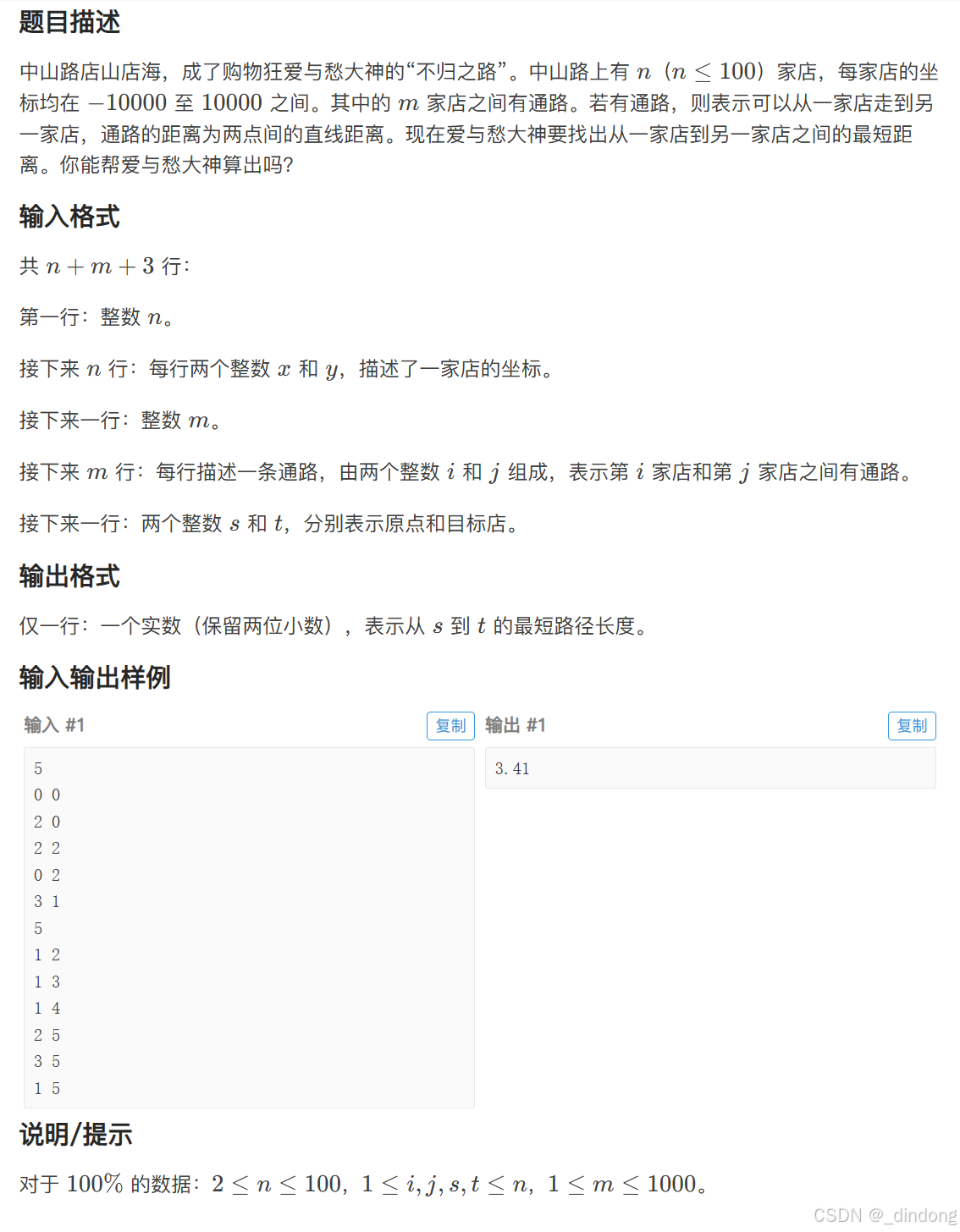
无向图/双向图,边数组不开两倍大小的时候,松弛时两边同时同时即可
因为bf写起来最简单,所以就写bf了
cpp
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=110,M=1010;
int n,m,s,t,x[N],y[N];
double dist[N];
struct node
{
int u,v;
double w;
}e[M];//无向图,不开二倍大小也行,松弛操作时两边都松弛即可
double calc(int p1,int p2)
{
int dx=x[p1]-x[p2];
int dy=y[p1]-y[p2];
return sqrt(dx*dx+dy*dy);
}
void bf()
{
//注意初始化
for (int i=1;i<=n;++i)dist[i]=1e10;
dist[s]=0;
for (int i=1;i<n;++i)
{
for (int j=1;j<=m;++j)
{
int u=e[j].u,v=e[j].v;
double w=e[j].w;
if (dist[v]>dist[u]+w)
{
dist[v]=dist[u]+w;
}
if (dist[u]>dist[v]+w)
{
dist[u]=dist[v]+w;
}
}
}
}
int main()
{
std::cin.tie(NULL);
std::cout.tie(NULL);
std::ios::sync_with_stdio(false);
cin>>n;
for (int i=1;i<=n;++i)cin>>x[i]>>y[i];
cin>>m;
for (int i=1;i<=m;++i)
{
int point1,point2;
cin>>point1>>point2;
e[i].u=point1,e[i].v=point2;e[i].w=calc(point1,point2);
}
cin>>s>>t;
bf();
cout<<fixed<<setprecision(2)<<dist[t]<<endl;
return 0;
}3.7 拉近距离(负环)
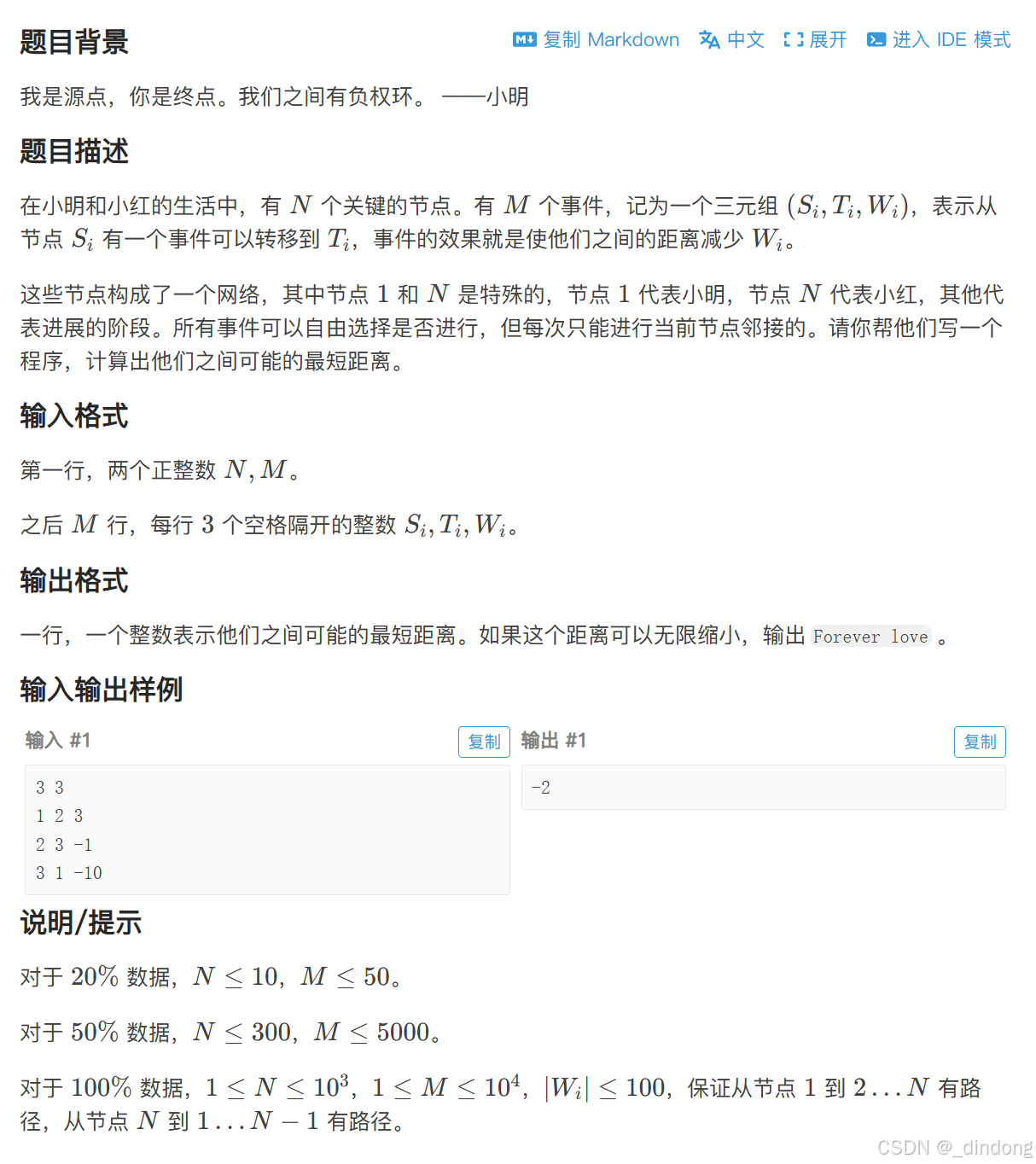
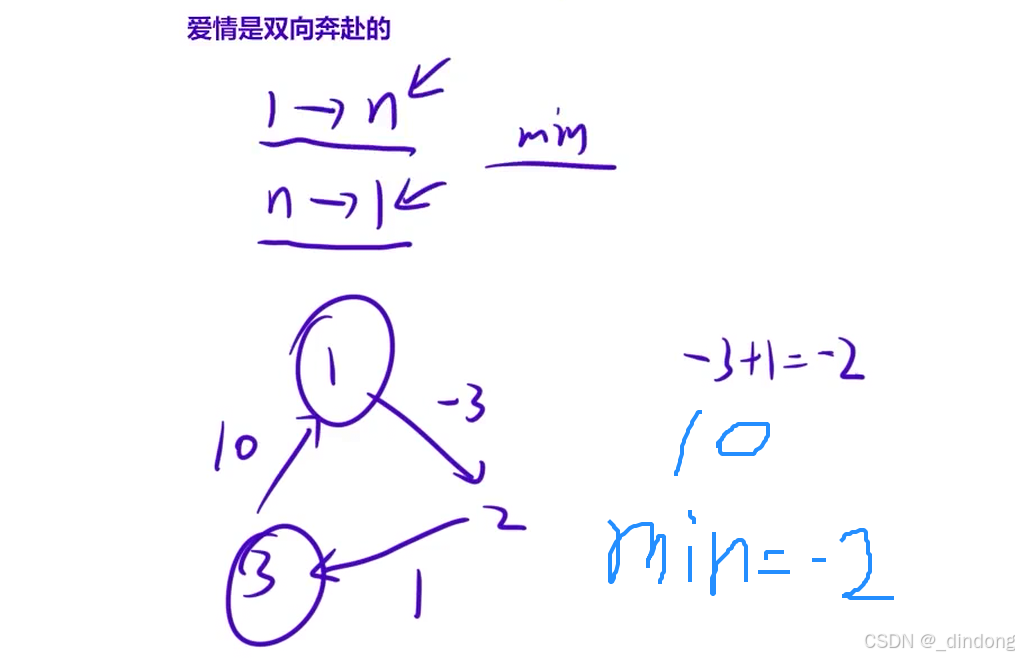
数据范围小,直接写bf了
cpp
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e3+10,M=1e4+10;
int pos,n,m,dist[N];
struct node
{
int u,v,w;
}e[M];
bool bf(int start)
{
memset(dist,0x3f,sizeof(dist));
dist[start]=0;
for (int i=1;i<=n;++i)
{
bool flag=true;
for (int j=1;j<=pos;++j)
{
int u=e[j].u,v=e[j].v,w=e[j].w;
if (dist[u]==0x3f3f3f3f)continue;
if (dist[v]>dist[u]+w)
{
dist[v]=dist[u]+w;
flag=false;
}
}
if (flag)return false;
}
return true;
}
int main()
{
std::cin.tie(NULL);
std::cout.tie(NULL);
std::ios::sync_with_stdio(false);
cin>>n>>m;
while(m--)
{
int u,v,w;cin>>u>>v>>w;
++pos;
e[pos].u=u,e[pos].v=v,e[pos].w=-w;//存负值
}
//1作起点
bool st=bf(1);
if (st)
{
cout<<"Forever love"<<endl;
return 0;
}
int ret=dist[n];
//n作起点
st=bf(n);
if (st)
{
cout<<"Forever love"<<endl;
return 0;
}
ret=min(ret,dist[1]);
cout<<ret<<endl;
return 0;
}3.8 最短路计数(重边处理+dp)

无向无权的图当然优先BFS了
这里的重边不能删去,因为是当作路径来考虑的,当两个点出现多条边,这几条边都是可以走的,都算一条路径。
如果边权不全相等就得保留最短的,当然如果有多条最短的都要保留。
插曲:最小边权相同的重边是否保留问题?
这里最小边权相同的重边是否保留,貌似是根据题目描述?
比如:
存在一条连接a,b的边,权值为w 和 a,b间存在一条权值为w边相连
前者可能需要保留最小边权重边,后者可能不需保留。
本题需要保留最小边权相同的边,不保留最小边权相同的边的路径统计问题链接:
回到本题,
注意每次更新状态方程的时候,需要拿出最短距离的节点,因为这里边权都相等,所以bfs,dijkstra,bf,spfa算法都是可用的,如果边权不等,那只能用dijkstra(bfs逻辑错误,bf/spfa超时)。
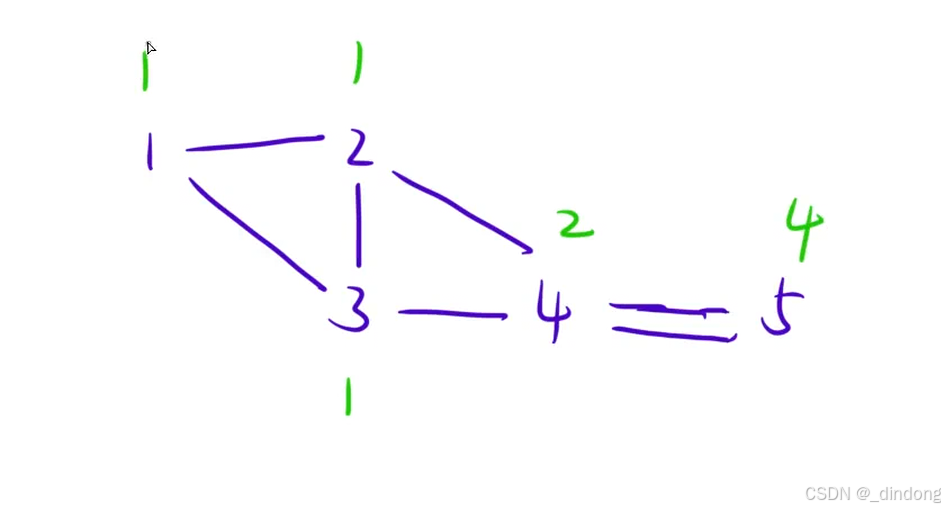
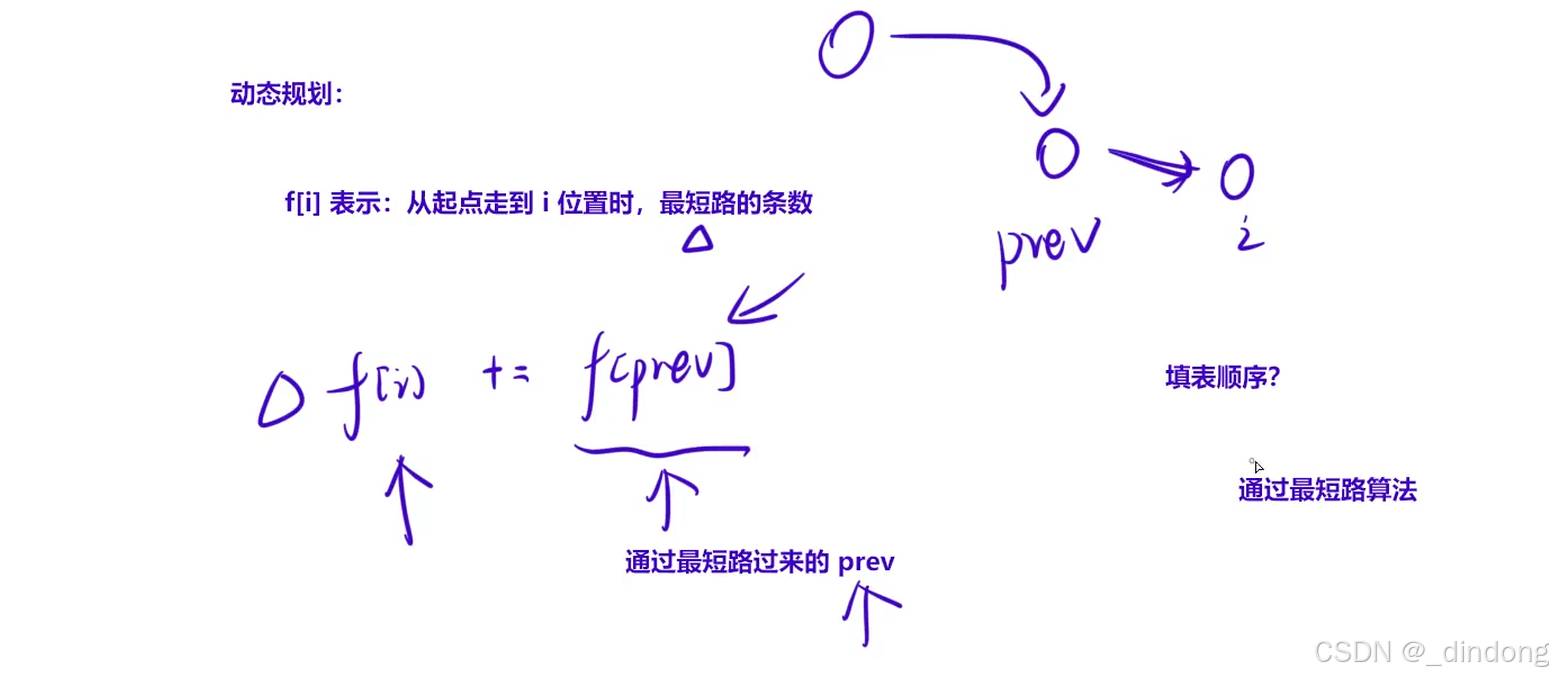
状态如何更新?
首先我们得确保到达v的时候是最短路,所以如果遇到更短路径直接赋值,这时就是第一次遇到该节点(bfs),赋值直接更新路径条数即可,然后纳入队列。
后续如果遇到相同小的路径+=操作即可。
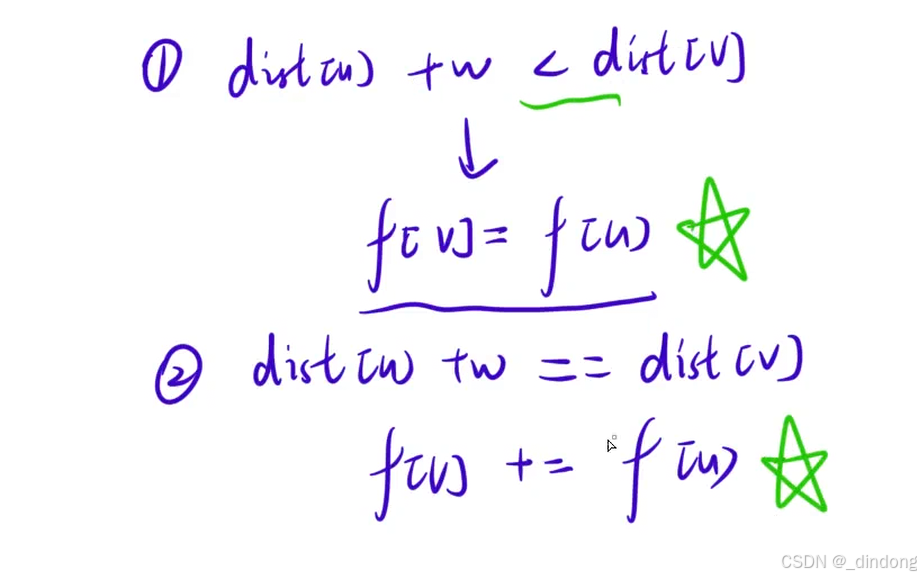
注意这里是不需要bool数组标记节点状态,因为我们要统计全部可能路径,如果一个节点是多条路径的交叉点,那么这个所有到达该点的路径都要考虑,如果标记了会漏掉一些路径。在Dijkstra算法中是需要标记节点状态的,因为每次标记的节点已经百分百确定是最短路。
代码实现如下:
BFS实现
cpp
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const int N=1e6+10,M=2e6+10,MOD=100003;
int n,m,f[N],dist[N];
vector<int> edges[N];
void bfs()
{
f[1]=1;
memset(dist,0x3f,sizeof(dist));
dist[1]=0;
queue<int> q;
q.push(1);
while(!q.empty())
{
int u=q.front();
q.pop();
for (auto v:edges[u])
{
if (dist[v]>dist[u]+1)
{
dist[v]=dist[u]+1;
f[v]=f[u];
q.push(v);//能更新说明是第一次遍历到v点
}
else if (dist[v]==dist[u]+1)
{
f[v]=(f[v]+f[u])%MOD;
}
}
}
}
int main()
{
std::cin.tie(NULL);
std::cout.tie(NULL);
std::ios::sync_with_stdio(false);
cin>>n>>m;
while(m--)
{
int u,v,w;cin>>u>>v;
edges[u].push_back(v);
edges[v].push_back(u);
}
bfs();
for (int i=1;i<=n;++i)cout<<f[i]<<endl;
return 0;
}Dijkstra实现
注意标记状态,以确定节点已在最短路
cpp
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
typedef pair<int,int> PII;
const int N=1e6+10,M=2e6+10,MOD=100003;
int n,m,f[N],dist[N];
vector<int> edges[N];
bool st[N];//标记已经确定最短路的节点
void dijkstra()
{
f[1]=1;//初始化!!
memset(dist,0x3f,sizeof(dist));
dist[1]=0;
priority_queue<PII,vector<PII>,greater<PII> > pq;
pq.push({0,1});
while(!pq.empty())
{
int u=pq.top().second;
pq.pop();
if (st[u])continue;
st[u]=true;
for (int v:edges[u])
{
if (dist[u]+1<dist[v])
{
dist[v]=dist[u]+1;
f[v]=f[u];
pq.push({dist[v],v});
}
else if (dist[u]+1==dist[v])
{
f[v]=(f[v]+f[u])%MOD;
}
}
}
}
int main()
{
std::cin.tie(NULL);
std::cout.tie(NULL);
std::ios::sync_with_stdio(false);
cin>>n>>m;
while(m--)
{
int u,v,w;cin>>u>>v;
edges[u].push_back(v);
edges[v].push_back(u);
}
dijkstra();
for (int i=1;i<=n;++i)cout<<f[i]<<endl;
return 0;
}4. 多源最短路
4.1 【模板】Floyd



打表有助于理解
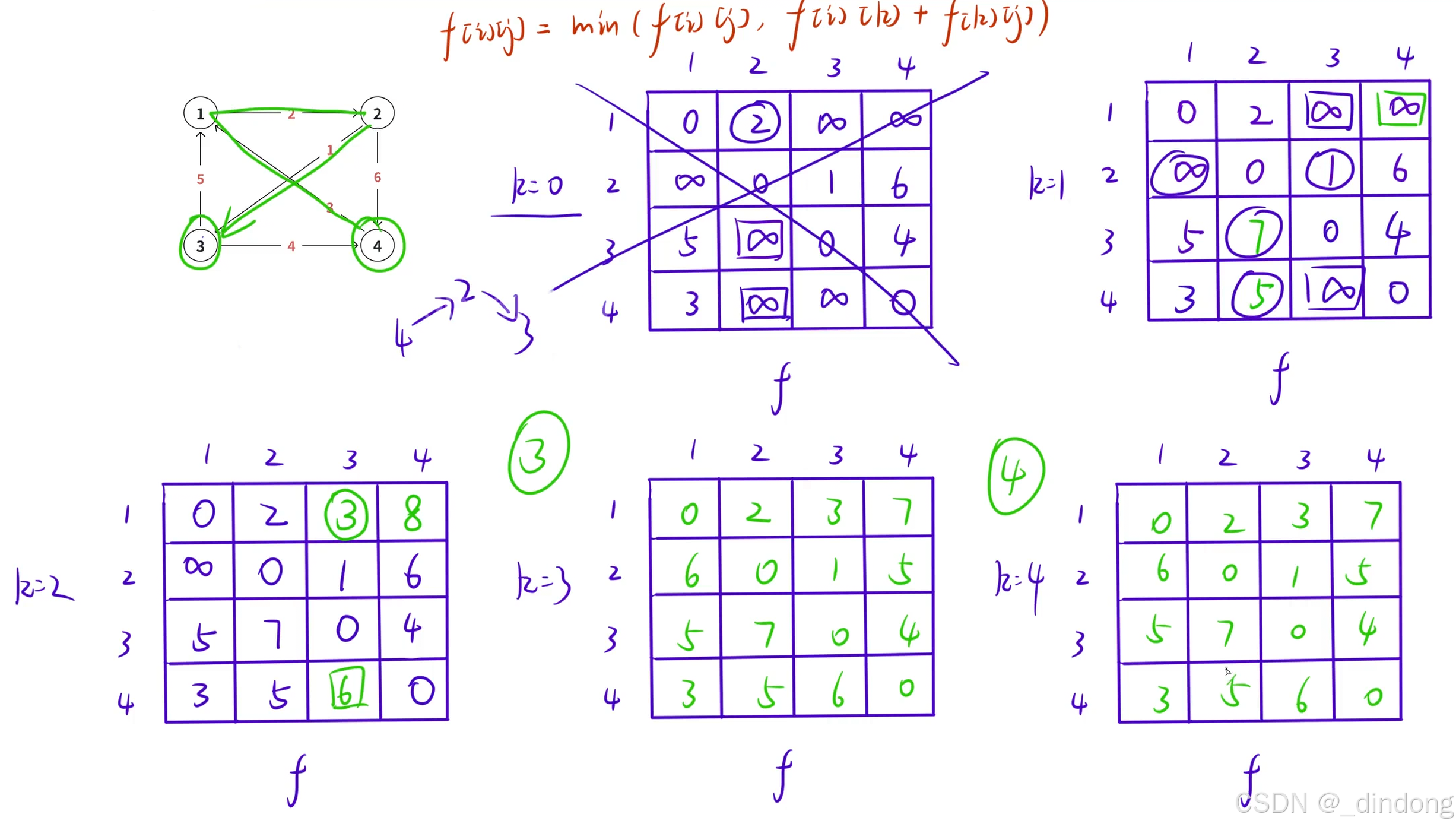
代码实现如下:
cpp
#include <bits/stdc++.h>
using namespace std;
const int N=110;
int n,m,f[N][N];
int main()
{
std::cin.tie(nullptr);
std::cout.tie(nullptr);
std::ios::sync_with_stdio(false);
cin>>n>>m;
memset(f,0x3f,sizeof(f));//初始化
for (int i=1;i<=n;++i)f[i][i]=0;
for (int j=1;j<=m;++j)
{
int u,v,w;
cin>>u>>v>>w;
f[u][v]=f[v][u]=min(f[u][v],w);
}
//按1~n顺序,选则插入点作为桥梁
for (int k=1;k<=n;++k)
for (int i=1;i<=n;++i)
for (int j=1;j<=n;++j)
f[i][j]=min(f[i][j],f[i][k]+f[k][j]);
for (int i=1;i<=n;++i)
{
for (int j=1;j<=n;++j)
{
cout<<f[i][j]<<" ";
}
cout<<endl;
}
return 0;
}4.2 Clear And Present Danger S
P2910 [USACO08OPEN] Clear And Present Danger S - 洛谷

跑一遍多源最短路算法即可
代码实现如下:
cpp
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const int N=110,M=1e4+10;
int n,m,road[M],f[N][N];
int main()
{
std::cin.tie(NULL);
std::cout.tie(NULL);
std::ios::sync_with_stdio(false);
cin>>n>>m;
for (int i=1;i<=m;++i)cin>>road[i];
for (int i=1;i<=n;++i)
for (int j=1;j<=n;++j)
cin>>f[i][j];
for (int k=1;k<=n;++k)
for (int i=1;i<=n;++i)
for (int j=1;j<=n;++j)
f[i][j]=min(f[i][j],f[i][k]+f[k][j]);
ll ans=0;
for (int i=1;i<=m-1;++i)
{
int s=road[i],d=road[i+1];
ans+=f[s][d];
}
cout<<ans<<endl;
return 0;
}4.3 灾后重建

修复时间非递减 以及 询问t是不下降的保证了Floyd算法的可行,询问是t的就把修复时间小于等于t的点插入。
代码实现如下:
cpp
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const int N=210,INF=0x3f3f3f3f;
int n,m,q,t[N],f[N][N];
//将序号为k点插入
void floyd(int k)
{
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
f[i][j]=min(f[i][j],f[i][k]+f[k][j]);
}
int main()
{
std::cin.tie(NULL);
std::cout.tie(NULL);
std::ios::sync_with_stdio(false);
cin>>n>>m;
for(int i=0;i<n;i++)cin>>t[i];
//表格初始化
memset(f,0x3f,sizeof(f));
for(int i=0;i<n;i++)f[i][i]=0;
//建图
while(m--)
{
int u,v,w;cin>>u>>v>>w;
f[u][v]=f[v][u]=min(f[u][v],w);
}
cin>>q;
int index=0;
while(q--)
{
int u,v,time;cin>>u>>v>>time;
while (index<n&&t[index]<=time)floyd(index++);//插入序号为index的点
//两个村子存在一个没修好,或者都修好了但是time时间时不连通,输出-1
if (t[u]>time||t[v]>time||f[u][v]==INF)cout<<-1<<endl;
else cout<<f[u][v]<<endl;
}
return 0;
}4.4 无向图的最小环问题

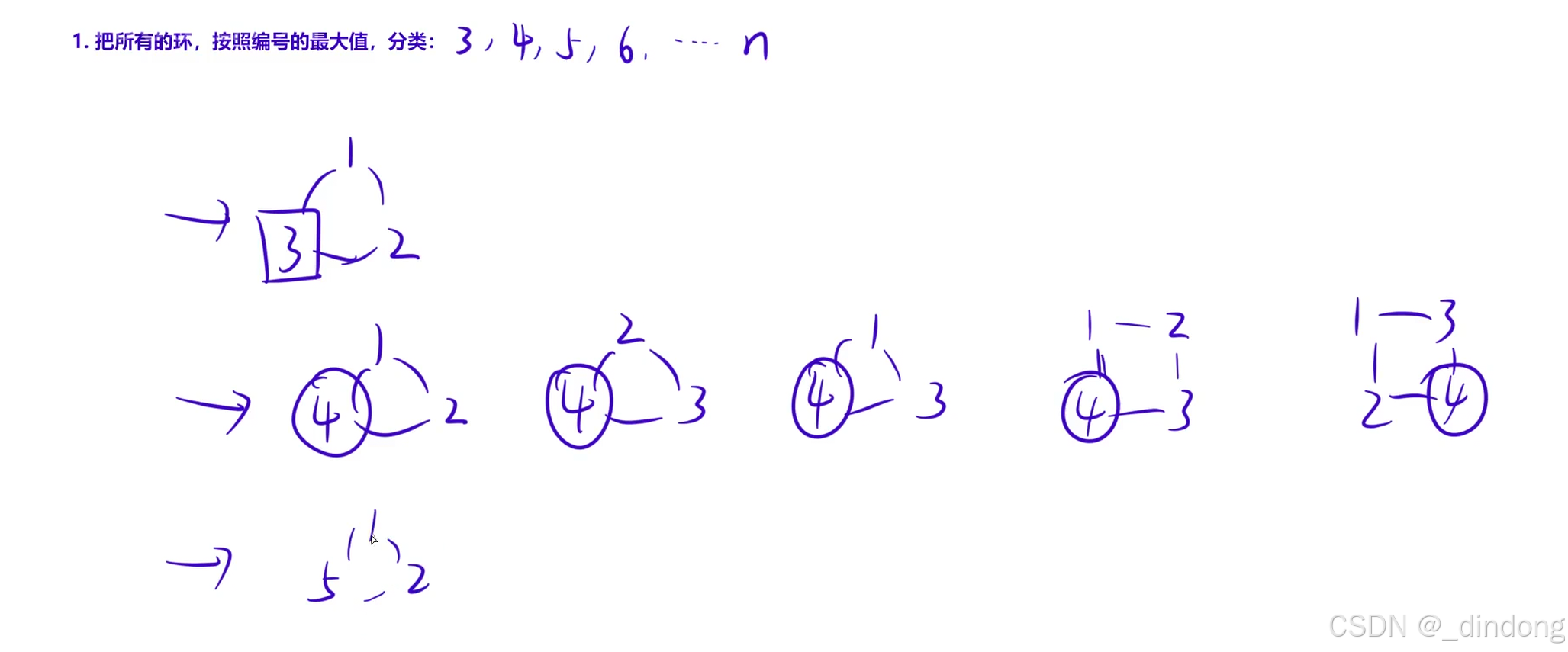
于是我们可以利用floyd算法,求出环编号最大为k时的最小环,环的权值和如下
在插入第k个点之前,i到j是考虑了前k-1个点当作桥梁确定i到j的最短路的,此时i到j就是最小路径,于是再添加k点即可组成编号最大为k的最小环
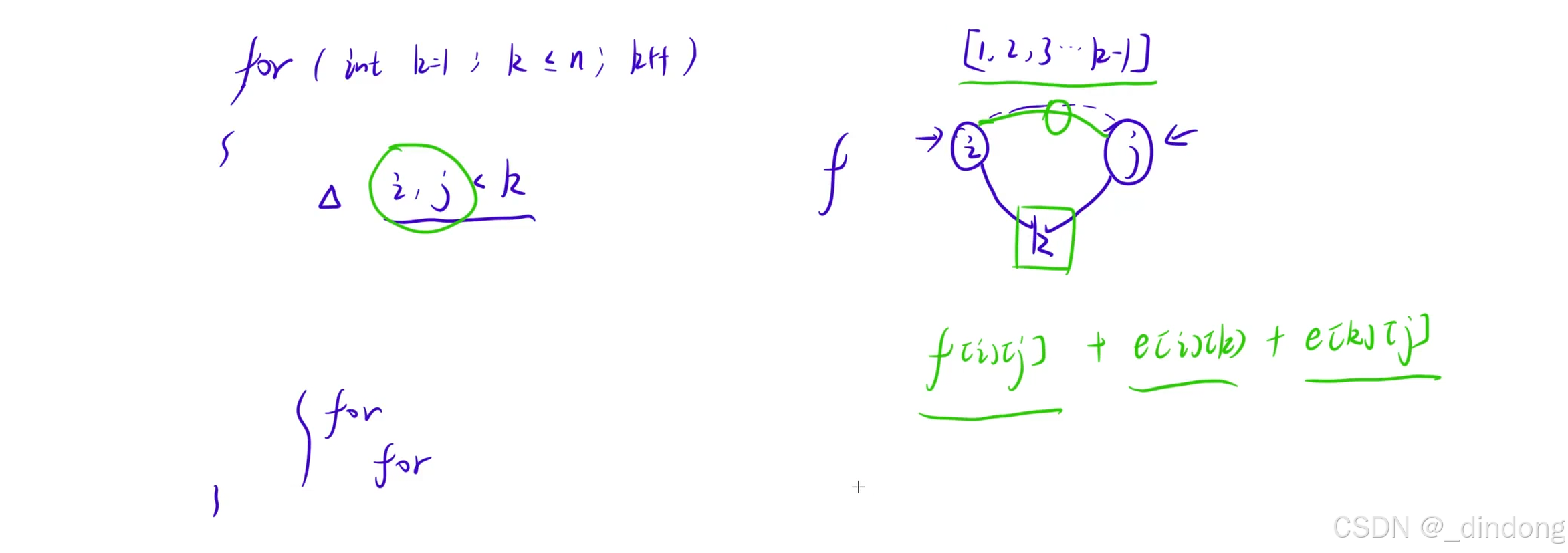
代码实现如下:
cpp
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const int N=110,INF=1e8;//1e9*3超int
int n,m,e[N][N],f[N][N];
int main()
{
std::cin.tie(NULL);
std::cout.tie(NULL);
std::ios::sync_with_stdio(false);
cin>>n>>m;
// 0x3f*3会溢出,改用1e8
// memset(e,0x3f,sizeof(e));
// memset(f,0x3f,sizeof(f));
for (int i=1;i<=n;++i)
for (int j=1;j<=n;++j)
e[i][j]=f[i][j]=(i==j?0:INF);
for (int i=1;i<=m;++i)
{
int u,v,w;cin>>u>>v>>w;
e[u][v]=e[v][u]=f[u][v]=f[v][u]=min(e[u][v],w);
}
int ret=INF;
for (int k=1;k<=n;++k)
{
for (int i=1;i<k;++i)
for (int j=i+1;j<k;++j)
ret=min(ret,f[i][j]+e[i][k]+e[k][j]);//小心溢出
for (int i=1;i<=n;++i)
for (int j=1;j<=n;++j)
f[i][j]=min(f[i][j],f[i][k]+f[k][j]);
}
if(ret==INF)cout<<"No solution."<<endl;
else cout<<ret<<endl;
return 0;
}------------------END------------------