Leetcode 116 相同的树 | 对称二叉树

im_AMBER2026-02-10 12:34

1 题目

100. 相同的树

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例 1：

复制代码 
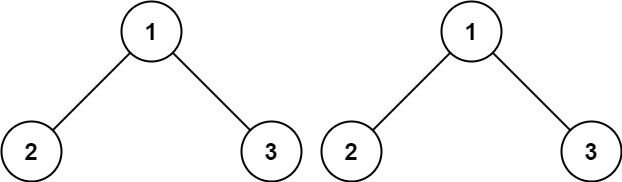
输入：p = [1,2,3], q = [1,2,3]
输出：true

示例 2：

复制代码 
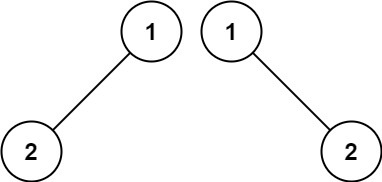
输入：p = [1,2], q = [1,null,2]
输出：false

示例 3：

复制代码 
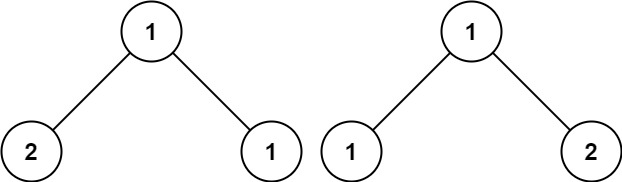
输入：p = [1,2,1], q = [1,1,2]
输出：false

提示：

  • 两棵树上的节点数目都在范围 [0, 100] 内
  • -104 <= Node.val <= 104

2 代码实现

c++

cpp 复制代码 
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        if (p == nullptr && q == nullptr){
            return true ;
        }
        if (p == nullptr || q == nullptr){
            return false ;
        }
        if (p -> val != q -> val ){
            return false;
        }
        return isSameTree(p -> left , q -> left ) && isSameTree(p -> right , q -> right);
    }
};

js

javascript 复制代码 
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {boolean}
 */
var isSameTree = function(p, q) {
    if(p == null && q == null){
        return true ;
    }
    if (p == null || q == null ){
        return false ;
    }
    if (p.val != q.val){
        return false ;
    }
    return isSameTree (q.left , p.left ) && isSameTree(q.right , p.right); 
};

思考

相同的树，一一遍历节点比较，应该就是一个递归遍历问题？深度优先搜索，递归。

3 题目

101. 对称二叉树

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

复制代码 
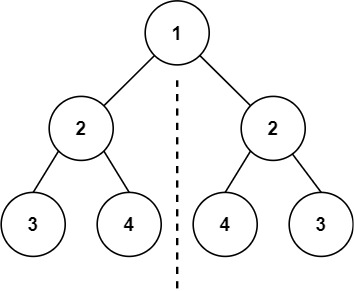
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

复制代码 
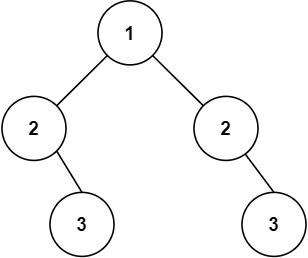
输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

  • 树中节点数目在范围 [1, 1000] 内
  • -100 <= Node.val <= 100

**进阶：**你可以运用递归和迭代两种方法解决这个问题吗？

4 代码实现

c++

cpp 复制代码 
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private:
    bool check (TreeNode* a , TreeNode* b ){
        if (a == nullptr && b == nullptr){
            return true;
        }
        if (a == nullptr || b == nullptr){
            return false ;
        }
        if (a -> val != b -> val){
            return false;
        }
        return check (a->left , b -> right) && check (a->right ,b -> left );
    }
public:
    bool isSymmetric(TreeNode* root) {
        if (root == nullptr){
            return true ;
        }
        return check (root -> left , root -> right);
    }
};

js

javascript 复制代码 
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isSymmetric = function(root) {
    const check = (a,b) =>{
        if (a == null && b == null) return true ;
        if (a == null || b == null) return false ;
        if (a.val != b.val) return false;
        return check (a.left , b.right )&& check(a.right ,b.left);
    } 
    if (root == null){
        return true ;
    }
    return check(root.left ,root.right);
};

思考

和前面一题比较类似，但是是轴对称，不是左右子树完全相同就可以的。

自己提交的错误代码

cpp 复制代码 
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if (root == nullptr){
            return true ;
        }
        if (root-> left == nullptr || root -> right == nullptr){
            return false;
        }
        if(root->left -> val != root -> right -> val ){
            return false ;
        }
        return isSymmetric(root -> left) && isSymmetric(root -> right );
    }
};

题解

你现在的核心需求是解决对称二叉树问题，并且你已经发现它和 "相同的树" 类似但有区别 ------ 轴对称要求的是 "镜像匹配" 而非 "完全相同"，同时你自己写的 C++ 代码存在逻辑错误，需要修正，还需要理解递归和迭代两种解法。

先分析你代码的问题

你当前的isSymmetric函数逻辑有明显错误：

  1. 错误认为 "根节点的左右子节点其一为空就返回 false"：但单节点树（root 无左右子节点）本身是对称的，比如root = [1]应该返回true。
  2. 递归逻辑错误：你直接递归判断left和right子树是否对称，但轴对称需要的是 "左子树的左节点 vs 右子树的右节点"、"左子树的右节点 vs 右子树的左节点"，而非直接递归左右子树本身。

正确解法：递归 + 迭代（C++）

解法 1：递归（核心是 "镜像比较"）

思路：

  • 定义辅助函数check，用于比较两个节点是否镜像匹配：
    1. 两个节点都为空 → 匹配（返回true）；
    2. 一个为空、一个不为空 → 不匹配（返回false）；
    3. 节点值不相等 → 不匹配（返回false）；
    4. 递归比较：A 的左节点 vs B 的右节点，且 A 的右节点 vs B 的左节点。
  • 主函数只需调用check(root->left, root->right)。
cpp 复制代码 
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    // 辅助函数：判断两个节点是否镜像匹配
    bool check(TreeNode* a, TreeNode* b) {
        // 情况1：两个节点都为空，镜像匹配
        if (a == nullptr && b == nullptr) {
            return true;
        }
        // 情况2：一个为空一个不为空，镜像不匹配
        if (a == nullptr || b == nullptr) {
            return false;
        }
        // 情况3：值不相等，镜像不匹配
        if (a->val != b->val) {
            return false;
        }
        // 核心：递归比较「a的左 vs b的右」且「a的右 vs b的左」
        return check(a->left, b->right) && check(a->right, b->left);
    }

    bool isSymmetric(TreeNode* root) {
        // 空树直接对称
        if (root == nullptr) {
            return true;
        }
        // 比较根节点的左右子树是否镜像
        return check(root->left, root->right);
    }
};
解法 2：迭代（广度优先搜索，BFS）

思路：

  • 用队列模拟递归，每次成对入队需要镜像比较的节点；
  • 每次出队两个节点，按镜像规则判断，再将 "左左 & 右右"、"左右 & 右左" 成对入队。
cpp 复制代码 
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if (root == nullptr) {
            return true;
        }
        // 队列存储需要成对比较的节点
        queue<TreeNode*> q;
        // 先入队根节点的左右子节点
        q.push(root->left);
        q.push(root->right);

        while (!q.empty()) {
            // 每次取出两个节点进行比较
            TreeNode* a = q.front();
            q.pop();
            TreeNode* b = q.front();
            q.pop();

            // 两个都为空，跳过后续判断
            if (a == nullptr && b == nullptr) {
                continue;
            }
            // 一个空一个非空，或值不等 → 不对称
            if (a == nullptr || b == nullptr || a->val != b->val) {
                return false;
            }

            // 按镜像规则入队下一组节点
            q.push(a->left);   // a的左
            q.push(b->right);  // b的右
            q.push(a->right);  // a的右
            q.push(b->left);   // b的左
        }
        // 所有节点都匹配完成
        return true;
    }
};

5 关键对比："相同的树" vs "对称二叉树"

问题 核心比较逻辑 递归对象
相同的树 A 的左 = B 的左，A 的右 = B 的右 (p.left, q.left)、(p.right, q.right)
对称二叉树 A 的左 = B 的右，A 的右 = B 的左 (a.left, b.right)、(a.right, b.left)

总结

  1. 对称二叉树的核心是镜像比较，而非 "左右子树相同"，必须交换左右节点的比较顺序；
  2. 递归解法需定义辅助函数，主函数仅需触发根节点左右子树的镜像检查；
  3. 迭代解法用队列成对存储待比较节点，按镜像规则入队 / 出队，逻辑和递归一致；
  4. 边界条件需注意：空树、单节点树都是对称的，不要错误排除这类情况。

很简单的两道题目！加油，打卡。

相关推荐
寻寻觅觅☆11 小时前
东华OJ-基础题-106-大整数相加（C++）
开发语言·c++·算法
偷吃的耗子11 小时前
【CNN算法理解】：三、AlexNet 训练模块(附代码)
深度学习·算法·cnn
今天只学一颗糖11 小时前
1、《深入理解计算机系统》--计算机系统介绍
linux·笔记·学习·系统架构
2013编程爱好者12 小时前
【C++】树的基础
数据结构·二叉树·树·二叉树的遍历
testpassportcn12 小时前
AWS DOP-C02 認證完整解析｜AWS DevOps Engineer Professional 考試
网络·学习·改行学it
化学在逃硬闯CS12 小时前
Leetcode1382. 将二叉搜索树变平衡
数据结构·算法
ceclar12312 小时前
C++使用format
开发语言·c++·算法
Gofarlic_OMS13 小时前
科学计算领域MATLAB许可证管理工具对比推荐
运维·开发语言·算法·matlab·自动化
夏鹏今天学习了吗13 小时前
【LeetCode热题100（100/100）】数据流的中位数
算法·leetcode·职场和发展
忙什么果14 小时前
上位机、下位机、FPGA、算法放在哪层合适？
算法·fpga开发
热门推荐
01GitHub 镜像站点02Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services03openclaw配置教程（linux+局域网ollama）04UV安装并设置国内源05243 行 microGPT：把“训练 + 推理”拆到骨头里06Linux下V2Ray安装配置指南07【软考经验分享】软考-中级-嵌入式备考08半小时搞定GitHub学生认证09AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南10Spring Flux方法总结