题型一:BFS解决最短路径问题
题目会给你唯一的起始位置和终止位置,中间可能途径若干点,让你求最短路径
解题大法:
一般会用队列和哈希表来完成,其中哈希表用于检测某一点是否入过队列
利用队列,先将起始位置加入队列,同时加入哈希表中,随后将这个点取出,并将其下一步途径点加入队列和哈希表,之后再同时将刚刚第二层加入的结点取出,并加入其下一步途径点,如此循环,直到队列为空,返回值即为所求!
例一:迷宫中离入口最近的出口
https://leetcode.cn/problems/nearest-exit-from-entrance-in-maze/
本题就是上面的大段文字的代码表示,不多说了~
class Solution {
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
bool visit[101][101];
int m,n;
public:
int nearestExit(vector<vector<char>>& maze, vector<int>& entrance)
{
memset(visit,0,sizeof visit);
int m=maze.size(),n=maze[0].size();
queue<pair<int,int>> q;
q.push({entrance[0],entrance[1]});
visit[entrance[0]][entrance[1]]=true;
int ret=0;
while(q.size())
{
ret++;
int sz=q.size();
for(int i=0;i<sz;i++)
{
auto [a,b]=q.front();
q.pop();
for(int k=0;k<4;k++)
{
int x=a+dx[k],y=b+dy[k];
if(x>=0&&x<m&&y>=0&&y<n&&maze[x][y]=='.'&&!visit[x][y])
{
if(x==0||x==m-1||y==0||y==n-1)
{
return ret;
}
q.push({x,y});
visit[x][y]=true;
}
}
}
}
return -1;
}
};例二:单词接龙
https://leetcode.cn/problems/word-ladder/
这个题乍一看可能感觉跟最短路径没啥关系,但是要是细分析一下会发现,你每一次改的一个字母会组成一个新单词,这些新单词不就是起始目标到终点目标的一个个节点嘛?只不过有些结点是不符合要求的~这个题的wordlist就相当于上一个题的通道,而其他不包含在wordlist的单词就是上一题不能走的墙!!!明确了这点后,我们可以开始做题了
这里我们可以用两个哈希表,一个用于存放wordlist,这样当我们新搞出来一个word时,直接hash.count(word)来查看其在不在worldlist里面即可,方便了很多,另外一个哈希表则用于判断看当前的这个word是否进过queue中~
代码:
class Solution {
public:
int ladderLength(string beginWord, string endWord, vector<string>& wordList)
{
unordered_set<string> hash(wordList.begin(),wordList.end());
unordered_set<string> vis;
if(!hash.count(endWord))
return 0;
queue<string> q;
q.push(beginWord);
vis.insert(beginWord);
int ret=1;
while(q.size())
{
ret++;
int sz=q.size();
while(sz--)
{
string t=q.front();
q.pop();
for(int i=0;i<t.size();i++)
{
auto tmp=t;
for(char j='a';j<='z';j++)
{
tmp[i]=j;
if(tmp==endWord)
return ret;
if(!vis.count(tmp)&&hash.count(tmp))
{
q.push(tmp);
vis.insert(tmp);
}
}
}
}
}
return 0;
}
};例三:为高尔夫比赛砍树
https://leetcode.cn/problems/cut-off-trees-for-golf-event/
这个题有一些复杂,首先我们要确定砍树的顺序,从低到高砍,所以我们要先确定砍树的顺序,加入哈希表中并排序,升序,排为升序后,对每两个点都求一次最小距离,此时转换为例题一,要注意的是那个vis数组如果设为全局的,那每次进入bfs时都要记得初始化0一下,因为每两个点之间的最小距离的判断都是独立的,不受前面的干扰~
class Solution {
int m,n;
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
public:
int cutOffTree(vector<vector<int>>& forest)
{
m=forest.size(),n=forest[0].size();
//确定砍树的顺序,加入哈希表中并排序,升序
vector<pair<int,int>> trees;
for(int i=0;i<m;i++)
for(int j=0;j<n;j++)
if(forest[i][j]>1)
trees.push_back({i,j});
sort(trees.begin(),trees.end(),[&](pair<int,int> p1,pair<int,int> p2){
return forest[p1.first][p1.second]<forest[p2.first][p2.second];
});
//现在已经是升序了,开始求每一步的最小路径
int bx=0,by=0;
int ret=0;
for(auto& [a,b]:trees)
{
int step =bfs(forest,bx,by,a,b);
if(step==-1)
return -1;
ret+=step;
bx=a,by=b;
}
return ret;
}
bool vis[51][51];
int bfs(vector<vector<int>>& forest,int bx,int by,int ex,int ey)
{
if(bx==ex&&by==ey)
return 0;
queue<pair<int,int>> q;
memset(vis,0,sizeof vis);
q.push({bx,by});
vis[bx][by]=true;
int step=0;
while(q.size())
{
step++;
int sz=q.size();
while(sz--)
{
auto [a,b]=q.front();
q.pop();
for(int k=0;k<4;k++)
{
int x=a+dx[k],y=b+dy[k];
if(x>=0&&x<m&&y>=0&&y<n&&!vis[x][y]&&forest[x][y]!=0)
{
if(x==ex&&y==ey)
return step;
q.push({x,y});
vis[x][y]=true;
}
}
}
}
return -1;
}
};题型二:多源bfs
这种题目往往会给你多个起始点,之后让你求边权为1的最短路问题。解决方式还是用队列
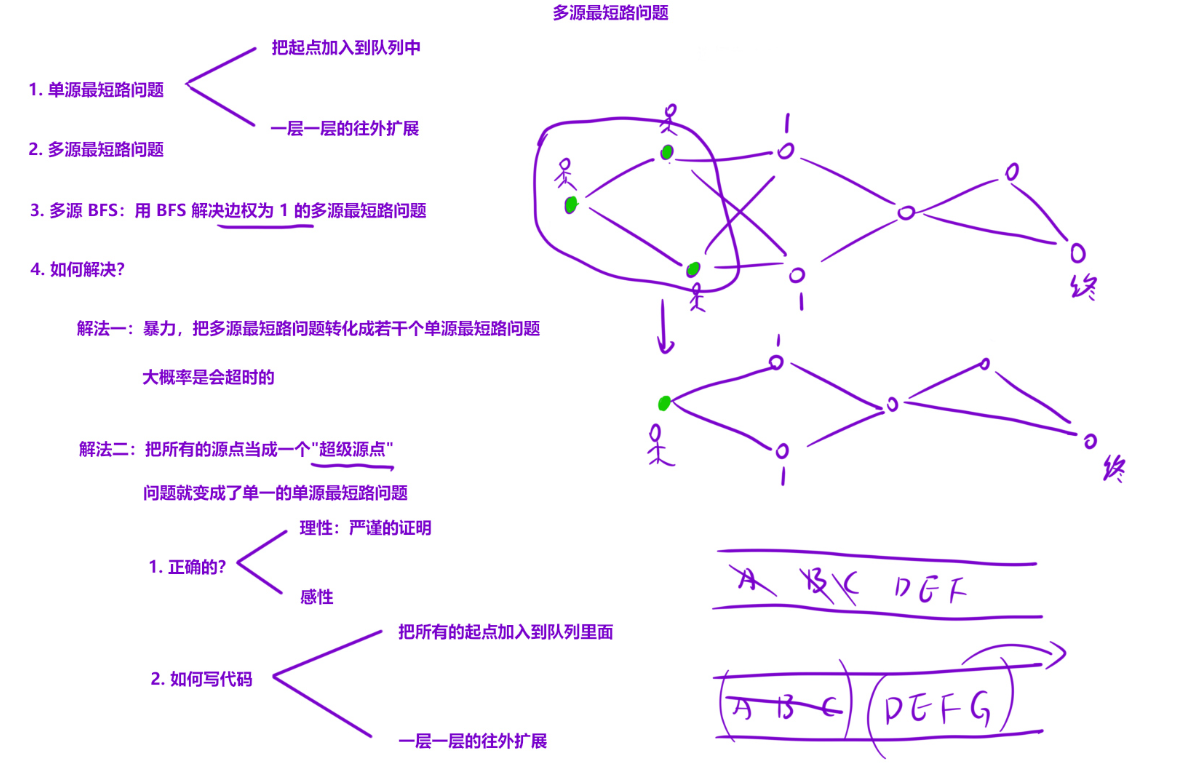
我们看几道题理解理解
例四:矩阵
https://leetcode.cn/problems/01-matrix/
这道题给人的感觉会很复杂,而且如果要是一个1一个1的bfs查找,理论上可行实际上会超时,因为这就相当于两层for循环里面再嵌套bfs,时间复杂度相当大了,我们这时不妨尝试一下多源bfs,即让这些源节点同时进队列,之后同时查找,效率会大大提升,主要代码和前面差不多,这里我们可以优化一下,用一个distance数组来代替求每层结点的个数~
代码:
class Solution {
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
public:
vector<vector<int>> updateMatrix(vector<vector<int>>& mat)
{
int m=mat.size(),n=mat[0].size();
vector<vector<int>> distance(m,vector<int>(n,-1));
//把多源点合并成单源点进行bfs
queue<pair<int,int>> q;
for(int i=0;i<m;i++)
for(int j=0;j<n;j++)
{
if(mat[i][j]==0)
{
distance[i][j]=0;
q.push({i,j});
}
}
//进行bfs
while(q.size())
{
auto [a,b]=q.front();
q.pop();
for(int k=0;k<4;k++)
{
int x=a+dx[k],y=b+dy[k];
if(x>=0&&x<m&&y>=0&&y<n&&distance[x][y]==-1)
{
distance[x][y]=distance[a][b]+1;
q.push({x,y});
}
}
}
return distance;
}
};例五:飞地数量
https://leetcode.cn/problems/number-of-enclaves/
让我们找出不去的1的连通块,直接找有点难找,所以我们正难则反,从出口进入,看有能走到哪些1,都给他标记上,之后再遍历原数组找那些没遍历过的就行~
代码:
class Solution {
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
public:
int numEnclaves(vector<vector<int>>& grid)
{
//正难则反,从出口往里面走
int m=grid.size(),n=grid[0].size();
vector<vector<bool>> visit(m,vector<bool>(n,false));
queue<pair<int,int>> q;
//从出口开始往里走
for(int i=0;i<m;i++)
for(int j=0;j<n;j++)
if(grid[i][j]==1&&(i==0||j==0||i==m-1||j==n-1)&&visit[i][j]==false)
{
visit[i][j]=true;
q.push({i,j});
}
//多源已经构成了,现在进行bfs
while(q.size())
{
auto [a,b]=q.front();
q.pop();
for(int k=0;k<4;k++)
{
int x=a+dx[k],y=b+dy[k];
if(x>=0&&x<m&&y>=0&&y<n&&grid[x][y]==1&&visit[x][y]==false)
{
visit[x][y]=true;
q.push({x,y});
}
}
}
int ret=0;
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
if(grid[i][j]==1&&visit[i][j]==false)
{
ret++;
}
}
}
return ret;
}
};题型三:拓扑排序
概念理解:
首先要理解一下什么是有向无环图,就是有方向,没有环路的图!如下图就是:
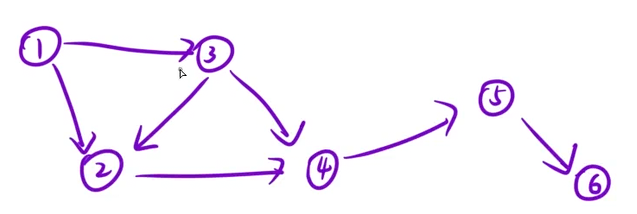
但要是在6和4之间加一笔就不是了:
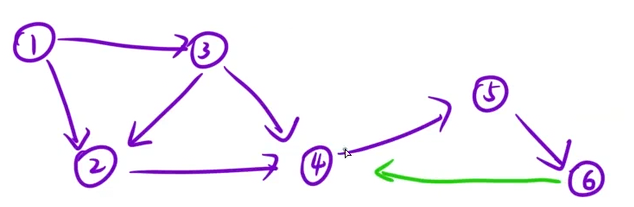
我们回到有向无环图,随后理解一下什么是入度,什么是出度:
入度就是有几个箭头指向我这个点,入度就是几,如图中1的入度为0,3的的入度为1,4的的入度为2。
入度就是有几个箭头背离我这个点,出度就是几,如图中1的出度为2,3的的出度为2,4的的出度为1。
而在拓扑排序中,我们只要确定入度就好~~
值得注意的是,拓扑排序的顺序是不唯一的!
具体操作方法如下图所示:

下面我们来实现下拓扑排序:
主要步骤包括:
1.作出图形
2.求出度值
3.度为0是让其进入队列
4.不断pop()队列元素,每次pop()时都更新与其有关联的数的度的值
5.重复上述过程,直到q.size()==0
6.检查是否有元素度不为0,有则说明题目要求实现不了!
例题展示:
例6:课程表
https://leetcode.cn/problems/course-schedule/
这个题难点就是在于构建那个图,难不成还真要在草纸上画一个图然后强塞给计算机吗?实际上我们可以很抽象的设计出这个图,通过C++提供的STL容器,我们之前学过哈希表unordered_map具有映射的功能,那在这里我们就可以利用这个哈希表,把相关的数据挂在这个数据下面,定义为
unordered_map<int,vector<int>> um;之后再设计一个度的vector,如此便可轻松解决本题!
这里先以上面的概念理解的图为例画一下:
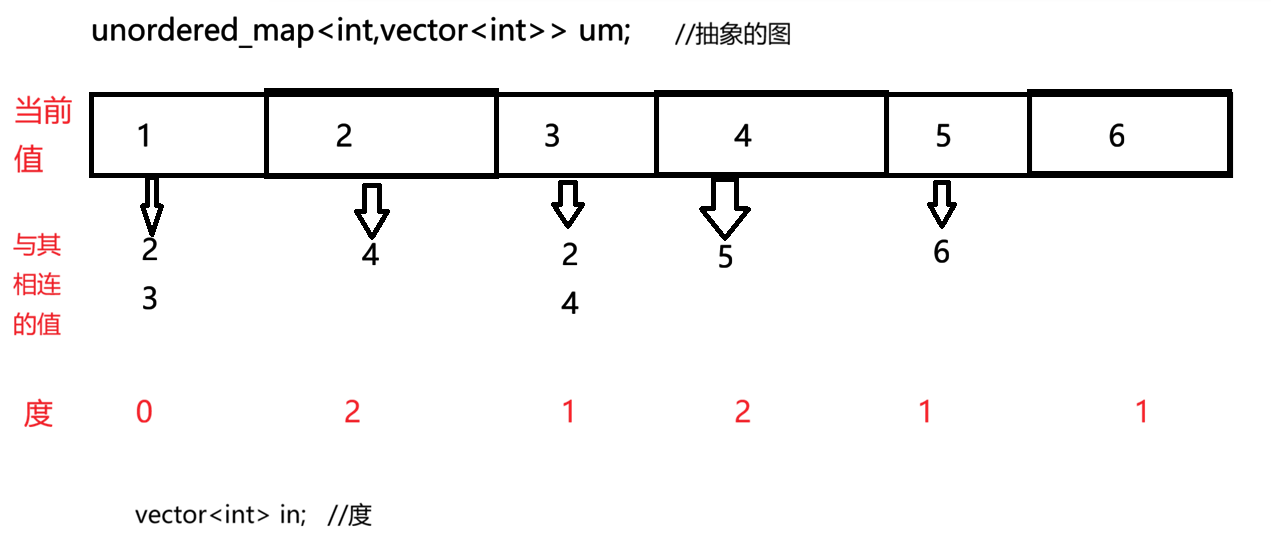
这样就把连接关系设计好了,之后度为0的时候让其入队列就好了!
好了,下面直接给出本题的代码,可以自行理解了~
参考代码:
class Solution {
public:
bool canFinish(int numCourses, vector<vector<int>>& prerequisites)
{
unordered_map<int,vector<int>> link; //有向无环图的设计链接
vector<int> in(numCourses); //入度
for(auto& e:prerequisites)
{
int a=e[0],b=e[1];
// b->a b指向a 相当于在b这个哈希桶里面插入a
link[b].push_back(a);
in[a]++; //度数加+1,代表有几条链接指向这个值
}
//此时已经建立好关系图
//让度为0的数先进入队列
queue<int> q;
for(int i=0;i<in.size();i++)
{
if(in[i]==0)
{
q.push(i); //注意不是push度的值而是度为0的对应的数值!!!
}
}
//队列已经装载完毕了,可以bfs了
while(q.size())
{
int t=q.front();
q.pop();
//修改和这个值相连的数值的度
for(auto e:link[t])
{
in[e]--;
//将度为0的值继续push进队列
if(in[e]==0)
q.push(e);
}
}
//此时检查看有没有度不是0的,有则说明有环
//实现不了题目要求
for(auto& e:in)
{
if(e)
return false;
}
return true;
}
};例7:课程表2
https://leetcode.cn/problems/course-schedule-ii/
思路一模一样,直接看代码吧
class Solution {
public:
vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites)
{
unordered_map<int, vector<int>> link;
vector<int> in(numCourses);
for (auto& e : prerequisites)
{
int a = e[0], b = e[1];
// b -> a
link[b].push_back(a);
in[a]++;
}
queue<int> q;
//入队列
for (int i = 0; i < in.size(); i++)
{
if (in[i] == 0)
q.push(i);
}
vector<int> ans;
while (q.size())
{
int t = q.front();
q.pop();
ans.push_back(t);
for (auto& e : link[t])
{
//修改度
in[e]--;
if (in[e] == 0)
{
q.push(e);
}
}
}
//看看有没有度不为0的情况,防止只能完成一半的情况出现
// for(int i=0;i<in.size();i++)
// {
// if(in[i])
// ans.clear(); //存在,总任务完不成,前面也做了也不算了
// }
//进行优化代码
if (ans.size() != numCourses)
ans.clear();
return ans;
}
};例8:火星文
这个题目有一点小难,我们主要了解设计图的方式方法:
由于这个是string,拆分统计度的时候也是一个一个的char,所以就不好直接统计度了,因此我们可以设计一个哈希表,<char,int>来存储度,之后在设计图的时候更为致命:
我一开始是想设计一个unordered_map<char,char[]>来设计我的图,但是有个问题,就是相同的映射关系不能存多次啊,就比如我这次存了a->b的连接关系,那下次我碰到这个链接关系的时候我就应该跳过他不存啊,所以我改了一下,用哈希表嵌套哈希表,即unordered_map<char,unordered_set<char>>的结构来存储,解决这两点后代码编写其实相对好写一下了:
class Solution {
unordered_map<char,unordered_set<char>> edgs; //存储图
unordered_map<char,int> in; //统计入度
bool check; //处理边界情况
public:
string alienOrder(vector<string>& words)
{
//初始化入度哈希表
for(auto& s:words)
{
for(auto& e:s)
{
in[e]=0;
}
}
//建图
int n=words.size();
//将字符串两两比较,确定字母顺序
for(int i=0;i<n;i++)
{
for(int j=i+1;j<n;j++)
{
add(words[i],words[j]);
if(check) return "";
}
}
//拓扑排序
queue<char> q;
for(auto& [a,b]:in)
{
if(b==0)
q.push(a);
}
string ret;
while(q.size())
{
char t=q.front();q.pop();
ret+=t;
for(char ch:edgs[t])
{
if(--in[ch]==0) q.push(ch);
}
}
//判断
for(auto& [a,b]:in)
{
if(b!=0)
return "";
}
return ret;
}
void add(string& s1,string& s2)
{
//在公共长度里面遍历就够了
int n=min(s1.size(),s2.size());
int i=0;
for(;i<n;i++)
{
if(s1[i]!=s2[i])
{
char a=s1[i],b=s2[i]; //a->b
//要保证a没在edges里出现过并且a对应的那个哈希桶里面没有b,才能将b放在a里面
if(!edgs[a].count(b) || !edgs.count(a))
{
edgs[a].insert(b);
in[b]++;
}
break;//两个字符串里面找到一个不同的字符时就可以不往下继续找了
}
}
//防止出现 abc ab这样的错误答案但是还能输出的例子
if(i==s2.size()&& i<s1.size())check=true;
}
};