FMCW雷达基本原理5
理论结合实际,才能读懂读通,当然实际雷达开发的过程中还会遇到别的问题,这里就简单的用matlab进行仿真,对FMCW雷达的应用有一个初步的认识就好。
verilog
clc; clear; close all;
%% ================= 1. 雷达参数设置 =================
c = 3e8; % 光速
fc = 77e9; % 载波频率 77GHz
lambda = c/fc; % 波长 (~3.9mm)
B = 150e6; % 带宽 150MHz
Tc = 40e-6; % Chirp 持续时间 (40us)
N_chirps = 64; % 一帧里的 Chirp 数量
Fs = 10e6; % 采样率
Ns = round(Tc * Fs); % 每个 Chirp 的采样点数
% 标准 DSP 时间轴 (0 ~ N-1)
t = (0:Ns-1) / Fs;
Slope = B/Tc; % 调频斜率
%% ================= 2. 目标设置 =================
% 目标1: 20m, 0m/s (静止)
R1 = 20; v1 = 0;
% 目标2: 50m, 10m/s (远离,产生多普勒)
R2 = 50; v2 = 10;
%% ================= 3. 信号生成 =================
Mix_Data_Matrix = zeros(N_chirps, Ns);
fprintf('正在生成雷达回波信号...\n');
for m = 1:N_chirps
t_slow = (m-1) * Tc; % 慢时间
% 更新目标位置 (R = R0 + v*t)
r1_curr = R1 + v1 * t_slow;
r2_curr = R2 + v2 * t_slow;
% 计算往返延迟
tau1 = 2 * r1_curr / c;
tau2 = 2 * r2_curr / c;
% 生成中频信号 (IF Signal)
Sig1 = exp(1j * 2*pi * (Slope * tau1 * t + fc * tau1));
Sig2 = exp(1j * 2*pi * (Slope * tau2 * t + fc * tau2));
% 叠加噪声 (SNR 调整)
Noise = 0.5 * (randn(1, Ns) + 1j*randn(1, Ns));
Mix_Data_Matrix(m, :) = Sig1 + Sig2 + Noise;
end
%% ================= 4. 信号处理 (FFT) =================
% --- 第一步: Range-FFT (对快时间做FFT) ---
Range_Map = fft(Mix_Data_Matrix, Ns, 2);
Range_Map = Range_Map(:, 1:Ns/2); % 取正半轴
% 生成距离轴
f_bin_res = Fs / Ns;
f_axis = (0:Ns/2-1) * f_bin_res;
R_axis = c * f_axis / (2 * Slope);
% --- 第二步: Doppler-FFT (对慢时间做FFT) ---
Doppler_Map = fft(Range_Map, N_chirps, 1);
Doppler_Map = fftshift(Doppler_Map, 1); % 零频移到中间
% 生成速度轴
v_res = lambda / (2 * N_chirps * Tc); % 速度分辨率
v_idx = -N_chirps/2 : N_chirps/2 - 1;
v_axis = v_idx * v_res;
%% ================= 5. 可视化绘图 =================
figure('Color', 'white', 'Position', [50, 50, 1200, 800]);
% --- 子图1: 混频器输出 (Mixer Output) ---
subplot(2,2,1);
plot(t*1e6, real(Mix_Data_Matrix(1,:)), 'LineWidth', 1);
title('1. 混频器输出 (单个Chirp时域)');
xlabel('时间 (us)'); ylabel('幅度');
grid on; axis tight;
subtitle('充满了噪声和杂波,看不出目标');
% --- 子图2: Range-FFT 结果堆叠 ---
subplot(2,2,2);
% 这里的维度是 [N_chirps x N_bins],所以 X轴是距离,Y轴是Chirp编号
imagesc(R_axis, 1:N_chirps, abs(Range_Map));
title('2. Range-FFT 结果 (垂直堆叠)');
xlabel('距离 (m)'); ylabel('Chirp 编号 (慢时间)');
colormap(jet);
xline(R1, 'w--', 'LineWidth', 1.5);
xline(R2, 'w--', 'LineWidth', 1.5);
xlim([0 80]);
subtitle('两条亮线位置不动,但颜色(相位)在变');
% --- 子图3: 相位旋转演示 (Phasor Rotation) ---
% 提取目标2 (50m) 的相位数据
[~, idx_target2] = min(abs(R_axis - R2));
phase_history = angle(Range_Map(:, idx_target2));
subplot(2,2,3);
% 画单位圆背景
theta = linspace(0, 2*pi, 100);
plot(cos(theta), sin(theta), 'k:', 'LineWidth', 1); hold on;
% 画前12个Chirp的相位矢量
for k = 1:12
phasor = exp(1j * phase_history(k));
col = [1 0 0] * (1 - (k-1)/15); % 颜色渐变
% 画箭头
quiver(0, 0, real(phasor), imag(phasor), 'Color', col, ...
'LineWidth', 2, 'MaxHeadSize', 0.5, 'AutoScale', 'off');
end
axis equal; grid on; xlim([-1.2 1.2]); ylim([-1.2 1.2]);
title('3. 目标2(50m, 10m/s) 的相位旋转');
xlabel('实部 I'); ylabel('虚部 Q');
text(-0.9, -1.1, '箭头随Chirp逆时针旋转 \rightarrow', 'Color', 'r', 'FontSize', 10);
% --- 子图4: 2D-FFT 最终结果 (已修正) ---
subplot(2,2,4);
% [重要修正] 转置 Doppler_Map 以匹配 (x=速度, y=距离)
% Doppler_Map.' 的维度变成 [200 x 64]
imagesc(v_axis, R_axis, abs(Doppler_Map).');
title('4. 最终结果: 距离-速度热力图');
xlabel('速度 (m/s)'); ylabel('距离 (m)');
axis xy; % 翻转Y轴方向,让0在下面
colormap(jet);
colorbar;
% 限制显示范围,聚焦目标
ylim([0 80]);
xlim([-15 15]);
% 加上辅助线验证 (理论位置)
hold on;
xline(v1, 'w--', 'LineWidth', 1.5);
yline(R1, 'w--', 'LineWidth', 1.5);
plot(v1, R1, 'wo', 'MarkerSize', 8, 'LineWidth', 2); % 画个圈
xline(v2, 'w--', 'LineWidth', 1.5);
yline(R2, 'w--', 'LineWidth', 1.5);
plot(v2, R2, 'wo', 'MarkerSize', 8, 'LineWidth', 2); % 画个圈
legend('理论位置', 'Location', 'best');
subtitle('红点精准落在白虚线交叉处');
fprintf('绘图完成!请查看弹出的窗口。\n');
这是一段MATLAB仿真的代码,分析一下:
第一部分:搭建雷达系统 (System Parameters)
这部分定义了雷达的物理属性,决定了它"能看多远"和"能看多细"。
matlab
c = 3e8; % 光速
fc = 77e9; % 载波频率 77GHz
lambda = c/fc; % 波长
B = 150e6; % 带宽 150MHz
Tc = 40e-6; % Chirp 持续时间
Slope = B/Tc; % [关键] 调频斜率 S
-
波长 λ \lambda λ:
λ = c f c ≈ 3.9 mm \lambda = \frac{c}{f_c} \approx 3.9 \text{mm} λ=fcc≈3.9mm
决定了雷达对微小位移(相位变化)的敏感度。测速全靠它。
-
调频斜率 S S S (Slope) :
S = B T c S = \frac{B}{T_c} S=TcB
这是 FMCW 的"刻度尺"。它定义了频率随时间增加得有多快。后续计算距离时,需要用它把"频率差"换算回"时间延迟"。
-
Tc = 40e-6; % Chirp 持续时间 (40us)
Fs = 10e6; % 采样率
Ns = round(Tc * Fs); % 每个 Chirp 的采样点数
这里采样点数是通过计算得出的,可以想想为什么这么计算。
第二部分:信号生成核心 (Signal Generation)
这是整个仿真中最"硬核"的部分,模拟了物理世界中的回波混频。
matlab
for m = 1:N_chirps
t_slow = (m-1) * Tc; % 慢时间
r1_curr = R1 + v1 * t_slow;% 实时距离
tau1 = 2 * r1_curr / c; % 往返延迟
% [核心公式] 生成中频信号
Sig1 = exp(1j * 2*pi * (Slope * tau1 * t + fc * tau1));
...
end对应的物理原理与公式推导
这行代码 exp(...) 实际上是 FMCW 混频输出公式 的直接实现。
-
发射信号 (Tx) :频率随时间 t t t 线性增加。
相位 ϕ T x ( t ) = 2 π ( f c t + 1 2 S t 2 ) \phi_{Tx}(t) = 2\pi (f_c t + \frac{1}{2} S t^2) ϕTx(t)=2π(fct+21St2)
-
接收信号 (Rx) :比发射晚了 τ \tau τ 秒。
相位 ϕ R x ( t ) = 2 π ( f c ( t − τ ) + 1 2 S ( t − τ ) 2 ) \phi_{Rx}(t) = 2\pi (f_c (t-\tau) + \frac{1}{2} S (t-\tau)^2) ϕRx(t)=2π(fc(t−τ)+21S(t−τ)2)
-
混频 (Mixer) :执行减法 Δ ϕ = ϕ T x − ϕ R x \Delta \phi = \phi_{Tx} - \phi_{Rx} Δϕ=ϕTx−ϕRx。
忽略掉高次项( S τ 2 S\tau^2 Sτ2 极小),剩下的相位差为:
Δ ϕ ( t ) ≈ 2 π ( S τ t ⏟ 频率项 + f c τ ⏟ 相位项 ) \Delta \phi(t) \approx 2\pi \left( \underbrace{S \tau t}{\text{频率项}} + \underbrace{f_c \tau}{\text{相位项}} \right) Δϕ(t)≈2π 频率项 Sτt+相位项 fcτ
解读代码中的两项:
-
第1项:
Slope * tau1 * t (距离频率项)这一项包含快时间 t t t。
对 t t t 求导得到频率: f = S τ f = S \tau f=Sτ。这就是拍频 (Beat Frequency) 。
-
作用: 给 Range-FFT 提供频率信息,用来算距离。
-
第2项:
fc * tau1 (多普勒相位项)这一项不包含 t t t,对于单个 Chirp 来说是个常数(初相)。
但在不同的 Chirp 之间( m m m 变化),由于物体运动, r c u r r r_{curr} rcurr 变了 → \rightarrow → τ \tau τ 变了。
相位变化量: Δ ϕ = 2 π f c Δ τ \Delta \phi = 2\pi f_c \Delta \tau Δϕ=2πfcΔτ。
-
作用: 给 Doppler-FFT 提供相位旋转信息,用来算速度。
第三部分:距离测量 (Range-FFT)
matlab
Range_Map = fft(Mix_Data_Matrix, Ns, 2); % 沿维度2(快时间)做FFT
% 坐标轴转换公式
f_bin_res = Fs / Ns;
f_axis = (0:Ns/2-1) * f_bin_res; % 得到拍频 fb
R_axis = c * f_axis / (2 * Slope); % 将 fb 转换为 距离 R对应的物理原理
这里利用的是 拍频与距离的线性关系。
-
拍频公式 :
由混频原理可知,拍频 f b f_b fb 等于斜率乘以延迟:
f b = S ⋅ τ f_b = S \cdot \tau fb=S⋅τ
-
代入延迟公式 τ = 2 R c \tau = \frac{2R}{c} τ=c2R:
f b = S ⋅ 2 R c f_b = S \cdot \frac{2R}{c} fb=S⋅c2R
-
反解距离 R R R(即代码中的最后一行):
R = c ⋅ f b 2 S R = \frac{c \cdot f_b}{2S} R=2Sc⋅fb
FFT 找到了信号里包含哪个频率 f b f_b fb,代码用上面的公式把这个频率直接翻译成了距离 R R R。
!NOTE
坐标中的转换公式,可以好好想想
第四部分:速度测量 (Doppler-FFT)
这是最神奇的一步,利用相位旋转测速。
matlab
Doppler_Map = fft(Range_Map, N_chirps, 1); % 沿维度1(慢时间)做FFT
% 坐标轴转换公式
v_res = lambda / (2 * N_chirps * Tc);
v_idx = -N_chirps/2 : N_chirps/2 - 1;
v_axis = v_idx * v_res;对应的物理原理
这里利用的是 多普勒效应引起的相位变化。
-
位移与相位 :
相邻两个 Chirp 间隔时间 T c T_c Tc。物体移动了 Δ d = v ⋅ T c \Delta d = v \cdot T_c Δd=v⋅Tc。
这导致的相位变化 Δ ϕ \Delta \phi Δϕ 为:
Δ ϕ = 4 π Δ d λ = 4 π v T c λ \Delta \phi = \frac{4\pi \Delta d}{\lambda} = \frac{4\pi v T_c}{\lambda} Δϕ=λ4πΔd=λ4πvTc
-
角频率与 FFT :
如果在慢时间轴上做 FFT,得到的"频率"索引 k k k (代码中的
v_idx) 代表了相位的旋转速度。其关系满足:
2 π k N c h i r p s = Δ ϕ = 4 π v T c λ 2\pi \frac{k}{N_{chirps}} = \Delta \phi = \frac{4\pi v T_c}{\lambda} 2πNchirpsk=Δϕ=λ4πvTc
-
反解速度 v v v:
v = λ 2 T c ⋅ k N c h i r p s v = \frac{\lambda}{2 T_c} \cdot \frac{k}{N_{chirps}} v=2Tcλ⋅Nchirpsk
观察代码:
v_res = lambda / (2 * N_chirps * Tc) 其实就是上面公式里的系数部分。所以
v = v_idx * v_res就是把 FFT 的索引变成了速度值。
!NOTE
同样,坐标轴的转换还是值得去想想为什么需要这么做。
结果
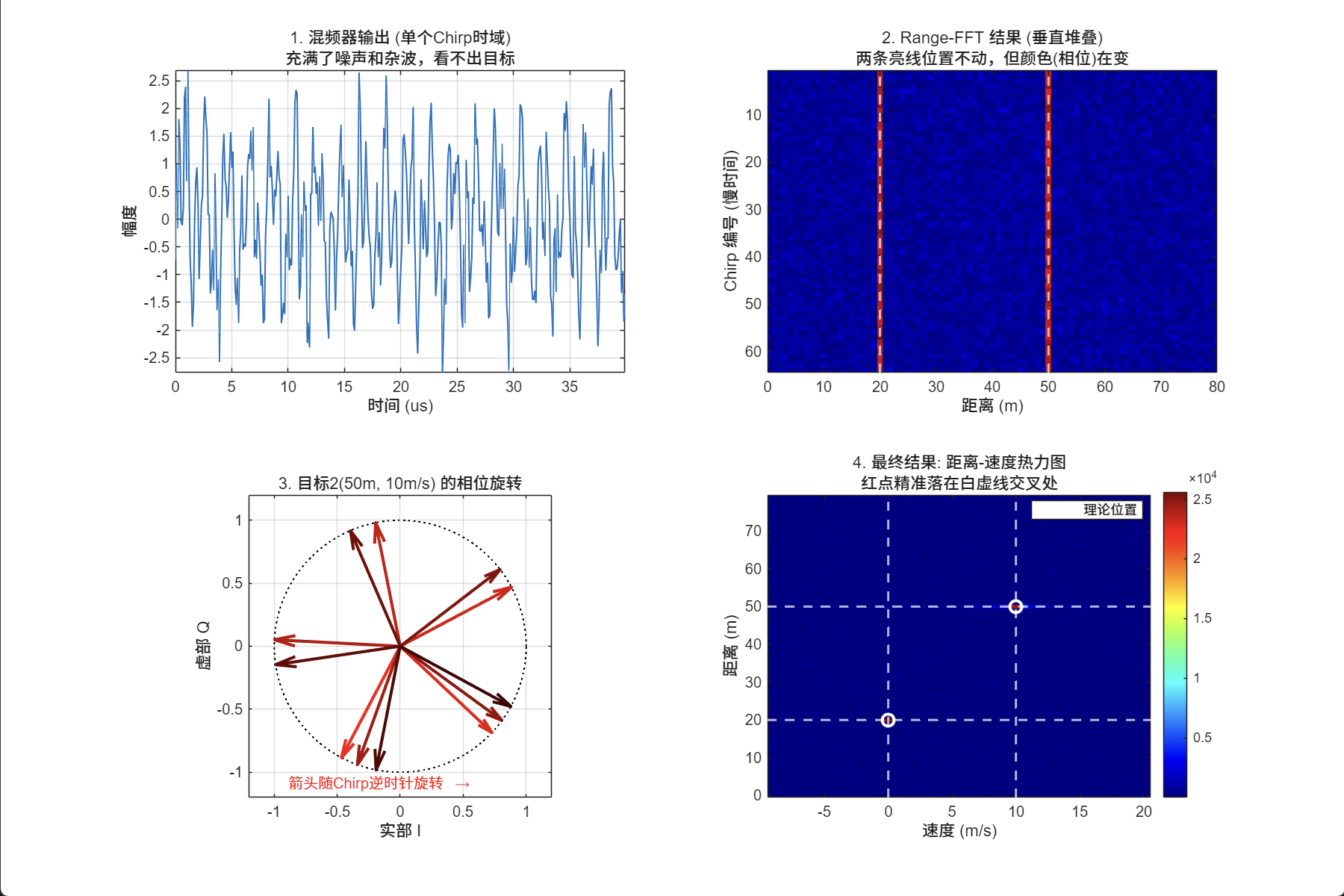
总结全流程
- S τ t S \tau t Sτt (快时间项) → Range-FFT \xrightarrow{\text{Range-FFT}} Range-FFT 提取出 f b f_b fb → R = c f b 2 S \xrightarrow{R=\frac{c f_b}{2S}} R=2Scfb 算出距离。
- f c τ f_c \tau fcτ (慢时间项) → Doppler-FFT \xrightarrow{\text{Doppler-FFT}} Doppler-FFT 提取出 Δ ϕ \Delta \phi Δϕ → v = λ Δ ϕ 4 π T c \xrightarrow{v=\frac{\lambda \Delta \phi}{4\pi T_c}} v=4πTcλΔϕ 算出速度。
坐标轴转换
FFT(快速傅里叶变换)本质上是一个数学工具,它只懂 "数字" (索引 Index 0, 1, 2...),不懂 "物理" (米、米/秒)。
之所以能把 FFT 的结果坐标轴画成"距离"和"速度",是因为在雷达设计之初,就建立了一套严密的物理映射关系。
一、 距离轴转换 (Range Axis)
代码源头:
matlab
f_bin_res = Fs / Ns; % 1. FFT的一个格子代表多少Hz
f_axis = (0:Ns/2-1) * f_bin_res; % 2. 生成频率轴 (Hz)
R_axis = c * f_axis / (2 * Slope);% 3. 把 Hz 换算成 米1. 第一步:从"格子(Bin)"到"频率(Hz)"
FFT 的输出是一个数组。数组的第 k k k 个元素(Bin k k k)代表什么频率?
这取决于你的采样参数:
- 总带宽: 也就是采样率 F s F_s Fs(Sampling Rate)。
- 切成几份: 也就是采样点数 N s N_s Ns。
所以,每一个格子代表的频率宽度(分辨率)是:
Δ f = F s N s \Delta f = \frac{F_s}{N_s} Δf=NsFs
第 k k k 个格子的频率就是: f = k ⋅ Δ f f = k \cdot \Delta f f=k⋅Δf。
2. 第二步:从"频率(Hz)"到"时间(s)"
这是 FMCW 的核心特性。
- 发射的 Chirp 是线性调频波,斜率是 S S S (Slope)。
- 意思是:每过 1秒,频率增加 S S S Hz。
- 反过来:如果你看到了 f b f_b fb 的频率差,说明信号延迟了 τ \tau τ 秒。
τ = f b S \tau = \frac{f_b}{S} τ=Sfb
3. 第三步:从"时间(s)"到"距离(m)"
- 信号是电磁波,以光速 c c c 飞行。
- 信号走了往返(去+回),所以路程是 2 R 2R 2R。
τ = 2 R c \tau = \frac{2R}{c} τ=c2R
4. 终极合并:从"频率"到"距离"
联立上面两步:
f b S = 2 R c \frac{f_b}{S} = \frac{2R}{c} Sfb=c2R
把 R R R 挪到左边:
R = c ⋅ f b 2 S R = \frac{c \cdot f_b}{2S} R=2Sc⋅fb
这就是代码中 R_axis = c * f_axis / (2 * Slope) 的物理来源。
- 直观理解: 频率越高 → \rightarrow → 延迟越大 → \rightarrow → 距离越远。
二、 速度轴转换 (Velocity Axis)
代码源头:
matlab
v_res = lambda / (2 * N_chirps * Tc); % 1. 一个格子代表多少速度
v_idx = -N_chirps/2 : N_chirps/2 - 1; % 2. 生成索引 (-32 ~ +31)
v_axis = v_idx * v_res; % 3. 生成速度轴这个转换稍微绕一点,因为它涉及到了相位。
1. 物理源头:相位差与速度
正如之前分析的,相邻两个 Chirp(间隔 T c T_c Tc)之间,物体移动距离 Δ d = v ⋅ T c \Delta d = v \cdot T_c Δd=v⋅Tc。
这导致的相位变化 Δ ϕ \Delta \phi Δϕ 是:
Δ ϕ = 4 π ⋅ ( v ⋅ T c ) λ \Delta \phi = \frac{4\pi \cdot (v \cdot T_c)}{\lambda} Δϕ=λ4π⋅(v⋅Tc)
2. FFT 的视角:角频率
我们在慢时间维度(Chirp 序列)上做 FFT。FFT 看到的"频率"(这里指数字角频率 ω \omega ω)其实就是相位变化率。
FFT 的第 k k k 个格子,代表的相位变化是:
Δ ϕ = 2 π ⋅ k N c h i r p s \Delta \phi = \frac{2\pi \cdot k}{N_{chirps}} Δϕ=Nchirps2π⋅k
(注:这里假设 k k k 覆盖一个完整周期)
3. 建立映射:从"格子"到"速度"
让上面两个 Δ ϕ \Delta \phi Δϕ 相等:
4 π v T c λ = 2 π k N c h i r p s \frac{4\pi v T_c}{\lambda} = \frac{2\pi k}{N_{chirps}} λ4πvTc=Nchirps2πk
4. 求解速度 v v v
我们把 v v v 解出来:
v = ( λ 2 ⋅ T c ⋅ N c h i r p s ) ⏟ 代码中的 v_res ⋅ k v = \underbrace{\left( \frac{\lambda}{2 \cdot T_c \cdot N_{chirps}} \right)}_{\text{代码中的 v\_res}} \cdot k v=代码中的 v_res (2⋅Tc⋅Nchirpsλ)⋅k
- λ \lambda λ:波长。波长越短,同样的移动产生的相位变化越大,测量越灵敏。
- T c ⋅ N c h i r p s T_c \cdot N_{chirps} Tc⋅Nchirps:这就是一帧的总时间 T f r a m e T_{frame} Tframe。观测时间越长,速度分辨率越高(分母越大,分辨率数值越小)。
这就是代码中 v_res 公式的由来。
总结表
| 维度 | FFT 输出 (数学) | 中间物理量 (桥梁) | 最终物理量 (人话) | 核心转换因子 |
|---|---|---|---|---|
| 距离轴 | 频率 Bin ( k k k) | 拍频 f b f_b fb (Hz) | 距离 R R R (m) | c 2 S \frac{c}{2S} 2Sc (光速除以2倍斜率) |
| 速度轴 | 频率 Bin ( k k k) | 相位差 Δ ϕ \Delta \phi Δϕ (rad) | 速度 v v v (m/s) | λ 2 T f r a m e \frac{\lambda}{2 T_{frame}} 2Tframeλ (波长除以2倍总时长) |
- 距离转换 依赖于 Slope (调频斜率) 。
- 速度转换 依赖于 Wavelength (波长) 和 Time (观测时长) 。