FMCW雷达第一部分:测距
外国文献写的相当透彻,所以拿过来研读一下。喜欢看原文的可以看这里https://wirelesspi.com/fmcw-radar-part-1-ranging/
文章分为3部分,我自己就看心情分了
3部分系列文章的第1部分,描述FMCW雷达如何找到多个静止目标的距离。
第2部分讨论如何通过形成雷达立方体结构来估计多个移动目标的速度和方向。
第3部分介绍了FMCW雷达的系统设计指南。
在《多速率信号处理》一书中,Fred Harris提到了一个很好的问题解决技巧:
"当面临一个无法解决的问题时,将其改变为你能解决的那个问题,然后解决它。"
我们将在本文中看到FMCW雷达是如何成为这种方法最美丽的应用之一。
- 显然,测量物体距离的逻辑方法是通过估计反射波的时间延迟(在纳秒量级),这既昂贵又不够准确。我们可以将距离与正弦波的频率关联起来,改为测量频率。这被证明要简单和准确得多。
- 这里还有另一种令人惊讶的方法可以应用这个想法,只有在深入了解细节后才能理解。因此,它将在结论部分提及。
背景

雷达(无线电探测和测距)是人类感官知觉的延伸。为了理解这个想法,请考虑以下两点。
- 想象一只蝙蝠在黑夜中或洞穴里。它利用一种称为回声定位的非凡方法来导航和定位猎物。这涉及通过它们的嘴或鼻子(发射器)发射高频超声波,这些波会从各种物体上反弹,然后被它们灵敏的耳朵(接收器)检测到。这使得蝙蝠能够检测到像蚊子一样小的昆虫猎物!
- 原则上,任何人都可以通过声音信号做同样的事情来检测物体,但我们的耳朵和大脑的分辨率要粗糙得多(此外,谁想一直嚎叫)。看看其他地方(没有双关语),虽然视觉是自然界赋予我们的最强大的传感器,但我们的眼睛只能充当被动雷达,利用环境中已有的光信号。
我们实际上可以做的就是设计一种利用相同原理但在可见光谱之外的电磁频谱(例如射频)中的机器。这种机器就是雷达,它整天发射高能量波并处理返回的信号,从不抱怨。
我们将讨论一种特定类型的雷达:调频连续波(FMCW)雷达。它特别适用于短距离应用,如自动驾驶汽车中的物体检测以避免碰撞、心跳监测、住宅和工业产品中的振动测量、无人机测距和入侵检测。有趣的是,FMCW雷达波形与长距离(LoRa)物理层有相似之处。
由于FMCW雷达广泛应用于汽车应用,我们以自动驾驶汽车为例来解释这个想法。
接下来,我们通过正式的方法描述雷达原理。
雷达原理
雷达在一个或多个方向上发射电磁能量,并在返回信号中搜索来自物体的反射。
我们描述信息提取过程时同时考虑实信号和复信号。
距离
假设Tx信号是一个正弦连续波(CW),给出为
x ( t ) = A cos ( 2 π f t ) x(t) = A \cos (2\pi ft) x(t)=Acos(2πft)
其中 A A A是振幅, f f f是频率。如果所有这些能量都消失在空旷的天空中,就没有返回信号。然而,如果被照射区域内有一个物体,例如建筑物墙壁,那么返回信号是
y ( t ) = A r cos [ 2 π f ( t − τ 0 ) ] = A r cos [ 2 π f t + ϕ ] y(t) = A_r \cos \big[2\pi f(t-\tau_0)\big] = A_r \cos \big[2\pi ft + \phi\big] y(t)=Arcos[2πf(t−τ0)]=Arcos[2πft+ϕ]
这里, A r A_r Ar是(现在非常微弱的)回波信号的振幅, τ 0 \tau_0 τ0是在雷达和目标之间的往返过程中产生的时间延迟。这个参数在其相位中包含了关于目标距离 d 0 d_0 d0的所有信息,因为根据上面的表达式我们可以写出:
ϕ = − 2 π f τ 0 , 或 τ 0 = − ϕ 2 π f (1) \phi = -2\pi f\tau_0, \qquad \text{或} \qquad \tau_0 = -\frac{\phi}{2\pi f} \tag{1} ϕ=−2πfτ0,或τ0=−2πfϕ(1)
从上图可以看出, d 0 d_0 d0是Tx和Rx之间的距离,由于波的往返行程而加倍。根据牛顿物理定律,如果时间延迟 τ 0 \tau_0 τ0等于 2 d 0 / c 2d_0/c 2d0/c,其中 c c c是电磁波的速度。
ϕ = − 2 π f 2 d 0 c = − 4 π d 0 λ \phi = -2\pi f \frac{2d_0}{c} = -4\pi \frac{d_0}{\lambda} ϕ=−2πfc2d0=−4πλd0
其中 λ \lambda λ是雷达的工作波长。从这里,距离被估计为
d 0 = λ 4 π ϕ (2) d_0 = \frac{\lambda}{4\pi}\phi\tag{2} d0=4πλϕ(2)
负号已经被移除,因为它源于延迟,与距离无关。正如我们很快将看到的,这种技术对测距没有用处 ,因为正弦波是周期性的,周期为 2 π 2\pi 2π。因此,相位 ϕ \phi ϕ只在 − π -\pi −π到 + π +\pi +π范围内是明确的。对于实用的无线电频率,这最多只有几厘米。
!NOTE
解释的已经非常到位了,本来想写点什么,真的插不上什么话,先从连续波入手,推导出连续波情况下的距离估计计算公式。但是有局限性,局限在于正弦波的周期性。至于工程上应用的测距技术,放在了后边进行讨论。
接下来,我们转向如何确定速度。
速度
在高中物理中作为移动物体中的频率变化引入,多普勒频移在无线信道中小尺度衰落的讨论中详细解释。
想象上图中的汽车以恒定的速度 v v v m/s朝相反方向行驶。对于所有进一步的时间 t t t,原本必须行进 d 0 d_0 d0 m的电磁波现在必须覆盖 d 0 + v t d_0 + v t d0+vt的距离。
y ( t ) = A r cos [ 2 π f ( t − 2 d 0 + 2 v t c ) ] = A r cos [ 2 π f { ( 1 − 2 v c ) t − 2 d 0 c } ] y(t) = A_r \cos \left[ 2\pi f \left( t - \frac{2d_0 + 2vt}{c} \right) \right] = A_r \cos \left[ 2\pi f \left\{ \left( 1 - \frac{2v}{c} \right) t - \frac{2d_0}{c} \right\} \right] y(t)=Arcos[2πf(t−c2d0+2vt)]=Arcos[2πf{(1−c2v)t−c2d0}]
显然,初始距离仍然与公式(2)相同,而多普勒频移 f d f_d fd是给定的频率变化
f d = 2 v c f = 2 v λ (3) f_d = \frac{2v}{c}f = \frac{2v}{\lambda}\tag{3} fd=c2vf=λ2v(3)
这产生了速度
v = f d 2 λ (4) v = \frac{f_d}{2}\lambda\tag{4} v=2fdλ(4)
以角度 ψ \psi ψ到达的波将具有按 cos ψ \cos \psi cosψ缩放的多普勒频移。由于它可以确定速度而不是距离,CW雷达主要用于运动和速度感应应用。
接收器框图
上面的距离推导相当简单。实际的CW雷达发送一个未调制的波,并在返回路径上移除载波以提取所需的信号,其框图如下所示。Rx链中显示的乘法器称为混频器,其输出是雷达设计师主要关注的。
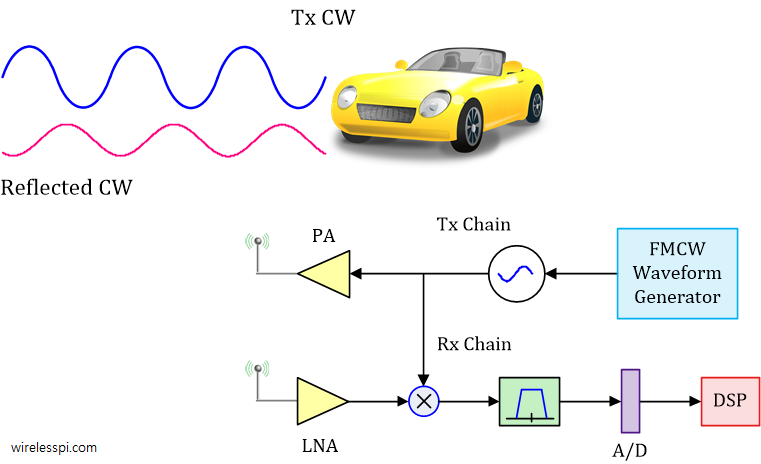
如果你是DSP初学者,请用以下术语思考以下数学表达式。当两个正弦波相乘时会发生什么?结果是两个正弦波,一个在差频,另一个在和频。
2 cos [ 2 π f ( t − τ 0 ) + θ ] ⋅ cos [ 2 π f t + θ ] = cos [ − 2 π f τ 0 ] + cos [ 2 π ⋅ 2 f t − 2 π f τ 0 + 2 θ ] ⏟ Filtered out 2 \cos[2\pi f(t - \tau_0) + \theta] \cdot \cos[2\pi f t + \theta] = \cos[-2\pi f \tau_0] + \underbrace{\cos[2\pi \cdot 2f t - 2\pi f \tau_0 + 2\theta]}_{\text{Filtered out}} 2cos[2πf(t−τ0)+θ]⋅cos[2πft+θ]=cos[−2πfτ0]+Filtered out cos[2π⋅2ft−2πfτ0+2θ]
和频被低通滤波,仅产生差频项。接下来,我们通过复信号描述如何得出相同的结果。
CW、复正弦波和IQ处理
在实践中,每当相位涉及检测或估计程序时,都会使用IQ信号。IQ形式的连续波(CW)被称为复正弦波,如下图所示。
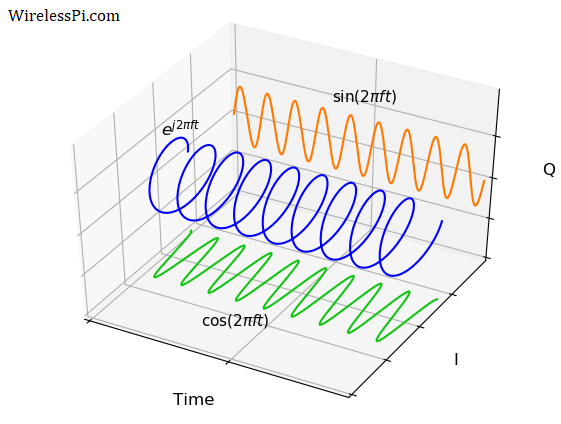
复正弦波的表达式由 e j 2 π f t e^{j2\pi f t} ej2πft给出,其中瞬时相位是时间的线性函数。
ϕ = 2 π f t \phi = 2\pi ft ϕ=2πft
该图还演示了欧拉关系
e j 2 π f t = cos ( 2 π f t ) + j sin ( 2 π f t ) e^{j2\pi f t} = \cos (2\pi f t) + j\sin (2\pi f t) ej2πft=cos(2πft)+jsin(2πft)
实部 cos ( 2 π f t ) \cos (2\pi f t) cos(2πft)可以看作是这个复正弦波在实平面(由时间和 I I I轴形成)上的投影。此外,虚部 sin ( 2 π f t ) \sin (2\pi f t) sin(2πft)可以看作是这个复正弦波在虚平面(由时间和 Q Q Q轴形成)上的投影。
现在我们可以重新审视复信号的结果。就复信号而言,让Tx信号为 e j ( 2 π f t + θ ) e^{j(2\pi f t+\theta)} ej(2πft+θ),其中我们包含了之前忽略的相位 θ \theta θ。接收到的信号是其延迟版本,写为 e j 2 π f ( t − τ 0 ) + θ e^{j2\pi f (t-\tau_0)+\theta} ej2πf(t−τ0)+θ。经过复杂的混合过程后,我们有
y ( t ) = e j [ 2 π f ( t − τ 0 ) + θ ] ⋅ e − j ( 2 π f t + θ ) = e − j 2 π f τ 0 y(t) = e^{j[2\pi f (t-\tau_0)+\theta]} \cdot e^{-j(2\pi f t+\theta)} = e^{-j2\pi f \tau_0} y(t)=ej[2πf(t−τ0)+θ]⋅e−j(2πft+θ)=e−j2πfτ0
它具有与上述差频相同的参数。现在让我们探讨为什么未调制的CW雷达不是一个很好的主意。
!NOTE
欧拉公式是联系复数与实数的枢纽,还有很多的解释,包括j是进行旋转等。复正弦波是一个螺旋的曲线,像一个弹簧一样。
未调制CW的缺点
在理想情况下,这个简单的CW为我们提供了我们想要的所有信息。然而,在实践中,这种方法存在一些问题,限制了CW雷达的应用。
- CW雷达无法测量目标的距离。如前所述,未调制的CW接收到的相位 ϕ \phi ϕ只在 − π -\pi −π到 + π +\pi +π范围内是明确的,因为混频器输出是周期性的,周期为 2 π 2\pi 2π。没有时间或频率标记,就无法区分第100个周期和第105个周期。
- 返回信号的幅度 A r A_r Ar比Tx信号的幅度 A A A小几个数量级。在混合和模数转换过程中,它几乎被Tx信号淹没。需要通过精心设计以最小化泄漏(单静态)或物理上分开的天线(双静态)来实现它们之间的分离。
- 用简单的CW对抗加性噪声更加困难。带内噪声无法被滤除,并且会对相位和频率的估计产生不利影响。事实上,频率估计算法会受到信噪比阈值效应的影响:低于某个信噪比,均方误差会迅速增加。
- 在多径环境中,这种信号的多个副本的总和表现出相同的频率,但由它们的相量加法给出旋转相位。正如我们稍后将看到的,调制的CW可以更好地处理多个反射。
- 很难区分雷达周围的多个目标,因为来自不同物体的返回波形彼此重叠,产生类似于多径环境的效果,扭曲相位并导致测距信息的丢失。
- CW的频谱是一个单一的窄脉冲。因此,它更容易受到其他传输的干扰。
因此,我们想要一种替代技术,这就是调制发挥作用的地方。