计数排序Counting Sort

计数排序是一种非基于比较的排序算法。当输入值范围相对于待排序元素数量较小时，它尤其高效。

计数排序的基本思想是统计输入数组中每个不同元素的频率，并利用这些信息将元素放置在正确的排序位置。

当输入元素的范围较小且与数组大小相当时，它表现良好。例如，对于输入 $1， 4， 0， 2， 1， 1$ ，数组大小为6，元素范围为0到4

如果输入数组的范围大于 n Log n，其中 n 是数组大小，那么我们可以用标准的比较排序算法（如合并排序）更好地排序。

计数排序算法

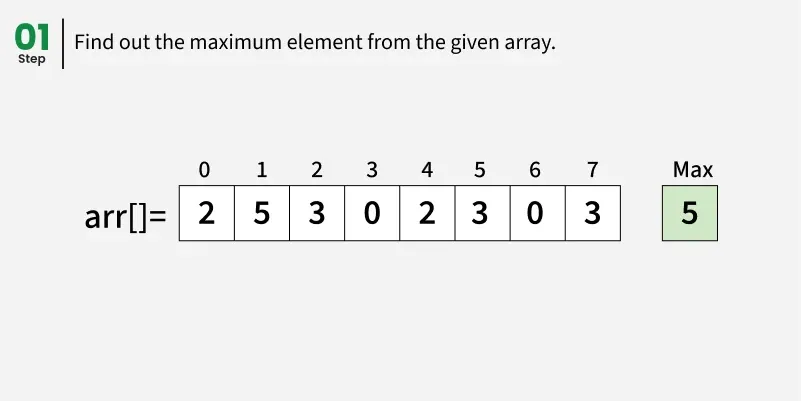
声明一个计数数组 cntArr\[\]，大小为 max（arr\[\]）+1，并初始化为 0。

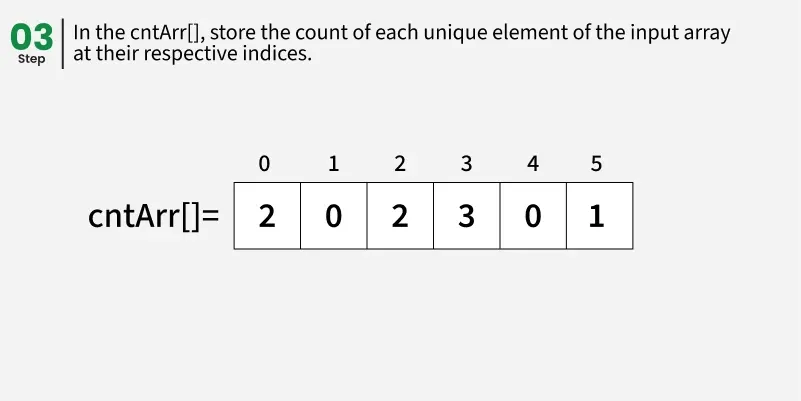
遍历输入数组 arr\[\]，并将 arr\[\] 中的每个元素映射为 cntArr\[\] 数组的索引，即对 0 <= i <和 N 执行 cntArr $arr\[i$ ]++。

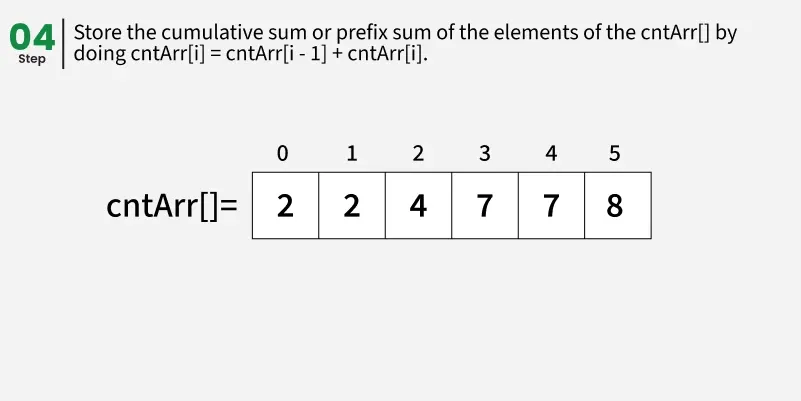
计算 cntArr\[\] 的每个索引处的前缀和。

创建一个大小为N的数组ans\[\]。

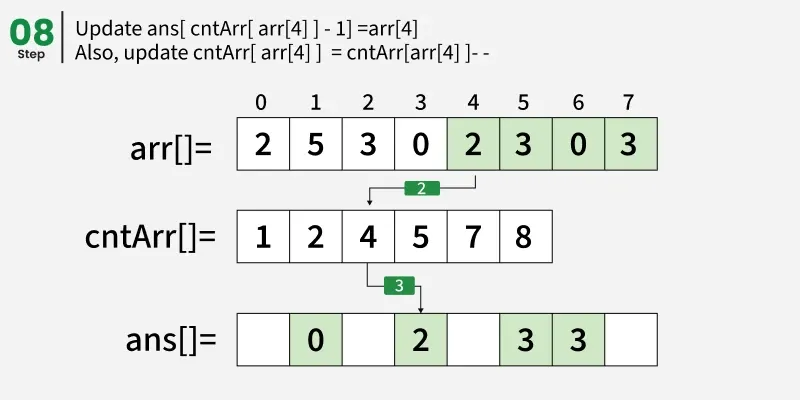
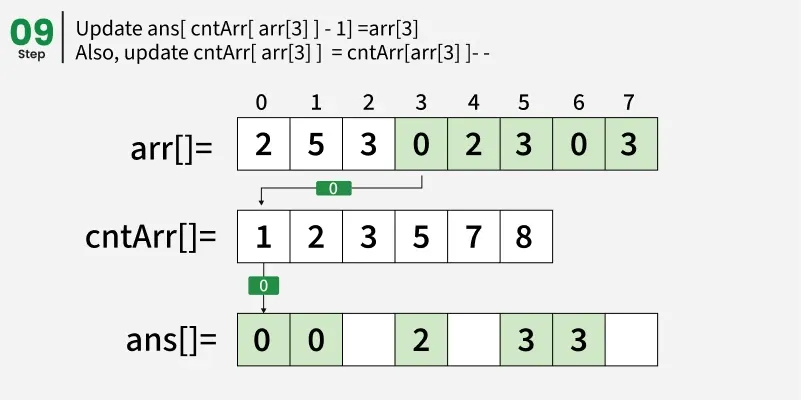
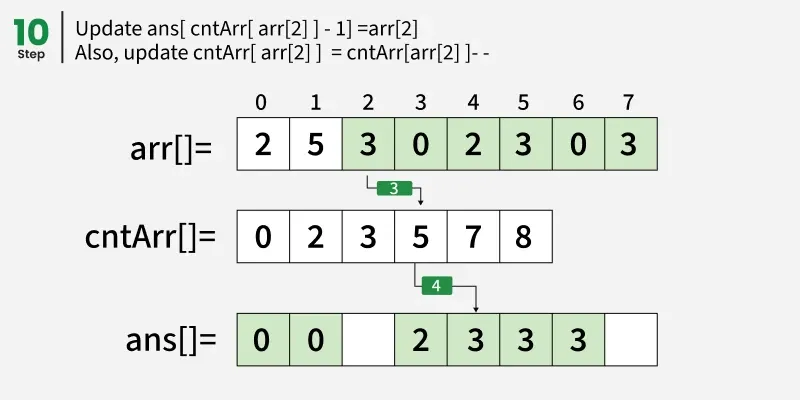
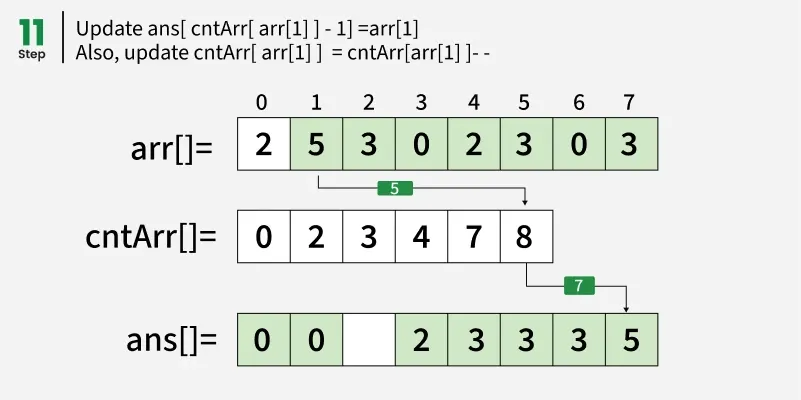
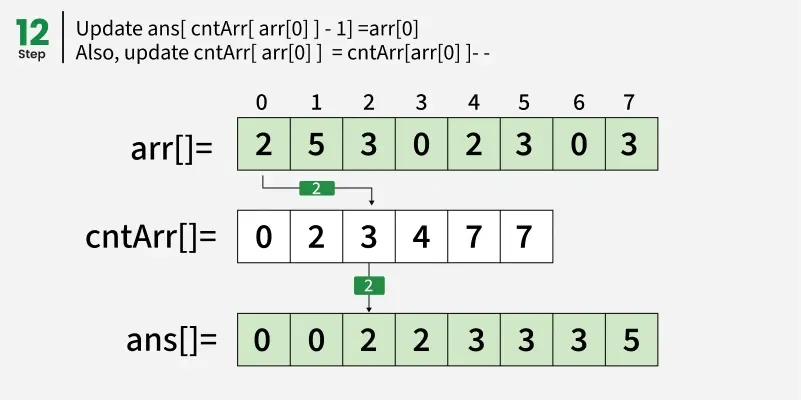
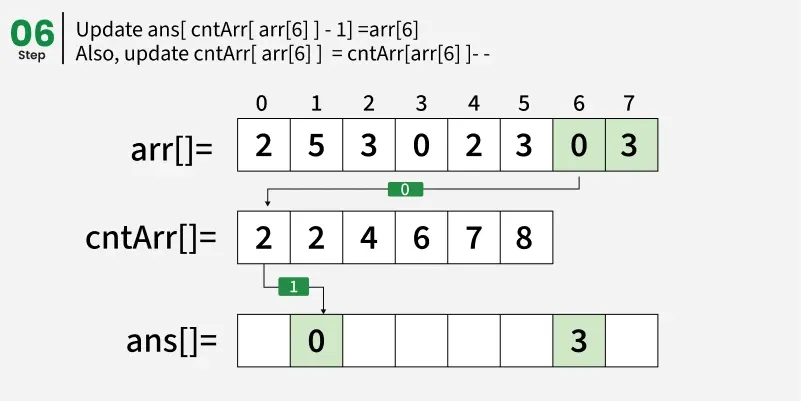
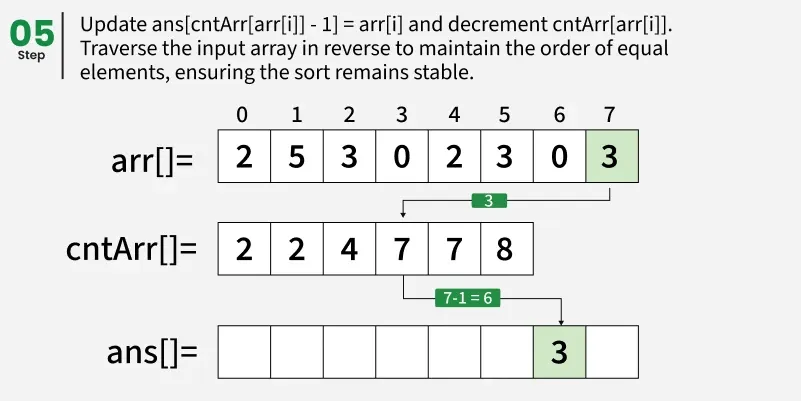
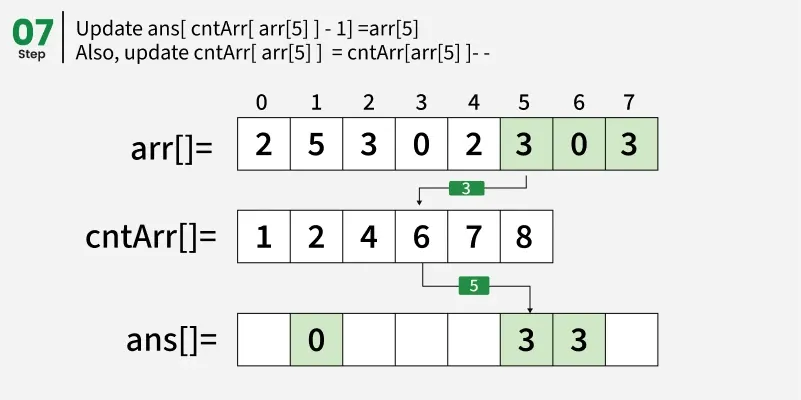
从结束处遍历阵列 arr\[\] 并更新 ans $cntArr\[ arr\[i$ ] - 1] = arr $i$ 。同时，更新 cntArr $arr\[i$ ] = cntArr $arr\[i$ ]- - 。

为什么我们要计算前缀和？

我们也可以简单地统计所有元素的出现次数，并逐一放入输出数组，但我们通过计算机前缀和来实现算法的稳定性。注意，在构建前缀和 cntArr\[\] 后，我们从右端遍历数组，确保最后一次出现会移动到排序后的数组中最后正确的位置。

计数类工作

复制代码

import java.util.Arrays;

public class CountingSort {

    public static int[] countSort(int[] arr) {
        int n = arr.length;
        if (n == 0) {
            return new int[0];
        }

        // find the maximum element
        int maxVal = arr[0];
        for (int i = 1; i < n; i++) {
            if (arr[i] > maxVal) {
                maxVal = arr[i];
            }
        }

        // create and initialize cntArr array
        int[] cntArr = new int[maxVal + 1];
        for (int i = 0; i <= maxVal; i++) {
            cntArr[i] = 0;
        }

        // count frequency of each element
        for (int i = 0; i < n; i++) {
            cntArr[arr[i]]++;
        }

        // compute prefix sum
        for (int i = 1; i <= maxVal; i++) {
            cntArr[i] += cntArr[i - 1];
        }

        // build output array
        int[] ans = new int[n];
        for (int i = n - 1; i >= 0; i--) {
            int v = arr[i];
            ans[cntArr[v] - 1] = v;
            cntArr[v]--;
        }

        return ans;
    }

    public static void main(String[] args) {
        int[] arr = {2, 5, 3, 0, 2, 3, 0, 3};
        int[] ans = countSort(arr);
        System.out.println(Arrays.toString(ans));
    }
}

输出

0 0 2 2 3 3 3 5

计数排序的复杂性分析：

时间复杂度：所有情况下均为 O（N+M），其中 N 和 M 分别是 inputArray\[\] 和 countArray\[\] 的大小。

辅助空间：O（N+M），其中 N 和 M 分别是 outputArray\[\] 和 countArray\[\] 所占的空间。

优势，计数方式：

如果输入范围与输入数量的阶数相等，计数排序通常比所有基于比较的排序算法（如合并排序和快速排序）更快。

稳定算法

计数排序的缺点：

不适用于十进制数值。

如果排序的值范围非常大，效率低下。

它不是原地排序算法，它会用额外的空间来排序数组元素。

计数排序的应用：

它是在距离有限的项目中常用的算法。例如，按年级排序学生，按时间、天、月、年等排序事件

它作为基排序中的子程序使用。

计数排序的理念被用于桶排序，将元素划分为不同的桶。

复制代码

编程资源
https://pan.quark.cn/s/7f7c83756948
更多资源
https://pan.quark.cn/s/bda57957c548