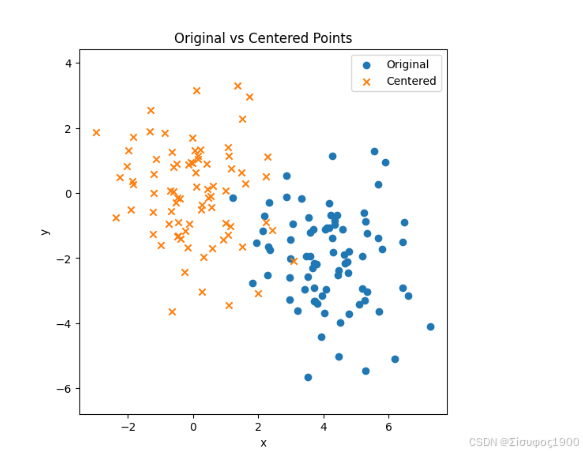
🎯 一、为什么必须去中心化?(核心数学原因)
在 ICP / Kabsch / Umeyama 中,我们需要求:
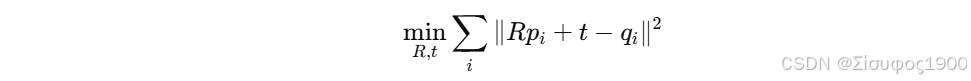
若不去中心化,SVD 得到的矩阵反映的是 同时包含旋转 + 平移混合的偏差,导致:
❌ 得不到真实的旋转
因为 SVD 只适用于纯旋转后的 协方差矩阵:
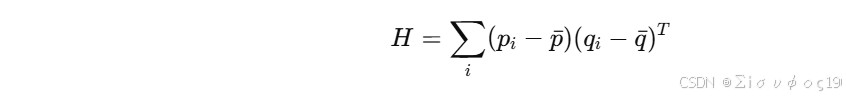
其中平移被去掉了。
🔍 去中心化的作用------消除平移影响

🧠 直观几何解释
👉 不去中心化的时候:
两个点云分别整体偏移 = 强制"旋转"来拟合平移误差
结果 SVD 会把 "平移差异" 当成 "旋转误差"
=> 得到错误旋转矩阵
👉 去中心化之后:
两个点云都以各自质心为坐标原点
只剩下姿态差异,因此能正确求出 R。
⭐ 一句话总结(记住这个!)
去中心化 = 去除平移,使点云之间的关系只剩下旋转,从而 SVD 才能正确分解出真实的 R。
二、MATLAB 演示:不去中心化 vs 去中心化(对比)
下面用真实点云模拟一个旋转 + 平移
并演示不去中心化会导致 SVD 求 R 失败。
📌 不去中心化:旋转和平移全部崩坏
📌 去中心化:恢复真实 R,t 精准无比

cpp
%% 1. 构造简单点云
P = randn(3,1000);
%% 2. 人为施加真实 R,t
R_true = angle2dcm(0.3,0.2,0.1);
t_true = [1;2;3]; % 大平移
Q = R_true * P + t_true;
%% =============== 不去中心化 ===============
H_raw = P * Q';
[U1,~,V1] = svd(H_raw);
R_wrong = V1*U1';
%% 平移
t_wrong = mean(Q,2) - R_wrong * mean(P,2);
%% =============== 去中心化 ===============
Pc = P - mean(P,2);
Qc = Q - mean(Q,2);
Hc = Pc * Qc';
[U2,~,V2] = svd(Hc);
R_correct = V2*U2';
t_correct = mean(Q,2) - R_correct * mean(P,2);
%% =============== 对比误差 ===============
fprintf("Rotation error (without centering): %.6f\n", norm(R_true-R_wrong,'fro'));
fprintf("Rotation error (centering): %.6f\n\n", norm(R_true-R_correct,'fro'));
fprintf("Translation error (without centering): %.6f\n", norm(t_true-t_wrong));
fprintf("Translation error (centering): %.6f\n", norm(t_true-t_correct));