题目:
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
图示两个链表在节点 c1 开始相交**:**
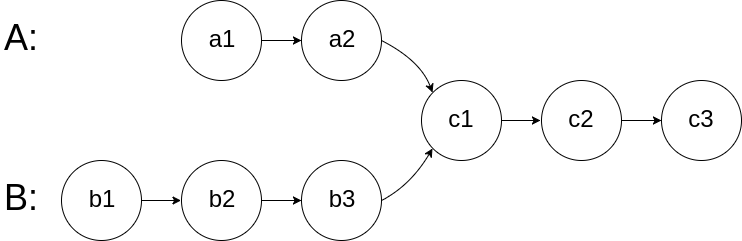
题目数据 保证 整个链式结构中不存在环。
示例 1:
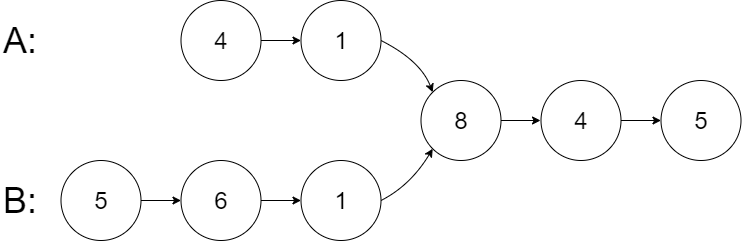
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出:Intersected at '8'
解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,6,1,8,4,5]。
在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
--- 请注意相交节点的值不为 1,因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说,它们在内存中指向两个不同的位置,而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点,B 中第四个节点) 在内存中指向相同的位置。
示例 2:
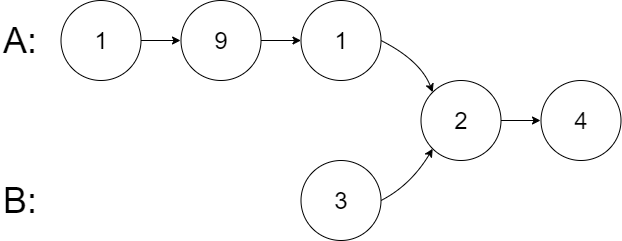
输入:intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出:Intersected at '2'
解释:相交节点的值为 2 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [1,9,1,2,4],链表 B 为 [3,2,4]。
在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例 3:
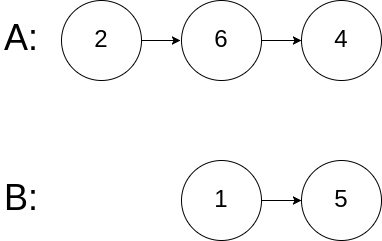
输入: intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出: No intersection
解释: 从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。
由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。
这两个链表不相交,因此返回 null 。
核心思路
双指针法:两个指针分别从两个链表头开始,走完自己的链表后切换到对方的链表头继续走。
关键认知:如果两个链表相交,两个指针最终会在相交点相遇;如果不相交,最终都会走到 null。
链表A: a1 → a2 → c1 → c2 → c3
链表B: b1 → b2 → b3 → c1 → c2 → c3
↑ 相交点
指针pA走的路径: a1 → a2 → c1 → c2 → c3 → b1 → b2 → b3 → c1
指针pB走的路径: b1 → b2 → b3 → c1 → c2 → c3 → a1 → a2 → c1
↑ 相遇题解:
java
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
if (headA == null || headB == null) return null;
ListNode pA = headA;
ListNode pB = headB;
// 两个指针各走一遍两个链表,相遇点就是相交点
while (pA != pB) {
// pA 走完 A 链表后,切换到 B 链表头
pA = (pA == null) ? headB : pA.next;
// pB 走完 B 链表后,切换到 A 链表头
pB = (pB == null) ? headA : pB.next;
}
return pA; // 相交返回交点,不相交返回 null
}
}
```
## 详细演示
### 示例1:有相交
```
链表A: 4 → 1 → 8 → 4 → 5
链表B: 5 → 6 → 1 → 8 → 4 → 5
↑ 相交点(值为8的节点)
A的长度: 5
B的长度: 6
公共部分长度: 3
pA 的路径(总共11步):
4 → 1 → 8 → 4 → 5 → null → 5 → 6 → 1 → 8
A链表(5步) 切换到B B链表(4步到相交点)
pB 的路径(总共11步):
5 → 6 → 1 → 8 → 4 → 5 → null → 4 → 1 → 8
B链表(6步) 切换到A A链表(2步到相交点)
第11步时,pA 和 pB 都指向节点8,相遇!
```
### 示例2:无相交
```
链表A: 1 → 2 → 3
链表B: 4 → 5
pA 的路径:
1 → 2 → 3 → null → 4 → 5 → null
A链表 切换到B B链表
pB 的路径:
4 → 5 → null → 1 → 2 → 3 → null
B链表 切换到A A链表
两个指针都走到 null,相遇在 null
返回 null(无相交)
```
## 为什么这个方法有效?
### 数学证明
假设:
- A 链表独有部分长度为 `a`
- B 链表独有部分长度为 `b`
- 公共部分长度为 `c`
```
链表A: [a 个节点] → [c 个节点]
链表B: [b 个节点] → [c 个节点]
↑ 相交点
pA 走的总距离:
a + c (A链表) + b (B链表的独有部分) = a + b + c
pB 走的总距离:
b + c (B链表) + a (A链表的独有部分) = a + b + c
两者走的总距离相同!
所以必然在相交点相遇
```
### 如果不相交
```
链表A: [a 个节点]
链表B: [b 个节点]
pA 走的距离: a + b
pB 走的距离: b + a
两者都走到 null,在 null 相遇
```
## 图解过程
```
示例:
A: 1 → 2 → 6 → 7
B: 3 → 4 → 5 → 6 → 7
↑ 相交点
步骤演示:
pA pB
↓ ↓
1 3 pA走1步,pB走1步
2 4 pA走2步,pB走2步
6 5 pA走3步,pB走3步
7 6 pA走4步,pB走4步
null 7 pA走5步,pB走5步
3 null pA切换到B头,pB切换到A头
4 1
5 2
6 6 相遇!返回节点6本质
双指针法的核心在于路径等长化:
- 让两个指针走相同的总距离
- 通过交换链表来抵消长度差
- 相交时在交点相遇,不相交时在 null 相遇
可以理解为:"你走过我走过的路,我走过你走过的路,我们终会相遇。"
这是一个非常优雅的算法,体现了对称性的美学。