目录
[【209. 长度最小的子数组】](#【209. 长度最小的子数组】)
引言:
滑动窗口?用两个指针维护一个动态的 "窗口" 区间,通过移动指针来扩大或缩小窗口,在一次遍历中完成计算,时间复杂度通常为 O (n)。
典型应用:
- 寻找最长无重复字符的子串
- 找到和为目标值的最短子数组
- 字符串的排列匹配
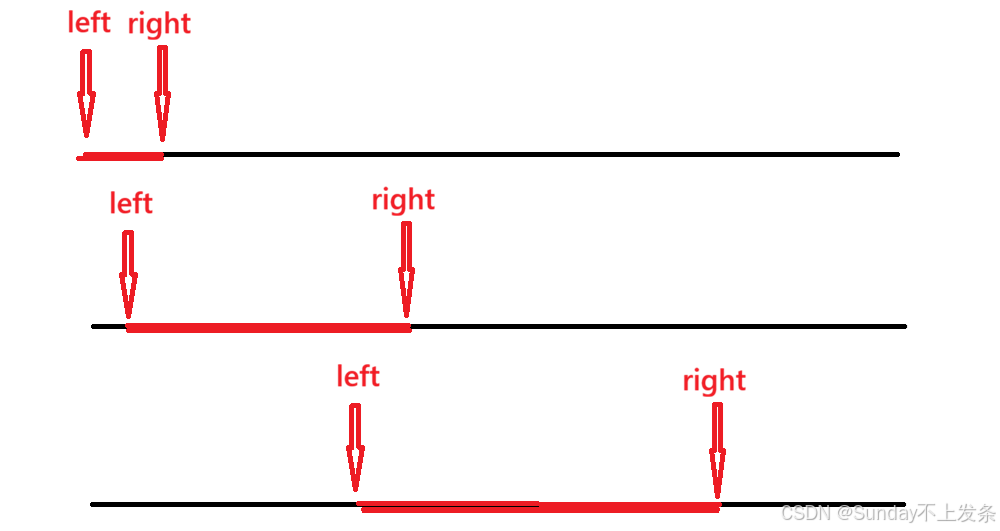
一般步骤(模板):(1)定义left 和 right 指针同时指向数组首元素;
(2)当符合要求时,right++,模拟进窗口;
(3)不满足要求时,left++,模拟出窗口;
(4)并根据具体情况更新结果。
结束条件:当right 越界。
具体我们通过下面的题目来深入认识它!!!
【209. 长度最小的子数组】
题目描述:
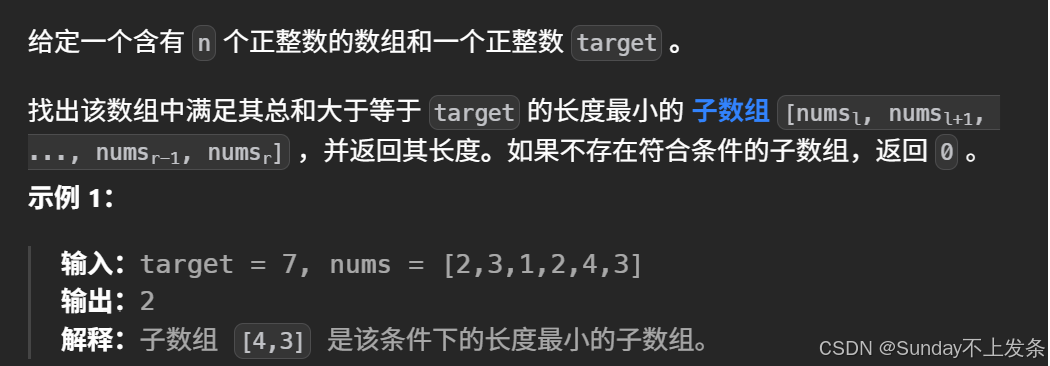
实现核心及思路:
由于数组元素均为正整数,所以当求和时满足单调性,套用上面的模板:
(1)定义left 和 right 指针,同时指向首元素;
(2)right 指针向右移动,进窗口,并求和 sum;当和 大于或等于target 时,更新结果;
(3)left指针向右移动,出窗口,同时让 sum 减去nums[left],直到sum小于target。
++注意:++在出窗口时,如果满足sum >= target,也要更新结果。
思路可视化:
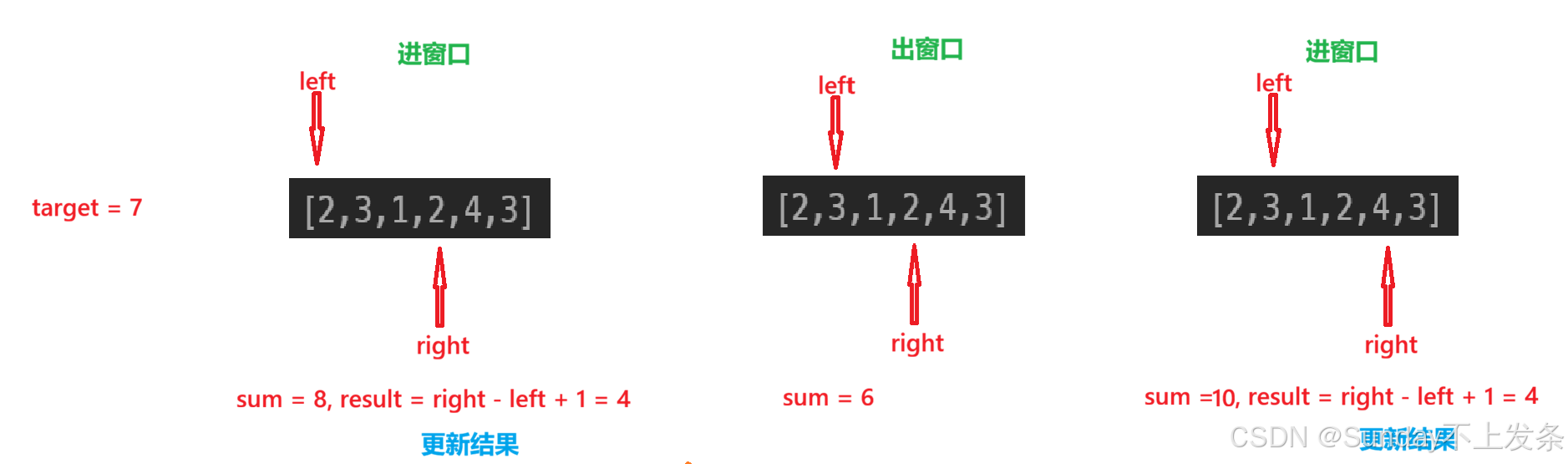
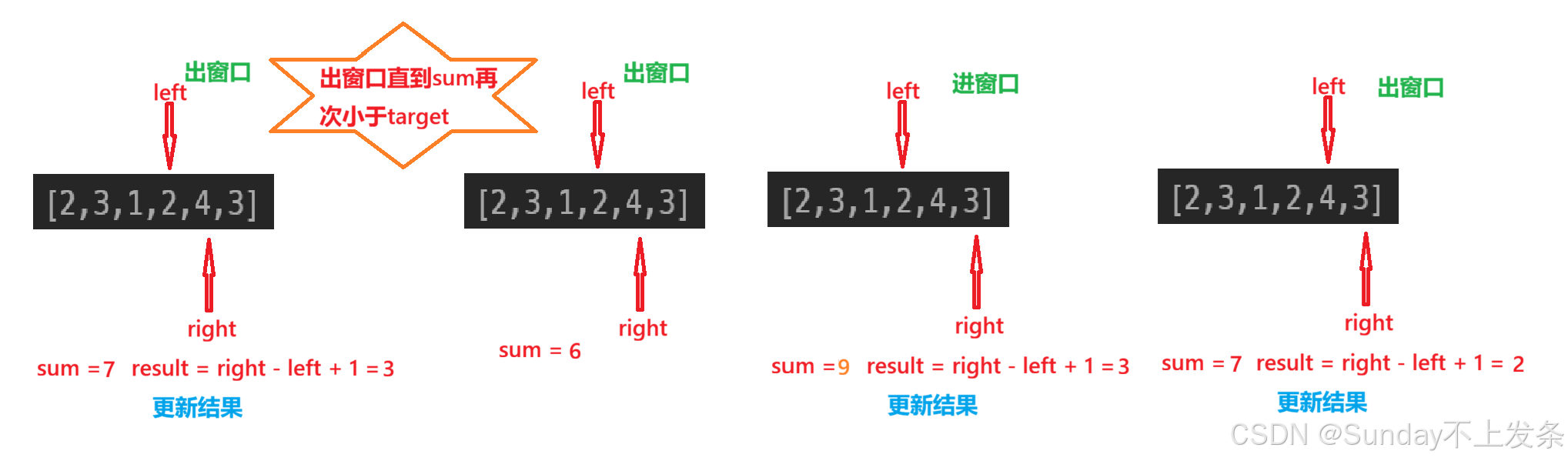
代码实现:
cpp
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums)
{
int left = 0, right = 0;
int len = INT_MAX, sum = 0;
while(right < nums.size())
{
sum += nums[right]; // 求和
while(sum >= target) // 保证窗口合法
{
len = min(len, right - left + 1); // 更新结果
sum -= nums[left++]; // 出窗口
}
right++; // 继续进窗口
}
return len == INT_MAX ? 0 : len;
}
};【无重复字符的最长子串】
题目描述:

实现核心及思路:
找不含重复字符的最长子串,我们需要一个标记来判断字符是否重复。ASCII总共有127个字符, 所以我们用一个大小为128的数组模拟哈希表,当一个字符进窗口就数组中与其映射位置上的元素++,只要值大于1就说明重复。
(1)定义left 和 right 指针,同时指向字符串开头;
(2)right 指针向右移动,进窗口,哈希表对应位置元素++,满足要求则更新结果;
(3)出现重复字符,left 指针向右移动,直到找到重复字符,然后继续让 right++;
++注意:++left向右移动过程中(出窗口),哈希表对应位置的元素要 --,因为这些字符已经不在窗口中了。
思路可视化:
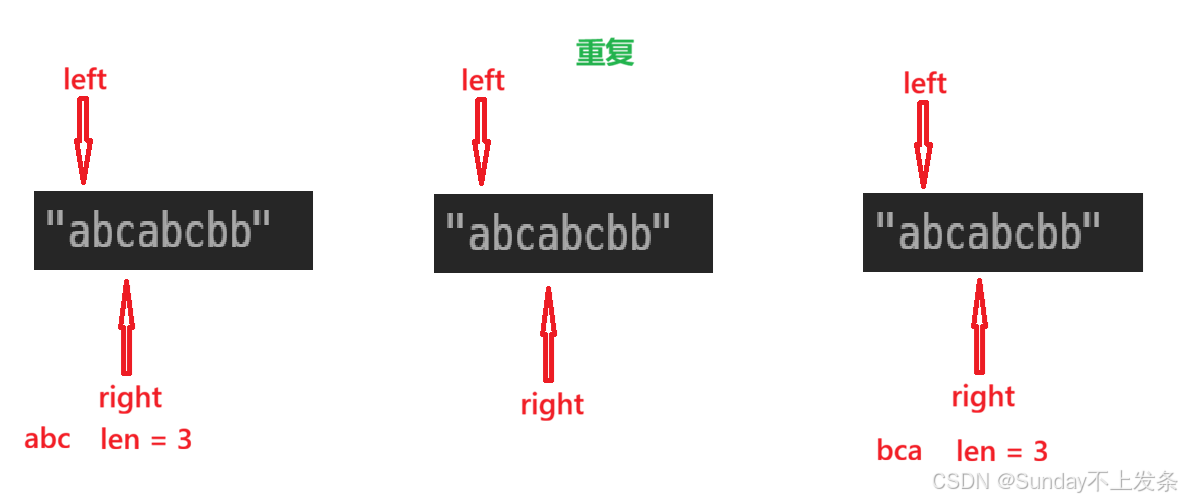
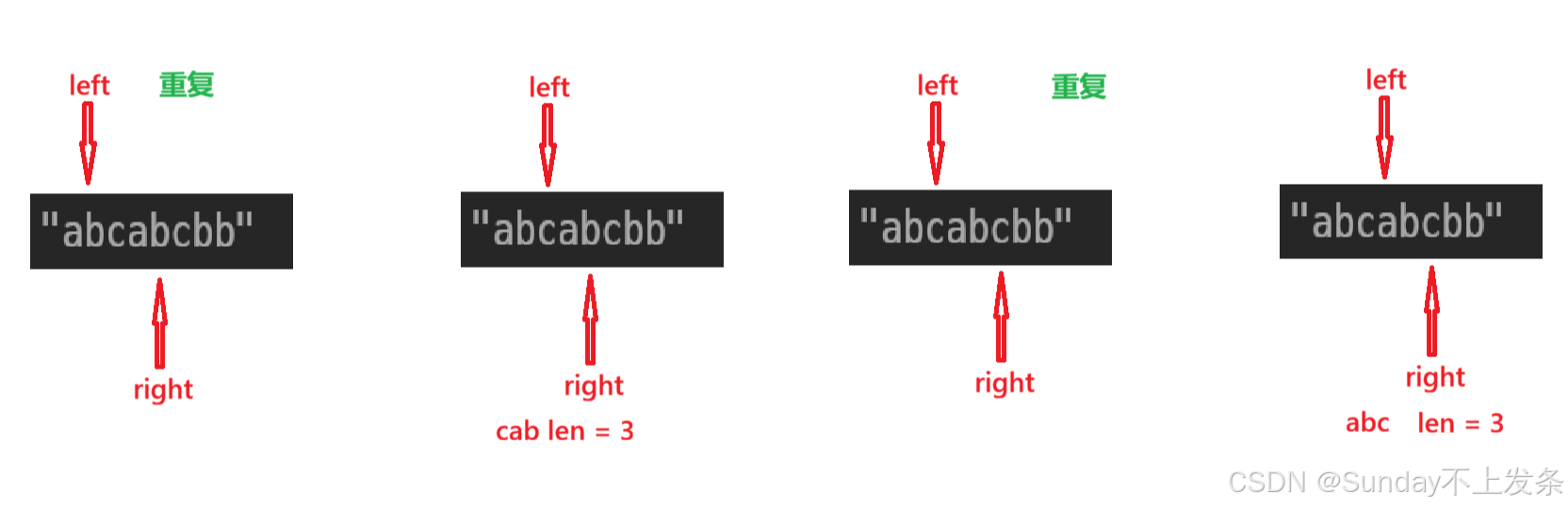
代码实现:
cpp
class Solution {
public:
int lengthOfLongestSubstring(string s)
{
int hash[128] = {0};
int left = 0, right = 0,size = s.size(), len = 0;
while(right < size)
{
hash[s[right]]++; // 标记
// 重复
if(hash[s[right]] > 1)
{
// 找重复字符,保证窗口合法(出窗口)
while(s[left] != s[right])
{
hash[s[left]]--; // 去掉标记
left++;
}
// 重复字符出窗口
hash[s[left]]--;
left++;
}
w = max(w, right - left + 1); // 更新结果
right++; // 继续进窗口
}
return w;
}
};【最大连续1的个数III】
题目描述:
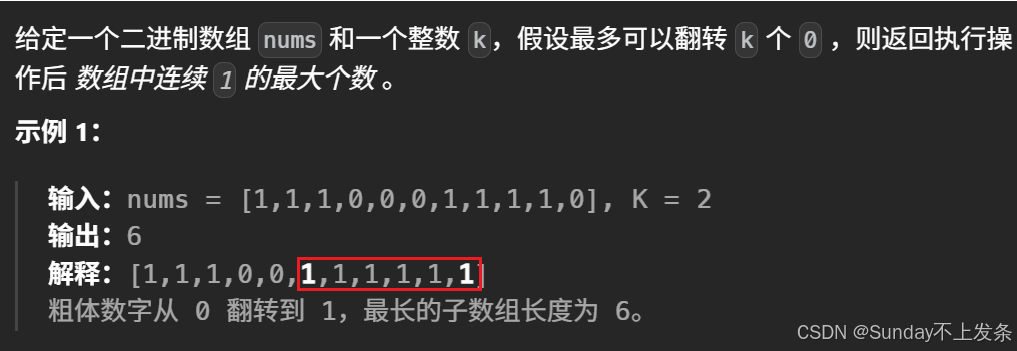
实现核心及思路:
相比上面找最长无重复的子串,此题就是在此基础上可以掺杂 k 个0,所以我们要控制窗口中0的个数,始终维护一个合法有效的窗口。
(1)定义left 和 right 指针,同时指向字符串开头;定义 cnt 记录0的个数(用来维护窗口合法);
(2)right 指针向右移动,进窗口:
- 如果nums[right] 等于1则right++,并更新结果;
- 如果等于0,则cnt++:如果cnt <= k,说明窗口合法,right++,并更新结果;如果cnt > k,则要多余的0出窗口,即让left++,直到找到0,让cnt--,使得cnt == k。
++优化:++ 最长子串其实在窗口中的0的个数等于k + 1时,所以,我们只需要在cnt > k时更新结果。但这样做,还需要在最后再更新一下结果,防止遍历完整个数组cnt 还是小于等于k。
代码实现:
cpp
class Solution {
public:
int longestOnes(vector<int>& nums, int k)
{
int left = 0, right = 0; // 左右指针,维护窗口
int size = nums.size();
int result = 0, cnt = 0; // 记录结果和当前遍历到的0的个数
while(right < size)
{
if(nums[right] == 0)
{
cnt++; // 0 个数更新
if(cnt > k) // 0个数不满足k
{
result = max(result, right - left); // 更新结果
// 左边的元素出窗口,直到0的个数重新满足要求
while(cnt > k)
{
if(nums[left] == 0)
{
cnt--; // 0个数--
}
left++;
}
}
}
right++;
}
result = max(result, right - left); // 再次更新结果
return result;
}
};【1658.将x减到0的最小操作数】
题目描述:


实现核心即思路:
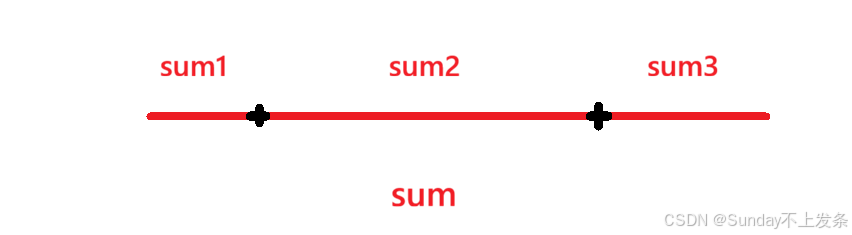
直接上手,其实非常麻烦,因为我们完全不知道该从左边找还是右边找,能够让x恰好被减到0。所以我们对这个问题进行转化:
假设从左边和右边找到了几个连续的元素,求和为x,则此时x可以被减到0。设数组所有元素之和为sum,又有sum1 + sum3 = x,则sum2 = sum - x。
我们只要在中间找到一个连续的和为sum - x的最长的子数组,就能找到最少的次数了。
又因为所有数组元素都大于0,则求和满足单调性,所以就能用滑动窗口来解决了。
(1)预处理:求数组所有元素之和sum,目标值 val = sum - x;
(2)left 和 right 指针维护窗口,add记录窗口中元素之和,len记录中间子数组长度;
***细节:***将len初始化为 -1,如果没找到满足的子数组,不会更新len的值,返回-1。
(3)right++,向右移动进窗口,add += nums[right]:
- 当 add < val,right继续向右移动,进窗口;
- 当 add > val,由于单调性,left++,出窗口,add -= nums[left],循环,直到add <= val,即当窗口合法;
- 当 add == val,更新len,记录len的最大值。
***结束条件:***right 越界。
(4)返回结果,nums.size() - len。
代码实现:
cpp
class Solution {
public:
int minOperations(vector<int>& nums, int x)
{
// 预处理:求和
int sum = 0;
for(auto e:nums) sum += e;
int left = 0, right = 0; // 左右窗口
// 转化为中间找一个和为sum - x的子数组
int val = sum - x;
// 处理特殊情况
if(val < 0) return -1;
int add = 0, len = -1; // 记录子数组和与长度
while(right < nums.size())
{
add += nums[right++]; // 进窗口
while(add > val)
{
add -= nums[left++]; // 出窗口
}
if(add == val)
{
len = max(len, right - left); // 更新结果
}
}
if(len == -1) return -1;
else return nums.size() - len;
}
};