多目标鲸鱼优化算法(Multi‑Objective Whale Optimization Algorithm, MOWOA )是基于单目标鲸鱼优化算法(WOA)扩展而来的多目标元启发式算法,核心是将座头鲸气泡网捕食行为与帕累托最优、非支配排序、外部存档等多目标优化机制融合,在平衡全局探索与局部开发的同时,高效逼近多目标优化问题(MOP)的帕累托最优前沿(PF)。其兼具WOA参数少、收敛快的优势,又适配多目标冲突场景,是工程与科学多目标优化的主流算法之一。
参考文献:
1\]I. R. Kumawat, S. J. Nanda and R. K. Maddila, "**Multi-objective whale optimization**," TENCON 2017 - 2017 IEEE Region 10 Conference, Penang, Malaysia, 2017, pp. 2747-2752, doi: 10.1109/TENCON.2017.8228329.
### 一、算法起源与生物学基础
#### 1.1 单目标WOA核心原理
WOA由Mirjalili与Lewis于2016年提出,模拟座头鲸**气泡网捕食**的三类核心行为:
1. **包围猎物**:鲸鱼向当前最优解(猎物)收缩移动,通过收敛因子控制搜索范围。
2. **气泡网攻击**:以螺旋路径逼近猎物,同时收缩包围圈,实现局部精细搜索。
3. **随机搜索**:当探索需求大于开发时,随机选择个体引导搜索,避免局部最优。
#### 1.2 MOWOA的扩展动机
单目标WOA仅优化单一目标,无法处理多目标冲突场景。MOWOA通过引入**帕累托支配、非支配排序、外部存档、拥挤距离**等机制,将单目标搜索逻辑升级为多目标协同优化,目标是获得一组均匀分布、收敛性强的帕累托最优解集。
### 二、MOP数学定义与核心概念
#### 2.1 多目标优化问题(MOP)
minF(x)=(f1(x),f2(x),...,fM(x))Ts.t.x∈Ω⊆RD \\begin{align\*} \\min \\quad \& \\mathbf{F}(\\mathbf{x}) = \\left(f_1(\\mathbf{x}), f_2(\\mathbf{x}), \\dots, f_M(\\mathbf{x})\\right)\^T \\\\ \\text{s.t.} \\quad \& \\mathbf{x} \\in \\Omega \\subseteq \\mathbb{R}\^D \\end{align\*} mins.t.F(x)=(f1(x),f2(x),...,fM(x))Tx∈Ω⊆RD
* x\\mathbf{x}x:DDD维决策向量;Ω\\OmegaΩ:决策空间;F(x)\\mathbf{F}(\\mathbf{x})F(x):MMM维目标向量(M≥2M\\ge2M≥2),目标间通常冲突。
* **帕累托支配** :x1≺x2 ⟺ ∀i,fi(x1)≤fi(x2)∧∃j,fj(x1)\1\|\\mathbf{A}\| \> 1∣A∣\>1)**
X(t+1)=Xr(t)−A⋅D \\mathbf{X}(t+1) = \\mathbf{X}_r(t) - \\mathbf{A} \\cdot \\mathbf{D} X(t+1)=Xr(t)−A⋅D
D=∣C⋅Xr(t)−X(t)∣ \\mathbf{D} = \|\\mathbf{C} \\cdot \\mathbf{X}_r(t) - \\mathbf{X}(t)\| D=∣C⋅Xr(t)−X(t)∣
Xr(t)\\mathbf{X}_r(t)Xr(t):种群中随机选取的个体,增强全局探索。
3. **气泡网螺旋攻击(p\>0.5p \> 0.5p\>0.5)**
X(t+1)=D′⋅ebl⋅cos(2πl)+X∗(t) \\mathbf{X}(t+1) = \\mathbf{D}' \\cdot e\^{bl} \\cdot \\cos(2\\pi l) + \\mathbf{X}\^\*(t) X(t+1)=D′⋅ebl⋅cos(2πl)+X∗(t)
D′=∣X∗(t)−X(t)∣ \\mathbf{D}' = \|\\mathbf{X}\^\*(t) - \\mathbf{X}(t)\| D′=∣X∗(t)−X(t)∣
D′\\mathbf{D}'D′:当前解与领导者的距离;螺旋路径实现局部精细开发。
### 四、标准MOWOA算法流程
#### 步骤1:初始化
1. 参数设置:N,Tmax,D,M,bN, T_{\\text{max}}, D, M, bN,Tmax,D,M,b,决策变量上下界lb,ub\\text{lb}, \\text{ub}lb,ub。
2. 种群初始化:随机生成NNN个初始解{Xi}i=1N\\{\\mathbf{X}_i\\}_{i=1}\^N{Xi}i=1N,计算目标向量F(Xi)\\mathbf{F}(\\mathbf{X}_i)F(Xi)。
3. 外部存档初始化:筛选初始种群中的非支配解,存入外部存档Archive\\text{Archive}Archive。
#### 步骤2:迭代进化(循环至TmaxT_{\\text{max}}Tmax)
1. **参数更新** :计算a,A,C,l,pa, \\mathbf{A}, \\mathbf{C}, l, pa,A,C,l,p。
2. **领导者选择** :从Archive\\text{Archive}Archive中随机选取一个领导者X∗\\mathbf{X}\^\*X∗。
3. **位置更新** :对每个个体Xi\\mathbf{X}_iXi,按p,∣A∣p, \|\\mathbf{A}\|p,∣A∣选择包围/随机/螺旋策略更新位置,得到新解Xi′\\mathbf{X}_i'Xi′,计算F(Xi′)\\mathbf{F}(\\mathbf{X}_i')F(Xi′)。
4. **非支配排序与存档更新** :
* 合并原种群与新解,执行非支配排序,划分层级。
* 按层级+拥挤距离筛选非支配解,更新Archive\\text{Archive}Archive(剔除被支配解,保留优质解)。
5. **种群更新** :从Archive\\text{Archive}Archive与新解中选取NNN个解,构成新一代种群。
#### 步骤3:终止与输出
达到最大迭代次数后,输出外部存档Archive\\text{Archive}Archive,作为MOP的帕累托最优近似解集。
### 五、关键技术模块解析
#### 5.1 外部存档管理(核心)
* **存档维护** :每次迭代后,合并新旧解,执行非支配排序,仅保留非支配解;若存档溢出,按**拥挤距离**剔除密集区域解,维持多样性。
* **领导者选择策略** :
* 随机选择:简单高效,适配多数场景。
* 拥挤距离优先:选择拥挤距离大的解,提升解集均匀性。
* 分解引导:结合MOEA/D的权重向量,按偏好选择领导者,适配特定目标方向。
#### 5.2 非支配排序与拥挤距离
* **非支配排序** :将解划分为F1,F2,...F_1, F_2, \\dotsF1,F2,...层级,F1F_1F1为第一级非支配解(最优),后续层级依次被前一层级支配。
* **拥挤距离**:计算每个解在目标空间中相邻解的目标差值之和,值越大表示解越稀疏,多样性越好;用于存档筛选与种群选择。
#### 5.3 探索‑开发平衡机制
* 收敛因子aaa:迭代前期aaa大,A\\mathbf{A}A易大于1,侧重随机搜索(探索);后期aaa小,A\\mathbf{A}A易小于1,侧重包围与螺旋攻击(开发)。
* 概率ppp:控制气泡网攻击与包围的比例,默认p=0.5p=0.5p=0.5,可自适应调整以适配问题特性。
### 六、MOWOA应用
MOWOA用于求解46个多目标测试函数(ZDT1、ZDT2、ZDT3、ZDT4、ZDT6、DTLZ1-DTLZ7、WFG1-WFG10、UF1-UF10、CF1-CF10、Kursawe、Poloni、Viennet2、Viennet3)以及1个工程应用(盘式制动器设计),并采用IGD、GD、HV、SP进行评价。
#### 6.1部分代码
```bash
close all;
clear ;
clc;
%%
% TestProblem测试问题说明:
%一共46个多目标测试函数,详情如下:
%1-5:ZDT1、ZDT2、ZDT3、ZDT4、ZDT6
%6-12:DZDT1-DZDT7
%13-22:wfg1-wfg10
%23-32:uf1-uf10
%33-42:cf1-cf10
%43-46:Kursawe、Poloni、Viennet2、Viennet3
%47 盘式制动器设计 温泽宇,谢珺,谢刚,续欣莹.基于新型拥挤度距离的多目标麻雀搜索算法[J].计算机工程与应用,2021,57(22):102-109.
%%
TestProblem=47;%1-47
MultiObj = GetFunInfo(TestProblem);
MultiObjFnc=MultiObj.name;%问题名
% Parameters
params.Np = 100; % Population size
params.Nr = 100; % Repository size
params.maxgen =100; % Maximum number of generations
[x,f] = MOwoa(params,MultiObj);
```
#### 6.2部分结果
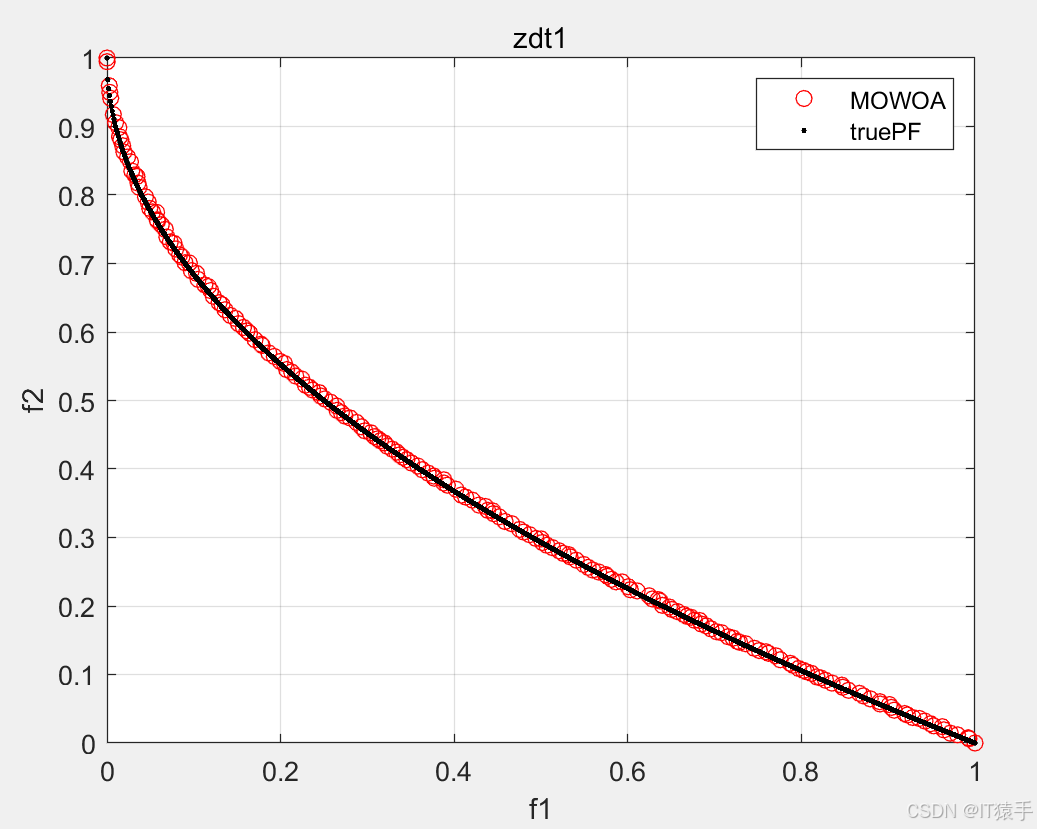
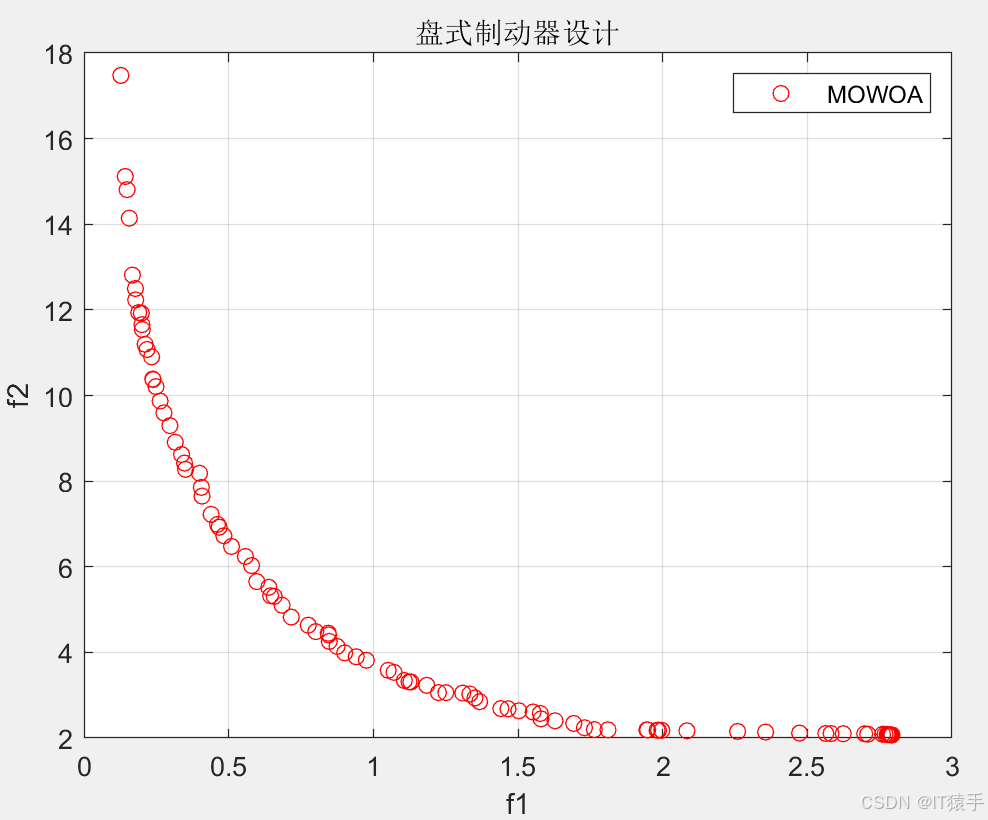
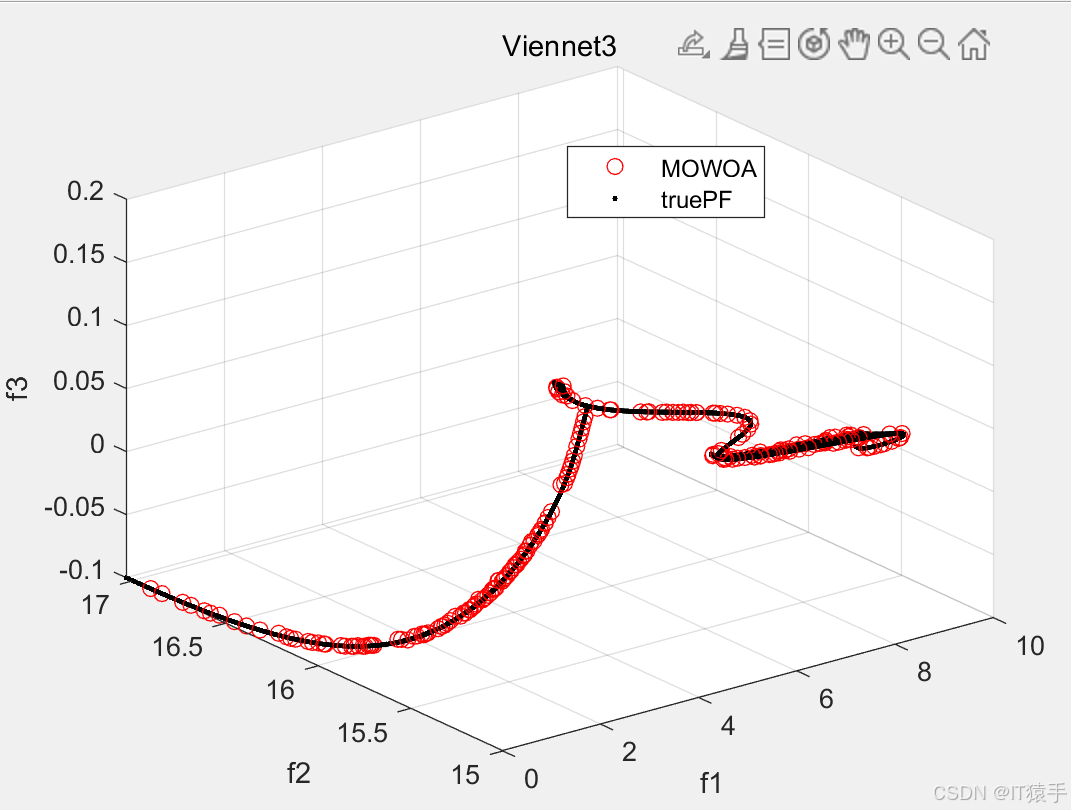
### 八、完整MATLAB代码见下方名片