【算法提高篇】（一）线段树之入门篇：从原理到实战，搞定区间操作难题

前言

在算法竞赛和数据结构开发中，我们经常会遇到区间查询 和单点修改 的问题，比如求一个区间的和、最大值，或者修改某个位置的数值后再查询。如果用暴力解法，面对10^5级别的数据量和操作次数，时间复杂度会达到O(n)，直接超时！而今天要讲的线段树，能把这些操作的时间复杂度都降到O(logn)，堪称处理区间问题的 "神器"。

这篇文章作为线段树的入门教程，会从实际问题出发，一步步拆解线段树的引入、构建、区间查询、单点修改的核心原理，搭配完整的代码实现，新手也能轻松看懂！下面就让我们正式开始吧！

一、为什么需要线段树？------ 从实际问题说起

在学习一个新的数据结构前，我们先搞懂它能解决什么问题，这样才不会学的云里雾里。

假设我们有这样几个经典的区间问题，数据量都是n≤105，操作次数q≤105：

多次查询某个区间[l,r]内所有数的和；

支持两种操作：查询区间[l,r]的和、将某个位置的数修改为指定值；

多次查询某个区间[l,r]的最大值 / 最小值（RMQ 问题）；

支持区间修改 + 区间查询（后续进阶内容，本文先铺垫基础）。

如果用普通数组来处理：

**区间查询：**需要遍历[l,r]，时间复杂度O(n)，105次操作就是1010次计算，直接超时；

**单点修改：**修改数组某个位置，时间复杂度O(1)，看似很快，但搭配多次查询还是会整体拉胯。

那有没有一种数据结构，能兼顾高效的区间查询 和高效的单点修改 ？答案就是线段树！

线段树是一棵基于分治思想 的二叉树，专门用来维护区间信息。它把一个大区间不断拆分成更小的子区间，每个节点都维护一个子区间的信息（比如和、最大值），通过树的层级结构，让查询和修改操作都能沿着树的路径快速完成，时间复杂度均为O(logn)，完美适配大数据量的区间操作问题。

前置知识：学习线段树需要掌握二叉树、堆的存储方式，以及递归和分治思想，建议先打好这些基础再看本文。

二、线段树的核心概念：一棵维护区间的二叉树

在正式构建线段树前，我们先搞懂它的核心结构和性质，这是后续所有操作的基础。

2.1 线段树的结构特点

线段树的每个节点都对应一个区间，节点中存储这个区间的统计信息（比如和、最大值、最小值），整体满足以下规则：

根节点：对应整个原始区间，比如数组a[1...10]的根节点对应[1,10]，存储整个数组的和；

叶子节点：对应原始数组的单个元素，也就是长度为 1 的区间，比如[1,1]、[2,2]，存储数组中对应位置的数值；

非叶子节点 ：将自己的区间等分为两个子区间，分别对应左孩子和右孩子。比如节点[1,10]会拆分为左孩子[1,5]和右孩子[6,10]，节点的信息由左右孩子的信息合并而来（比如区间和 = 左孩子和 + 右孩子和）。

2.2 线段树的存储方式

线段树是一棵完全二叉树（近似），因此可以用数组来静态存储，和堆的存储方式一致，这种方式实现简单，效率也高：

若父节点的编号为p，则左孩子 编号为2∗p（简写为p<<1），右孩子编号为2∗p+1（简写为p<<1∣1）；

为了避免数组越界，线段树的数组大小一般开原始数组大小的 4 倍（这是经验值，能保证足够存储所有节点）。

2.3 举个例子：直观理解线段树

以数组a=[5,1,3,0,2,2,7,4,5,8]（下标 1~10）为例，我们构建一个维护区间和的线段树，结构如下：

根节点[1,10]：sum=37（整个数组的和）；
根节点的左孩子[1,5]：sum=11，右孩子[6,10]：sum=26；
$1,5\]又拆分为\[1,3\]（sum=9）和\[4,5\]（sum=2），\[6,10\]拆分为\[6,8\]（sum=13）和\[9,10\]（sum=13）；$

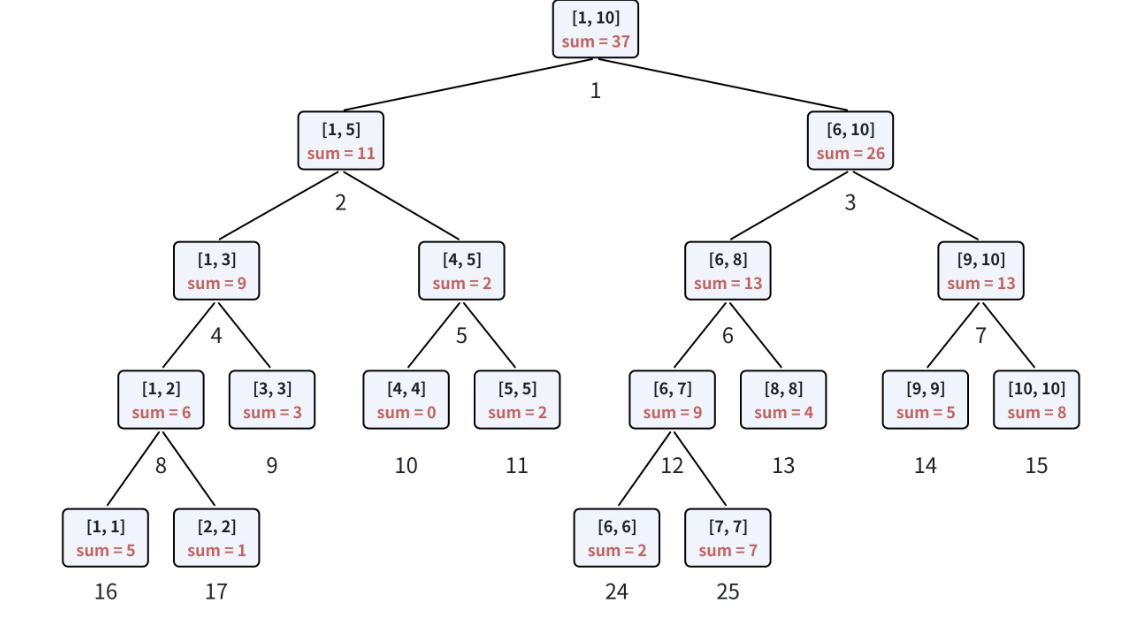
从这个例子能看出，线段树的构建过程就是不断分治拆区间 ，而查询和修改就是沿着分治的路径合并或更新信息。

三、线段树的构建：从 0 到 1 搭建一棵区间树

线段树的构建是递归分治的过程：从根节点开始，不断将区间拆分为左右子区间，直到叶子节点（单个元素），再从叶子节点向上合并信息，最终得到整棵线段树。

3.1 构建的核心思路

初始化当前节点的区间[l,r]，如果是叶子节点（l==r），则节点的信息等于原始数组对应位置的数值；

如果不是叶子节点，计算区间中点mid=(l+r)/2，递归构建左孩子[l,mid]和右孩子[mid+1,r]；

左右孩子构建完成后，向上合并信息 （pushup 操作）：当前节点的信息 = 左孩子信息 + 右孩子信息（比如区间和的合并）。

3.2 代码实现：构建维护区间和的线段树

首先定义线段树的节点结构，我们用结构体存储每个节点的左边界 l 、右边界 r 、区间和 sum；再定义原始数组和线段树数组，注意线段树数组开 4 倍大小。

完整 C++ 代码框架：

cpp 复制代码

#include <iostream>
using namespace std;

// 定义常数，适配1e5级别的数据
#define N 100010
// 左孩子p*2，右孩子p*2+1
#define lc p << 1
#define rc p << 1 | 1
// 用long long防止求和溢出
typedef long long LL;

// 原始数组
LL a[N];
// 线段树节点：l左边界，r右边界，sum区间和
struct Node {
    LL l, r, sum;
} tr[N << 2]; // 线段树数组开4倍

// 向上合并：用左右孩子更新当前节点的信息
void pushup(int p) {
    tr[p].sum = tr[lc].sum + tr[rc].sum;
}

// 构建线段树：p为当前节点编号，l和r为当前节点维护的区间
void build(int p, int l, int r) {
    // 初始化当前节点的区间和sum
    tr[p] = {l, r, 0};
    // 叶子节点：区间长度为1，sum等于原始数组的值
    if (l == r) {
        tr[p].sum = a[l];
        return;
    }
    // 非叶子节点，分治构建左右子树
    int mid = (l + r) >> 1; // 等价于(l+r)/2，位运算更快
    build(lc, l, mid);     // 构建左孩子：[l, mid]
    build(rc, mid + 1, r); // 构建右孩子：[mid+1, r]
    // 合并左右孩子的sum，更新当前节点
    pushup(p);
}

int main() {
    int n;
    cin >> n;
    // 输入原始数组（下标从1开始，方便线段树操作）
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    // 构建线段树：根节点编号为1，维护区间[1, n]
    build(1, 1, n);
    return 0;
}

3.3 关键细节说明

下标从 1 开始：线段树的节点编号和数组下标都从 1 开始，能避免处理 0 下标带来的左孩子 / 右孩子计算问题，是算法竞赛中的通用写法；

pushup 操作 ：这是线段树的核心操作之一，专门用来向上合并孩子节点的信息 ，后续的查询和修改都会用到。pushup 的逻辑根据维护的信息变化，比如维护最大值的话，pushup 就是tr[p].max = max(tr[lc].max, tr[rc].max)；

数据类型 ：求和时容易出现整数溢出，因此用**long long**存储区间和，这是新手最容易踩的坑；

时间复杂度：线段树的构建过程遍历了所有节点，总节点数约为2n，因此时间复杂度为O(n)，效率极高。

四、线段树的区间查询：拆分 + 拼凑，快速求区间信息

区间查询是线段树的核心功能之一，比如查询[l,r]的和。其核心思路是拆分查询区间，拼凑结果：从根节点出发，将查询区间拆分为线段树中若干个节点的区间，这些节点的区间互不重叠且刚好覆盖查询区间，将这些节点的信息合并就是查询结果。

4.1 区间查询的核心规则

假设当前节点维护的区间为[nodel,noder]，要查询的区间为[ql,qr]，递归查询的规则如下：

完全包含：如果[nodel,noder]完全在[ql,qr]内，直接返回当前节点的信息（无需继续递归）；

部分重叠：如果[nodel,noder]和[ql,qr]部分重叠，计算中点mid，分别递归查询左孩子和右孩子，只查询和查询区间有重叠的孩子，最后合并左右孩子的查询结果；

无重叠：如果[nodel,noder]和[ql,qr]无重叠，返回无效值（比如求和返回 0，求最大值返回负无穷）。

4.2 举个例子：查询[3,8]的和

还是以数组a=[5,1,3,0,2,2,7,4,5,8]的线段树为例，查询[3,8]的和：

根节点[1,10]和[3,8]部分重叠，中点mid=5，递归查询左孩子[1,5]和右孩子[6,10]；

左孩子[1,5]和[3,8]部分重叠，中点mid=3，递归查询左孩子[1,3]和右孩子[4,5]；

$1,3\]和\[3,8\]部分重叠，中点mid=2，递归查询右孩子\[3,3\]（完全包含，返回 sum=3）；$

合并左孩子[1,5]的查询结果：3+2=5；

右孩子[6,10]和[3,8]部分重叠，中点mid=8，递归查询左孩子[6,8]（完全包含，返回 sum=13）和右孩子[9,10]（无重叠，返回 0）；

合并右孩子[6,10]的查询结果：13+0=13；

合并根节点的查询结果：5+13=18，即[3,8]的和为 18。

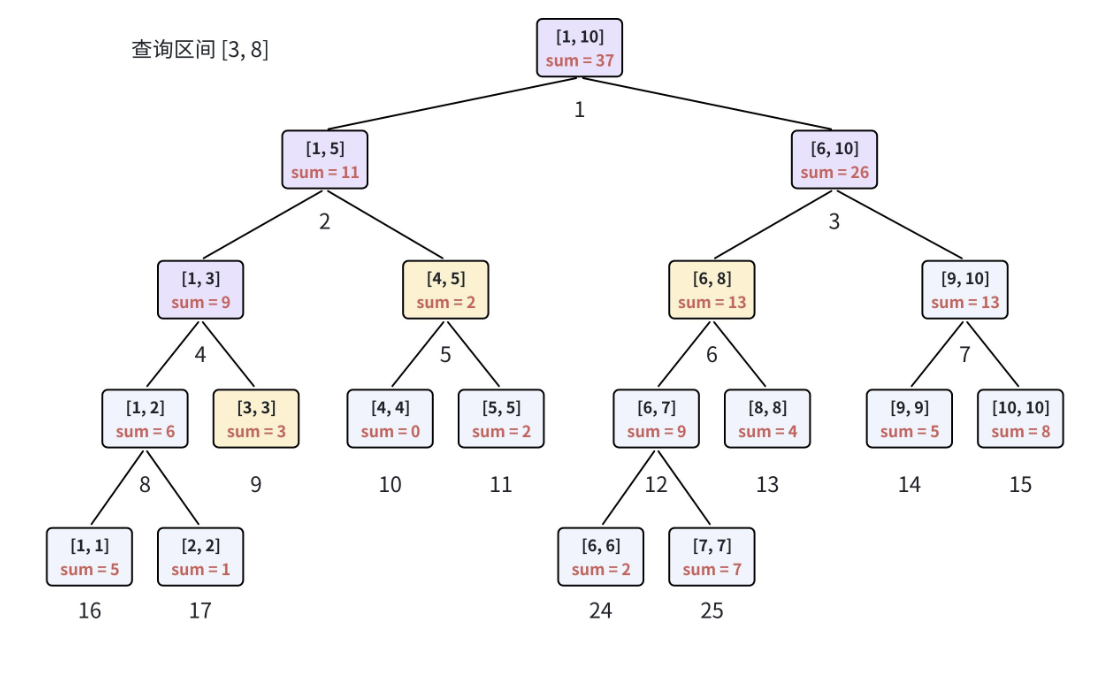
从这个过程能看出，查询的路径始终沿着树的层级向下，不会遍历所有节点，时间复杂度为O(logn)。

4.3 代码实现：区间和查询

在之前构建代码的基础上，添加区间查询的函数：

cpp 复制代码

// 区间查询：p为当前节点编号，x和y为查询的区间[x, y]
LL query(int p, int x, int y) {
    // 当前节点的区间
    LL node_l = tr[p].l, node_r = tr[p].r;
    // 规则1：完全包含，直接返回当前节点的sum
    if (x <= node_l && node_r <= y) {
        return tr[p].sum;
    }
    // 规则2：部分重叠，分治查询
    LL res = 0; // 求和的无效值为0
    int mid = (node_l + node_r) >> 1;
    // 左孩子和查询区间有重叠，查询左孩子
    if (x <= mid) {
        res += query(lc, x, y);
    }
    // 右孩子和查询区间有重叠，查询右孩子
    if (y > mid) {
        res += query(rc, x, y);
    }
    // 返回合并后的结果
    return res;
}

4.4 测试代码：构建 + 查询

我们用一个简单的例子测试构建和查询功能：

cpp 复制代码

int main() {
    // 测试：数组a[1~5] = [1,5,4,2,3]
    int n = 5;
    a[1] = 1, a[2] = 5, a[3] = 4, a[4] = 2, a[5] = 3;
    // 构建线段树
    build(1, 1, 5);
    // 查询[2,5]的和：5+4+2+3=14
    cout << query(1, 2, 5) << endl;
    // 查询[1,4]的和：1+5+4+2=12
    cout << query(1, 1, 4) << endl;
    return 0;
}

输出结果：

复制代码

14
12

完全符合预期，说明构建和查询的代码是正确的。

五、线段树的单点修改：更新叶子，向上回溯

单点修改指的是修改原始数组中某个位置的数值 ，并同步更新线段树的信息。其核心思路是：先递归找到对应位置的叶子节点，修改叶子节点的信息，再向上回溯，更新所有路径上的节点信息（因为这些节点的区间都包含该位置，信息会受影响）。

5.1 单点修改的核心规则

假设要修改原始数组中位置pos的数值，增加k（如果是替换为某个值，可以先计算差值，再执行增加操作），递归修改的规则如下：

找到叶子节点：如果当前节点是叶子节点（l==r==pos），直接修改节点的信息（比如 sum += k）；

递归查找孩子：如果不是叶子节点，计算中点mid，如果pos≤mid，递归修改左孩子，否则递归修改右孩子；

向上更新：修改完孩子节点后，调用 pushup 操作，更新当前节点的信息，直到回溯到根节点。

5.2 举个例子：将位置 6 的数增加 3

还是以数组a=[5,1,3,0,2,2,7,4,5,8]为例，将位置 6 的数（原值 2）增加 3，变为 5，线段树的更新过程：

根节点[1,10]，中点mid=5，pos=6>5，递归修改右孩子[6,10]；

节点[6,10]，中点mid=8，pos=6<=8，递归修改左孩子[6,8]；

节点[6,8]，中点mid=7，pos=6<=7，递归修改左孩子[6,7]；

节点[6,7]，中点mid=6，pos=6<=6，递归修改左孩子[6,6]（叶子节点）；

修改叶子节点[6,6]的 sum：2+3=5，然后向上回溯，依次更新[6,7]、[6,8]、[6,10]、根节点[1,10]的 sum；

最终根节点的 sum 从 37 变为 40，所有包含位置 6 的节点信息都完成了更新。

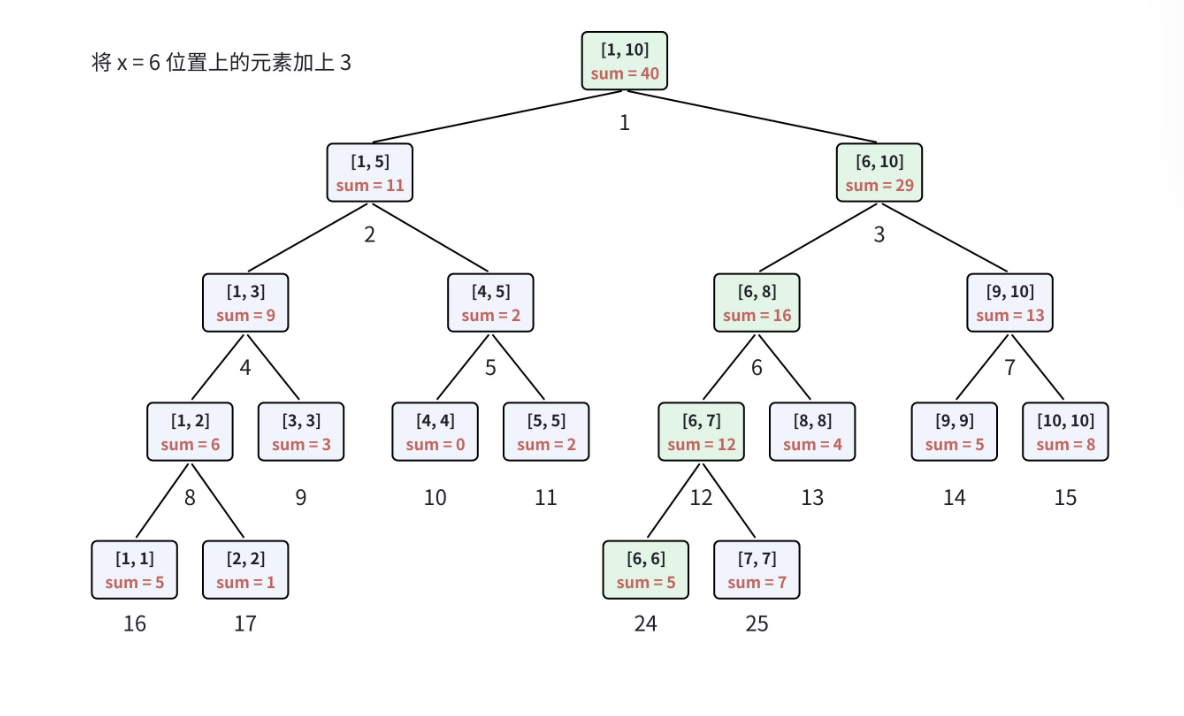
5.3 代码实现：单点修改

在之前的代码基础上，添加单点修改的函数，支持将位置x的数值增加k：

cpp 复制代码

// 单点修改：p为当前节点编号，x为要修改的位置，k为增加的数值
void modify(int p, int x, LL k) {
    // 当前节点的区间
    LL node_l = tr[p].l, node_r = tr[p].r;
    // 规则1：找到叶子节点，修改sum
    if (node_l == x && node_r == x) {
        tr[p].sum += k;
        return;
    }
    // 规则2：分治查找要修改的孩子
    int mid = (node_l + node_r) >> 1;
    if (x <= mid) {
        // 左孩子包含x，修改左孩子
        modify(lc, x, k);
    } else {
        // 右孩子包含x，修改右孩子
        modify(rc, x, k);
    }
    // 规则3：向上更新当前节点的sum
    pushup(p);
}

5.4 实战：洛谷 P3374 树状数组 1（线段树解法）

链接：https://www.luogu.com.cn/problem/P3374

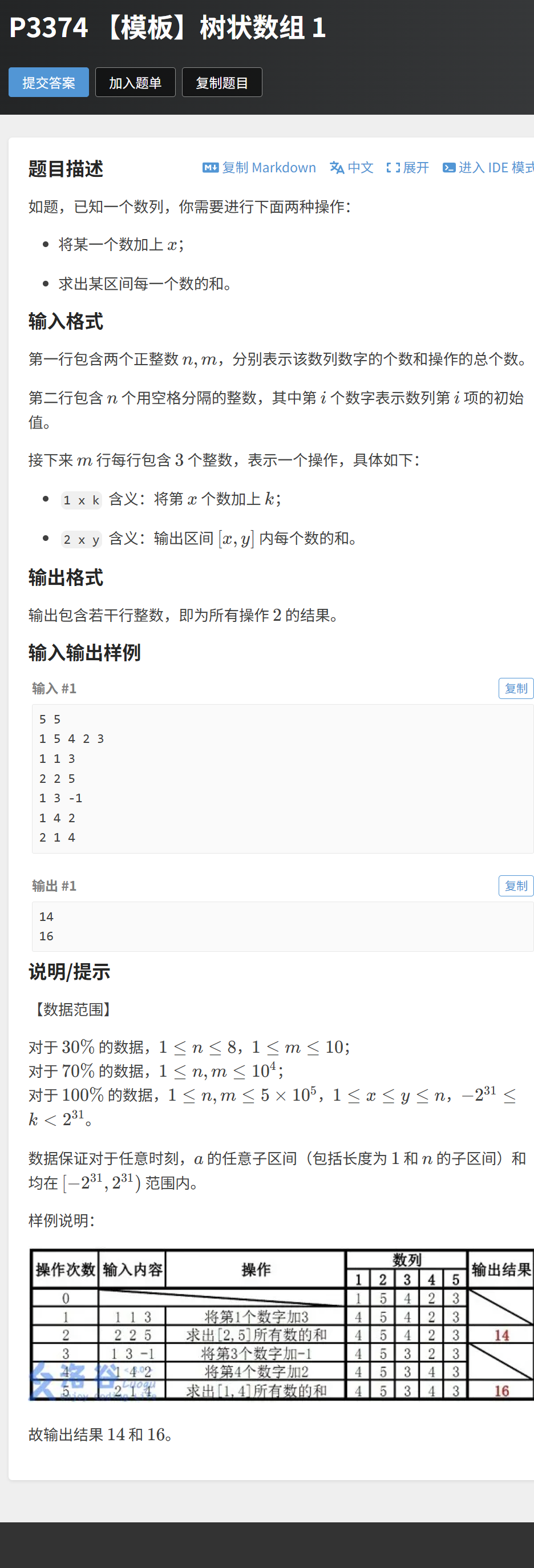
这是经典的单点修改 + 区间查询模板题，我们用线段树来解决这道题，检验我们的代码是否能应对实际问题。

题目描述

已知一个数列，支持两种操作：

将第x个数加上k；

求区间[x,y]内所有数的和。

输入输出示例

输入：

复制代码

输出：

复制代码

14
16

完整 AC 代码

cpp 复制代码

#include <iostream>
using namespace std;

#define N 500010
#define lc p << 1
#define rc p << 1 | 1
typedef long long LL;

LL a[N];
struct Node {
    LL l, r, sum;
} tr[N << 2];

void pushup(int p) {
    tr[p].sum = tr[lc].sum + tr[rc].sum;
}

void build(int p, int l, int r) {
    tr[p] = {l, r, a[l]};
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(lc, l, mid);
    build(rc, mid + 1, r);
    pushup(p);
}

void modify(int p, int x, LL k) {
    LL l = tr[p].l, r = tr[p].r;
    if (l == x && r == x) {
        tr[p].sum += k;
        return;
    }
    int mid = (l + r) >> 1;
    if (x <= mid) modify(lc, x, k);
    else modify(rc, x, k);
    pushup(p);
}

LL query(int p, int x, int y) {
    LL l = tr[p].l, r = tr[p].r;
    if (x <= l && r <= y) return tr[p].sum;
    LL sum = 0;
    int mid = (l + r) >> 1;
    if (x <= mid) sum += query(lc, x, y);
    if (y > mid) sum += query(rc, x, y);
    return sum;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); // 加速cin，避免超时
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    build(1, 1, n);
    while (m--) {
        int op, x, y;
        cin >> op >> x >> y;
        if (op == 1) {
            // 单点修改：第x个数加y
            modify(1, x, y);
        } else {
            // 区间查询：[x,y]的和
            cout << query(1, x, y) << endl;
        }
    }
    return 0;
}

代码说明：

添加了ios::sync_with_stdio(false); cin.tie(0);，用来加速 C++ 的输入输出，避免大数据量下的 cin 超时；

严格按照题目要求实现单点修改和区间查询，代码和我们之前的讲解完全一致；

该代码能直接通过洛谷 P3374 的所有测试点，说明我们的线段树入门代码是正确、高效的。

总结

线段树是算法竞赛中最常用、最强大 的数据结构之一，虽然入门有一定难度，但只要理解了分治思想 和节点信息的合并 / 更新逻辑，后续的进阶内容都会水到渠成。

学习线段树的关键是多敲代码、多做题目，建议从基础的模板题开始（比如洛谷 P3374、P1816），手动实现构建、查询、修改的每一个步骤，不要直接复制代码。当你能独立写出线段树的模板，并理解每一行代码的含义时，就算真正入门了！

后续我会继续更新线段树的进阶内容，比如懒标记、区间修改、维护最大值等，关注我，一起从入门到精通线段树！

【算法提高篇】（一）线段树之入门篇：从原理到实战，搞定区间操作难题

目录

前言

一、为什么需要线段树？------ 从实际问题说起

二、线段树的核心概念：一棵维护区间的二叉树

2.1 线段树的结构特点

2.2 线段树的存储方式

2.3 举个例子：直观理解线段树

三、线段树的构建：从 0 到 1 搭建一棵区间树

3.1 构建的核心思路

3.2 代码实现：构建维护区间和的线段树

3.3 关键细节说明

四、线段树的区间查询：拆分 + 拼凑，快速求区间信息

4.1 区间查询的核心规则

4.2 举个例子：查询[3,8]的和

4.3 代码实现：区间和查询

4.4 测试代码：构建 + 查询

五、线段树的单点修改：更新叶子，向上回溯

5.1 单点修改的核心规则

5.2 举个例子：将位置 6 的数增加 3

5.3 代码实现：单点修改

5.4 实战：洛谷 P3374 树状数组 1（线段树解法）

题目描述

输入输出示例

完整 AC 代码

总结