[算法竞赛]二、链表

_Twink1e2026-02-14 11:09

链表是一种动态数据结构，可以增删节点来插入和删除数据，但寻找与读取数据性能较低

单向链表

每个链表的节点由其内容和指针所决定

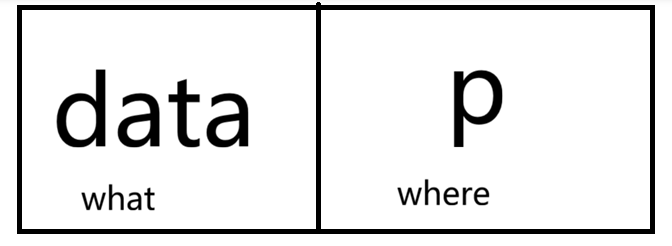
如图，这是一个节点，这个节点中data指的是这个节点存放的数据 这个节点中p表示这个节点的指针，即节点在哪个位置

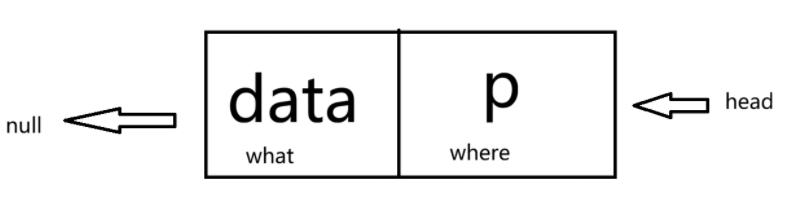
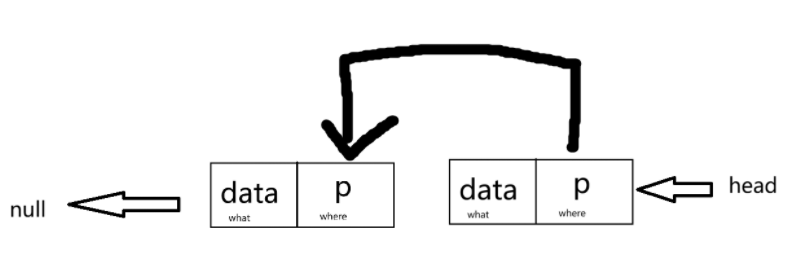
单向链表既然是单向，就肯定是有头有尾的，我们通常用head指针来指向第一个节点以此来找到头结点，将最后一个节点指向null表示该节点为最后一个节点（因为没有下一个节点了）

复制代码 
struct listnode {
    int data;
    struct listnode *next;
};
struct listnode *head;

遍历节点

注意这里只是遍历节点的操作

我们需要设置一个工作结点，让这个结点不断等于下一个结点直到我们需要用的节点即可

复制代码 
    listnode *temp1 = head; // 从链表头开始遍历
    for (int i = 0; i < num ; i++) {
        temp1 = temp1->next;
    }

插入节点

接下来我们想在链表中插入节点

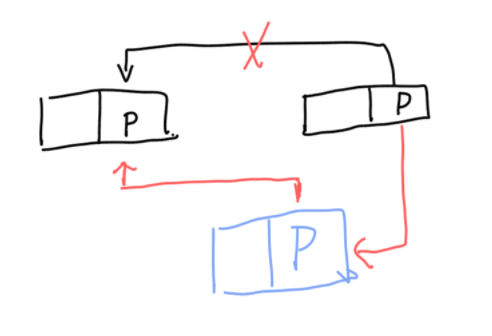
过程是这样的：首先我们创建一个新节点，并初始化这个新节点，如果新节点的位置是头节点，那么新节点的下一个节点就是头结点，如果不是，那么先找到要插入节点的位置。

然后遍历一个节点到我们需要的位置 让新节点的下一个节点变成这个节点的下一个节点，让这个节点的下一个节点变成新节点即可

复制代码 
void insert(int data, int num) {
    listnode *temp = new listnode();//初始化操作
    temp->data = data;
    temp->next = NULL;

    //  找到第num-1个节点（要插入位置的前驱节点）
    listnode *temp1 = head; // 从链表头开始遍历
    // 循环num-1次，找到前驱节点
    for (int i = 0; i < num - 1 ; i++) {
        temp1 = temp1->next;
    }
    //  插入新节点
    temp->next = temp1->next;
    temp1->next = temp;
}

删除节点

删除节点就是插入节点的反操作

复制代码 
void del(int num) {
    listnode *del_node = NULL; // 待删除的节点
    listnode *prev = head;
    for (int i = 0; i < num - 1; i++) {
        prev = prev->next;
    }
    del_node = prev->next;          // 记录待删除节点
    prev->next = del_node->next;    // 前驱节点跳过待删除节点
}

循环链表

就是把尾指针的指向null换成指向头就行

链表反转

复制代码 
node* reverselist(node *head) {
    node *pre=NULL;
    node *next=NULL;
    while (head!=NULL) {
        next=head->next;
        head->next=pre;
        pre=head;
        head=next;
    }
    return pre;
}

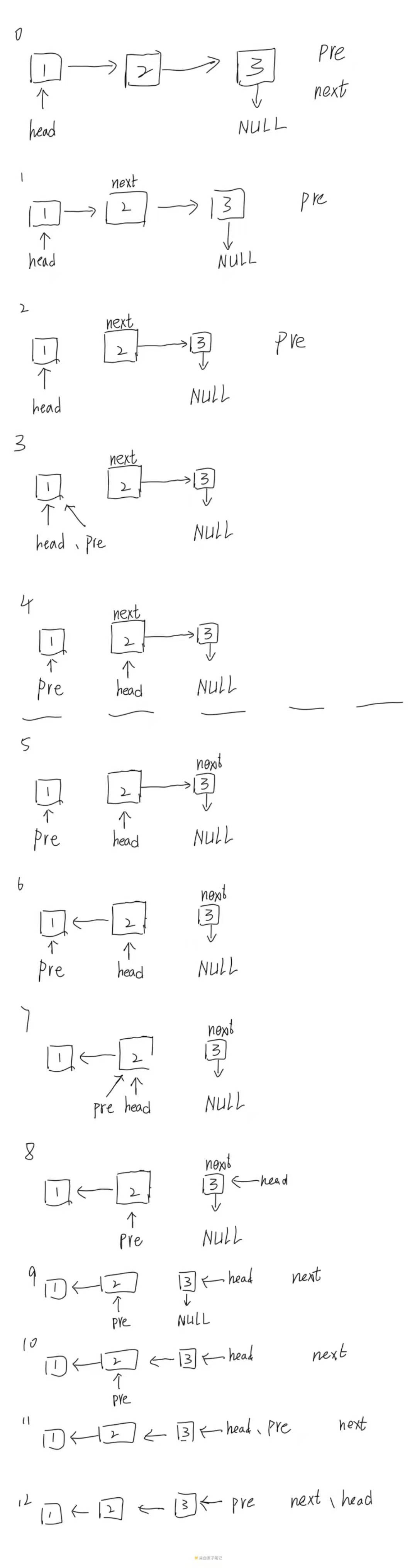
给这段代码画了一个过程图，把链表反转的操作理解为指针swap即可

两个有序链表的合并

复制代码 
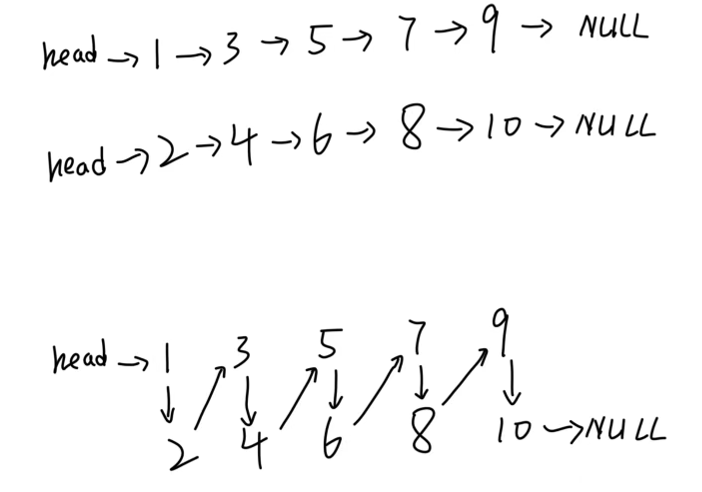
node* merge(node *head1,node *head2) {
    if (head1==NULL||head2==NULL) return head1==NULL?head2:head1;
    node *head=head1->data<head2->data?head1:head2;
    node *cur1=head->next;
    node *cur2=head==head1?head1:head2;
    node *pre=head;
    while (cur1!=NULL&&cur2!=NULL) {
        if (cur1->data<cur2->data) {
            pre->next=cur1;
            cur1=cur1->next;
        }
        else {
            pre->next=cur2;
            cur2=cur2->next;
        }
        pre=pre->next;
    }
    pre->next=cur1!=NULL?cur1:cur2;
    return head;
}

两个链表相加（高精度加法用链表解决）

复制代码 
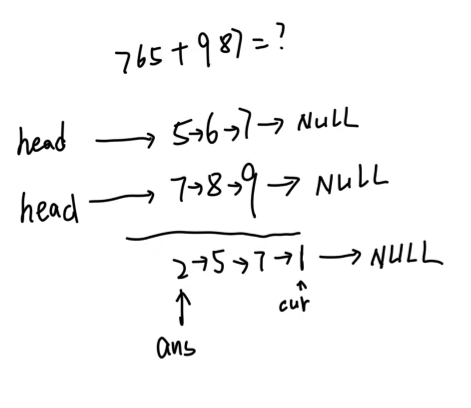
node* add(node* head1,node* head2) {
    node *ans=NULL;
    node *cur=NULL;
    int carry=0;
    for (int sum,val;
        head1!=NULL||head2!=NULL||carry!=0;
        head1=head1==NULL?NULL:head1->next,
        head2=head2==NULL?NULL:head2->next)

        {
        sum=(head1==NULL?0:head1->data)+
            (head2==NULL?0:head2->data)+carry;
        val=sum%10;
        carry=sum/10;

        node* temp=new node;
        temp->data=val;
        temp->next=NULL;

        if (ans==NULL) {
            ans=temp;
            cur=ans;
        }
        else {
            cur->next=temp;
            cur=cur->next;
        }
    }
    return ans;
}

双向链表

复制代码 
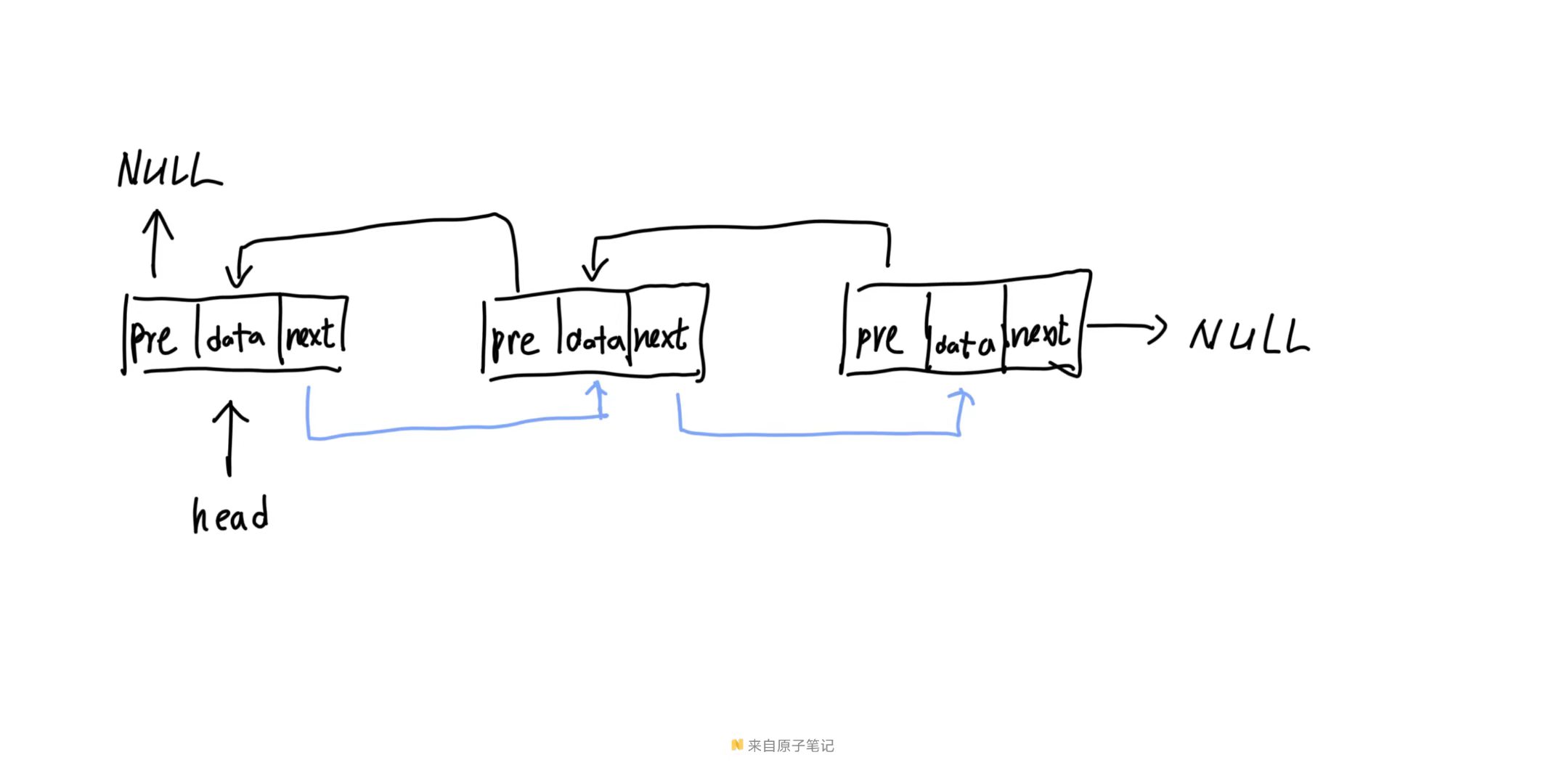
struct doublenode {
    int data;
    doublenode* next;
    doublenode* prev;
};
doublenode* head;

插入节点

其实跟单向链表一样，就是多了个需要设置节点上一个节点的操作；

复制代码 
void doubleinsert(int x,int n) {
    doublenode *newnode = new doublenode;
    newnode->data=x;
    newnode->next=NULL;
    newnode->prev=NULL;
    doublenode* temp=head;

    for (int i=1;i<n-1;i++)temp=temp->next;
    newnode->next=temp->next;
    newnode->prev=temp;
    temp->next=newnode;
    temp->next->prev=newnode;
}

经典例题

约瑟夫环（洛谷P1996）橙题

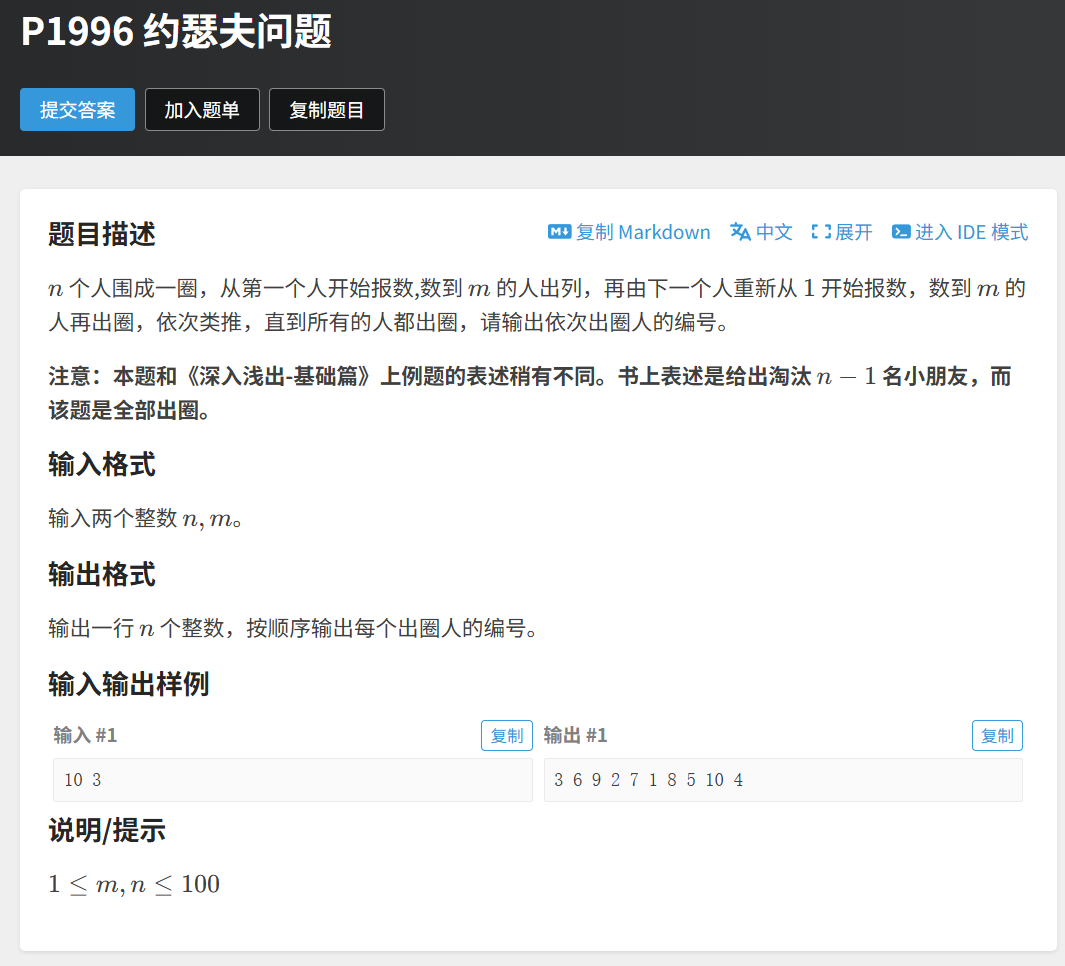
单向链表解

复制代码 
#include<bits/stdc++.h>
using namespace std;

struct node {
    int data;
    node *next;
};
node *head=NULL;
node *temp;
node *cur;
node *pre;

int main() {//初始化链表
    int n,m;
    cin>>n>>m;
    head=new node;
    head->data=1;
    head->next=NULL;
    cur=head;
    for(int i=2;i<=n;i++) {
        temp=new node();
        temp->data=i;
        cur->next=temp;
        cur=temp;
    }
    cur->next=head;
//以下为约瑟夫环操作
    cur=head;
    pre=head;
    while (--n) {
        for (int i=1;i<m;i++){
            pre=cur;
            cur=cur->next;
        }
        cout<<cur->data<<" ";
        pre->next=cur->next;
        delete cur;
        cur=pre->next;
    }
    cout<<cur->data;
return 0;
}

STL解

复制代码 
#include<bits/stdc++.h>
using namespace std;

int main() {
    int n,m;
    cin>>n>>m;
    list<int> node;
    for(int i=1;i<=n;i++) {//初始化链表
        node.push_back(i);
    }
    list<int>::iterator it = node.begin();
    while (node.size() > 1) {
        for (int i=1; i<m; i++) {
            ++it;
            if (it == node.end()) {//循环链表
                it = node.begin();
            }
        }
        cout << *it << " ";
        list<int>::iterator next_it = next(it);//因为删除节点it后it就找不到，所以设置一个nextit变量用来存储it的位置
        if (next_it == node.end()) {//循环链表
            next_it = node.begin();
        }
        node.erase(it);//删除结点
        it = next_it;
    }
    cout << *it << endl;
    return 0;
}

队列安排（洛谷P1160）黄题

题解

步骤 1：初始化队列
  • 先将 1 号同学入队，作为初始队列；
  • 记录 1 号同学的迭代器到 pos[1]。
步骤 2：处理 2~N 号同学的插入

对每个同学 i（2≤i≤N）：

  1. 输入 k（目标同学）和 p（插入方向）；
  2. 通过 pos[k] 快速找到 k 号同学的迭代器；
  3. 根据 p 的值选择插入位置：
    • p=0：插入到 k 号左侧（list.insert(pos[k], i)）；
    • p=1：插入到 k 号右侧（list.insert(next(pos[k]), i)）；
  4. 记录新插入元素 i 的迭代器到 pos[i]。
步骤 3：处理 M 次删除操作

对每个删除指令 x：

  1. 检查 pos[x] 是否为 list.end()（标记「元素是否存在」）；
  2. 若存在（pos[x] != list.end()）：
    • 执行 list.erase(pos[x]) 删除元素；
    • 将 pos[x] 置为 list.end()，标记该元素已被删除；
  3. 若不存在（pos[x] == list.end()）：直接跳过，避免崩溃。
步骤 4：输出最终队列

遍历 list，按顺序输出剩余元素。

复制代码 
#include <bits/stdc++.h>
using namespace std;

int main() {
    int N;
    cin >> N;
    list<int> node;
    // 辅助数组，用于找到编号x对应的迭代器
    vector<list<int>::iterator> pos(N + 1);
    node.push_back(1);
    pos[1] = node.begin();
    for (int i = 2; i <= N; ++i) {
        int k, p;
        cin >> k >> p;
        auto it_k = pos[k]; // 直接找到k号同学的迭代器
        if (p == 0) {
            // 插入到k号的左边
            auto new_it = node.insert(it_k, i);
            pos[i] = new_it;
        } else {
            // 插入到k号的右边
            auto new_it = node.insert(next(it_k), i);
            pos[i] = new_it;
        }
    }
    // 删除M个同学
    int M;
    cin >> M;
    while (M--) {
        int x;
        cin >> x;
        // 如果x号同学还在队列中，则删除
        if (pos[x] != node.end()) {
            node.erase(pos[x]);
            pos[x] = node.end(); // 标记为已删除，因为我们事先开的N+1大小的数组，而且只有N个同学，所以我们可以把最后一个用不到的元素拿出来标记已为删除的元素。
        }
    }

    // 输出
    for (auto it = node.begin(); it != node.end(); ++it) {
        if (it != node.begin()) cout << " ";
        cout << *it;
    }
    return 0;
}

总结

什么时候选链表？ 链表的核心操作是 在指定位置插入 和 删除指定元素 ，对比常见数据结构： 数组的插入删除需要移动大量元素，时间复杂度 O (n)，效率低；

一些难度比较低的且题目核心是插入和删除指定元素的题就可以优先考虑列表，而手动实现的链表需要自己管理节点指针，易出现野指针、空指针错误；因此比赛中我们一般优先考虑STL list【O (1) 时间的插入删除操作，且封装了指针管理】

相关推荐
民乐团扒谱机1 小时前
【读论文】引力与惯性的起源：从全息原理到牛顿定律与爱因斯坦方程
算法·量子力学·熵·万有引力·爱因斯坦方程·全息原理·牛顿定律
努力学算法的蒟蒻1 小时前
day84（2.13）——leetcode面试经典150
算法·leetcode·面试
@––––––1 小时前
力扣hot100—系列8-回溯算法
javascript·算法·leetcode
!停2 小时前
数据结构二叉树—堆(2)&链式结构(上)
数据结构·算法
C++ 老炮儿的技术栈2 小时前
万物皆文件：Linux 抽象哲学的开发之美
c语言·开发语言·c++·qt·算法
im_AMBER2 小时前
Leetcode 120 求根节点到叶节点数字之和 | 完全二叉树的节点个数
数据结构·学习·算法·leetcode·二叉树·深度优先
1027lonikitave2 小时前
FFTW的expr.ml怎么起作用
算法·哈希算法
TracyCoder1232 小时前
LeetCode Hot100（54/100）——215. 数组中的第K个最大元素
算法·leetcode·排序算法
We་ct2 小时前
LeetCode 92. 反转链表II ：题解与思路解析
前端·算法·leetcode·链表·typescript
热门推荐
01GitHub 镜像站点02Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services03爬虫逆向之观安（观镜WEB应用安全防护系统）04openClaw安装飞书插件｜核心踩坑：spawn EINVAL 错误终极解决指南05BongoCat - 跨平台键盘猫动画工具06HTB 赛季10 - Pterodactyl - user07UV安装并设置国内源08243 行 microGPT：把“训练 + 推理”拆到骨头里09openclaw配置教程（linux+局域网ollama）10openclaw 配置飞书 报错 应用未建立长连接