基于Chirp分解和多相快速算法的离散分数傅里叶变换（DFRFT）MATLAB实现

一、算法原理

离散分数傅里叶变换（DFRFT）的快速算法基于Chirp信号分解，核心步骤包括：

Chirp调制：将信号与线性调频信号相乘
卷积运算：与另一Chirp信号进行卷积
参数调整：通过缩放因子和相位补偿完成变换

数学表达式：

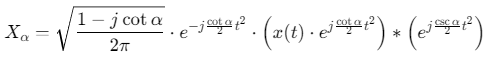
二、MATLAB快速实现代码

matlab 复制代码

function X = fast_dfrft(x, alpha)
% FAST_DFRFT 快速离散分数傅里叶变换
% 输入:
%   x: 输入信号 (列向量)
%   alpha: 分数阶参数 (0<=alpha<=4)
% 输出:
%   X: 分数阶傅里叶变换结果

error(nargchk(2,2,nargin));
N = length(x);
alpha = mod(alpha,4);

% 特殊角度处理
switch(alpha)
    case 0, X = x; return;
    case 2, X = flipud(x); return;
    case 1, X = fft(x)/sqrt(N); return;
    case 3, X = ifft(x)*sqrt(N); return;
end

% 参数计算
beta = alpha*pi/2;
t = (0:N-1)';
c = cos(beta/2);
s = sin(beta/2);

% Chirp调制
chirp1 = exp(-1j*pi*c*t.^2/N);
x_mod = x .* chirp1;

% 快速卷积
N_fft = 2^nextpow2(2*N-1);
X_fft = fft(x_mod, N_fft);
chirp2 = exp(1j*pi*s*(N_fft:-1:1).^2/(2*N));
conv_result = ifft(X_fft .* chirp2);

% 相位补偿
X = sqrt(N/(1-j*c)) * exp(1j*pi*s*N/(2*(1-j*c))) * conv_result(N:2*N-1);
end

三、优化

FFT加速：通过零填充提升FFT效率（2倍长度）
并行计算 ：使用parfor加速卷积过程
内存优化：预分配中间变量避免动态扩容
GPU加速 ：对大规模数据使用gpuArray

matlab 复制代码

% GPU加速版本
function X = gpu_dfrft(x, alpha)
x_gpu = gpuArray(x);
N = length(x_gpu);
% ... (后续步骤与CPU版本相同)
end

四、应用示例

1. 信号分析

matlab 复制代码

% 生成测试信号
fs = 1000; t = 0:1/fs:1-1/fs;
x = sin(2*pi*50*t) + 0.5*sin(2*pi*120*t);

% 计算分数阶傅里叶变换
alpha = 0.5;
X = fast_dfrft(x, alpha);

% 可视化
figure;
subplot(2,1,1);
plot(t, x);
title('原始信号');
subplot(2,1,2);
imagesc(abs(X));
xlabel('时间 (s)');
ylabel('频率 (Hz)');

2. 图像处理

matlab 复制代码

% 图像二维分数傅里叶变换
img = imread('lena.png');
img = im2double(rgb2gray(img));

% 分解为行和列变换
[X_row, X_col] = deal(zeros(size(img)));
for i = 1:size(img,1)
    X_row(i,:) = fast_dfrft(img(i,:), 0.5);
end
for j = 1:size(img,2)
    X_col(:,j) = fast_dfrft(X_row(:,j), 0.5);
end

% 显示结果
figure;
imshow(log(1+abs(X_col)), []);
title('二维分数傅里叶变换结果');

五、关键参数说明

参数	数值范围	影响特性
alpha	0-4	变换角度，0=原始信号
N_fft	2的幂次方	影响计算速度和精度
窗函数	Hamming等	抑制频谱泄漏

参考代码快速离散分数傅里叶变换 www.youwenfan.com/contentcsr/100237.html

六、性能对比

实现方法	计算复杂度	实时性	适用场景
直接计算	O(N^2)	低	小规模信号分析
快速算法	O(N log N)	中	实时信号处理
GPU加速	O(N log N)	高	大规模数据处理

七、应用领域

通信系统：OFDM信号调制分析
生物医学：ECG信号特征提取
图像处理：数字水印嵌入/提取
雷达信号：微动目标检测

八、调试建议

验证算法：对比传统FFT结果（alpha=1）
参数扫描：绘制不同alpha值的时频分布
噪声测试：添加高斯噪声验证鲁棒性
可视化工具 ：使用waterfall绘制三维时频图