第 3 章:动态规划与策略迭代
本章目标:学习使用动态规划 (DP) 算法在已知环境模型的情况下求解最优策略,掌握策略迭代 (Policy Iteration) 与价值迭代 (Value Iteration) 的核心逻辑。
📖 目录 (Table of Contents)
- 动态规划的前提
- 策略评估 (Policy Evaluation)
- 策略改进 (Policy Improvement)
- 策略迭代 (Policy Iteration)
- 价值迭代 (Value Iteration)
- 广义策略迭代 (GPI)
- 总结与预告
1. 动态规划的前提
动态规划 (DP) 需要完整的环境模型:
- 状态转移概率 P ( s ′ ∣ s , a ) P(s'|s,a) P(s′∣s,a) 已知
- 奖励函数 R ( s , a , s ′ ) R(s,a,s') R(s,a,s′) 已知
这意味着我们不需要去"探索"环境,而是可以直接计算最优解(Planning)。
2. 策略评估 (Policy Evaluation)
目标 :给定策略 π \pi π,计算其状态价值函数 V π V^\pi Vπ。
V k + 1 ( s ) = ∑ a π ( a ∣ s ) [ R ( s , a ) + γ ∑ s ′ P ( s ′ ∣ s , a ) V k ( s ′ ) ] V_{k+1}(s) = \sum_a \pi(a|s) \left[ R(s,a) + \gamma \sum_{s'} P(s'|s,a) V_k(s') \right] Vk+1(s)=a∑π(a∣s)[R(s,a)+γs′∑P(s′∣s,a)Vk(s′)]
代码实现 (Policy Evaluation)
python
def policy_evaluation(env, policy, gamma=0.99, theta=1e-6):
"""策略评估:迭代计算 V^π"""
states = env.get_states()
V = {s: 0.0 for s in states}
while True:
delta = 0
for s in states:
v = V[s]
# 根据策略计算期望
new_v = 0
for a in env.get_actions():
prob = policy.get((s, a), 0)
if prob > 0:
s_next, r, _ = env.step(s, a)
new_v += prob * (r + gamma * V.get(s_next, 0))
V[s] = new_v
delta = max(delta, abs(v - V[s]))
if delta < theta:
break
return V3. 策略改进 (Policy Improvement)
目标 :基于当前的 V π V^\pi Vπ,修改策略以获得更大的长期回报。
贪婪策略 (Greedy Policy) :
π ′ ( s ) = arg max a [ R ( s , a ) + γ ∑ s ′ P ( s ′ ∣ s , a ) V π ( s ′ ) ] \pi'(s) = \arg\max_a \left[ R(s,a) + \gamma \sum_{s'} P(s'|s,a) V^\pi(s') \right] π′(s)=argamax[R(s,a)+γs′∑P(s′∣s,a)Vπ(s′)]
代码实现 (Policy Improvement)
python
def policy_improvement(env, V, gamma=0.99):
"""策略改进:基于 V 提取贪婪策略"""
policy = {}
for s in env.get_states():
action_values = {}
for a in env.get_actions():
s_next, r, _ = env.step(s, a)
action_values[a] = r + gamma * V.get(s_next, 0)
best_action = max(action_values, key=action_values.get)
policy[s] = best_action
return policy4. 策略迭代 (Policy Iteration)
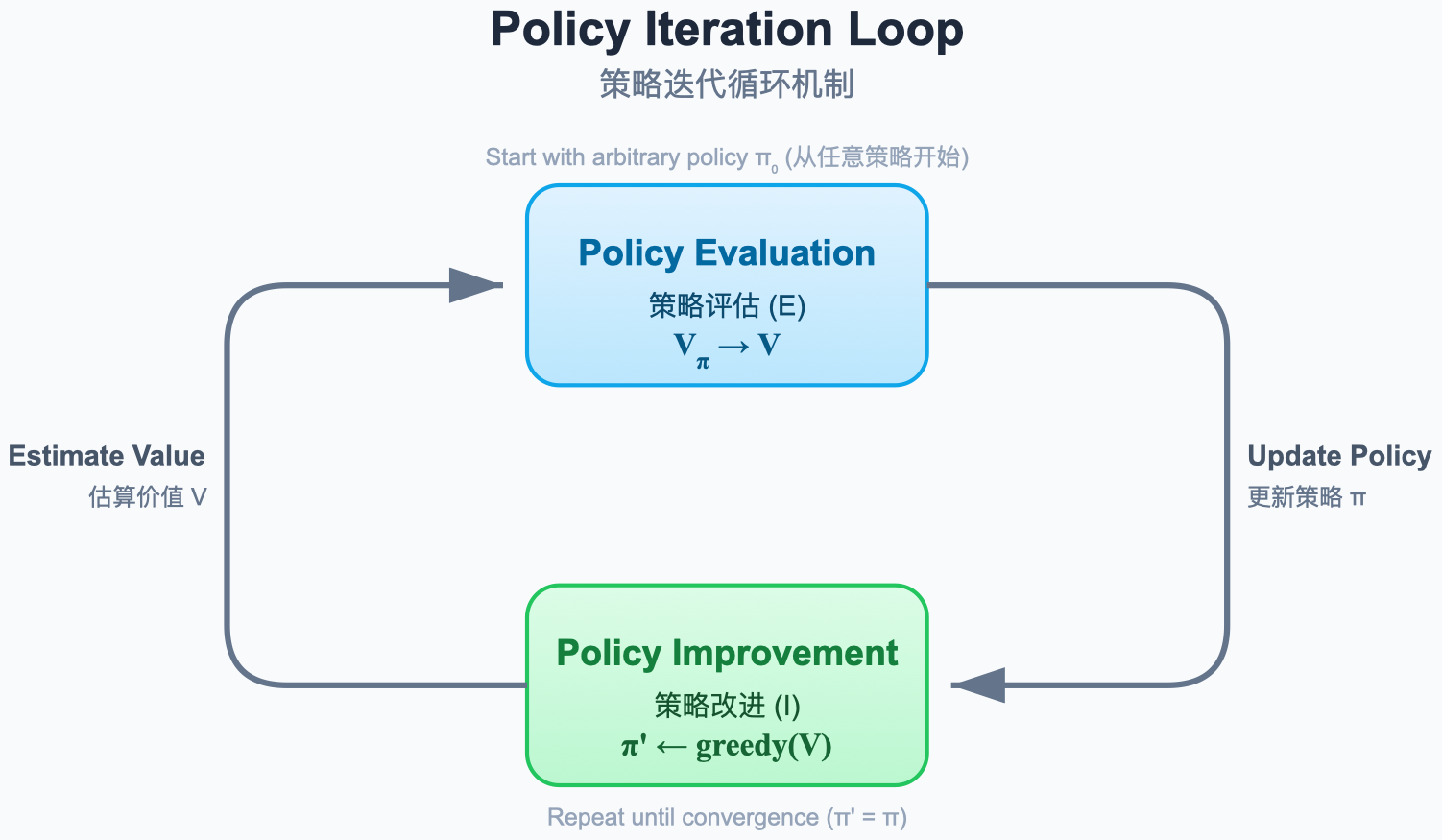
图解说明:
- 蓝色循环:策略评估 (Evaluation) - 计算当前策略的价值 V。
- 红色循环:策略改进 (Improvement) - 根据价值 V 改进策略 π。
- 收敛 :两者交替进行,直到策略不再改变,此时达到最优策略 π ∗ \pi^* π∗。
代码实现 (Policy Iteration)
python
import numpy as np
def policy_iteration(env, gamma=0.99):
"""策略迭代:交替评估和改进"""
# 初始化随机策略
states = env.get_states()
actions = env.get_actions()
policy = {s: np.random.choice(actions) for s in states}
while True:
# 1. 策略评估
V = policy_evaluation(env, policy, gamma)
# 2. 策略改进
new_policy = policy_improvement(env, V, gamma)
# 检查收敛
if new_policy == policy:
break
policy = new_policy
return policy, V5. 价值迭代 (Value Iteration)
思想:不必等待策略评估完全收敛,我们可以每更新一次 V 就贪婪地改进策略,或者直接合并这两个步骤。
V k + 1 ( s ) = max a [ R ( s , a ) + γ ∑ s ′ P ( s ′ ∣ s , a ) V k ( s ′ ) ] V_{k+1}(s) = \max_a \left[ R(s,a) + \gamma \sum_{s'} P(s'|s,a) V_k(s') \right] Vk+1(s)=amax[R(s,a)+γs′∑P(s′∣s,a)Vk(s′)]
代码实现 (Value Iteration)
python
def value_iteration(env, gamma=0.99, theta=1e-6):
"""价值迭代:直接计算 V*"""
states = env.get_states()
V = {s: 0.0 for s in states}
while True:
delta = 0
for s in states:
v = V[s]
# 直接取最大动作价值
action_values = []
for a in env.get_actions():
s_next, r, _ = env.step(s, a)
action_values.append(r + gamma * V.get(s_next, 0))
V[s] = max(action_values) if action_values else 0
delta = max(delta, abs(v - V[s]))
if delta < theta:
break
# 最后提取一次最优策略
policy = policy_improvement(env, V, gamma)
return policy, V6. 广义策略迭代 (GPI)
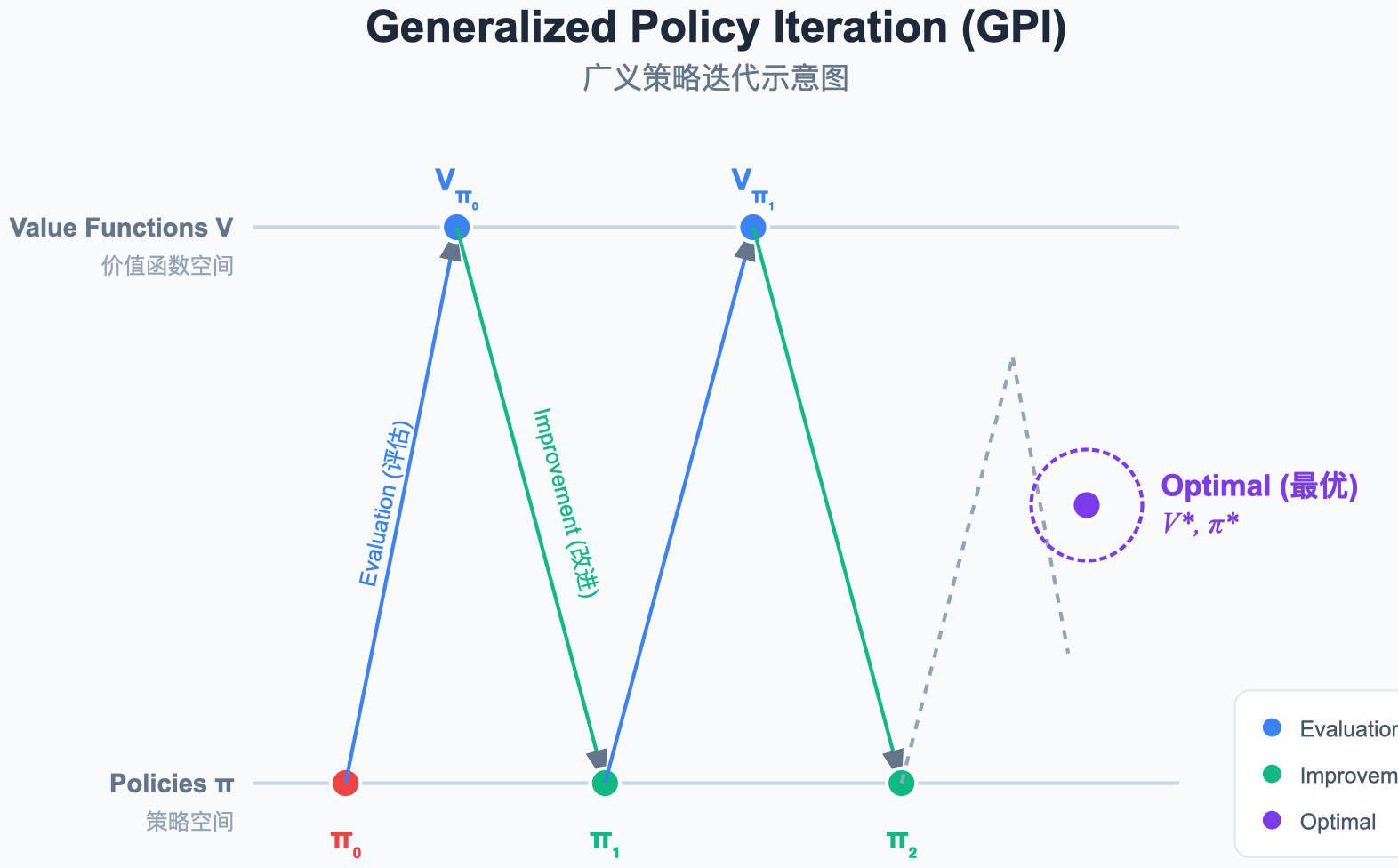
图解说明:
- 核心思想:策略评估(让价值函数逼近当前策略的真实价值)和策略改进(让策略对于当前价值函数贪婪)是两个竞争又合作的过程。
- GPI:并不要求每次步骤都完美收敛,只要这两个过程持续进行,最终就会收敛到最优解。
7. 总结与预告
本章核心:
- 动态规划 是一种基于模型的规划方法 (Planning)。
- 策略迭代 分离了评估和改进,比较稳健。
- 价值迭代 融合了两者,通常收敛更快。
下一章预告 :
如果我们不知道环境模型(不知道 P 和 R 怎么办)?我们将进入 Model-Free 的世界,学习蒙特卡洛方法。