【读论文】深度学习中的卷积算术指南 A guide to convolution arithmetic for deep learning

文章目录

[第1章引言](#第1章引言)
- [1.1 离散卷积](#1.1 离散卷积)
- [1.2 池化](#1.2 池化)
[第2章卷积算术](#第2章卷积算术)
- [2.1 无零填充、单位步长](#2.1 无零填充、单位步长)
- [2.2 有零填充、单位步长](#2.2 有零填充、单位步长)
- - [2.2.1 半填充（等尺寸填充）](#2.2.1 半填充（等尺寸填充）)
  - [2.2.2 全填充](#2.2.2 全填充)
- [2.3 无零填充、非单位步长](#2.3 无零填充、非单位步长)
- [2.4 有零填充、非单位步长](#2.4 有零填充、非单位步长)
[第3章池化算术](#第3章池化算术)
[第4章转置卷积算术](#第4章转置卷积算术)
- [4.1 卷积的矩阵运算形式](#4.1 卷积的矩阵运算形式)
- [4.2 转置卷积](#4.2 转置卷积)
- [4.3 无零填充、单位步长的转置卷积](#4.3 无零填充、单位步长的转置卷积)
- [4.4 有零填充、单位步长的转置卷积](#4.4 有零填充、单位步长的转置卷积)
- - [4.4.1 半填充的转置卷积](#4.4.1 半填充的转置卷积)
  - [4.4.2 全填充的转置卷积](#4.4.2 全填充的转置卷积)
- [4.5 无零填充、非单位步长的转置卷积](#4.5 无零填充、非单位步长的转置卷积)
- [4.6 有零填充、非单位步长的转置卷积](#4.6 有零填充、非单位步长的转置卷积)
[第5章其他类型的卷积](#第5章其他类型的卷积)
- [5.1 空洞卷积](#5.1 空洞卷积)
参考文献

作者：文森特·迪穆兰¹⋆、弗朗西斯科·维辛²⋆†
⋆加拿大蒙特利尔大学米拉人工智能研究所 †意大利米兰理工大学人工智能实验室
2018年1月12日
邮箱：1dumouliv@iro.umontreal.ca 2francesco.visin@polimi.it
arXiv预印本：1603.07285v2 [stat.ML]，2018年1月11日
乔治·博克斯名言 ：所有模型都是错的，但有些模型是有用的。

致谢

本指南的作者感谢大卫·沃德-法利、纪尧姆·阿兰和贾拉尔·居尔切雷提供的宝贵反馈。同时，也感谢所有通过有益的评论、建设性的批评和代码贡献帮助完善本教程的读者，期待大家继续提出建议！

特别感谢《日光色》配色方案的创作者伊桑·斯库诺弗，本指南中的图表均采用了该配色方案的色彩。

反馈

我们诚挚欢迎各位的反馈！我们已尽最大努力保证内容的准确性、信息量和简洁性，但若你发现任何错误，或认为部分内容需要重新表述以提升精准度和易懂性，敬请随时联系我们。此外，如果你有认为适合纳入本技术报告的内容并希望我们展开探讨，也请告知，我们会尽力对本文档进行更新。

源代码与动画

用于生成本指南及相关图表的代码已发布在GitHub上，读者还可在该平台找到图表的动画版本。

1 网址：http://ethanschoonover.com/solarized

2 网址：https://github.com/vdumoulin/conv_arithmetic

第1章引言

深度卷积神经网络（CNN）是深度学习领域取得突破性进展的核心。尽管早在90年代，卷积神经网络就已被用于解决字符识别任务（乐康等人，1997），但它之所以能得到如今的广泛应用，归功于一项较近期的研究------当时一个深度卷积神经网络在ImageNet图像分类挑战赛中取得了超越当前最优水平的成绩（克里热夫斯基等人，2012）。

因此，卷积神经网络成为机器学习从业者的重要工具。然而，初次学习使用卷积神经网络往往是一个颇具挑战性的过程。卷积层的输出形状受输入形状、卷积核形状、零填充和步长的选择共同影响，而这些参数之间的关联并非易事推导。这与全连接层形成鲜明对比，全连接层的输出尺寸与输入尺寸无关。此外，卷积神经网络通常还包含池化阶段 ，这相较于全连接网络又增加了一层复杂度。最后，所谓的转置卷积层（也称为分数步长卷积层）近年来被越来越多的研究采用（蔡勒等人，2011；蔡勒和弗格斯，2014；朗等人，2015；拉德福德等人，2015；维辛等人，2015；林等人，2016），而其与普通卷积层的关联，现有研究的阐释清晰程度参差不齐。

本指南的目标主要有两个：

阐释卷积层与转置卷积层之间的关联；
帮助读者直观理解卷积层、池化层和转置卷积层中，输入形状、卷积核形状、零填充、步长与输出形状之间的关系。

为保证内容的广泛适用性，本指南给出的结论与具体实现细节无关，适用于所有常用的机器学习框架，如Theano（贝尔斯特拉等人，2010；巴斯蒂安等人，2012）、Torch（科洛贝尔特等人，2011）、TensorFlow（阿巴迪等人，2015）和Caffe（贾扬清等人，2014）。

本章将简要回顾卷积神经网络的核心构建模块，即离散卷积和池化。若想深入学习该主题，可参考《深度学习》教材的第9章（古德费洛等人，2016）。

1.1 离散卷积

神经网络的基础是仿射变换：接收一个向量作为输入，将其与矩阵相乘得到输出（通常在将结果传入非线性激活函数前，还会加上一个偏置向量）。这种变换适用于任何类型的输入，无论是图像、音频片段还是无序的特征集合：无论其维度如何，都可先将其展平为向量，再进行变换。

图像、音频片段及其他诸多类似数据具有内在结构。更具体地说，它们具备以下重要特性：

以多维数组的形式存储；
存在一个或多个有序轴（例如，图像的宽度轴和高度轴、音频片段的时间轴）；
存在一个通道轴，用于获取数据的不同维度信息（例如，彩色图像的红、绿、蓝通道，立体音轨的左、右声道）。

仿射变换无法利用这些特性；事实上，该变换会将所有轴同等对待，忽略数据的拓扑信息 。但在解决计算机视觉、语音识别等任务时，利用数据的隐含结构往往能起到事半功倍的效果，此时最好保留这些结构信息------这正是离散卷积的用武之地。

离散卷积是一种能保留有序性 的线性变换，具有稀疏性 （仅有少量输入单元参与单个输出单元的计算）和参数共享性 （相同的权重会应用于输入的多个位置）。

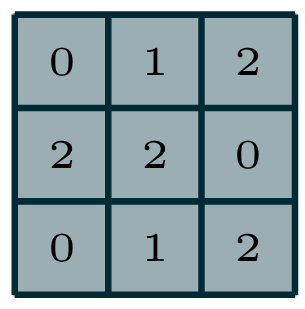
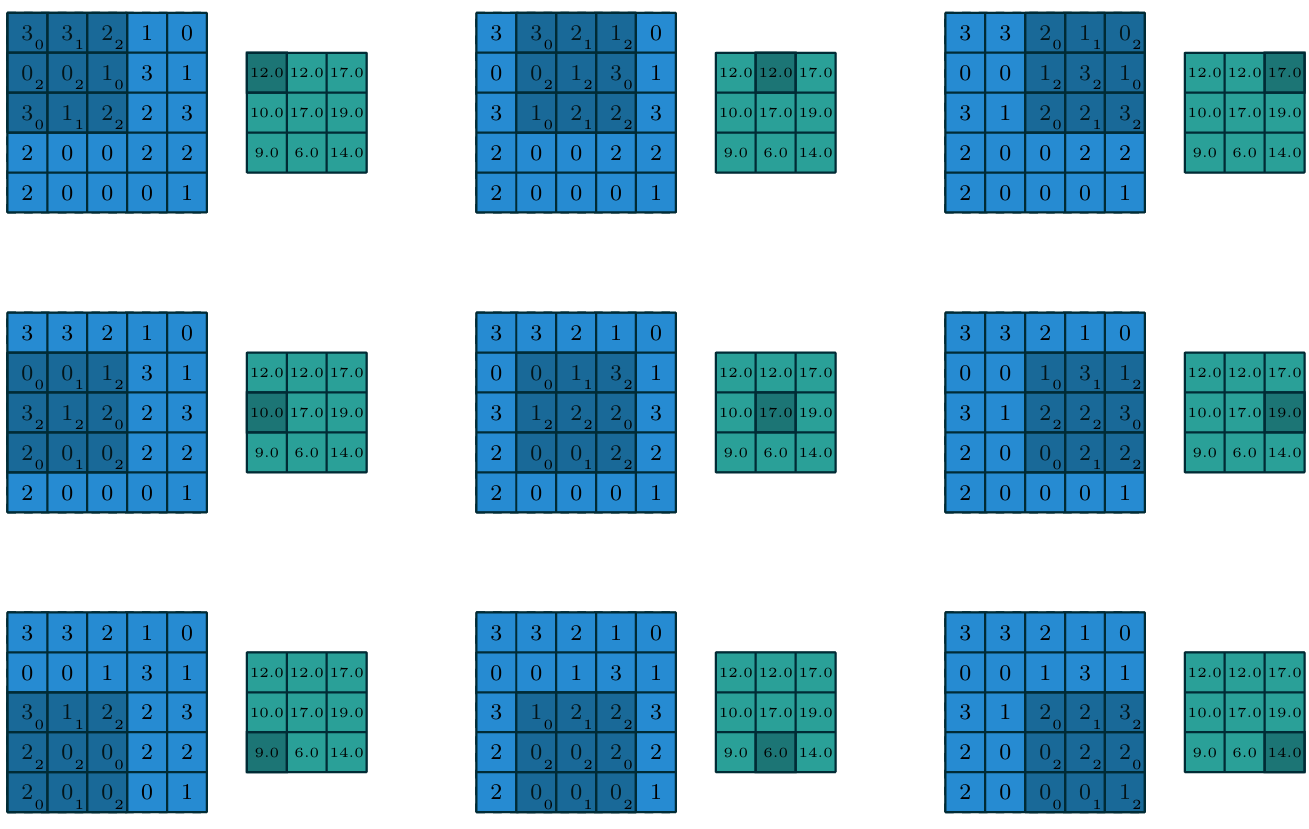
图 1.1离散卷积的输出值计算过程

图1.1展示了离散卷积的一个示例。浅蓝色的网格为输入特征图 。为简化绘图，本示例仅展示了单个输入特征图，但实际应用中，多个输入特征图堆叠的情况也十分常见 。带有阴影的区域是卷积核 ，其元素取值为固定数值，卷积核会在输入特征图上进行滑动。在每个滑动位置，将卷积核的每个元素与对应的输入元素相乘，再将所有乘积结果求和，即可得到该位置的输出值。使用不同的卷积核重复此过程，可得到任意数量的输出特征图（图1.3），该过程的最终结果即为输出特征图 ⁱⁱ。若存在多个输入特征图，卷积核需为三维结构（或等价地，为每个输入特征图分配一个独立的卷积核），并将所有输入特征图与对应卷积核卷积后的结果按元素求和，得到最终的输出特征图。

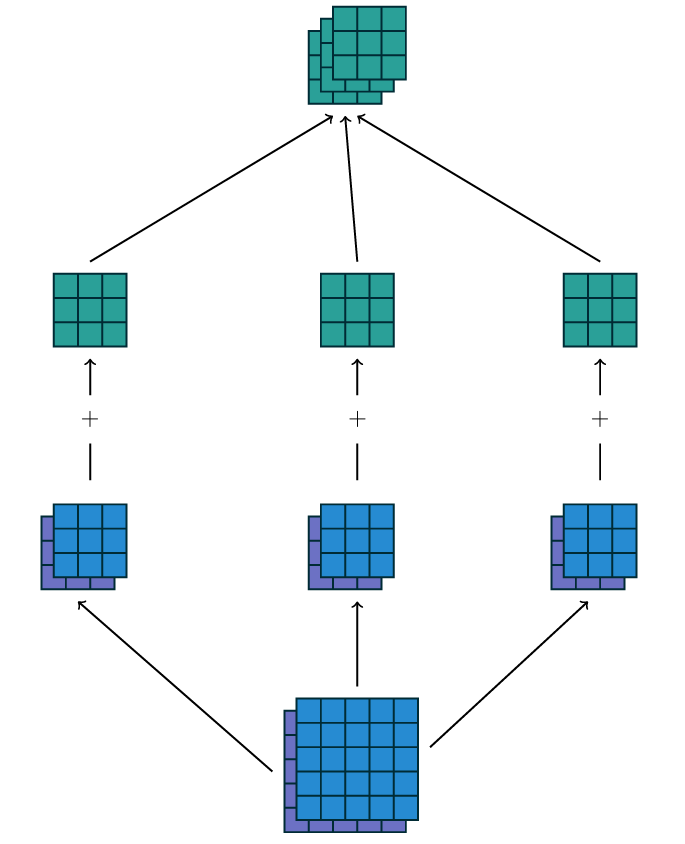
【图1.3 通过3×2×3×3的卷积核集合 w w w，实现从2个输入特征图到3个输出特征图的卷积映射过程。在左侧映射路径中，输入特征图1与卷积核 w 1 , 1 w_{1,1} w1,1卷积、输入特征图2与卷积核 w 1 , 2 w_{1,2} w1,2卷积，将两个结果按元素求和得到第一个输出特征图；中间和右侧路径执行相同操作，分别得到第二个和第三个输出特征图，最终将三个输出特征图整合为卷积的最终输出。】

本文示例中的卷积为二维卷积 ，但其可推广至N维卷积。例如，在三维卷积中，卷积核为立方体结构，会在输入特征图的高度、宽度和深度三个维度上滑动。

定义一个离散卷积的卷积核集合，其形状可表示为 ( n , m , k 1 , . . . , k N ) (n, m, k_1, ..., k_N) (n,m,k1,...,kN)的某种排列，其中：

n n n：输出特征图的数量；
m m m：输入特征图的数量；
k j k_j kj：第 j j j个轴上的卷积核尺寸。

卷积层在第 j j j个轴上的输出尺寸 o j o_j oj受以下参数影响：

i j i_j ij：第 j j j个轴上的输入尺寸；
k j k_j kj：第 j j j个轴上的卷积核尺寸；
s j s_j sj：第 j j j个轴上的步长（卷积核两个连续滑动位置之间的距离）；
p j p_j pj：第 j j j个轴上的零填充（在轴的起始和末尾位置补零的数量）。

例如，图1.2展示了一个3×3的卷积核，以2×2的步长，在带有1×1零填充边界的5×5输入特征图上进行卷积的过程。

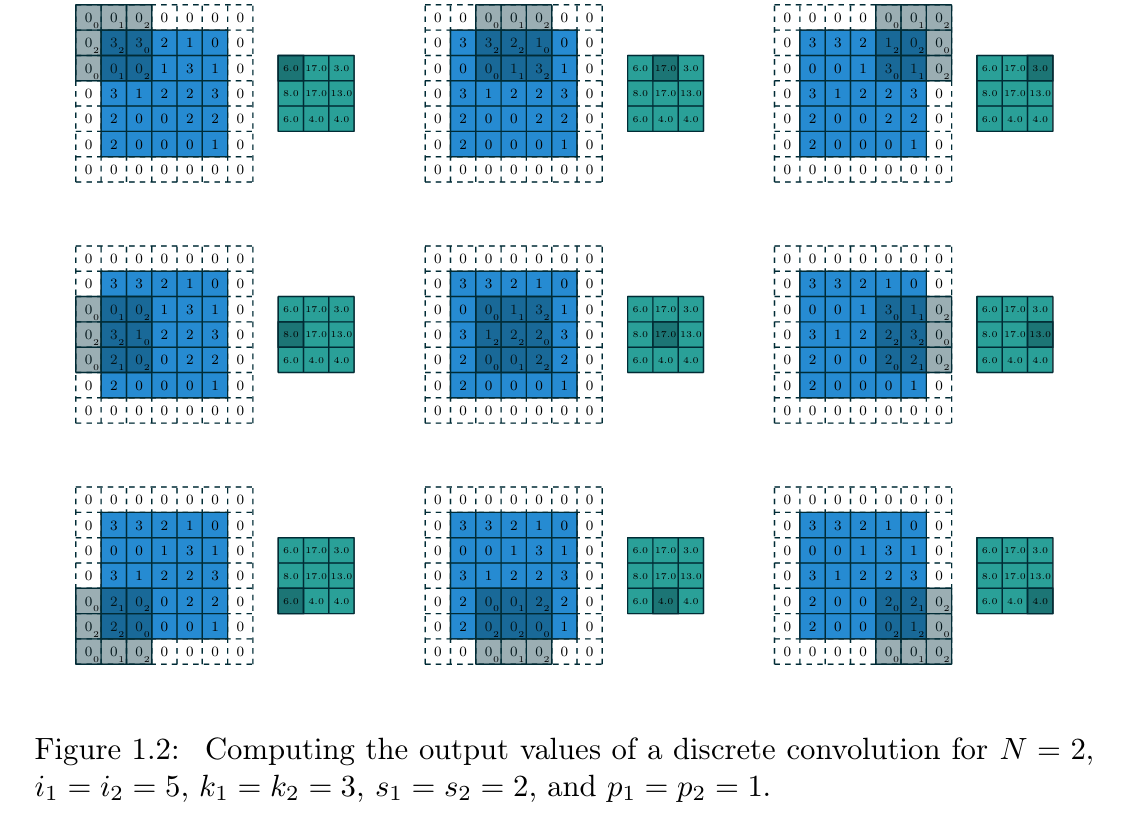
【图1.2 离散卷积的输出值计算过程（参数设置： N = 2 N=2 N=2、输入尺寸 i 1 = i 2 = 5 i_1=i_2=5 i1=i2=5、卷积核尺寸 k 1 = k 2 = 3 k_1=k_2=3 k1=k2=3、步长 s 1 = s 2 = 2 s_1=s_2=2 s1=s2=2、零填充 p 1 = p 2 = 1 p_1=p_2=1 p1=p2=1）】

需要注意的是，步长本质上是一种下采样 方式。步长除了被解释为卷积核的滑动步距，也可理解为输出的保留比例：例如，卷积核以步长2滑动，等价于卷积核以步长1滑动，但仅保留奇数位置的输出元素（图1.4）。

ⁱ 前文提及的图像通道、音频通道，就是多输入特征图的典型例子。

ⁱⁱ 从信号处理的角度来看，卷积与互相关存在区别，但当卷积核为可学习参数时，二者可以互换。为简化表述并与大多数机器学习文献保持一致，本指南中统一使用"卷积"一词。

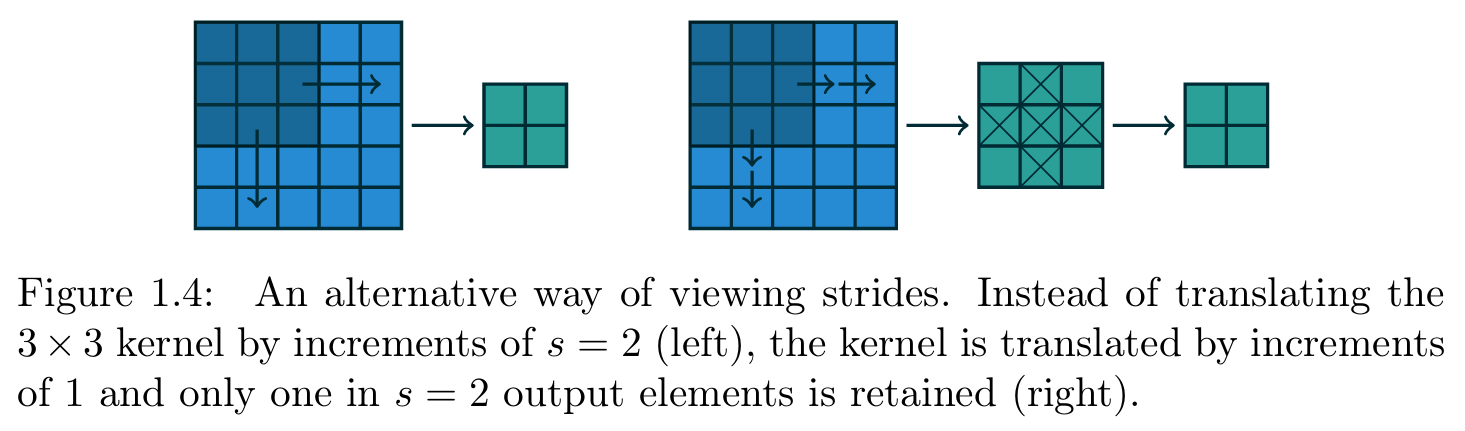
【图1.4 步长的另一种理解方式：左侧为卷积核以步长s=2滑动，右侧为卷积核以步长1滑动，但仅保留每s=2个输出中的1个元素（二者效果等价）】

1.2 池化

除离散卷积外，池化操作 是卷积神经网络的另一核心构建模块。池化操作通过对输入特征图的局部子区域进行聚合统计（如取平均值或最大值），实现特征图尺寸的缩小。

池化的操作方式与离散卷积十分相似：将一个池化窗口 在输入特征图上滑动，将窗口内的输入元素传入池化函数 进行计算。从某种意义上说，池化与卷积的唯一区别在于，将卷积中基于卷积核的线性组合替换为了其他聚合函数。图1.5为平均池化 的示例，图1.6为最大池化的示例。

池化层在第 j j j个轴上的输出尺寸 o j o_j oj受以下参数影响：

i j i_j ij：第 j j j个轴上的输入尺寸；
k j k_j kj：第 j j j个轴上的池化窗口尺寸；
s j s_j sj：第 j j j个轴上的池化窗口步长。

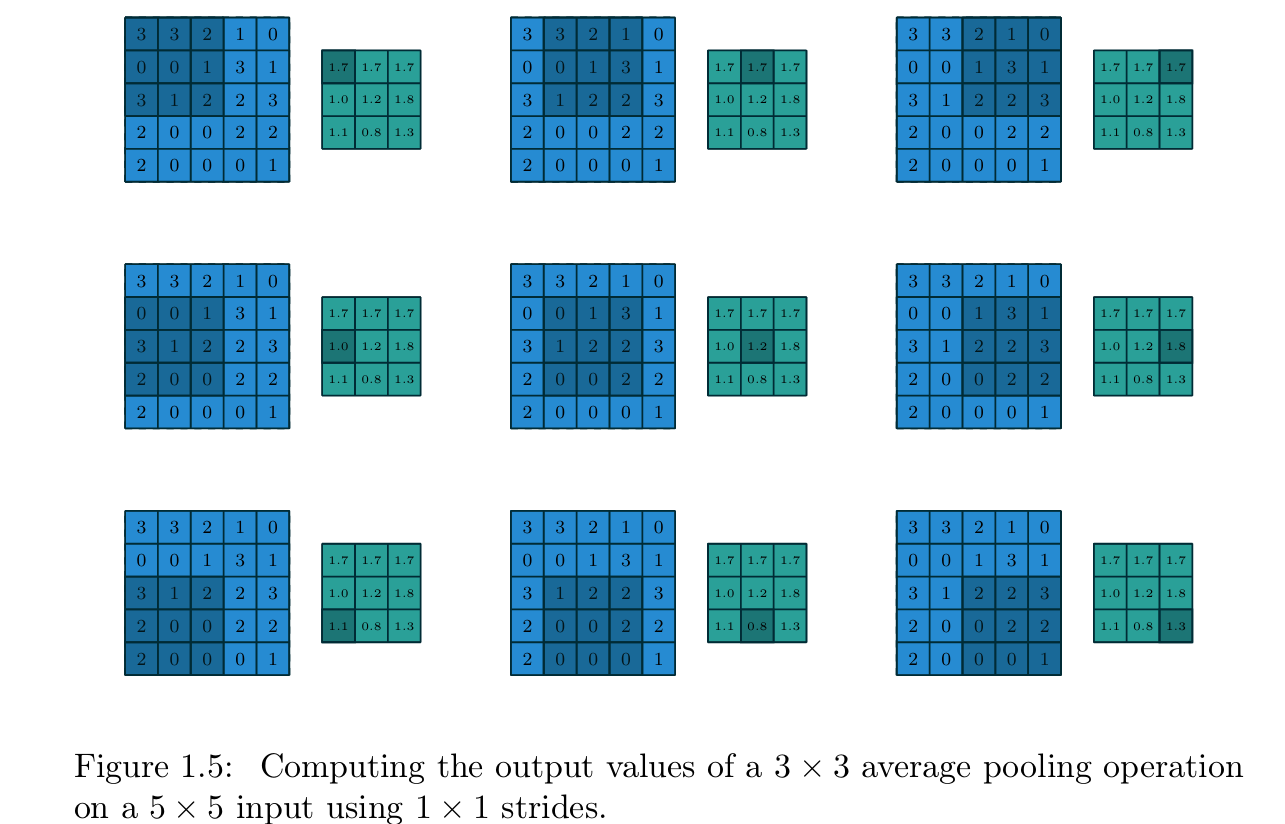
【图1.5 3×3平均池化的输出值计算过程（参数设置：5×5输入、步长1×1）】

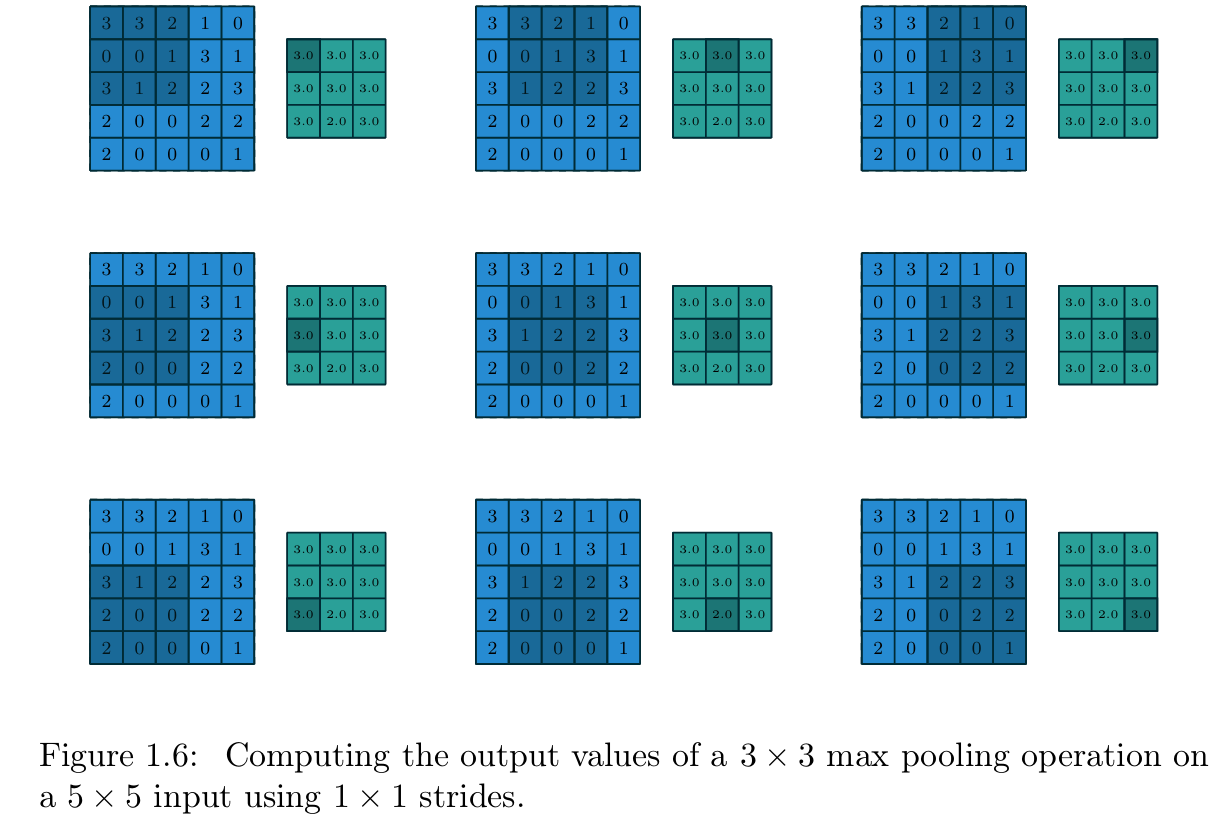
【图1.6 3×3最大池化的输出值计算过程（参数设置：5×5输入、步长1×1）】

第2章卷积算术

卷积层的各参数仅对对应轴的输出尺寸产生影响，不同轴之间无相互作用------这一特性为分析卷积层参数与输出尺寸的关系提供了便利。因此，本章将基于以下简化设定展开分析：

二维离散卷积（ N = 2 N=2 N=2）；
正方形输入（ i 1 = i 2 = i i_1=i_2=i i1=i2=i）；
正方形卷积核（ k 1 = k 2 = k k_1=k_2=k k1=k2=k）；
各轴步长相同（ s 1 = s 2 = s s_1=s_2=s s1=s2=s）；
各轴零填充数量相同（ p 1 = p 2 = p p_1=p_2=p p1=p2=p）。

该简化设定便于分析和可视化，且本章节得出的结论可直接推广至N维卷积 和非正方形的一般情况。

2.1 无零填充、单位步长

最易分析的情况是卷积核在输入特征图的所有位置 滑动（即 s = 1 s=1 s=1、 p = 0 p=0 p=0），图2.1展示了 i = 4 i=4 i=4、 k = 3 k=3 k=3时的该类卷积示例。

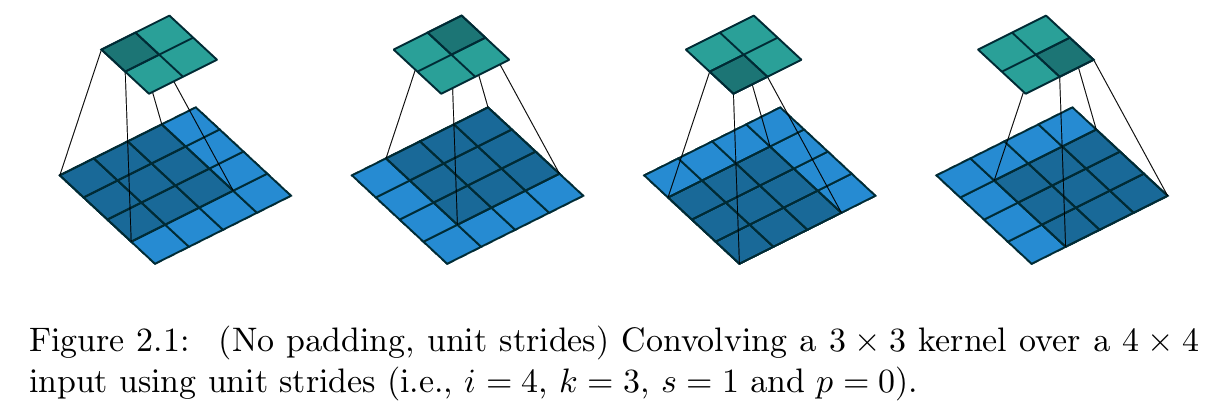
【图2.1 无填充、单位步长的卷积操作（参数设置：输入尺寸 i = 4 i=4 i=4、卷积核尺寸 k = 3 k=3 k=3、步长 s = 1 s=1 s=1、零填充 p = 0 p=0 p=0，即3×3卷积核以单位步长在4×4输入上做卷积）】

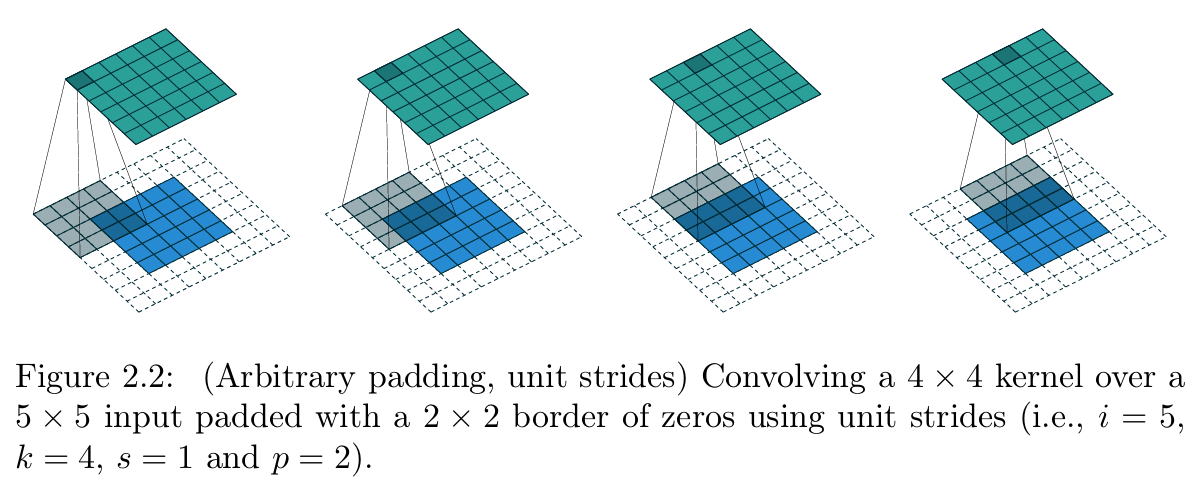
【图2.2 任意填充、单位步长的卷积操作（参数设置：输入尺寸 i = 5 i=5 i=5、卷积核尺寸 k = 4 k=4 k=4、步长 s = 1 s=1 s=1、零填充 p = 2 p=2 p=2，即4×4卷积核以单位步长在带2×2零填充边界的5×5输入上做卷积）】

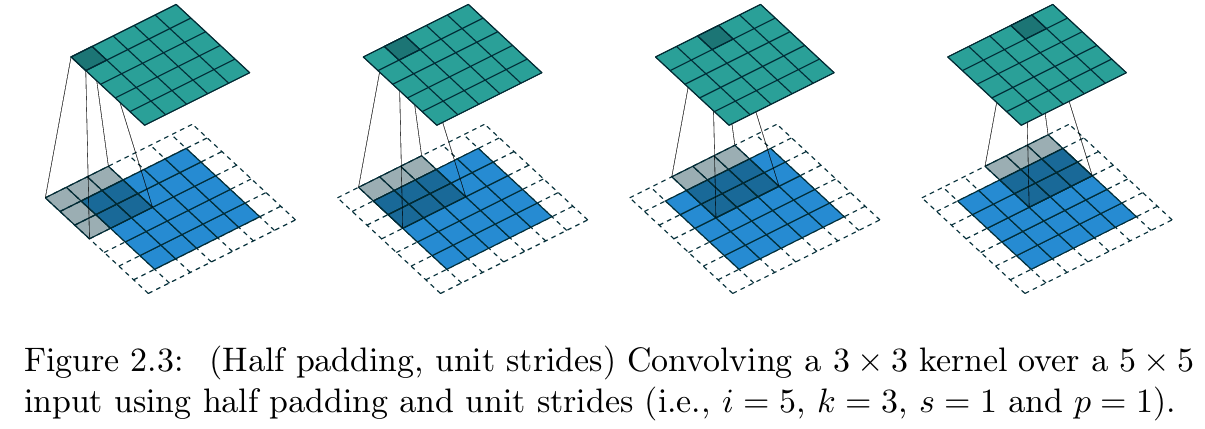
【图2.3 半填充、单位步长的卷积操作（参数设置：输入尺寸 i = 5 i=5 i=5、卷积核尺寸 k = 3 k=3 k=3、步长 s = 1 s=1 s=1、零填充 p = 1 p=1 p=1，即3×3卷积核以单位步长在带1×1零填充边界的5×5输入上做半填充卷积）】

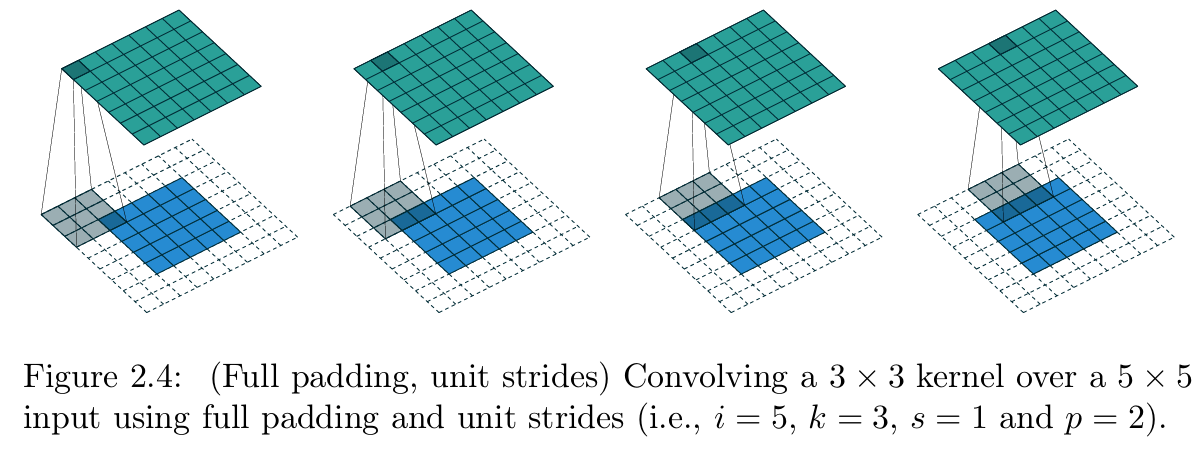
【图2.4 全填充、单位步长的卷积操作（参数设置：输入尺寸 i = 5 i=5 i=5、卷积核尺寸 k = 3 k=3 k=3、步长 s = 1 s=1 s=1、零填充 p = 2 p=2 p=2，即3×3卷积核以单位步长在带2×2零填充边界的5×5输入上做全填充卷积）】

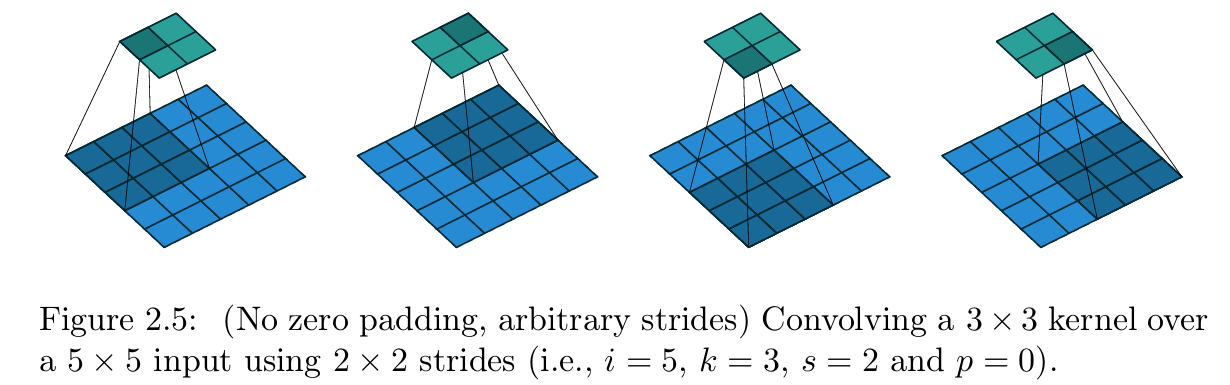
【图2.5 无零填充、任意步长的卷积操作（参数设置：输入尺寸 i = 5 i=5 i=5、卷积核尺寸 k = 3 k=3 k=3、步长 s = 2 s=2 s=2、零填充 p = 0 p=0 p=0，即3×3卷积核以2×2步长在5×5输入上做卷积）】

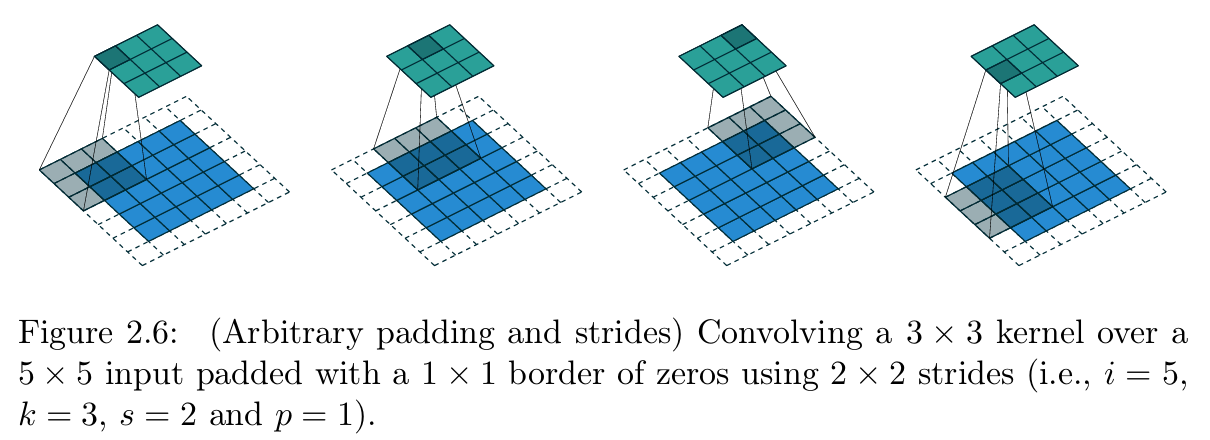
【图2.6 任意填充、任意步长的卷积操作（参数设置：输入尺寸 i = 5 i=5 i=5、卷积核尺寸 k = 3 k=3 k=3、步长 s = 2 s=2 s=2、零填充 p = 1 p=1 p=1，即3×3卷积核以2×2步长在带1×1零填充边界的5×5输入上做卷积）】

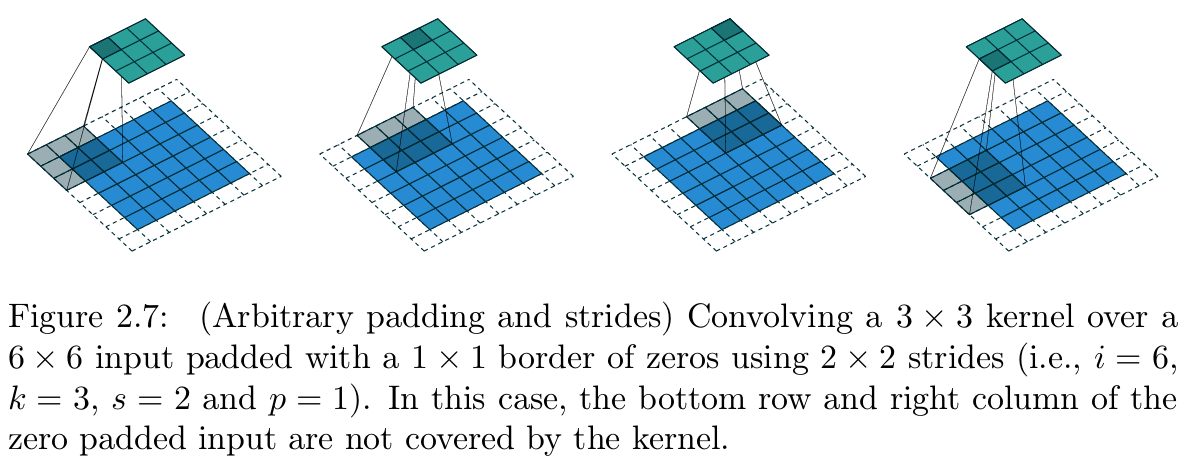
【图2.7 任意填充、任意步长的卷积操作（参数设置：输入尺寸 i = 6 i=6 i=6、卷积核尺寸 k = 3 k=3 k=3、步长 s = 2 s=2 s=2、零填充 p = 1 p=1 p=1，即3×3卷积核以2×2步长在带1×1零填充边界的6×6输入上做卷积）；本案例中，零填充后的输入特征图，其最后一行和最后一列未被卷积核覆盖】

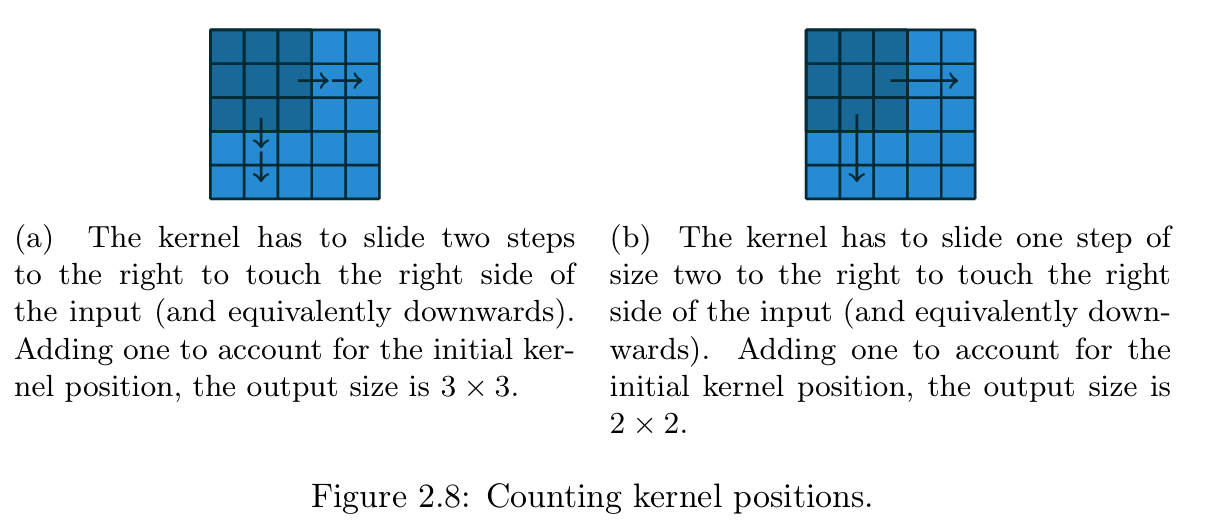
【图2.8 卷积核可行放置次数的计数方式

(a) 卷积核需向右滑动2步才能触达输入的右边界（向下滑动同理），计入卷积核初始位置，最终输出尺寸为3×3

(b) 卷积核需以步长2向右滑动1步才能触达输入的右边界（向下滑动同理），计入卷积核初始位置，最终输出尺寸为2×2】

该情况下的输出尺寸，可通过卷积核在输入上的可行放置次数来定义。以宽度轴为例：卷积核从输入特征图的最左侧开始，以步长1向右滑动，直至卷积核的右边界与输入的右边界重合。输出尺寸等于卷积核的滑动步数加1（加1是为了计入卷积核的初始位置）（图2.8a），高度轴的计算逻辑同理。

更形式化地，可推导出如下关系：
关系式1 ：对于任意输入尺寸 i i i和卷积核尺寸 k k k，当步长 s = 1 s=1 s=1、零填充 p = 0 p=0 p=0时，输出尺寸为：
o = ( i − k ) + 1 o=(i-k)+1 o=(i−k)+1

2.2 有零填充、单位步长

为纳入零填充 的影响（仅限定步长 s = 1 s=1 s=1），我们先分析其对有效输入尺寸 的改变：在输入的两侧各补 p p p个零后，有效输入尺寸从原输入尺寸 i i i变为 i + 2 p i+2p i+2p。基于此，可结合关系式1推导出有零填充、单位步长下的输出尺寸关系：

关系式2 ：对于任意输入尺寸 i i i、卷积核尺寸 k k k和零填充数量 p p p，当步长 s = 1 s=1 s=1时，输出尺寸为：
o = ( i − k ) + 2 p + 1 o=(i-k)+2p+1 o=(i−k)+2p+1

图2.2展示了 i = 5 i=5 i=5、 k = 4 k=4 k=4、 p = 2 p=2 p=2时的该类卷积示例。

在实际应用中，有两种特殊的零填充方式因各自的特性被广泛使用，下文将对其展开详细分析。

2.2.1 半填充（等尺寸填充）

输出尺寸与输入尺寸相等 （ o = i o=i o=i）是一种常用的需求，此时可采用半填充，其参数满足以下关系：

关系式3 ：对于卷积核尺寸为奇数的情况（ k = 2 n + 1 k=2n+1 k=2n+1， n n n为自然数），当步长 s = 1 s=1 s=1、零填充 p = ⌊ k / 2 ⌋ = n p=\lfloor k/2 \rfloor=n p=⌊k/2⌋=n时，输出尺寸为：
o = i + 2 ⌊ k / 2 ⌋ − ( k − 1 ) = i + 2 n − 2 n ≡ i \begin{aligned} o &=i+2\lfloor k/2 \rfloor-(k-1) \\ &=i+2n-2n \\ &\equiv i \end{aligned} o=i+2⌊k/2⌋−(k−1)=i+2n−2n≡i

这种填充方式也被称为等尺寸填充（same padding） ，图2.3展示了 i = 5 i=5 i=5、 k = 3 k=3 k=3（因此 p = 1 p=1 p=1）时的半填充卷积示例。

2.2.2 全填充

卷积操作通常会使输出尺寸小于输入尺寸，但实际应用中有时需要输出尺寸大于输入尺寸 ，这一需求可通过合理的零填充实现，即全填充：

关系式4 ：对于任意输入尺寸 i i i和卷积核尺寸 k k k，当零填充 p = k − 1 p=k-1 p=k−1、步长 s = 1 s=1 s=1时，输出尺寸为：
o = i + 2 ( k − 1 ) − ( k − 1 ) = i + ( k − 1 ) \begin{aligned} o &=i+2(k-1)-(k-1) \\ &=i+(k-1) \end{aligned} o=i+2(k−1)−(k−1)=i+(k−1)

全填充的命名源于：该方式下，卷积核与输入特征图的所有部分重叠和完全重叠的情况 都会被纳入计算。图2.4展示了 i = 5 i=5 i=5、 k = 3 k=3 k=3（因此 p = 2 p=2 p=2）时的全填充卷积示例。

2.3 无零填充、非单位步长

前文推导的所有关系式均仅适用于单位步长 的卷积，纳入非单位步长 的影响需要进一步推导。为便于分析，本节先暂时忽略零填充（即 s > 1 s>1 s>1、 p = 0 p=0 p=0），图2.5展示了 i = 5 i=5 i=5、 k = 3 k=3 k=3、 s = 2 s=2 s=2时的该类卷积示例。

与单位步长的情况类似，该情况下的输出尺寸仍可通过卷积核的可行放置次数 定义。以宽度轴为例：卷积核从输入特征图的最左侧开始，以步长 s s s向右滑动，直至卷积核的右边界与输入的右边界重合，输出尺寸等于滑动步数加1（计入初始位置）（图2.8b），高度轴的计算逻辑同理。

由此可推导出如下关系：
关系式5 ：对于任意输入尺寸 i i i、卷积核尺寸 k k k和步长 s s s，当零填充 p = 0 p=0 p=0时，输出尺寸为：
o = ⌊ i − k s ⌋ + 1 o=\left\lfloor\frac{i-k}{s}\right\rfloor+1 o=⌊si−k⌋+1

式中的向下取整函数是为了处理一种特殊情况：卷积核的最后一次滑动无法使其右边界与输入右边界完全重合，即部分输入元素未被卷积核覆盖（图2.7为该情况的示例）。

2.4 有零填充、非单位步长

有零填充、非单位步长 是卷积的一般情况 ，其输出尺寸的推导可类比关系式2的思路：将有效输入尺寸 i + 2 p i+2p i+2p代入关系式5，即可得到该情况的输出尺寸关系：

关系式6 ：对于任意输入尺寸 i i i、卷积核尺寸 k k k、零填充数量 p p p和步长 s s s，输出尺寸为：
o = ⌊ i + 2 p − k s ⌋ + 1 o=\left\lfloor\frac{i+2p-k}{s}\right\rfloor+1 o=⌊si+2p−k⌋+1

与关系式5一致，式中的向下取整函数意味着：不同的输入尺寸可能会得到相同的输出尺寸 。具体来说，若 i + 2 p − k i+2p-k i+2p−k能被 s s s整除，那么所有满足 j = i + a j=i+a j=i+a（ a ∈ { 0 , . . . , s − 1 } a\in\{0,...,s-1\} a∈{0,...,s−1}）的输入尺寸 j j j，都会得到相同的输出尺寸。需要注意的是，这种模糊性仅在 s > 1 s>1 s>1时存在。

图2.6展示了 i = 5 i=5 i=5、 k = 3 k=3 k=3、 s = 2 s=2 s=2、 p = 1 p=1 p=1的卷积示例，图2.7展示了 i = 6 i=6 i=6、 k = 3 k=3 k=3、 s = 2 s=2 s=2、 p = 1 p=1 p=1的卷积示例。值得注意的是，尽管两个示例的输入尺寸不同，但输出尺寸完全一致。这一特性对普通卷积的分析无影响，但会增加转置卷积分析的复杂度。

第3章池化算术

在神经网络中，池化层的作用是使模型对输入的微小平移具有不变性 。最常用的池化方式是最大池化：将输入特征图划分为若干（通常不重叠的）子区域，取每个子区域的最大值作为输出。除此之外，还有平均池化等其他池化方式，其核心思想均为：对输入的局部子区域应用非线性聚合函数，实现局部特征的聚合（布罗等人，2010a、2010b、2011；萨克斯等人，2011）。

读者可能已经发现，卷积算术的分析仅基于一个前提：某个函数在输入的局部子区域上重复应用 。这意味着，第2章中推导的卷积尺寸关系式，可直接迁移至池化算术的分析中。由于池化操作不涉及零填充，因此池化输出尺寸的通用关系式为：

关系式7 ：对于任意输入尺寸 i i i、池化窗口尺寸 k k k和步长 s s s，池化层的输出尺寸为：
o = ⌊ i − k s ⌋ + 1 o=\left\lfloor\frac{i-k}{s}\right\rfloor+1 o=⌊si−k⌋+1

该关系式适用于所有类型的池化操作。

第4章转置卷积算术

转置卷积 的需求，通常源于希望实现普通卷积的逆变换：将某个卷积的输出形状，映射回其输入形状，同时保持与原卷积兼容的连接模式。例如，在卷积自编码器中，可将转置卷积作为解码层；或利用转置卷积将特征图投影至更高维的空间。

与全连接层相比，卷积层的逆变换要复杂得多------全连接层的逆变换仅需使用形状转置后的权重矩阵即可。但由于任何卷积操作，本质上都是矩阵运算的高效实现，因此从全连接层逆变换中得到的思路，也可用于解决卷积层的逆变换问题。

与卷积算术类似，转置卷积的各参数仅对对应轴的输出尺寸产生影响，不同轴之间无相互作用，这一特性简化了转置卷积算术的分析。

本章将基于以下简化设定展开分析：

二维转置卷积（ N = 2 N=2 N=2）；
正方形输入（ i 1 = i 2 = i i_1=i_2=i i1=i2=i）；
正方形卷积核（ k 1 = k 2 = k k_1=k_2=k k1=k2=k）；
各轴步长相同（ s 1 = s 2 = s s_1=s_2=s s1=s2=s）；
各轴零填充数量相同（ p 1 = p 2 = p p_1=p_2=p p1=p2=p）。

同样，本章得出的结论可直接推广至N维转置卷积 和非正方形的一般情况。

4.1 卷积的矩阵运算形式

以图2.1中的卷积为例，若将输入和输出按从左到右、从上到下 的顺序展平为向量，那么该卷积操作可表示为一个稀疏矩阵 C C C ，矩阵中的非零元素即为卷积核的元素 w i , j w_{i,j} wi,j（ i i i、 j j j分别为卷积核的行、列索引）：

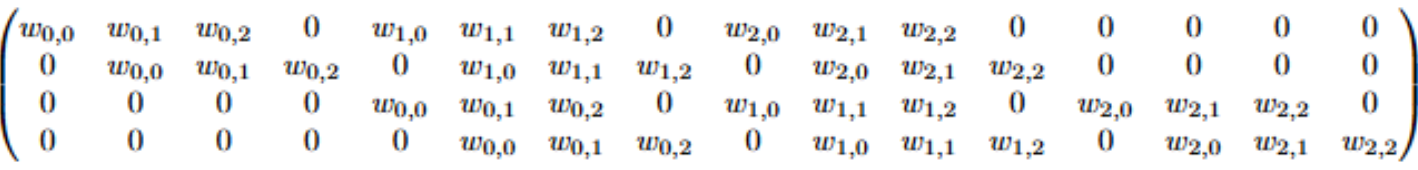
该线性运算将展平为16维向量的4×4输入矩阵，转换为4维向量，再将其重塑为2×2的输出矩阵。

基于卷积的矩阵表示，反向传播 过程可通过矩阵转置 轻松实现：将损失值与 C T C^T CT相乘，即可完成误差的反向传播。该操作将4维的误差向量转换为16维的向量，其连接模式由矩阵 C C C的结构天然保证与原卷积兼容。

值得注意的是，卷积核 w w w同时定义了正向传播的矩阵 C C C和反向传播的矩阵 C T C^T CT。

4.2 转置卷积

现在我们考虑一个问题：如何实现从4维空间到16维空间的映射，同时保持与图2.1中卷积相同的连接模式？这一操作即为转置卷积。

转置卷积也被称为分数步长卷积 或反卷积 ⁱ，其核心是交换普通卷积的正向传播和反向传播过程 。简单来说：卷积核定义了一个卷积操作，而该操作是普通卷积还是转置卷积，由正向传播和反向传播的计算方式决定。

例如，卷积核 w w w定义的普通卷积，正向传播为与 C C C相乘，反向传播为与 C T C^T CT相乘；而由该卷积核定义的转置卷积，正向传播为与 C T C^T CT相乘，反向传播为与 ( C T ) T = C (C^T)^T=C (CT)T=C相乘ⁱⁱ。

最后需要说明的是，任何转置卷积都可通过普通卷积模拟实现，但这种方式的缺点是：通常需要在输入中添加大量的零行和零列，导致实现效率极低。

基于前文的铺垫，本章将采用与卷积算术章节相反的推导思路：通过转置卷积对应的普通卷积（二者共享同一卷积核），推导转置卷积的参数特性，并定义其等价的普通卷积形式。

ⁱ 文献中有时会使用"反卷积"一词，但本指南不建议使用------因为数学上的反卷积是卷积的逆运算 ，与转置卷积并非同一概念。

ⁱⁱ 转置卷积可被理解为普通卷积对输入的梯度，这也是实际框架中实现转置卷积的常用方式。

4.3 无零填充、单位步长的转置卷积

理解转置卷积的一个简单思路是：将转置卷积的输入，视为某个普通卷积作用于初始特征图后的输出，那么转置卷积的作用，就是恢复该初始特征图的形状ⁱ。

考虑这样一个普通卷积：3×3的卷积核，以单位步长、无零填充的方式，在4×4的输入上进行卷积（即 i = 4 i=4 i=4、 k = 3 k=3 k=3、 s = 1 s=1 s=1、 p = 0 p=0 p=0）。如图2.1所示，该卷积的输出为2×2的特征图。那么，该卷积对应的转置卷积，作用于2×2的输入时，输出形状将为4×4。

实现转置卷积的另一种方式，是应用其等价的普通卷积 （效率更低）。对于上述示例，其等价的普通卷积为：3×3的卷积核，以单位步长，在带有2×2零填充边界的2×2输入上进行卷积（即 i ′ = 2 i'=2 i′=2、 k ′ = k k'=k k′=k、 s ′ = 1 s'=1 s′=1、 p ′ = 2 p'=2 p′=2），如图4.1所示。值得注意的是，等价普通卷积的卷积核尺寸和步长，与原转置卷积完全相同，仅需对转置卷积的输入进行零填充ⁱⁱ。

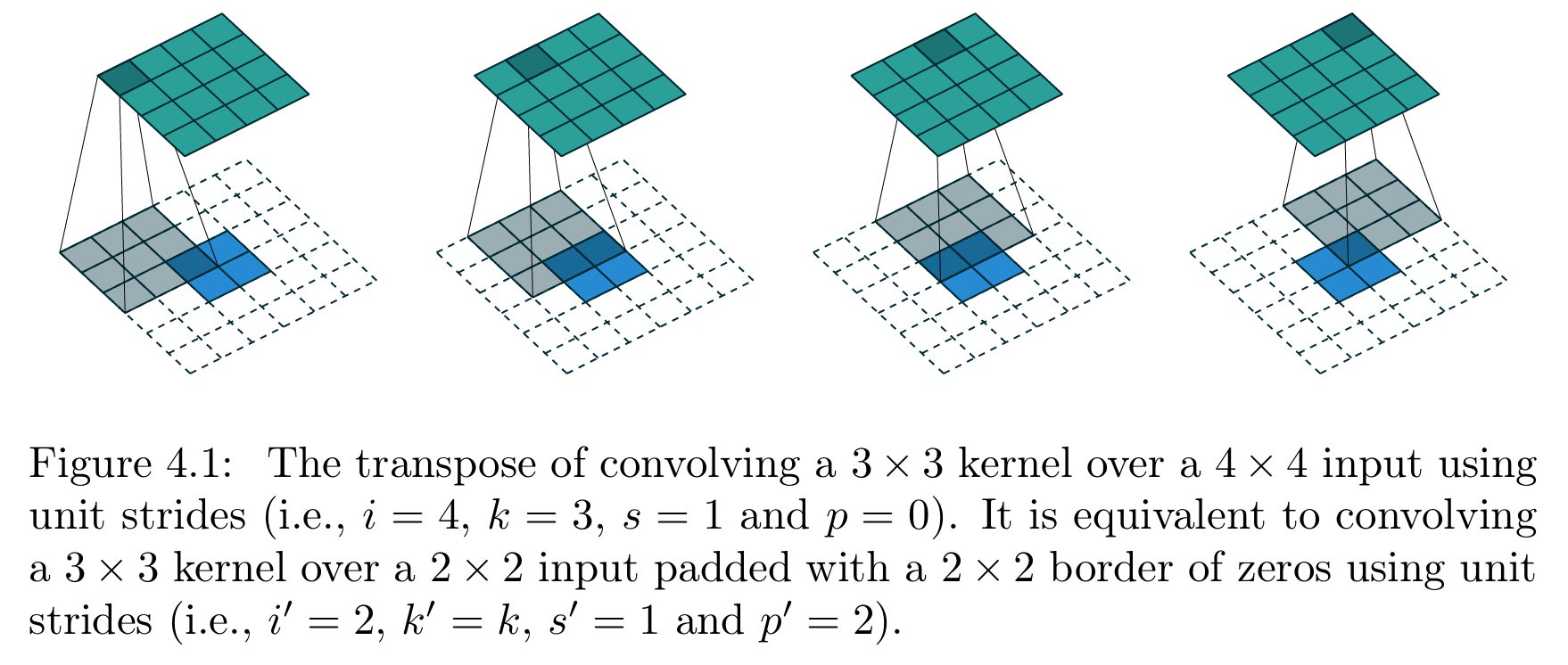
【图4.1 无填充、单位步长卷积的转置卷积操作（原卷积参数：输入尺寸 i = 4 i=4 i=4、卷积核尺寸 k = 3 k=3 k=3、步长 s = 1 s=1 s=1、零填充 p = 0 p=0 p=0，即3×3卷积核以单位步长在4×4输入上做卷积）；该转置卷积等价于：3×3卷积核以单位步长在带2×2零填充边界的2×2输入上做卷积（参数设置：输入尺寸 i ′ = 2 i'=2 i′=2、卷积核尺寸 k ′ = k k'=k k′=k、步长 s ′ = 1 s'=1 s′=1、零填充 p ′ = 2 p'=2 p′=2）】

零填充的设计逻辑，可通过转置卷积的连接模式 理解：为保持与原卷积相同的连接模式，等价普通卷积的零填充需满足：卷积核的第一次（左上角）滑动，仅与输入的左上角像素重叠------这意味着，零填充的数量需等于卷积核尺寸减1。

对输入特征图的所有像素应用这一逻辑，可推导出无零填充、单位步长转置卷积的尺寸关系：

关系式8 ：对于步长 s = 1 s=1 s=1、零填充 p = 0 p=0 p=0、卷积核尺寸为 k k k的普通卷积，其对应的转置卷积参数为：卷积核尺寸 k ′ = k k'=k k′=k、步长 s ′ = s s'=s s′=s、零填充 p ′ = k − 1 p'=k-1 p′=k−1，转置卷积的输出尺寸为：
o ′ = i ′ + ( k − 1 ) o'=i'+(k-1) o′=i′+(k−1)

有趣的是，该等价普通卷积正是单位步长的全填充卷积。

ⁱ 需注意，转置卷积无法保证恢复原输入特征图的数值 ------因为其并非卷积的逆运算，仅能恢复与原输入相同的宽度和高度。

ⁱⁱ 尽管该可视化方式与转置矩阵的运算结果等价，但通过零填充引入了大量无意义的"零相乘"操作。本指南仅将其作为可视化手段，实际的框架实现会规避这些无效运算，提升效率。

4.4 有零填充、单位步长的转置卷积

由"无零填充卷积的转置卷积，等价于对输入进行零填充的普通卷积"可合理推断：有零填充卷积的转置卷积，等价于对输入进行更少零填充的普通卷积。

这一推断已得到验证，图4.2展示了 i = 5 i=5 i=5、 k = 4 k=4 k=4、 p = 2 p=2 p=2时的有零填充卷积对应的转置卷积示例。

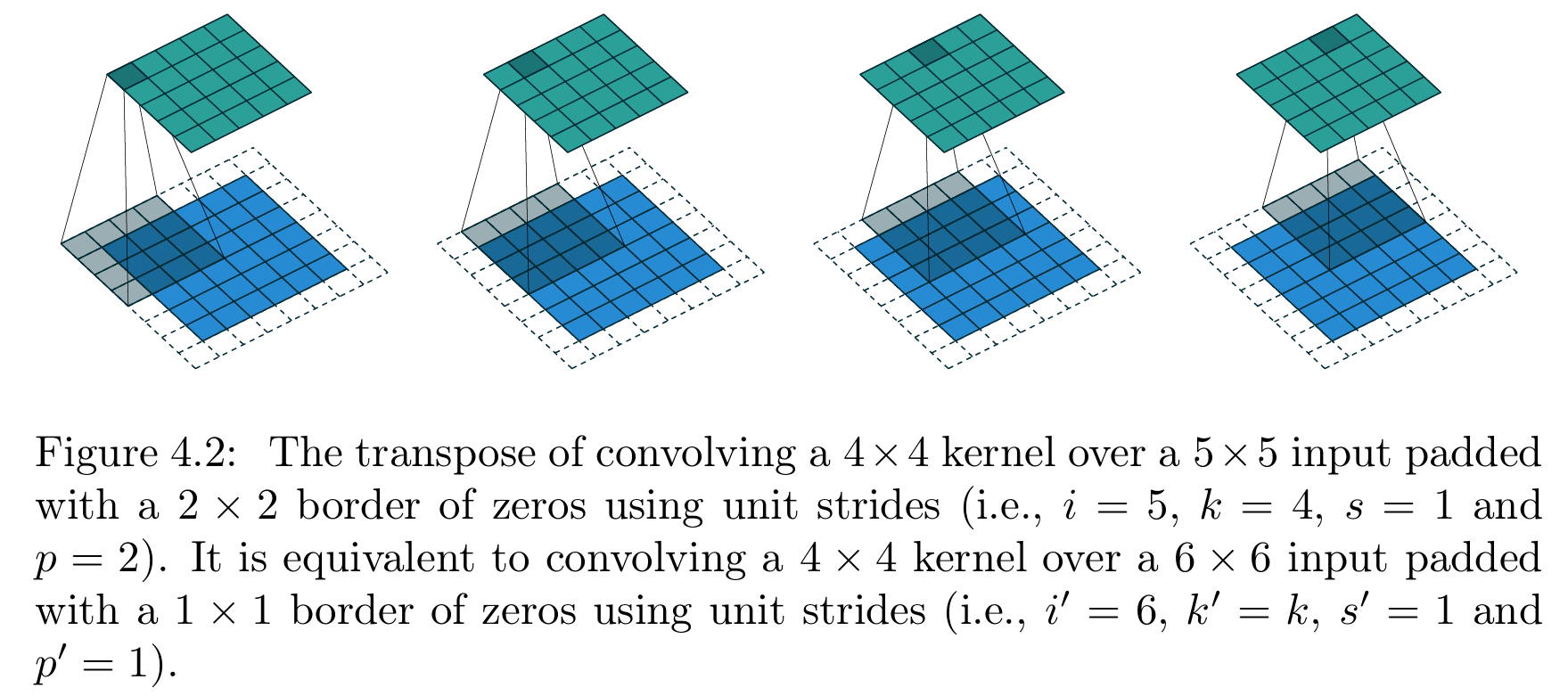
【图4.2 带填充、单位步长卷积的转置卷积操作（原卷积参数：输入尺寸 i = 5 i=5 i=5、卷积核尺寸 k = 4 k=4 k=4、步长 s = 1 s=1 s=1、零填充 p = 2 p=2 p=2，即4×4卷积核以单位步长在带2×2零填充边界的5×5输入上做卷积）；该转置卷积等价于：4×4卷积核以单位步长在带1×1零填充边界的6×6输入上做卷积（参数设置：输入尺寸 i ′ = 6 i'=6 i′=6、卷积核尺寸 k ′ = k k'=k k′=k、步长 s ′ = 1 s'=1 s′=1、零填充 p ′ = 1 p'=1 p′=1）】

形式化地，有零填充、单位步长卷积对应的转置卷积，满足以下关系：
关系式9 ：对于步长 s = 1 s=1 s=1、卷积核尺寸为 k k k、零填充数量为 p p p的普通卷积，其对应的转置卷积参数为：卷积核尺寸 k ′ = k k'=k k′=k、步长 s ′ = s s'=s s′=s、零填充 p ′ = k − p − 1 p'=k-p-1 p′=k−p−1，转置卷积的输出尺寸为：
o ′ = i ′ + ( k − 1 ) − 2 p o'=i'+(k-1)-2p o′=i′+(k−1)−2p

4.4.1 半填充的转置卷积

通过归纳推理可合理推断：半填充卷积的转置卷积，其等价普通卷积也为半填充卷积------因为半填充卷积的输出尺寸与输入尺寸相等。因此，半填充卷积对应的转置卷积满足以下关系：

关系式10 ：对于卷积核尺寸为奇数（ k = 2 n + 1 k=2n+1 k=2n+1， n n n为自然数）、步长 s = 1 s=1 s=1、零填充 p = ⌊ k / 2 ⌋ = n p=\lfloor k/2 \rfloor=n p=⌊k/2⌋=n的半填充卷积，其对应的转置卷积参数为：卷积核尺寸 k ′ = k k'=k k′=k、步长 s ′ = s s'=s s′=s、零填充 p ′ = p p'=p p′=p，转置卷积的输出尺寸为：
o ′ = i ′ + ( k − 1 ) − 2 p = i ′ + 2 n − 2 n = i ′ \begin{aligned} o' &=i'+(k-1)-2p \\ &=i'+2n-2n \\ &=i' \end{aligned} o′=i′+(k−1)−2p=i′+2n−2n=i′

图4.3展示了 i = 5 i=5 i=5、 k = 3 k=3 k=3（因此 p = 1 p=1 p=1）时的半填充卷积对应的转置卷积示例。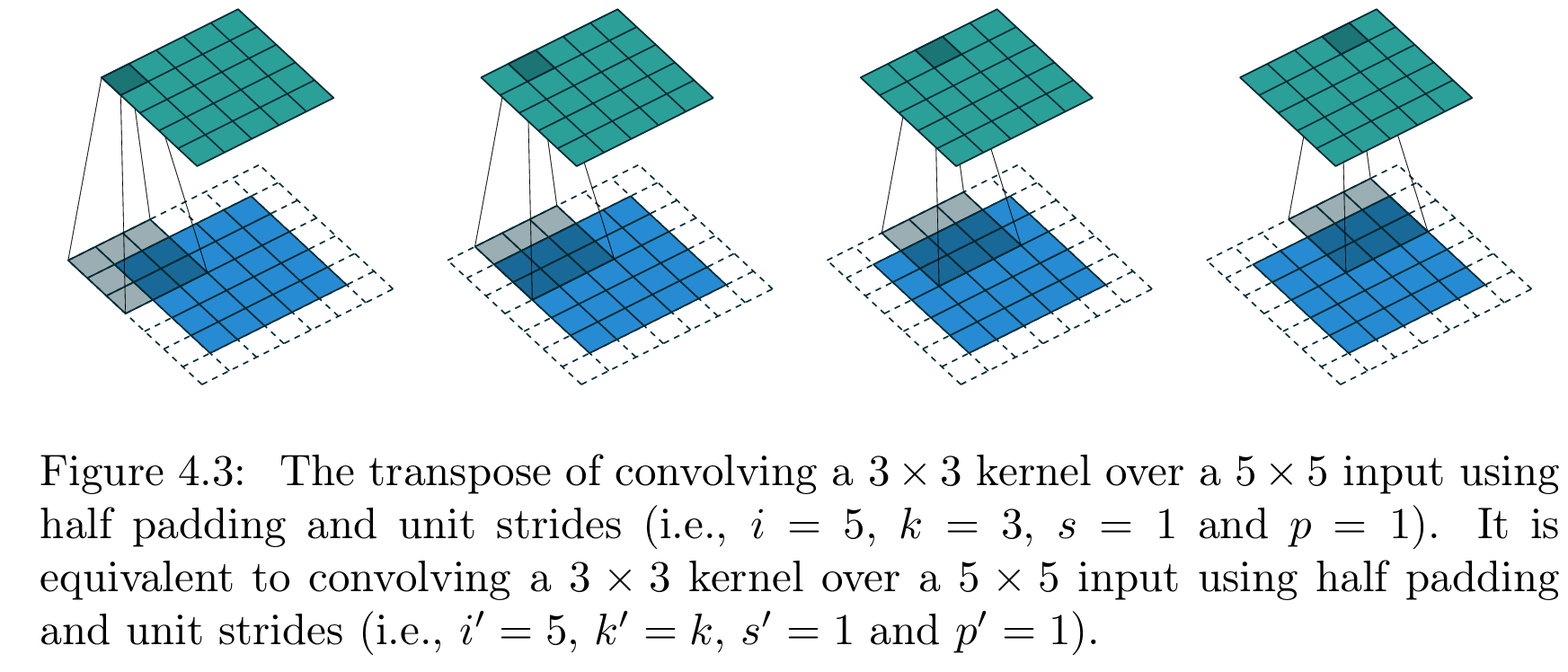

【图4.3 半填充、单位步长卷积的转置卷积操作（原卷积参数：输入尺寸 i = 5 i=5 i=5、卷积核尺寸 k = 3 k=3 k=3、步长 s = 1 s=1 s=1、零填充 p = 1 p=1 p=1，即3×3卷积核以单位步长在5×5输入上做半填充卷积）；该转置卷积等价于：3×3卷积核以单位步长在5×5输入上做半填充卷积（参数设置：输入尺寸 i ′ = 5 i'=5 i′=5、卷积核尺寸 k ′ = k k'=k k′=k、步长 s ′ = 1 s'=1 s′=1、零填充 p ′ = 1 p'=1 p′=1）】

4.4.2 全填充的转置卷积

由"无零填充卷积的转置卷积等价于全填充的普通卷积"可自然推断：全填充卷积的转置卷积，等价于无零填充的普通卷积：

关系式11 ：对于步长 s = 1 s=1 s=1、卷积核尺寸为 k k k、零填充 p = k − 1 p=k-1 p=k−1的全填充卷积，其对应的转置卷积参数为：卷积核尺寸 k ′ = k k'=k k′=k、步长 s ′ = s s'=s s′=s、零填充 p ′ = 0 p'=0 p′=0，转置卷积的输出尺寸为：
o ′ = i ′ + ( k − 1 ) − 2 p = i ′ − ( k − 1 ) \begin{aligned} o' &=i'+(k-1)-2p \\ &=i'-(k-1) \end{aligned} o′=i′+(k−1)−2p=i′−(k−1)

图4.4展示了 i = 5 i=5 i=5、 k = 3 k=3 k=3（因此 p = 2 p=2 p=2）时的全填充卷积对应的转置卷积示例。

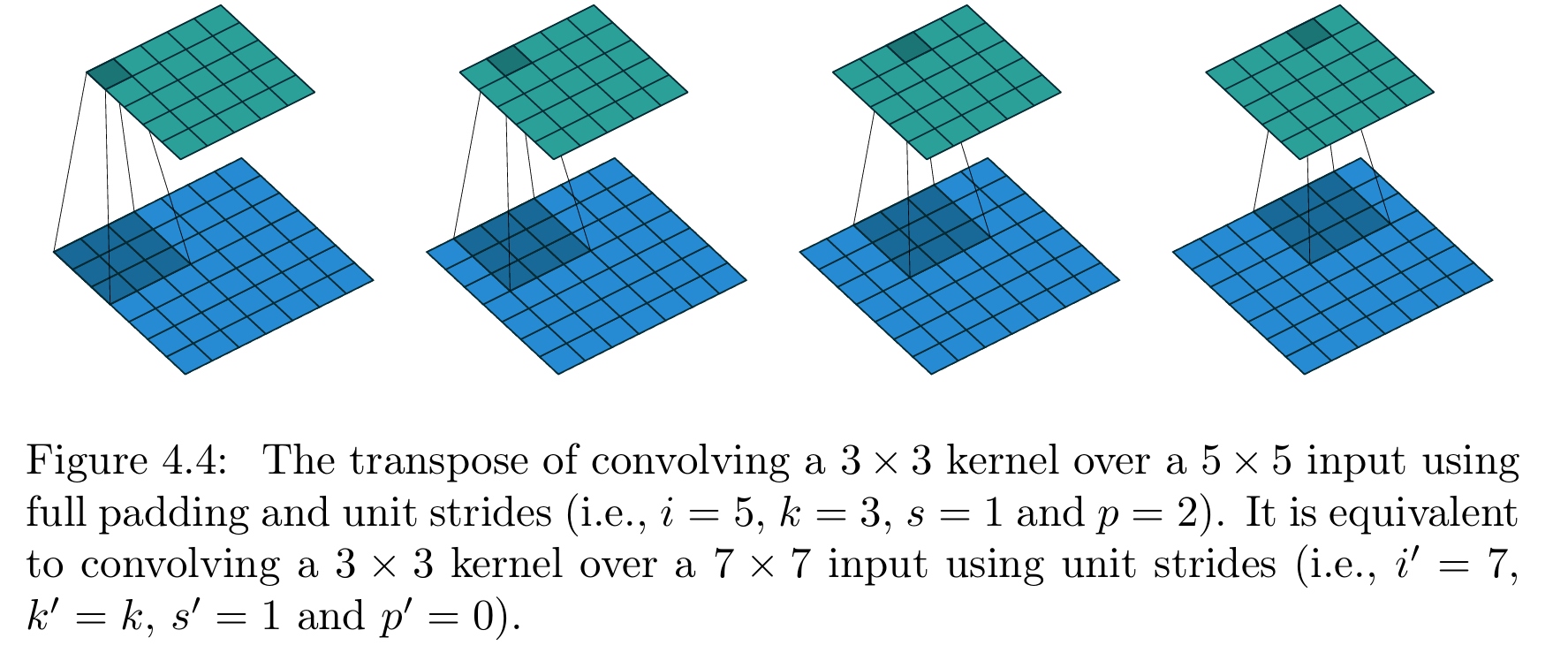
【图4.4 全填充、单位步长卷积的转置卷积操作（原卷积参数：输入尺寸 i = 5 i=5 i=5、卷积核尺寸 k = 3 k=3 k=3、步长 s = 1 s=1 s=1、零填充 p = 2 p=2 p=2，即3×3卷积核以单位步长在5×5输入上做全填充卷积）；该转置卷积等价于：3×3卷积核以单位步长在7×7输入上做卷积（无填充，参数设置：输入尺寸 i ′ = 7 i'=7 i′=7、卷积核尺寸 k ′ = k k'=k k′=k、步长 s ′ = 1 s'=1 s′=1、零填充 p ′ = 0 p'=0 p′=0）】

，即3×3卷积核以膨胀率2、单位步长在7×7输入上做空洞卷积）】

4.5 无零填充、非单位步长的转置卷积

通过与有零填充卷积转置的归纳推理相同的逻辑，可推断：步长 s > 1 s>1 s>1的卷积，其转置卷积等价于步长 s < 1 s<1 s<1的普通卷积 。这一直觉是合理的，这也是转置卷积被称为分数步长卷积的原因。

图4.5展示了 i = 5 i=5 i=5、 k = 3 k=3 k=3、 s = 2 s=2 s=2时的无零填充、非单位步长卷积对应的转置卷积示例，该示例可帮助理解分数步长 的本质：在输入元素之间插入零 ，使卷积核的滑动步距小于单位步长ⁱ。

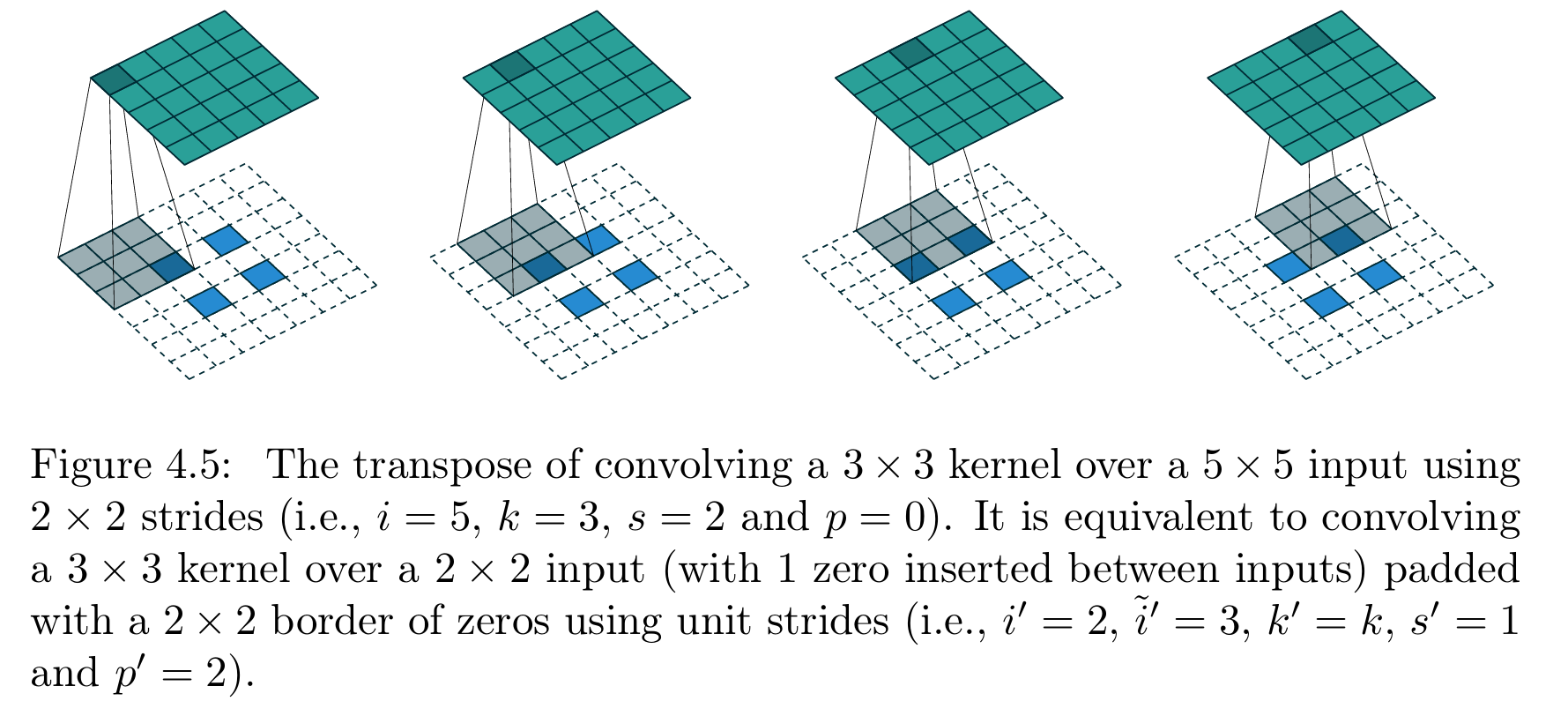
【图4.5 无填充、非单位步长卷积的转置卷积操作（原卷积参数：输入尺寸 i = 5 i=5 i=5、卷积核尺寸 k = 3 k=3 k=3、步长 s = 2 s=2 s=2、零填充 p = 0 p=0 p=0，即3×3卷积核以2×2步长在5×5输入上做卷积）；该转置卷积等价于：3×3卷积核以单位步长在带2×2零填充边界的输入插零后 的2×2特征图上做卷积（参数设置：原始输入尺寸 i ′ = 2 i'=2 i′=2、插零后输入尺寸 i ~ ′ = 3 \tilde{i}'=3 i~′=3、卷积核尺寸 k ′ = k k'=k k′=k、步长 s ′ = 1 s'=1 s′=1、零填充 p ′ = 2 p'=2 p′=2，输入插零规则：相邻元素间插入1个零）】

本节先做一个前提假设：卷积为无零填充 （ p = 0 p=0 p=0），且输入尺寸 i i i满足 i − k i-k i−k能被 s s s整除。在该假设下，无零填充、非单位步长卷积对应的转置卷积满足以下关系：

关系式12 ：对于零填充 p = 0 p=0 p=0、卷积核尺寸为 k k k、步长为 s s s，且输入尺寸满足 i − k i-k i−k能被 s s s整除的普通卷积，其对应的转置卷积参数为：输入尺寸为 i ′ i' i′（ i ′ i' i′为原输入插入零后的拉伸尺寸，相邻输入元素间插入 s − 1 s-1 s−1个零）、卷积核尺寸 k ′ = k k'=k k′=k、步长 s ′ = 1 s'=1 s′=1、零填充 p ′ = k − 1 p'=k-1 p′=k−1，转置卷积的输出尺寸为：
o ′ = s ( i ′ − 1 ) + k o'=s\left(i'-1\right)+k o′=s(i′−1)+k

ⁱ 这种实现方式效率较低，实际框架会规避无意义的零相乘操作，但从概念上，这是理解非单位步长卷积转置的有效方式。

4.6 有零填充、非单位步长的转置卷积

当普通卷积的输入尺寸 i i i满足 i + 2 p − k i+2p-k i+2p−k能被 s s s整除时，可结合关系式9和关系式12，将转置卷积的分析推广至有零填充、非单位步长的一般情况：

关系式13 ：对于卷积核尺寸为 k k k、步长为 s s s、零填充数量为 p p p，且输入尺寸满足 i + 2 p − k i+2p-k i+2p−k能被 s s s整除的普通卷积，其对应的转置卷积参数为：输入尺寸为 i ~ ′ \tilde{i}' i~′（ i ~ ′ \tilde{i}' i~′为原输入插入零后的拉伸尺寸，相邻输入元素间插入 s − 1 s-1 s−1个零）、卷积核尺寸 k ′ = k k'=k k′=k、步长 s ′ = 1 s'=1 s′=1、零填充 p ′ = k − p − 1 p'=k-p-1 p′=k−p−1，转置卷积的输出尺寸为：
o ′ = s ( i ′ − 1 ) + k − 2 p o'=s\left(i'-1\right)+k-2p o′=s(i′−1)+k−2p

图4.6展示了 i = 5 i=5 i=5、 k = 3 k=3 k=3、 s = 2 s=2 s=2、 p = 1 p=1 p=1时的有零填充、非单位步长卷积对应的转置卷积示例。

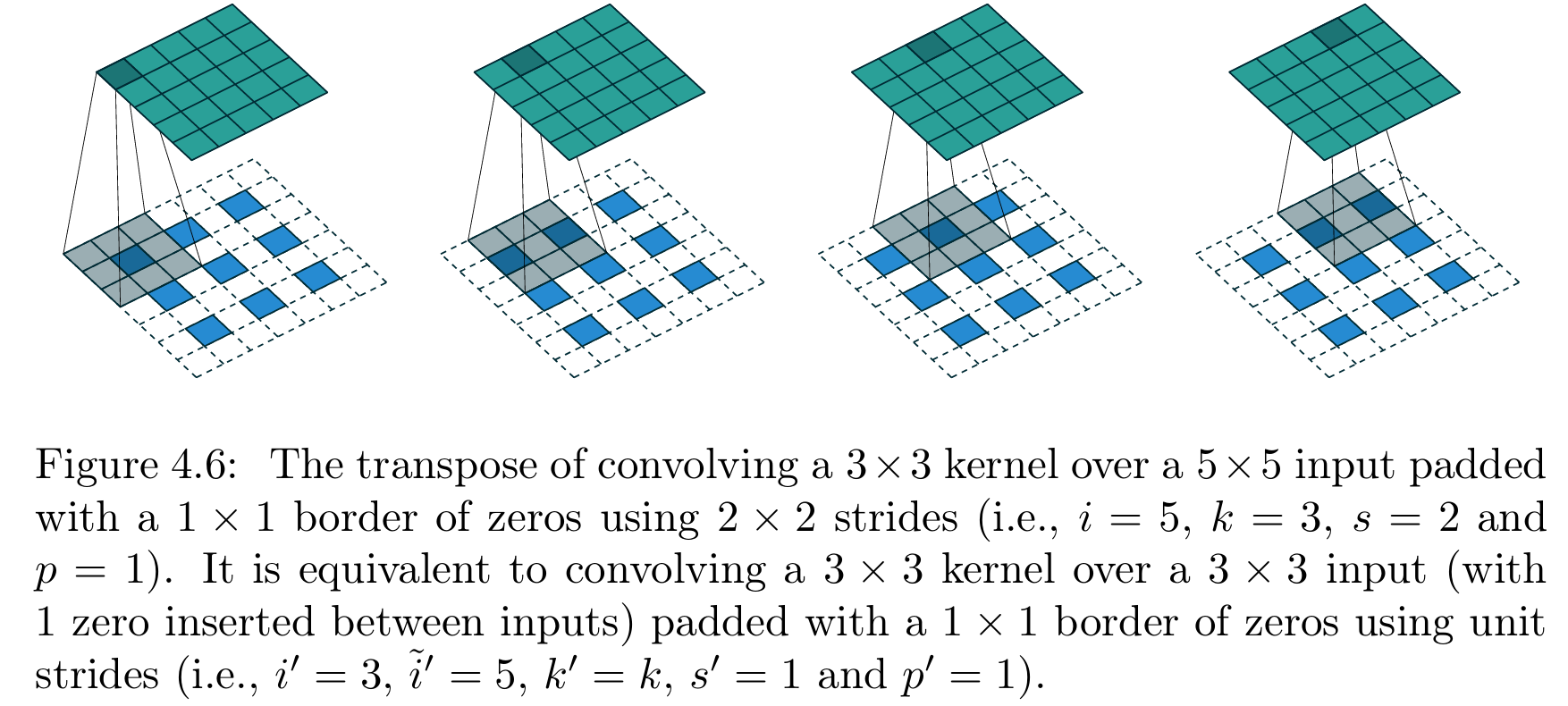
【图4.6 带填充、非单位步长卷积的转置卷积操作（原卷积参数：输入尺寸 i = 5 i=5 i=5、卷积核尺寸 k = 3 k=3 k=3、步长 s = 2 s=2 s=2、零填充 p = 1 p=1 p=1，即3×3卷积核以2×2步长在带1×1零填充边界的5×5输入上做卷积）；该转置卷积等价于：3×3卷积核以单位步长在带1×1零填充边界的输入插零后 的3×3特征图上做卷积（参数设置：原始输入尺寸 i ′ = 3 i'=3 i′=3、插零后输入尺寸 i ˉ ′ = 5 \bar{i}'=5 iˉ′=5、卷积核尺寸 k ′ = k k'=k k′=k、步长 s ′ = 1 s'=1 s′=1、零填充 p ′ = 1 p'=1 p′=1，输入插零规则：相邻元素间插入1个零）】

引入参数 a ∈ { 0 , . . . , s − 1 } a\in\{0,...,s-1\} a∈{0,...,s−1}，可解除对输入尺寸 i i i的整除约束，该参数用于区分能得到相同 i ′ i' i′的 s s s种不同输入情况：

关系式14 ：对于卷积核尺寸为 k k k、步长为 s s s、零填充数量为 p p p的普通卷积，其对应的转置卷积参数为：参数 a a a、输入尺寸为 i ~ ′ \tilde{i}' i~′（ i ~ ′ \tilde{i}' i~′为原输入插入零后的拉伸尺寸，相邻输入元素间插入 s − 1 s-1 s−1个零）、卷积核尺寸 k ′ = k k'=k k′=k、步长 s ′ = 1 s'=1 s′=1、零填充 p ′ = k − p − 1 p'=k-p-1 p′=k−p−1，其中 a = ( i + 2 p − k ) m o d s a=(i+2p-k) \mod s a=(i+2p−k)mods为输入的底部和右侧边缘补零的数量，转置卷积的输出尺寸为：
o ′ = s ( i ′ − 1 ) + a + k − 2 p o'=s\left(i'-1\right)+a+k-2p o′=s(i′−1)+a+k−2p

图4.7展示了 i = 6 i=6 i=6、 k = 3 k=3 k=3、 s = 2 s=2 s=2、 p = 1 p=1 p=1时的该类转置卷积示例。

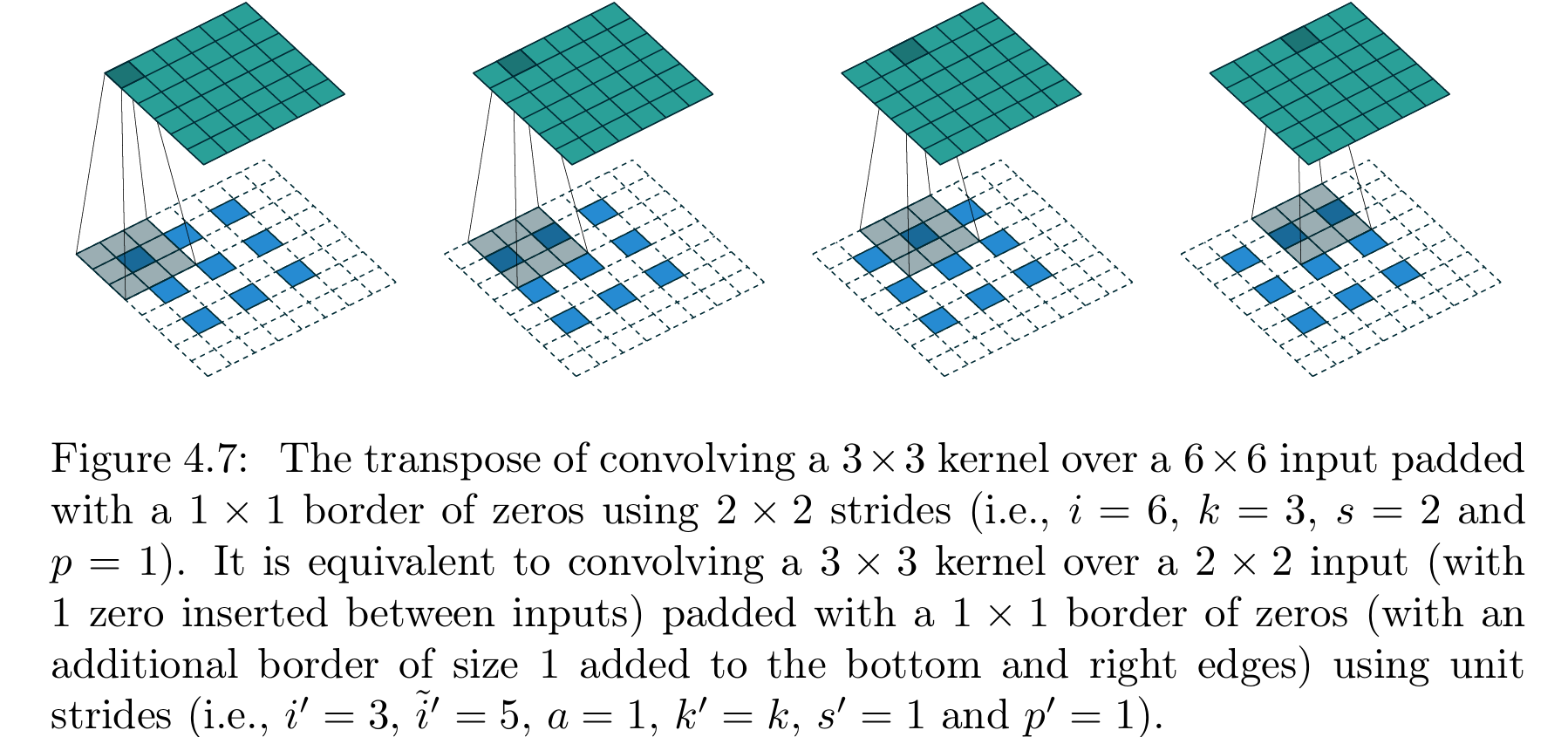
【图4.7 带填充、非单位步长卷积的转置卷积操作（原卷积参数：输入尺寸 i = 6 i=6 i=6、卷积核尺寸 k = 3 k=3 k=3、步长 s = 2 s=2 s=2、零填充 p = 1 p=1 p=1，即3×3卷积核以2×2步长在带1×1零填充边界的6×6输入上做卷积）；该转置卷积等价于：3×3卷积核以单位步长在带额外零填充+基础1×1零填充 的输入插零后2×2特征图上做卷积（参数设置：原始输入尺寸 i ′ = 3 i'=3 i′=3、插零后输入尺寸 i ˉ ′ = 5 \bar{i}'=5 iˉ′=5、额外填充参数 a = 1 a=1 a=1、卷积核尺寸 k ′ = k k'=k k′=k、步长 s ′ = 1 s'=1 s′=1、零填充 p ′ = 1 p'=1 p′=1；输入处理规则：先在相邻元素间插入1个零，再在特征图底部和右侧各加1个零的边界，最后做1×1基础零填充）】---

第5章其他类型的卷积

5.1 空洞卷积

熟悉深度学习文献的读者可能会发现，空洞卷积（dilated convolution） （也称为扩张卷积（atrous convolution），源自法语"convolutions à trous"）在近年来的研究中频繁出现。本节将帮助读者直观理解空洞卷积，若想深入学习其原理及应用场景，可参考陈等人（2014）、余和科尔通（2015）的研究。

空洞卷积的核心是在卷积核的元素之间插入间隔 ，实现卷积核的"膨胀"。其膨胀率由一个额外的超参数 d d d控制，不同框架的实现细节可能略有差异，但通常的规则是：在卷积核元素之间插入 d − 1 d-1 d−1个间隔，因此当 d = 1 d=1 d=1时，空洞卷积退化为普通卷积。

空洞卷积的优势是：无需增大卷积核尺寸，即可低成本地扩大输出单元的感受野，当多个空洞卷积堆叠时，该优势尤为明显。一个具体的应用案例是Oord等人（2016）提出的WaveNet模型------该模型是一个用于原始音频的自回归生成模型，通过空洞卷积，使新音频帧的生成能基于大量的历史音频帧上下文。

要推导膨胀率 d d d与输出尺寸 o o o的关系，首先需分析膨胀率对有效卷积核尺寸 的影响：尺寸为 k k k的卷积核，在膨胀率为 d d d时，其有效卷积核尺寸为：
k ^ = k + ( k − 1 ) ( d − 1 ) \hat{k}=k+(k-1)(d-1) k^=k+(k−1)(d−1)

将有效卷积核尺寸代入关系式6，即可得到空洞卷积的输出尺寸关系式：

关系式15 ：对于任意输入尺寸 i i i、卷积核尺寸 k k k、零填充数量 p p p、步长 s s s，以及膨胀率 d d d，空洞卷积的输出尺寸为：
o = ⌊ i + 2 p − k − ( k − 1 ) ( d − 1 ) s ⌋ + 1 o=\left\lfloor\frac{i+2p-k-(k-1)(d-1)}{s}\right\rfloor+1 o=⌊si+2p−k−(k−1)(d−1)⌋+1

图5.1展示了 i = 7 i=7 i=7、 k = 3 k=3 k=3、 d = 2 d=2 d=2时的空洞卷积示例。

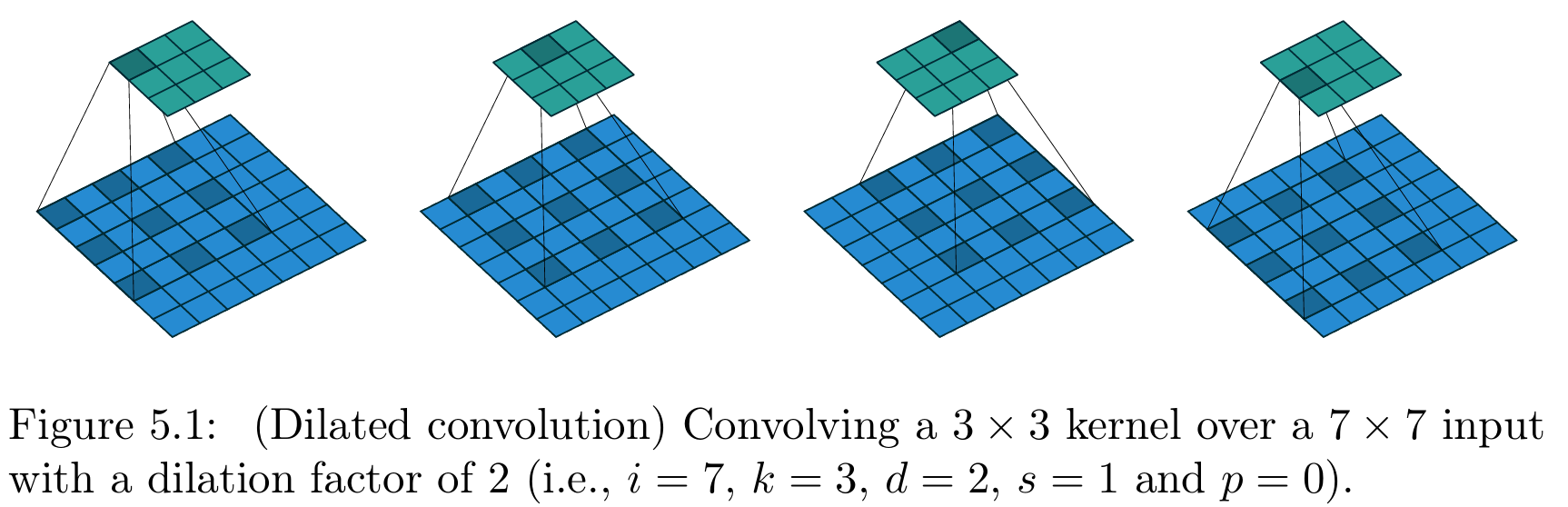
【图5.1 空洞卷积操作（参数设置：输入尺寸 i = 7 i=7 i=7、卷积核尺寸 k = 3 k=3 k=3、膨胀率 d = 2 d=2 d=2、步长 s = 1 s=1 s=1、零填充 p = 0 p=0 p=0

参考文献

（注：因参考文献为英文文献标引，为保证准确性，此处保留原文形式）

Abadi, M., Agarwal, A., Barham, P., Brevdo, E., Chen, Z., Citro, C., Corrado, G. S., Davis, A., Dean, J., Devin, M., et al. (2015). Tensorflow: Large-scale machine learning on heterogeneous systems. Software available from tensorflow.org.

Bastien, F., Lamblin, P., Pascanu, R., Bergstra, J., Goodfellow, I., Bergeron, A., Bouchard, N., Warde-Farley, D., and Bengio, Y. (2012). Theano: new features and speed improvements. arXiv preprint arXiv:1211.5590.

Bergstra, J., Breuleux, O., Bastien, F., Lamblin, P., Pascanu, R., Desjardins, G., Turian, J., Warde-Farley, D., and Bengio, Y. (2010). Theano: A cpu and gpu math compiler in python. In Proc. 9th Python in Science Conf , pages 1--7.

Boureau, Y., Bach, F., LeCun, Y., and Ponce, J. (2010a). Learning mid-level features for recognition. In Proc. International Conference on Computer Vision and Pattern Recognition (CVPR'10). IEEE.

Boureau, Y., Ponce, J., and LeCun, Y. (2010b). A theoretical analysis of feature pooling in vision algorithms. In Proc. International Conference on Machine learning (ICML'10).

Boureau, Y., Le Roux, N., Bach, F., Ponce, J., and LeCun, Y. (2011). Ask the locals: multi-way local pooling for image recognition. In Proc. International Conference on Computer Vision (ICCV'11). IEEE.

Chen, L.-C., Papandreou, G., Kokkinos, I., Murphy, K., and Yuille, A. L. (2014). Semantic image segmentation with deep convolutional nets and fully connected crfs. arXiv preprint arXiv:1412.7062.

Collobert, R., Kavukcuoglu, K., and Farabet, C. (2011). Torch7: A matlab-like environment for machine learning. In BigLearn, NIPS Workshop, number EPFL-CONF-192376.

Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep learning. Book in preparation for MIT Press.

Im, D. J., Kim, C. D., Jiang, H., and Memisevic, R. (2016). Generating images with recurrent adversarial networks. arXiv preprint arXiv:1602.05110.

Jia, Y., Shelhamer, E., Donahue, J., Karayev, S., Long, J., Girshick, R., Guadarrama, S., and Darrell, T. (2014). Caffe: Convolutional architecture for fast feature embedding. In Proceedings of the ACM International Conference on Multimedia, pages 675--678. ACM.

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Imagenet classification with deep convolutional neural networks. In Advances in neural information processing systems, pages 1097--1105.

Le Cun, Y., Bottou, L., and Bengio, Y. (1997). Reading checks with multilayer graph transformer networks. In Acoustics, Speech, and Signal Processing, 1997. ICASSP-97., 1997 IEEE International Conference on, volume 1, pages 151--154. IEEE.

Long, J., Shelhamer, E., and Darrell, T. (2015). Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 3431--3440.

Oord, A. v. d., Dieleman, S., Zen, H., Simonyan, K., Vinyals, O., Graves, A., Kalchbrenner, N., Senior, A., and Kavukcuoglu, K. (2016). Wavenet: A generative model for raw audio. arXiv preprint arXiv:1609.03499.

Radford, A., Metz, L., and Chintala, S. (2015). Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv preprint arXiv:1511.06434.

Saxe, A., Koh, P. W., Chen, Z., Bhand, M., Suresh, B., and Ng, A. (2011). On random weights and unsupervised feature learning. In L. Getoor and T. Scheffer, editors, Proceedings of the 28th International Conference on Machine Learning (ICML-11), ICML '11, pages 1089--1096, New York, NY, USA. ACM.

Visin, F., Kastner, K., Courville, A. C., Bengio, Y., Matteucci, M., and Cho, K. (2015). Reseg: A recurrent neural network for object segmentation.

Yu, F. and Koltun, V. (2015). Multi-scale context aggregation by dilated convolutions. arXiv preprint arXiv:1511.07122.

Zeiler, M. D. and Fergus, R. (2014). Visualizing and understanding convolutional networks. In Computer vision--ECCV 2014, pages 818--833. Springer.

Zeiler, M. D., Taylor, G. W., and Fergus, R. (2011). Adaptive deconvolutional networks for mid and high level feature learning. In Computer Vision (ICCV), 2011 IEEE International Conference on, pages 2018--2025. IEEE.