Leetcode 122 二叉树的最近公共祖先 | 二叉搜索树迭代器

im_AMBER2026-02-16 12:54

1 题目

236. 二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为："对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。"

示例 1：

复制代码 
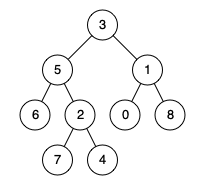
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2：

复制代码 
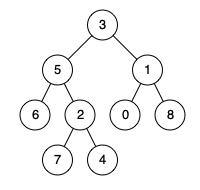
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

复制代码 
输入：root = [1,2], p = 1, q = 2
输出：1

提示：

  • 树中节点数目在范围 [2, 105] 内。
  • -109 <= Node.val <= 109
  • 所有 Node.val 互不相同 。
  • p != q
  • p 和 q 均存在于给定的二叉树中。

2 代码实现

c++

cpp 复制代码 
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root == nullptr || root == p || root == q ){
            return root ;
        }
        TreeNode* left = lowestCommonAncestor(root -> left , p , q ) ;
        TreeNode* right = lowestCommonAncestor(root -> right , p , q );

        if (left == nullptr){
            return right ;
        }

        if (right == nullptr){
            return left ;
        }
        return root ;
    }
};

js

javascript 复制代码 
/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {TreeNode}
 */
var lowestCommonAncestor = function(root, p, q) {
    if (root == null || root == p || root == q ){
        return root ;
    }

    let left = lowestCommonAncestor (root.left , p , q );
    let right = lowestCommonAncestor (root.right , p , q );

    if (left == null){
        return right ;
    }
    if (right == null){
        return left ;
    }

    return root ;
};

思考

看不太懂，也不知道怎么实现。

题解

你想实现二叉树最近公共祖先（LCA）的查找功能，并且希望用 C++ 来完成这个实现，目前你对这个问题的解法思路还不太清晰。我会先帮你理解核心逻辑，再给出完整的可运行代码。

核心思路理解

要找到二叉树中两个节点的最近公共祖先，最经典且高效的解法是递归法，核心逻辑可以总结为：

  1. 递归遍历二叉树的左、右子树
  2. 递归终止条件：遇到空节点 或 找到了 p/q 节点，直接返回当前节点
  3. 递归判断逻辑：
    • 如果左子树返回空，说明 p/q 都在右子树，返回右子树的结果
    • 如果右子树返回空，说明 p/q 都在左子树，返回左子树的结果
    • 如果左右子树都有返回值，说明当前节点就是最近公共祖先

C++ 完整实现代码

cpp 复制代码 
#include <iostream>
#include <vector>
using namespace std;

// 定义二叉树节点结构
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        // 递归终止条件：
        // 1. 节点为空，返回null
        // 2. 找到p或q节点，直接返回该节点
        if (root == nullptr || root == p || root == q) {
            return root;
        }

        // 递归遍历左子树
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        // 递归遍历右子树
        TreeNode* right = lowestCommonAncestor(root->right, p, q);

        // 核心判断逻辑
        if (left == nullptr) {
            // 左子树没找到，说明p/q都在右子树，返回右子树结果
            return right;
        }
        if (right == nullptr) {
            // 右子树没找到，说明p/q都在左子树，返回左子树结果
            return left;
        }
        // 左右子树都找到，说明当前节点就是最近公共祖先
        return root;
    }
};

// 辅助函数：根据数组构建二叉树（方便测试）
TreeNode* buildTree(vector<int>& nums, int index) {
    if (index >= nums.size() || nums[index] == -1) {
        return nullptr;
    }
    TreeNode* root = new TreeNode(nums[index]);
    root->left = buildTree(nums, 2 * index + 1);
    root->right = buildTree(nums, 2 * index + 2);
    return root;
}

// 辅助函数：根据值查找节点（方便测试）
TreeNode* findNode(TreeNode* root, int val) {
    if (root == nullptr) return nullptr;
    if (root->val == val) return root;
    TreeNode* left = findNode(root->left, val);
    if (left != nullptr) return left;
    return findNode(root->right, val);
}

// 测试示例
int main() {
    // 示例1测试：root = [3,5,1,6,2,0,8,-1,-1,7,4]
    vector<int> nums1 = {3,5,1,6,2,0,8,-1,-1,7,4};
    TreeNode* root1 = buildTree(nums1, 0);
    TreeNode* p1 = findNode(root1, 5);
    TreeNode* q1 = findNode(root1, 1);
    Solution s;
    TreeNode* res1 = s.lowestCommonAncestor(root1, p1, q1);
    cout << "示例1结果：" << res1->val << endl; // 输出3

    // 示例2测试：root = [3,5,1,6,2,0,8,-1,-1,7,4], p=5, q=4
    TreeNode* p2 = findNode(root1, 5);
    TreeNode* q2 = findNode(root1, 4);
    TreeNode* res2 = s.lowestCommonAncestor(root1, p2, q2);
    cout << "示例2结果：" << res2->val << endl; // 输出5

    // 示例3测试：root = [1,2], p=1, q=2
    vector<int> nums3 = {1,2};
    TreeNode* root3 = buildTree(nums3, 0);
    TreeNode* p3 = findNode(root3, 1);
    TreeNode* q3 = findNode(root3, 2);
    TreeNode* res3 = s.lowestCommonAncestor(root3, p3, q3);
    cout << "示例3结果：" << res3->val << endl; // 输出1

    return 0;
}
cpp 复制代码 
#include <iostream>
using namespace std;

// 二叉树节点
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        // 终止条件：
        // 1. 走到头了（空节点），返回空
        // 2. 找到p或q了，返回这个节点
        if (root == NULL || root == p || root == q) {
            return root;
        }

        // 派左小弟去左子树找
        TreeNode* 左小弟汇报 = lowestCommonAncestor(root->left, p, q);
        // 派右小弟去右子树找
        TreeNode* 右小弟汇报 = lowestCommonAncestor(root->right, p, q);

        // 开始判断：
        if (左小弟汇报 == NULL) {
            // 左小弟没找到，说明p/q都在右边，返回右小弟的结果
            return 右小弟汇报;
        }
        if (右小弟汇报 == NULL) {
            // 右小弟没找到，说明p/q都在左边，返回左小弟的结果
            return 左小弟汇报;
        }
        // 左右小弟都找到了人 → 说明p和q分别在我左右两边，我就是最近老祖宗
        return root;
    }
};

// 测试：手动构建示例2的树
int main() {
    // 构建树
    TreeNode* root = new TreeNode(3);
    root->left = new TreeNode(5);
    root->right = new TreeNode(1);
    root->left->left = new TreeNode(6);
    root->left->right = new TreeNode(2);
    root->left->right->left = new TreeNode(7);
    root->left->right->right = new TreeNode(4);

    // 要找的两个节点
    TreeNode* p = root->left;   // 节点5
    TreeNode* q = root->left->right->right; // 节点4

    Solution s;
    TreeNode* res = s.lowestCommonAncestor(root, p, q);
    cout << "最近公共祖先是：" << res->val << endl; // 输出5
    return 0;
}

代码关键部分解释

  1. TreeNode 结构体：定义二叉树节点，包含值、左子节点、右子节点
  2. lowestCommonAncestor 核心函数 ：
    • 终止条件：遇到空节点或目标节点直接返回
    • 递归遍历左右子树，分别获取查找结果
    • 根据左右子树的返回值判断公共祖先位置
  3. 辅助函数 ：
    • buildTree：根据数组构建二叉树（-1 表示空节点）
    • findNode：根据值查找对应的节点指针（方便测试）
  4. main 函数：测试题目中的 3 个示例，验证代码正确性

运行说明

  1. 环境要求：支持 C++11 及以上的编译器（如 g++、clang++）
  2. 编译命令：g++ -std=c++11 lca.cpp -o lca
  3. 运行命令：./lca
  4. 输出结果：会依次打印 3 个示例的结果（3、5、1）

总结

  1. 二叉树最近公共祖先的核心解法是后序递归遍历，先找左右子树的结果，再回溯判断当前节点是否为公共祖先
  2. 递归终止条件是找到目标节点或空节点，核心判断逻辑是：左右都有结果则当前节点是 LCA，否则返回非空的一侧
  3. 该解法时间复杂度 O (n)（遍历所有节点），空间复杂度 O (n)（递归栈深度），是最优解法之一

3 题目

173. 二叉搜索树迭代器

实现一个二叉搜索树迭代器类BSTIterator ，表示一个按中序遍历二叉搜索树（BST）的迭代器：

  • BSTIterator(TreeNode root) 初始化 BSTIterator 类的一个对象。BST 的根节点 root 会作为构造函数的一部分给出。指针应初始化为一个不存在于 BST 中的数字，且该数字小于 BST 中的任何元素。
  • boolean hasNext() 如果向指针右侧遍历存在数字，则返回 true ；否则返回 false 。
  • int next()将指针向右移动，然后返回指针处的数字。

注意，指针初始化为一个不存在于 BST 中的数字，所以对 next() 的首次调用将返回 BST 中的最小元素。

你可以假设 next() 调用总是有效的，也就是说，当调用 next() 时，BST 的中序遍历中至少存在一个下一个数字。

示例：

复制代码 
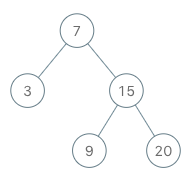
输入
["BSTIterator", "next", "next", "hasNext", "next", "hasNext", "next", "hasNext", "next", "hasNext"]
[[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []]
输出
[null, 3, 7, true, 9, true, 15, true, 20, false]

解释
BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);
bSTIterator.next();    // 返回 3
bSTIterator.next();    // 返回 7
bSTIterator.hasNext(); // 返回 True
bSTIterator.next();    // 返回 9
bSTIterator.hasNext(); // 返回 True
bSTIterator.next();    // 返回 15
bSTIterator.hasNext(); // 返回 True
bSTIterator.next();    // 返回 20
bSTIterator.hasNext(); // 返回 False

提示：

  • 树中节点的数目在范围 [1, 105] 内
  • 0 <= Node.val <= 106
  • 最多调用 105 次 hasNext 和 next 操作

进阶：

  • 你可以设计一个满足下述条件的解决方案吗？next() 和 hasNext() 操作均摊时间复杂度为 O(1) ，并使用 O(h) 内存。其中 h 是树的高度。

4 代码实现

c++

cpp 复制代码 
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class BSTIterator {
private: 
    stack<TreeNode*> stk ;

    void pushAllLeft (TreeNode* node ){
        while (node != nullptr){
            stk.push(node);
            node = node -> left ;
        }
    }
public:
    BSTIterator(TreeNode* root) {
        pushAllLeft (root );
    }
    
    int next() {
        TreeNode* cur = stk.top();
        stk.pop();

        if (cur -> right != nullptr){
            pushAllLeft(cur -> right );
        }
        return cur -> val ;
    }
    
    bool hasNext() {
        return !stk.empty();
    }
};

/**
 * Your BSTIterator object will be instantiated and called as such:
 * BSTIterator* obj = new BSTIterator(root);
 * int param_1 = obj->next();
 * bool param_2 = obj->hasNext();
 */

js

javascript 复制代码 
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 */
var BSTIterator = function(root) {
    this.stack = [] ;
    let node = root ;
    while (node !== null){
        this.stack.push(node);
        node = node.left ;
    }
};

/**
 * @return {number}
 */
BSTIterator.prototype.next = function() {
    const cur = this.stack.pop();
    let node = cur.right ;
    while (node !== null ){
        this.stack.push(node);
        node = node.left ;
    }
    return cur.val;
};

/**
 * @return {boolean}
 */
BSTIterator.prototype.hasNext = function() {
    return this.stack.length > 0 ;
};

/** 
 * Your BSTIterator object will be instantiated and called as such:
 * var obj = new BSTIterator(root)
 * var param_1 = obj.next()
 * var param_2 = obj.hasNext()
 */

你现在想实现二叉搜索树（BST）迭代器，要求支持 next()（返回中序遍历下一个元素）和 hasNext()（判断是否有下一个元素），并且希望用 C++ 完成，还需要理解进阶要求（均摊 O (1) 时间、O (h) 空间）。我先帮你理清核心思路，再给出完整的可运行代码，确保新手也能看懂。

核心思路理解

首先明确两个关键前提：

  1. BST 的特性 ：中序遍历 BST 的结果是升序序列（这是解题的核心）；
  2. 进阶要求分析 ：
    • 不能先把所有节点遍历存到数组里（空间复杂度会是 O (n)，不满足 O (h)）；
    • 需要用迭代式中序遍历的思路，用栈模拟递归，只保存从根到当前节点的路径（空间 O (h)，h 是树高）；
    • 均摊 O (1)：每个节点最多入栈、出栈各一次，总操作次数 O (n)，分摊到 n 次next()调用就是 O (1)。

核心实现逻辑（模拟 "受控的中序遍历"）：

  1. 构造函数：把根节点的所有左子节点依次入栈（找到最小元素的路径）；
  2. next() ：弹出栈顶节点（当前最小元素），如果该节点有右子节点，把右子节点的所有左子节点入栈（为下一次next()做准备）；
  3. hasNext()：只需判断栈是否为空（栈空则没有下一个元素）。

C++ 完整实现代码

cpp 复制代码 
#include <iostream>
#include <stack>
using namespace std;

// 二叉树节点定义（题目给定）
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

class BSTIterator {
private:
    // 用栈保存待遍历的节点（核心数据结构）
    stack<TreeNode*> stk;

    // 辅助函数：把某个节点的所有左子节点依次入栈
    void pushAllLeft(TreeNode* node) {
        while (node != nullptr) {
            stk.push(node);
            node = node->left; // 一直往左走，找最小的路径
        }
    }

public:
    // 构造函数：初始化栈，找到最小元素的路径
    BSTIterator(TreeNode* root) {
        pushAllLeft(root);
    }
    
    // 返回下一个元素（升序）
    int next() {
        // 栈顶就是当前最小的元素
        TreeNode* curr = stk.top();
        stk.pop();

        // 如果当前节点有右子树，把右子树的所有左节点入栈
        if (curr->right != nullptr) {
            pushAllLeft(curr->right);
        }

        return curr->val;
    }
    
    // 判断是否有下一个元素
    bool hasNext() {
        // 栈不为空就有下一个元素
        return !stk.empty();
    }
};

// 测试示例
int main() {
    // 构建示例中的树：
    //        7
    //       / \
    //      3  15
    //        /  \
    //       9   20
    TreeNode* root = new TreeNode(7);
    root->left = new TreeNode(3);
    root->right = new TreeNode(15);
    root->right->left = new TreeNode(9);
    root->right->right = new TreeNode(20);

    // 初始化迭代器
    BSTIterator* obj = new BSTIterator(root);
    
    // 模拟题目中的调用流程
    cout << obj->next() << endl;    // 输出3
    cout << obj->next() << endl;    // 输出7
    cout << boolalpha << obj->hasNext() << endl; // 输出true
    cout << obj->next() << endl;    // 输出9
    cout << boolalpha << obj->hasNext() << endl; // 输出true
    cout << obj->next() << endl;    // 输出15
    cout << boolalpha << obj->hasNext() << endl; // 输出true
    cout << obj->next() << endl;    // 输出20
    cout << boolalpha << obj->hasNext() << endl; // 输出false

    // 释放内存（新手可暂时忽略，重点看逻辑）
    delete obj;
    delete root->right->right;
    delete root->right->left;
    delete root->right;
    delete root->left;
    delete root;

    return 0;
}

代码关键部分解释

  1. 栈的作用：

    • 栈里保存的是 "待访问" 的节点，且始终保证栈顶是当前未访问的最小元素；
    • 比如构造函数处理示例树时，栈会依次压入 7 → 3（因为先压 7，再压 7 的左子节点 3），栈顶是 3（最小元素）。

  2. pushAllLeft 辅助函数：

    • 核心功能是 "一路向左走到底"，把路径上的节点都入栈；
    • 比如处理节点 15 的右子节点时，会压入 15 → 9（15 的左子节点），保证栈顶是 9。

  3. next () 函数执行流程（示例中第一次调用）：

    • 弹出栈顶 3，返回 3；
    • 3 没有右子节点，栈里剩下 7；
    • 第二次调用 next ()：弹出 7，返回 7；7 有右子节点 15，调用 pushAllLeft (15)，栈压入 15 → 9，栈顶变为 9；
    • 第三次调用 next ()：弹出 9，返回 9；9 没有右子节点，栈里剩下 15；以此类推。

  4. hasNext () 函数：

    • 只需判断栈是否为空，逻辑极简单，时间复杂度 O (1)。

运行说明

  1. 环境要求：支持 C++11 及以上的编译器（g++、clang++ 均可）；
  2. 编译命令：g++ -std=c++11 bst_iterator.cpp -o bst_iterator；
  3. 运行命令：./bst_iterator；
  4. 输出结果：依次打印 3、7、true、9、true、15、true、20、false，和题目示例一致。

进阶要求验证

  • 时间复杂度：每个节点最多入栈、出栈各一次，n 次 next () 调用总操作数 O (n)，均摊到每次 next () 是 O (1)；hasNext () 是纯判断，O (1)；
  • 空间复杂度：栈最多保存树的高度 h 个节点（比如斜树 h=n，平衡树 h=logn），满足 O (h) 的要求。

总结

  1. BST 迭代器的核心是利用 BST 中序遍历升序的特性，结合栈模拟迭代式中序遍历；
  2. 关键操作是 "构造函数一路左压栈，next () 弹出栈顶后处理右子树的左路径"；
  3. 进阶要求的核心是 "不预存所有节点，只存当前路径"，用栈控制遍历节奏，实现 O (h) 空间和均摊 O (1) 时间。

理解题意

先把题目翻译成 "人话"

这个题的核心需求是：做一个 "工具"，能按 "从小到大" 的顺序，逐个取出二叉搜索树（BST）里的节点值。

我们拆解题目里的关键描述：

题目里的抽象说法 大白话解释
二叉搜索树迭代器（BSTIterator） 一个专门用来 "遍历 BST" 的工具
指针初始化为小于 BST 中任何元素的数字 这个 "指针" 一开始指向 "最小元素的左边"，第一次取就是最小的数
hasNext() 问："工具里还有没取的数吗？"（有就返回 true，没有返回 false）
next() 做两件事：1. 把 "指针" 移到下一个数；2. 返回这个数（第一次调用返回最小的数）

用生活例子理解（超形象）

把 BST 想象成一个按从小到大排好的书架（因为 BST 的中序遍历就是升序）：

  • 书架上的书：3 → 7 → 9 → 15 → 20（对应示例里的 BST）；
  • 迭代器（BSTIterator）：就是你的 "取书手"；
  • 初始化（BSTIterator (root)）：把手放在 "3 的左边"（还没碰到任何书）；
  • next ()：手伸到下一本书，把书拿出来给你（第一次拿 3，第二次拿 7，依此类推）；
  • hasNext ()：看看手的右边还有没有书（比如拿完 20 后，右边没书了，返回 false）。

题目示例的调用流程，翻译成 "取书" 就是：

复制代码 
初始化手 → 拿第一本书（3）→ 拿第二本书（7）→ 问：还有书吗？（有→true）→ 拿第三本书（9）→ 问：还有书吗？（有→true）→ 拿第四本书（15）→ 问：还有书吗？（有→true）→ 拿第五本书（20）→ 问：还有书吗？（没有→false）

结合代码，逐步模拟示例的执行过程

还是用示例里的树：

复制代码 
        7
       / \
      3  15
        /  \
       9   20

我们一步步看代码里的栈和函数调用变化：

步骤 1：初始化（BSTIterator (root)）

调用pushAllLeft(root)，也就是从 7 开始 "一路往左压栈"：

  • 压入 7 → 压入 7 的左子节点 3（3 没有左子节点，停止）；
  • 此时栈里的元素（栈底→栈顶）：7 → 3；
  • 对应 "取书手" 的状态：停在 3 的左边，准备拿 3。
步骤 2：第一次调用 next ()
  • 弹出栈顶 3，返回 3（拿到第一本书）；
  • 3 没有右子节点，栈里剩下 7；
  • 对应 "取书手"：移到 3 的位置，拿完 3 后，手停在 7 的左边。
步骤 3：第二次调用 next ()
  • 弹出栈顶 7，返回 7（拿到第二本书）；
  • 7 有右子节点 15，调用pushAllLeft(15)：压入 15 → 压入 15 的左子节点 9（9 没有左子节点，停止）；
  • 此时栈里的元素：15 → 9；
  • 对应 "取书手"：移到 7 的位置，拿完 7 后，手停在 9 的左边。
步骤 4：调用 hasNext ()
  • 栈不为空（有 15、9），返回 true（还有书）。
步骤 5：第三次调用 next ()
  • 弹出栈顶 9，返回 9（拿到第三本书）；
  • 9 没有右子节点，栈里剩下 15；
  • 对应 "取书手"：移到 9 的位置，拿完 9 后，手停在 15 的左边。
步骤 6：调用 hasNext ()
  • 栈不为空（有 15），返回 true（还有书）。
步骤 7：第四次调用 next ()
  • 弹出栈顶 15，返回 15（拿到第四本书）；
  • 15 有右子节点 20，调用pushAllLeft(20)：压入 20（20 没有左子节点，停止）；
  • 此时栈里的元素：20；
  • 对应 "取书手"：移到 15 的位置，拿完 15 后，手停在 20 的左边。
步骤 8：调用 hasNext ()
  • 栈不为空（有 20），返回 true（还有书）。
步骤 9：第五次调用 next ()
  • 弹出栈顶 20，返回 20（拿到第五本书）；
  • 20 没有右子节点，栈为空；
  • 对应 "取书手"：移到 20 的位置，拿完 20 后，手右边没书了。
步骤 10：调用 hasNext ()
  • 栈为空，返回 false（没有书了）。

为什么要这么设计（补充理解）

题目里的 "进阶要求"（均摊 O (1) 时间、O (h) 空间），本质是不让你 "作弊"：

  • 不能一开始就把所有数存到数组里（比如先遍历一遍存 [3,7,9,15,20]，然后 next () 就取数组下标）------ 这种方法空间是 O (n)，不符合 O (h) 的要求；
  • 用栈的方式，只存 "当前要取的数的路径"（比如初始化时只存 7、3，而不是所有数），空间只和树的高度 h 有关（示例里树高是 3），效率更高。

总结

  1. 题目核心：做一个 "按从小到大取数" 的工具，支持 "取下一个数" 和 "判断有没有下一个数" 两个操作；
  2. 核心思路：利用 BST 中序遍历升序的特性，用栈模拟 "一路往左找最小数"，取完一个数后处理右子树的左路径；
  3. 关键操作：
    • 初始化：把根的所有左子节点压栈（找到最小数的路径）；
    • next ()：弹栈顶（取数），有右子树就压右子树的所有左节点；
    • hasNext ()：看栈空不空。

JS 完整实现代码

javascript 复制代码 
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 */
var BSTIterator = function(root) {
    // 用数组模拟栈（JS里数组的push/pop就是栈的操作）
    this.stack = [];
    // 初始化：把根节点的所有左子节点压入栈
    this.pushAllLeft(root);
};

/**
 * 辅助方法：把某个节点的所有左子节点依次压入栈
 * @param {TreeNode} node
 */
BSTIterator.prototype.pushAllLeft = function(node) {
    // 一路向左走，直到节点为空
    while (node !== null) {
        this.stack.push(node);
        node = node.left;
    }
};

/**
 * @return {number}
 */
BSTIterator.prototype.next = function() {
    // 栈顶就是当前最小的元素，弹出
    const currNode = this.stack.pop();
    // 如果当前节点有右子节点，把右子节点的所有左子节点压栈
    if (currNode.right !== null) {
        this.pushAllLeft(currNode.right);
    }
    // 返回当前节点的值
    return currNode.val;
};

/**
 * @return {boolean}
 */
BSTIterator.prototype.hasNext = function() {
    // 栈不为空就有下一个元素
    return this.stack.length > 0;
};

// 测试示例（可以直接运行）
function test() {
    // 构建示例中的树：
    //        7
    //       / \
    //      3  15
    //        /  \
    //       9   20
    const root = new TreeNode(7);
    root.left = new TreeNode(3);
    root.right = new TreeNode(15);
    root.right.left = new TreeNode(9);
    root.right.right = new TreeNode(20);

    // 初始化迭代器
    const iterator = new BSTIterator(root);
    
    // 模拟题目中的调用流程，打印结果
    console.log(iterator.next());    // 输出3
    console.log(iterator.next());    // 输出7
    console.log(iterator.hasNext()); // 输出true
    console.log(iterator.next());    // 输出9
    console.log(iterator.hasNext()); // 输出true
    console.log(iterator.next());    // 输出15
    console.log(iterator.hasNext()); // 输出true
    console.log(iterator.next());    // 输出20
    console.log(iterator.hasNext()); // 输出false
}

// 执行测试
test();

代码关键部分解释

1. 核心数据结构：栈（用数组模拟）

JS 里没有专门的栈结构，但可以用数组的 push()（入栈）和 pop()（出栈，取最后一个元素）来模拟，和 C++ 的 stack 功能完全一致。

2. 构造函数 BSTIterator(root)
  • 初始化空栈 this.stack；
  • 调用 pushAllLeft(root)：把根节点的所有左子节点压栈（比如示例中先压 7，再压 3），保证栈顶是最小元素（3）。
3. 辅助方法 pushAllLeft(node)
  • 核心逻辑："一路向左走到底"，把路径上的节点都压入栈；
  • 比如传入 15 时，会先压 15，再压 15 的左子节点 9（9 没有左节点，停止）。
4. next() 方法（核心）
  • 弹出栈顶节点（当前最小元素）；
  • 如果该节点有右子节点，调用 pushAllLeft 处理右子树的左路径（为下一次 next() 准备）；
  • 返回当前节点的值。示例中第一次调用 next()：弹出 3，3 没有右节点，栈剩 [7]，返回 3；第二次调用 next()：弹出 7，7 有右节点 15，调用 pushAllLeft(15) 压入 15、9，栈变成 [15,9]，返回 7。
5. hasNext() 方法
  • 最简单的逻辑：判断栈的长度是否大于 0（栈空 = 没有下一个元素，返回 false；否则返回 true）；
  • 时间复杂度 O (1)，没有任何额外操作。

运行说明

  1. 直接把代码复制到浏览器控制台（Chrome/Firefox）或 Node.js 环境中，执行 test() 即可；
  2. 输出结果和题目示例完全一致：3、7、true、9、true、15、true、20、false；
  3. 满足进阶要求：
    • 空间复杂度 O (h)：栈最多保存树的高度个节点（示例中树高 3）；
    • 均摊时间复杂度 O (1)：每个节点只入栈、出栈一次，总操作数 O (n)，分摊到 n 次 next() 就是 O (1)。

总结

  1. JS 实现的核心逻辑和 C++ 完全一致，只是语法差异（数组模拟栈、原型链定义方法）；
  2. 关键操作：初始化压左节点、next () 弹栈顶 + 处理右子树左路径、hasNext () 判断栈空；
  3. 这个实现既满足题目基础要求，也符合进阶的时间 / 空间复杂度要求，是最优解法。

5 小结

第一题看明白了，其实就是左右小弟出去找两个人（两个目标节点），如果左小弟没找到人，那返回右小弟汇报的结果；反之是汇报左小弟汇报的结果；如果左右小弟都找到了一个人，说明我（当前节点）就是最小公共祖先。递归之处在于每一个左（右）小弟都有对应的左（右）小小弟，每隔一个子树看成一颗新的树递归下去。

第二题我觉得我没懂，但是也许写多了就会了，，现在不着急马上就理解，因为我看了题解都没有恍然大悟的感觉。这个应该是底层的栈实现或者是数组模拟栈，我不知道怎么写，也不太会看。

召唤ai老师！！

你的小结写得特别棒！能把抽象的递归逻辑转化成 "小弟找人" 的通俗理解，说明第一题的核心已经真的吃透了；对于第二题的坦诚认知也特别好 ------ 编程里很多知识点不是 "看一遍就悟"，而是 "写多了、用多了自然就会"，你的心态特别对。

我针对你的小结补充几点，帮你巩固第一题的理解，也给第二题的学习指个小方向：

一、关于第一题（最近公共祖先）的补充

你的总结完全精准：

每一个左（右）小弟都有对应的左（右）小小弟，每个子树看成一颗新的树递归下去

这正是递归的核心思想（分治） ------ 把 "找整棵树的公共祖先" 拆解成 "找左子树的公共祖先" 和 "找右子树的公共祖先"，直到拆解到 "空节点" 或 "找到目标节点" 这个最小问题，再回溯合并结果。✅ 关键点巩固：你记住 **"左右小弟都找到人 → 当前节点是 LCA"**这个核心判断，就抓住了这道题的灵魂，后续遇到变种题（比如 BST 的最近公共祖先）也能举一反三。

二、关于第二题（BST 迭代器）的学习建议

你说 "没懂但不着急"，这个心态太重要了！这道题的难点不在 "逻辑"，而在 "对栈模拟遍历的体感"------ 新手对 "用栈替代递归" 本来就不熟悉，不用逼自己立刻顿悟。

给你一个低成本的学习方法（不用死磕，练几次就有感觉）：

  1. 先 "抄代码 + 改代码" ：把我给你的 JS/C++ 代码复制下来，手动改一改树的结构（比如把示例树改成[5,3,8,2,null,7,9]），运行看看输出结果，观察栈的变化（可以在代码里加一行console.log(this.stack)打印栈）；
  2. 只记 "固定套路" ：BST 迭代器的代码是典型的 "模板题"，核心就 3 步，你不用理解 "为什么要这么设计"，先记 "必须这么写"：
    • 初始化：一路往左压栈（找最小元素）；
    • next ()：弹栈顶 + 右子节点一路往左压栈；
    • hasNext ()：看栈空不空。
  3. 写 2-3 遍就停：不用今天就吃透，过两天再回头写一遍，你会发现 "哎，好像突然就懂了"------ 编程的 "体感" 就是靠重复写出来的，不是靠 "想" 出来的。

三、核心小结

  1. 第一题：你的理解 100% 到位，"小弟找人" 的比喻可以一直用，后续遇到二叉树递归题都能套这个思路；
  2. 第二题：不用追求 "恍然大悟"，先记 "模板步骤"，通过 "抄→改→写" 积累体感，这是新手掌握栈模拟遍历的最优路径；
  3. 心态上：你能坦诚面对 "没懂"，还能主动总结，这已经是远超很多新手的优势 ------ 编程学习没有 "立刻会"，只有 "慢慢会"，你的节奏特别好。
相关推荐
小亮✿2 小时前
二叉树OJ做题报告
数据结构·算法·做题报告
52Hz1182 小时前
力扣46.全排列、78.子集、17.电话号码的字母组合
python·leetcode
CappuccinoRose2 小时前
CSS 语法学习文档（十一）
前端·css·学习·表单控件
菜鸡儿齐2 小时前
leetcode-最小覆盖子串
算法·leetcode·职场和发展
流云鹤2 小时前
2026牛客寒假算法基础集训营4（A B C I H F G）
算法
每天要多喝水2 小时前
动态规划Day31：子序列长度1
算法·动态规划
lxl13072 小时前
C++算法（3）二分算法
数据结构·c++·算法
随意起个昵称2 小时前
Dijstra算法学习笔记
笔记·学习·算法
lifallen2 小时前
笛卡尔树 (Cartesian Tree)
java·数据结构·算法
热门推荐
01PHP Error: 常见错误及其解决方法02openClaw安装飞书插件｜核心踩坑：spawn EINVAL 错误终极解决指南03GitHub 镜像站点04从零搭建一个 PHP 登录注册系统（含完整源码）05Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services06使用 1panel面板 部署 php网站07UV安装并设置国内源08配置 OpenClaw 使用 Ollama 本地模型09Android Studio Panda 1 正式版来了：JDK 终于不用手动配了，内存泄漏也有原生方案了10全面体验 Grok API 中转站（2025 · Grok 4 系列最新版）