3483. 2的幂次方（上海交通大学考研机试题目）

3483. 2的幂次方

⭐️难度：中等

⭐️类型：分治、递归

📖题目：题目链接

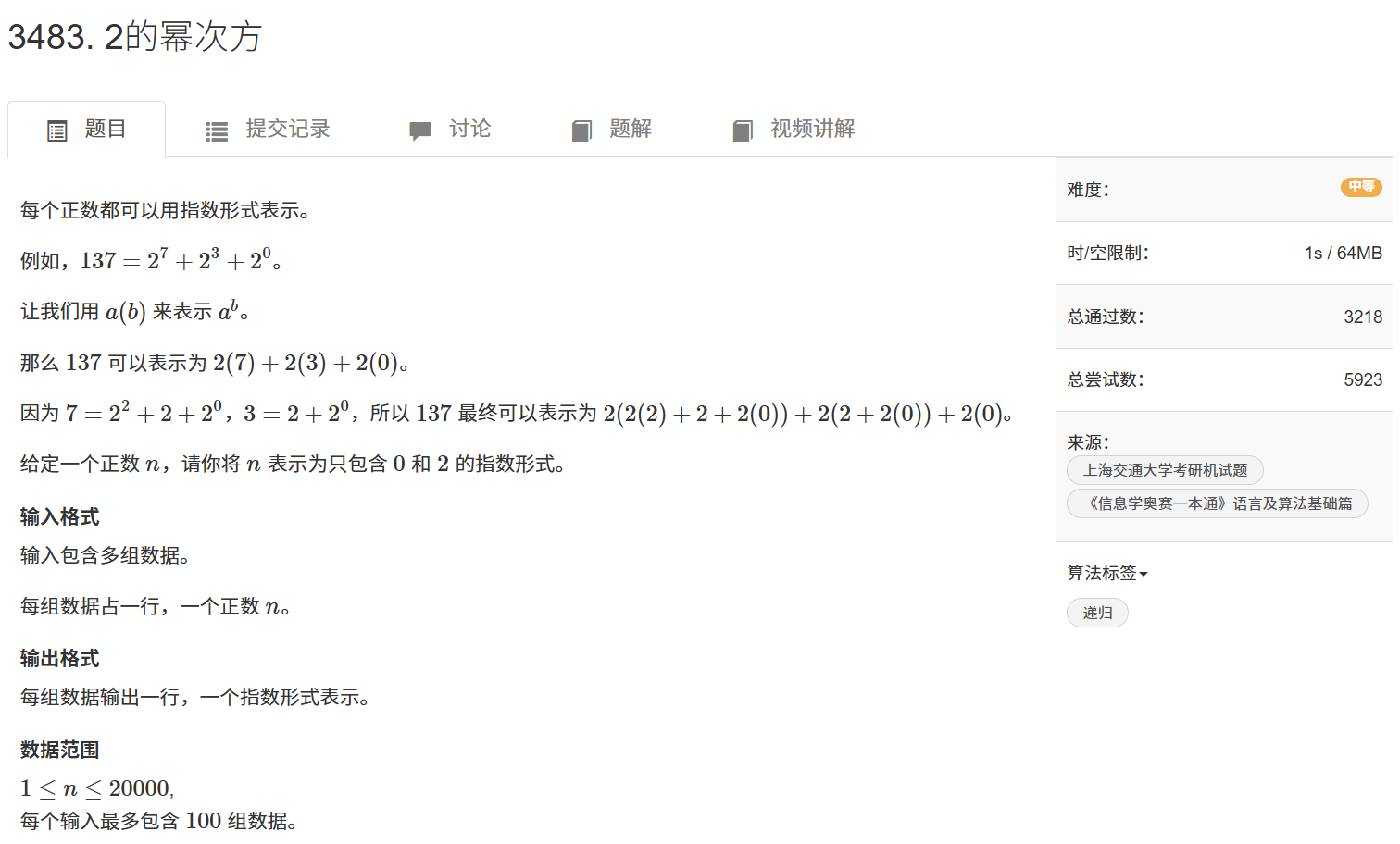
输入样例：

1315

输出样例：

2(2(2+2(0))+2)+2(2(2+2(0)))+2(2(2)+2(0))+2+2(0)

🌟思路：

以题目例子为例：

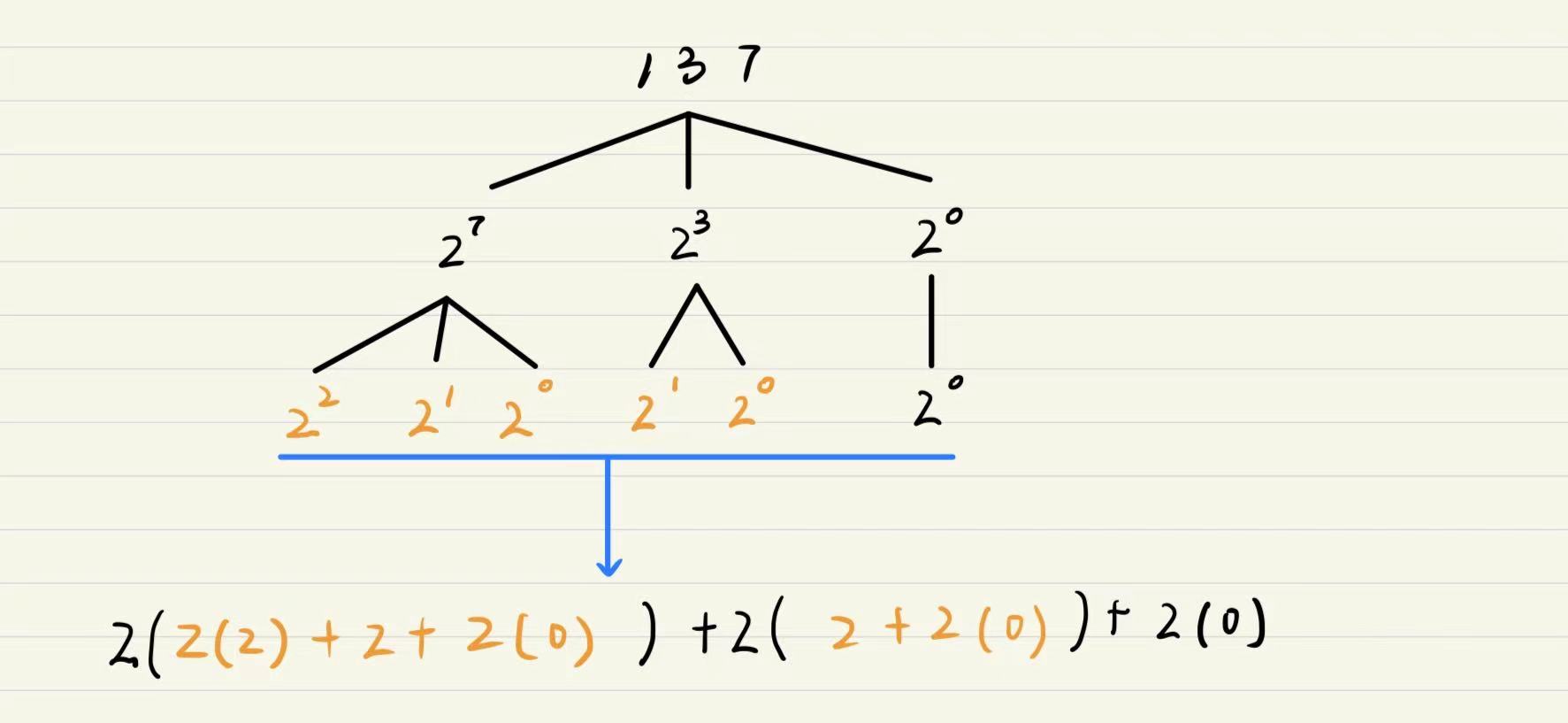
总结：

1、只包含指数为0，1，2的数，

2、指数1不用写出来，

不难发现问题的解决符合：大问题拆分成若干相似的小问题，符合分治法 的思想。

步骤：

1️⃣先获得n的2指数形式

把数字转化成机器数，不难看出，获得任何一个数的2指数形式，只需要知道机器数中哪些比特是1，

只需要与1相与，就能得出哪些比特是1。

n最大为20000，所以与n 相与机器数 最多是1000000000000000(15个0)，

2¹⁴=16384，2¹⁵=32768

所以：2¹⁴<20000<2¹⁵

cpp 复制代码

string Get2sExponet(int n) {
    vector<int> exp;
    for (int i = 15;i >= 0;i--) {  // 先压入高次幂
        if ((n & (1 << i)) != 0) {
            exp.push_back(i);
        }
    }
    // n = 2^(exp[0] + 2^(exp[1]) + ... + 2^(exp[size - 1])
}

2️⃣构建结果字符串

每一个黑色部分都是一个小问题，

cpp 复制代码

tring Get2sExponet(int n) {
    if (n == 0) {
        return "0";
    }
    
    /*vector<int> exp;
    for (int i = 15; i >= 0; --i) {
        if ((n & (1 << i)) != 0) {
            exp.push_back(i);
        }
    }*/
    // n = 2^(exp[0]) + 2^(exp[1]) + ... + 2^(exp[size-1])
    
    string res = "";
    for (int i = 0; i < exp.size(); ++i) {
        if (i != 0) {
            res += "+";
        }
        if (exp[i] == 1) {  // 特殊：2^1^不用加（）
            res += "2";
        }
        else {
            res += "2(" + Get2sExponet(exp[i]) + ")";
        }
    }
    return res;
}

📚题解：

cpp 复制代码

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<string.h>
#include<vector>  // vector不需要.h
#include<list>
#include<set>  // // 可以用 set 和 multiset
#include<unordered_set> // 可以用 unordered_set 和 unordered_multiset
#include<map>  // 可以用 map 和 multimap
#include<unordered_map> // 可以用 unordered_map 和 unordered_multimap
#include<algorithm>
#include<string>
#include<iostream>
#include<queue>
#include<stack>

using namespace std;

string Get2sExponet(int n) {
    if (n == 0) {
        return "0";  // 2^0^递归出口，0的次方不存在，返回本身
    }

    vector<int> exp;
    for (int i = 15; i >= 0; --i) {
        if ((n & (1 << i)) != 0) {  // 先压高次幂
            exp.push_back(i);
        }
    }
    // n = 2^(exp[0]) + 2^(exp[1]) + ... + 2^(exp[size-1])

    string res = "";
    for (int i = 0; i < exp.size(); ++i) {
        if (i != 0) {
            res += "+";
        }
        if (exp[i] == 1) {  // 2^1^递归出口，不用加（）
            res += "2";
        }
        else { 
            res += "2(" + Get2sExponet(exp[i]) + ")";
        }
    }
    return res;
}
int main() {
    int n;
    while (scanf("%d", &n) != EOF) {
        printf("%s\n", Get2sExponet(n).c_str());
    }
  

    return 0;
}