递归_二叉树_50 . 从前序与中序遍历序列构造二叉树

题目介绍

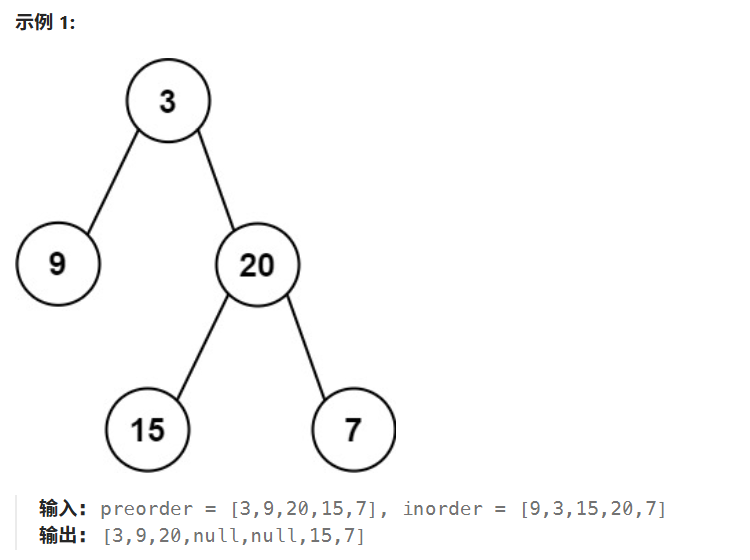
给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历 ， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

提示:

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证为二叉树的前序遍历序列
inorder 保证为二叉树的中序遍历序列

本文（文末代码）约 2000 字，阅读+思考10 min

检验答案网址：105. 从前序与中序遍历序列构造二叉树 - 力扣（LeetCode）

解析

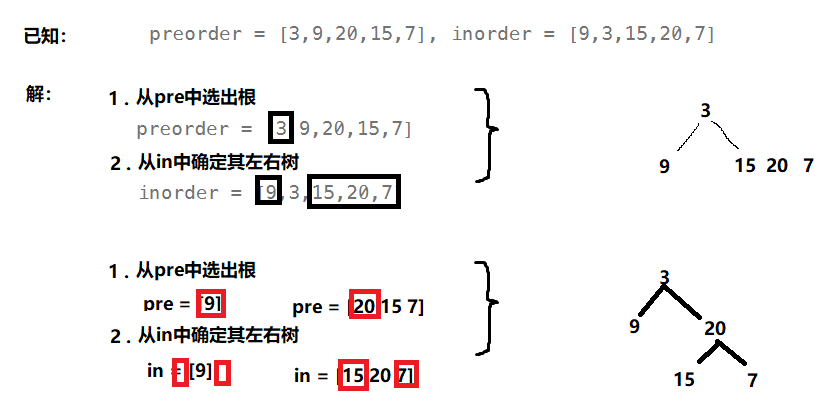
1 . 本题需求很明确：根据已知的前序序列和中序序列构建该二叉树------该二叉树具有唯一性

2 . 因为二叉树的前序序列（整体和局部都以根 - 左 - 右）能确定根；而二叉树的中序序列（整体和局部都以左 - 根 - 右）能确定 左右子树

3 . 以往在课本上学习，都是以选择题形式出现：解决这类题都是自己在演草纸上构建

4 . 代码如何解决呢
5 . 其实也是从手动计算中总结出规律，进而用代码表示------这也算是"建模"吧

6 . 我们开始用手搓：

再直观一点：
真正直接确定唯一位置的------是从pre选出根
7 . 递归方法构建树：

a . 核心任务：肯定是构建当前的根节点

b . 当根节点的val 来源于 pre的第一个数字

c . 然后划分出左右子树的范围------方便后序深度构建左子树，右子树

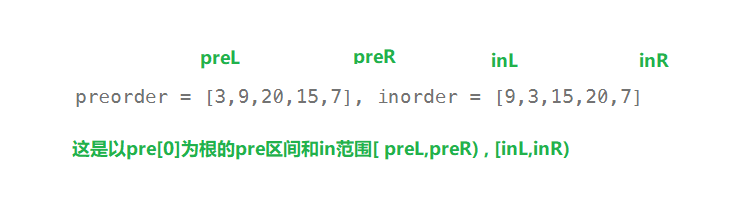
8 . 难点：分别找到左子树和右子树在两个序列的区间

a . 已知：根val的左边都是左子树的所有结点；右边都是右子树的所有结点

b . 已知：val 在一个序列中不会重复------那么可以使用不允许重复插入的哈希表

c . unordered_map<int ,int >为了快速映射根val 在in中的下标------进而划分

9 .

10 . 左子树的区间
左闭右开

11 . 右子树的区间
左闭右开

12 . 先来试着写代码：
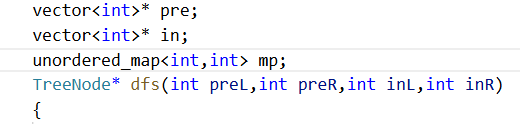1 . 虽然参数只传递区间，但是为了找到preorder和inorder需要两个指针
1 . 由于每个子树的具体区间不一样，所以参数传两个区间

注：

a . 该函数里只有一句代码，正是构建当前树的根节点------括号里root的val填什么呢？

b . 很明显，由前序序列确定根------
2 . 核心任务完成

13 . 接下来需要完整构建树------自己的左右子树也是同样逻辑：
3 . 最后root构建完成，返回本层构建好的树给上层 14 . 那括号里的区间怎么填呢？
从图上看得出来，要得到in中的左右具体哪些结点------得先确定根节点3的位置

代码：

cpp 复制代码

int rootPos = mp[rootVal];//先确定rootval在in中的位置

15 . 现在in中的左右划分明了：

左子树： inL = inL inR = rootPos

右子树 : inL = rootPos+1 inR = inR

16 . 那如何得到左右子树在pre中的分布：

cpp 复制代码

 int rootPos = mp[rootVal];//先确定rootval在in中的位置
int leftSize = rootPos - inL; // 确定左子树占多宽

注：

之所以会纠结，是不确定左子树有多宽------由于已经确定了in的划分：自然知晓左子树有多宽

17 . 所以，pre中的左右子树划分：

左子树： preL = preL+1 preR = preL+leftSize+1

右子树 : preL = preL+leftSize+1 preR = preR

所以代码补充一下：

cpp 复制代码

    TreeNode* dfs(int preL,int preR,int inL,int inR)
    {
        int rootVal = (*pre)[preL];// *pre -> 得到 vector; 再[preL] ->得到int
        TreeNode* root = new TreeNode(rootVal);
        int rootPos = mp[rootVal];//先确定rootval在in中的位置
        int leftSize = rootPos - inL; // 确定左子树占多宽
        root->left = dfs(preL+1,preL+leftSize+1,inL,rootPos);
        root->right = dfs(preL+leftSize+1,preR,rootPos+1,inR);
        return root;
    }

18 . 再加上递归出口：由于区间采取左闭右开原则，自然左边不能和右边相等，更不能大于之

cpp 复制代码

TreeNode* dfs(int preL,int preR,int inL,int inR)
    {
        if(preL >= preR || inL >= inR) return nullptr;
}

19 . 主函数里再调用一下：把哈希表也初始化一下

cpp 复制代码

    vector<int>* pre;
    vector<int>* in;
    unordered_map<int,int> mp;
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        pre = &preorder;
        in = &inorder;
        for(int i = 0;i < inorder.size();i++)
        {
            mp[inorder[i]] = i;
        }
        return dfs(0,preorder.size(),0,inorder.size());
    }

完整代码：

cpp 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
   
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        pre = &preorder;
        in = &inorder;
        for(int i = 0;i < inorder.size();i++)
        {
            mp[inorder[i]] = i;
        }
        return dfs(0,preorder.size(),0,inorder.size());
    }
    vector<int>* pre;
    vector<int>* in;
    unordered_map<int,int> mp;
    TreeNode* dfs(int preL,int preR,int inL,int inR)
    {
        if(preL >= preR || inL >= inR) return nullptr;
        int rootVal = (*pre)[preL];// *pre -> 得到 vector; 再[preL] ->得到int
        TreeNode* root = new TreeNode(rootVal);
        int rootPos = mp[rootVal];//先确定rootval在in中的位置
        int leftSize = rootPos - inL; // 确定左子树占多宽
        root->left = dfs(preL+1,preL+leftSize+1,inL,rootPos);
        root->right = dfs(preL+leftSize+1,preR,rootPos+1,inR);
        return root;
    }
};

总结以及完整参考代码

cpp 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
   
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        pre = &preorder;
        in = &inorder;
        for(int i = 0;i < inorder.size();i++)
        {
            mp[inorder[i]] = i;
        }
        return dfs(0,preorder.size(),0,inorder.size());
    }
    vector<int>* pre;
    vector<int>* in;
    unordered_map<int,int> mp;
    TreeNode* dfs(int preL,int preR,int inL,int inR)
    {
        if(preL >= preR || inL >= inR) return nullptr;
        int rootVal = (*pre)[preL];// *pre -> 得到 vector; 再[preL] ->得到int
        TreeNode* root = new TreeNode(rootVal);
        int rootPos = mp[rootVal];//先确定rootval在in中的位置
        int leftSize = rootPos - inL; // 确定左子树占多宽
        root->left = dfs(preL+1,preL+leftSize+1,inL,rootPos);
        root->right = dfs(preL+leftSize+1,preR,rootPos+1,inR);
        return root;
    }
};